我国埋深在1 000 m以下煤炭资源储量为2.95万亿t，约占煤炭资源总量的53%[1]。《国家中长期科学和技术发展规划纲要》(2006—2020)明确提出:重点研究开发煤炭高效开采技术及配套装备，建设千米深井以开发深部矿物资源已成为应对能源紧缺问题的必然选择[2]。在千米煤矿深井中，提升容器以速度高达16 m/s、载重量达45 t的高速重载工况下装卸载物料，系统运行过程中，卷筒卷绕速度、卷筒及钢丝绳制造尺寸偏差等因素会造成钢丝绳出现提升不同步现象，由于柔性罐道对于容器的约束作用较弱，2根钢丝绳的提升不同步会造成提升容器倾斜，影响提升系统的安全运行。
双绳缠绕式深井提升系统是一个复杂的非线性系统，系统模型存在大量的非线性因素，例如:系统参数不确定性，包括钢丝绳刚度、阻尼的不同和时变特性，卷筒、天轮及钢丝绳等尺寸的不同，浮动天轮液压系统非线性特性等;除此之外，还包括钢丝绳与卷筒之间的摩擦力，浮动天轮液压缸活塞杆与缸筒之间的摩擦力、提升容器与罐道之间摩擦等外部干扰。以上因素使得传统的PID控制器难以完成提升容器调平控制。
滑模控制器可以用来处理非线性系统控制问题。DING 等[3]设计了一种非奇异终端滑模面与饱和函数相结合的新型滑模面，进一步设计了鲁棒控制器;王婕等[4]利用齐次性方法设计了连续有限时间收敛的高阶滑模跟踪控制器;QI 等[5]为一种永磁同步电动机的速度控制设计了新型二阶积分滑模控制器，积分滑模面可以在滑动阶段进一步减小稳态误差，为此通过 Lyapunov 函数方法设计了一种二阶滑模控制器。
进一步地，针对控制设计过程中状态量难以直接测量的问题，在控制器中引入状态观测器。状态观测器可以将非线性系统参数不确定性和外部干扰进行处理，起到优化部分状态变量的作用，得到状态变量的观测值。近年来,状态观测器已在电机控制系统[6-9]、飞行器姿态控制[10-11]、机器人控制[12-13]、机械加工[14]等领域得到了广泛的应用。文献[15-16]证明了扩展状态观测器的收敛性和稳定性，表明扩展状态观测器能够将干扰估计误差和状态估计误差保持在一个很小的范围内。文献[17]利用线性观测器得到快变子系统的观测速度矢量，基于这个观测速度矢量与线性系统的最优控制理论设计系统的快变控制力矩，实现两柔性杆振动的抑制。文献[18]针对一类具有多重不确定性的非线性系统，提出了一种基于扩展状态观测器的控制方法，并将其应用于导弹的部分集成制导控制设计。
针对柔性罐道工况下双绳缠绕式煤矿深井提升系统运行过程中容器倾斜问题，笔者提出了容器位姿调平控制方法。首先，建立双绳缠绕式深井提升系统容器位姿调平控制模型;然后，考虑提升系统运行过程中控制量在钢丝绳中传递存在的不确定延时问题，构建了容器位姿调平主动控制矩阵模型，设计了控制信号信号传输延时补偿观测器，证明了包含延时补偿观测器的容器位姿调平主动控制模型的稳定性;然后，设计滑模控制器实现容器位姿调平控制，考虑到控制器设计过程中需要容器角度的微分信号，利用高增益观测器为滑模控制器提供光滑的角度微分信号。综上，笔者提出的控制算法不仅可以补偿控制输入延时，而且可以削弱信号干扰导致的系统抖振，保证良好的控制性能。为验证提出控制方法的有效性，利用双绳缠绕式煤矿深井提升试验台对提出的控制方法开展了实验验证，实验结果表明，与传统的控制方法相比，容器位姿调平控制方法可以更有效地减小容器运行过程中的倾斜角度。
1 容器位姿调平控制模型
图1为双绳缠绕式深井提升系统，主要包括:卷筒、提升钢丝绳、浮动天轮系统和提升容器。双绳缠绕式提升系统中，一个容器利用两条钢丝绳进行提升和下放，在系统运行过程中，卷筒卷绕速度、卷筒及钢丝绳制造尺寸偏差等因素会造成钢丝绳出现提升不同步现象，在柔性罐道工况下，由于罐道对于容器的约束作用较弱，2根钢丝绳的提升不同步会造成提升容器倾斜。在浮动天轮系统中，液压缸可以驱动浮动天轮，从而改变天轮的高度，进而调整垂直段提升钢丝绳长度，最终起到调节容器位姿的效果。
图1 双绳缠绕式深井提升系统
Fig.1 Double-rope winding deep well hoisting system
图2为双绳缠绕式深井提升系统原理图，其中图2(a)为提升系统工作原理图，由图2(a)可以看出，本文将提升钢丝绳及柔性罐道离散为若干具有时变特性的质量-弹簧-阻尼系统;图2(b)为提升系统各组成部分的几何关系示意图。其中，提升系统本体的主要参数可表示为:i=1,2分别为提升系统左右两侧;lri(i=1,2)为2根钢丝绳在卷筒上的卷绕长度;lci(i=1,2)为容器提升或下降过程中钢丝绳弦绳长度;lhi(i=1,2)为容器提升或下降过程中垂直提升钢丝绳长度;ui(i=1,2)为浮动天轮位移;α为钢丝绳弦绳与水平面之间的夹角;ai(i=1,2)为两根钢丝绳与提升容器连接点到提升容器重心的水平距离;bi(i=1,2)为提升容器上平面与下平面到提升容器重心的垂直距离;khi(i=1,2)为提升钢丝绳弹簧阻尼器模型的等效刚度;chi(i=1,2)为提升钢丝绳弹簧阻尼器模型的等效阻尼;ksj(j=1,2,3,4)为4对弹簧阻尼器模型的横向等效刚度;csj(j=1,2,3,4)为4对弹簧阻尼器模型的横向等效阻尼。
图2 双绳缠绕式深井提升系统原理
Fig.2 Schematic diagram of double-rope winding deep well
hoisting system
在容器提升过程中，将其上升方向看作坐标正方向，则提升系统两根钢丝绳在系统运行过程中的长度可写为
lhi=lhi0-lri-uisin α
(1)
式中，lhi0为容器在最底部时2根垂直提升钢丝绳的初始长度。
笔者主要研究提升容器提升过程中的问题，因此忽略容器的横向和纵向振动，则容器的广义坐标可以表示为q=[xc,yc,θc]，其中xc和yc分别为提升容器重心的横向和纵向位移;θc为容器沿逆时针方向旋转的角度，基于此，双绳缠绕式深井提升系统的拉格朗日方程可写为
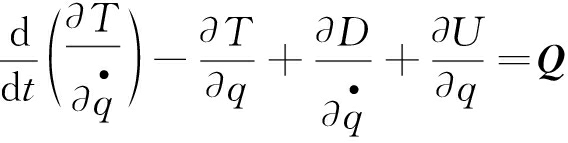
(2)
式中，T，U，D和Q分别为双绳缠绕式深井提升系统在系统运行过程中的动能、势能、瑞利耗散函数和非有势力向量;t为时间。
根据图2(b)所示浮动天轮运动时钢丝绳与天轮之间的几何关系，则左右两侧浮动天轮与钢丝绳弦绳切点的位移为lri-uisin α，通过左右两侧浮动天轮与垂直提升钢丝绳切点的钢丝绳的位移为lri+(1+sin α)ui。因此，s段长度内左右两侧弦绳的单位长度位移sli和y段长度内左右两侧垂直钢丝绳单位长度的位移yli可分别表示为
(3)
yli=lri+(1+sin α)ui+[(xc-aiθc)-
(4)
基于式(3)，(4)可得系统左右两侧弦绳和垂直段提升钢丝绳的动能Tlci,Tlhi分别为
(5)
(6)
式中，ρl为钢丝绳单位长度质量。
左右两侧浮动天轮的动能Thi可分别写为
(7)
式中，mi分别为左右两侧浮动天轮的质量;ri分别为左右两侧浮动天轮的直径;Ii分别为左右两侧浮动天轮的转动惯量。
提升容器的动能Tc可表示为
(8)
式中，mc为提升容器的质量;Ic为提升容器的转动惯量。
左、右两根钢丝绳的势能Uli可分别表示为
(9)
式中，kci分别为左、右两侧弦绳的刚度;khi分别为左、右两侧垂直提升钢丝绳的刚度;g为重力加速度，10 m/s2。
左、右两侧浮动天轮的势能Uhi可分别表示为
Uhi=migui
(10)
在系统运行过程汇总，容器倾斜和水平方向位移会使提升系统罐道产生势能，容器和罐道的总势能Uc可写为
(11)
左、右两根钢丝绳的瑞丽耗散函数Dli可表示为
(12)
式中，cci分别为左、右两侧钢丝绳弦绳的阻尼系数;chi分别为左、右两侧垂直提升钢丝绳的阻尼系数。
提升容器和容器罐道的总瑞利耗散函数Dc可表示为
(13)
综上，双绳缠绕式深井提升系统的总动能、总势能和总瑞利耗散函数可分别表示为
T=Tlc1+Tlc2+Tlh1+Tlh2+Th1+Th2+Tc
(14)
U=Ul1+Ul2+Uh1+Uh2+Uc
(15)
D=Dl1+Dl2+Dc
(16)
将式(14)～(16)进行结合，可得提升系统本体动力学模型的矩阵方程形式
(17)
式中，
和q分别为提升系统的广义加速度、广义速度和广义位移;M，C，K和F分别为系统的质量矩阵、阻尼矩阵、刚度矩阵和非有势力向量，分别可表示为
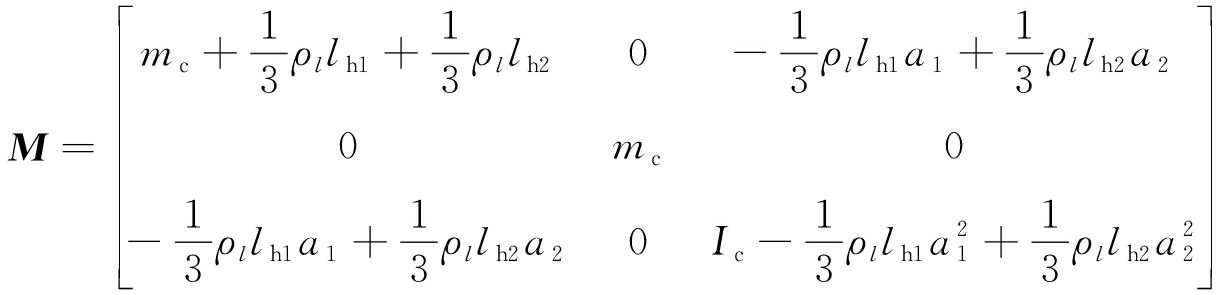
(18)
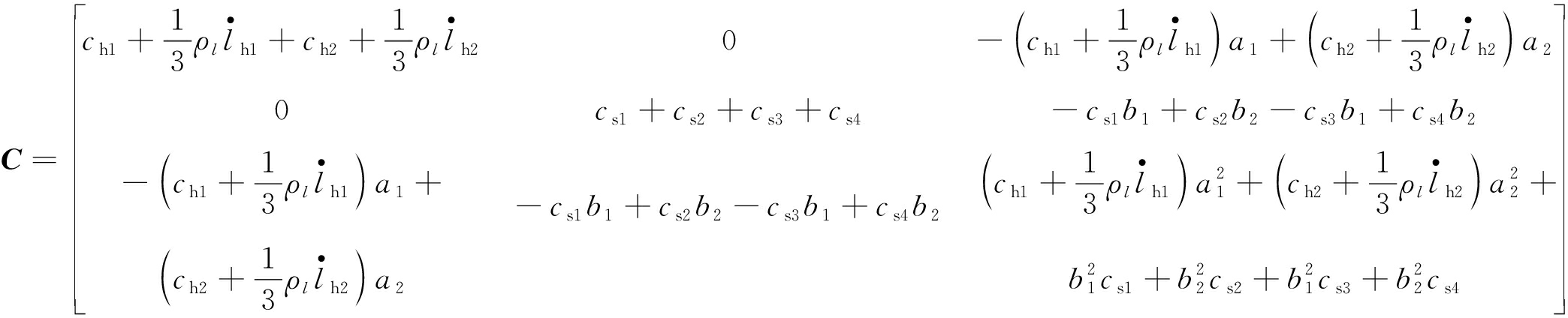
(19)
(20)
(21)
对于容器位姿调平，其最终控制目的为容器倾角控制，因此可将提升系统本体动力学模型的矩阵方程简化为
(K31xc+K33θc)=F31
(22)
式中，Mmn,Cmn,Kmn和Fmn(m=1,2,3;n=1,2,3)为提升系统质量矩阵、阻尼矩阵、刚度矩阵和非有势力向量中的相应元素。
由于容器位姿实际是通过两根对称的钢丝绳进行调节的，因此可将控制输入进一步简化，写作u1=u=-u2，则式(22)可表示为
(23)
式中,
提升系统钢丝绳刚度的值通常远大于其阻尼值，则式(22)可进一步简化为
(24)
则提升系统容器位姿调平控制系统可以写成如下状态空间方程的形式:
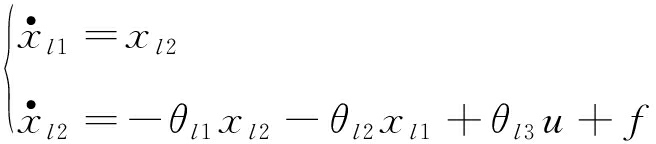
(25)
式中，各状态方程中的系数具体表示为θl1=B/A,θl2=C/A,θl3=R/A,f=F0/A，定义状态变量
2 浮动天轮驱动信号延时补偿观测器
由于浮动天轮位移传递至容器需要经过钢丝绳，驱动信号从发出到产生作用存在时变延时，因此需要对容器位姿调平控制模型控制信号输入时变延时补偿。
针对式(25)所示的状态空间方程，考虑控制输入存在的控制输入时变延时，可将式(25)改写为如下提升系统时间延时模型:
(26)
式中，xct(t)为包含提升系统状态变量的矩阵;uct(t-τct)为存在时变延时的控制输入;yct(t)为系统状态输出;
为控制输入不确定延时的上限值，该值看作是已知的，则上述提升系统控制输入时变延时模型为
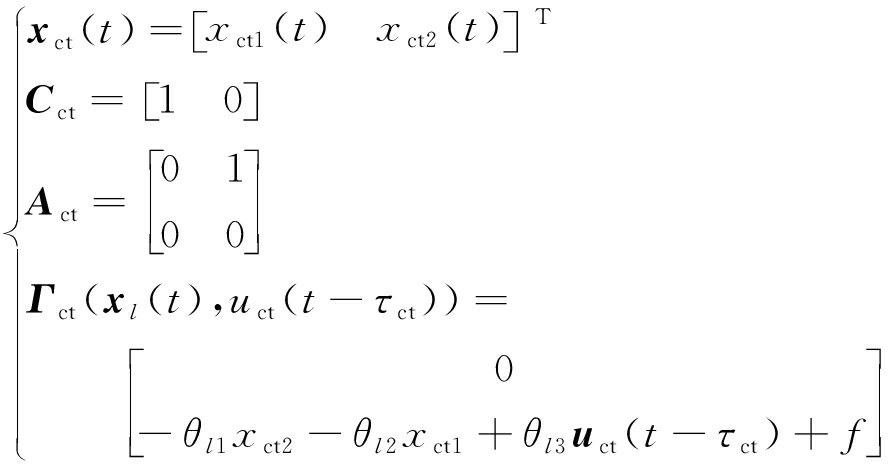
其中，τct为控制输入的不确定延时。
针对式(26)，提出控制输入不确定延时补偿观测器，并作出如下假设:假设1:状态变量和控制输入均为有界的;假设2:Γct(xl(t),uct(t-τct))均满足Lipschitz连续性条件;假设3:不确定的控制输入延时τct满足如下特性:① 不确定输入延时τct的上界
② 存在大于0的参数Ect，满足
进而，时变延时观测器可设计为
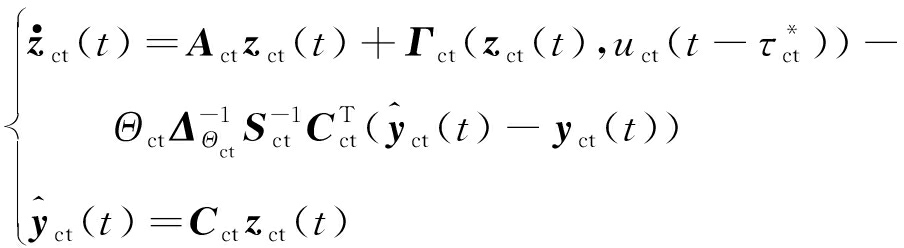
(27)
式中，zct(t)为引入延时观测器后的状态变量值，即为xct(t)的观测值;Θct为需要设计的变量；
为yct(t)的观测值;ΔΘct为需要设计的矩阵，对于容器位姿调平系统，需要设计的矩阵可分别表示为
(28)
式中，Θct>0，Sct为正定的对称矩阵，并且满足如下矩阵方程
(29)
定义加入时变延时观测器后提升系统和钢丝绳张力平衡系统中实际状态变量与观测得到的状态变量之间的偏差为εct，表示为
εct=zct(t)-xct(t)
(30)
结合式(28)～(30)，则状态变量观测偏差关于时间的导数
可以表示为
Γct(xct(t),xct(t-τct))
(31)
定义为ect=ΔΘctεct，然后基于式(28)，系统(31)的参数及变量满足如下变化:
式(31)基于变换后的状态变量估计偏差ect可以重新表示为
(32)
定义关于状态变量估计偏差ect的Lyapunov-Krasovskii[19]函数V(ect)为
(33)
式中，αct为将在后续进行定义的正常数。
结合式(32),(33)，Lyapunov-Krasovskii函数V(ect)关于时间的导数可写为
(34)
为验证系统整体的稳定性，最终的目的是要证明式(32)是收敛的，因此，式(34)应该被改写为关于观测误差的表达形式，为此，提出引理1。
引理1:对于
‖ect(σ)‖2dσ>0，其满足:
(35)
式中，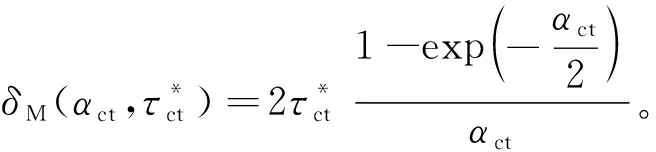
证明:结合式(35)和Hölder不等式，可得
(36)
基于上述引理1，式(34)可以改写为
V(ect(t))≤λct2‖ect(t)‖2+
(37)
式中，
结合式(33),(37)，可得
(38)
因此，‖ect(t)‖可以按如下不等式表示
(39)
然后，存在δl,in1>0，δl,in2>0，Tl,in0>0，使状态变量观测偏差满足
(40)
其中，
然后，根据之前所述的观测偏差变换关系ect=ΔΘctεct，观测误差εct满足
(41)
由此可见，设计的延时观测器满足ζ-practically[21]稳定性条件，其中δct对应ζ-practically稳定性条件中的参数ζ，稳定性。
3 提升系统容器位姿调平控制方法
提出了将滑模控制与高增益观测器相结合的控制方法进行容器位姿调平控制律设计，其中滑模控制器用来设计初始控制输出，高增益观测器为滑模控制器提供光滑的角度微分信号，优化控制输出。
图3为提升系统容器位姿调平控制原理图，容器倾角反馈至滑模控制器，提升系统状态量反馈至高增益观测器，可得到观测后的容器倾角一阶导数，该数值同样进入滑模控制器，进而得到浮动天轮液压缸的驱动电压值，该电压值经延时补偿观测器处理后，得到相位提前的阀控电压值，调节两浮动天轮位移，进而减小容器倾角值。
图3 容器位姿调平控制原理
Fig.3 Principle diagram of conveyance leveling control
3.1 高增益观测器设计
针对提升系统状态方程(25)，高增益观测器可设计为
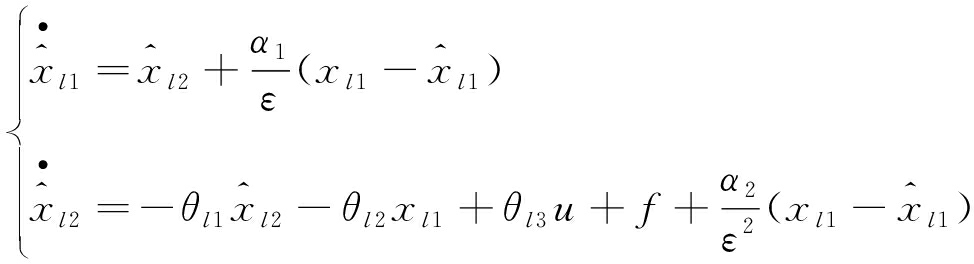
(42)
式中，α1和α2为正实数，ε≪1。
取
则观测器可写为
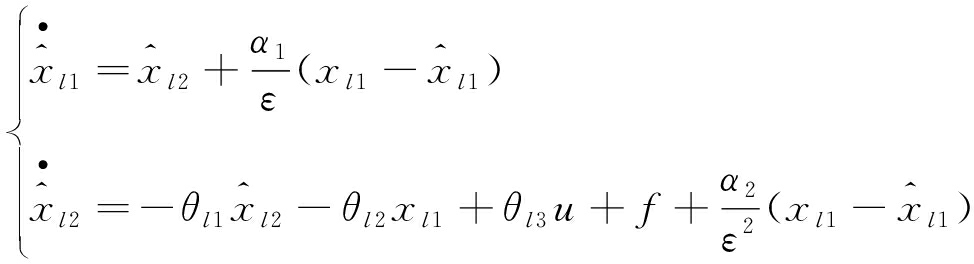
(43)
定义
结合式(42)和(43)，可得
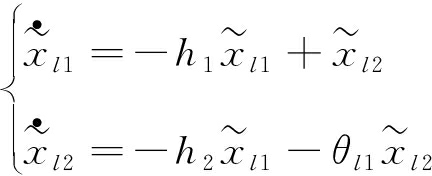
(44)
即
(45)
式中，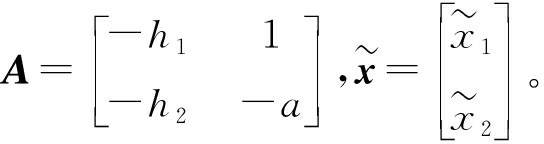
如果取Α为Hurwitz，即Α的特征值为负，则应对h1和h2的值进行设计，使Α满足Hurwitz。进而根据式(45)，可得
指数收敛:
(46)
式中，φ0和σ0为正常数。
特征方程
即s2+(h1+a)s+h2=0。对应(s+p)2=0，得
(47)
其中，p的设计需要满足p>0，h1=2p-a>0。
3.2 基于高增益观测器的滑模控制器设计
针对系统状态方程(25)，设计滑模函数为
取
(48)
式中，
为期望容器倾角，θc为实际容器倾角。取控制律为
(49)
取滑模控制的Lyapunov函数Vs为
(50)
由于
(51)
(52)
则
(53)
其中，
因此
(54)
式中，k1=-ηc，k2=θl1-η-c。
由于
则
(55)
式中，η>1。
则闭环系统Lyapunov函数为
V=Vs+V0
(56)
其中，
则
即
同样指数收敛。
由于高增益观测器是指数收敛的，则
(57)
式中，η1=2(η-1)>0;χ(·)为
的K类函数，σ0>0。
引理2:针对V:[0,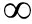
)∈R，不等式方程
的解为
V(t)≤e-σ0(t-t0)V(t0)+
e-σ0(t-τ)F(τ)dτ
式中，α为任意常数。
采用引理2，不等式方程
的解为
e-η1(t-t0)V(t0)+χ(·)e-η1t+σ0t0
e-η1τe-σ0τdτ=
(58)
即
(59)
由于V(t)≥0，故t→时，V(t)=0，且V(t)指数收敛，收敛精度取决于η。
图4 双绳缠绕式深井提升试验台
Fig.4 Double-rope winding deep well hoisting experimental
system
从上述控制算法推导过程可以看出，利用高增益观测器可以在仅有单一状态量的情况下，对其余状态量进行观测，因此本文提出的控制方法不仅可以提高控制性能，而且可以简化控制系统对传感器信号的需求。
4 实验结果及分析
为验证本文提出的容器位姿调平控制方法的有效性，搭建了双绳缠绕式深井提升试验台，试验系统硬件主要包括提升系统井架、提升卷筒、钢丝绳、浮动天轮、浮动天轮液压缸、容器、罐道。提升容器上安装有倾角传感器，可以实时反馈容器在提升过程中的位姿，倾角传感器选择svt628t型号，量程为±90°，精度为±0.1%。表1为双绳缠绕式深井提升试验台参数。
表1 双绳缠绕式深井提升试验台参数配置
Table 1 Parameters of double-rope winding deep well
hoisting experimental system
工作参数数值最大提升高度/m6配重尺寸/(m×m×m)0.375×0.375×0.125液压缸行程/mm±100最大提升加速度/(m·s-2)1最大提升速度/(m·s-1)1配重质量/kg200
图5 双绳缠绕式深井提升试验系统控制方案
Fig.5 Control scheme of double-rope winding deep well hoisting
experimental system
图5为双绳缠绕式深井提升试验系统控制方案。双绳缠绕式深井提升试验台运行过程中的容器倾角由位姿传感器采集，浮动天轮液压缸伸缩量由位移传感器采集，采集到4～20 mA电流信号经信号调理系统处理后转换为±10 V电压信号，由研华公司A/D板卡PCI-1716采集，提升系统卷筒转速通过编码器采集，采集到的信号传输至PCI-1784板卡。工控机实时控制系统中具有卷筒转速控制算法，可以保证提升系统按指定速度运行;工控机中具有容器位姿调平控制算法，该算法通过处理容器倾角信号可得到浮动天轮液压缸控制信号，该信号由凌华公司D/A板卡ACL-6126生成±10 V内的电压信号，该电压信号通过信号调理系统优化处理后驱动比例伺服阀进行工作，进而驱动浮动天轮液压缸运动，起到调节容器位姿的作用。
图6为设定的试验系统提升容器运行速度曲线，为尽量贴近实际工况，提升曲线设定为六段速曲线，加速度值分别设为0.35，0.70 m/s2。
图6 提升容器运行速度
Fig.6 Running velocity of conveyance
图7为正常工况即2根钢丝绳无提升不同步下系统运行过程中的容器倾角，从图7可以看出，在该工况下，容器倾角较小，下方阶段容器倾角大于提升阶段容器倾角。
图7 正常工况下容器倾角
Fig.7 Title angle of the conveyance under normal condition
为验证控制器有效性，设置了卷筒直径误差即提升系统钢丝绳不同步，图8为两根提升钢丝绳的卷绕高度。在两根钢丝绳卷绕高度不一致的情况下，容器在提升过程中产生倾斜，如图9所示，容器倾角在系统提升阶段不断增大，在下放阶段不断减小，容器倾角峰值为10.52°。
图8 存在卷筒直径偏差工况下两钢丝绳提升高度
Fig.8 Hoisting height of two wire ropes when two drums have
diameter deviation
图9 存在卷筒直径偏差工况下容器倾角
Fig.9 Title angle of the conveyance when two drums have
diameter deviation
图10 不同控制器下的容器倾角调节效果
Fig.10 Title angle of the conveyance with three different
controllers
图10为不同控制器下的容器倾角调节效果，分别使用PI、反步及本文提出的控制器。从图中可以看出，与存在卷筒直径偏差的工况相比，PI、反步及本文提出的控制器均可以有效减小提升系统运行过程中的容器倾角，其中反步和提出的控制器相对于PI控制器具有更优越的响应速度，而提出的控制算法由于添加了延时补偿观测器和高增益观测器，具有更好的控制效果。图11为不同控制器下两浮动天轮液压缸位移。表2对不同控制器下的容器倾角调节效果进行了量化比较，进一步证明了提出的控制方法的优越性。表3中给出了本文提出控制方法的控制参数。
表2 不同控制器下容器倾角调节结果
Table 2 Tilt angle adjust results of conveyance with
three different controllers
控制方法峰值/(°)均方根误差无控制器10.527.71PI控制器2.140.93反步控制器1.080.69提出控制器0.820.51
图11 不同控制器下液压缸位移
Fig.11 Displacements of two hydraulic cylinders with three
different controllers
表3 提出控制器控制参数
Table 3 Control parameters of the proposed controller
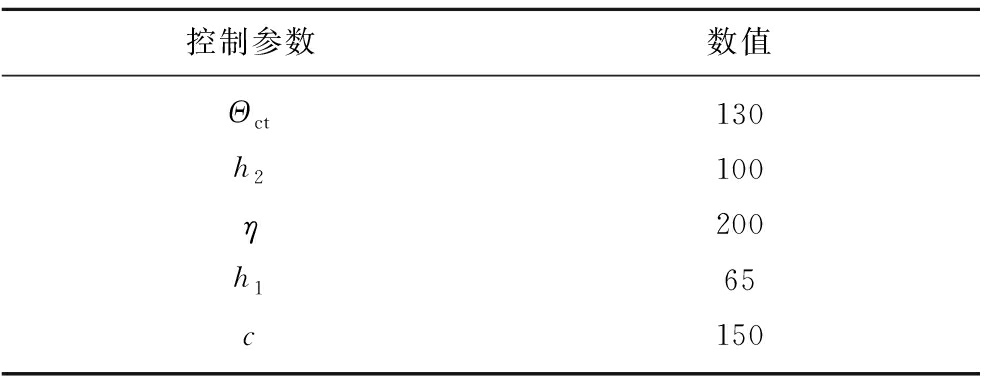
控制参数数值Θct130h2100η200h165c150
5 结 论
(1)建立了双绳缠绕式深井提升系统本体模型，搭建了双绳缠绕式深井提升试验台及其控制系统，设定了六段速提升容器运行曲线，分析了正常工况与存在卷筒直径偏差工况下容器倾角；正常工况下，容器倾角小于1°，存在卷筒直径偏差工况下，容器倾角峰值达10.52°。
(2)构建了容器倾角控制模型，考虑控制信号在钢丝绳中传递存在得延时问题，设计了浮动天轮驱动信号延时补偿观测器，并证明了系统加入延时补偿观测器后的稳定性。
(3) 将高增益观测器与滑模控制器相结合，设计了双绳缠绕式深井提升系统容器位姿调平控制方法，为验证提出控制方法的有效性，在搭建的双绳缠绕式深井提升试验台上进行了实验验证，并与PI控制器和反步控制器进行了对比，其中PI控制器可将容器倾角峰值从10.52°减小至2.14°，反步控制器可将容器倾角峰值从10.52°减小至1.08°，提出的控制器可将容器倾角峰值从10.52°减小至0.82°，证明了所提出控制器的优越性。
[1] 刘劲军,邹声勇,张步斌,等.我国大型千米深井提升机械的发展趋势[J].矿山机械,2012,40(7):1-6.
LIU Jinjun,ZOU Shengyong,ZHANG Bubin,et al.Discussion trend of domestic large hoisting equipments for deep shafts of thousands meters[J].Mining & Processing Equipment,2012,40(7):1-6.
[2] 张胜利.超深竖井提升系统钢丝绳纵向振动仿真优化研究[D].郑州:郑州大学,2016.
ZHANG Shengli.Study on simulation optimization of the steel wire rope’s longitudinal vibration in ultra-deep vertical shaft hoisting system[D].Zhengzhou:Zhengzhou University,2016.
[3] DING S H,ZHENG W X.Nonsingular terminal sliding mode control of nonlinear second-order systems with input saturation[J].International Journal of Robust Nonlinear Control,2016,26(9):1857-1872.
[4] WANG J,ZONG Q,SU R,et al.Continuous high order sliding mode controller design for a flexible air-breathing hypersonic vehicle[J].ISA Transactions,2014,53(3):690-698.
[5] QI L,BAO S,SHI H B.Permanent-magnet synchronous motor velocity control based on second-order integral sliding mode control algorithm[J].Transactions of the Institute of Measurement and Control,2015,37(7):875-882.
[6] 黄进.直流直线电机保证精度的自适应全维状态观测器极点配置[J].测控技术,2018,37(5):137-142.
HUANG Jin.Adaptive full dimensional state observer pole placement for guaranteed accuracy of DC linear motor[J].Measurement and Control Technology,2018,37(5):137-142.
[7] ELHASSEN B,ABDELLAH M,AZEDDINE B,et al.Nonlinear adaptive observer for sensorless passive control of permanent magnet synchronous motor[J].Journal of King Saud University-Engineering Sciences,2019,doi.org/10.1016/j.jksues.2019.06.003.
[8] PIMKUMWONG N,WANG M S.Full-order observer for direct torque control of induction motor based on constant V/F control technique[J].ISA Transactions,2018,73:189-200.
[9] GAN M G,ZHANG M,ZHENG C Y,et al.An adaptive sliding mode observer over wide speed range for sensorless control of a brushless DC motor[J].Control Engineering Practice,2018,77:52-62.
[10] LIU J J,SUN M W,CHEN Z Q,et al.Output feedback control for aircraft at high angle of attack based upon fixed-time extended state observer[J].Aerospace Science and Technology,2019,95:105468.
[11] 檀姗姗,杨洪玖,路继勇,等.基于扩张状态观测器的飞行器姿态控制研究[J].燕山大学学报,2017,41(6):521-527.
TAN Shanshan,YANG Hongjiu,LU Jiyong,et al.Attitude control of aircraft based on extended state observer[J].Journal of Yanshan University,2017,41(6):521-527.
[12] UEKI S,MOURI T,KAWASAKI H.Nonlinear disturbance observer for object grasping/manipulation by multi-fingered robot hand[J].IFAC-Papers OnLine,2017,50(1):12704-12709.
[13] 郭一军,俞立,徐建明.基于扩张状态观测器的轮式移动机器人全阶滑模控制[J].重庆邮电大学学报(自然科学版),2017,29(3):382-388.
GUO Yijun,YU Li,XU Jianming.Full-order sliding mode control of wheeled mobile robot based on extended state observer[J].Journal of Chongqing University of Posts and Telecommunications (Natural Science Edition),2017,29(3):382-388.
[14] LING Z,ZHANG B,YANG H G,et al.Optimized linear active disturbance rejection control for pneumatic servo systems via least squares support vector machine[J].Neurocomputing,2017,242:178-186.
[15] LING Z,LIU X,WANG T.Trajectory tracking control for double-joint manipulator systems driven by pneumatic artificial muscles based on a nonlinear extended state observer[J].Mechanical Systems and Signal Processing,2019,122:307-320.
[16] 王军晓,戎佳艺,俞立.直流降压变换器的降阶扩张状态观测器与滑模控制设计与实现[J].控制理论与应用,2019,36(9):1486-1492.
WANG Junxiao,RONG Jiayi,YU Li.Design and implementation of reduced-order extended state observer and sliding mode control for DC-DC buck converter[J].Control Theory & Applications,2019,36(9):1486-1492.
[17] 于潇雁,陈力.漂浮基柔性两杆空间机械臂基于状态观测器的鲁棒控制及振动控制[J].机械工程学报,2016,52(15):28-35.
YU Xiaoyan,CHEN Li.Observer based robust control and vibration control for a free-floating flexible space manipulator[J].Journal of Mechanical Engineering,2016,52(15):28-35.
[18] WANG Q,RAN M P,DONG C Y.Robust partial integrated guidance and control for missiles via extended state observer[J].ISA Transactions,2016,65:27-36.
[19] GAO H J，CHEN T E．Network-based output tracking control[J].IEEE Transactions on Automatic Control，2008，53(3):655-667．
[20] BENAMOR A,MESSAOUD H.Robust adaptive sliding mode control for uncertain systems with unknown time-varying delay input[J].ISA Transactions,2018,79:1-12.
[21] HE Q,LIU J.An observer for a velocity-sensorless VTOL aircraft with time-varying measurement delay[J].International Journal of Systems Science,2016，47(3):1-10.
