实现井下工作面少人乃至无人作业是安全开采和智慧矿山建设的重要目标之一[1]。滚筒式采煤机是综采工作面的主要设备之一，实现采煤机自动截割对提高采煤机自动化水平，促进煤矿自动化建设有重要意义。实现采煤机自动截割的重点和难点之一是采煤机自动调高问题。
为解决该难题，国内外学者对此进行了大量研究，一方面是直接煤岩识别技术，诸如将γ射线探测[2]、雷达探测[3]、声波探测[4]、图像识别[5]等技术应用于煤岩界面识别，然而由于煤矿地质条件复杂,煤层赋存状态和煤岩属性多变使得上述方法不具有普适性标准,同时由于工作面环境恶劣、识别实时性的原因使得这些技术均未获得工程应用[6]。另一方面则是记忆截割技术，区别于直接的煤岩分界识别方法，记忆截割根据煤矿工作面和截割过程的特点，通过采煤机在示教截割过程中产生的截割参数，如滚筒高度、截割电流等来预测之后的截割轨迹，并以此作为采煤机滚筒自动调高的依据，因而不易受到直接煤岩分界识别所受到的限制。虽然传统记忆截割在一定程度上提高了采煤机的自动化水平，但是同时也有着截割精度低，难适应煤岩分界面变化的缺点。张丽丽等使用微粒群算法[7]和遗传算法对截割路径进行优化[8]，还将灰色系统理论应用于截割轨迹预测并取得了较传统记忆截割更优的预测效果[9];樊启高等则提出利用灰色马尔科夫组合模型的采煤机自适应记忆截割策略，显著提升了采煤机的自动化水平[10];王福忠等还提出了使用迭代学习对截割轨迹进行追踪[11];田立勇等提出一种基于滚筒采煤机摇臂惰轮轴受力分析的综合截割识别方法[12]。
近年来随着机器学习技术研究的广泛开展，深度学习在诸多领域都得到了广泛应用，但在记忆截割方面的研究却鲜有报道。为了提高记忆截割的截割效率与截割精度，笔者在前人的研究基础上，提出一种采用深度LSTM神经网络对截割轨迹进行预测的方法，并对深度LSTM神经网络的超参数进行了优化，实现了对截割轨迹更精准的预测。然后通过改进神经网络结构提出一种MSLSTM神经网络，提升了模型在多步预测中的能力。
1 基于LSTM神经网络的记忆截割轨迹预测建模
1.1 LSTM神经网络
LSTM神经网络可以看作是一种特殊的RNN网络，其具备RNN所具有的递归属性，同时还具有特殊的门结构来控制神经单元间的历史信息传递，因而避免了传统递归神经网络在训练过程中可能出现的梯度爆炸和梯度消失问题。
本文所使用的Peephole LSTM神经网络[13]比原始LSTM神经网络添加了Peephole结构，其基础结构如图1所示，其中，xt为t时刻神经网络单元的输入;h为tanh函数;C为神经网络单元的记忆状态。
图1 LSTM神经网络单元
Fig.1 LSTM neural network block
每一个LSTM神经单元在其t时刻的记忆状态为ct。对LSTM神经单元记忆状态的修改和输出通过对输入门(Input gate)、遗忘门(Forget gate)和输出门(Output gate)的控制来实现。在每一个时刻，LSTM单元通过3个门接受当前时刻输入和上个时刻神经单元输出。在使用输入门、遗忘门控制记忆状态的更新后，通过非线性激活函数和输出门的控制形成LSTM神经单元的输出。一个LSTM神经单元内的计算过程如下。
输入门it为
it=σ(Wi[ht-1,xt]+Pi∘ct-1+bi)
(1)
遗忘门ft为
ft=σ(Wf[ht-1,xt]+Pf∘ct-1+bf)
(2)
输出门ot为
ot=σ(Wo[ht-1,xt]+Po∘ct-1+bo)
(3)
单元记忆状态
为
(4)
(5)
单元输出ht为
ht=ot∘tanh ct
(6)
式中，Wi，Wf，Wo，Wc，Pi，Pf，Po，Pc以及偏置项bi，bf，bo，bc为需要训练的权值;ht-1为上一时刻神经单元的输出;xt为当前神经单元的输入;ct-1为上一时刻神经单元的记忆状态;σ和tanh起到激活函数的作用，其分别为sigmoid函数和双曲正切函数;∘为Hadamard积。
1.2 深度LSTM神经网络
深度神经网络可以更好地提取复杂的数据特征，建立输入变量和输出变量之间的非线性映射关系。为提升预测准确度，本文将原始LSTM神经网络扩展到多层，使用深度LSTM神经网络对记忆截割轨迹进行预测，如图2所示，深度LSTM神经网络由1个输入层、多个LSTM神经网络层和1个全连接层构成。在网络中上一个LSTM层的输出作为下一个LSTM层的输入，数据输入层与LSTM层共同实现输入截割数据特征的提取。最后一个全连接层的输出为列向量，是经神经网络计算后所得到的预测值。
图2 深度LSTM神经网络结构
Fig.2 Deep LSTM neural network structure
1.3 预测流程
针对本文研究问题并结合深度LSTM神经网络，提出的采用深度LSTM神经网络模型对截割轨迹进行预测的方法，设计模型训练、预测步骤如下:
(1)确定深度LSTM神经网络模型的输入输出变量，对输入数据集进行归一化预处理，并将预处理后的数据集划分成为训练集以及测试集2个部分。
(2)构造深度LSTM预测模型。使用Adam算法[14]，利用训练集对模型进行迭代训练，每次迭代后判断误差是否满足设定要求，若满足则结束循环，若不满足则再进行下一次迭代，并使迭代计数加一。若迭代次数达到迭代上限但仍不满足误差要求则重置神经网络并重新开始训练。训练流程如图3所示。
图3 深度LSTM神经网络迭代训练流程
Fig.3 Flow chart of training deep LSTM neural network
(3)使用随机搜索，对超参数进行寻优，选取合适的超参数。
(4)利用测试集对训练完成的网络模型进行测试，记录其误差。
记忆截割轨迹预测多采用逐点预测的方式，每隔固定距离设置一个预测节点，同时也是截割数据的采样点。深度LSTM神经网络的输入数据X即为在采样点多次连续的循环截割中获得的采煤机前滚筒的高度值。网络的输出Y即为所预测的对应预测节点处的截割滚筒高度值。
1.4 数据采集及预处理
本文用于训练预测模型的截割数据为中国平煤神马集团十三矿在实际生产中采煤机的运行记录数据，见表1，表1中数据为采煤机在多次截割过程中，截割滚筒在每个采样节点(x1-x40)处的高度值，在工作面每隔3 m，采煤机自动记录一次前滚筒的中心高度，采煤机截深为0.8 m，每一刀包含40个采样点。总共循环次数为16次，然后将前12次作为神经网络的训练集，后4次作为测试集。
在将数据输入神经网络前需将数据进行归一化处理，则归一化的公式为
式中，xuv为第u刀截割中的第v个采样点的截割滚筒高度值;xmin与xmax分别为样本数据中的极小值和极大值;上角R为用R语言进行标准化(归一化)。
表1 煤岩分布数据
Table 1 Distribution data of coal and rock
截割循环次数x1x2x3x4x5x6…x34x35x36x37x38x39x40第1刀3.023.123.143.233.133.22…3.973.873.763.733.723.643.65第2刀3.123.213.313.213.323.45…4.043.963.803.723.703.753.72第3刀3.273.473.603.703.813.85…4.083.993.983.803.763.723.74…………
1.5 预测效果评估标准
本文选取了平均绝对误差(Mean Absolute Error，EMA)、平均绝对百分误差(Mean Absolute Percentage Error，EMAP)和均方根误差(Root Mean Squared Error，ERMS)作为评价各预测模型与预测方法的预测效果的依据。
以测试集数据为例，其表达式为
式中，
和yi分别为测试中第i个预测点的预测值和实际值;N为测试样本的个数。
1.6 超参数选择
本文提出的深度LSTM网络涉及到的超参数主要包括:网络层数、每层网络的隐层神经元个数等。
表2中的超参数为深度LSTM神经网络的结构参数。其中深度LSTM网络层数与隐藏层神经元个数以及输入序列长度对于训练效果有较大影响。依据经验将隐层的神经元个数的搜索范围限制为[30,150]。损失函数采用均方误差(Mean Square Error，EMS)，其计算公式为
2 算例仿真分析
本文的深度LSTM 网络训练由MATLAB软件实现，硬件平台CPU为Intel(R)Core(TM)i7-7700HQ CPU @ 2.80GHz。
表2 深度LSTM网络的超参数选择与搜索范围
Table 2 Experimental settings of deep LSTM hyper-
parameters
超参数设定值(项)深度LSTM 层数{2,3}第1层隐藏层神经元个数[30,150]第2层隐藏层神经元个数[30,150]第3层隐藏层神经元个数[30,150]训练样本集个数560最大迭代次数2 000训练优化算法Adam损失函数MSE
2.1 不同LSTM神经网络模型预测效果对比
首先经过随机搜索，选取合适的步长。在预先选取的搜索范围内进行寻优。获得最优初始步长的值后，在依据经验所预定的范围内对深度LSTM神经网络的结构超参数采用随机搜索的方法进行优化，并在相同训练数据集下选取MAPE值为对照标准。表3为选取的部分训练结果展示。
从表3中可以看出随着层数和隐层节点数的增加，预测结果误差呈现出先降后增的趋势，说明过低的模型参数会带来欠拟合的问题，而过大的超参数则会导致过拟合。
2.2 不同预测算法预测效果对比
为了显示深度LSTM神经网络的优势，选取支持向量回归(Support Vector Regression，SVR)与梯度提升回归树(Gradient Boosting Regression Tree，GBRT)在相同的数据集下进行对截割轨迹预测效果的对比。深度LSTM的超参数为经过寻优搜索后的数值。
表3 深度LSTM神经网络不同模型参数预测效果
Table 3 Prediction effect of different model parameters
under deep LSTM
层数第1层第2层第3层EMA/mmEMAP/%ERMS/mm23030085.342.26897.41210030082.162.18395.602150100072.631.94188.23350505069.711.86283.883100505066.081.76881.4931001005071.111.89886.06315010010073.821.97089.62
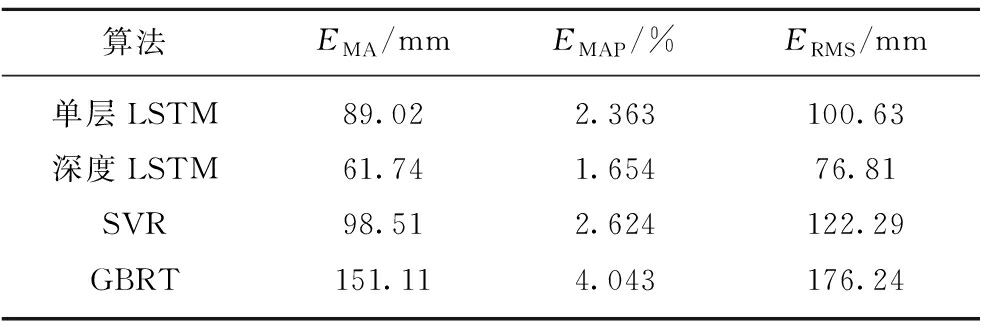
表4 不同算法与神经网络预测结果比较
Table 4 Prediction results under different algorithms
算法EMA/mmEMAP/%ERMS/mm单层LSTM89.022.363100.63深度LSTM61.741.65476.81SVR98.512.624122.29GBRT151.114.043176.24
从表4中可以看出，深度LSTM网络可以更好的提取学习截割高度的非线性变化特征，并获得更精准的预测。将LSTM神经网络扩展为多层神经网络，可以有效提升网络的预测能力。深度LSTM神经网络相对于SVR和GBRT，EMA降低了35%和59%，EMAP降低 37%和59%，ERMS降低37%和56%，预测准确度得到了较大提高。
使用深度LSTM神经网络对于一次截割中的40个节点进行连续预测并与其他算法进行对比。结果如图4所示，可见SVR与GBRT的预测效果较差，在x=[5,15]的曲线中可以看出明显的偏差。
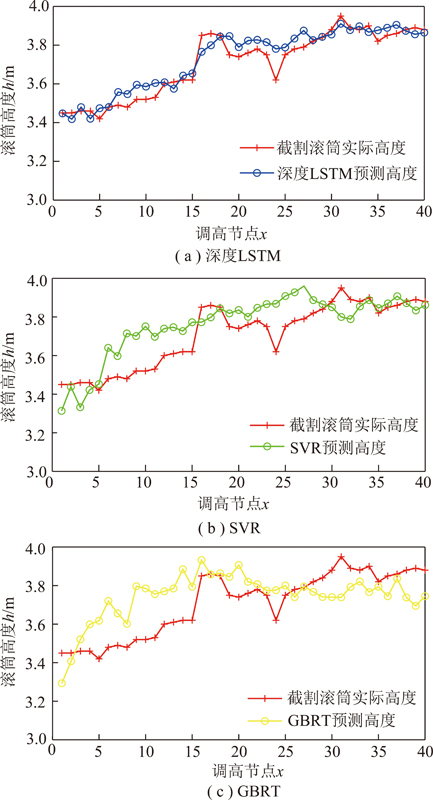
图4 深度LSTM，SVR，GRBT预测效果对比
Fig.4 Comparison of deep LSTM,SVR,GRBT prediction effect
3 预测模型优化
考虑到实际生产中的实时性问题，采煤机一般需要进行多次连续截割，故需对截割路径进行多步预测，但由式(1)～(5)可得
(7)
式(7)中存在着由遗忘门引入的乘法项:
(8)
式中，
分别为其对应下角标时刻的遗忘门，输入门，单元记忆更新输入，单元输出，单元输入，peepholes结构引入的系数，单元记忆的值。
由于1≥fj，随着t-j的增大，该项也随之减小。因此LSTM对于[xl,hl-1]的响应不可避免的减小。
为了解决这个问题，本文提出1种MSLSTM神经网络(Memory Strengthen Long Short-term Memory)，该神经网络通过引入1个比例因子kt来补偿响应的衰减问题。
(9)
其中,kt∈
N，则可得
(10)
由式(6)可得
(11)
可见对于∀Wf∈M×N，∃kt∈N使得
(12)
因此，MSLSTM的记忆长度会大于LSTM，可以更好保存数据的历史记忆。然后，由随时间的反向传播[15](Back Propagation Trough Time，BPTT)则可得
δkt=δyt∘[1-tanh(ct)2]∘ft∘ct-1
(13)
式中，δkt为损失函数对kt的梯度;yt为神经网络t时刻的输出。
由Adam算法可得kt的更新计算步骤为
当t=l时，若令gl=δkt，则
ml=β1ml-1+(1-β1)gl
(14)
(15)
(16)
(17)
(18)
其中，l为一个特指的时刻;ml和vl分别为一阶和二阶矩估计;gl用来在推导公式中代指
为gl的平方;vl-1为l-1时的二阶矩估计;
为β1的l次幂;
为β2的l次幂;kl+1为t=l+1时的kt;kl为t=l时的
为对v的偏差修正;
分别为对ml和vl的偏差修正;α为更新步长;衰减速率β1，β2分别为0.9和0.99;用于稳定数值的小常数ε为10-8。
4 基于MSLSTM神经网络的记忆截割轨迹预测
将改进后的MSLSTM神经网络加深为深度神经网络并与深度LSTM神经网络进行预测效果对比。为增加对比的可靠性，仍使用第3节中使用的滚筒高度数据，并将数据集中前10刀划分为训练集，后6刀划分为测试集。利用重新划分后的数据集分别对原模型和改进后的模型进行预测测试。每刀中，预测误差见表5。
表5 深度LSTM神经网络与深度MSLSTM神经网络预测效果对比
Table 5 Comparison of prediction effect between deep LSTM neural network and deep MSLSTM neural network
项目第1刀EMA/mmEMAP/%ERMS/mm第2刀EMA/mmEMAP/%ERMS/mm第3刀EMA/mmEMAP/%ERMS/mm第4刀EMA/mmEMAP/%ERMS/mmLSTM63.481.70178.2265.731.76683.8167.181.80584.2578.172.08896.50MSLSTM65.481.75881.2866.081.76881.4966.261.77881.9169.231.85385.13
由表5可知，由于训练集数据规模的下降，第1刀时，深度LSTM神经网络的预测误差有所变大，但比深度MSLSTM神经网络略小，LSTM的EMA，EMAP，ERMS较MSLSTM分别低3.1%，3.2%，3.7%，随着预测步数的增加，深度MSLSTM神经网路具有更好的表现，其在第3,4刀的各项误差评价指标均小于深度LSTM神经网络。第4刀时MSLSTM的EMA，EMAP，ERMS较LSTM分别低11.4%，11.3%，11.3%。
由此可见，深度MSLSTM神经网络对于多步预测更具优势。
5 结 论
(1)针对综采工作中采煤机记忆截割精度不足的问题，提出了基于深度学习的记忆截割轨迹预测方法。利用深度LSTM神经网络对记忆截割轨迹预测进行了建模，并对神经网络超参数进行了优化。
(2)使用真实的采煤机截割前滚筒高度数据对深度LSTM预测模型进行了验证，并就预测误差与SVR，GRBT进行了对比。实验结果证明，深度LSTM神经网络在采煤机记忆截割方面较SVR，GRBT等机器学习方法具有更好的表现，其EMA为61.74 mm，EMAP为1.654%，ERMS为76.81 mm，均低于SVR与GRBT。
(3)在模型中引入比例因子，提高了神经网络的记忆保持能力，并将MSLSTM与LSTM进行了对比。实验结果表明，MSLSTM在多步预测方面比LSTM具有更好的效果，且其优势随着预测步数的增加而变大。
[1] 张帆,徐志超.基于残差神经网络的矿井图像重构方法[J].煤炭学报，2019,44(11):3614-3624.
ZHANG Fan,XU Zhichao.A mine image reconstruction method based on residual neural network[J].Journal of China Coal Society，2019,44(11):3614-3624.
[2] BESSINGER S L,NELSON M G.Remnant roof coal thickness measurement with passive gamma ray instruments in coal mines[J].IEEE Transactions on Industry Applications,1993,29(3):562-565.
[3] BAUSOV I Y,STOLARCZYK G L,STOLARCZYK L G,et al.Look-ahead radar and horizon sensing for coal cutting drums[A].2007 4th International Workshop on,Advanced Ground Penetrating Radar[C].IEEE,2007:208-211.
[4] 杨文萃,邱锦波,张阳,等.煤岩界面识别的声学建模[J].煤炭科学技术,2015,43(3):100-103．
YANG Wencui,QIU Jinbo,ZHANG Yang,et al.Acoustic modeling of coal-rock interface identification[J].Coal Science and Technology,2015,43(3):100-103．
[5] 孙继平,佘杰.基于小波的煤岩图像特征抽取与识别[J].煤炭学报,2013,38(10):1900-1904.
SUN Jiping,SHE Jie.Wavelet-based coal-rock image feature extrac-tion and recognition[J].Journal of China Coal Society,2013,38(10):1900-1904.
[6] 杨恩,王世博,葛世荣,等.煤岩界面的高光谱识别原理[J].煤炭学报,2018,43(S2):646-653.
YANG En,WANG Shibo,GE Shirong,et al.Study on the principle of hyperspectral recognition of coal-rock interface[J].Journal of China Coal Society,2018,43(S2):646-653.
[7] 张丽丽,谭超,王忠宾,等.基于微粒群算法的采煤机记忆截割路径优化[J].煤炭科学技术,2010,38(4):69-71.
ZHANG Lili,TAN Chao,WANG Zhongbin,et al.Optimization of mnemonic cutting path for coal shearer based on corpuscular group algorithm[J].Coal Science and Technology,2010,38(4):69-71.
[8] 张丽丽,谭超,王忠宾,等.基于遗传算法的采煤机记忆截割路径优化[J].煤炭工程,2011(2):111-113.
ZHANG Lili,TAN Chao,WANG Zhongbin,et al.Optimization of memory cutting path of shearer based on genetic algorithm[J].Coal Engineering,2011(2):111-113.
[9] 周斌,王忠宾,权国通.灰色系统理论在采煤机记忆截割技术中的应用[J].矿山机械,2011,39(4):20-23.
ZHOU Bin,WANG Zhongbin,QUAN Guotong.Application of grey system theory to memory cutting technology of shearers[J].Mining & Processing Equipment,2011,39(4):20-23.
[10] 樊启高,李威,王禹桥,等.一种采用灰色马尔科夫组合模型的采煤机记忆截割算法[J].中南大学学报(自然科学版),2011,10(42):3054-3058.
FAN Qigao,LI Wei,WANG Yuqiao,et al.An algorithm of shearer memory cutting based on grey-markovian model[J].Journal of Central South University (Science and Technology),2011,10(42):3054-3058.
[11] 王福忠,高颖.采煤机截割滚筒轨迹的迭代学习跟踪控制[J].控制工程,2018,25(6):966-971.
WANG Fuzhong,GAO Ying.Tracking control of shearer cutting-drum using iterative learning[J].Control Engineering of China,2018,25(6):966-971.
[12] 田立勇,毛君,王启铭.基于采煤机摇臂惰轮轴受力分析的综合煤岩识别方法[J].煤炭学报,2016,41(3):782-787.
TIAN Liyong,MAO Jun,WANG Qiming.Coal and rock identification method based on the force of idler shaft in shearer’s ranging arm[J].Journal of China Coal Society,2016,41(3):782-787.
[13] GERS F A,SCHMIDHUBER J.Recurrent nets that time and count[A].IEEE-INNS-ENNS International Joint Conference on Neural Networks[C].IEEE,2000,3:189-194.
[14] KINGMA D P,BA J.Adam:A method for stochastic optimization[J].ArXiv Preprint ArXiv，2014，9:1-10.
[15] BODEN M.A guide to recurrent neural networks and backpropagation[J].The Dallas Project,2002.
[16] BERGSTRA J,BENGIO Y.Random search for hyper-parameter optimization[J].Journal of Machine Learning Research,2012,13(2):281-305.
[17] 朱乔木,李弘毅,王子琪,等．基于长短期记忆网络的风电场发电功率超短期预测[J].电网技术,2017,41(12):3797-3802.
ZHU Qiaomu,LI Hongyi,WANG Ziqi,et al.Short-term wind power forecasting based on LSTM[J].Power System Technology,2017,41(12):3797-3802.
[18] 张宇帆,艾芊,林琳,等.基于深度长短时记忆网络的区域级超短期负荷预测方法[J].电网技术,2019,43(6):1884-1892.
ZHANG Yufan,AI Qian,LIN Lin,et al.A very short-term load forecasting method based on deep LSTM RNN at zone level[J].Power System Technology,2019,43(6):1884-1892.
[19] TAN C,XU R,WANG Z,et al.An improved genetic fuzzy logic control method to reduce the enlargement of coal floor deformation in shearer memory cutting process[J].Computational Intelligence and Neuroscience,2016,2016:9.
[20] LI W,LUO C,YANG H,et al.Memory cutting of adjacent coal seams based on a hidden Markov model[J].Arabian Journal of Geosciences,2014,7(12):5051-5060.
[21] XU Zhipeng,WANG Zhongbin.Modelling and simulation on shearer self-adaptive memory cutting[J].Procedia Engineering,2012,37:37-41.
[22] GREFF K,SRIVASTAVA R K,KOUTN
K J,et al.LSTM:A search space odyssey[J].IEEE transactions on neural networks and learning systems,2016,28(10):2222-2232.
[23] GERS F A,SCHMIDHUBER J,CUMMINS F.Learning to forget:Continual prediction with LSTM[J].Neural Computation,2000,12(10):2451-2471.
[24] 苏秀平,李威,樊启高.采煤机滚筒调高滑模变结构控制策略[J].煤炭学报,2012,37(12):2107-2111.
SU Xiuping,LI Wei,FAN Qigao.A shearer drum height adjusting strategy using sliding-mode variable structure control[J].Journal of China Coal Society,2012,37(12):2107-2111.
[25] 苏秀平.采煤机自动调高控制及其关键技术研究[D].徐州:中国矿业大学,2013．
SU Xiuping.Study on key technologies of auto-height adjustment for shearer[D].Xuzhou:China University of Mining and Technology,2013.
[26] 薛红梅.基于Elman神经网络的采煤机自动调高控制算法研究[D].西安:西安科技大学,2014．
XUE Hongmei.Research on memory lifting control algorithm for shearer based on elman neural network[D].Xi’an:Xi’an University of Science and Technology,2014.
[27] HARGRAVE C O,JAMES C A,RALSTON J C.Infrastructure-based localisation of automated coal mining equipment[J].International Journal of Coal Science & Technology,2017,4(3):252-261.
[28] NAJAFI Mehdi,JALALI Seyed Mohammad Esmaiel,KHALO Kakaie Reza,et al.Prediction of cavity growth rate during underground coal gasification using multiple regression analysis[J].International Journal of Coal Science & Technology,2015,2(2):318-324.
