高瓦斯矿井发生火灾,建立封闭过程时,十分容易发生瓦斯爆炸,甚至连续爆炸[1-3]。尤其在火区初次封闭后,发生过多次在短时间内爆炸的重大事故,在2013-03-29与2013-04-01,吉林通化八宝煤矿采空区自然发火封闭过程中诱发多次瓦斯爆炸,造成53人死亡[4];2003-10-24,宁夏白芨沟矿井下构筑封闭防爆墙时先后发生4次瓦斯爆炸。针对此类事故,国内学者开展了相关研究,周西华等[5-6]采用COMSOL软件研究了不同风速条件下,封闭火区巷道中心垂直断面速度场、气体体积分数场变化规律,给出了判定甲烷爆炸危险区域的方法。翟小伟等[7]推导了短时间内封闭火区CH4和O2体积分数变化规律,得到了甲烷爆炸的可能性及发生时间。LUO等[8]通过球形爆炸实验分析CO及烃类混合物的加入对CH4爆炸的链式反应影响并测定了反应后的爆炸极限。秦波涛等[9]通过实验研究表明可燃混合气体爆炸上、下限范围变大,瓦斯爆炸危险性增加。波兰中央矿山救护总站通过一系列转换系数将火区内混合爆炸性气体转换为单一的爆炸三角形,以此判断瓦斯爆炸危险性[2]。张辛亥等[10]研究了封闭火区内O2,CH4体积分数与封闭时间数学关系,绘制了瓦斯爆炸危险性的理论变化曲线,得到了发生爆炸的时间。邓存宝等[11]研究了煤矿封闭火区后O2,CO气体运移规律,理论推导了有效扩散系数计算式,建立了封闭火区内热量传递模型和火区启封时间计算模型。DUAN等[12]研究了构筑密闭时期大气扰动造成火区氧体积分数变化对火区瓦斯爆炸危险性的影响。焦宇等[13]分析了惰性气体在矿井火灾引发瓦斯爆炸事故的抑爆机理并分析了影响构筑火区封闭时期瓦斯爆炸事故的发生规律。赵洪宝等[14]等研发了一种采空区瓦斯体积分数区域分布三维实测装置,测定具有严重的瓦斯爆炸威胁区域。彭斌[15]研究了采空区气体交换及不同漏风量系数条件下爆炸危险系数的变化规律。
煤矿火灾发生后,封闭火区过程中,生成高温气体与煤巷、采空区瓦斯涌出,极易发生火灾诱发瓦斯爆炸事故,目前相关学者主要研究了火区封闭与启封时间计算模型、封闭区内CH4与O2积聚规律、瓦斯爆炸危险性定性分析等发面,关于火区封闭过程中瓦斯爆炸危险性影响因素及对其演化规律、煤矿火灾发生后引发次生瓦斯爆炸事故危险性定量分析,预测封闭过程中可能发生瓦斯爆炸时间研究甚少。为此,笔者结合前期瓦斯爆炸影响因素实验及数据拟合原理,构建了一种火区瓦斯爆炸危险性估算预测数学模型,为矿井火区安全封闭与事故应急抢险救援提供借鉴。
1 煤矿火区瓦斯爆炸危险性预测理论
瓦斯爆炸必须同时满足3个条件:① 环境甲烷体积分数在可爆极限区间内;② 氧气体积分数大于临界氧体积分数;③ 有大于引燃甲烷最小点火能的火源存在。因此,矿井发生火灾后,火区内高温区域分布范围广,伴随瓦斯不断涌出,O2体积分数短时间内依然高于临界氧体积分数。火区内瓦斯爆炸界限并非传统的5%~16%,受高温、CO、压力等多因素综合作用影响,爆炸界限范围变大。火区封闭过程中火灾生成气体、巷道空间瓦斯涌出与风量缩减多因素耦合作用,极易发生火灾诱发次生瓦斯爆炸事故。
火区封闭过程中,根据不同时间火区状态参数监测结果,绘制并拟合出最易爆炸点位置变化过程曲线与方程,结合气体体积分数随时间变化趋势,预测可能发生次生瓦斯爆炸时间,达到预测爆炸危险性的目的。火区瓦斯爆炸危险性预测原理图如图1所示。定义图1中,可能爆炸点M(XM(CH4),YM(O2))为火区环境诱发瓦斯最易爆炸状态点随时间变化过程与爆炸下限交点,临界点E(xE,yE)为不同温度与CO体积分数条件下,发生瓦斯爆炸的CH4与O2体积分数点。根据不同时刻监测的火区易爆点参数变化,ti时刻为(xi,yi),如图1所示。曲线1为火区状态点参数变化曲线,曲线2为瓦斯爆炸下限曲线,对曲线1与曲线2求方程交点即可得到发生瓦斯爆炸时CH4与O2体积分数,从而可以反演出发生瓦斯爆炸时间t。

图1 火区瓦斯爆炸危险性预测原理
Fig.1 Principle diagram of the burning gas explosion
hazard prediction
2 温度与CO气体耦合作用对瓦斯爆炸界限影响
2.1 试验装置及方案
实验采用的20 L爆炸实验装置分为配气系统、温度及压力等参数控制采集系统、点火系统。具体装置结构如图2所示。

图2 爆炸装置系统
Fig.2 System diagram of explosive device
2.2 实验结果
环境温度和可燃性气体CO耦合条件下瓦斯爆炸界限实验数据见表1。当环境温度为50~100 ℃、可燃性气体CO体积分数为1.0%~10.0%,通过分析实验数据,观察爆炸极限随环境温度计CO体积分数变化规律,以保证相关度为前提,利用二元二次多项式曲面进行函数拟合。将环境温度T和CO体积分数n作为自变量,甲烷爆炸极限L作为因变量,拟合方程:
L=a+bT+cn+dTn+eT2+fn2
(50<T<100,1%<n<10%)
(1)
式中,a,b,c,d,e,f为拟合系数。
经拟合后,瓦斯爆炸上限Lu、下限Ll随环境温度、CO体积分数变化的表达式分别为
Lu=17.459-0.027T-0.209n-
0.001Tn+0.000 3T2-0.014n2
Ll=6.371-0.001T-0.563n-0.001Tn-
0.000 1T2-0.002n2
表1 温度与CO体积分数耦合条件瓦斯爆炸界限实验结果
Table 1 Experimental results of gas explosion limit under coupling condition of temperature and CO concentration

环境温度T/℃瓦斯体积分数(爆炸上限)/%n=1%n=5%n=10%瓦斯体积分数(爆炸下限)/%n=1%n=5%n=10%5016.416.014.15.43.60.97517.116.514.25.23.20.810017.716.615.84.52.80.7

图3 温度与CO气体耦合作用下甲烷爆炸上限和
下限拟合曲面
Fig.3 Fitting surface of methane upper and lower explosion
limits under coupling condition of temperature and pressure
由图3可知,随着温度T不断上升,瓦斯爆炸下限下降,爆炸上限上升,瓦斯可爆炸条件范围增大。随着环境中CO体积分数升高,瓦斯爆炸上限、下限均随之降低,瓦斯可爆炸条件范围增大。煤矿发生煤燃烧火灾时,燃烧煤体温度为600~800 ℃,峰值可达1 200 ℃。因此火区瓦斯爆炸界限范围较大,更容易发生瓦斯爆炸。
3 瓦斯爆炸时间预测数学模型
3.1 曲线拟合原理
数据拟合基于最小二乘法原理,原理为:对于给定的一组数据{(xi,S(xi)),(i=1,2,…,m)},若拟合曲线模型为y=f(x),则第i误差距离为f(xi)-P(xi),所有点的平方和就是![]() 进而求出
进而求出![]() 的最小值对应的参数,因此得到拟合曲线P(x)=f(x)。
的最小值对应的参数,因此得到拟合曲线P(x)=f(x)。
根据图1中(x1,y1),(x2,y2),(x3,y3),…,(xi,yi),选取合理的拟合公式,将瓦斯易爆点数据代入上述拟合公式中,求解系数a0,a1,…,ai,确定拟合曲线方程。
3.2 瓦斯爆炸下限方程求解
不同温度、不同CO体积分数条件下瓦斯爆炸下限点B(xB,yB)可由式(1)得到。由于式(1)二次型系数较小,对计算结果影响十分有限,此处省略方程二次项,临界点E瓦斯体积分数方程C(CH4)[16]为
C(CH4)=5.73-4.9×10-3T
(2)
根据式(1)与式(2),可求出火区不同温度、CO体积分数条件下下限点B(xB,yB)、临界点E(xE,yE)CH4与O2体积分数,根据B,E两点CH4与O2体积分数获得CH4随O2体积分数变化关系式为
C(CH4)=f(C(O2))
(3)
式中,C(O2)为O2体积分数;f(C(O2))为关于O2体积分数的函数。
3.3 发生瓦斯爆炸时对应瓦斯与氧气体积分数
根据不同时刻ti火区气体成分C(CH4)i,C(O2)i,温度Ti等测试数据拟合的曲线方程C(CH4)=f(C(O2)),与式(3)联立,求解可能发生瓦斯爆炸时对应的瓦斯体积分数和氧气体积分数点M(XM(CH4),YM(O2))。
3.4 瓦斯爆炸时间预测
根据不同时刻ti火区气体成分C(CH4)i,C(O2)i变化的数据,如图4所示,可拟合出气体体积分数C(CH4),C(O2)随时间ti的变化曲线方程:
C(O2)=f(t(O2))
(4)
C(CH4)=g(t(CH4))
(5)
式中,f(t(O2))为关于O2爆炸时间的函数;g(t(CH4))为关于CH4爆炸时间的函数。
根据火区不同时刻测试O2体积分数C(O2)i(i=1,2,…,n)、CH4体积分数C(CH4)i(i=1,2,…,n)和当前测量时间t。进行瓦斯爆炸预测时,至少进行2次以上测量,并分别将C(CH4),C(O2)与t进行曲线拟合,得到瓦斯C(CH4)与C(O2)随时间t变化拟合方程(4)和(5),然后根据求出的可能爆炸时的瓦斯体积分数与氧气体积分数M(XM(CH4),YM(O2))代入式(4)与式(5),反演求出可能发生瓦斯爆炸时间:
t(O2)=f-1(C(O2))
(6)
t(CH4)=g-1(C(CH4))
(7)

图4 火区CH4体积分数随时间变化曲线
Fig.4 Change curve of burning methane concentration with time
4 瓦斯爆炸危险性预测时间确定原则
4.1 瓦斯与氧气体积分数交点确定原则
根据瓦斯爆炸影响因素建立的不同因素条件下(温度、CO等)瓦斯爆炸下限变化公式,确定该温度、CO等条件下瓦斯爆炸下限方程:C(CH4)min=g(C(O2)),根据不同时刻ti监测的火区状态点参数变化(xi,yi),拟合出火区状态点的变化方程:C(CH4)=f(C(O2)),两个方程联立求解,即可预测出可能发生爆炸点M(XM(CH4),YM(O2))的瓦斯体积分数和氧气体积分数。
4.2 瓦斯爆炸时间确定
根据火区监测的CH4与O2随时间变化拟合曲线,结合可能爆炸的瓦斯体积分数、氧气体积分数M(XM(CH4),YM(O2))。若可能爆炸点M(XM(CH4),YM(O2))的氧气体积分数小于临界点E的氧气体积分数,即YM(O2)<YE(O2),则氧气体积分数不足,不爆炸。如果氧气体积分数大于临界点E的氧气体积分数YM(O2)>YE(O2),氧气体积分数充足,则将可能爆炸点M(XM(CH4),YM(O2))的氧气体积分数YM(O2)代入式(7),即可求解出时间t(CH4),发生瓦斯爆炸时间则依据CH4体积分数变化的爆炸时间t(CH4)确定。
5 火区气体状态点分布规律及其监测
5.1 火区气体状态点分布规律
巷道平均风速条件下烟流逆流层判别式[17]为
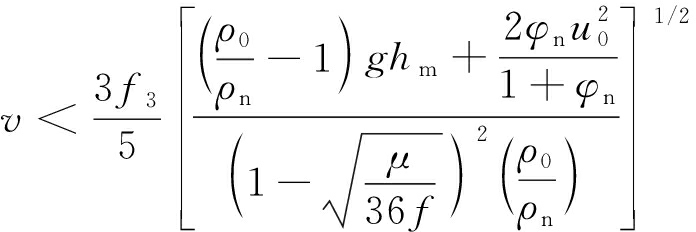
(8)
式中,v为井巷平均风速,m/s;f3为转换系数,表示烟流最大垂直速度与水平逆流速度之比;ρn为经燃烧生成气体密度,kg/m3;hm为井巷高度;φn为混合比,φn=mn/m;u0为燃烧生成气体在脱离可燃物的速度,m/s;μ为巷道摩擦因数;f为实验常数,取0.004~0.004 6,平均值为0.004 3;mn为烟流微团里燃烧生成物的质量,kg;m为烟流微团里风流的质量,kg;ρ0为巷道风流密度,kg/m3。
火区封闭过程中,风量减少,风速降低,由式(8)可知,巷道顶端极易形成逆流层。当火区封闭后,烟流必然在火区内形成高温逆流层。煤矿火灾发生后,热风压与体积力共同作用使环境中气体在火焰周围产生自循环流动的逆流层,引起瓦斯积聚,火源上风侧为高温区域。根据瓦斯爆炸三要素,火源点上风侧为瓦斯最易爆炸危险区域。
5.2 火区气体状态点监测
笔者前期研究得到,水平巷道封闭火区后(入口风速0.1 m/s),火灾最易爆炸点位于火源点上风侧10.45 m处[18]。为此,一旦矿井发生火灾事故应重点监测火源上风侧气体体积分数变化(由于火区温度较高,一般传感器极易毁坏,可以采用耐温性能好的光纤分布式传感器),准确及时地监测掌握火区气体体积分数、温度等参数变化,根据监测与监测参数绘制变化曲线,判定易爆点进入瓦斯爆炸三角形趋势与时间。
6 火灾诱发瓦斯爆炸危险性预测案例
6.1 火灾发生发展背景
煤矿火灾常发生在采空区、煤巷中。笔者利用COMSOL数值模拟软件研究水平巷道中煤巷底板发生火灾事故后在不同风速条件下,气体温度场,体积分数场分布[19]。50 m×4 m×3 m长方体水平巷道模型如图5所示 。巷道四周岩石厚度设为0.5 m,左侧为风流入口,右侧为风流出口。坐标(16,2,0) 处设置一下底面直径为1 m,上顶面直径0.5 m,垂高0.2 m的圆台形热源。

图5 计算模型
Fig.5 Calculation model
6.2 边界条件及火源设置
矿井火灾火源处反应极为复杂,为简化火区模拟计算条件,坐标(16,2,0)处圆台即为模拟中火源为煤堆中心,将其视为不断释放高温烟气的恒温区。煤堆及巷道四周为固体传热,外部为原岩温度,风流为流体传热,初始温度为20 ℃。风流入口O2体积分数取21%,CH4体积分数取0.05%,CO2体积分数设为0.03%,CO体积分数设为0。火灾初期氧气消耗量较大,煤堆表面燃烧反应耗氧量按照O2体积分数不低于15%计算,火源温度达到1 300 ℃前生成CH4,CO2,CO气体体积比为0.05∶1∶1,火源温度达到1 300 ℃后生成CH4,CO2,CO气体体积比为0.05∶1∶2,巷道壁面瓦斯涌出量为定值0.048 m3/s。为研究火区封闭过程中瓦斯爆炸易爆区域范围变化趋势,入口端风速分别取0.10,0.25,0.50,1.00和1.50 m/s。传热采用固-气耦合传热,出口边界为自由出口。
6.3 模拟结果
根据火区封闭过程中气体体积分数场与温度场分布情况,绘制出瓦斯易爆点变化拟合曲线如图6中曲线1所示,常温常压下瓦斯爆炸下限变化曲线如图6中曲线2所示,笔者仅考虑温度对临界点瓦斯体积分数与氧气体积分数影响,临界点瓦斯体积分数方程C(CH4)=5.73-4.9×10-3T,临界氧体积分数拟合方程为C(O2)=12.669-0.012 69T,确定临界点E′,结合瓦斯爆炸特性影响因素实验结论,确定瓦斯爆炸上下限点B′和C′,3点连线可构建不同温度时变化的瓦斯爆炸三角形。

图6 瓦斯易爆点拟合曲线
Fig.6 Fitting curve of gas explosive point
拟合图6中瓦斯易爆点变化曲线与变温度条件下瓦斯爆炸下限,得到瓦斯易爆点变化曲线1:C(O2)=20.507 39-0.325 64C(CH4),当温度为565 ℃时,瓦斯爆炸三角形如图5中△B′C′E′所示,瓦斯爆炸下限对应曲线2′方程为:C(O2)=32.623 9C(CH4)-94.148 15,曲线1与曲线2′交点为(3.48%,19.37%)。
假设供风量呈线性下降,在60 min内完成封闭,封闭后存在少量漏风(1.2 m3/s),则入口速度边界改为时间的分段函数即

(9)
根据火区封闭时风速变化方程知,风速为1.5 m/s时,对应时间t1=900 s,对应易爆点气体体积分数为C(CH4)=0.638%,C(O2)=20.52%;风速为1.0 m/s时,对应时间t2=1 800 s,对应易爆点气体体积分数为C(CH4)=1.01%,C(O2)=19.91%;风速为0.5 m/s时,对应时间t3=2 700 s,对应易爆点气体体积分数为C(CH4)=1.55%,C(O2)=19.94%;风速为0.25 m/s时,对应时间t4=3 150 s,对应易爆点气体体积分数为C(CH4)=2.667%,C(O2)=19.74%;风速为0.1 m/s时,对应时间t5=3 420 s,对应易爆点气体体积分数为C(CH4)=4.114%,C(O2)=19.16%。
根据不同风速以及易爆点瓦斯与氧气体积分数,绘制出CH4随时间变化曲线(图7)与O2随时间变化曲线(图8)。

图7 CH4体积分数随时间变化拟合曲线
Fig.7 Fitting curve of CH4 concentration changing with time

图8 O2体积分数随时间变化拟合曲线
Fig.8 Fitting curve of O2 concentration changing with time
通过对CH4体积分数随时间变化曲线,对易爆点进行数据拟合,得到瓦斯体积分数随时间变化曲线为:C(CH4)=0.114 15e0.001 03t。根据瓦斯爆炸下限与易爆点变化曲线交点得出的瓦斯体积分数为3.479 73%,反演求出对应瓦斯爆炸时间ti=3 317.7 s。
通过对O2体积分数随时间变化曲线,对易爆点进行数据拟合,得到氧气随时间变化曲线为,C(O2)=20.865 36-4.215 71×10-4t。根据瓦斯爆炸下限与易爆点变化曲线交点得出的O2体积分数为19.374 25%,反演求出对应瓦斯爆炸时间ti=3 537.0 s=58.95 min。CH4体积分数为3.479 73%时,反演求出瓦斯爆炸时间为ti=3 317.7 s=55.30 min。根据瓦斯爆炸时间确定原则,确定瓦斯爆炸时间为3 317.7 s=55.30 min。
7 结 论
(1)构建了一种火区瓦斯爆炸危险性估算预测模型,应用变化的瓦斯爆炸三角形与曲线拟合理论,火区参数获取简单,可为矿井火区封闭提供参考建议。
(2)基于瓦斯爆炸条件与时间最小理论求得的瓦斯可能爆炸时间,若可能爆炸点M(XM(CH4),YM(O2))O2体积分数小于临界点E的O2体积分数,不爆炸。若O2体积分数大于临界点E的O2体积分数,发生瓦斯爆炸时间依据CH4体积分数变化的爆炸时间t(CH4)确定。
(3)该预测模型的应用限制条件较多,模型的进一步发展过程还需要进一步考虑多因素耦合作用下瓦斯爆炸三角形变化规律、惰化火区措施对火区气体体积分数影响等方面。
[1] 周心权.矿井火灾防治[M].徐州:中国矿业大学出版社,2002:146-160.
[2] BAI Gang,LI Xueming,ZHOU Xihua,et al.Evaluation of lignite combustion characteristics and gas explosion risks under different air volumes[J].Energy Sources,Part A:Recovery,Utilization,and Environmental Effects,2020,doi:10.1080/15567036.2020.1770375.
[3] 梁运涛,罗海珠.中国煤矿火灾防治技术现状与趋势[J].煤炭学报,2008,33(2):126-130.
LIANG Yuntao,LUO Haizhu.Current situation and development trend for coal mine fire prevention & extinguishing techniques in China[J].Journal of China Coal Society,2008,33(2):126-130.
[4] 丁百川.四天里的五次爆炸[J].劳动保护,2013,12:32-35.
DING Baichuan.Five explosions in four days[J].Labour protection,2013,12:32-35.
[5] 周西华,李诚玉,张丽丽,等.封闭后火区气体运移规律的数值模拟[J].中国地质灾害与防治学报,2015,26(2):116-122.
ZHOU Xihua,LI Chengyu,ZHANG Lili,et al.Closed during fire gas migration law of numerical simulation[J].Geological Disasters in China and Prevention Journal,2015,26(2):116-122.
[6] 周西华,孟乐,史美静,等.高瓦斯矿发火区封闭时对瓦斯爆炸界限因素的影响[J].爆炸与冲击,2013,33(4):351-356.
ZHOU Xihua,MENG Le,SHI Meijing,et al.Influences of sealing fire zone in high gas mine on impact factors of gas explosion limit[J].Explosion and Shock Waves,2013,33(4):351-356.
[7] 翟小伟,来兴平.瓦斯矿井工作面火区封闭后爆炸危险性快速预测方法[J].煤炭学报,2016,41(9):2251-2255.
ZHAI Xiaowei,LAI Xingping.Rapid prediction method for explosion hazard in gas mine after sealing fire working face[J].Journal of China Coal Society,2016,41(9):2251-2255.
[8] LUO Z,SU B,LI Q,et al.Micromechanism of the initiation of a multiple flammable gas explosion[J].Energy & Fuels,2019,33(8):7738-7748.
[9] 秦波涛,张雷林,王德明,等.采空区煤自燃引爆瓦斯的机理及控制技术[J].煤炭学报,2009,34(12):1655-1659.
QIN Botao,ZHANG Leilin,WANG Deming,et al.Mechanism and restraining technology on spontaneous combustion of coal detonating gas in goaf[J].Journal of China Coal Society,2009,34(12):1655-1659.
[10] 张辛亥,徐精彩,刘继勇,等.高瓦斯矿发火区封闭时瓦斯爆炸危险性预测[J].西安矿业学院学报,1999,6(2):110-113.
ZHANG Xinhai,XU Jingcai,LIU Jiyong,et al.Analysis of the danger of gas explosion in coal mine after sealing the fire zone[J].Journal of Xi’an Mining Institute,1999,19(2):110-113.
[11] 邓存宝,王继仁,洪林.矿井封闭火区内气体运移规律[J].辽宁工程技术大学学报,2004,23(3):296-298.
DENG Cunbao,WANG Jiren,HONG Lin.Gas transfer law in closed fire zone of a coal mine[J].Journal of Liaoning Technical University,2004,23(3):296-298.
[12] DUAN Yulong,WANG Shuo,WANG Wenhe,et al.Atmospheric disturbance on the gas explosion in closed fire zone[J].International Journal of Coal Science & Technology,2020,doi:10.1007/s40789-020-00295-3.
[13] 焦宇,段玉龙,周心权,等.煤矿火区密闭过程自燃诱发瓦斯爆炸的规律研究[J].煤炭学报,2012,37(5):850-856.
JIAO Yu,DUAN Yulong,ZHOU Xinquan,et al.The law of methane explosion induced by spontaneous combustion process in closed fire zone of coal mines[J].Journal of China Coal Society,2012,37(5):850-856.
[14] 赵洪宝,张欢,王宏冰,等.采空区瓦斯体积分数区域分布三维实测装置研制与应用[J].煤炭学报,2018,43(12):3411-3418.
ZHAO Hongbao,ZHANG Huan,WANG Hongbing,et al.Development and application of a three-dimensional measurement device for gas concentration[J].Journal of China Coal Society,2018,43(12):3411-3418.
[15] 彭斌.老空区与外界气体交换规律及瓦斯爆炸防控理论与应用[D].北京:中国矿业大学(北京),2019.
PENG Bin.Law of gas exchange between sealed goaf and outside space and application of gas explosion prevention theory[D].Beijing:China University of Mining and Technology (Beijing),2019.
[16] 何博文,高广伟,汪洪彬.用不同温度下的爆炸三角形判定火灾瓦斯的爆炸危险性[J].煤矿安全,1990(8):9-12.
HE Bowen,GAO Guangwei,WANG Hongbin.The explosion risk of fire gas is determined by explosion triangle at different temperature[J].Coal Mine Safety,1990(8):9-12.
[17] 张兴凯.地下工程火灾原理及应用[M].北京:首都经济贸易大学出版社,1997.
[18] 李诚玉.煤矿火区瓦斯爆炸危险性演化规律研究[D].阜新:辽宁工程技术大学,2015.
LI Chengyu.Research on evolution law of CH4 explosion hazard in fire area of coal mine[D].Fuxin:Liaoning Technical University,2015.
[19] 周西华,白刚,孙宝铁,等.煤矿水平巷道火区瓦斯爆炸易爆区域判定研究[J].中国安全科学学报,2015,25(9):78-84.
ZHOU Xihua,BAI Gang,SUN Baotie,et al.Research on judgement of gas easily explosive area in horizontal tunnel fire area of coal mine[J].China Safety Science Journal,2015,25(9):78-84.
