土工合成材料在加筋工程中的应变硬化与应变软化是土工合成材料常见力学特性，关于筋土界面相互作用的试验研究[1-2]中都强调了筋材的这一显著特性。史旦达等[3]对比单、双向土工格栅加筋工况，认为单向格栅加筋时的直剪和拉拔曲线表现为应变软化型，而双向格栅加筋的2种试验曲线一般表现为应变硬化型;而杨敏等[4]研究土工布与黄土界面摩擦作用时发现，直剪试验曲线表现为硬化型，拉拔曲线表现成软化型。
一般情况下，对筋土界面特性理论方面研究需考虑剪应力与位移之间的关系[5-7]，刘续等[8]和易富等[9]认为在拉拔位移较小的情况下剪应力和位移呈线性关系;GURUNG等[10]采用双曲线计算模型分析界面剪应力与位移的变化关系;ESTERHULZEN等[11]提出了峰值前和峰值后都采用双曲线表示的位移软化模型;林明飞等[12]将剪应力-位移曲线前后2部分均采用双曲线模型进行模拟;王军等[13]在试验基础上提出一种能够描述筋土界面力学性能的组合本构模型，该模型包含峰值及残余强度包络线、峰值前的双曲线模型、峰值后位移软化模型和界面剪胀模型;林伟岸等[14]将峰值前、峰值后塑性软化和塑性流动的剪应力与位移变化均采用直线模拟;而张鹏等[15]提出三阶段弹塑性剪应力-位移模型，峰值前采用双曲线模拟，峰值后的塑性软化和塑性流动阶段采用直线模拟。上述筋拉拔土界面模型虽能较好的模拟界面拉拔行为，但未能考虑筋材拉拔全过程不同阶段界面的的渐进破坏特性。
为了真实描述筋土界面拉拔过程中不同阶段的渐进破坏作用特性，国内外学者针对筋材应变软化特性提出了很多计算模型，如ZHU等[16]和CHEN等[17]通过三参数模型推导了筋土界面轴力和剪应力在不同拉拔阶段的解析表达式。在关于筋土界面特性的研究中，对于应变硬化特性只有较少计算模型，而且还未有同时包含筋材应变硬化和应变软化2种塑性变形特征的计算模型。
笔者在筋土拉拔界面理想弹塑性模型[18]基础上，针对加筋材料拉拔曲线的应变硬化和应变软化2种形式(以下简称应变硬化筋材和应变软化筋材)，提出应变硬化筋材在拉拔过程中经历3个连续阶段，应变软化筋材在拉拔过程中经历5个连续阶段，分别推导出2种类型筋材拉拔试验过程中不同拉拔阶段的拉力、剪应力和位移的分布规律，同时还分析了界面剪应力在不同拉拔阶段的演化规律，以期为实际加筋工程中筋材的选择与设计提供参考。
1 筋土界面基本方程
图1为筋材拉拔试验示意图，试验中，试验槽底部和侧向边界固定，在承压板上可以施加竖向上覆压力。筋材的长度和厚度分别为L，t，拉伸模量为E。
设筋材在x处的剪应力为τ，在其上取长度为dx的微单元体进行分析，宽度取筋材的单位宽度，忽略筋材的边界效应，则根据受力平衡可以得出
(T+dT)-T+2τ(dx+εdx)=0
(1)
式中，T为筋材在x处单位宽度拉力;εdx为微元体的单元变形长度;ε为应变。
根椐应变的定义，在x处筋材应变可写为
(2)
式中，u为x处筋材相对位移。
假定应变与单位宽度的拉力线性相关，即
ε=T/(Et)
(3)
由式(1)～(3)可以求出
(4)
一般在拉拔过程中的实际应变ε很小[19]，可忽略，故式(4)近似表示为
(5)
式(5)即为筋土界面基本方程，对研究筋土界面特性具有重要意义。
图1 筋材拉拔示意
Fig.1 Pull-out sketch of reinforcement
根据文献[20],界面剪应力峰值τp可由式(6)计算:
τp=σntan φ′gs=(qs+γh)tan φ′gs
(6)
式中，σn为法向应力,σn=qs+γh;qs为附加应力;γ为试验填料的容重;h为加筋以上填料的铺筑高度;φ′gs为界面综合摩擦角。
2 应变硬化筋材拉拔界面分析
2.1 硬化筋材模型
应变硬化筋材界面剪应力与位移试验曲线达到峰值前可近似表现为弹性关系，之后表现为应变硬化特征。将这种曲线形式简化为如图2所示的双线性线性剪应力-位移(τ-u)关系[21]。由图2可见，第1阶段(OA段)，以直线表示剪应力达到峰值前的剪应力与位移关系;第2阶段(AB段)，以直线表示筋材的应变硬化。图2中,Ks1和Ks2分别为OA段和AB段的斜率，也叫做界面剪切刚度，up为对应的拉拔位移，Ks1=τp/up。当筋材拉拔端剪应力增大到筋材极限剪应力τult时，筋材发生破坏，定义两者之间的比值为破坏比Rf[15]，即Rf=τp/τult，其值一般在0.5～1.0。
(7)
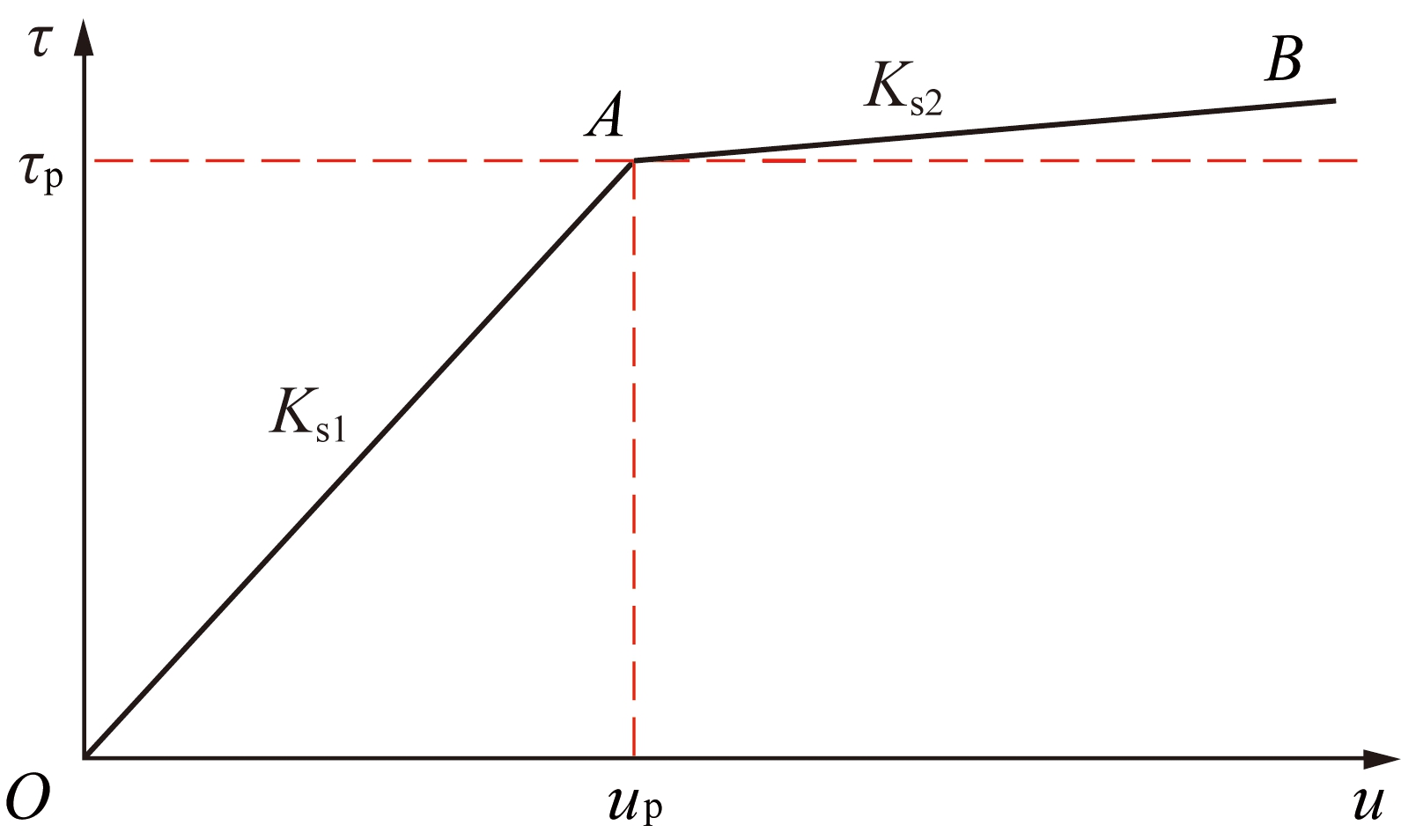
图2 双线性界面剪应力与位移(τ-u)关系
Fig.2 Relationship between interface shear stress and
displacement of bilinear (τ-u)
基本假定:根据上述应变硬化筋材理论模型的定义，认为拉拔荷载下筋土界面将经历弹性阶段、弹性-硬化过渡阶段、完全硬化阶段，分别对应图3中的Ⅰ,Ⅱ,Ⅲ阶段(Le，Lh分别为筋材拉拔过程中弹性区长度和硬化区长度)。通过理论计算可得到各个拉拔阶段拉力、剪应力和位移的计算表达式。
图3 拉拔模型分析中应变硬化筋材渐进拉拔过程
Fig.3 Progressive pull-out process of strain hardening
reinforcement in pull-out model analysis
2.2 硬化模型验证
为验证硬化模型的准确性与适用性，引入几种经典的筋土界面模型进行对比分析，包括理想弹塑性模型[18]、双曲线模型[10]。笔者选取文献[3]中法向应力为100 kPa、相对密度为70%条件下双向土工格栅与砂土的拉拔试验结果进行模拟验证，模拟参数见表1，模拟结果如图4所示。从图4可以看出，理想弹性模型和双曲线模型无法体现界面的硬化过程，而双线性剪应力-位移弹塑性硬化模型能够较好的反映界面硬化特性，而且计算更为简便，具有更好的适用性。硬化模型可适用于加筋土拉拔试验时试验曲线呈现应变硬化特征情况时，该模型能够合理的模拟硬化型筋材的拉拔行为，但图中阶段Ⅱ即弹性-硬化过渡阶段区间很小，这是由于该筋材弹性模量很大而加筋长度较小导致筋材的渐进性破坏不明显。双向土工格栅加筋土产生应变硬化现象的主要原因是由于双向格栅横肋的阻挡作用。
表1 拉拔试验的模拟参数[3]
Table 1 Simulation parameters of pull-out test[3]
σn/kPaL/mt/mmE/GPaKs1/(MPa·m-1)Ks2/(MPa·m-1)tan φ'gs1000.2254.230.470.56
图4 双向土工格栅拉拔试验结果[3]
Fig.4 Pull-out test results of bidirectional geogrids in
reference[3]
2.3 硬化拉拔界面全历程分析
2.3.1 弹性阶段(Ⅰ阶段)
当0≤u<up时，剪应力和位移呈弹性关系，二者关系满足关系式τ=Ks1u，联立式(5)和(7)可得到此阶段的控制方程
(8)
式中，
解式(8)可得
Te(x)=C1exp(-αx)+C2exp(αx)
(9)
式中，Te(x)为筋材在弹性阶段的拉力;C1,C2为积分常数。
拉拔试验中，拉拔端即x=0的拉力为T01，在自由端即x=L的拉力为0，则有边界条件
(10)
将边界条件式(10)代入式(9)可求得
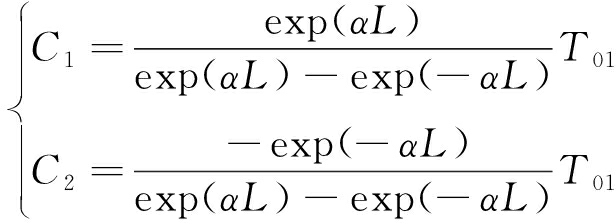
(11)
则可求得Ⅰ阶段的拉力表达式:
(12)
根据式(5)和(7)可得到Ⅰ阶段相应的剪应力τe(x)和位移ue(x)关系式
(13)
(14)
让x=0代入到式(14)中可得到拉拔端的位移(即拉拔位移ue0)的变换式为
(15)
当ue0=up时，τp=Ks1ue0，由式(15)可得弹性阶段与弹性-硬化过渡阶段的临界拉力
也就是在弹性阶段的最大拉力为
(16)
2.3.2 弹性-硬化过渡阶段(Ⅱ阶段)
随着拉力的不断增长，界面剪应力从拉拔端逐渐向尾部传递，直至达到峰值，然后拉拔端开始发生塑性特征，出现应变硬化现象，进入Ⅱ阶段。定义临界点P(x=Lh)划分弹性区和硬化区，当0≤x<Lh，界面处于Ⅱ阶段硬化区，而当Lh<x≤L，界面处于Ⅱ阶段弹性区(其中，Lh为硬化区的长度)。
(1)弹性区(Lh<x≤L)。Ⅱ阶段弹性区界面拉力、剪应力和位移的分布规律与完全弹性阶段相似，可得
(17)
(18)
(19)
式中，T02为过渡点P的拉拔力。
考虑到过渡点P的界面剪应力等于峰值剪应力，则可以得到
(20)
(2)硬化区(0≤x≤Lh)。Ⅱ阶段硬化区界面剪应力与剪切位移的关系由式(7)定义，联立式(5)和(7)可得
(21)
式中，
Th(x)=C3exp(-βx)+C4exp(βx)
(22)
式中，Th(x)为筋材在完全弹性阶段的拉力;C3,C4为积分常数。
考虑边界条件:
(23)
式中，T03为弹性硬化阶段的极限拉力。
将式(23)边界条件代入式(22)可求得
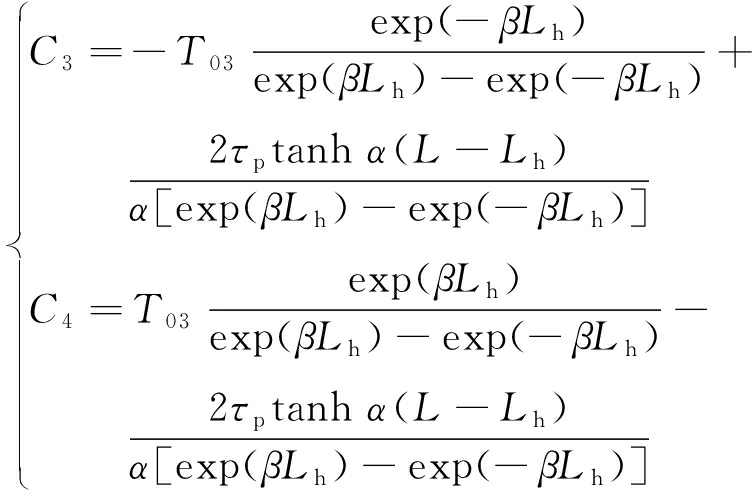
(24)
则可求得Ⅱ阶段拉力、剪应力和位移的表达式分别为
(25)
(26)
(27)
由于弹性区与硬化区的过渡点P剪应力连续，即τe(x=Lh)=τh(x=Lh)，则可以求得T03:
(28)
当Lh=L时，由式(28)可得弹性-硬化过渡阶段与完全硬化阶段的临界拉力
为
(29)
2.3.3 完全硬化阶段(Ⅲ阶段)
类似于Ⅱ阶段硬化区的分析，式(22)仍然适用于完全硬化阶段，边界条件为
(30)
式中，T04为完全硬化阶段的极限拉力。
Ⅱ阶段的拉力、剪应力和位移表达式为
(31)
(32)
(33)
将x=0代入式(33)中得到此阶段拉拔位移uh0的变换式为
(34)
式中，uh0为完全硬化阶段x=0时筋材的拉拔位移。
在完全硬化阶段，界面拉拔端拉拔力和剪应力均增大，当筋材拉拔端处的剪应力增大到筋材的极限应力τult时，筋材发生破坏，则τult=Ks2(uh0-up)+τp，结合Rf=τp/τult，所以式(34)可写成
(35)
综上，应变硬化筋材拉拔试验过程中的3个阶段均得到了封闭解，每2个阶段间临界拉力的结果见表2。
2.4 界面剪应力分布规律
为直观反映应变硬化筋材拉拔试验过程中界面不同拉拔阶段的受力演化规律，对3个阶段界面剪应力分布进行分析。所选取的模型参数见表1。为简化分析，对模型参数进行归一化处理，归一化筋材位置为X=x/L，归一化界面剪应力为ρ=τ/τp。
表2 硬化拉拔模型2个阶段间的临界拉力
Table 2 Critical tensile force between two stages of
hardening pull-out model
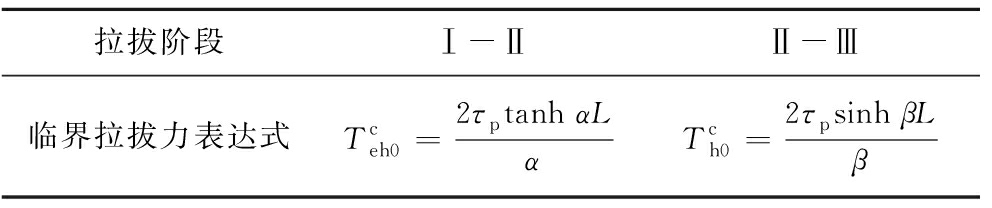
拉拔阶段Ⅰ-ⅡⅡ-Ⅲ临界拉拔力表达式Tceh0=2τptanh αLαTch0=2τpsinh βLβ
计算得到
根据所给出的模型参数，代入以下各式:
2.4.1 弹性阶段
代入式(13)得到:
代入式(16)求得完全弹性与弹性-硬化过渡段的临界拉力
2.4.2 弹性-硬化过渡阶段
(1)弹性区(0.5≤X≤1.0)。令Lh=L/2代入式(18)得:
(2)硬化区(0≤X≤0.5)。将Lh=L/2代入式(26)得到
由式(29)可求得弹性-硬化过渡与完全硬化阶段的临界拉力
2.4.3 完全硬化阶段
代入式(32)得到
代入式(35)求得完全硬化阶段的极限拉力
根据上述界面剪应力计算表达式，可得应变硬化筋材拉拔过程中弹性、弹性-硬化过渡和完全硬化3个阶段的界面剪应力演化规律，如图5所示。由图5可知:当T≤22.15 kN/m时，界面处于弹性阶段，剪应力从拉拔端到自由端呈非线性减小，当T=22.15 kN/m时，界面处于弹性与弹性-硬化过渡的临界阶段，拉拔端达到剪应力峰值56 kPa;当22.15 kN/m≤T≤22.41 kN/m时，界面处于弹性-硬化过渡阶段，此阶段拉拔端剪应力达到峰值后带动自由端继续增大，剪应力从拉拔端到自由端整体呈减小趋势，当T=22.41 kN/m时，即自由端也达到峰值后，界面将进入完全硬化阶段;当22.41 kN/m≤T≤27.96 kN/m时，界面处于完全硬化阶段，此阶段拉拔端剪应力继续增大，直至T=27.96 kN/m时，拉拔端剪应力达到筋材极限应力，筋材发生破坏。
图5 拉拔过程各阶段剪应力演化规律(硬化筋材)
Fig.5 Evolution of shear stress in different stages of pull-out
process (hardened reinforcement)
3 应变软化筋材拉拔界面分析
3.1 软化筋材模型
应变软化筋材界面剪应力与位移试验曲线达到峰值前可近似表现为弹性关系，之后表现为塑性软化和塑性流动。本文将这种曲线特征简化为如图6所示的三线性剪应力-位移关系(τ-u)。由图6可知，第1阶段(OA段)，以直线表示剪应力达到峰值前剪应力与位移关系;第2阶段(AB段)，以直线表示筋材的应变软化;第3阶段(BC段)，以水平直线表示筋材的塑性流动。图6中,ks1为OA段斜率，ks1=τp/up;ks2为AB段斜率，τr为界面残余剪应力，ur为对应位移，ks2=(τr-τp)/(ur-up)<0;类比破坏比的定义，将两者之间的比值定义为R′f，即R′f=τr/τp。
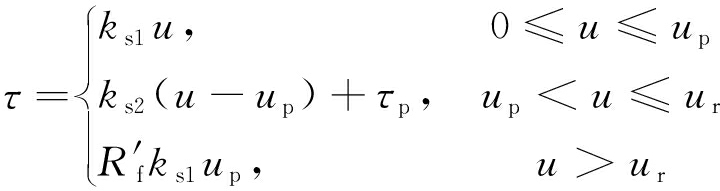
(36)
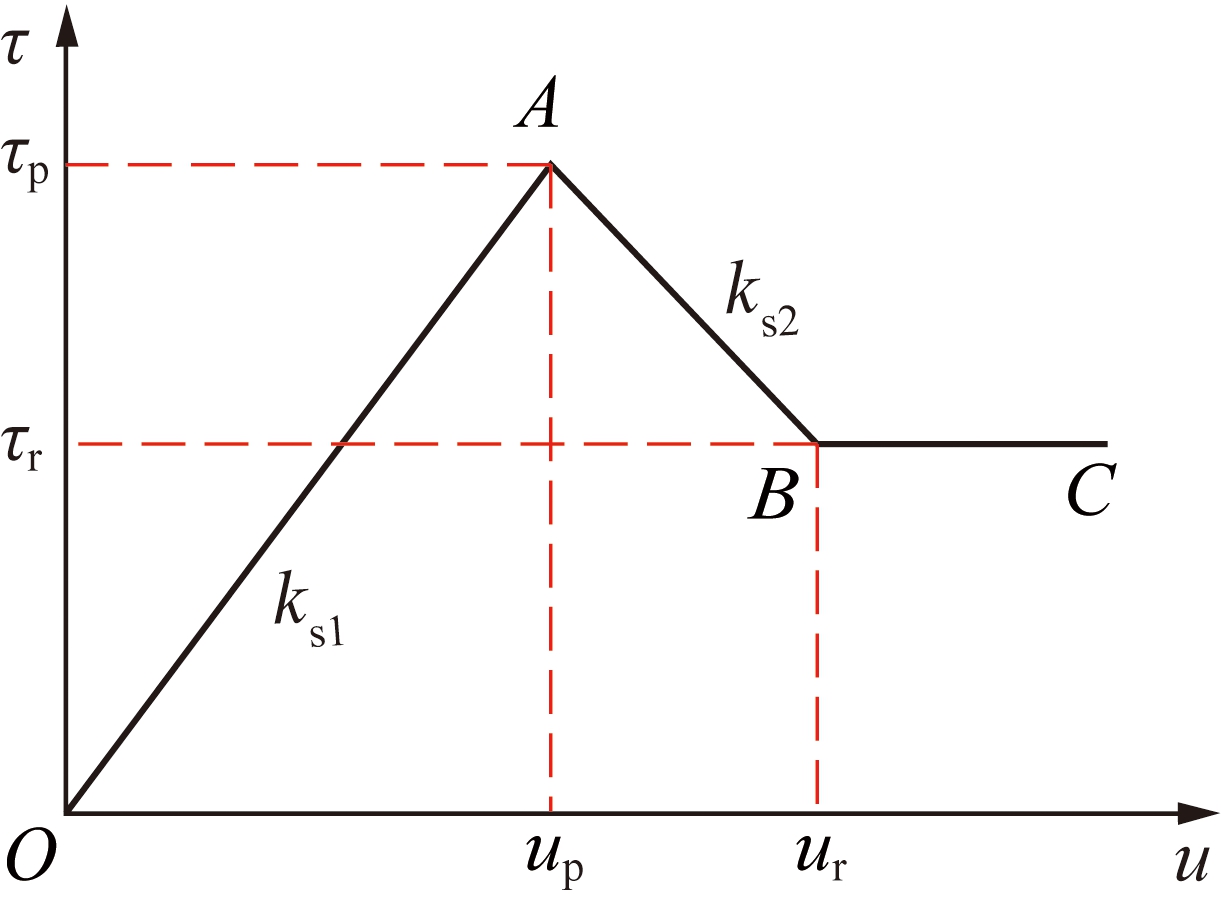
图6 三线性界面剪应力与位移(τ-u)关系
Fig.6 Relationship between interface shear stress
and displacement of trilinear (τ-u)
基本假定:将应变软化筋材筋土拉拔过程划分为弹性、弹性-软化过渡、完全软化、软化-残余过渡和完全残余5个阶段[16]，分别对应图7(a)～(e)(Ls为筋材拉拔过程中软化区的长度)。通过理论计算可得到各个拉拔阶段的界面拉力、剪应力和位移计算表达式。
3.2 软化模型验证
笔者选取文献[3]中法向应力100 kPa压实度为0.85条件下单向土工格栅与黏性土的拉拔试验结果进行模拟，模拟参数见表3。为验证软化模型的准确性与适用性，引入理想弹塑性模型[18]和弹性-指数软化模型[19]2种经典筋土界面模型进行对比分析，模拟结果如图8所示。从图8可以看出，理想弹性模型在无法体现界面的软化过程，而弹性-指数软化模型和三线性剪应力-位移弹塑性软化模型能够较好的反映界面软化特性，但三线性软化模型更为计算简便，表达式简洁，具有更好的适用性。在加筋土拉拔试验时试验曲线出现应变软化特征时可适用于此软化模型，该模型能够合理的模拟应变软化筋材界面的拉拔特性，而且图8中阶段Ⅱ和Ⅳ两个过渡阶段区间不明显。单向格栅加筋土产生应变软化现象是因为在加筋过程中当拉拔力随着拉拔位移的增大达到峰值时，筋材整体出现滑动而发生应变软化特征。
图7 拉拔模型分析中应变软化筋材渐进拉拔过程
Fig.7 Progressive pull-out process of strain softening
reinforcement in pull-out model analysis
表3 拉拔试验的模拟参数[3]
Table 3 Simulation parameters of pull-out test in reference[3]
σn/kPaL/mt/mmE/GPaks1/(MPa·m-1)ks2/(MPa·m-1)tan φgsR'f1000.220.41.73-0.520.210.64
图8 单向土工格栅拉拔试验结果[3]
Fig.8 Pull-out test results of unidirectional geogrids[3]
3.3 软化拉拔界面全历程分析
3.3.1 弹性阶段(Ⅰ阶段)
与上述应变硬化型筋材在弹性阶段的分布规律相同，联立式(5)和(36)可得到此阶段的拉力、剪应力和位移关系表达式为
(37)
(38)
(39)
将x=0代入式(39)中可得拉拔位移ue0的变换式
(40)
当ue0=up时，τp=ks1ue0，由式(40)可得弹性阶段与弹性-硬化过渡阶段的临界拉力也就是在弹性阶段的最大拉力
(41)
3.3.2 弹性-软化过渡阶段(Ⅱ阶段)
界面剪应力逐渐增大并从拉拔端向尾部传递，直至拉拔端剪应力达到峰值，开始发生应变软化现象，进入Ⅱ阶段。定义临界点Q1(x=Ls)划分弹性区和软化区，当0≤x<Ls，界面处于Ⅱ阶段软化区，而当0≤x<Ls，界面处于Ⅱ阶段弹性区(其中，Ls为软化区的长度)。
(1)弹性区(Ls≤x≤L)。Ⅱ阶段弹性区界面拉力、剪应力和位移的分布规律与完全弹性阶段相似，则可以得到
(42)
(43)
(44)
考虑到过渡点Q1的界面剪应力等于峰值剪应力，则可以得到
(45)
(2)软化区(0≤x≤Ls)。软化区界面剪应力与剪切位移的关系由式(36)定义，联立式(45)和式(36)可得
(46)
式中，
解式(46)可得
Ts(x)=C′3cos βx+C′4sin βx
(47)
式中，Ts(x)为筋材在完全弹性阶段的拉力;C′3,C′4为积分常数。
考虑边界条件:
(48)
将式(48)边界条件代入到式(47)可得
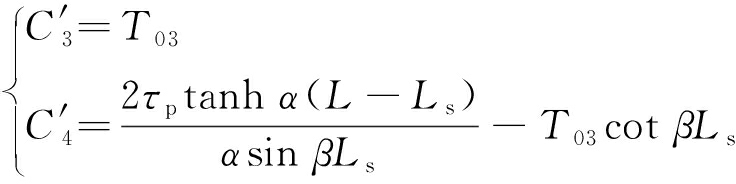
(49)
由于弹性区与软化区的过渡点Q1的剪应力连续，即τe(x=Ls)=τs(x=Ls)，则可以求得T03:
(50)
则可求得Ⅱ阶段软化区拉力、剪应力和位移的表达式:
(51)
(52)
(53)
当Ls=L时，由式(50)可得弹性-软化过渡阶段与完全软化阶段的临界拉拔力
(54)
3.3.3 完全软化阶段(Ⅲ阶段)
类似与Ⅱ阶段软化区的分析，式(47)仍然适用于完全软化阶段，边界条件为
(55)
则完全软化阶段的解为
Ts(x)=T04(cos βx-cot βLsin βx)
(56)
(57)
(58)
将x=0代入式(58)可得此阶段拉拔位移us0的变换式:
(59)
在完全软化阶段，界面拉力和剪应力均减小，当us0=ur时，τr=ks2(us0-up)+τp，由式(59)可得弹性-软化过渡阶段与完全软化阶段的临界拉拔力
也就是完全软化阶段的最小拉拔力为
(60)
3.3.4 软化-残余过渡阶段(Ⅳ阶段)
当拉拔力减小到筋材拉拔端开始进入残余状态并逐渐向筋材尾部延伸，进入Ⅳ阶段。定义过渡点Q2(x=Lr)划分软化区和残余区，当0≤x<Lr，界面处于Ⅱ阶段残余区，而当Lr<x≤L，界面处于Ⅱ阶段软化区(其中，Lr为残余区长度)。
(1)软化区(Ls≤x≤L)。在完全软化阶段得到拉力、剪应力和位移的分布规律与软化-残余过渡阶段相似，根据式(56)～(59)可以得到Ⅳ阶段弹性区的拉力、剪应力和位移的关系式为
Ts(x)=T05[cos β(x-Lr)-cot β(L-Lr)×
sin β(x-Lr)]
(61)
cos β(x-Lr)]
(62)
(63)
由于过渡点Q2处的界面剪应力等于残余剪应力τs(x=Lr)=τr，则根据式(61)可以得到
(64)
(2)残余区(0≤x≤Lr)。残余区界面剪应力与残余抗剪强度相等，由式(5)和(36)可得
(65)
考虑边界条件:
(66)
式中，Tr(x)为筋材在完全残余阶段的拉力。
则可得
(67)
(68)
(69)
(70)
将x=0,Lr=L代入式(67)得到软化-残余过渡阶段与完全残余阶段的临界拉力
(71)
3.3.5 完全残余阶段(Ⅴ阶段)
将x=0,Lr=L代入式(69)得到筋材拉拔端的临界剪切位移:
(72)
假定筋材在拉拔端的位移为u′0，则剪切位移的分布可导出为
(73)
此阶段拉力
和界面剪应力τr保持常数。因此，拉力在筋材不同位置的分布为
Tr(x)=2τr(L-x)
(74)
综上，应变软化筋材拉拔试验过程中的5个阶段均得到了封闭解，每2个阶段间临界拉力的结果见表4。
3.4 界面剪应力分布规律
为直观反映应变软化筋材筋土界面不同拉拔阶段的受力演化规律，对5个阶段界面剪应力的分布进行分析，所选的模型参数见表3。
计算得到
根据所给出的模型参数，代入以下各式。
表4 软化拉拔模型两个阶段间临界拉力
Table 4 Critical tensile force between two stages of
softening pull-out model
拉拔阶段临界拉拔力表达式Ⅰ-ⅡTces0=2τptanh αLαⅡ-ⅢTcs0=2τpsin βLβⅢ-ⅣTcsr0=2τrtan βLβⅣ-ⅤTcs0=2τrL
(1)弹性阶段。
代入式(38)得到:代入式(41)求得完全弹性阶段与弹性-软化过渡阶段的临界拉力
(2)弹性-软化过渡阶段。
① 弹性区(0.5≤X≤1)。令Ls=L/2代入式(45)得到
② 软化区(0≤X≤0.5)。将Ls=L/2代入式(52)得到
由式(54)可求得弹性-软化过渡阶段与完全软化阶段的临界拉力
(3)完全软化阶段。
代入式(57)得到ρ=R′f(tan βLsin βLX+cos βLX)，代入式(60)求得完全软化阶段与软化-残余阶段的临界拉力
(4)软化-残余过渡阶段。
① 软化区(0.5≤X≤1)。令Lr=L/2代入式(62)得到ρ=R′f[tan(βL/2)sin βL(X-0.5)+cos βL(X-0.5)];
② 残余区(0≤X≤0.5)。进入残余区的界面剪应力ρ=R′f=0.64。由式(71)可求得软化-残余过渡阶段与完全残余阶段的临界拉力
(5)完全残余阶段。
完全残余阶段界面剪应力ρ=R′f=0.64。根据上述界面剪应力计算表达式，可得土工合成材料拉拔过程中弹性阶段、弹性-软化过渡阶段、完全软化阶段、软化-残余过渡阶段和完全残余阶段的界面剪应力演化规律，如图9所示。
图9 拉拔过程各阶段剪应力演化规律(软化筋材)
Fig.9 Evolution of shear stress in different stages of pull-out process soil (softened reinforcement)
由图9可知,当T≤7.95 kN/m时，界面处于弹性阶段，剪应力从拉拔端到自由端呈非线性减小，当T=7.95 kN/m时，界面处于弹性与弹性-软化过渡的临界阶段，拉拔端达到剪应力峰值21 kPa;当7.95 kN/m≤T≤8.33 kN/m时，界面处于弹性-软化过渡阶段，剪应力整体呈先增大后减小变化趋势，峰值点位于弹性区与软化区交界;随着拉力增大，软化区长度也不断增大，自由端剪应力逐渐向峰值靠近，当T≤8.33 kN/m时，自由端也达到峰值后，界面将进入完全软化阶段;当5.47 kN/m≤T≤8.33 kN/m时，界面处于完全软化阶段，剪应力从拉拔端到自由端呈非线性增大，当T≤5.47 kN/m时，拉拔端剪应力达到残余应力，界面将进入软化-残余过渡阶段。当5.38 kN/m≤T≤5.47 kN/m时，界面处于软化-残余过渡阶段阶段，此阶段拉拔端开始进入残余状态并逐渐向自由端过渡;当T≤5.38 kN/m时，即自由端也达到残余应力后，界面将进入完全残余阶段，此阶段剪应力保持残余应力不变。
4 结 论
(1)针对土工合成材料拉拔时出现的应变硬化和应变软化现象，提出了双线性剪应力-位移弹塑性硬化模型和三线性剪应力-位移弹塑性软化模型，将应变硬化筋材的筋土拉拔过程分为弹性阶段、弹性-硬化过渡阶段和完全硬化阶段，将应变软化筋材的筋土拉拔过程分为弹性阶段、弹性-软化过渡阶段、完全软化阶段、软化-残余过渡阶段和完全残余阶段。
(2)通过界面基本控制方程，分别推导了拉拔荷载下应变硬化和应变软化2种塑性变形特征筋材不同阶段界面拉力、剪应力和位移的解析解;同时分析了界面剪应力在不同拉拔阶段的演化规律，反映了筋土界面的渐进性破坏。
(3)2组模型预测结果与拉拔试验数据基本吻合，验证了所提出2种弹塑性模型对筋材在拉拔界面中渐进破坏分析的有效性;在筋材的拉拔过程中，一般过渡阶段不明显。
[1] 施建勇,钱学德,朱月兵.垃圾填埋场土工合成材料的界面特性试验方法研究[J].岩土工程学报,2010,32(5):699-692.
SHI Jianyong,QIAN Xuede,ZHU Yuebing.Experimental methods for interface behaviors of geosynthetics in landfills[J].Chinese Journal of Geotechnical Engineering,2010,32(5):699-692.
[2] 林伟岸,张宏伟,詹良通,等.土工膜/土工织物界面大型斜坡模型试验研究[J].岩土工程学报,2012,34(10):1590-1596.
LIN Weian,ZHANG Hongwei,ZHAN Liangtong,et al.Large-scale ramp model tests on geomembrane/geotextile interface[J].Chinese Journal of Geotechnical Engineering,2012,34(10):1590-1596.
[3] 史旦达,刘文白,水伟厚.单双向塑料土工格栅与不同填料界面作用特性对比试验研[J].岩土力学,2009,30(8):2237-2244.
SHI Danda,LIU Wenbai,SHUI Weihou.Comparative experimental studies of interface characteristics between uniaxial/biaxial plastic geogrids and different soils[J].Rock and Soil Mechanics,2009,30(8):2237-2244.
[4] 杨敏,李宁,刘新星,等.土工布加筋土界面摩擦特性试验研究[J].西安理工大学报,2016,32(1):46-51.
YANG Min,LI Ning,LIU Xinxing,et al.Experimental research on interface frictional behaviors of the geotextile-reinforced soil[J].Journal of Xi’an University of Technology,2016,32(1):46-51.
[5] SAWICKI A.Modelling of geosynthetic reinforcement in soil retaining walls[J].Geosynthetics International,1998,5(3):327-345.
[6] 陈榕,栾茂田,赵维,等.土工格栅拉拔试验及筋材摩擦受力特性研究[J].岩土力学,2009,30(4):960-964.
CHEN Rong,LUAN Maotian,ZHAO Wei,et al.Research on pull-out test and frictional resistance characteristic of geogrids[J].Rock and Soil Mechanics,2009,30(4):960-964.
[7] LIU H Y,HAN H Y,AN H M,et al.Hybrid finite-discrete element modelling of asperity degradation and gouge grinding during direct shearing of rough rock joints[J].International Journal of Coal Science & Technology,2016,3(3):295-310.
[8] 刘续,唐晓武,申昊,等.加筋土结构中筋材拉拔力的分布规律研究[J].岩土工程学报,2013,35(4):800-804.
LIU Xu,TANG Xiaowu,SHEN Hao,et al.Stress distribution of reinforcement of reinforced soil structures under drawing force[J].Chinese Journal of Geotechnical Engineering,2013,35(4):800-804.
[9] 易富,张旖旎,王世杰,等.土工格栅与尾矿拉拔试验及筋材拉力研究[J].硅酸盐通报,2018,37(6):1836-1840,1851.
YI Fu,ZHANG Yini,WANG Shijie.Research on pull-out test and tensile of geogrids and tailings[J].Bulletin of the Chinese Ceramic Society,2018,37(6):1836-1840,1851.
[10] GURUNG N,IWAO Y,MADHAV M R.Pullout test model for extensible reinforcement[J].International Journal for Numerical and Analytical Methods in Geomechanics,1999,23(12):1337-1348.
[11] ESTERHUIZEN J B,FLIZ G M,DUNCAN J M.Constitutive behavior of geosynthetic interface[J].Journal of Geotechnical and Geoenvironmental Engineering,2001,127(10):834-840.
[12] 李明飞,郑效峰,那达慕,等.土工合成材料界面应变软化特性的一种本构新模型[J].沈阳工业大学学报,2015,37(1):97-101.
LI Mingfei,ZHENG Xiaofeng,NA Damu.A new constitutive model for strain softening behavior in geosynthetic interface[J].Journal of Shenyang University of Technology,2015,37(1):97-101.
[13] 王军,林旭,符洪涛.砂土-格栅筋土界面特性的本构模型研究[J].岩土力学,2014,35(S2):75-84.
WANG Jun,LIN Xu,FU Hongtao.Study of constitutive model of sand-geogrid interface behavior in geogrid/geotextile reinforced soil[J].Rock and Soil Mechanics,2014,35(S2):75-84.
[14] 林伟岸,朱斌,陈云敏,等.考虑界面软化特性的垃圾填埋场斜坡上土工膜内力分析[J].岩土力学,2008,29(8):2063-2069.
LIN Weian,ZHU Bin,CHEN Yunmin,et al.Tension analysis of geomembrane in landfill slope considering interface strain-softening[J].Rock and Soil Mechanics,2008,29(8):2063-2069.
[15] 张鹏,王建华,陈锦剑.土工织物拉拔试验中筋土界面力学特性[J].上海交通大学学报,2004,38(6):999-1002.
ZHANG Peng,WANG Jianhua,CHEN Jinjian.MechanicaI behavior of the interface between reinforcement and soil in pull-out tests on geotextiles[J].Journal of Shanghai Jiaotong University,2004,38(6):999-1002.
[16] ZHU H H,ZHANG C C,TANG C S,et al.Modeling the pullout behavior of short fiber in reinforced soil[J].Geotextiles and Geomembranes,2014,42(4):329-338.
[17] CHEN J H,SAYDAM S,HAGAN P C.An analytical model of the load transfer behavior of fully grouted cable bolts[J].Construction and Building Materials,2015,101(1):1006-1015.
[18] HONG C Y,YIN J H,ZHOU W H,et al.Analytical study on progressive pullout behavior of a soil nail[J].Journal of Geotechnical and Geoenvironmental Engineering,2012,138(4):500-507.
[19] 赖丰文,李丽萍,陈福全.土工格栅筋土拉拔界面的弹性-指数软化模型与性状[J].工程地质学报,2018,26(4):852-860.
LAI Fengwen,LI Liping,CHEN Fuquan.Elastic-exponential softening model for behavior of interface between geogrid reinforcement and soil against pullout[J].Journal of Engineering Geology,2018,26(4):852-860.
[20] SOBHI S,WU J T H.Interface pullout formula for extensible sheet reinforcement[J].Geosynthetics International,1996,11(5):565-581.
[21] MADHAV M R,GURUNG N,IWAO Y.A theoretical model for pull-out response of extensible reinforcements[J].Geosynthetics International,1998,5(4):399-424.
