在岩石力学与工程地质领域，岩体通常被认为具有结构特征。节理作为构成岩体结构重要的两个因素(节理与岩石整块)之一，其存在使得岩体结构存在裂隙、薄弱层、以及断面之间的相互咬合，这些不均匀性影响着岩体力学的性质[1-5]。节理的存在往往会削弱岩体的强度以及稳定性，对工程安全有重要影响，控制着岩石工程中岩体结构的变形及稳定。节理的粗糙度对节理剪切与闭合性质有重要影响。合理的节理粗糙度指标能够全面反映节理形貌几何特点(起伏特点、粗糙光滑度、节理走向)，并且是基于节理三维形貌特点的三维粗糙度指标，同时能从物理意义上与节理抗剪强度联系起来。若能确定符合上述条件的节理粗糙度指标然后结合节理其他物理力学参数来确定出节理峰值抗剪强度模型，那么节理峰值抗剪强度预测的问题就能迎刃而解。
目前描述岩石表面形貌特征的二维剖面线方法主要可分为统计参数描述、分形描述、JRC曲线描述[6]。统计参数将节理形貌线离散为点，将点的高度或形成的曲线作为研究对象，研究其高度分布以及函数的特征参数，常见的统计参数有表面形貌一阶导数的均方根Z2，轮廓粗糙度指标Ra[7]，线伸长率δL[8]，形貌线极限坡度λ[9]，形貌线坡度均方根指数Rq[10]等。分形维数测定方法是基于节理形貌自相似的性质，基于数学分形维数来分析节理粗糙度，常用的方法有方盒计数法、功率谱法、尺码法、结构函数法等[11-16]。BARTON等[9]提出了10条标准JRC曲线，这10条标准曲线与岩石节理剪切强度建立了很好的联系。在所研究节理上可用表面形态测量仪器测量并绘制出至少3条相应方向的节理轮廓线，然后通过视觉对比的方法确定出JRC值[17]。另外一些学者建立了JRC数值与节理轮廓线统计参数、分形维数及其他定义的粗糙度指标之间的关系[18-20]，这些方法均可客观定量描述节理粗糙度。二维粗糙度指标由于信息量的限制导致描述的结果与节理实际形貌有一定的偏差和局限，不能完全表示岩石节理形貌的粗糙程度。基于节理形貌三维特征BELEM等[21-22]定义了节理剪切倾角平均值θs、表面粗糙度系数Rs、各向异性度Ka、节理弯曲度Ts、平均正向坡度参数θp+与平均负向坡度参数θp-来描述节理三维粗糙度;唐志成等[23]在二维坡度均方根基础上提出了三维坡度均方根。TANG等[24]基于光照部分所占整个节理形貌面积的比值提出了三维粗糙度指标BAP。CHEN等[25]基于多重分维思想来描述节理形貌粗糙度。GRASSELLI等[26-27]基于等效倾角的分布规律提出了三维粗糙度指标。孙辅庭等[28-29]在Grasselli有效剪切倾角的基础上提出了具有分维性质的粗糙度指标。班力壬等[30]探讨了不同几何参数的微凸体对剪切强度的影响，提出了一个三维粗糙度系统。
研究结果表明，节理在压剪作用下，仅仅是一小部分较陡微凸体发生接触而相互作用[31]。以往在描述粗糙度时是考虑整个形貌面微凸体的分布特点，这使得所得粗糙度指标弱化了较陡微凸体作用而强化了较平缓微凸体对剪切强度的作用(实际上大多平缓微凸体在剪切过程中未接触)[31]。因此合理的粗糙度描述方法应基于实际接触微凸体分布特点来进一步探求。笔者基于实际接触节理的微凸体分布特点，将实际接触节理微凸体的等效视倾角的平均值作为节理粗糙度。对自然节理面进行了新的粗糙度描述，与节理峰值剪胀角对比表明该粗糙度描述方法可以较好的与节理剪切强度联系起来。
1 较陡视倾角的作用
节理面的真实形貌可用三角形网格微元近似表示，三角形微元通过节理面测量的数据点生成。通过统计数据发现[26-27]：
(1)
式中,θ*为节理微凸体有效倾角;Aθ*为有效倾角大于θ*的微元面积总和与节理面面积总和比;A0为所有节理微元等效倾角大于0时的面积总和与节理表面面积总和之比;
为沿剪切方向节理微元有效倾角最大值;C为公式拟合系数，描述角度分布情况。
将面积比Aθ*/A0视为θ*的函数来研究该函数f(θ*)的性质,则有
(2)
则视倾角在(θ*，θ*+dθ*)之间的微凸体面积比含量xθ*为
xθ*=f(θ*)-f(θ*+dθ*)=-[df(θ*)]
(3)
则
(4)
当θ*取值较大和较小时，θ*变化范围分别为
(5)
式中，
与
分别为θ*取值较大和较小的倾角。
基于式(4)，则有
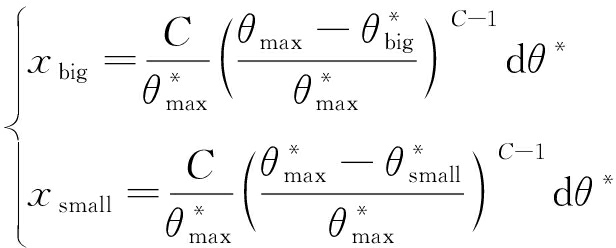
(6)
当C>1时,则有
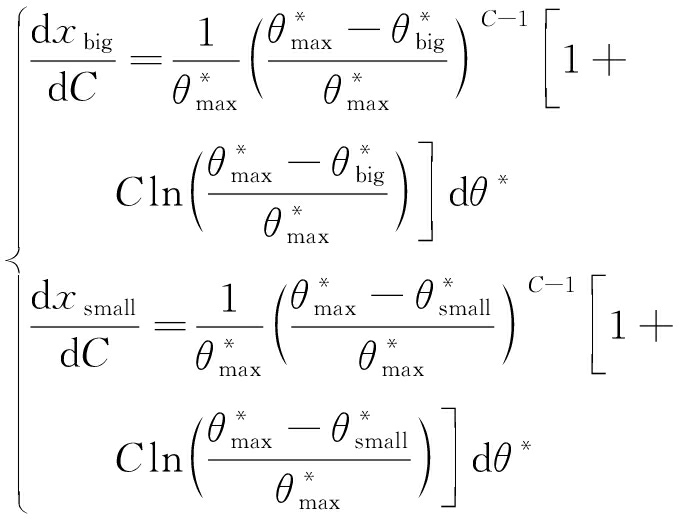
(7)
令式(7)=0，解得的C分别为Cbig,Csmall，则
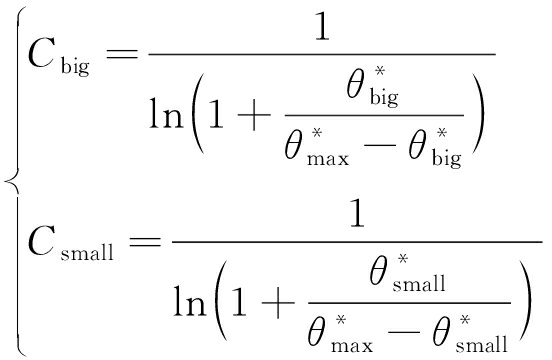
(8)
Cbig≈0，实际中C>Cbig，Cbig<0，为单调减函数;Csmall≈∞，实际中C<Csmall，Csmall>0，为单调增函数。随着C值的增大，节理中较陡视倾角的面积比含量降低。TATONE[32]定义粗糙度指标为
随着C值的增大，节理粗糙度降低。基于以上分析可知，C值是通过反映节理面中较陡视倾角的比例，从而间接影响节理面的粗糙度。当节理为随机粗糙节理时，在剪切过程中仅仅是节理上的一小部分较陡视倾角发生了接触，所以在分析节理抗剪强度时应该重点考虑接触微凸体之间的相互作用。
2 实际接触面积
TERZAGHI[33]最早进行了关于摩擦理论与接触理论的研究，研究发现真实的接触面积等于法向应力与节理面壁强度的比值。随后BOWDEN 和 TABOR等[33]研究发现上述结论适用于大部分材料的摩擦行为。接触理论中认为在微观层次中，所有的接触面都是粗糙的表面，即使接触面表观很光滑。并且接触的部位仅仅在与剪切方向相反的较陡的一小部分微凸体表面上。在接触部位，由于法向应力比较集中，少数接触的微凸体应力水平较大以至于达到材料的屈服极限。该屈服是针对微凸体尺度上的屈服，并不是整个接触面的屈服。
GREENWOOD和WILLIAMSON(GW)模型[34]，如图1所示。
图1 GW模型
Fig.1 GW model
图1中假设相邻微凸体变形独立，其位置分布可用微凸体顶点高度z的函数φ(z)来描述微凸体高度概率密度。自然形成的粗糙表面微凸体顶峰高度分布为
(9)
式中,m为粗糙度，数值为微凸体顶点高度的均方根。
模型中施加荷载的过程可等效为刚性平面下移的过程。微凸体接触深度为d=h-h0，h为微凸体顶点至节理平均高度线的距离，h0为刚性平面至节理平均高度线的距离。图1中h箭头上的半圆图形实际情况下为变形的微凸体。为表示初始顶点与刚性面之间的位置关系，本文未表示接触之后变形情况。接触微凸体与刚性平面接触半径
则单个微凸体的接触面积ΔA为
ΔA=πa2=πdR=π(z-h0)R
(10)
单个微凸体的作用力ΔF为
(11)
式中，E*为等效弹性模量；R为微凸体曲率半径。
若微凸体总数为N0，分别对式(9)～(11)进行积分，可以得到实际接触面积Ac和法向力F分别为
Ac=
N0φ(z)πR(z-h0)dz
(12)
(13)
则实际接触面积与压力的比值为
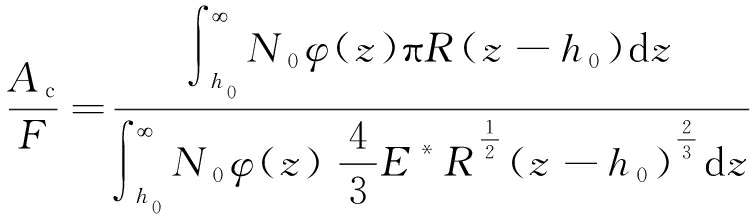
(14)
对式(14)无量纲化，则ζ=z/m并且ζ0=h0/m，则有
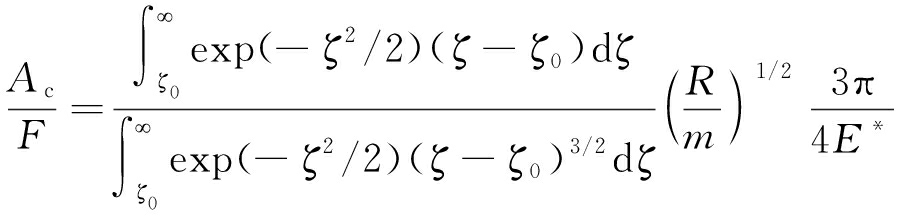
(15)
在典型的平均应力范围内ζ0的取值为2.5～3.5[35]，在这个范围内，假设变量S为
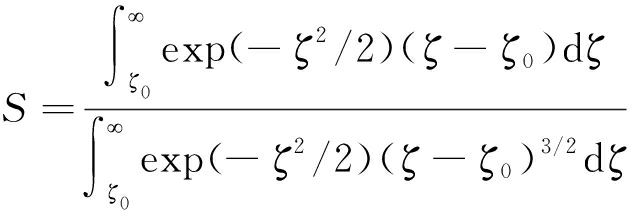
计算可知S在1.4左右少量变化，则可近似为
(16)
由式(16)可知随着法向应力的增大，所接触的微凸体数目逐渐增多，接触面积也逐步加大。法向应力与接触面积的比例关系与节理上微凸体分布情况有关。
GREENWOOD与TRIPP[36]继续对模型进行了改进，改进模型适用于两个粗糙表面接触的问题，也得到了相同的结论。对于完全耦合的并且没有填充物的节理，当承受法向荷载时，节理少部分接触微凸体会发生弹性变形，在最初接触的微凸体部分会发生屈服。随着法向应力继续增加，会有更多的微凸体相互接触并发生屈服，这一过程会连续发生直至相互接触的微凸体面积足够大能够承受给定法向荷载的作用。因此，可以假设所有接触微凸体中的最小倾角为在一定荷载作用下刚好屈服的微凸体的倾角。基于GREENWOOD与TRIPP的研究成果，SWAN对节理性质进行了研究[37]，研究发现对于压剪作用下的岩石节理，接触的微凸体应力水平较高以至于微凸体发生屈服或破坏。因此对于岩石节理在法向应力下的剪切问题，实际接触面积Ac也可以近似认为是作用在节理面上法向荷载N除以岩石的单轴抗压强度σc。
(17)
式中,A为节理面名义面积;σn为法向应力。
3 考虑真实接触微凸体的粗糙度指标
GRASSELLI 等[26-27]在岩石节理直剪试验中发现:① 剪切接触面积与剪切方向密切相关，只有面向剪切方向的接触部分才能够对剪切提供抵抗力，背向剪切方向的区域都发生分离。② 剪切时的压剪破坏都集中在面向剪切方向的陡倾角区域。③ 施加剪切荷载时，剪切应力在粗糙节理表面的重新分布首先从节理面面向剪切方向最陡的部分开始。在剪切过程中仅仅是节理上的一小部分较陡微凸体发生了接触，所以在分析节理抗剪强度时应该重点考虑接触微凸体之间的相互作用[28]。因此具有明确物理意义同时可以与节理抗剪强度联系起来的节理粗糙度指标应该是考虑实际接触微凸体的分布特点得到的。
GRASSELLI[26-27]研究发现
能够表征节理粗糙度。TATONE等[32]认为在C=0时没有数学意义，提出了粗糙度指标
目前
已经成为国际上公认的粗糙度指标。唐志成等[38]对TATONE提出的粗糙度指标采用平均有效视倾角θavg进行了物理意义上的解释,即
(18)
然而θavg是节理形貌所有有效倾角的平均值，并不是接触部分节理微凸体有效倾角的平均值。为了考虑剪切过程中实际接触部分节理微凸体的作用，设在某一应力水平下接触时最小的视倾角为
则接触部分微凸体等效倾角平均值为
范围内的视倾角的平均值。基于式(4)则实际接触节理微凸体等效倾角平均值为
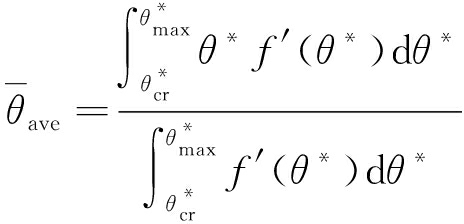
(19)
其中,f′(θ*)为视倾角在(θ*，θ*+dθ*)之间的微凸体面积比含量；
为所有接触微凸体的等效倾角和；
为所有接触微凸体个数，则
为所有接触微凸体等效倾角平均值。式(19)相较于式(18)考虑了节理接触部分形貌特征，显然更为合理。则
(20)
当节理完全接触时
而
即为TATONE提出的粗糙度指标。只是本文提出的粗糙度指标的一种特殊形式。
对于完全耦合的并且没有填充物的节理，当承受法向荷载时，节理少部分接触微凸体会发生弹性变形，在最初接触的微凸体部分会发生屈服。随着法向应力继续增加，会有更多的微凸体相互接触并发生屈服，这一过程会连续发生直至相互接触的微凸体面积足够大能够承受给定法向荷载的作用。因此，可以假设所有接触微凸体中的最小倾角为在一定荷载作用下刚好屈服的微凸体的倾角。
基于以上假设，结合式(1)与(17)，得到所有接触微凸体中的最小倾角为
(21)
结合式(20)与式(21)，则实际接触部分节理微凸体倾角的平均值为
(22)
式(22)为粗糙节理接触部分所有有效倾角的平均值，将定义为实际接触节理粗糙度，则可以反映实际接触微凸体的三维粗糙度。
4 节理面的制作与三维扫描试验
为探索是否实际接触节理粗糙度
可与节理剪切强度较好的联系起来。本节进行了巴西劈裂试验获取了劈裂节理面来代替自然节理面研究。进行了节理形貌面的扫描试验获取了节理坐标数据以定量表征节理形貌三维粗糙度。通过不同剪切公式计算出了节理峰值剪胀角，探索了实际接触节理粗糙度与剪切强度的联系。
巴西劈裂法制备岩石节理是采用测试岩石抗拉强度的巴西劈裂试验拉断试样形成节理。采用这种方法得到的节理粗糙不平呈不规则的弯曲状并与自然岩石表面形貌特征很相似，制备过程较为简单。对于有层理结构的节理，沿层理劈开能够保证节理的方向较为平直，因此该方法为常用制备节理的方法[27]。笔者选取岩石工程中常遇到的花岗岩作为岩石材料来研究其节理形貌特征，所有试块的制备都是从同一大块完整岩石中切割获取。所制备岩石试块尺寸为200 mm×100 mm×100 mm。制备好试块后，选取200 mm×100 mm的长方形作为加载面，加载线位于面沿长轴方向的中心。加载速率为0.5 mm/min直到岩石劈裂，最后得到5组劈裂节理面。
为定量描述岩石节理粗糙度特征，5组劈裂所得花岗岩节理面扫描试验在武汉大学自制的三维激光扫描仪上进行(图2)。三维激光扫描仪是由高精度CCD位移传感器、计算机控制的高精度二维位移工作台、计算机控制系统及数据处理系统组成。节理形貌经传感器扫描后，由数据采集软件保存并处理。
图2 三维扫描测量仪
Fig.2 3D scanning machine
使用三维激光扫描仪进行节理形貌测量工作具体步骤如下:① 将岩石节理待测样本放置扫描仪承台板上，节理形貌面向扫描仪激光测头;② 调整激光扫描仪范围确保节理能够完全被测量范围覆盖;③ 设置扫描起始位置，调节试样放置角度，确保起始扫描边缘与扫描路径重合;④ 通过扫描控制系统设置扫描采样间距为0.25 mm，采样频率为20 kHZ;⑤ 启动扫描仪开始扫描，数据采集系统自动采集节理高程坐标信息并保存。试验中节理由劈裂试验所得，上下节理吻合较好，因而仅对其中一个面进行扫描。
通过上述方法扫描5组节理得到了节理形貌几何信息，得到三维节理形貌图如图3所示。
图3 节理形貌
Fig.3 Morphology of rock joints
在采样间距为0.25 mm时，剪切方向为图中长方向正向时所得形貌参数见表1。
在获取节理形貌数字模型基础上，通过3D打印技术制作了复制节理试样所用的5组PLA底模(形貌与图3一致)，将质量配合比水∶水泥∶砂=1∶2.3∶4.5的水泥砂浆浇筑在PLA底模上即可得到水泥砂浆节理。耦合节理试块尺寸为200 mm×100 mm×100 mm。所有节理具有5种形貌，每组形貌相同的试块4个，共20个试块。按照不同的形貌标记试块为JM-1，JM-2，JM-3，JM-4，JM-5。为获取节理力学参数，试块制作过程中制备了若干个高度为100 mm，直径为50 mm的砂浆试件。为保证材料性质一致，在制作过程中测试力学参数所用砂浆柱与节理试块配合比相同、振捣过程一致，养护条件均一致。测定其单轴抗压强度为29 MPa、单轴抗拉强度为2.1 MPa。
表1 节理面三维形貌参数计算结果
Table 1 Joint surface morphology parameter
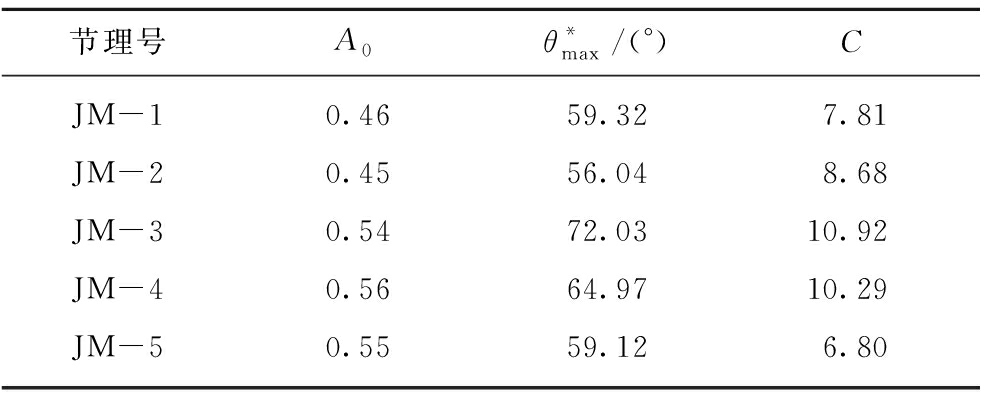
节理号A0θ*max/(°)CJM-10.4659.327.81JM-20.4556.048.68JM-30.5472.0310.92JM-40.5664.9710.29JM-50.5559.126.80
与剪切强度的联系
最早BARTON提出τp=σntan(φb+ip)，其中，φb为基本摩擦角;ip为峰值剪胀角[9]。在剪切过程中，基本摩擦角不变而峰值剪胀角会随着法向应力与剪切位移而变化。
GRASSELLI[27]基于粗糙度指标提出了节理峰值抗剪强度公式:
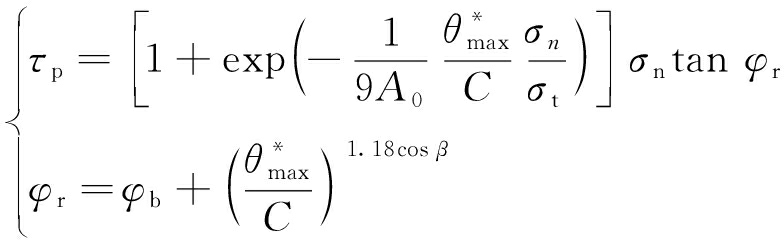
(23)
式中，τp为峰值抗剪强度;φr为残余摩擦角;β为片节理面的倾角(一般β=0);σt为材料抗拉强度。
TATONE[32]基于粗糙度指标提出了新的节理峰值抗剪强度公式:
(24)
式中,l为采样间距,mm。
TIAN等[39]认为式(23)中与A0不是描述粗糙度的关键指标，为了凸显参数C的作用，提出以下节理峰值抗剪强度公式:
(25)
其中，峰值剪胀角ip为
(26)
TIAN模型形式简洁，符合摩尔库伦准则。但是该模型中峰值剪胀角量纲和基本摩擦角不一致，仅为经验模型。
XIA等[40]认为GRASSELLI峰值抗剪强度模型不符合摩尔-库伦公式形式，未能体现峰值膨胀角的影响以及演化规律，物理意义不够明确。XIA等提出了用式(27)来预测节理峰值抗剪强度τ，即
(27)
其中,剪胀角ip为
(28)
YANG等[41]提出了含三维形貌参数的剪切强度准则
(29)
其中，剪胀角ip为
(30)
该模型中
为初始膨胀角，与节理形貌面粗糙度有关;
部分描述了节理峰值膨胀角与初始膨胀角的关系。
唐志成等[38]基于复制节理的剪切试验，分析了粗糙度、法向应力对剪切强度的影响,提出了含三维形貌参数的剪切强度准则:
(31)
其中，剪胀角为
(32)
节理峰值剪胀角反映了某一应力下的剪切实际情况，并且可以准确的反映节理峰值抗剪强度。基于上述模型计算出峰值剪胀角与节理实际接触节理粗糙度对比如图4所示。
由图4可以看出各模型计算所得峰值剪胀角不尽相同，当节理法向应力较低时，各模型计算峰值剪胀角差别不大;随着法向应力的增大，计算结果离散值较大。但是各模型计算结果的趋势都是随着法向应力增大峰值剪胀角呈抛物线形式减小。黄色实线为4个模型计算峰值剪胀角的平均值，可见随着法向应力增大峰值剪胀角呈抛物线形式减小。
黑色实线为计算实际接触节理粗糙度。可以看出实际接触节理粗糙度也是随着法向应力增大呈抛物线形式减小，并且曲线也较为光滑。可知节理实际接触粗糙度指标随着法向应力的变化趋势与节理峰值剪胀角的变化趋势很类似。节理峰值剪胀角反映了某一应力下的剪切实际情况，并且可以准确的反映节理峰值抗剪强度。上述趋势变化一致的现象表明节理实际粗糙度指标可以与节理峰值抗剪强度很好的联系起来。
图4 节理实际粗糙度指标与峰值剪胀角对比
Fig.4 Real contact joint roughness and the peak dilatation angle
定量分析计算实际接触节理粗糙度与各模型节理峰值剪胀角均值可知在法向力较小时两者较为接近。本文定义的实际接触节理粗糙度为微凸体等效倾角的平均角度。当节理为规则节理并且法向应力较低时，节理抗剪强度符合PATTON[42]线性准则，该模型中由于节理为规则齿形节理，在剪切作用发生前节理是完全吻合的，所以在剪切过程中峰值剪胀角即为规则齿形节理的角度，也是接触部分所有节理倾角的平均值。当法向应力较大时，在剪切过程中一些微凸体发生剪断，节理形貌发生磨损导致节理粗糙度降低。但初始粗糙度的描述是不考虑剪切过程中的磨损的，所以本文所提粗糙度指标在法向应力较大时大于峰值剪胀角。
本文粗糙度指标与其他4个目前较为经典的模型进行了比较，同时与这4个模型的平均值进行了比较。定性分析与定量分析都表明实际接触节理粗糙度可以很好的与剪切强度联系起来。下一步工作是进行节理剪切试验，提出基于新粗糙度指标的峰值抗剪强度公式。由图4发现随着法向应力增大，实际接触节理粗糙度与各模型节理峰值剪胀角均值差值会变大，此时应考虑法向应力的影响。节理剪切强度与考虑实际接触节理的粗糙度之间的定量关系需要进一步探索。
6 结 论
(1)基于Grasselli 视倾角分布函数研究了不同视倾角的面积比含量，分析了较陡接触微凸体对节理抗剪强度的作用。基于接触理论研究发现对于压剪作用下的岩石节理，接触的微凸体应力水平较高以至于微凸体发生屈服或破坏。对于岩石节理在法向应力下的剪切问题，实际接触面积Ac可以近似认为是作用在节理面上法向荷载N除以岩石的单轴抗压强度σc。
(2)基于指标的实际物理意义，考虑剪切过程中实际接触部分节理微凸体的作用，基于实际接触部分节理上微凸体分布特征，得到了合理的三维粗糙度指标。该指标为实际接触节理微凸体等效视倾角的平均值。
(3)节理峰值剪胀角反映了某一应力下的剪切实际情况，并且可以准确的反映节理峰值抗剪强度。对比分析了实际接触节理粗糙度与节理峰值剪胀角趋势变化，结果表明节理粗糙度新指标可以与节理峰值抗剪强度很好的联系起来，该研究为进一步研究节理抗剪强度准则提供了理论基础。
[1] TIAN Y,LIU Q,MA H,et al.New peak shear strength model for cement filled rock joints[J].Engineering Geology,2018,233:269-280.
[2] 陶志刚,庞仕辉,张博,等.大尺度边坡岩体开裂解体破坏规律试验研究[J].矿业科学学报，2016,1(3):222-227.
TAO Zhigang，PANG Shihui，ZHANG Bo,et al.Experimental study on failure law of cracking and disintegration of rock mass in large-scale slope[J].Journal of Mining Science and Technology，2016,1(3):222-227.
[3] ZHANG X B,YI B,JIANG Q H,et al.Evaluation Models for the Peak Shear-Strength and Shear-Resistance Components of Rough Rock Joints[J].Journal of Testing & Evaluation,2017,45(6):1-12.
[4] SHE C X,SUN F T.Study of the peak shear strength of a cement-filled hard rock joint[J].Rock Mechanics & Rock Engineering,2017:1-16.
[5] 张振宇,李豪杰,贾长恒,等.带有橡胶垫层混凝土接触摩擦特性的试验研究[J].矿业科学学报，2018，3(1):20-28.
ZHANG Zhenyu，LI Haojie，JIA Changheng，et al．Characteristics of direct shear test for plain concrete joint with rubber cushion[J].Journal of Mining Science and Technology，2018，3(1):20-28.
[6] 易成,王长军,张亮,等.基于两体相互作用问题的粗糙表面形貌描述指标系统的研究[J].岩石力学与工程学报,2006,25(12):2481-2492.
YI Cheng，WANG Changjun，ZHANG Liang,et al.Study on description index system of rough surface based on bi-body interaction[J].Chinese Journal of Rock Mechanics and Engineering，2006,25(12):2481-2492.
[7] DONG W P,MAINSAH E,STOUT K J.Reference planes for the assessment of surface roughness in three dimensions[J].International Journal of Machine Tools & Manufacture,1995,35(2):263-271.
[8] WANG Q.Study on determination of rock joint roughness by using elongation rate R[A].Proceedings of the undergoing constructions[C].Jinchuan:1982:343-348.
[9] BARTON N,QUADROS E F D.Joint aperture and roughness in the prediction of flow and groutability of rock masses[J].International Journal of Rock Mechanics & Mining Sciences,1997,34(3-4):252.e1-252.e14.
[10] TSE R,CRUDEN D M.Estimating joint roughness coefficients[J].International Journal of Rock Mechanics & Mining Sciences & Geomechanics Abstracts,1979,16(5):303-307.
[11] GAGNEPAIN J J,ROQUES-CARMES C.Fractal approach to two-dimensional and three-dimensional surface roughness[J].Wear,1986,109(1-4):119-126.
[12] FEDER J.Fractal[M].New York:plenum press,1988.
[13] MAJUMDAR A,TIEN C L.Fractal characterization and simulation of rough surfaces[J].Aip Advances,2015,136(1):313-327.
[14] STUPAK P R,KANG J H,DONOVAN J A.Fractal characteristics of rubber wear surfaces as a function of load and velocity[J].Wear,1990,141(1):73-84.
[15] BROWN C A,SAVARY G.Describing ground surface texture using contact profilometry and fractal analysis[J].Wear,1991,141(2):211-226.
[16] GANTI S,BHUSHAN B.Generalized fractal analysis and its applications to engineering surfaces[J].Wear,1995,180(1-2):17-34.
[17] 丁增志.节理表面形貌研究及在非贯通节理岩体强度准则中的应用[D].上海:同济大学,2007.
DING Zengzhi.Study of joint surface topography and application in strength criterion of roughness containing discontinuous joints[D].Shanghai:Tongji University,2017.
[18] MAERZ N H,FRANKLIN J A,BENNETT C P.Joint roughness measurement using shadow profilometry[J].International Journal of Rock Mechanics & Mining Sciences & Geomechanics Abstracts,1990,27(5):329-343.
[19] LEE Y H,CARR J R,BARR D J,et al.The fractal dimension as a measure of the roughness of rock discontinuity profiles[J].International Journal of Rock Mechanics & Mining Sciences & Geomechanics Abstracts,1990,27(6):453-464.
[20] BARTON N,BANDIS S.Review of Predictive Capabilities of JRC-JCS Model in Engineering Practice[A].Barton N,Stephansson O,eds,Rock Joints[C].Balkema,Rotterdam:1990:603-610.
[21] BELEM T,HOMAND-ETIENNE F,SOULEY M.Quantitative parameters for rock joint surface roughness[J].Rock Mechanics & Rock Engineering,2000,33(4):217-242.
[22] HOMAND F,BELEM T,SOULEY M.Friction and degradation of rock joint surfaces under shear loads[J].International Journal for Numerical & Analytical Methods in Geomechanics,2001,25(10):973-999.
[23] 唐志成,黄润秋,张建明,等.含坡度均方根的结构面峰值剪切强度经验公式[J].岩土力学,2015(12):3433-3438.
TANG Zhicheng，HUANG Runqiu，ZHANG Jianming，et al．Empirical peak shear strength criterion for rock joints based on slope root-mean-square [J].Rock and Soil Mechanics，2015(12):3433-3438.
[24] TANG H,GE Y,WANG L,et al.Study on estimation method of rock mass discontinuity shear strength based on three-dimensional laser scanning and image technique[J].Journal of Earth Science,2012,23(6):908-913.
[25] CHEN S J,ZHU W C,YU Q L,et al.Characterization of anisotropy of joint surface roughness and aperture by variogram approach based on digital image processing technique[J].Rock Mechanics & Rock Engineering,2016,49(3):855-876.
[26] GRASSELLI G,EGGER P.Constitutive law for the shear strength of rock joints based on three-dimensional surface parameters[J].International Journal of Rock Mechanics & Mining Sciences,2003,40(1):25-40.
[27] GRASSELLI G.Shear strength of rock joints based on quantifiedsurface description[D].Lausanne，Switzerland:Swiss Federal Institute of Technology，2001.
[28] SUN F T,JIANG Q R,SHE C X.Research on three-dimensional roughness characteristics of tensile granite joint[J].Applied Mechanics & Materials,2012,204-208:514-519.
[29] 孙辅庭,佘成学,万利台.新的岩石节理粗糙度指标研究[J].岩石力学与工程学报,2013,32(12):2513-2519.
SUN Futing，SHE Chengxue，WAN Litai.Research on a new roughness index of rock joint[J].Chinese Journal of Rock Mechanics and Engineering，2013,32(12):2513-2519.
[30] 班力壬,戚承志,单仁亮,等.一种新的表征岩石节理粗糙度指标系统[J].煤炭学报，2018,43(12):3356-3363.
BAN Liren,QI Chengzhi,SHAN Renliang,et al.A new 3D roughness parameter system for rock joint[J].Journal of China Coal Society,2018,43(12):3356-3363.
[31] 陈曦，曾亚武，孙翰卿，等.基于Grasselli形貌参数的岩石节理初始剪胀角新模型[J].岩石力学与工程学报，2019，38(1):133-152.
CHEN Xi,ZENG Yawu,SUN Hanqing,et al.A new model of the initial dilatancy angle of rock joints based on Grasselli’s morphological parameters[J].Chinese Journal of Rock Mechanics and Engineering，2019，38(1):133-152.
[32] TATONE B S.Quantitative characterization of natural rock discontinuity roughness in situ and in the laboratory[D].Toronto:University of Toronto，2009.
[33] 波波夫.接触力学与摩擦学的原理及其应用[M].北京：清华大学出版社,2011.
[34] GREENWOOD J A,WILLIAMSON J B P.Contact of nominally flat surfaces[A].Proceedings of the Royal Society of London[C].London:1966,295(1442):300-319.
[35] POPOV V L.Contact mechanics and friction physical principles and applications[M].Beijing:Tsinghua University Press,2011:66-67.
[36] GREENWOOD J A,TRIPP J H.The contact of two nominally flat rough surfaces[J].ARCHIVE Proceedings of the Institution of Mechanical Engineers,1971,185:625-634.
[37] SWAN G.Determination of stiffness and other joint properties from roughness measurements[J].Rock Mechanics & Rock Engineering,1983,16(1):19-38.
[38] 唐志成,刘泉声,刘小燕.节理的剪切力学性质与含三维形貌参数的剪切强度准则比较研究[J].岩土工程学报,2014,36(5):873-879.
TANG Zhicheng,LIU Quansheng,LIU Xiaoyan.Shear behavior of rock joints and comparative study on shear strength criteria with three-dimensional morphology parameters[J].Chinese Journal of Geotechnical Engineering,2014,36(5):873-879.
[39] TIAN Y，LIU Q，LIU D，et al.Updates to grasselli’s peak shear strength model[J].Rock Mechanics and Rock Engineering，2018，51,2115-2133.
[40] XIA C C,TANG Z C,XIAO W M,et al.New peak shear strength criterion of rock joints based on quantified surface description[J].Rock Mechanics and Rock Engineering，2014，47:387-400.
[41] YANG J,RONG G,HOU D,et al.Experimental study on peak shear strength criterion for rock joints[J].Rock Mechanics and Rock Engineering，2016,49:821-835.
[42] PATTON F D.Multiple modes of shear failure in rock[A].Proceedings of the 1st ISRM Congress[C].Portugal:1966:509-513.
