在岩土工程和采矿领域，深部岩体的力学行为近年来备受学者关注，研究表明，深部岩石材料在加载过程中常表现出应变软化特征、弹塑性耦合特征和塑性变形破坏特征等非线性力学行为[1]。在实践中，岩石工程中实际研究对象往往为破裂后的围岩，因此如何科学描述峰后围岩的非线性力学行为进而建立相应的本构模型是一项具有挑战性的工作。与地面岩体力学中受弱面控制不同，大量试验结果表明，深部岩石的峰后力学特性多呈现一定的围压依赖效应，且随着破裂程度的加剧，弹性参数也将会发生一定程度的劣化[2-6]，即围岩所处的应力水平和塑性变形的变化均会在一定程度上引起岩石力学参数(弹性模量、剪胀角、黏聚力和摩擦力)的变化。然而在工程应用中，这一特征常常被忽视或被简化，如剪胀角，在非关联流动法则中，其值恒定为0，在关联流动法则中，其值等于内摩擦角，又如在FLAC中应用较多的应变软化模型(SS模型)中，虽然允许用户定义内摩擦角、黏聚力与剪胀角等计算参数作为等效塑性应变的分段线性函数，但却未考虑围压的影响效应。上述简化对于复杂应力状态下的工程尤其是承受高围压作用的深部地下工程而言，其计算误差往往不可忽略。
国内外众多学者对此开展了相应的研究:MARTIN C D等通过开展花岗岩的循环加卸载试验[7]，研究了岩石材料在峰后不同损伤状态下的变形及强度特征，内摩擦角随塑性体积应变先增加后缓慢衰减;黏聚力则先快速衰减，后趋于定值。尤明庆等通过模拟地下岩体破坏的三轴卸围压试验，指出岩样的弹性模量随围压升高而增大，残余强度也随之升高[8];张凯基于对2种大理岩循环加、卸载试验得到了黏聚力和内摩擦角随塑性内变量的演化规律即随塑性变形量的增加，黏聚力逐渐减小，内摩擦角逐渐增加[9];黄润秋等通过室内三轴卸荷试验和破裂断口的SEM细观扫描信息，对高地应力下锦屏一级大理岩的变形破裂及强度特征进行了研究，分析指出随着初始围压的增大，岩石脆性特征明显，得到了各强度参数的不同变化规律[10];张春会等通过扩容指数建立了剪胀角和围压之间的关系，得出剪胀角对岩石的承载能力发挥的作用，在同条件下岩石的强度会随着剪胀角的增加而略有提高，岩石破坏单元的体积膨胀变大[11]。
上述学者分别研究了塑性累积变形和围压2者对围岩力学特性的影响，但没有同时考虑2者的综合作用影响。笔者针对性开展了相关研究，利用三轴循环加卸载的方法获得各级围压下不同塑性累积阶段的岩石力学参数，进而研究塑性变形与围压2者综合影响下的围岩受力变形特征，建立深部岩体弹塑性耦合效应的应变软化分析模型并利用数值分析方法对模型的适用性进行了验证。
1 三轴循环加卸载试验
试样选用取自山东莱州某采石厂的白色大理岩，室温下其平均密度为2.82 g/cm3。试件采自同一整体岩块，并按照ISRM要求，经取芯、切割、打磨等步骤加工成高50 mm，直径100 mm 的标准圆柱体试样，试样两端面不平整度小于0.05 mm，利用声波波速测试筛除差异较大的岩样(图1)。分为6组开展不同围压条件下的循环加卸载试验研究，每组岩样首先进行2～3次常规三轴试验，确定其在该级围压下的峰值强度及最大塑性变形，而后进行4～10次三轴循环加卸载试验，研究塑性应变及围压影响下的岩石力学特性。
图1 大理岩试样及超声波检测
Fig.1 Sample and ultrasonic testing
试验在中国矿业大学深部岩土力学与地下工程国家重点实验室的MTS815.0型电液伺服三轴试验机上进行，如图2所示，首先施加围压至目标值，预定围压目标值分别为:5，10，15，20，25和30 MPa，随后采用荷载和环向变形相结合的方式控制整个加卸载过程。在塑性之前的加载阶段，采用轴向荷载控制方式进行等梯度加卸载，荷载梯度40 kN为一个循环，加载速率为1.0 kN/s，卸载速率为2.0 kN/s，围压保持恒定;当荷载到达峰值强度的80%左右时，加载方式转换为环向变形控制，加载速率为0.002 mm/s，环向变形每增长0.2 mm为一个循环卸载点，卸载速率设为1.0 kN/s，卸载到围压，等梯度递增循环，直至到达岩石的残余强度试验终止，试验流程如图3所示。不同围压下岩石的破坏形态如图4所示，试验获得的应力应变曲线如图5所示。
图2 MTS815.02 岩石电液伺服三轴试验机
Fig.2 MTS815.02 rock electro-hydraulic servo triaxial
testing machine
图3 三轴循环加卸载试验流程
Fig.3 Triaxial cyclic loading-unloading test flow chart
图4 不同围压下的大理岩破坏形态
Fig.4 Failure morphology of marble under different
confining pressure
从岩样的破坏形态和应力应变曲线可获得一些直观结论:① 岩石力学特性受围压和塑性应变影响较大:随围压升高，岩石的强度、弹性模量等力学参数有明显升高;随累积塑性应变增大，岩石的弹性模量产生明显劣化，如图5所示;② 从岩石破坏后形态可以看出，岩石在三轴条件下的破坏多为与水平面呈一定角度的剪切破坏，破裂角随围压升高而逐渐减小，这与岩石强度的静水压力效应是相一致的。
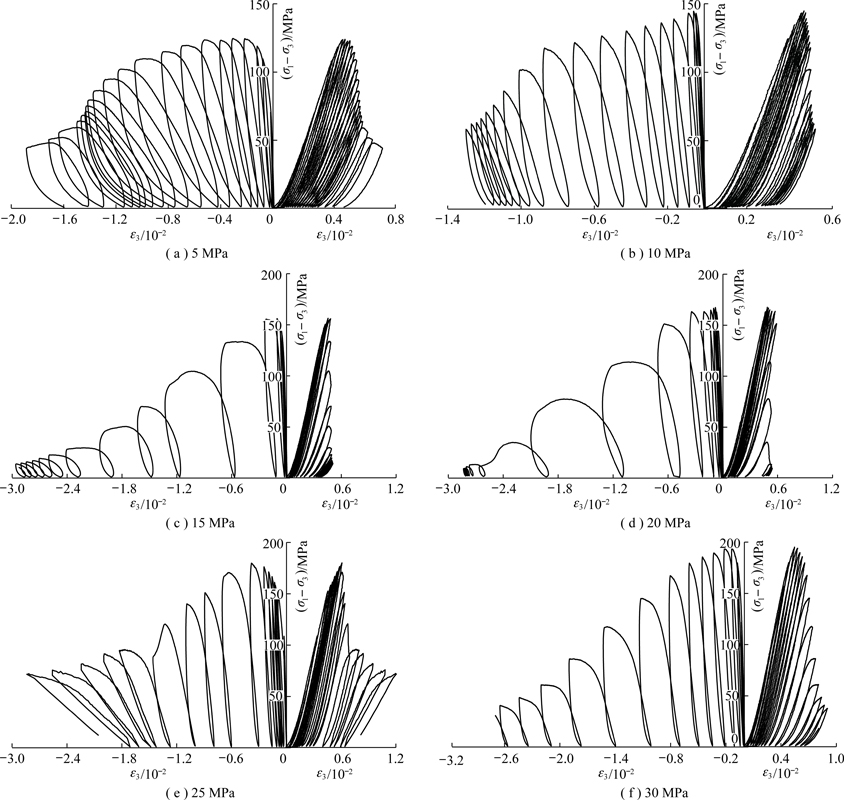
图5 大理岩试样不同围压下循环加卸载压缩试验结果
Fig.5 Triaxial compression test results of marble under cyclic loading-unloading conditions
根据试验所获取的应力应变数据，整理分析后，分别研究了应变软化阶段的强度参数、弹性模量和剪胀角随累积塑性变形和围压的变化规律。
2 结果分析与模型建立
2.1 塑性参数的选择
塑性参数被引入表征岩体发生的塑性破坏程度，常见的塑性参数有增量和全量形式，FLAC应变软化模型中采用增量形式的塑性体积应变Δεps，然而在理论模型分析时，更多的选取形式较简便的全量形式[12-14]。本文考虑简洁性，采用二维塑性剪切应变γp为塑性参数，来表征岩体内部的塑性破坏程度。γp的物理意义为材料受压产生塑性变形后其最大主塑性压缩应变和最小主塑性膨胀应变绝对值之和。其表达式为
(1)
其中, η为塑性参数;
分别为最大和最小主塑性应变。γp形式简单，物理意义明确,γp与Δεps可以相互转换，其表达式为
(2)
式中,Nψ为过程参数;Nψ=(1+sin ψ)/(1-sin ψ)，ψ为剪胀角。
2.2 强度参数分析
对于三轴压缩试验，岩石强度一般指在某一特定围压下岩石所能承受的最高偏应力水平，其本质是强度参数演化过程中的应力极值点。决定岩石强度特征的力学参数是黏聚力c和内摩擦角φ，M-C准则、H-B准则均采用二者来表征岩石的强度特征。针对塑性应变对岩石强度的影响，不同学者通过循环加卸载试验开展了相关研究[2,9,15-18]，然而专门针对峰后应变软化阶段的强度参数的分析尚且不多，且均未同时考虑围压和塑性应变的综合作用影响(图6，σn为任意点的正应力;τ为剪应力;
为临界塑性剪切应变)，因此针对性的开展了相关工作。
图6 受围压及塑性应变影响的摩尔强度包络线
Fig.6 Mohr strength envelopes associated with confining
pressure and plastic strain
对理想塑性而言，材料的屈服面是固定不变的，应力状态不能落在屈服面之外，但对于岩石材料，随着塑性变形的发展，岩石破碎程度不同，处于峰值状态和残余状态的岩石屈服面是不同的，即后继屈服面不同于初始屈服面。岩石的后继屈服面不只与其应力状态有关，还与其损伤程度，即塑性变形历史有关[19]。后继屈服面可表示为
f(σi,j,κ)=0
(3)
式中，σi,j,κ为任意一点的应力;κ为强化参数。
对于有固定表达式的传统强度理论，例如M-C准则来说，由于未考虑这方面因素，因此将其应用于峰后强度预测时，其拟合精度往往较低。针对这种情况，将其参数设计为围压和塑性应变的函数是合理的[18]，M-C准则的表达式为
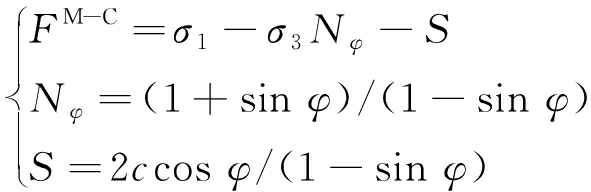
(4)
其中，σ1和σ3分别为最大和最小主应力;Nφ，S均为过程参数;c，φ分别为岩石的黏聚力与内摩擦角。当FM-C<0时，岩体处于弹性状态，此时应力应变关系符合广义胡克定律。而当FM-C=0时，进入屈服状态，产生塑性流动，其变形取决于塑性流动法则:
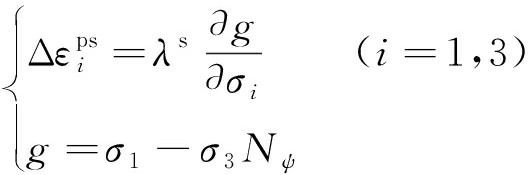
(5)
其中，
为塑性应变增量;λs为塑乘因子;σi为主应力;g为塑性势函数。式(4)和(5)构成了M-C准则。实际岩石工程中，天然岩体受构造运动或人为因素扰动，大多处于塑性屈服状态，后继屈服特征对于岩体工程的稳定和工程安全尤为重要。而由于传统M-C准则未考虑塑性剪应变的影响，虽然考虑了围压但由于其表达形式是线性的，仍不能很好反映围岩的峰后强度特征。例如在深部开挖中，围岩峰后受到高围压的约束作用，其破坏形态趋近于理想塑性，使用该准则评估的岩石三轴强度与实测强度数据偏差较大。因此，需对其进行改造。将式(4)中的N，S看作围压σ3与塑性剪切应变γp的函数，则式(4)可表示为
(6)
为进一步研究围岩的峰后应变软化的后继屈服强度特征，需获得黏聚力c(σ3,γp)和内摩擦角φ(σ3,γp)与围压σ3及塑性剪切应变γp的函数关系。根据图5，以应力卸载到初始加载应力时的环向塑性应变与轴向塑性应变的差值为塑性参数，以各循环中不同塑性应变下对应的各峰值点为后继屈服强度，构建后继屈服强度与塑性剪切应变的结果，而后通过差值的办法获得每0.2个塑性剪切应变下，后继屈服强度与围压的对应关系，得到的结果如图7所示。
图7 不同围压下后继屈服强度与塑性剪应变关系
Fig.7 Relationship between strength and plastic shear
strain under different confining pressures
利用图7得到的不同塑性剪切应变和不同围压下对应的极限应力状态，绘制在同一塑性剪应变下，不同围压对应的不同极限应力状态而生成的若干组摩尔圆，每2组圆的外切线与x轴夹角为内摩擦角与y轴的截距为黏聚力，如图8所示。对某级围压下所对应的摩尔圆分别与其他围压下的各摩尔圆两两做公切线并获得各切点坐标，而后利用最小二乘法对各切点坐标进行拟合，从而得到该级围压下的强度包络线方程，通过对该包络线方程与摩尔圆相切位置进行求导，则其斜率和截距即为该级围压下的内摩擦角对应的正切值和黏聚力值，如图9所示。以黏聚力为例，由此获得各级围压下的黏聚力随塑性剪应变的变化如图10所示。由图10可以看出，黏聚力随塑性剪应变增加而逐步降低，且下降幅度逐步减缓并趋于平缓，二者均符合负指数型函数规律，因此采用最小二乘法对其进行负指数函数的曲线拟合。
图8 摩尔圆及其包络线求解c,φ值
Fig.8 Mohr’s strength envelope and c,φ solving
图9 强度包络线及其切线
Fig.9 Strength envelope and its tangent
图10 不同围压下黏聚力随塑性剪应变变化规律
Fig.10 Variation of cohesion with plastic shear strain under
different confining pressure
另一方面，为研究围压的影响，根据图10的数据，绘制在同一塑性剪应变下，黏聚力随围压变化情况，可看出黏聚力随围压增加而增大，符合线性递减的变化规律，因此采用最小二乘法对其进行线性函数拟合，拟合结果如图11所示。
图11 不同塑性剪应变下黏聚力随围压变化规律
Fig.11 Variation of cohesion with confining pressure
under different plastic shear strains
图12 内摩擦角在围压-塑性剪切应变空间的散点分布
及三维拟合曲面
Fig.12 Values of friction angle on the confining pressure-plastic
shear strain space and its fitting surface
综合图10，11，可以看出围岩在峰后应变软化阶段的强度参数是在由围压和塑性剪切应变二者的二维曲面上演化。根据插值获得的内摩擦角/黏聚力-围压-塑性剪切应变数据，图12，13分别给出了围压峰后应变软化状态时的黏聚力c 和内摩擦角φ在由围压σ3及塑性剪切应变γp构成的二维面上空间点的分布情况。由图12，13可以看出，塑性剪切应变对黏聚力c和内摩擦角φ的影响非常明显:内摩擦角和黏聚力随等效塑性应变γp均呈现出负指数减小的特征(图12，13)，另一方面，围压σ3对峰后黏聚力c和内摩擦角φ影响也非常明显，随着围压σ3的增加，内摩擦角φ值单调减小，而黏聚力c单调增加。这与众多三轴压缩试验中岩石强度特征的结果是相吻合的[18,20-22]。经典的弹塑性理论中认为的材料强度参数是材料的固有特性从而保持不变，由于没有考虑岩土类材料的峰后应变软化特征，其适用性受到局限，在本文中，充分考虑了塑性变形对黏聚力和内摩擦角的弱化作用，可以理解为材料在变形过程中损伤对晶粒间黏聚力的劣化作用以及晶格间的滑动摩擦劣化作用。
图13 黏聚力在围压-塑性剪切应变空间的散点分布
及三维拟合曲面
Fig.13 Values of cohesion on the confining pressure-plastic
shear strain space and its fitting surface
为建立黏聚力c和内摩擦角φ与围压σ3及塑性剪切应变γp的二维函数关系，根据上述分析结果，设定黏聚力c和内摩擦角φ与围压σ3为线性关系(0≤σ3≤30)，与塑性剪切应变γp为负指数衰减关系(0≤γp≤2.2%)，同时需要指出的是，塑性剪切应变γp与偏应力大小相关，与围压σ3则不存在相关性，因此2者符合叠加原理，由此构建的二维函数表达式为
(7)
式(7)构成了内摩擦角和黏聚力的数学模型，其中,φ1～φ4，c1～c4为拟合系数。利用Matlab分别对其进行最小二乘曲面拟合，拟合结果如图12,13所示，拟合系数及相关系数见表1。
表1 黏聚力和内摩擦角的拟合系数
Table 1 Fitting coefficients of cohesion and friction angle
φ1φ2φ3φ4R234.481.44-1.2425.560.99c1c2c3c4R267.863.680.79-39.190.99
可根据式(1)～(3)反算循环加卸载各峰值点的应力状态，并与试验获得的实测值进行对比，以此验证所推导方程的适用性。选取围压为20 MPa时计算的后继屈服点与原实验值的对比结果如图14所示，可以看出2者具有较好的拟合精度。
图14 后继屈服点计算值与试验值对比
Fig.14 Comparison of calculated value and test value about
the post-peak strengthen
2.3 弹性模量特征分析
从图5可看成，岩石峰后加卸载过程中应力应变曲线仍保留线性段，定义此过程中峰值应力点的割线模量为应变软化阶段的弹性模量，可以看出，随塑性剪切应变的增加，斜率值趋于减小。大量学者针对其劣化特性开展了相关室内试验和理论研究工作，表明弹性模量随塑性变形的增大而逐渐减小[23-25];另一方面，围压对弹性模量的影响也非常明显[4,7,20-22]。众多试验表明，围压增大有利于岩样内部的裂隙以及孔隙等闭合，从而增加了岩样的刚度，致使岩样的弹性模量也随之相应的增大[5,21,26-29]。然而，综合考虑塑性应变和围压二者共同作用对变形参数影响的研究尚未开展，事实上，与地面岩石工程不同，对深部地下工程而言，岩石的变形特征需要考虑其所处的应力状态和蕴含的塑性损伤程度的影响。
在弹性阶段，表征岩石材料的重要参数为其弹性模量与泊松比。材料变形符合广义胡克定律，在不同围压下弹性模量和泊松比的计算公式为
(8)
其中，E为弹性模量;μ为泊松比;ε1和ε3分别为最大和最小主应变。尤明庆、赖勇根据不同围压下岩样的变形分析，并结合细观损伤理论的思路，均认为可采用负指数型函数来表达岩石的弹性模量E与围压σ3的关系[28-29]，其表达式分别为
E0-E=(E0-Ea)exp(-σ3/Q)
(9)
(10)
式中，E0为弹性模量的极限值;Ea为单轴压缩时的弹性模量;Q为与试样黏聚力和内摩擦角有关的参数;
为与裂隙密度有关的参数;A，B为拟合系数，由不同围压下的弹性模量经过回归分析获得。
另一方面，弹性模量随塑性应变的增加而出现劣化[8,16,23]。李英杰将弹性模量随塑性变形简化为线性折减，考虑折减因子分别为1.0，0.5，0.3三种情形进行对比分析[25];类似的，张凯、周辉等采用体积模量和剪切模量来描述，认为体积模量保持不变，剪切模量随塑性应变线性减小[2,9,16]。
通过分析线弹性段的应力应变关系可以得到在不同围压下的弹性模量随塑性剪切应变的变化曲线，如图15所示。可以看出，弹性模量随塑性剪切应变大致呈线性衰减的规律，即
E=ea1+ea2γp
(11)
其中，ea1，ea2为拟合参数，采用式(11)，对试验数据进行曲线拟合，相应的拟合参数见表2，结果如图15所示。
图15 不同围压下弹性模量-塑性应变关系
Fig.15 Relationship between elasticity modulus and plastic
shear strain under different confining pressures
表2 弹性模量随塑性剪切应变拟合系数
Table 2 Fitting coefficients of elasticity modulus with the
plastic shear strain
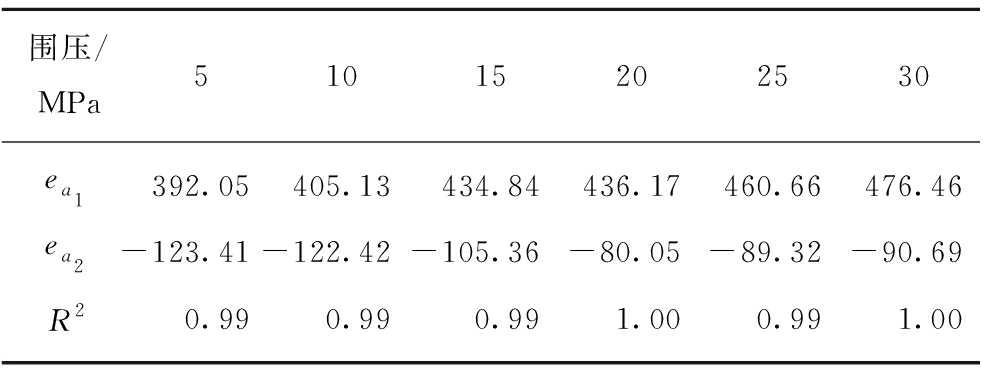
围压/MPa51015202530ea1392.05405.13434.84436.17460.66476.46ea2-123.41-122.42-105.36-80.05-89.32-90.69R20.990.990.991.000.991.00
受围压约束作用，围岩的变形特性会产生一定的强化，弹性模量随围压的增加而增加，但增长幅度逐渐减缓，其对应关系可看作负指数型增长[28-29]，可表示为
E=eb1exp(-σ3/eb2)
(12)
其中，eb1，eb2为拟合参数，根据图15，通过插值方法获得每0.2个塑性应变增长下的弹性模量与围压的对应关系，根据式(12)，对插值数据进行曲线拟合，拟合曲线如图16所示，得到的拟合系数见表3。
图16 不同塑性应变下弹性模量-围压关系
Fig.16 Relationship between elasticity modulus and confining
pressures under different plastic shear strain
表3 弹性模量随围压拟合系数
Table 3 Fitting coefficients of elasticity modulus with the confining pressure
剪切应变0.20.40.60.81.01.21.41.61.82.02.2eb1434.64416.81399.16381.80364.84350.01337.83327.56319.90316.21319.14eb20.370.340.310.280.250.180.150.130.110.090.07R20.750.780.800.820.840.760.800.840.880.910.93
从表2和图16可以看出，所提出的模型符合弹性模量的变化规律:随围压的升高而升高，但提升速率逐渐减慢。综合式(11)，(12)，可以看出与强度参数一样，围岩的弹性模量也是在由围压和塑性剪切应变2者的二维曲面上演化。据此，根据插值获得弹性模量-围压-塑性剪切应变数据，获得数据的空间分布如图17所示。根据式(11)，(12)可看出，弹性模量随塑性剪应变γp增加呈线性衰减关系(0≤γp≤2.2%)，随围压σ3增加呈负指数型增长关系(0≤σ3≤30)，由此构建的二维拟合函数关系为
E=e1exp(-σ3/e2)+e3γp+e4
(13)
式中，e1～e4为拟合系数。
由MATLAB拟合的曲面如图17所示，得到的拟合系数见表4。
图17 弹性模量-围压-塑性应变空间的三维拟合曲面
Fig.17 Three-dimensional fitting surface on elasticity
modulus-confining pressure-plastic shear strain
表4 弹性模量-围压-塑性剪切应变三维曲面拟合系数
Table 4 Fitting coefficients of elasticity modulus with the
confining pressure and plastic shear stain
e1e2e3e4R2-235.117.22-90.69517.60.98
2.4 剪胀角特征分析
岩石材料进入塑性状态后，其变形呈非线性特征，微观裂纹的形成和扩展导致岩石宏观上的体积膨胀，剪胀角被引入来描述岩石材料的扩容行为。
根据式(4)，对应的主应力进行偏微分，则主塑性应变率为
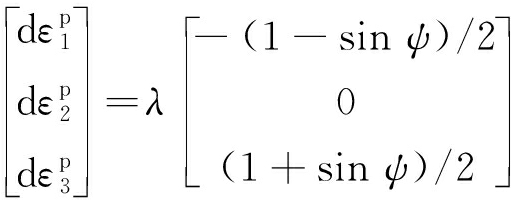
(14)
式中，
分别为3个主塑性应变;λ为塑乘因子。
根据上述屈服条件可知，当材料在某一点上发生屈服时，总的应变率可由2个独立的流动法则分别单独作用之和来表征:
(15)
式(15)中需要确定2个塑乘因子λ1，λ2，其中塑性势函数g1,g2为
将式(16)，(17)代入式(15)，可得
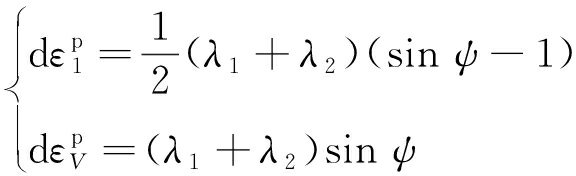
(18)
因此
(19)
其中，
为塑性体积应变增量,
为塑性轴向应变增量;
为塑性环向应变增量。赵星光等根据式(19)，利用塑性应变轨迹来计算剪胀角[30]。对于常规假三轴试验σ1=σ3，因此ε2=ε3。则式(19)可进一步简化为
(20)
由实验获得的轴向应变和环向应变，按式(20)计算不同塑性剪应变下试样的剪胀角，如图18中各散点所示。可以看出，剪胀角随塑性剪应变增加呈先增加后减小的变化(0≤γp≤2.2%)，在0.7～1.0时达到最大值。根据这一特征，构建指数差值型函数对剪胀角-塑性剪应变数据进行曲线拟合，获得较好拟合精度:
ψ=da3[exp(-da1γp)-exp(-da2γp)]+da4
(21)
式中，da1～da4为拟合参数，各围压下的拟合参数及相关系数见表5。
图18 不同围压下剪胀角-塑性剪应变关系
Fig.18 Relationship between dilation angle and plastic
shear strain under different confining pressures
表5 剪胀角随塑性剪切应变拟合系数
Table 5 Fitting coefficients of dilation angle with the
plastic shear strain
围压/MPa0.21.03.5102040da10.200.160.120.140.290.21da23.393.494.493.832.153.31da389.39109.47106.91104.0895.0879.44da4-12.62-33.52-43.33-39.86-18.82-31.09R20.991.001.001.001.000.99
另一方面，受围压约束作用的影响，围岩的扩容特性会随围压的升高而逐步降低，其对应关系符合式(22)的线性衰减模型，相应的拟合参数见表6。
ψ=db1+db2σ3
(22)
表6 剪胀角随围压拟合系数
Table 6 Fitting coefficients of dilation angle with the confining pressure
塑性剪切应变0.20.40.60.81.01.21.41.61.82.02.22.4db130.0053.8963.3266.1265.9164.3862.2759.9657.6055.2652.9750.74db2-0.86-1.06-1.10-1.08-1.06-1.04-1.02-1.01-1.00-1.00-1.00-1.00R20.950.940.940.940.930.920.910.900.900.910.910.91
剪胀角用来表征岩石材料扩容的参量，其变化规律与体积膨胀直接相关。而从岩石的三轴试验过程可以知道，峰后阶段围岩扩容随塑性应变增加呈先急剧增加后逐步衰减的趋势，同时，由于围压的约束作用，围岩扩容随围压增加而呈衰减趋势。基于以上2方面的分析，同时结合图18,19的变化规律，构建了同时考虑围压和塑性变形影响的二维剪胀角模型，由最小二乘法进行数据拟合处理，得出了剪胀角模型的拟合公式，为
ψ=d3[exp(-d1γp)-exp(-d2γp)]+d4σ3+d5
(23)
式中，d1～d5为拟合系数。
图19 不同塑性应变下剪胀角-围压关系
Fig.19 Relationship between dilation angel and different
confining pressures under plastic shear strain
根据式(23)，对基于试验和插值的剪胀角数据进行曲面拟合，拟合系数见表7，拟合结果如图20所示。
图20 剪胀角-围压-塑性应变空间的三维拟合曲面
Fig.20 Three-dimensional fitting surface on dilation angle-
confining pressure-plastic shear strain space
表7 剪胀角-围压-塑性剪切应变曲面拟合系数
Table 7 Fitting coefficients of dilation angle with the
confining pressure and plastic shear stain
d1d2d3d4d5R20.183.4093.91-1.01-10.390.96
该指数差值型函数较好的体现了剪胀角随着围压的增加呈线性衰减，同时随着塑性剪应变的增加呈先增后减的趋势，这与实际的试验现象也是相符的。
3 模型的数值实现
利用FLAC3D 5.0程序自带的二次开发插件FLAC3D500VS2010Addin，在Visual Studio 2010开发平台中对所提出的本构模型进行项目开发。以M-C模型代码为原型进行重新编写，编写完成后须设置合适断点调试，调试成功后进行数值计算。
3.1 模型的验证
(1)初步验证。建立边长为1，仅含一个单元的立方体模型。因其只包含一个单元，因此其内部各变量应与理论值严格一致，方便检验所构建的本构模型自身的正确性。
按1.0×10-5 m/s的位移加载速率加载，不考虑重力影响，本构模型分别选取应变软化模型(S-S Model)和弹塑性耦合应变软化模型(EPCSS Model)进行计算。计算参数取自室内三轴试验结果，利用内置FISH语言，提取各变量随塑性剪应变的变化曲线，任意选择围压为30 MPa时的对比结果如图21所示。从图21中可看出，黏聚力、内摩擦角和剪胀角3个参量变化规律几乎是一致的，但由于S-S Model是采用Table差值的形式，曲线光滑度与EPCSS Model有一定差异;而对于弹性模量，S-S Model中未考虑其随塑性变形的劣化，因此是一水平线而EPCSS Model中反映出了其随塑性变形增大线性衰减直到残余的特征。
图21 FLAC3D记录的EPCSS模型与应变软化模型各
变量随塑性剪应变变化曲线
Fig.21 Variables’ changes recorded in FLAC3D
with EPCSS model and S-S model
分别提取围压为10，20和30 MPa时随塑性剪应变的变化曲线与理论值的对比如图22所示。可以看出FLAC3D计算结果与理论值具有较高的一致性，证明该模型的二次开发是正确的。
(2)试验验证。按照室内三轴压缩试验的试验尺寸和试验条件，创建模型和设置边界条件进行数值模拟。在试样四周施加相应围压，在底面设置位移约束，顶面施加竖向荷载。加载速率为1.0×10-5 m/s。由于大理石自身存在的天然孔隙，在室内压缩试验中，存在初始压密现象，因此数值模拟获得的应力应变曲线需要水平向外移动从而忽略初始压密段的影响，则在30 MPa围压下数值模拟结果与室内试验结果的对比情况如图23所示。
图22 不同围压下各参数随塑性剪切应变变化曲线
Fig.22 Variation curves of EPCSS model parameters with plastic shear strain under different confining pressures
图23 三轴压缩数值模拟应力应变曲线与试验结果对比
Fig.23 Comparison of marble simulation with the experimental
从图23可以看出，数值模拟所得的应力应变曲线与试验曲线具有较好的一致性，因此该模型能够合理揭示岩石峰后破裂阶段的体积非线性增长行为。
3.2 模型的应用
选取广泛采用的算例参数[13-14,31]:取开挖半径3 m的圆形隧道，密度ρ为 2 500 kg/m3、临界塑性应变为 2.2%，弹性模量E0为 4 GPa，泊松比μ为 0.25，支护抗力P0为 0。计算模型如图24所示，计算模型为边长 60 m的矩形，隧道周围划分为辐射性网格，在小变形及平面应变条件下进行计算。地应力σ0分别选取 5，10，15，20，25和30 MPa六个方案。
本构模型采用FLAC3D内置的M-C模型、应变软化模型(S-S Model)和弹塑性耦合应变软化模型(EPCSS Model)。M-C模型、应变软化模型的计算参数见表8，9。EPCSS模型的参数取值可按照如下方法获取，即将零围压零塑性剪切应变时的力学参数与初始条件相对应，反算得到模型参数，而后将其代入FLAC3D中进行计算。
图24 计算模型
Fig.24 Diagram for numerical simulation model
表8 M-C模型和应变软化模型计算通用参数
Table 8 Functions of material parameters in self-
constitutive model
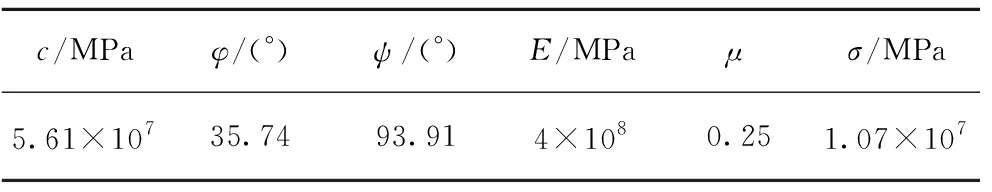
c/MPaφ/(°)ψ/(°)E/MPaμσ/MPa5.61×10735.7493.914×1080.251.07×107
表9 应变软化模型参数
Table 9 Functions of material parameters in self-constitutive model
塑性剪应变/10-20.10.20.40.60.81.01.21.41.61.82.02.2黏聚力/MPa51.2246.7338.7431.8426.0021.1016.9413.3310.227.635.423.53内摩擦角/(°)35.3735.0234.3133.6132.9232.2331.5630.9030.2429.6028.9628.33剪胀角/(°)02.3022.6331.4834.5734.7933.6131.7529.6027.3525.0822.84
从数值模拟结果可看出EPCSS模型充分体现围压和塑性剪切应变共同作用对围岩力学参数的影响。对径向位移，与S-S模型仅考虑塑性应变影响不同，EPCSS模型同时考虑了围压对强度参数的增强作用，因此塑性区面积介于2者之间，无量纲位移也介于2者之间(图25)。图25中，r/R0为无量纲半径； uE0/ (σ0R0)为无量纲径向位移。对应力分布，随初始地应力增加，塑性区扩展，与M-C模型相比，考虑强度参数劣化的S-S模型和EPCSS模型此时径向应力小于M-C模型，切向应力峰值点比M-C模型更进一步向围岩深部发展，而S-S模型由于未考虑围压的作用，上述变化比EPCSS模型更为显著(图26)。从以上变形与应力分析可以看出，在圆形隧洞开挖问题中，考虑弹塑性耦合效应的应变软化模型(EPCSS Model)能够反映:① 围岩力学参数随围压升高，在塑性区扩展有限时，与S-S模型相比，EPCSS模型的塑性区和径向位移略小;② 围岩力学参数随塑性区扩展而劣化，塑性区扩展较为快速，径向位移增长明显;③ 应力向深部传递的特征明显，从而进一步造成深部岩体的破坏。因此该模型较为合理描述了深部岩体的实际特点和工程破坏特征。
4 结 论
(1)峰后围岩力学行为归纳为受应力状态和塑性损伤共同影响。通过循环加卸载条件下的三轴压缩试验，研究了围岩峰后应变软化阶段的强度参数、变形参数和剪胀角的变化规律，构建了考虑弹塑性耦合的应变软化模型。
(2)开展大理岩的循环加卸载力学特性试验验证模型的合理性，结果表明，提出的二维面模型反映了细观力学响应与宏观变形破坏过程的一致性。随围压的增大，岩石强度、刚度增大，塑性特征增强，随塑性损伤增大，岩石刚度降低。
图25 σ3=20 MPa径向位移对比
Fig.25 Comparison of radial displacements when σ3=20 MPa
图26 σ3=20 MPa径向应力和切向应力对比
Fig.26 Comparison of radial and tangential stress when σ3=20 MPa
(3)将所提出模型在FLAC内二次开发，与S-S模型和M-C模型相比，在塑性区扩展、径向位移增长、应力场分布规律等方面都更为合理的描述了深部岩体的实际特点和工程破坏特征。
[1] 何满潮，谢和平，彭苏萍，等.深部开采岩体力学研究[J].岩石力学与工程学报,2005,24(16):2803-2813.
HE Manchao,XIE Heping,PENG Suping,et al.Study on rock mechanics in deep mining engineering[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(16):2803-2813.
[2] 张凯，周辉，冯夏庭，等.大理岩弹塑性耦合特性试验研究[J].岩土力学,2010，31(8):2425-2434.
ZHANG Kai,ZHOU Hui,FENG Xiating,et al.Experimental research on elastoplastic coupling character of marble[J].Rock and Soil Mechanics,2010,31(8):2425-2434.
[3] 曲圣年，殷有泉.弹塑性耦合和广义正交法则[J].力学学报,1982,18(1):63-70.
QU Shengnian,YIN Youquan.Elastoplastic coupling and generalized normality rule[J].Chinese Journal of Theoretical and Applied Mechanics,1982,18(1):63-70.
[4] 江权.高地应力下硬岩弹脆塑性劣化本构模型与大型地下洞室群围岩稳定性分析[D].武汉:中国科学院武汉岩土力学研究所,2007.
JIANG Quan.Study on model and stability of surrounding rock of large underground caverns under high geo-stress condition[D].Wuhan:Institute of Rock and Soil Mechanics,Chinese Academy of Sciences,2007.
[5] KANG Hongpu.Support technologies for deep and complex roadways in underground coal mines:A review[J].International Journal of Coal Science & Technology,2014,1(3):261-277.
[6] 钱七虎.非线性岩石力学的新进展--深部岩体力学的若干关键问题[A].第八次全国岩石力学与工程学术大会论文集[C].成都,2004.
QIAN Qihu.New development of nonlinear rock mechanics-some key problems of deep rock mechanics[A].Proceedings of the 8th National Conference on Rock Mechanics and Engineering[C].Chengdu,2004.
[7] MARTIN C D,CHANDLER N A.The progressive fracture of Lac du Bonnet granite[J].International Journal of Rock Mechanics & Mining Science & Geomechanics Abstracts,1994,31(6):643-659.
[8] 尤明庆，苏承东.大理岩试样循环加载强化作用的试验研究[J].固体力学学报,2008,29(1):66-72.
YU Mingqing,SU Chengdong.Experimental study on strengthening of marble specimen in cyclic loading of uniaxial or pseudo-triaxial compression[J].Chinese Journal of Solid Mechanics,2008，29(1):66-72.
[9] 张凯.脆性岩石力学模型与流固耦合机理研究[D].武汉:中国科学院武汉岩土力学研究所,2010.
ZHANG Kai.Study on mechanical model and fluid-solid coupling mechanism for brittle rocks[D].Wuhan:Institute of Rock and Soil Mechanics,Chinese Academy of Sciences,2010.
[10] 黄润秋，黄达.高地应力条件下卸荷速率对锦屏大理岩力学特性影响规律试验研究[J].岩石力学与工程学报,2010,29(1):21-33.
HUANG Runqiu,HUANG Da.Experimental research on affection laws of unloading rates on mechanical properties of jinping marble under high geostress[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(1):21-33.
[11] 张春会，徐晓攀，王锡朝，等.考虑围压影响的岩石弹脆塑力学模型[J].采矿与安全工程学报,2015，32(1):132-137.
ZHANG Chunhui,XU Xiaopan,WANG Xichao,et al.Elastic-brittle-plastic mechanical model for rock with confining pressure[J].Journal of Mining & Safety Engineering,2015，32(1):132-137.
[12] 李鹏飞，赵星光，郭政，等.北山花岗岩在三轴压缩条件下的强度参数演化[J].岩石力学与工程学报,2017,36(7):1599-1610.
LI Pengfei,ZHAO Xingguang,GUO Zheng,et al.Variation of strength parameters of Beishan granite under triaxial compression[J].Chinese Journal of Rock Mechanics and Engineering,2017,36(7):1599-1610.
[13] CUI L,ZHENG J J,ZHANG R J,et al.Elasto-plastic analysis of a circular opening in rock mass with confining stress-dependent strain-softening behaviour[J].Tunnelling and Underground Space Technology,2015,50:94-108.
[14] WANG S,YIN X,TANG H,et al.A new approach for analyzing circular tunnel in strain-softening rock masses[J].International Journal of Rock Mechanics & Mining Sciences,2010,47(1):170-178.
[15] 朱珍德，孙林柱.不同频率循环荷载作用下岩石阻尼比试验与变形破坏机制细观分析[J].岩土力学,2010，31(S1):8-12.
ZHU Zhende,SUN Linzhu.Damping ratio experiment and mesomechanical analysis of deformation failure mechanism on rock under different frequency cyclic loadings[J].Rock and Soil Mechanics,2010,31(S1):8-12.
[16] 周辉，张凯，冯夏庭，等.脆性大理岩弹塑性耦合力学模型研究[J].岩石力学与工程学报,2010,29(12):2398-2409.
ZHOU Hui,ZHANG Kai,FENG Xiating,et al.Elastoplastic coupling mechanical model for brittle marble[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(12):2398-2409.
[17] 周辉，杨凡杰，张传庆，等.考虑围压效应的大理岩弹塑性耦合力学模型研究[J].岩石力学与工程学报,2012,31(12):2389-2399.
ZHOU Hui,YANG Fanjie,ZHANG Chuanqing,et al.An elastoplastic coupling mechanical model for marble considering confining pressure effect[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(12):2389-2399.
[18] 陆银龙，王连国，杨峰，等.软弱岩石峰后应变软化力学特性研究[J].岩石力学与工程学报,2010,29(3):640-648.
LU Yinlong,WANG Lianguo,YANG Feng,et al.Post-peak strain softening mechanical properties of weak rock[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(3):640-648.
[19] 陈惠发，萨里普.弹性与塑性力学[M].北京:中国建筑工业出版社,2005.
[20] 李斌.高围压条件下岩石破坏特征及强度准则研究[D].武汉:武汉科技大学,2015.
LI Bin.Study on rock failure characteristics and ROCK strength criteria under high confining pressure[D].Wuhan:Wuhan University of Science and Technology,2015.
[21] 苏承东，韦四江，杨玉顺，等.高温后粗砂岩常规三轴压缩变形与强度特征分析[J].岩石力学与工程学报,2015,34(S1):2792-2800.
SU Chengdong,WEI Sijiang,YANG Yushun,et al.Analysis of strength and conventional triaxial compression deformation characters of coarse sandstone after high temperature[J].Chinese Journal of Rock Mechanics and Engineering,2015,34(S1):2792-2800.
[22] 刘泉声，刘恺德，朱杰兵，等.高应力下原煤三轴压缩力学特性研究[J].岩石力学与工程学报,2014,33(1):24-34.
LIU Quansheng,LIU Kaide,ZHU Jiebing,et al.Study of mechanical properties of raw coal under high stress with triaxial compression[J].Chinese Journal of Rock Mechanics and Engineering,2014,33(1):24-34.
[23] 张强，葛修润，王水林，等.考虑材料变形和破坏特性的强度折减方法研究[J].岩石力学与工程学报,2011,30(S1):2764-2769.
ZHANG Qiang,GE Xiurun,WANG Shuilin,et al.study of strength reduction method considering material deformation and failure characteristics[J].Chinese Journal of Rock Mechanics and Engineering,2011,30(S1):2764-2769.
[24] MOGI K.Experimental rock mechanics[M].Florida:CRC Press,2006:45-52.
[25] 李英杰，张顶立，刘保国.考虑变形模量劣化的应变软化模型在FLAC3D中的开发与验证[J].岩土力学,2011,32(S1):647-659.
LI Yingjie,ZHANG Dingli,LIU Baoguo.Development and verification of strain-softening model considering deformation modulus degradation in FLAC3D[J].Rock and Soil Mechanics,2011,32(S1):647-659.
[26] 吕颖慧，刘泉声，胡云华.基于花岗岩卸荷试验的损伤变形特征及其强度准则[J].岩石力学与工程学报,2009,28(10):2096-2103.
LÜ Yinghui,LIU Quansheng,HU Yunhua.Damage deformation characteristics and strength criterion based on unloading experiments of granite[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(10):2096-2103.
[27] 张浩，康毅力，陈景山，等.变围压条件下致密砂岩力学性质实验研究[J].岩石力学与工程学报,2007,26(S2):4227-4231.
ZHANG Hao,KANG Yili,CHEN Jingshan,et al.Experimental study on mechanical properties of dense sandstone under variable confining pressures[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(S2):4227-4231.
[28] 赖勇.围压对杨氏模量的影响分析[J].重庆交通大学学报(自然科学版),2009，28(2):246-249.
LAI Yong.Effect analysis of confining pressure on young’s modulus[J].Journal of Chongqing Jiaotong University (Naturalscience),2009,28(2):246-249.
[29] 尤明庆.岩石试样的杨氏模量与围压的关系[J].岩石力学与工程学报,2003,22(1):53-60.
YOU Mingqing.Effect of confining pressure on the Young’s modulus of rock specimen[J].Chinese Journal of Rock Mechanics and Engineering,2003,22(1):53-60.
[30] ZHAO X G,CAI M.A mobilized dilation angle model for rocks[J].International Journal of Rock Mechanics and Mining Sciences,2010,47(3):368-384.
[31] ZHANG Qiang,JIANG Binsong,WANG Shuilin,et al.Elasto-plastic analysis of a circular opening in strain-softening rock mass[J].International Journal of Rock Mechanics and Mining Sciences,2012,50:38-46.
