矿山工程和煤矿开采经常伴随着由于地下水压力引发的围岩失稳破坏问题出现。水-力耦合作用下岩石(体)力学特性一直是矿山岩石力学研究的热点问题之一[1-4],水-力耦合作用下岩石(体)变形过程的应力变化情况比较复杂,岩石(体)的骨架结构、应力状态与其变形相关联,许多岩石(体)工程的失稳破坏与两场耦合作用下应力与变形相关。目前许多学者在水-力耦合作用下岩石的强度、变形和破坏特性方面做了大量的研究[5-13]。陈秀铜等[5]对大理岩、砂岩和板岩进行了高水压、高围压渗流条件下的全应力-应变过程三轴压缩实验,分析了高围压、高水压对岩石强度及变形的影响;佘成学等[6]、陈子全等[7]的研究表明:在高孔隙水压力作用下,岩石的强度大大降低,破坏应变也降低,虽然破坏都是以剪切破坏为主,但在有高孔隙水压力作用下,岩石的破坏更具有突然性,其脆性破坏特征增强;李邦翔[8]、郭孔灵[9]、刘泉声[10]等分别对水-力耦合作用下岩石裂隙扩展和破坏强度进行了研究,发现随水压升高岩石起裂应力、损伤应力和峰值强度均持续降低;赵延林等[11-12]、宋战平等[13]和WANG等[14]分别研究了全应力-应变过程中灰岩、粗砂岩的水-力耦合特性,发现渗透压的存在导致岩石的峰值强度和变形模量变小,而且岩石的渗透率大小与体积应变演化密切相关。
水对岩石的力学特性有着重要的影响,孔隙率高的岩石,水很容易充满岩石内部的微孔隙裂隙,形成较强的水-力耦合效应[15-17]。但孔隙率低或极低的难渗流或不渗透岩石,水很难或无法进入岩石的微孔隙裂隙内,水对岩石的作用力只能以面力的形式作用于岩石表面,形成水-力隔离状态。尽管目前国内外在岩石水-力耦合方面取得了不少研究成果,但现有研究很少关注极低渗透率下岩石的水-力隔离作用。为揭示在水-力耦合与水-力隔离2种不同力学状态下岩石力学特性的差异性,笔者以孔道砂岩为试验对象,在MTS815岩石力学试验系统上进行不同围压和孔压下的常规三轴压缩试验,对比研究全应力-应变过程中水-力耦合和水-力隔离2种不同条件下孔道砂岩的力学特性。该研究成果对于研究水-力耦合相关的矿山突水灾害和处于水-力隔离状态的致密岩石工程(如地下储库)的稳定性具有重要理论意义和工程应用价值。
1 试验方案
1.1 孔道砂岩水-力耦合和水-力隔离的实现
孔道砂岩水-力耦合是指水压加载在孔道砂岩的内孔里,孔压渗入试件的微孔隙裂隙内,从而形成水-力耦合作用(图1(a))。水-力隔离是指孔道水压没有渗入试件的微孔隙裂隙内,孔压仅作用于试件的内孔壁上,对内孔壁形成一个面力,即为水-力隔离作用(图1(b))。进行水-力隔离试验时,在MTS815三轴腔内上下两个水压加载头之间,内置隔水装置(图2)。该隔水装置为一种高强度的胶管,该胶管穿过孔道砂岩的内孔,水压加载在胶管内,通过胶管将孔压传递给孔道砂岩内孔壁,使孔压无法渗入试件的微孔隙裂隙内。

图1 水-力耦合与隔离状态下孔道砂岩示意
Fig.1 Sketch of hollow sandstone under hydro-mechanical
coupling and isolation conditions

图2 MTS815三轴腔内孔道砂岩内壁加装隔水胶管
Fig.2 Installation of water proof hose in hollow sandstone
inside the triaxial cell of MTS815
1.2 试件制备与孔隙度测试
砂岩岩样取自湖南宝山有色金属矿业有限责任公司新建箕斗主井,埋深为203~240 m处的砂岩含水层,将其制备成内孔径为6 mm、直径50 mm、高100 mm的圆柱体标准试件,如图3所示,并用塑料薄膜进行包裹,密封岩样防止风化。该砂岩呈灰色,岩性为细砂岩,主要成分为石英。采用煮沸法测定孔道砂岩的饱和吸水率,经计算砂岩平均饱水率在4.6%左右,采用AiniMR-60核磁共振分析仪对孔道砂岩试件进行孔隙率测试,获得孔道砂岩试件的平均孔隙率为7.17%。

图3 孔道砂岩试件与尺寸
Fig.3 Hollow sandstone specimens and their sizes
1.3 试验装置和程序

图4 MTS815岩石力学试验系统
Fig.4 MTS815 rock mechanics test system
在湖南科技大学岩石力学实验室的MTS815岩石力学试验系统上进行试验(图4)。整个试验围压σ3分成10,20,30 MPa共 3个系列,每个系列围压试验中,孔压P设为4个级别,分别是围压σ3的20%,40%,60% 和80%。试验具体步骤如下:① 对水-力耦合下的岩石试件用热缩管进行包裹,对水-力隔离下的岩石试件加装隔水装置(图2),然后用热缩管进行包裹,随后将试件置于试验系统内,安装好水管、环向位移计和轴向位移计,放下三轴腔。② 以0.05 MPa/s的速率预加载轴压σ1至1 MPa,随后以0.05 MPa/s的加载速率依次加载围压σ3与孔压到试验设计值,保持轴压σ1与围压σ3的大小一致,使其达到三轴静水压力的状态(σ1=σ2=σ3)。③ 采用0.005 mm/s的加载率对试件进行轴向加载,直到试件破坏。试验过程中轴压、围压、孔压和轴向位移加载过程如图5所示。

图5 试验加载过程示意
Fig.5 Schematic diagram of test loading paths
2 水-力耦合下孔道砂岩力学特性
2.1 应力-应变曲线分析
水-力耦合下孔道砂岩力学特性试验数据见表1,代表性的偏应力-应变曲线如图6所示。可以看出,偏应力-轴向应变曲线主要分为5个阶段[18-21]。阶段I:原生孔隙裂隙压缩闭合阶段;阶段 II:线弹性变形阶段;阶段III:裂纹稳定发展阶段,岩石内部出现新生微裂纹,随着轴应力增大微裂纹稳定扩展;阶段IV:裂纹的非稳定扩展阶段,进入该阶段的应力阈值为扩容起始应力,此时岩石内部出现贯通裂纹,岩石体积开始膨胀,出现体积扩容现象;随着轴向应力进一步增大,达到峰值偏应力强度(σ1-σ3)max而破坏,出现宏观贯通裂纹;此后进入峰后阶段V:在峰后阶段,应力跌落明显,呈现出脆性破坏特征,由于围压约束作用,试件仍保持一定的残余强度。部分试件在峰后应力-应变曲线快速跌落后又出现小幅上扬,这是由于MTS岩石力学试验机具有可靠的峰后围压保持系统,在峰后,轴向应力跌落到较低水平,而围压仍保持不变,在持续的围压作用下试件破裂面摩擦咬合,当破裂面的抗剪强度高于其承载的轴向应力时,随应变的增加应力会小幅增长,直至达到破裂面的抗剪强度。
表1 力学参数对比分析
Table 1 Comparative analysis of mechanical parameters

围压σ3/MPa状态孔压P/MPa峰值偏应力强度(σ1-σ3)max/MPa变形模量E50/GPa泊松比μ残余偏应力强度/MPa扩容起始偏应力/MPa10水-力耦合水-力隔离254.435.650.3018.4734.15449.885.370.3624.7534.89644.064.860.4022.2933.26841.464.310.4311.5031.76249.496.010.3921.2632.98461.965.900.4146.4520.22663.395.630.3833.9649.15864.695.840.3644.2861.5020水-力耦合水-力隔离465.446.150.3327.1349.78859.025.180.3722.8942.401250.383.640.4115.7140.211642.622.600.4519.9535.34469.556.320.3532.7840.62872.536.460.3141.7563.191275.146.350.3454.6172.051677.966.660.2958.3575.2730水-力耦合水-力隔离674.136.430.3336.8456.971265.884.570.3537.8151.981857.843.680.3731.1041.852449.122.890.3827.6435.06682.866.670.2646.5878.781283.196.630.3070.3765.5118100.917.140.2572.3991.2424107.977.510.2279.0394.67

图6 代表性的偏应力-应变曲线
Fig.6 Representative deviatoric stress-strain curves
偏应力-体积应变曲线主要分为2个阶段:体积压缩阶段与体积扩容阶段,体积压缩阶段体积应变随应力增加而减小,达到扩容起始偏应力点时体积变形曲线向左偏转,岩石扩容。
图7为水-力耦合作用下,不同围压和孔压下孔道砂岩的偏应力-应变曲线。结合应力-应变关系曲线和表1可知:恒定围压下,随着孔压的增大,孔道砂岩的峰值偏应力强度、扩容起始偏应力、残余偏应力强度均有不同程度的减小。以围压σ3=20 MPa为例,当孔压从4 MPa增加至16 MPa时,峰值偏应力强度从65.44 MPa减至42.62 MPa,减小了34.9%;扩容起始偏应力从49.78 MPa减小至35.34 MPa,减小了29.1%;残余强度从27.13 MPa减至19.95 MPa,减小了26.5%。孔压恒定时,峰值偏应力强度、扩容起始偏应力、残余偏应力强度随围压σ3增加而增大。以孔压P=8 MPa为例,当围压σ3从10 MPa增加至20 MPa时,峰值偏应力强度从41.46 MPa增至59.02 MPa,增幅为42.4%;扩容起始偏应力从31.76 MPa增至42.4 MPa,增幅为33.5%;残余偏应力强度从11.5 MPa增至22.89 MPa,增幅达99.0%。

图7 水-力耦合下孔道砂岩的偏应力-应变曲线
Fig.7 Deviatoric stress-strain curves of hollow sandstone
under hydro-mechanical coupling condition
2.2 变形特性分析
常规三轴压缩条件下,孔道砂岩在50% 峰值强度下的变形模量E50和泊松比μ[11-12]分别为
![]()
(1)
![]()
(2)
![]()
(3)
式中,σ1为50%峰值强度时的轴向应力;σ3为作用于试件上的围压;ε1为50%峰值强度时的轴向应变;ε3为50%峰值强度时的环向应变。
图8分别为变形模量E50和泊松比μ随孔压的变化曲线,由图8可以发现:水-力耦合作用下,围压σ3保持恒定时,变形模量E50随孔压增加而减小。以围压σ3=20 MPa为例,当孔压从4 MPa增加至16 MPa时,变形模量E50从6.15 GPa减少至2.60 GPa,减少了57.7%。孔压保持恒定时,变形模量E50随围压σ3增加整体呈上升趋势,以孔压P=6 MPa为例,当围压σ3从10 MPa增加至30 MPa时,变形模量E50从4.86 GPa增加至6.43 GPa,增幅达32.3%。

图8 水-力耦合下变形模量E50和泊松比μ随孔压P的变化
Fig.8 Relationship curves of E50 and μ versus P under hydro-
mechanical coupling condition
围压σ3保持恒定时,泊松比μ随孔压的增加而增大,同时随着围压σ3的增大,泊松比μ随孔压增加的趋势逐渐减缓。以围压σ3=20 MPa为例,当孔压从4 MPa增加至16 MPa时,泊松比μ从0.33 增加至0.45。当孔压P保持恒定时,泊松比μ随围压σ3增加整体呈下降趋势。以孔压P=6 MPa为例,当围压σ3从10 MPa增加至30 MPa时,泊松比μ从0.40减小至0.33。
2.3 有效峰值强度分析
水-力耦合下,孔道砂岩固体骨架之间的孔隙在压缩过程中将受到轴压、围压与孔压共同作用。为进一步分析孔道砂岩的水力耦合效应,引入有效轴向应力σ′1(轴向应力σ1与孔压P的差值)与有效围压σ′3(围压σ3与孔压P的差值)。在常规的三轴试验中,有效最小主应力就是有效围压σ′3;有效偏应力σ′d为有效轴向应力σ′1与有效围压σ′3的差值。孔道砂岩的有效峰值强度σ′1,max 和有效最小主应力σ′3 可以通过下式计算:
σ′1,max=σ1,max-P
(4)
σ′3=σ3-P
(5)
图9为水-力耦合下有效峰值强度σ′1,max与有效最小主应力σ′3的关系曲线。由图9可知,有效峰值强度σ′1,max随有效围压σ′3增加呈线性增长。对有效峰值强度σ′1,max与最小主应力σ′3之间的关系进行拟合:
σ′1,max=kσ′3+d
(6)
式中,k,d为拟合参数,k=2.53,d=39.23。

图9 水-力耦合下有效峰值强度σ′1,max与有效最小主
应力σ′3 关系曲线
Fig.9 Relationship curve of σ′1,max versus σ′3 under hydro-
mechanical coupling condition
根据莫尔-库伦屈服准则,有效峰值强度σ′1,max与最小主应力σ′3之间的关系可以表示为
![]()
(7)
获得水-力耦合作用下,饱水砂岩的有效黏聚力c′=1.04 MPa,有效内摩擦角φ′=33.95 MPa。
3 水-力隔离下孔道砂岩力学特性
3.1 应力-应变关系曲线分析
水-力隔离下孔道砂岩力学特性试验数据见表1,偏应力-应变曲线如图10所示。类似于水-力耦合,偏应力-轴向应变曲线也可分为5个阶段,其偏应力-体积应变曲线可分为2个阶段。
处于水-力隔离状态下的孔道砂岩试件在恒定围压下,随孔压的增大,孔道砂岩的峰值偏应力强度、扩容起始偏应力、残余偏应力强度均有不同程度的增加。以围压σ3=20 MPa为例,当孔隙水压从4 MPa增至16 MPa时,峰值偏应力强度从69.55 MPa增至77.96 MPa,增幅为12.1%;扩容起始偏应力从40.62 MPa增至75.27 MPa,增幅达85.3%;残余偏应力强度从32.78 MPa增至58.35 MPa,增幅达78.0%。孔压恒定时,孔道砂岩的峰值偏应力强度、扩容起始偏应力、残余偏应力强度随围压σ3增加而增大。以孔压P=6MPa为例,当围压σ3从10 MPa增加至30 MPa时,峰值偏应力强度从63.39 MPa增至82.86 MPa,增幅为30.7%;扩容起始偏应力从49.15 MPa增至78.78 MPa,增幅达60.3%;残余偏应力强度从33.96 MPa增至46.58 MPa,增幅为37.2%。
3.2 变形特性分析
为研究水-力隔离状态下,围压σ3和孔压P对孔道砂岩变形特性的影响,由式(1)~(3)计算获得试件的变形模量E50和泊松比μ。获得水-力隔离状态下变形模量E50、泊松比μ随孔压P的变化规律(图11)。

图10 水-力隔离状态下孔道砂岩的偏应力-应变曲线
Fig.10 Deviatoric stress-strain curves of hollow sandstone
under hydro-mechanical isolation condition

图11 水-力隔离下变形模量E50和泊松比μ随孔压P的变化
Fig.11 Relationship curves of E50 and μ versus P under
hydro-mechanical isolation condition
水-力隔离状态下,围压σ3保持恒定时,除围压σ3=10 MPa外,在σ3=20 MPa和30 MPa的情况下,随孔压增加,变形模量 E50整体呈上升趋势(图11(a))。以围压σ3=30 MPa为例,当孔压从6 MPa增加至24 MPa时,变形模量E50从6.67 GPa增加至7.51 GPa;当孔压一定时,随围压σ3的增长,试件的变形模量 E50同步增加。如在孔压P=6 MPa下,当围压σ3从10 MPa增加至30 MPa时,E50从5.63 GPa增加至6.67 GPa。在围压σ3一定下,泊松比μ随孔压的增加整体呈减小趋势(图11(b))。以围压σ3=30 MPa为例,当孔压从6 MPa增加至24 MPa时,泊松比μ从0.26减小至0.22;当孔压一定时,试件泊松比 μ随围压σ3的增加整体呈减小趋势。以孔压P=6 MPa为例,当围压σ3从10 MPa增加至30 MPa时,泊松比μ从0.38减小至0.26。
3.3 平均应力梯度分析
水-力隔离状态下在围压σ3和孔压P共同作用下,孔道砂岩内部的径向应力σr和切向应力σθ分布如图12所示,其大小由式(8)计算得到:
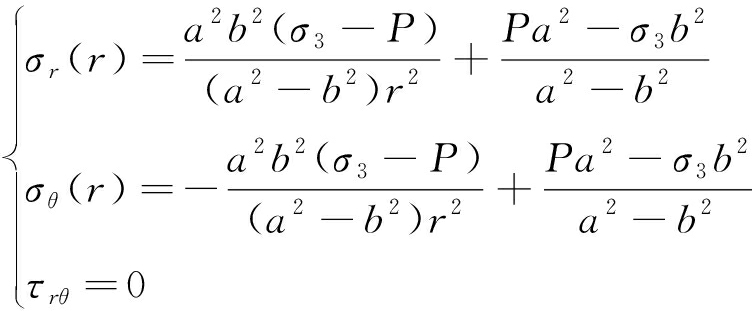
(8)
式中,a和b为孔道砂岩试样的内半径和外半径;r为离孔道中心的径向距离;τrθ为剪切应力;θ为极坐标中的环向坐标。

图12 垂直于轴向截面的平面应力分析
Fig.12 A plane stress diagram perpendicular to the axial section
由式(8)可知,外力一定时,径向应力σr和切向应力σθ随着r的改变而改变,因此在围压和孔压共同作用下,平面径向和切向应力场是非均匀的。为了表征总体应力场的变化和径向应力场的不均匀程度,引入平均应力梯度的概念,径向和切向应力的平均应力梯度![]() 和
和![]() 分别为
分别为
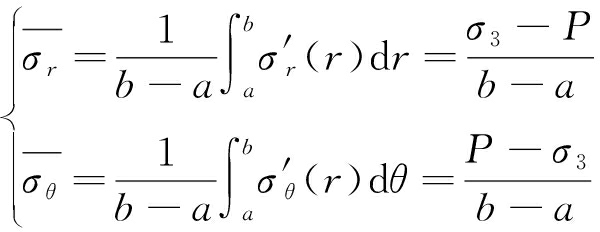
(9)
其中,σ′r(r)和σ′θ(r)分别为微元体上的径向和切向应力梯度;![]() 这表明径向和切向应力场的走势是一致的。当孔压P与围压σ3相等时,平均径向应力梯度
这表明径向和切向应力场的走势是一致的。当孔压P与围压σ3相等时,平均径向应力梯度![]() 此时孔道试件等同于实心试件,当孔压为0时,平均径向应力梯度
此时孔道试件等同于实心试件,当孔压为0时,平均径向应力梯度![]() 有最大值。孔道砂岩的峰值偏应力强度与其平均径向应力梯度关系如图13所示。
有最大值。孔道砂岩的峰值偏应力强度与其平均径向应力梯度关系如图13所示。

图13 水-力隔离下孔道砂岩的峰值偏应力强度与平均
径向应力梯度的关系曲线
Fig.13 Relation curves between peak deviatoric stress and
average radial stress gradient under hydro-mechanical
isolation condition
当围压σ3恒定、P<σ3时,随孔压的增加,平均径向应力梯度减小,峰值偏应力强度呈非线性增长趋势。这表明,水-力隔离下在孔道砂岩内孔壁施加适量应力可以明显提高试件的三轴承载力。以围压σ3=30 MPa为例,当孔压P=6 MPa时,![]() 峰值偏应力强度为82.86 MPa,当孔压增加到24 MPa时,
峰值偏应力强度为82.86 MPa,当孔压增加到24 MPa时,![]() MPa/mm,峰值偏应力强度为107.97 MPa,增幅达30.3%。
MPa/mm,峰值偏应力强度为107.97 MPa,增幅达30.3%。
4 讨 论
4.1 力学特性对比
图14为水-力耦合与水-力隔离2种不同力学状态下,峰值偏应力强度、变形模量、扩容起始偏应力和泊松比随孔压的变化规律。对比分析发现:除个别离散点外,总体上在围压σ3与孔压相同的情况下,处于水-力隔离状态下试件的峰值偏应力强度和变形模量要大于水-力耦合状态下的相应量值,但与泊松比的关系趋于相反,而且随围压和孔压的增加以上变化趋势愈明显。
用水-力隔离状态下的峰值偏应力强度和变形模量除以水-力耦合状态下的相应值,获得水-力隔离下强度增强系数λS 和模量增强系数λE:
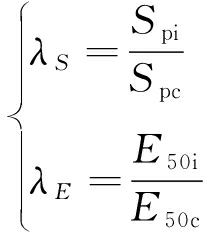
(10)
式中,Spi,Spc 分别为水-力隔离和耦合状态下的峰值偏应力强度;E50i,E50c 分别为水-力隔离和耦合状态下的变形模量。
水-力隔离下强度增强系数λS 和模量增强系数λE随孔压的变化规律也显示在图14(a),(b)中,可以发现:随着孔压的增加,λS和λE 非线性增长,如围压σ3=30 MPa下,当孔压从6 MPa增至24 MPa时,λS和λE分别从1.11增至2.20,从1.04增加到2.59。这表明随着孔压的增加,水-力耦合与水-力隔离2种力学状态下岩石力学特性的差异越大。
4.2 破裂模式对比
图15,16分别为水-力耦合与水-力隔离2种不同力学状态下试件破裂模式。可以发现:水-力耦合下试件呈现出明显的剪切破裂,且剪切破裂面单一,破裂角分布在53°~69°,在较低围压10 MPa和20 MPa下,随孔压的增加破裂角逐渐增大,破裂面向轴向偏移。以围压σ3=20 MPa下的试件为例,孔压从4 MPa增加到16 MPa时,试件破裂角从55°增加到69°。而在较高围压30 MPa下,试件的破裂角先增后减,当孔压达到24 MPa时,试件出现X型剪切破坏的痕迹。这种破裂面向轴向偏移和X型共轭破坏的出现,表明在当孔压接近围压时,试件会呈现出类似单轴破坏的形式。
而水-力隔离下试件破裂角随孔压的变化不明显,随围压的增加,试件中剪切细小裂纹和轴向细小裂纹增加,试件出现多个剪切破裂面,主破裂面和最小主应力的夹角约为60°,与围压和孔压的关系不大。剪切破坏主导试件破坏形式,平均径向应力梯度的变化对试件破裂模式没有明显影响。

图14 水-力耦合与隔离2种状态下峰值偏应力强度、变形模量、扩容起始偏应力和泊松比的对比
Fig.14 Comparisons of peak deviatoric stress,deformation modulus,initial expansion deviatoric stress and Poisson’s ratio under
hydro-mechanical coupling and isolation conditions

图15 水-力耦合状态下试件破裂模式
Fig.15 Failure mode of under hydro-mechanical coupling condition

图16 水-力隔离状态下试件破裂模式
Fig.16 Failure mode of under hydro-mechanical isolation condition
4.3 工程意义
水-力耦合和水-力隔离分别对应于2种不同的水岩相互作用状态。地下含水层(如砂岩,灰岩含水层)大多为孔隙率较高的岩层,其水-力耦合效应显著。开采(挖)导致地下含水层渗流场发生变化,在变化的水力梯度驱动下,围岩渗透压发生改变,其水-力耦合状态随之变化,研究不同孔压下岩石的水-力耦合特性对于揭示诸如矿山开采突水、立井掘进突水和岩溶隧道涌突水等灾害机理有重要理论意义和工程应用价值。
水-力隔离问题是针对极低渗透岩石工程中的一类力学问题,对于极低渗透岩石(如花岗岩,盐岩),流体很难或无法进入岩石的微孔隙裂隙内,从而形成水-力隔离状态。水-力隔离问题研究在核废弃物的地下埋储、地下油气储藏等致密岩石工程领域都具有非常重要的意义。研究发现水-力隔离下在孔道内孔壁施加适量应力可以明显提高试件的三轴承载力,这一研究成果对于合理确定致密岩石储库工程的运行内压有理论参考价值。
5 结 论
(1)水-力耦合状态下,孔道砂岩的峰值偏应力强度、扩容起始偏应力、残余偏应力强度和变形模量与围压呈正相关关系,与孔压呈负相关关系,而泊松比的关系则正好相反。
(2)水-力隔离状态下孔道砂岩试件径向应力分布不均匀,峰值偏应力强度、扩容起始偏应力和残余偏应力强度均与围压和孔压在总体上呈正相关趋势,该状态下在内孔壁施加适量应力可以明显提高试件的三轴承载力。
(3)在一定的围压与孔压下,处于水-力耦合下试件峰值偏应力强度和变形模量在总体上要低于水-力隔离状态下的相应量值,而泊松比的关系则正好相反;随孔压的增加2种力学状态下的岩石力学特性差异越大。
(4)水-力耦合状态下试件呈现出明显的单一剪切面破裂,破裂角分布在53°~69°变化,而水-力隔离状态下试件破裂角变化不明显。
[1] DUBE A K SINGH B.Effect of humidity on tensile strength of sandstone[J].Journal of Mines,Metals & Fuels,1972,20(1):8-10.
[2] BAUD P,ZHU W,WONG T.Failure mode and weakening effect of water on sandstone[J].Journal of Geophysical Research:Solid Earth,2000,105(B7):16371-16389.
[3] 邢福东,朱珍德,刘汉龙,等.高围压高水压作用下脆性岩石强度变形特性试验研究[J].河海大学学报(自然科学版),2004,32(2):184-187.
XING Fudong,ZHU Zhende,LIU Hanlong,et al.Experimental study on strength and deformation characteristics of brittle rocks under high confining pressure and hydraulic pressure[J].Journal of Hohai University(Natural Sciences),2004,32(2):184-187.
[4] 李根,唐春安,李连崇.水岩耦合变形破坏过程及机理研究进展[J].力学进展,2012,42(5):593-619.
LI Gen,TANG Chunan,LI Lianchong.Advances in rock deformation and failure process under water-rock coupling[J].Advances in Mechanics,2012,42(5):593-619.
[5] 陈秀铜,李璐.高围压、高水压条件下岩石卸荷力学性质试验研究[J].岩石力学与工程学报,2008,27(S1):2694-2699.
CHEN Xiutong,LI Lu.Experimental study of unloading mechanical properties of rock under high confining pressure and high water pressure[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(S1):2694-2699.
[6] 佘成学,崔旋.高孔隙水压力对岩石蠕变特性的影响[J].岩石力学与工程学报,2010,29(8):1603-1609.
SHE Chengxue,CUI Xuan.Influence of high pore water pressure on creep properties of rock[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(8):1603-1609.
[7] 陈子全,李天斌,陈国庆,等.水力耦合作用下的砂岩声发射特性试验研究[J].岩 土 力 学,2014,35(10):2815-2822.
CHEN Ziquan,LI Tianbin,CHEN Guoqing,et al.Experimental study of acoustic emission characteristics of sandstone under hydro-mechanical coupling action[J].Rock and Soil Mechanics,2014,35(10):2815-2822.
[8] 李邦翔,朱维申,杨磊,等.水力耦合作用下三维中空裂隙扩展模式与材料破坏强度的试验研究[J].中南大学学报(自然科学版),2019,50(5):1192-1202.
LI Bangxiang,ZHU Weishen,YANG Lei,et al.Experimental research on propagation mode of 3D hollow crack and material failure strength under hydro-mechanical coupling[J].Journal of Central South University (Science and Technology),2019,50(5):1192-1202.
[9] 郭孔灵,杨磊,盛祥超,等.水力耦合作用下含三维裂隙类岩石材料的破裂力学行为及声发射特征[J].岩土力学,2019,40(11):4380-4390.
GUO Kongling,YANG Lei,SHENG Xiangchao,et al.Fracture mechanical behavior and AE characteristics of rock-like material containing 3-D crack under hydro-mechanical coupling[J].Rock and Soil Mechanics,2019,40(11):4380-4390.
[10] 刘泉声,刘学伟.多场耦合作用下岩体裂隙扩展演化关键问题研究[J].岩土力学,2014,35(2):305-320.
LIU Quansheng,LIU Xuewei.Research on critical problem for fracture network propagation and evolution with multifield coupling of fractured rock mass[J].Rock and Soil Mechanics,2014,35(2):305-320.
[11] ZHAO Y L,TANG J Z,CHEN Y,et al.Hydromechanical coupling tests for mechanical and permeability characteristics of fractured limestone in complete stress-strain process[J].Environmental Earth Sciences,2017,76:1-18.
[12] 赵延林,付成成,汪亦显,等.全应力-应变过程中裂隙灰岩的水-力耦合特性试验研究[J].岩石力学与工程学报,2016,35(S2):3763-3773.
ZHAO Yanlin,FU Chengcheng,WANG Yixian,et al.Tests on hydro-mechanical coupling characteristics of fractured limestone in complete stress-strain process[J].Chinese Journal of Rock Mechanics and Engineering,2016,35(S2):3763-3773.
[13] 宋战平,程昀,杨腾添,等.渗透-应力耦合作用下灰岩压缩破坏及声发射特性分析[J].煤炭学报,2019,44(9):2751-2759.
SONG Zhanping,CHENG Yun,YANG Tengtian,et al.Analysis of compression failure and acoustic emission characteristics of limestone under permeability-stress coupling[J].Journal of China Coal Society,2019,44(9):2751-2759.
[14] WANG L,LIU J F,PEI J L,et al.Mechanical and permeability characteristics of rock under hydro-mechanical coupling conditions[J].Environmental Earth Sciences,2015,73(10):5987-5996.
[15] 王广荣,薛东杰,郜海莲.煤岩全应力-应变过程中渗透特性的研究[J].煤炭学报,2012,37(1):107-112.
WANG Guangrong,XUE Dongjie,GAO Hailian,et al.Study on permeability characteristics of coal rock in complete stress-strain process[J].Journal of China Coal Society,2012,37(1):107-112.
[16] 陈跃都.水力耦合作用下岩体粗糙裂隙渗流及滑移失稳机理研究[D].太原:太原理工大学,2018.
CHEN Yuedu.study on flow and slip instability mechanism in rough rock fractures under hydro-mechanical coupling effects[D].Taiyuan:Taiyuan University of Technology,2018.
[17] 薛维培,李昊鹏,姚直书,等.考虑脆性损伤和水力耦合影响的立井井壁临界突水水压理论解[J].采矿与安全工程学报,2019,36(3):566-573.
XUE Weipei,LI Haopeng,YAO Zhishu,et al.Theoretical solutions to critical water inrush pressure in vertical shaft lining under the influence of brittle damage and hydraulic coupling[J].Journal of Mining & Safety Engineering,2019,36(3):566-573.
[18] CHEN Xu,YU Jin,TANG Chunan,et al.Experimental and numerical investigation of permeability evolution with damage of sandstone under triaxial compression[J].Rock Mechanics and Rock Engineering,2017,50(6):1529-1549.
[19] BIENIAWSKI Z T.Mechanism of brittle fracture of rock[J].International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts,1967,4(4):395-430.
[20] MARTIN C D,CHANDLER N A.The progressive fracture of Lac du Bonnet granite[J].International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts,1994,31(6):643-659.
[21] GOKTAN R M,YILMAZ N G.A new methodology for the analysis of the relationship between rock brittleness index and drag pick cutting[J].The Journal of the South African Institute of Mining and Metallurgy,2005,105:727-733.
