黏土岩是深部地下工程中常见的岩土介质,这一介质具有非常复杂的物理力学性质[1]。为在施工过程中选择合理的支护措施[2],需对其力学特性进行研究。LI[3]通过CT扫描技术对黏土岩试样进行观测后发现,在各向等压渗透试验后黏土岩内部会产生大量的微裂纹。因此构建合理的本构模型来反应其力学特性对深部地下工程施工尤为重要。
近些年损伤力学的发展为这种加载过程中内部产生缺陷的岩土材料的力学性能研究提供了一种方法。细观损伤力学采用平均化的方法将材料的细观损伤机制反映到宏观的力学行为中,这种方法既避免了复杂的统计学计算,又可以提供很好的物理背景。
陈新等[4]将岩土材料假设成含微孔洞的球形单元集合体,将微孔洞作为损伤基元,通过微孔洞所占比例大小来衡量损伤程度,提出了适用于花岗岩的塑性损伤模型。韦立德等[5]综合考虑剪胀效应对岩体变形和渗流的影响以及损伤对于岩体渗流的影响提出了岩石损伤本构模型。谢和平等[6]认为岩石的变形与破坏是一个与外界能量交换的过程,基于能量耗散原理建立了损伤演化的宏-细-微观多层次岩石力学体系。SHAO等[7]对岩石的损伤演化与微裂纹发展进行了系统的研究,建立连续损伤模型,分析非饱和条件下损伤对于岩石渗透系数的影响并建立流固耦合有限元模型。WANG等[8]通过分析强度准则和残余强度对岩土材料的软化影响建立了统计损伤模型并考虑了软化效应。王军详等[9]在弹塑性理论和损伤理论的基础上引入修正有效应力原理建立适用于脆性岩石的弹塑性损伤本构模型。袁小平等[10]认为软化分为塑性软化和损伤软化,损伤软化是由于岩石内部微裂纹的扩展引起。基于Drucker-Prager准则建立适用于脆性岩石的弹塑性损伤本构模型。陈亮等[11]基于北山花岗岩的试验结果,通过岩石的宏观力学性能推导岩石在外力作用下微裂纹的发展规律,在热力学框架的基础下提出了适用于花岗岩的唯象弹塑性损伤本构模型。
笔者以黏土岩为研究对象,将黏土岩内部的微裂纹作为损伤基元在修正Drucker-Prager帽盖模型的基础上引入了塑性损伤和硬化,构建了适用于黏土岩的本构模型。基于有限元软件ABAQUS,在UMAT子程序中将塑性硬化和损伤引入迭代算法中编制了该模型的本构程序。通过对常温条件下黏土岩的三轴压缩试验进行数值模拟,并与试验结果进行比较,对比结果表明新模型不仅可以很好地反映黏土岩的硬化和软化现象,还很好的反映了黏土岩的塑性流动特性。最后将新模型应用在黏土岩隧硐开挖算例上,验证了新模型在地下工程施工数值模拟上的适用性。
1 基于塑性损伤的黏土岩本构模型
龚哲,于洪丹等[12-13]等对黏土岩进行了一系列的三轴压缩试验,试验结果表明黏土岩是一种具有明显硬化和软化现象的介质,且整个试验过程的应力-应变曲线可以划分为4个阶段,分别为:弹性阶段、塑性硬化阶段、塑性软化阶段以及塑性流动阶段。
1.1 屈服函数与塑性势函数
BALDI等[14]在总结大量试验结果的基础上得到了黏土岩的屈服面,发现Drucker-Prager对于黏土岩的力学行为描述更加准确。在修正Drucker-Prager准则的基础上引入“帽盖模型”来描述黏土岩在静水压力下屈服的特性[15]。修正Drucker-Prager帽盖模型的屈服函数由剪切屈服面和帽盖屈服面两段组成,连接处光滑,在p′-q平面内的屈服面如图1所示,图1中,b=(αpa+k)。
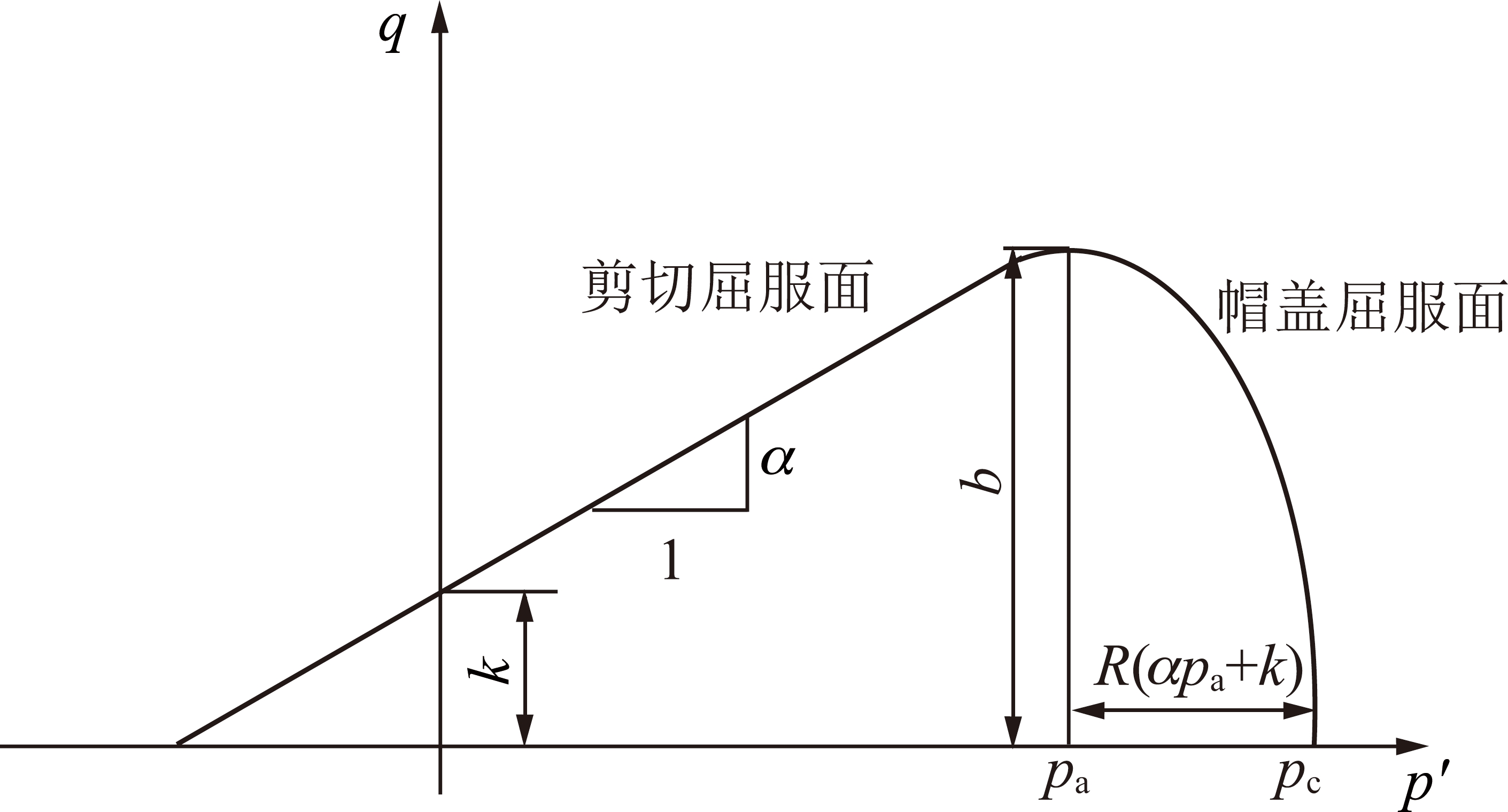
图1 修正Drucker-Prager帽盖模型
Fig.1 Modified Drucker-Prager cap model
其中剪切屈服面Fs的表达式为
Fs=q-αp′-k=0
(1)
式中,![]() 为一种运算符号,求解矩阵的迹,即对角线元素之和,
为一种运算符号,求解矩阵的迹,即对角线元素之和,![]() 为应力张量,s为偏应力张量,δ为Kronecker函数;a和k分别为剪切屈服面在p′-q平面上的斜率和截距,其表达式为
为应力张量,s为偏应力张量,δ为Kronecker函数;a和k分别为剪切屈服面在p′-q平面上的斜率和截距,其表达式为
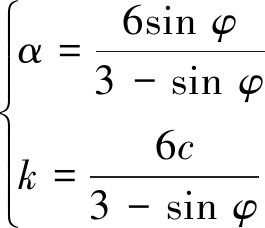
(2)
式中,φ,c分别为内摩擦角(°)和黏聚力(Pa)。
帽盖屈服面Fc为一段椭圆弧,其表达式为
![]()
(3)
其中,R为控制帽盖几何形状的参数;pa的表达为
![]()
(4)
式中,pc为先期固结应力,Pa。
传统塑性力学中假设塑性势函数与屈服函数采用相同的数学表达式,即在计算过程中采用关联流动法则。但是关联流动法则并不适用于岩土材料,已经有证据证明岩土材料的屈服函数与塑性势函数并不相同,因此塑性计算时应当采用非关联流动法则[16]。
本文假设塑性势函数与屈服函数形状相似但数学表达式不相同[17],其两段表达式Gs和Gc分别为
Gs=q-α′p′-k′=0
(5)
![]()
(6)
式中,Gs,Gc分别为剪切屈服面Fs对应的塑性势函数和帽盖屈服面Fc对应的塑性势函数; a′和k′表达式为
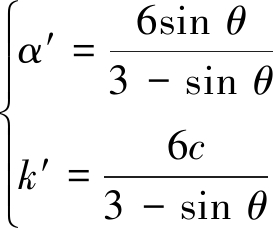
(7)
式中,θ为膨胀角,(°)。
1.2 硬化变量及损伤变量演化方程
本文考虑使用损伤理论来描述黏土岩内部的缺陷[18-19]。损伤理论从细观力学的角度解释了材料力学性能的弱化,黏土岩在加载过程中会产生很多微裂纹[20-22],微裂纹在加载过程中不断地扩展与聚集,从而引起材料力学性能的下降[23]。已有试验研究也证实了黏土岩在加载过程中存在微裂纹扩展的现象[13,24]。笔者将以微裂纹作为损伤基元构建损伤变量,并引入到本构模型中来描述黏土岩的力学特性。
1.2.1 塑性损伤变量
在塑性阶段认为塑性损伤是存在于整个塑性过程中的,选择合理的损伤演化方程对于描述黏土岩的塑性软化和塑性流动十分重要。随着塑性应变的不断累积,塑性损伤不断增大。然而,由于明显的塑性流动阶段的存在,假设的塑性损伤不能随着塑性应变一直增大,而应存在一个上限值,接近上限值时塑性损伤几乎不变,材料进入塑性流动阶段。塑性损伤变量Dp演化方程为
![]()
(8)
式中,![]() 为塑性损伤变量Dp的上限值;α1和βp为模型参数;ξp为等效塑性应变。
为塑性损伤变量Dp的上限值;α1和βp为模型参数;ξp为等效塑性应变。
1.2.2 塑性硬化变量
黏土岩的应力-应变曲线的塑性阶段在宏观上先表现为硬化。因此,为了描述其塑性硬化力学特性引入合理的硬化法则十分重要。本文采用双曲线型塑性硬化方程,塑性硬化变量hp表达式为
![]()
(9)
式中,hp0和bp为模型参数。
SCHMERTMANn和OSTERBERG[25],LAMBE[26]以及HAJIABDOLMAJID等[27]对不同的岩土材料研究发现在三轴压缩试验过程中,当材料进入塑性阶段后内摩擦角随着应变的累积呈负指数的形式升高,此后并没有明显的降低,而黏聚力在整个塑性过程中随着应变的累积先增大后减小。
因此模型中黏聚力c和内摩擦角φ的演化方程采用:
![]()
(10)
式中,c0为黏聚力的初始值,Pa;φ0为内摩擦角的初始值,(°)。
先期固结应力pc的演化受塑性体应变的影响,其表达式为
![]()
(11)
式中,pc0为先期固结应力的初始值,Pa;cp为模型参数;![]() 为塑性体应变。
为塑性体应变。
2 本构积分算法
进入塑性阶段时,材料本身的屈服面会随着塑性应变的累积(硬化变量和损伤变量的变化)不断地发生变化(硬化过程屈服面扩张/软化过程屈服面收缩),且在屈服面变化的整个过程应力始终位于屈服面之上。第1节给出了塑性阶段屈服面的变化规律,本节将介绍在屈服面变化过程中如何通过数值方法使得应力始终位于屈服面之上。
塑性阶段计算时,先假设只发生弹性变形,计算弹性试探应力,当试探应力超出屈服面时,需要通过本构积分算法[28-30]将超出屈服面的应力拉回到屈服面上。

图2 本构积分算法示意
Fig.2 Schematic diagram of constitutive integral algorithm
本文采用的积分算法除了考虑塑性硬化变量之外,还引入了塑性损伤变量,在算法迭代过程中塑性硬化变量和塑性损伤变量将随着塑性应变的变化与应力一起进行调整,并通过更新后的塑性硬化变量和塑性损伤变量对屈服面进行更新,从而使得每一个增量步更新后的应力始终位于更新后的屈服面上(图2)。
2.1 向后欧拉式本构积分算法
由弹塑性增量理论可知,应变增量可以写成:
Δε=Δεe+Δεp
(12)
式中,Δε,Δεe,Δεp分别为总应变增量、弹性应变增量和塑性应变增量的二阶张量。
本文采用非关联流动法则,则塑性应变增量的形式可以写成
![]()
(13)
其中,dλi为塑性因子;σ为应力二阶张量;G为塑性势函数。塑性势函数求导如下:
![]()
(14)
![]()
(15)
式(15)中平均主应力p′和偏应力q对应力张量的求导结果写成向量矩阵的形式:
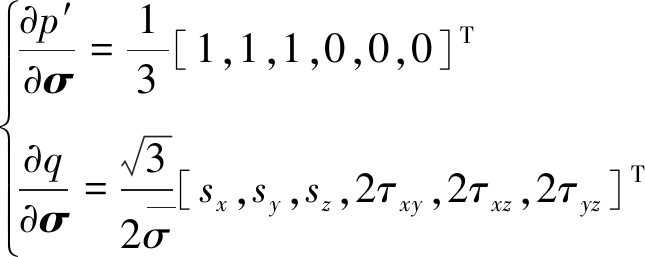
(16)
式中,![]() 其中,J2为偏应力第二不变量;sx=σx-(σx+σy+σz)/3;sy=σy-(σx+σy+σz)/3;sz=σz-(σx+σy+σz)/3,σx,σy,σz,τxy,τxz,τyz为6个应力分量。
其中,J2为偏应力第二不变量;sx=σx-(σx+σy+σz)/3;sy=σy-(σx+σy+σz)/3;sz=σz-(σx+σy+σz)/3,σx,σy,σz,τxy,τxz,τyz为6个应力分量。
当增量步开始时,假设该增量步内的总应变增量全部是弹性应变增量,则可根据下式计算第n+1增量步的弹性试探应力![]()
![]()
(17)
式中,De为刚度矩阵的张量形式;σn为上一增量步结束时应力张量;Δεn+1为第n+1增量步的应变增量张量。
当试探应力超出屈服面时,需要通过向后欧拉算法将其拉回到屈服面上。进入塑性阶段后实际应力为
![]()
(18)
式中,![]() 为第n+1增量步的塑性应变增量张量。
为第n+1增量步的塑性应变增量张量。
将式(13),(17)代入式(18)可得
![]()
(19)
式中,Δλn+1为更新后的塑性因子。
此时的应力状态σn+1需要满足一致性条件,即
F[(p′)n+1,qn+1,(Dp)n+1,(hp)n+1]=0
(20)
式中,(p′)n+1,qn+1,(Dp)n+1和(hp)n+1分别为更新后的平均主应力、偏应力、塑性损伤变量和塑性硬化变量。
将式(13)代入式(8),(9)中可得到塑性硬化变量和塑性损伤变量:
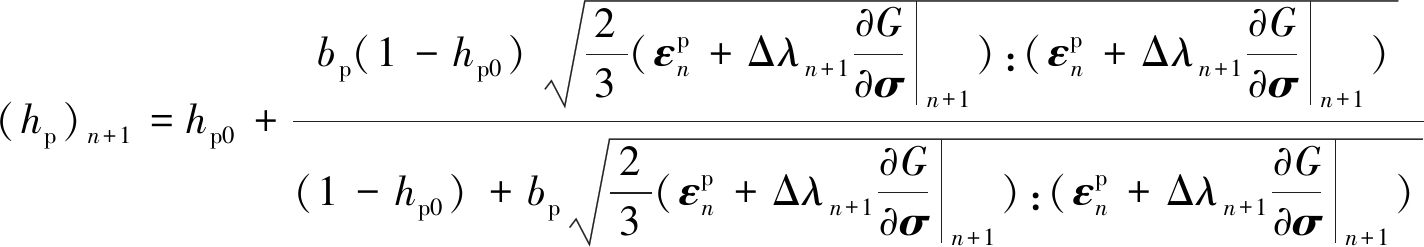
(21)
![]()
(22)
将式(21)和式(22)代入式(20)中可以消除未知量(Dp)n+1和(hp)n+1。则式(19)和(20)变成求解σn+1和Δλn+1的隐式方程组,采用牛顿法求解得Δλn+1和更新后的应力σn+1。将Δλn+1代回到式(21)和(22)更新硬化变量和损伤变量再带回式(20)更新屈服面。
2.2 一致性切线刚度矩阵
由前人的研究结果可知[31],在本构积分算法中一致切线刚度矩阵可以在提高计算精度和稳定性的同时加速收敛。
向后欧拉算法式(19)可以写成矩阵形式:
![]()
(23)
对式(23)进行微分可得
![]()
(24)
对式(24)进行化简可以得到
![]()
(25)
式中,I为单位矩阵。
根据一致性准则可得
![]()
(26)
将式(25)代入式(26)并化简可得
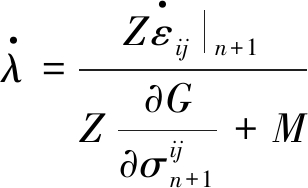
(27)
式中,![]()
将式(27)代入式(25)中可以得到
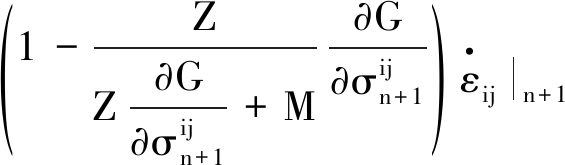
(28)
则一致切线刚度矩阵的表达式为
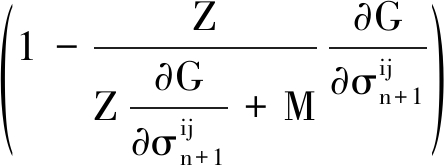
(29)
式中,Dct为一致性刚度矩阵。
2.3 UMAT子程序调用流程
ABAQUS提供了用Fortran语言编写的UMAT子程序接口,供用户二次开发之用。ABAQUS每个增量步计算流程大致如下(图3):
(1)增量步开始时,ABAQUS会将应力、应变、应变增量以及时间增量传输给UMAT子程序,同时通过PROPS(n)将固体参数导入子程序中,通过子程序计算得到新的应力、应变以及一致切线刚度矩阵返回主程序中。
(2)ABAQUS主程序再调用流体参数并通过SOILS分析步进行平衡迭代计算。
(3)如若迭代不收敛或者迭代达到最大次数,则减小增量步时长重新开始计算;如若迭代收敛则更新应力、应变以及其他参数,进入下一增量步开始计算。

图3 ABAQUS调用UMAT子程序计算流程
Fig.3 Calculation flow chart of ABAQUS calls UMAT subroutine
3 黏土岩三轴压缩试验数值模拟
编写新模型的UMAT子程序,经编译调试后对常温条件下黏土岩的三轴压缩试验进行有限元模拟,并与室内试验结果进行比较验证该子程序的有效性。
3.1 试验结果
常温条件下,黏土岩三轴压缩试验在双联动软岩渗流-应力耦合流变仪上进行[13]。试验考虑不同初始围压条件(4.7,3.7 MPa),初始孔压1.2 MPa,采用不排水压缩(压缩速率20 μm/min),得到应力-应变曲线和超孔压曲线,如图4所示。从图4可以看出,黏土岩进入塑性阶段之后,除了有非常明显的塑性硬化外,还有明显的塑性软化以及塑性流动现象;整个加载过程中试样的孔隙水压力在逐渐增大,且进入塑性阶段后,其增长速率逐渐减小。

图4 黏土岩不同围压下三轴压缩试验曲线[13]
Fig.4 Triaxial compression test curves of claystone under different confining pressures[13]
3.2 模型参数反演及模拟结果对比
建立黏土岩试样有限元模型(图5),模型直径为38 mm、高度为76 mm,模型采用HM耦合4节点轴对称减缩积分单元(CAX4RP),约束试样底部轴向自由度和轴心径向自由度。模型四周为不排水边界。按照试验流程施加相应的围压和孔压,再对模型顶部施加轴向位移。

图5 试验模拟有限元模型
Fig.5 Finite element model of test simulation
表1中给出了黏土岩数值模拟的主要物理参数。这些参数是通过大量的现场试验、室内试验以及现场声波探测得到的结果[32]。模型中有关参数主要通过反演获得。反演过程中的对比试验数据为三轴压缩试验所得应力-应变曲线,反演采用贾善坡[33]提出的Nelder-Mead法与有限元联合反演法,将有限元程序作为一个单独模块嵌入Nelder-Mead算法程序中,通过数值算例对反演结果进行求解。在整个反演过程中,需要对比的数据是试验与计算所得的相同应变下对应的应力值与超孔隙水压力值,为了同时利用这两种数据,需要为两种数据设置一个权重关系,权重的大小关系与试验过程中测得该类数据的可靠度有关。其表达式为
(1-λ)φ1+λφ2→min
(30)
式中,λ为两种误差函数所占比重;φ1,φ2分别为试验值与计算值在偏差应力和孔压上的误差函数;当λ=1时,则认为第1种物理量所测数据不可信,当λ=0时,则认为第2种物理量所测数据不可信。
表1 黏土岩基本力学参数[32]
Table 1 Basic mechanical parameters of claystone[32]
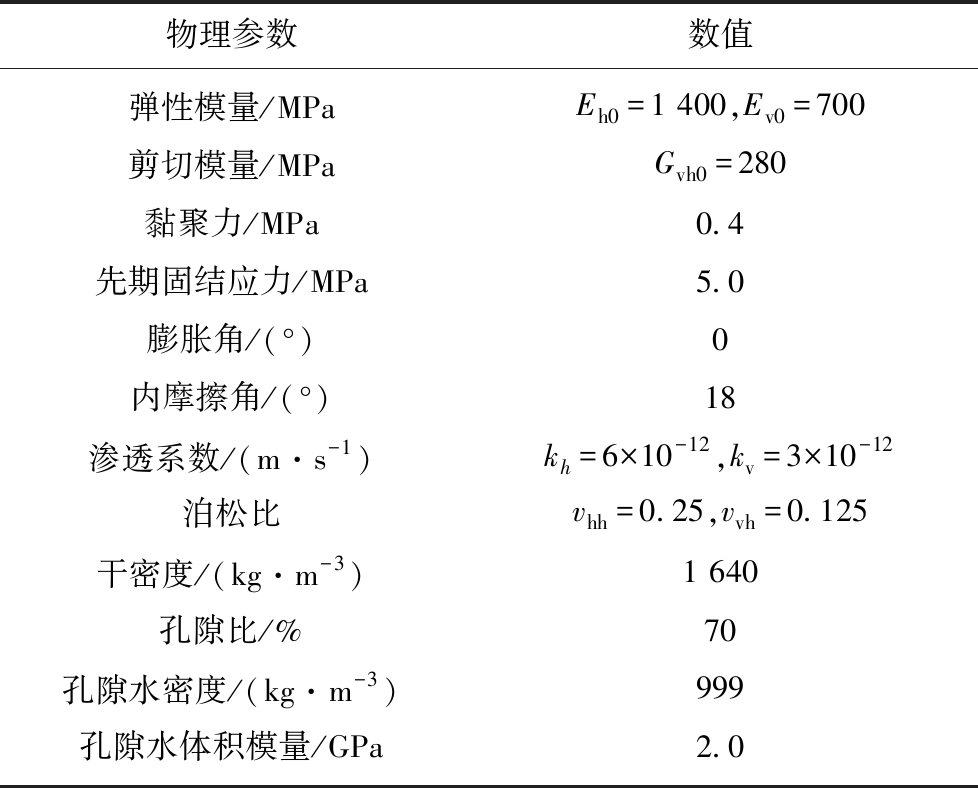
物理参数数值弹性模量/MPaEh0=1 400,Ev0=700剪切模量/MPaGvh0=280黏聚力/MPa0.4先期固结应力/MPa5.0膨胀角/(°)0内摩擦角/(°)18渗透系数/(m·s-1)kh=6×10-12,kv=3×10-12泊松比vhh=0.25,vvh=0.125干密度/(kg·m-3)1 640孔隙比/%70孔隙水密度/(kg·m-3)999孔隙水体积模量/GPa2.0
由计算所得和试验所得的偏差应力数据构成的误差函数表达式为
![]()
(31)
式中,![]() 为不同的轴向应变所对应的偏应力试验值;
为不同的轴向应变所对应的偏应力试验值;![]() 为相应的反演分析计算值;l为参与反演分析的试验值个数。
为相应的反演分析计算值;l为参与反演分析的试验值个数。
由计算所得和试验所得的超孔隙水压力数据构成的误差函数表达式为
![]()
(32)
式中,![]() 为不同的轴向应变所对应的试验孔压值;
为不同的轴向应变所对应的试验孔压值;![]() 为相应的反演分析计算值;w为孔隙水压力。
为相应的反演分析计算值;w为孔隙水压力。
模型参数的反演结果见表2[22]。
表2 黏土岩本构模型参数[22]
Table 2 Claystone constitutive model parameters[22]
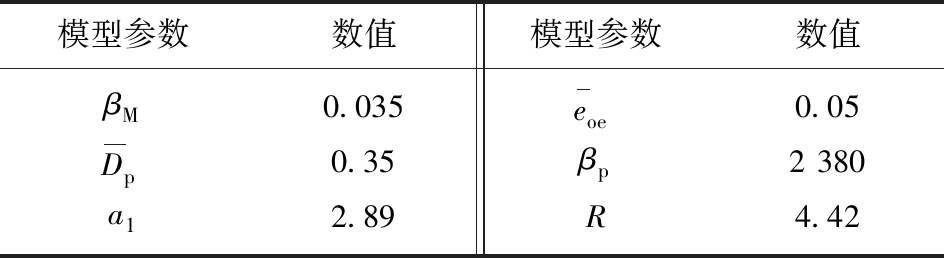
模型参数数值模型参数数值βM0.035eoe0.05Dp0.35βp2 380a12.89R4.42
图6给出了新模型计算得到的不同围压条件下不排水三轴压缩试验与模拟应变曲线的对比结果。从图6可以看出:塑性阶段模拟结果与试验结果相似表现为先硬化再软化;塑性阶段后期试验结果与新模型的模拟结果均表现出明显的塑性流动特性,这是因为塑性损伤存在损伤上限,试样内的损伤不可能无限制的增加,当试样内的损伤达到上限值时,宏观上表现为塑性流动阶段。
图7给出了试验和模拟的超孔压曲线对比图。从图7可以看出,模拟的超孔压结果可以较好的反应超孔压的演化趋势,即进入塑性阶段后,超孔压增大的速率逐渐减小。

图6 试验与模拟结果应变曲线对比
Fig.6 Comparison results of test and simulation for strain curves

图7 试验结果与模拟结果超孔压曲线对比
Fig.7 Comparison results of test and simulation for excessive pore pressure
4 算 例
为进一步验证新模型在地下工程施工数值模拟中的适用性,建立黏土岩隧硐开挖的平面模型如图8所示,模型宽度和高度分别为10 m,开挖隧硐位于模型中心直径为1 m,不设置衬砌支护。有限元网格模型共340个单元,369个节点,单元类型为CPE4RP。模型的边界条件及初始条件设置如下:网格模型底部节点采用固定约束,侧面采用法向约束,顶部施加6.1 MPa的面荷载;模型的初始地应力设置底部为3.7 MPa,顶部为3.6 MPa;初始孔压设置底部为2.6 MPa,顶部为2.5 MPa。共设置2个分析步分别为地应力平衡分析步和开挖分析步,其中开挖分析步为瞬态分析。围岩物理参数及模型参数取自表1,2。

图8 隧硐开挖有限元模型
Fig.8 Finite element model of tunnel excavation
开挖分析步中隧硐岩体被挖除后,随着围岩收敛变形的增大,围岩的损伤变量、Mises应力以及孔隙水压力的变化如图9~11所示。

图9 隧硐开挖后损伤变量演化
Fig.9 Damage variable evolution after tunnel excavation

图10 隧硐开挖后Mises应力演化
Fig.10 Mises stress evolution after tunnel excavation

图11 隧硐开挖后孔隙水压力演化
Fig.11 Pore pressure evolution law after tunnel excavation
从图9可以看出,损伤变量随着围岩收敛变形的累积逐渐增大,部分围岩损伤达到上限后不再增加。从图10可以看出,围岩的Mises应力随着围岩收敛变形的累积逐渐增大,但靠近隧硐的围岩在应力增大后出现明显的应力下降现象,这是因为此区域围岩应力达到峰值后进入软化阶段,应力开始逐渐跌落。从图11可以看出,开挖初始阶段,围岩进入塑性阶段时,硐室周边围岩均向内部收敛,同时孔压也开始逐渐降低。
通过黏土岩隧硐开挖的算例验证了新模型在地下硐室开挖计算中也可以反映黏土岩的软化以及塑性流动的特性。
5 结 论
(1)本文考虑黏土岩加载过程中产生的缺陷,以微裂纹作为损伤基元构建损伤变量,并将其与硬化变量一同引入至修正Drucker-Prager帽盖模型中,建立了能够描述黏土岩HM耦合条件下力学特性的本构模型。
(2)基于原有的向后欧拉算法,引入塑性硬化和塑性损伤变量参与迭代计算,通过控制屈服面的变化来描述材料的硬化与软化现象。
(3)模拟结果与试验结果对比发现,新模型不仅能很好地模拟试样的硬化和软化阶段,还能很好的反应黏土岩的塑性流动阶段。
(4)建立黏土岩隧硐平面模型,通过隧硐开挖计算验证了新模型的适用性,为以后的地下硐室开挖数值模拟提供了指导。
[1] 于洪丹.Boom 黏土渗流-应力耦合长期力学特性研究[D].武汉:中国科学院武汉岩土力学研究所,2010.
YU Hongdan.Hydro-mechanical coupled creep behavior of Boom clay[D].Wuhan:Wuhan Institute of Rock and Soil Mechanics,Chinese Academy of Sciences,2010.
[2] KANG Hongpu.Support technologies for deep and complex roadways in underground coal mines:A review[J].International Journal of Coal Science & Technology,2014,1(3):261-277.
[3] LI X L.Thermal impact on the damaged zone around a radioactive waste disposal in clay host rocks[J].Deliverable 2.State of The Art on THMC.
[4] 陈新,杨强,周维垣.岩土材料塑性损伤模型及拱坝的变形局部化分析[J].岩土力学,2007,28(5):865-870.
CHEN Xin,YANG Qiang,ZHOU Weiyuan.An elastoplastic damage model for geomaterials and analysis of strain localizaion of arch dams[J].Rock and Soil Mechanics,2007,28(5):865-870.
[5] 韦立德,杨春和.压剪应力条件下各向异性岩石损伤本构模型和渗流模型(Ⅰ):理论模型[J].岩土力学,2006,27(3):429-434.
WEI Lide,YANG Chunhe.Constitutive model and seepage model of anisotropic rock in compression with micromechanics(I):Theoretical models[J].Rock and Soil Mechanics,2006,27(3):429-434
[6] 谢和平,彭瑞东,鞠杨.岩石变形破坏过程中的能量耗散分析[J].岩石力学与工程学报,2004,23(21):3565-3570.
XIE Heping,PENG Ruidong,JU Yang.Energy dissipation of rock deformation and fracture[J].Chinese Journal of Rock Mechanics and Engineering,2004,23(21):3565-3570.
[7] SHAO J F,RUDNICKI J W.A microcrack-based continuous damage model for brittle geomaterials[J].Mechanics of Materials,2000,32(10):607-619.
[8] WANG Z,LI Y,WANG J G.A damage-softening statistical constitutive model considering rock residual strength[J].Computers & Geosciences,2007,33(1):1-9.
[9] 王军祥,姜谙男.岩石弹塑性损伤本构模型建立及在隧道工程中的应用[J].岩土力学,2015,36(4):1147-1158.
WANG Junxiang,JIANG Annan.An elastoplastic damage constitutive model of rock and its application to tunnel engineering[J].Rock and Soil Mechanics,2015,36(4):1147-1158.
[10] 袁小平,刘红岩,王志乔.基于Drucker-Prager准则的岩石弹塑性损伤本构模型研究[J].岩土力学,2012,33(4):1104-1108.
YUAN Xiaoping,LIU Hongyan,WANG Zhiqiao.Study of elastoplastic damage constitutive model of rocks based on Drucker-Prager criterion[J].Rock and Soil Mechanics,2012,33(4):1104-1108.
[11] 陈亮,刘建锋,王春萍,等.北山深部花岗岩弹塑性损伤模型研究[J].岩石力学与工程学报,2013,32(2):290-298.
CHEN Liang,LIU Jianfeng,WANG Chunping,et al.Elastoplastic damage model of Beishan deep granite[J].Chinese Journal of Rock Mechanics and Engineering,2013,32(2):290-298.
[12] 龚哲,陈卫忠,于洪丹.Boom 黏土热-力耦合弹塑性损伤模型研究[J].岩土力学,2016,37(9):2433-2450.
GONG Zhe,CHEN Weizhong,YU Hongdan.A thermo-mechanical coupled elastoplastic damage model for Boom clay[J].Rock and Soil Mechanics,2016,37(9):2433-2450.
[13] YU H D,CHEN W Z,JIA S P,et al.Experimental study on the hydro-mechanical behavior of Boom clay[J].International Journal of Rock Mechanics and Mining Sciences,2012,53:159-165.
[14] BALDI G,HUECKEL T,PEANO A,et al.Developments in modelling of thermo-hydro-geomechanical behaviour of Boom clay and clay-based buffer materials[R].Luxembourg:Office for Official Publications of the European Communities,1991.
[15] DOLAREVIC S,IBRAHIMBEGOVIC A.A modified three-surface elasto-plastic cap model and its numerical implementation[J].Computers & Structures,2007,85(7-8):419-430.
[16] KIM MK,LADE PV.Single hardening constitutive model for frictional materials[J].Computers and Geotechnics,1988,5(4):307-324.
[17] 贾善坡,陈卫忠,杨建平,等.基于修正Mohr-Coulomb 准则的弹塑性本构模型及其数值实施[J].岩土力学,2010,31(7):2051-2058.
JIA Shanpo,CHEN Weizhong,YANG Jianping,et al.An elastoplastic constitutive model based on modified Mohr-Coulomb criterion and its numerical implementation[J].Rock and Soil Mechanics,2010,31(7):2051-2058.
[18] SIMO J C,JU J W.Strain- and stress-based continuum damage models-I.Formulation[J].International Journal of Solids and Structures,1987,23(7):821-840.
[19] SIMO J C,JU J W.Strain- and stress-based continuum damage models-II.Computational aspects[J].International Journal of Solids and Structures,1987,23(7):841-869.
[20] LITEWKA A,DEBINSKI J.Load-induced oriented damage and anisotropy of rock-like materials[J].International Journal of Plasticity,2003,19(12):2171-2191.
[21] CHABOCHE J L.Continuous damage mechanics-a tool to describe phenomena before crack initiation[J].Nuclear Engineering and Design,1981,64(2):233-247.
[22] 马永尚.Boom Clay温度-渗流-应力耦合非线性损伤及流变机理研究[D].武汉:中国科学院武汉岩土力学研究所.2017.
MA Yongshang.Study on thermo-hydro-mechanical coupled nonlinear damage and rheological mechanism of Belgian Boom Clay[D].Wuhan:Institute of Rock and Soil Mechanics,Chinese Academy of Sciences,2017.
[23] GIRAUD A,ROUSSET G.Time-dependent behaviour of deep clays[J].Engineering Geology,1996,41(1):181-195.
[24] BASTIAENS W,BERNIER F,LI X L.An overview of long-term HM measurements around HADES URF[A].Proceedings of International Symposium on multiphysics coupling and long-term behaviour in rock mechanics[C].Lieege,2006:15-26.
[25] SCHMERTMANN J H,OSTERBERG J O.An experimental study of the development of cohesion and friction with axial strain in saturated cohesive soils[A].Research Conference on Shear Strength of Cohesive Soils[C].ASCE,1960:643-694.
[26] LAMBE T W.A mechanical picture of shear strength in clay[A].Research Conference on Shear Strength of Cohesive Soils.University of Colorado[C].Boulder,Colorado,1960:555-580.
[27] HAJIABDOLMAJID V,KAISER PK,MARTIN C D.Modelling brittle failure of rock[J].International Journal of Rock Mechanics and Mining Sciences,2002,39(6):731-741.
[28] 庄茁.连续体和结构的非线性有限元[M].北京:清华大学出版社,2002.
[29] WANG X,WANG L B,XU L M.Formulation of the return mapping algorithm for elastoplastic soil models[J].Computers and Geotechnics,2004,31:315-338.
[30] CRISFIELD M A.Non-linear finite element analysis of solids and structures[M].New York:John Wiley & Sons,2000.
[31] SIMO J C,TAYLOR R L.Consistent tangent operators for rate-independent elastoplasticity[J].Computer Methods in Applied Mechanics and Engineering,1985,48(1):101-118.
[32] CHEN G J,SILLEN X,VERSTRICHT J,et al.ATLAS III in-situ heating test in Boom clay:Field data,observation and interpretation[J].Computers and Geotechnics,2011,38(5):683-696.
[33] 贾善坡.Boom Clay渗流应力损伤耦合流变模型、参数反演与工程应用[D].武汉:中国科学院武汉岩土力学研究所,2009.
JIA Shanpo.Hydro-mechanical coupled creep damage constitutive model of Boom Clay,back analysis of model parameters and its engineering application[D].Wuhan:Institute of Rock and Soil Mechanics,Chinese Academy of Sciences,2009.

 [J].煤炭学报,2020,45(2):633-642.doi:10.13225/j.cnki.jccs.2019.0167
[J].煤炭学报,2020,45(2):633-642.doi:10.13225/j.cnki.jccs.2019.0167