全应力应变关系是开展岩体工程变形与应力分析的基础，统计损伤本构模型已被广泛应用于模拟脆性岩石变形破坏全过程。由于脆性岩石内部含有大量微裂隙或微孔隙等初始空隙，导致当前模型理论尤其是能够反映脆性岩石峰前变形力学特性的统计损伤模型理论仍是岩体变形力学研究中的热点和难点之一。
自从提出全应力应变关系曲线概念并在岩石刚性伺服试验机上得到完全体现以来，国内外学者[1-3]对脆性岩石变形破坏全过程模拟方法进行了大量探索并取得了丰硕的研究成果。由于脆性岩石变形破坏过程本质上属于空隙孕育、扩展及相互贯通的过程，而损伤理论正是用来研究岩石材料变形破坏及其空隙的形成演化过程，其中，基于连续损伤理论和统计强度理论建立的统计损伤本构模型是除经典弹塑性模型以外受到广泛应用的脆性岩石变形破坏全过程模拟方法之一。近年来，统计损伤模型理论研究内容主要集中在应力状态和损伤阈值的影响[4]、微元强度的度量方式及其随机分布形式[5]、模型参数的确定方法以及残余强度变形特性模拟[6]等方面，从而使其能够较好地反映脆性岩石变形破坏全过程。然而，该类模型理论仍然存在一定缺陷或不足，尤其在反映脆性岩石峰前变形力学特性方面，主要体现在如下几点:① 当前理论提出普适的损伤模型将脆性岩石视为无初始损伤岩块，而实际上脆性岩石在地质演化形成或人为扰动作用过程中不可避免地产生大量的初始空隙，这些既有缺陷使脆性岩石含有初始损伤，从而影响其宏观变形力学性质;② 当前本构模型难以模拟出脆性岩石变形破坏全过程中的初始空隙压密变形阶段，然而对于某些脆性岩石，如煤岩，很多情况下其初始宏观应力应变关系表现出强烈的非线性行为，且其非线性变形曲率随着脆性岩石所处的应力水平变化而变化;③ 当前本构模型在推导过程中将脆性岩石弹性模量视为常数，虽然这与其事先假定脆性岩石为致密岩块相符合，但众多试验表明脆性岩石弹性模量与初始空隙闭合变形紧密相关并随着应力水平变化而变化。由此可见，脆性岩石峰前变形力学特性与其内部初始空隙及应力水平密不可分，为此，曹文贵等[7]将脆性岩石抽象为由岩石骨架和空隙两部分组成，采用宏观与微观相结合的分析方法建立了能够反映脆性岩石初始宏观非线性变形力学行为的模拟方法。LIU等[8]基于传统Hooke定律提出了一种能够考虑岩石非线性弹性行为的双应变Hooke模型，李连崇等[9]利用该模型进行有效的数值验证，并在大尺度岩石工程中进行了可行性分析。郝宪杰等[10]在分析煤体非线性弹性特征基础上提出了描述非线性弹性力学行为的弹塑性本构方程，并进行了数值编程。上述研究结果均很好地推动了对于脆性岩石峰前变形力学特性的认识，但是不难发现，其获得的理论模型曲线与试验曲线仍有较大差距，且未探讨初始空隙闭合与脆性岩石力学性质之间的联系，仅将初始空隙闭合笼统地视为引起初始宏观非线性变形特征的原因欠妥，因此，探究应力作用下初始空隙闭合变形进而提出一种能够很好地反映脆性岩石变形破坏全过程尤其是峰前变形力学特性的统计损伤本构模型正是本研究的核心内容。
为此，笔者在脆性岩石变形力学特征基础上探讨初始空隙闭合对脆性岩石峰前变形力学性质产生的影响，利用当前脆性岩石统计损伤本构模型理论的优点，对考虑初始空隙闭合影响的脆性岩石非线性变形破坏全过程模拟方法进行探索，以期完善统计损伤本构模型研究内容与方法。
1 脆性岩石变形力学特征
脆性岩石变形力学特征是分析初始空隙在闭合变形过程中脆性岩石变形力学参数演化的基础。国内外学者[11-13]基于岩石刚性伺服试验机开展三轴压缩试验，普遍认为不同围压作用下脆性岩石变形破坏全过程如图1所示，简要分析如下。
图1 不同围压作用下脆性岩石变形破坏全过程示意
Fig.1 Sketch map of complete failure process of brittle rocks under different confining pressures
(1)不同围压作用下脆性岩石阶具有阶段性变形特征，一般可分为初始压密、线性、屈服硬化、软化和残余强度等变形阶段，其全应力应变过程中的关键特征点如屈服应力、峰值强度和残余强度均随围压增大而增大。
(2)对于含有大量初始空隙的脆性岩石，在偏应力作用下将表现出非常明显的初始压密变形阶段，随着围压逐渐增大，初始宏观非线性变形曲率不断减小直至几乎为零，随着围压再次递增，脆性岩石在偏应力作用下初始压密变形阶段可忽略不计，其变形破坏全过程与致密岩块表现一致。
(3)随着围压逐渐增大，脆性岩石弹性模量不断增大直至保持为常数，体现出脆性岩石抵抗弹性变形的能力随着应力水平的改变而发生变化，显然这与将弹性模量视为常数的致密岩块有显著区别。
由此可以看出，初始空隙闭合对初始压密变形阶段、初始宏观非线性变形曲率及弹性模量等脆性岩石峰前变形力学特性产生显著影响。因此，笔者将基于脆性岩石变形力学特征探讨不同应力水平作用下初始空隙闭合与脆性岩石峰前变形力学特性之间的联系。
2 初始空隙闭合及其影响
由于初始空隙能否发生闭合变形取决于脆性岩石所处的应力状态[14]，因此探讨初始空隙闭合及其影响即为探讨应力状态及其相应的变形力学特性。基于三轴压缩试验规程可知脆性岩石先被施加围压待变形稳定后，再被施加轴向压力直至发生变形破坏。于是基于不同应力状态下脆性岩石变形力学特征将初始空隙分为两类:仅能够在静水压力状态下发生闭合的初始空隙(第1类初始空隙)和能够在静水压力状态和偏应力状态下均发生闭合的初始空隙(第2类初始空隙)，下面分别对其探讨。
2.1 第1类初始空隙
为了能够探讨第1类初始空隙闭合及其影响，假设其形状为半长度等于a的硬币形椭圆[15]，由于初始空隙张开度与其纵横比λ呈正相关，可得围压σ3与λ之间的关系[15]，即
σ3=πEs(λ0-λ)/[4(1-μ2)]
(1)
其中，λ0为第1类初始空隙的初始纵横比;Es和μ分别为致密岩块的弹性模量和泊松比。由于第1类初始空隙在静水压力状态下不断发生闭合变形直至完全闭合，其纵横比λ不断减小直至为0，第1类初始空隙闭合应力
可由式(2)得
(2)
由于每条第1类初始空隙张开度不相同，故与其相应的闭合应力也不相等，由式(2)可得第i条第1类初始空隙闭合应力
为
(3)
其中，λi为第i条第1类初始空隙的初始纵横比。随着围压σ3逐渐增大，第1类初始空隙未闭合总条数N不断减少直至为0，忽略第1类初始空隙各条数之间的相互作用[15]可得
(4)
其中，E2为脆性岩石弹性模量;V为岩石基质体积。为了简单起见，假设λi服从均匀分布，则其可表示为
λi=iλm/N0
(5)
其中，N0和λm分别为第1类初始空隙的总条数和初始纵横比最大值。由式(3)和式(5)可得第1类初始空隙已闭合条数i与围压σ3之间的关系，即
(6)
式中，
为第N0条第1类初始空隙闭合应力。则围压σ3作用下第1类初始空隙未闭合条数N为
(7)
将式(7)代入式(4)可得脆性岩石弹性模量E2与围压σ3之间的关系，即
(8)
其中，
η=Es/E0-1
(9)
E0=Es/(1+ωN0)
(10)
ω=16a3(1-μ2)/[9V(1-2μ)]
(11)
由式(8)可知，E2是关于σ3的递增函数且适用于σ3不大于的情况。由于第1类初始空隙全部闭合时E2不随σ3增大而变化且近似于Es，于是，脆性岩石弹性模量E2可表示为
(12)
式(12)中参数可基于脆性岩石三轴压缩试验资料并采用最小二乘法方法获取。由此可见，随着第1类初始空隙在静水压力状态下发生闭合的条数逐渐增多，脆性岩石弹性模量不断增大，当第1类初始空隙完全闭合时脆性岩石弹性模量将保持为常数即致密岩块弹性模量，显然第1类初始空隙闭合将直接影响着脆性岩石弹性模量的变化。
2.2 第2类初始空隙
由脆性岩石变形力学特征可以看出，随着围压逐渐增大，脆性岩石初始宏观非线性变形曲率不断减小，表明某特定静水压力状态下脆性岩石内部有一定数量的第2类初始空隙发生闭合。当第2类初始空隙在某特定静水压力状态下全部发生闭合时，脆性岩石在偏应力作用下将直接进入线性变形阶段;若某特定静水压力状态下脆性岩石变形稳定后仍有一定数量的第2类初始空隙未发生闭合，则脆性岩石继续在偏应力状态作用下发生闭合，且随着偏应力逐渐增大，第2类初始空隙发生闭合的条数不断增多直至全部闭合，从而使脆性岩石表现出初始压密变形阶段并进入线性变形阶段。由此可见，第2类初始空隙闭合将直接影响着脆性岩石初始宏观非线性变形曲率以及偏应力作用下脆性岩石是否表现出初始压密变形阶段。值得注意的是，由于脆性岩石在偏应力作用下必将进入线性变形阶段，因此第2类初始空隙能够全部发生闭合。
综上分析，初始空隙闭合使脆性岩石内部初始缺陷得到了改善，从而使脆性岩石峰前变形力学性质得到了强化，因此将处于线性变形阶段的脆性岩石可视为由岩石骨架和未发生闭合的第1类初始空隙两部分组成，于是在此基础上可建立考虑初始空隙闭合影响的脆性岩石变形分析方法。
3 脆性岩石变形分析方法
由于低初始空隙率的脆性岩石初始压密变形阶段很不明显，众多学者在研究脆性岩石峰前变形力学性质时往往将其忽略，但对于高初始空隙率的脆性岩石，其初始压密变形阶段在峰前变形全过程中的占比较大，不能忽略[10]。无论何种脆性岩石，其内部都含有初始空隙，故笔者将零应力状态下脆性岩石构成要素即岩石骨架和初始空隙作为分析出发点来研究脆性岩石变形分析方法。
将应力作用下脆性岩石进行细观化处理，取出能够表征脆性岩石构成要素及初始构成比的代表性柱状单元，将其视为由骨架材料和裂隙材料两部分组成，如图2所示，其中，骨架材料可视为由岩石骨架和第1类初始空隙组成，裂隙材料可视为由第2类初始空隙及相关软物质组成。设代表性柱状单元、骨架材料和裂隙材料的长度在加载之前分别为
和
在轴向应力σ加载之后产生的变形量分别为
和
于是，由材料变形力学分析方法可得代表性柱状单元轴向应变εi为
(13)
其中，γ0为裂隙材料初始构成比;
和
分别为骨架材料和裂隙材料的轴向应变。由此可见，建立脆性岩石变形分析方法即需获得裂隙材料和骨架材料的变形分析方法。
图2 脆性岩石变形分析
Fig.2 Sketch for brittle rocks deformation analysis
3.1 裂隙材料变形分析方法
研究表明裂隙材料服从负指数变形规律[16]，即
(14)
其中，E1为裂隙材料弹性模量。由于裂隙材料弹性模量较低[17]，当脆性岩石进入线性变形阶段时，exp(-σ/E1)趋向于0，裂隙材料变形基本结束，此时第2类初始空隙已全部闭合，从而验证了前述对第2类初始空隙闭合及其影响探讨的合理性。
3.2 骨架材料变形分析方法
骨架材料变形破坏全过程必然伴随着空隙的孕育、扩展及相互贯通。根据空隙成因及演化特征，空隙可分为由第1类初始空隙和附加空隙组成。第1类初始空隙是地质演化或人为扰动所形成，在静水压力状态下发生闭合使脆性岩石弹性模量不断增大，起到增强岩石抵抗弹性变形能力的作用，因此，可认为第1类初始空隙闭合实际上使脆性岩石内部结构发生自愈合行为;附加空隙是骨架材料所受应力超过屈服应力产生的新空隙，并在应力持续作用下不断扩展及贯通，使脆性岩石强度发生破坏，起到弱化岩石抵抗变形能力的作用。由于微空隙是损伤的典型表现，于是可将未闭合第1类初始空隙和附加空隙分别视为骨架材料的初始损伤和附加损伤，因此，获得骨架材料变形分析方法的关键在于建立骨架材料损伤模型。
当前损伤理论提出的损伤模型大都基于应变等价性假设[18]建立起来的，它们在模拟无初始损伤岩块变形破坏全过程方面取得了较好效果，但无法反映初始损伤对岩石变形力学性质的影响，然而无论如何为本文建立含初始损伤的骨架材料损伤模型奠定了基础。
静水压力状态脆性岩石内部第1类初始空隙发生闭合，其中，闭合部分改善了骨架材料变形力学性质，未闭合部分构成了骨架材料初始损伤。骨架材料所受应力达到屈服应力时发生附加损伤并随着变形逐渐增大，附加损伤不断提高并达到上限值，但此时骨架材料仍具有一定的承载能力。于是，基于几何损伤理论将骨架材料抽象为未损伤部分、损伤部分和未闭合第1类初始裂隙3部分组成，如图3所示。
图3 骨架材料损伤模型
Fig.3 Damage model for skeleton material
设骨架材料所受名义应力为σi，其作用面积为A，其中，未损伤部分和损伤部分所受微观应力分别为σ′i和
作用面积分别为A1和A2，未闭合第1类初始裂隙面积为A0且不承担荷载。由微观受力分析方法可建立骨架材料损伤模型，即
(15)
其中，
Dt=D0+Dn
(16)
其中，D0为初始损伤变量，D0=A0/A;Dn为附加损伤变量，Dn=A2/A;Dt为骨架材料损伤变量。当D0=0时，Dt=Dn，式(15)即为当前提出普适的岩石损伤模型。
考虑到骨架材料损伤部分和未损伤部分紧密混在在一起，因此，对于骨架材料宏观与微观各部分应变的关系可利用文献[19]思路确定出骨架材料宏观轴向应变与未损伤部分材料轴向应变相同，由于σ′i是未损伤部分材料的微观应力，可认为未损伤部分骨架材料变形服从广义胡克定律，即
(17)
其中，μs为骨架材料泊松比;σ′j 和σ′k分别为未损伤部分材料在j和k方向的微观应力。由于裂隙材料在脆性岩石线性变形阶段变形已基本结束，骨架材料弹性模量及其泊松比可近似认为与致密岩块相同。设骨架材料损伤沿着最大主应变方向发生[6]，于是结合式(15)和式(17)可获得骨架材料变形分析方法，即
(18)
式中，σj和σk为骨架材料在j和k方向的名义应力。
4 脆性岩石变形模拟方法
将式(14)和式(18)分别代入式(13)则建立出三轴压缩条件下脆性岩石统计损伤本构模型，即
σ1=(1-Dt)Es[ε1-γ0exp(-σ1/E1)]/(1-γ0)+
(19)
其中，
为致密岩块残余强度。由此可见要建立考虑初始空隙闭合及其影响的脆性岩石统计损伤本构模型，还需给出D0和Dn的确定方法。
4.1 D0的确定方法
由骨架材料变形分析方法可知，随着围压不断增大，第1类初始空隙闭合条数逐渐增多，D0不断减小，E2不断增大;当第1类初始空隙全部闭合时，D0变为0，E2保持为常数。由此可见，D0和E2与围压的变化关系类似，D0可表示为脆性岩石弹性模量劣化程度，即
D0=1-E2/Es
(20)
4.2 Dn的确定方法
由于骨架材料变形破坏过程可视为一个发生连续损伤的过程，且微元强度的破坏具有随机性，其破坏概率与应力状态紧密相关，于是，为了考虑附加损伤阈值和应力状态对骨架材料微元强度的影响，基于Mohr-Coulomb强度准则将微元强度度量方法F表示为
F=σ′1-ασ′3-k0
(21)
α=(1+sin φy)/(1-sin φy)
(22)
k0=2cycos φy/(1-sin φy)
(23)
其中，σ′1和σ′3分别为未损伤骨架材料在i=1和j=k=3方向的微观应力;α和k0分别为与骨架材料发生附加损伤时的黏聚力cy和内摩擦角φy有关的常数。将式(17)代入式(21)可得微元强度的另一度量方法，即
(24)
由式(24)可知，F取值有3种情况:当骨架材料未达到附加损伤阈值时，F<0;恰好发生附加损伤时，F=0;已经发生附加损伤时，F>0。引入统计损伤理论常用的Weibull概率密度函数以表征骨架材料微元强度破坏的随机性，随着微元强度破坏数目不断增多，其分布函数Dn由0逐渐递增。由于D0是由未闭合第1类初始裂隙引起的，当骨架材料完全损伤时Dt等于1，则由式(16)可知Dn上限值为1-D0。于是，Dn的确定方法可表示为
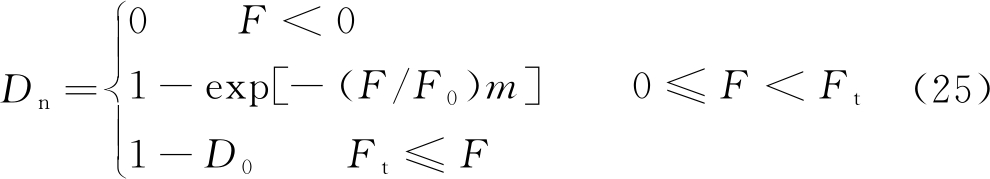
式中，Ft为Dn等于1-D0时F度量值，可基于损伤函数连续性确定;m和F0为随机分布参数。
当骨架材料发生附加损伤时裂隙材料变形已基本结束，即exp(-σ1/E1)趋向于0。于是，将式(25)代入式(19)可得考虑初始空隙闭合及其影响的脆性岩石变形破坏全过程模拟方法，即
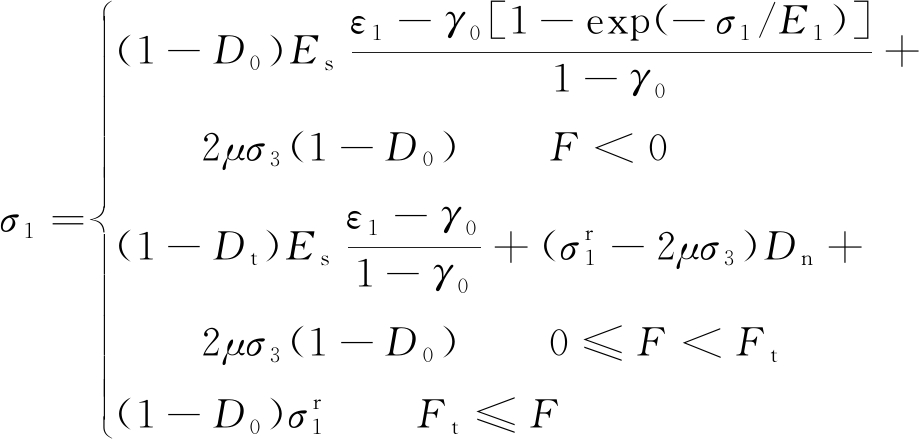
(26)
5 参数的确定方法
参数cy和φy可基于常规力学试验确定，参数Es,μ,E0,E2和D0的确定方法已于前述介绍，参数γ0和E1可采用文献[7]方法确定。因此，还需给出参数m和F0的确定方法。
脆性岩石具有应变软化特性，其应力应变关系曲线在峰值点(σ1=σsc，ε1=εsc)处具有极值特性，即
(27)
式中，σsc和εsc分别为峰值点的应力和应变。
同时，峰值点又需满足式(26)中的第2式。于是联立方程即可确定参数m和F0：
m=(1-D0-Dnsc)(1-γ0)Fsc/{(1-Dnsc)×
(28)
F0=Fsc[-ln(1-Dnsc)]-1/m
(29)
其中，
Fsc=Es(εsc-γ0)/(1-γ0)+(2μ-α)σ3-k0
(30)
(31)
值得注意的是，在参数m和F0求解过程中需弄清两个问题:
(1)F的求导。
当脆性岩石处于峰值强度时，F>0，exp(-σ1/E1)趋近0，于是，将式(13)代入式(24)可得F另一表达式:
F=Es(ε1-γ0)/(1-γ0)+(2μ-α)σ3-k0
(32)
于是，基于式(32)求得F关于ε1的导函数，即
∂F/∂ε1=Es/(1-γ0)
(33)
(2)峰值点的取值。
三轴压缩条件下脆性岩石应力应变曲线为某特定围压作用下偏应力应变试验曲线，该试验曲线是以脆性岩石受到偏应力作用为记录始点进行绘制的，它忽略了脆性岩石在静水压力状态下产生的初始应变εc，然而高初始空隙率的脆性岩石初始应变不能忽略，并且本构模型中σ1和ε1分别代表最大主应力与最大主应变，因此，在偏应力应变曲线基础上分析σ1和ε1还需分别包含σ3和εc。于是，本构模型理论应力应变曲线峰值点(σsc,εsc)与偏应力应变试验曲线峰值点
的关系可表示为
σsc=σ′sc+σ3
(34)
εsc=ε′sc+εc
(35)
由于静水压力状态下脆性岩石在仅具有初始损伤，于是，基于式(26)中第1式可得εc，即
γ0[1-exp(-σ3/E1)]
(36)
至此，已建立考虑初始空隙闭合及其影响的脆性岩石变形破坏全过程模拟方法并给出了参数的确定方法，但其合理性与可行性有待验证，下面进行分析。
6 模型验证
文献[20]给出了红砂岩在围压分别为0,10,20,30和40 MPa条件下偏应力应变试验曲线，如图4所示。采用本文方法可确定参数α=4.60,k0=51.47 MPa，γ0=0.001，E0=14.62 GPa,Es=22.52 GPa,μ=0.25，不同围压下脆性岩石相关模型参数见表1。值得注意的是，这些参数是基于三轴压缩条件下脆性岩石变形力学参数的变化规律以及前述参数的确定方法进行确定。于是，可获得不同围压作用下红砂岩模型理论曲线，并将其与试验曲线进行比较，如图5所示。
图4 红砂岩偏应力应变试验曲线
Fig.4 Deviatoric stress-axial strain test curves of red sandstone
表1 模型参数
Table 1 Model parameters
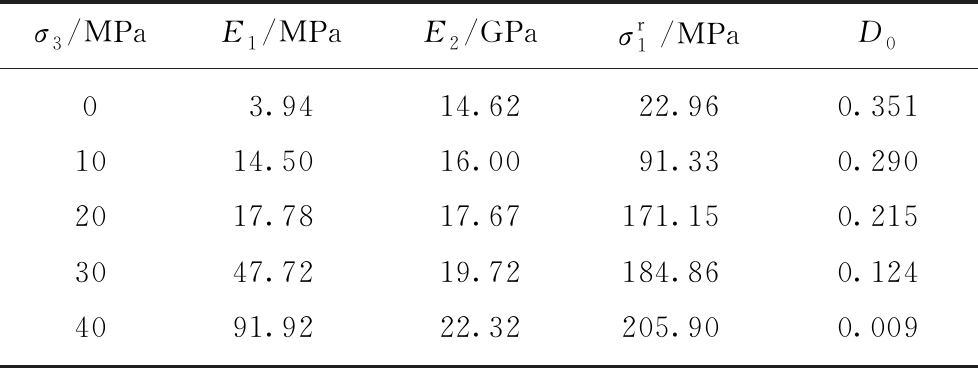
σ3/MPaE1/MPaE2/GPaσr1/MPaD003.9414.6222.960.3511014.5016.0091.330.2902017.7817.67171.150.2153047.7219.72184.860.1244091.9222.32205.900.009
图5 本文理论模型曲线与试验曲线的比较
Fig.5 Comparison of theoretical model curves in this paper and test curves
为了进一步验证本文理论模型和方法的合理性与可行性，分别根据文献[6]和文献[7]中同类型脆性岩石本构模型，采用相同试验资料获取相应的模型理论曲线，并将它们分别与试验曲线进行比较，如图6，7所示。
图6 文献[6]理论模型曲线与试验曲线的比较
Fig.6 Comparison of theoretical model curves in reference[6] and test curves
图7 文献[7]理论模型曲线与试验曲线的比较
Fig.7 Comparison of theoretical model curves in reference[7] and test curves
由此可以看出:
(1)文献[6]理论模型能够反映线性、屈服硬化、软化和残余强度等变形阶段，但不能反映初始空隙压密变形阶段及弹性模量变化特征，这是由于该理论将脆性岩石视为致密岩块且其内部不含有初始空隙，显然其理论模型应用范围受到了一定限制。
(2)文献[7]理论模型能够反映初始空隙压密、线性、屈服硬化和软化等变形阶段，但不能反映脆性岩石残余强度变形阶段，这是该理论认为损伤部分材料不能承受载荷所致，同时，该理论模型不能反映初始宏观非线性变形曲率及弹性模量变化特征。尽管该理论认为脆性岩石存在初始空隙，但其忽视了初始空隙闭合与其应力状态有紧密关系从而无法考虑初始空隙闭合及其影响，因此其理论模型仍然存在一定缺陷。
(3)本文理论模型不仅能够很好地反映脆性岩石变形破坏全过程5个变形阶段，也能够很好地反映初始宏观非线性变形曲率及弹性模量变化特征。
为了进一步反映初始空隙闭合及其影响，根据本文模型和方法可得红砂岩损伤演化规律以及附加损伤演化规律，分别如图8,9所示。
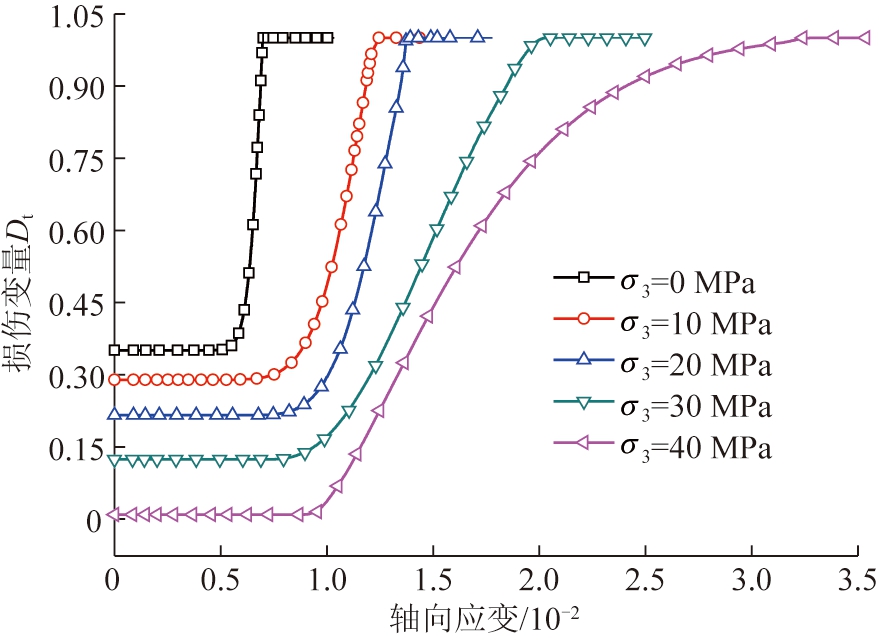
图8 红砂岩损伤演化规律
Fig.8 Evolution law of damage for red sandstone
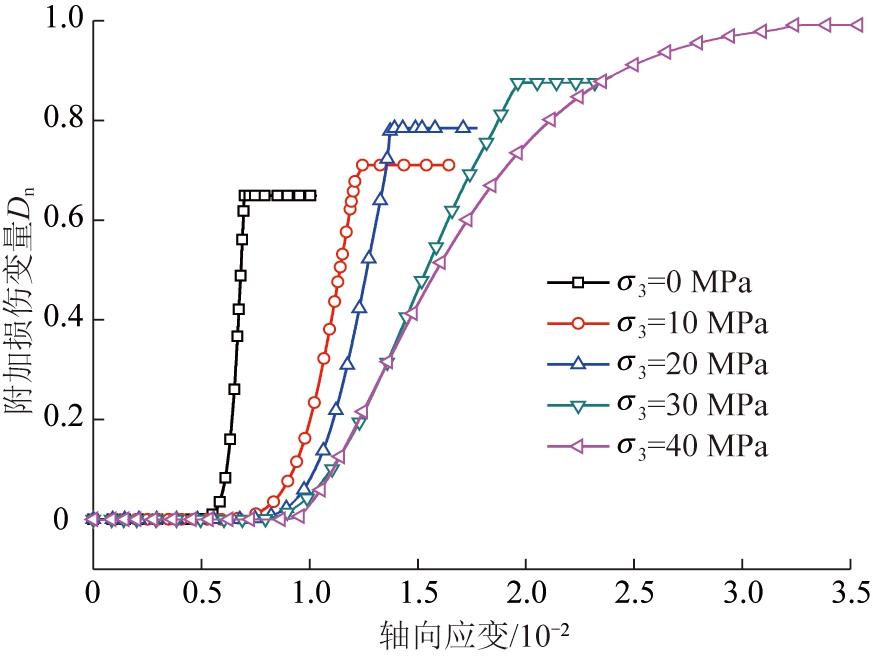
图9 红砂岩附加损伤演化规律
Fig.9 Evolution law of additional damage for red sandstone
由此可以看出:
(1)随着围压逐渐增大，初始损伤变量不断减小，表明静水压力状态下红砂岩内部结构产生自愈合行为，由初始空隙引起的初始损伤不断降低;当第一类初始空隙在静水压力状态下完全闭合时，初始损伤变量为0，其损伤演化规律与致密红砂岩块相同，阐释了增大围压具有消除红砂岩内部初始缺陷的作用[21]。
(2)当红砂岩所受应力未达到附加损伤阈值时，红砂岩将维持恒定的初始损伤程度，一旦所受应力达到附加损伤阈值时，随着轴向变形逐渐增大，红砂岩损伤变量及附加损伤变量不断增大;随着围压逐渐增大，红砂岩附加损伤速率不断降低，阐释了增大围压具有抑制红砂岩附加损伤的作用[21]。
(3)红砂岩损伤及附加损伤演化规律呈S型，随着轴应变不断增大，损伤变量由D0递增至1，附加损伤变量由0逐渐递增至1-D0，表明初始空隙引起的初始损伤在红砂岩损伤演化规律中起着重要作用。
7 结 论
(1)初始空隙可分为2类:第1类初始空隙和第2类初始空隙，前者闭合引起脆性岩石弹性模量发生变化，后者闭合引起脆性岩石具有初始压密变形阶段以及初始宏观非线性变形曲率发生变化，且在初始宏观变形过程中能够完全闭合。
(2)脆性岩石损伤可分为2类:初始损伤和附加损伤，前者由未闭合第1类初始空隙引起，后者由脆性岩石达到附加损伤阈值时产生附加空隙引起。
(3)建立了考虑初始空隙闭合及其影响的脆性岩石变形破坏全过程模拟方法并给出其参数的确定方法。通过分析本文以及同类理论模型曲线分别与试验曲线并探讨红砂岩损伤演化规律，表明本文理论模型能够很好地反映红砂岩变形破坏全过程，并能阐释围压、初始空隙和峰前变形力学特性3者之间的关系，从而验证了本文模型和方法的合理性与可行性。
[1] KRAJCINOVIC D,SILVA M A G.Statistical aspects of the continuous damage theory[J].International Journal of Solids and Structures,1982,18(7):551-562.
[2] 何明明,李宁,朱才辉,等.岩石分数阶体积变形模型及其试验研究[J].岩土力学,2016,37(11):3137-3144.
HE Mingming,LI Ning,ZHU Caihui,et al.The volume deformation behavior of rock based on fractional calculus and its experimental study[J].Rock and Soil Mechanics,2017,37(11):3137-3144.
[3] 杜修力,黄景琦,金浏,等.岩石三维弹塑性损伤本构模型研究[J].岩土工程学报,2017,39(6):978-985.
DU Xiuli,HUANG Jingqi,JIN Liu,et al.Three-dimension elastic-plastic damage constitutive model for intact rock[J].Chinese Journal of Geotechnical Engineering,2017,39(6):978-985.
[4] LI X,CAO W G,SU Y H.A statistical damage constitutive model for softening behavior of rocks[J].Engineering Geology,2012(143/144):1-17.
[5] 刘冬桥,王焯,张晓云.岩石应变软化变形特性及损伤本构模型研究[J].岩土力学,2017,38(10):2901-2908.
LIU Dongqiao,WANG Zhuo,ZHANG Xiaoyun.Characteristics of strain softening of rocks and its damage constitutive model[J].Rock and Soil Mechanics,2017,38(10):2901-2908.
[6] ZHAO H,SHI C J,ZHAO M H,et al.Statistical damage constitutive model for rocks considering residual strength[J].International Journal of Geomechanics,2016,17(1):04016033.
[7] 曹文贵,张超,贺敏,等.考虑空隙压密阶段特征的岩石应变软化统计损伤模拟方法[J].岩土工程学报,2016,38(10):1754-1761.
CAO Wengui,ZHANG Chao,HE Min,et al.Statistical damage simulation method of strain softening deformation process for rocks considering characteristics of void compaction stage[J].Chinese Journal of Geotechnical Engineering,2016,38(10):1754-1761.
[8] LIU H H,RUTQVIST J,BERRYMAN J G.On the relationship between stress and elastic strain for porous and fractured rock[J].International Journal of Rock Mechanics and Mining Sciences,2009,46(2):289-296.
[9] 李连崇,LIU Huihai,赵瑜.基于双应变胡克模型的岩石非线性弹性行为分析[J].岩石力学与工程学报,2012,31(10):2119-2126.
LI Lianchong,LIU Huihai,ZHAO Yu.Investigation on nonlinear elastic behavior of rocks based on a two-part hook’s model[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(10):2119-2126.
[10] 郝宪杰,袁亮,卢志国,等.考虑煤体非线性弹性力学行为的弹塑性本构模型[J].煤炭学报,2017,42(4):896-901.
HAO Xianjie,YUAN Liang,LU Zhiguo,et al.An elastic plastic soften constitutive model of coal considering its nonlinear elastic mechanical behavior[J].Journal of China Coal Society,2017,42(4):896-901.
[11] 刘学伟,刘泉声,刘滨,等.侧向压力对裂隙岩体破坏形式及强度特征的影响[J].煤炭学报,2014,39(12):2405-2411.
LIU Xuewei,LIU Quansheng,LIU Bin,et al.Effects of lateral pressure on failure modes and strength characteristics of fractured rock mass[J].Journal of China Coal Society,2014,39(12):2405-2411.
[12] 李冰洋，尤明庆.岩石黏结摩擦特性及非线性强度的指数准则描述[J].岩石力学与工程学报,2016,35(10):1945-1953.
LI Bingyang,YOU Mingqing.Nonlinear strength of rocks with cohesion and friction using the exponential criterion[J].Chinese Journal of Rock Mechanics and Engineering,2016,35(10):1945-1953.
[13] ASEF M R，REDDISH D J.The impact of confining stress on the rock mass deformation modulus[J].Geotechnique,2002,52(4):235-241.
[14] 陈颙.岩石物理学[M].北京:北京大学出版社,2001.
[15] WALSH J B.The effect of cracks on the compressibility of rock[J].Journal of Geophysical Research-atmospheres,1965,70(2),381-388.
[16] ZHAO Y,LIU H H.An elastic strain-stress relationship for porous rock under anisotropic stress conditions[J].Rock Mechanics and Rock Engineering,2012,45(3):389-399.
[17] 左建平,陈岩,宋洪强,等.煤岩组合体峰前轴向裂纹演化与非线性模型[J].岩土工程学报,2017,39(9):1609-1615.
ZUO Jianping,CHEN Yan,SONG Hongqiang,et al.Evolution of pre-peak axial crack strain and nonlinear model for coal-rock combined body[J].Chinese Journal of Geotechnical Engineering,2017,39(9):1609-1615.
[18] LEMAITRE J.How to use damage mechanics[J].Nuclear Engineering and Design,1984,80(3):233-245.
[19] 曹文贵，张升，赵明华.软化与硬化特性转化的岩石损伤统计本构模型之研究[J].工程力学,2006,23(11):110-115.
CAO Wengui,ZHANG Sheng,ZHAO Minghua.Study on a statistical damage constitutive model with conversion between softening and hardening properties of rock[J].Engineering Mechanics,2006,23(11):110-115.
[20] 张军,艾池,李玉伟,等.基于岩石破坏全过程能量演化的脆性评价指数[J].岩石力学与工程学报,2017,36(6):1326-1340.
ZHANG Jun,AI Chi,LI Yuwei,et al.Brittleness evaluation index based on energy variation in the whole process of rock failure[J].Chinese Journal of Rock Mechanics and Engineering,2017,36(6):1326-1340.
[21] 张慧梅,谢祥妙,彭川,等.三向应力状态下冻融岩石损伤本构模型[J].岩土工程学报,2017,39(8):1444-1452.
ZHANG Huimei,XIE Xiangmiao,PENG Chuan,et al.Constitutive model for damage of freeze-thaw rock under three-dimensional stress[J].Chinese Journal of Geotechnical Engineering,2017,39(8):1444-1452.
