

能量耗散是岩石发生破坏的根本原因,岩石损伤破坏过程本质上是岩石在能量驱动下由稳定态向不稳定态再向稳定态转变的过程[1]。岩石是具有不均匀性、各向异性的脆性材料,包含层理、节理、断面等结构,当岩石中的层理沿一定方向排列就构成了层状岩石[2]。隧道、水电站、核电站废料存储设施等常基于层状岩石建设[3-4],采矿过程与页岩气开发中也经常遇到层状岩石[5-7],建设与开发过程中的冲击钻进、爆破和切削等工艺是破碎岩石的主要方式。因此,深入了解冲击荷载作用下层状岩石的动力学特性,研究其破碎过程中能量传递规律、耗散特性、破碎形态及碎块分布特征,对提高钻进效率、矿石产出率和能量利用率具有重要意义[8-9]。
目前已有许多学者从能量与块度特征角度对岩石破碎过程进行分析。谢和平等[10]基于能量耗散分析建立的岩石损伤演化方程较好地描述了岩石的损伤演化过程,给出了复杂应力条件下卸荷弹性模量的变化公式。ZHANG等[11]通过对岩石试样施加不同速率的荷载,研究了不同加载速率下岩石的断裂与能量耗散特性。GRADY[12]利用能量恒定原理,基于岩石耗散能全部用于岩石断裂的假定建立了岩石块度与能量公式。LUNDBERG[13]通过霍普金森杆(SHPB)研究了岩石块度分布特征与能量吸收特征,认为岩石输入能越高,岩石破碎越完全。李地元等[14]简单分析了层状砂岩冲击载荷下破碎时吸收能占输入能的比例,认为层面与加载方向平行时,岩石的能量吸收率最高。HONG等[15]利用大直径SHPB装置,分析了不同加载速率下岩石的能量吸收率与破碎形态。不同于一般岩石,层状岩石破碎过程中,不仅需考虑有效能量相对于总输入能占比、冲击速度快慢等的影响,还需考虑冲击方向与层理方向不同夹角下岩石的块度分布特征,而目前还少有相关研究。
基于此,笔者对层状岩石进行不同冲击速度、不同层理倾角的动态压缩试验,对比分析了层状岩石动态破坏下的块度分布特征,探讨不同入射能对层状岩石反射能、透射能、耗散能密度和块度分布的影响。
选用层状千枚岩制作冲击荷载试验所用试样。岩样取自江西省九江市,由典型的庐山第四纪沉积岩经变质作用形成。试验所用层状试样根据国际岩石力学学会(ISRM)推荐标准[16],加工成φ50 mm×50 mm大小,打磨后试样两端面不平整度与不垂直度均在±0.02 mm。经成分分析,所用试样岩石成分包括白云母、斜绿泥石与石英。表1为岩石矿物成分构成。在偏光镜下对试样进行观察,表明其具有明显的层理状构造,如图1所示。
表1 矿物成分
Table 1 Mineral composition

矿物名称百分比/%白云母31.89斜绿泥石26.91石英24.47钠长石13.22透辉石3.51

图1 偏光镜下的千枚岩层状结构
Fig.1 Phyllite layered structure under polarizer
定义层面倾角θ为层面法线方向与加载方向的夹角,层状试样倾角示意图如图2所示,εi,εr,εt分别为测得的入射、反射及透射应变。按照层理倾角θ与冲击速度不同将45个试样分为15组,每组包含0°,22.5°,45°,67.5°和90°试样各3个。分别对冲头施加6.96,10.86,14.83 m/s的冲击速度。

图2 层状试样加载示意
Fig.2 Dynamic impact layered specimen
层状岩石动态冲击压缩试验在中国科学院武汉岩土力学研究所的分离式霍普金森杆试验系统(Splitting Hopkinson Pressure bar,SHPB)上进行。试验系统的输入杆、输出杆、吸能杆采用同种材料,直径均为50 mm,长度分别为2 500,2 500和1 000 mm。为生成波形光滑、弥散效应小的钟型波,采用锥形冲头,并在输入杆杆端粘贴橡胶垫作为波形整形器。为减少摩擦效应,防止不必要的干扰,在试样两端涂抹凡士林。在输入杆与输出杆距试件端部1 m处粘贴应变片,并通过光电法测量弹头初速。
采用基于一维应力波传播和应力均匀性假定的三波法处理应变片与超动态应变仪采集的数据,得到层状岩石应力σ、应变ε及应变率![]() 为
为
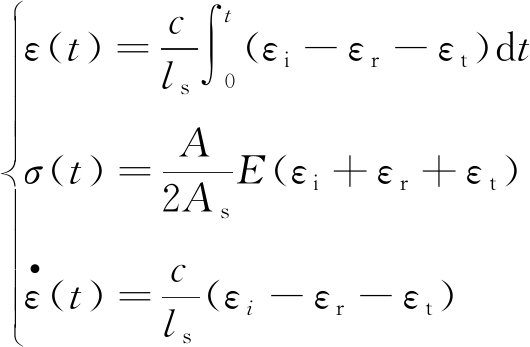
(1)
式中,ls和As为试样的长度及截面积;c,E和A为杆件的弹性波波速、弹性模量及截面积。
整个加载过程中入射波、反射波和透射波所携带的能量分别为Wi,Wr和Wt,其计算公式为
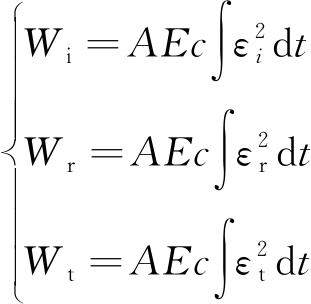
(2)
动态冲击压缩试验过程中试样吸收的能量Ws计算为
Ws=Wi-Wr-Wt
(3)
试样吸收能Ws主要构成方程为
Ws=Wd+Wk+Wo
(4)
其中,Wd为用于扩展原有裂纹、生成新断裂面和微裂纹的岩石破碎耗散能;Wk为岩石破碎飞出时携带的弹射动能;Wo为破碎时的声能、热能与辐射能等其他损耗。根据ZHANG等[11]在高速摄像机下对动能的计算研究,动能Wk占吸收能的比例为
![]()
(5)
式中,vo为冲头的冲击速度。
计算得到的值大部分在10%以内,动能只占试样破坏吸收能量的很少一部分,冲击载荷下吸收能量主要由破碎耗能构成,因此高速冲击下可忽略弹射动能及其他耗能[17-18],岩石破碎耗散能Ws=Wd。
考虑试样间的尺寸差异,采用更客观的破碎耗能密度wd反映岩石破碎能耗情况,即单位体积层状岩石破碎耗能:
![]()
(6)
式中,Vs为试样体积。
根据式(1),求得不同冲击速度下层状岩石各倾角的动态抗压强度,如图3所示。任意冲击速度下,倾角为0°试样动态抗压强度最高,倾角67.5°的动态抗压强度最低。随冲击速度的增加,岩石动态抗压强度逐渐增大,低倾角下试样抗压强度增加趋势明显,45°~90°试样线性拟合线的斜率较低,表明试样动态抗压强度随冲击速度增大趋势较慢。

图3 不同冲击速度下层状岩石动态抗压强度
Fig.3 Dynamic compressive strength of layered rocks under different impact velocities
均质岩石受冲击载荷下产生的块度大致为正六面体,即长宽高各个方向的尺寸相差较小,可以使用任意方向尺寸对破碎后块度进行测量[19]。由于层状岩石中层理的存在,导致破碎后的试样呈现典型的片状结构,如图4所示。在不同方向测量会产生尺寸误差,因此为研究层状岩石破碎块度分布,需首先确定层状岩石试样块度尺寸的测量方法。
考虑以方孔筛筛分冲击载荷下层状岩石破碎块度,因此假设以六面体包络岩块[19],取该六面体3个互相垂直的棱长,其中最长的棱为长度,次之为宽度,长度最小的棱为宽度。筛分时将长度与宽度棱所在的面置于筛孔上,最长的棱决定岩块是够能通过筛孔,因此定义长度即最大尺寸棱为块度的粒径。
对破碎后的试样碎块进行收集,典型冲击速度下的破坏形态如图4所示,由图4可知,随着冲击速度增大,层状岩石试样破碎程度逐渐加剧,破碎块度逐渐减小。根据碎块特征,选用尺寸为31.5,25.0,20,16.0,10.0,5.0,2.5 mm的标准方孔筛进行筛选,通过高灵敏度电子称确定筛上碎块质量。为对比不同尺寸试样下的块度分布特征,以各筛孔筛上累积质量百分比标定筛分试验结果,不同冲击速度下层状岩石碎块筛分试验结果见表2。

图4 不同冲击速度和倾角下层状岩石破坏形态
Fig.4 Failure modes of layered rock under different impact velocities and dip angles
表2 层状岩石冲击载荷下碎块筛分试验结果
Table 2 Screening test results of impact fragments of layered samples

编号层理倾角θ/(°)冲击速度/(m·s-1)各筛孔筛上累积质量百分比/%>31.5 mm25~31.5 mm25~20 mm20~16 mm16~10 mm10~5 mm5~2.5 mm<2.5 mm块度平均粒径/mm分形维数D13-1-106.86 100000000050.000 —13-2-106.93 99.8420000000.15835.695 —13-3-106.80 100000000050.000—10-1-122.56.97 98.724000000.7340.54235.328 1.355 10-2-122.57.02 98.639000000.7900.57135.300 1.374 10-3-122.56.84 98.926000000.4250.64935.390 1.365 7-1-1457.06 76.36514.98404.2781.7590.8641.4520.29832.655 1.615 7-2-1457.02 81.54713.59603.11200.8070.9430.19633.652 1.454 7-3-1456.92 74.91810.2876.5235.2041.8690.5420.4320.22532.396 1.454 4-1-167.56.94 74.13319.34203.4511.3060.8690.6260.27432.850 1.498 4-2-167.56.85 77.83715.86503.0291.8230.7390.4960.21133.167 1.419 4-3-167.56.80 73.1638.5329.1925.1281.7011.3500.6330.30131.907 1.602 1-1-1906.96 99.8200000000.18035.688 1.116 1-2-1906.85 91.2638.04600000.4870.20434.920 1.378 1-3-1906.94 98.17700001.1330.4630.22735.203 1.154 14-1-2010.73 99.142000000.4230.43535.465 1.262 14-2-2010.47 59.58333.0656.2240000.6390.48932.072 1.595
续 表

编号层理倾角θ/(°)冲击速度/(m·s-1)各筛孔筛上累积质量百分比/%>31.5 mm25~31.5 mm25~20 mm20~16 mm16~10 mm10~5 mm5~2.5 mm<2.5 mm块度平均粒径/mm分形维数D14-3-2010.65 77.64414.34203.4562.1791.1470.6700.56232.833 1.701 11-1-222.510.93 96.72400002.0790.6510.54634.766 1.393 11-2-222.510.75 93.2380003.5721.8550.7140.62133.971 1.550 11-3-222.510.69 80.66810.182004.5362.2731.6150.72632.545 1.813 8-1-24510.96 61.043021.8396.4413.7824.8241.4650.60628.812 1.744 8-2-24510.96 65.34213.1637.8024.6594.008 3.1871.3160.52330.488 1.823 8-3-24510.85 60.831019.9768.2415.4453.2351.5890.68328.744 1.748 5-1-267.510.98 63.14111.00611.5078.5871.9452.3691.0250.42030.291 1.703 5-2-267.510.94 53.13414.82512.0738.9725.6682.7601.8490.71928.537 1.868 5-3-267.510.76 57.27916.2389.8539.1763.2532.2471.3190.63529.582 1.798 2-1-29010.70 87.2168.544002.3181.2350.4490.23834.007 1.439 2-2-29010.78 88.8278.090001.5950.8500.4210.21634.331 1.424 2-3-29010.48 85.7728.965003.0441.3130.6180.28833.717 1.503 15-1-3014.82 34.16340.05718.8762.9842.0320.9480.5970.34328.676 1.517 15-2-3014.97 49.03128.71516.8633.60900.8210.6540.30730.174 1.462 15-3-3014.86 41.76735.35813.3823.0681.7430.8950.6090.37828.805 1.557 12-1-322.514.82 74.15821.25302.279001.1450.85232.979 1.847 12-2-322.514.96 51.8367.45112.427014.4308.4353.9521.46926.107 2.202 12-3-322.514.79 62.46226.2167.035002.2381.3060.74331.545 1.768 9-1-34514.97 44.10927.84011.8025.2394.2443.8671.7391.16028.154 1.984 9-2-34514.84 17.65655.20511.7044.4264.9692.7592.2541.02726.288 2.027 9-3-34514.89 13.87247.50621.0715.6414.2313.6682.9831.02825.086 2.061 6-1-367.514.72 049.47321.71912.1488.3325.0742.1201.13422.607 2.036 6-2-367.514.74 043.98422.99713.9369.8315.7022.2481.30221.915 2.073 6-3-367.514.94 047.30221.67311.13410.5954.9062.1411.24922.085 2.047 3-1-39014.83 049.65118.03513.09710.8584.6512.6151.09322.314 1.985 3-2-39014.85 050.98616.34014.5319.4515.2022.3561.13422.417 1.997 3-3-39014.98 052.86515.39512.3747.2498.5912.4531.07322.318 1.953
为量化比较层状岩石破碎块度大小,采用块度平均粒径ds来表征岩石破碎程度[18-19],即
![]()
(7)
式中,di为不同孔径筛上滞留岩石破碎块度的平均尺寸;ηi为对应di的碎块质量百分比。
块度平均粒径ds的计算结果见表2,由表2可知,对同一层理倾角,随着冲击速度的增大,ds逐渐减小,表明试样破碎程度逐渐增大;在同一冲击速度下,层理倾角为67.5°的试样破碎后ds最小,层理倾角为0°的试样ds最大,表明相同冲击速度下67.5°试样破碎程度最大,0°试样破碎程度最小。
分析表2和图4可知,使用块度平均粒径ds可以简单直观的比较层状岩石破碎程度,但并不能直观反映破碎块度的分布特征,即具有相同ds并不意味着各筛上碎块质量相同,也就无法真正量化破碎块度分布特征。许多学者的研究结果表明,岩石破碎后的块度具有分形特征[21-22]。按质量-块度关系可以获得岩石破碎块度分布方程
![]()
(8)
其中,x为岩石破碎块度;m(x)为尺寸小于x的破碎块度累积质量;mt为破碎块度总质量;D为破碎块度分布分形维数。对式(8)两边取对数计算得
![]()
(9)
由式(9)可知,(3-D)即为ln[m(x)/mt]~ln x坐标图中拟合直线的斜率。将求得的分形维数列于表2。
由表2分析可知,对同一层理倾角,随着冲击速度的增大,破碎块度逐渐减小,分形维数D逐渐增大,且不同分布下分形维数差别较大,表明分形维数D可以量化破碎块度分布特征,相较于di表征意义更加广泛。
根据式(1)~(6),求得不同层理倾角与冲击速度下试样的平均入射能、反射能、透射能、耗散能与破碎耗能密度,分别讨论相关能量关系。
图5为层状岩石在冲击载荷作用下反射能随入射能的变化关系。由图5可以看出,各层理倾角下,反射能随入射能增大而逐渐增加,对不同层理倾角试样而言,二者均呈线性关系,但斜率不同表明增长趋势也不同。高倾角下增长趋势较快,0°,22.5°试样斜率较小,增长趋势较慢。结合试样破坏形态分析可知[23-26],0°,22.5°试样未完全破裂,此时反射能随入射能增多缓慢增加,而对于高倾角试样,试样完全破裂,反射能增大趋势显著。
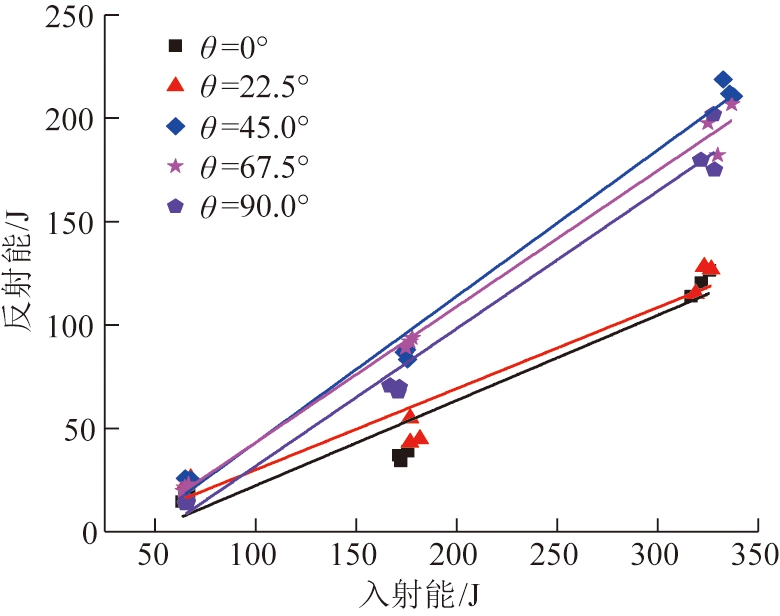
图5 层状岩石试样入射能和反射能关系
Fig.5 Relationship between incident energy and reflected energy of layered samples
对不同层理倾角而言,45.0°,67.5°和90.0°的试样在入射能大致相同时反射能较大,表明大倾角下无用功大多以反射波形式耗散。式(10)为入射能与反射能拟合公式。

(10)
图6为层状岩石在冲击载荷作用下透射能随入射能的变化关系。由图6可见,与反射能对应,各层理倾角下,透射能随入射能增大逐渐增大,但45.0°,67.5°和90.0°的增大趋势平稳。0°,22.5°层状岩石透射能较大,透射能与入射能呈现线性关系,表明低倾角下无用功大多以透射波形式耗散。式(11)为入射能与透射能拟合公式,67.5°数据较离散,相关度较低,但由图6可知,拟合公式能够很好的反映数据点变化趋势。

(11)
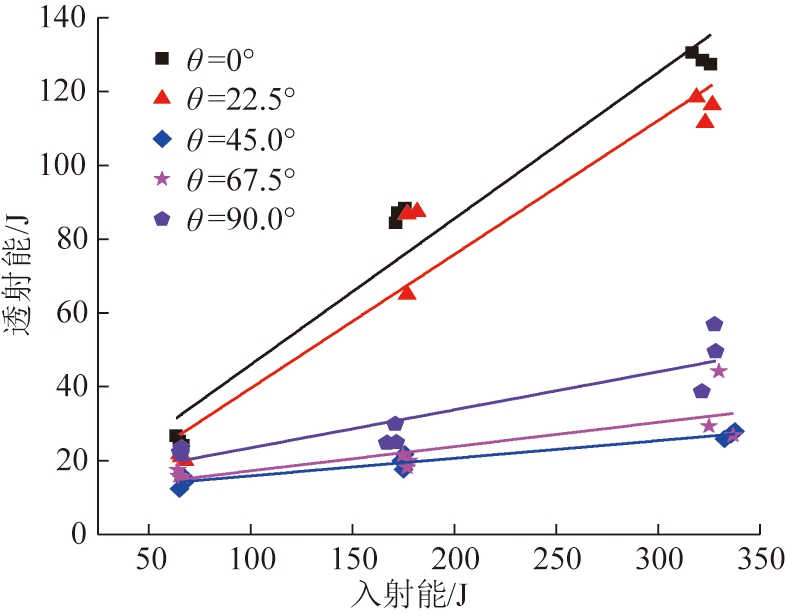
图6 层状岩石入射能和透射能关系
Fig.6 Relationship between incident energy and transm- ission energy of layered samples
层状岩石各倾角下破碎耗散能密度与入射能的关系如图7所示。在入射能相近时,层理倾角为90.0°的试样耗散能密度最大,层理倾角为0°,22.5°的试样耗散能密度较小。

图7 层状岩石破碎耗能密度与入射能关系
Fig.7 Relation between broken energy density and incident energy of layered samples
由图7可见,层状岩石各层理倾角下破碎耗能密度随入射能增加而增多,呈现较好的相关性,且各倾角下增加趋势大致相同。各层理倾角拟合关系式为

(12)
层状岩石各倾角破碎耗散能与分形维数的关系如图8所示。
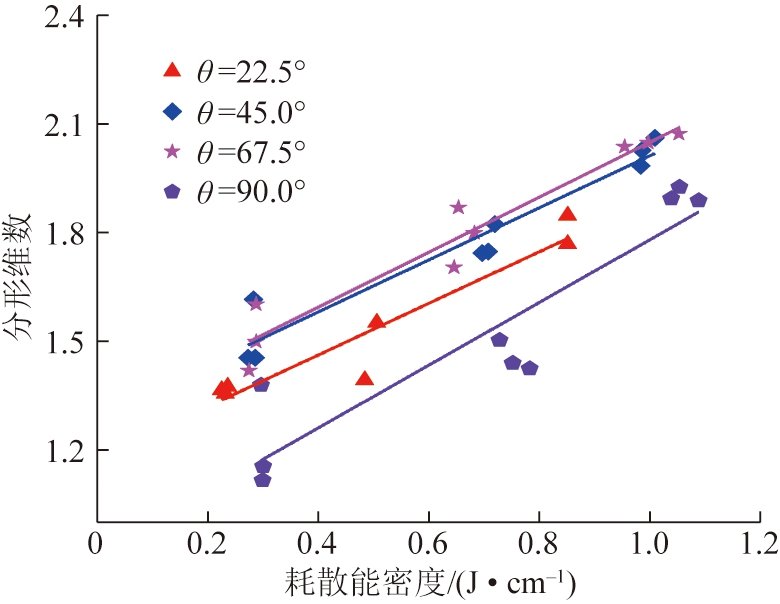
图8 层状岩石试样破碎耗能密度与分形维数关系
Fig.8 Relation between broken energy density and fractal dimension of layered samples
由图8可见,各倾角下分形维数随耗散能密度增大而增加,相关性系数较高。各层理倾角分形维数与耗散能密度拟合关系式为

(13)
高倾角时斜率较大,表明在大倾角下随能耗增大,试样破碎程度越剧烈;而低倾角时增加趋势较小,表明此时随耗散能密度增大,试样破碎趋势变化较小,产生新裂纹与破裂面所需能量较多。
(1)对同一层理倾角,随着冲击速度的增大,块度平均粒径ds逐渐减小,表明试样破碎程度逐渐增大;在同一冲击速度下,层理倾角为67.5°的试样破碎后ds最小,层理倾角为0°的试样ds最大,表明相同冲击速度下67.5°试样破碎程度最大,0°试样破碎程度最小。对同一层理倾角,随着冲击速度的增大,破碎块度逐渐减小,分形维数D逐渐增大,表明分形维数D可以量化破碎块度分布特征。
(2)在冲击速度相近时,入射能的差别不大;在任意冲击速度下,层理倾角为90°时耗散能密度最大,但与45°~67.5°相差不大;低冲击速度下,22.5°的耗散能密度最小,高冲击速度下,层理倾角为0°的试样耗散能密度最小。表明相同入射能时,高倾角试样能量利用率高,0°或22.5°的利用率较低。
(3)层理倾角为45.0°,67.5°和90.0°的试样在入射能大致相同时反射能较大,层理倾角为0°,22.5°的试样透射能较大,表明高倾角下无用功大多以反射波形式耗散,低倾角下无用功大多以透射波形式耗散。反射能、透射能与耗散能密度随入射能增大而增加。
(4)各倾角下分形维数随耗散能密度增大而增加。高倾角时增加幅度较大,表明在大倾角下随能耗增大,试样破碎程度越剧烈;而低倾角时增加趋势平稳,表明此时随耗散能密度增大,试样破碎趋势变化较小,产生新裂纹与破裂面所需能量较多。
(5)在层状岩矿开采与隧洞开挖过程中,任意动载下,选择45°~67.5°倾角的加载角度,不仅岩石强度较低,岩石破碎程度高,且能量利用率较高,耗散能密度较大。
[1] BIENIAWSKI Z T.Stability concept of brittle fracture propagation in rock[J].Engineering Geology,1967,2(3):149-162.
[2] PARK B,MIN K B.Bonded-particle discrete element modeling of mechanical behavior of transversely isotropic rock[J].International Journal of Rock Mechanics & Mining Sciences,2015,76:243-255.
[3] 裴建良,刘建锋,徐进.层状大理岩卸荷力学特性试验研究[J].岩石力学与工程学报,2009,28(12):2496-2502.
PEI Jianliang,LIU Jianfeng,XU Jin.Experimental study of mechanical properties of layered marble under unloading condition[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(12):2496-2502.
[4] 李林,陈结,姜德义,等.单轴条件下层状盐岩的表面裂纹扩展分析[J].岩土力学,2011,32(5):1394-1398.
LI Lin,CHEN Jie,JIANG Deyi,et al.Analysis of surface crack growth in layered salt rock under uniaxial compression[J].Rock and Soil Mechanics,2011,32(5):1394-1398.
[5] 赵毅鑫,龚爽,黄亚琼.冲击载荷下煤样动态拉伸劈裂能量耗散特征实验[J].煤炭学报,2015,40(10):2320-2326.
ZHAO Yixin,GONG Shuang,HUANG Yaqiong.Experimental study on energy dissipation characteris-tics of coal samples under impact loading[J].Journal of China Coal Society,2015,40(10):2320-2326.
[6] TAVALLALI A,VERVOORT A.Failure of transversely isotropic rock material:Effect of layer orientation and material properties[A].The 6th International Symposium on Ground Support in Mining and Civil Engineering Construction[C].Cape Town,South Africa,2008.
[7] BAI Xiangfei,WANG Yue,LI Wenhua.Mineralogy,distribution,occurrence and removability of trace elements during the coal preparation of No.6 coal from Heidaigou mine[J].International Journal of Coal Science & Technology,2014,1(4):402-420.
[8] QIU Jiadong,LI Diyuan,LI Xibing.Dynamic failure of a phyllite with a low degree of metamorphism under impact Brazilian test[J].International Journal of Rock Mechanics & Mining Sciences,2017,94:10-17.
[9] JU Yang,SUN Huafei,XING Mingxu,et al.Numerical analysis of the failure process of soil-rock mixtures through computed tomography and PFC3D models[J].International Journal of Coal Science & Technology,2018,5(2):126-141.
[10] 谢和平,鞠杨,黎立云,等.岩体变形破坏过程的能量机制[J].岩石力学与工程学报,2008,27(9):1729-1740.
XIE Heping,JU Yang,LI Liyun,et al.Energy mechanism of deformation and failure of rock masses[J].Chinese Journal of Rock Mechanics and Engineering.2008,27(9):1729-1740.
[11] ZHANG Z X,KOU S Q,JIANG L G,et al.Effects of loading rate on rock fracture:fracture characteristics and energy partitioning[J].International Journal of Rock Mechanics and Mining Sciences,2000,37(5):745-762.
[12] GRADY D E.Length scales and size distributions in dynamic fragmentation[J].International Journal of Fracture,2010,163:85-99.
[13] LUNDBERG B.A split Hopkinson bar study of energy absorption in dynamic rock fragmentation[J].International Journal of Rock Mechanics and Mining Science & Geomechanics Abstracts,1976,13(6):187-197.
[14] 李地元,邱加冬,李夕兵.冲击载荷作用下层状砂岩动态拉压力学特性研究[J].岩石力学与工程学报,2015,(10):2091-2097.
LI Diyuan,QIU Jiadong,LI Xibing.Experimental study on dynamic tensile and compressive properties of bedding sandstone under impact loading[J].Chinese Journal of Rock Mechanics and Engineering,2015(10):2091-2097.
[15] HONG L,ZHOU Z L,YIN T B,et al.Energy consumption in rock fragmentation at intermediate strain rate[J].Journal of Central South University of Technology,2009,16(4):677-682.
[16] ZHOU Y X,XIA K,LI X B,et al.Suggested methods for determining the dynamic strength parameters and mode-I fracture toughness of rock materials[J].International Journal of Rock Mechanics and Mining Sciences,2012,49:105-112.
[17] 李淼,乔兰,李庆文.高应变率下预制单节理岩石SHPB劈裂试验能量耗散分析[J].岩土工程学报,2017,39(7):1336-1343.
LI Miao,QIAO Lan,LI Qingwen.Energy dissipation of rock specimens under high strain rate with single joint in SHPB tensile tests[J].Chinese Journal of Geotechnical Engineering,2017,39(7):1336-1343.
[18] LI X F,ZHANG Q B,LI H B,et al.Grain-based discrete element method(GB-DEM) modelling of multi-scale fracturing in rocks under dynamic loading[J].Rock Mechanics and Rock Engineering,2018,51:3785-3817.
[19] 王维华,李宏艳,齐庆新,等.基于分形理论的采动裂隙时空演化规律研究[J].煤炭学报,2014,39(6):1023-1030.
WANG Weihua,LI Hongyan,QI Qingxin,et al.Study on fissure development rule of overlying strata influenced by mining based on fractal theory[J].Journal of China Coal Society,2014,39(6):1023-1030.
[20] LI X F,LI H B,ZHANG Q B,et al.Dynamic fragmentation of rock material:Characteristic size,fragment distribution and pulverization law[J].Engineering Fracture Mechanics,2018,199:739-759.
[21] 张继春.岩体爆破的块度理论及其应用[M].成都:西南交通大学出版社,2001:48-51.
[22] 谢和平,高峰,周宏伟,等.岩石断裂和破碎的分形研究[J].防灾减灾工程学报,2003,23(4):1-9.
XIE Heping,GAO Feng,ZHOU Hongwei,et al.Fractal fractureand fragmentation in rocks[J].Journal of Disaster Prevention and Mitigation Engineering,2003,23(4):1-9.
[23] 王利,高谦.岩石块度的分形演化模型及其应用[J].煤炭学报,2007,32(11):1170-1174.
WANG Li,GAO Qian.Fragmentation predicition of rock based on damage energy dissipation[J].Journal of China Coal Society,2007,32(11):1170-1174.
[24] LI X F,LI X,LI H B,et al.Dynamic tensile behaviours of heterogeneous rocks:The grain scale fracturing characteristics on strength and fragmentation[J].International Journal of Impact Engineering,2018,118:98-118.
[25] ZHANG Haixia,YU Kuangshi,ZHU Zhiping.Effect of operating parameters on coal gasification[J].International Journal of Coal Science & Technology,2018,5(2):244-252.
[26] 李晓锋,李海波,刘凯,等.冲击荷载作用下岩石动态力学特性及破裂特征研究[J].岩石力学与工程学报,2017,36(10):2393-2405.
LI Xiaofeng,LI Haibo,LIU Kai,et al.Dynamic properties and fracture characteristics of rocks subject to impact loading[J].Chinese Journal of Rock Mechanics and Engineering,2017,36(10):2393-2405.