为解决矿区水资源保护与利用问题,神东矿区提出了通过建造煤矿地下水库来进行地下水资源储存、循环利用的技术途径,即在工作面开采后,利用密闭墙等人工构筑物将煤柱连接起来形成挡水坝体,使采空区成为一相对密闭的储水空间[1-7]。与地面水库坝体的受力条件不同,煤矿地下水库中的人工构筑物(人工坝体)除了要承受水压作用外,还会受到上覆岩层残余沉降引起的垂直载荷的影响,因此如何在综合考虑水压和上覆垂直载荷影响的条件下进行人工坝体承载结构的合理设计对于水库的安全运行显得尤为重要。大柳塔煤矿作为地下水库技术成功应用的典型代表,经过多年的探索与实践,已在人工坝体结构设计与施工方面形成了一套较完整的方法。它将人工坝体设计为防渗墙-承载墙组合结构,其中防渗墙一般为砖墙,以黄土等防渗材料为充填物;承载墙以工字钢为骨架,以混凝土为胶结充填料,墙体嵌入两侧煤柱一定深度,左右侧和顶底边均通过全螺纹锚杆与四周围岩相连;为了增强墙体的承载稳定性,在其外侧增设了一与之垂直的支撑墙结构,由此形成了由挡水坝墙和支撑墙组成的“T”字形人工坝体结构。现场实践表明,该坝体结构安全、可靠,能满足长期使用的承载能力要求,且相关理论测算结果显示,其最大挡水高度可达到60~90 m[8],已远超水库的日常储水水位(15~20 m),由此说明该坝体结构强度富余系数过高,坝体结构设计存在可优化的空间。因此在兼顾储水安全性和建设经济性的基础上对诸如大柳塔煤矿的“T”字形人工坝体结构进行优化显得十分必要。
针对煤矿地下水库坝体稳定性问题,目前已有许多学者开展了研究,但多集中于煤柱坝体稳定性分析,而对于人工坝体稳定性分析相对较少。如程阳[9]模拟计算了煤矿地下水库3种不同类型的煤柱坝体周围的渗流场,为坝体防渗工程措施提供了参考依据;顾大钊等[10]研究了在不同强度震动作用下,煤柱坝体的应变分布规律与危险区位置,提出了坝体安全系数,为煤柱坝体抗震安全性评价提供了参考依据。对于人工坝体稳定性问题,陈苏社[8]利用FLAC数值软件分析了煤矿地下水库人工坝体的位移场和应力场分布,并根据强度折减法,得到了坝体安全系数。白东尧等[11]运用弹性薄板理论对李家壕煤矿地下水库人工坝体中的素混凝土墙(无钢筋骨架)承载性能进行了分析。上述研究虽从不同角度对坝体承载稳定性进行了分析,但基本未考虑上覆垂直载荷对坝体承载性能的影响。而实际上,虽然在构筑完人工坝体后的初始阶段,坝体顶部没有受到垂直载荷作用,但随着坝体服务时间的增加,受残余沉降变形的影响,上覆岩层会挤压坝体顶部,从而使坝体顶部受到垂直载荷的作用,因此有必要在考虑垂直载荷作用的条件下对坝体结构进行优化。
由人工坝体组成结构特征可知,坝体结构强度主要与坝墙厚度、工字钢骨架结构和支撑墙结构有关,因此人工坝体结构优化可从这3个方面进行。为了评价支撑墙设置的必要性,在坝体承载性分析中,先单独计算坝墙是否满足承载力要求(若满足,则在坝墙结构的基础上进行厚度和骨架结构的优化;否则,在坝体承载性分析中有必要考虑支撑墙的影响)。考虑到坝体中的挡水坝墙属于以工字钢为骨架的混凝土结构,其弹性参数难以计算,因此为便于计算分析,可依据强度等效原则,将工字钢骨架结构简化为另一种结构形式,由于以圆形钢筋为骨架的混凝土结构的弹性参数计算比较简单,因此可将坝墙内布置的工字钢骨架结构等效为强度相等的圆形钢筋骨架结构,将坝墙简化为一定配筋率的以圆形钢筋为骨架的混凝土墙结构,利用建筑工程领域常用的“正交异性板模型”[12-13]来对其进行承载性能分析,从而确定适用于大柳塔矿地质储水与工况条件下的坝体结构优化形式。
1 大柳塔煤矿地下水库人工坝体结构
如图1所示,大柳塔地下水库人工坝体一般由砖墙(防渗墙)和工字钢混凝土墙(承载墙)组成,其整体结构呈“T”字形,主要材料为砼、工字钢、锚杆和钢筋网片,其中混凝土强度等级为C30,骨架为11号工字钢。坝墙左侧和右侧均嵌入同侧煤柱0.3 m,墙体顶部嵌入顶板0.3 m,墙体底部嵌入底板0.2 m,墙的左右侧和顶、底边均通过锚杆与两侧煤柱体和顶、底板相连接,并通过铅丝将锚杆、工字钢和钢筋网片固接在一起。坝墙中的工字钢混凝土墙的尺寸为5 000 mm×4 000 mm×1 000 mm,工字钢布置方式如图2所示,横向3根,竖向5根,间排距均为1 m,为了增强坝墙的稳定性,坝墙平面外施工了一支撑墙体,其内部的工字钢布置方式为横向3根、竖向1根,工字钢间通过焊接联结成整体,前后铺设两层钢筋网,采用C30级混凝土将坝墙浇筑成一整体。相关理论测算结果显示,大柳塔地下水库人工坝体最大挡水高度可达60~90 m[8],而水库的日常储水水位一般为15~20 m,因此可得出该坝体结构强度富余系数过高,坝体结构设计存在可优化的空间。

图1 一般坝体施工设计
Fig.1 Sketch of dam construction design
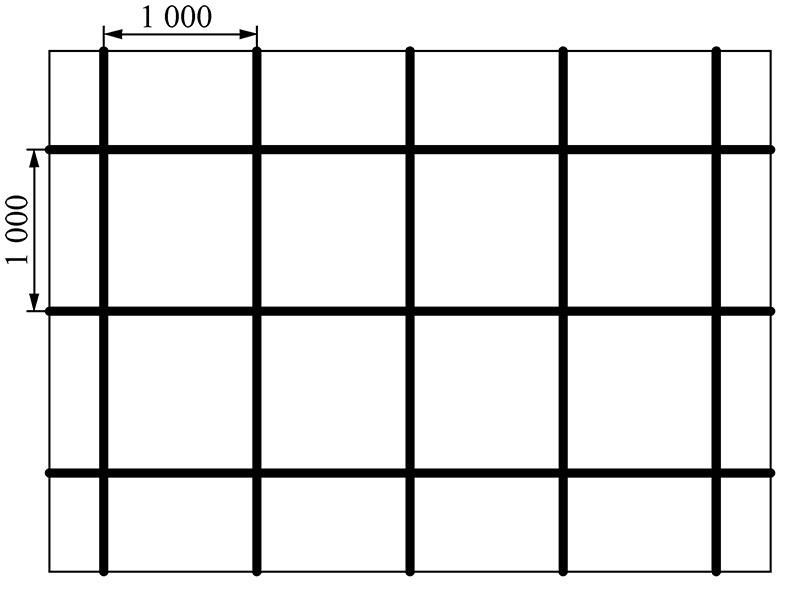
图2 坝墙内工字钢布置示意
Fig.2 Schematic diagram of I-beam layout in dam wall
2 坝墙的正交异性薄板力学模型
2.1 模型的简化
基于评价坝墙外设置支撑墙的必要性和便于计算的目的,先单独对坝墙进行承载性分析。考虑到坝墙中主体受力结构为承载墙,所以只对坝墙中的承载墙,即工字钢混凝土墙的承载性能进行分析。坝墙中的工字钢混凝土墙在宽度(x)和高度(y)方向均等间距布置有工字钢,按照强度等效原则,可将工字钢骨架结构等效为根数相同、钢材等级相同和横截面积相同的圆形钢筋骨架结构,因此工字钢混凝土墙结构可简化为一定配筋率的以圆形钢筋为骨架的混凝土墙结构,可利用正交异性板模型对其进行计算。
对于正交异性板的计算,运用薄板理论计算的结果跟中厚板理论相比是有一定的差异的,其中按中厚板理论计算得到的结果精度较高,但计算复杂,求解困难。工程上对于板的分类,一般来说,薄板是指板的厚度与板面最小尺寸之比在0.01~0.2内的平板,中厚板是指板的厚度与板面最小尺寸之比大于0.2的平板。现场工字钢与混凝土组合墙的厚度与墙面最小尺寸比为0.25,由文献[14]可知,板的厚度与板面最小尺寸之比为0.15和0.25的平板分别按薄板理论计算得到的结果的精度接近相等,因此,在满足工程精度的要求下,可使用薄板理论对板厚与板面最小尺寸之比为0.25的平板进行求解。
由图1可知,坝墙左、右侧和底部均嵌入于围岩中,且均通过锚杆与围岩相连接,因此墙体左右侧、底边边界约束条件可看作固支;考虑到墙体顶部与顶板间的喷砼连接方式难以使两者得到充分接触,因此墙体顶部边界约束条件可看作简支。据此,可将坝墙中的工字钢混凝土墙简化为如图3所示的受水压和垂直载荷作用,边界约束条件为三边固支、一边简支,配筋方式为横三竖五,横向配筋率ρx为0.249%,竖向配筋率ρy为0.332%的正交异性薄板模型,图中,2a为坝体宽度;b为坝体高度;h为坝体厚度;p为坝体顶边界所受的采动覆岩应力;q(y)为坝体内表面所受的水压大小。

图3 坝墙的正交异性薄板力学模型
Fig.3 Orthotropic thin plate mechanical model of dam wall
由弹性力学理论可知,叠加原理适用于小变形和线弹性变形情况,故薄板应力解可看作是薄板分别在水压和顶板上覆垂直载荷作用下的应力之和。
2.2 正交异性薄板在水压作用下的应力解
正交异性板的伽辽金方程[15]为
ωmdxdy=0
(1)
式中,ω为薄板的挠度函数,其表达式一般为![]() 和D2为薄板在弹性主方向的抗弯刚度;D3为折算刚度;dx与dy分别为板中微小单元体的横向和竖向边长。
和D2为薄板在弹性主方向的抗弯刚度;D3为折算刚度;dx与dy分别为板中微小单元体的横向和竖向边长。
设挠度函数为
(m,n=1,3……)
(2)
令m=n=1,则
![]()
(3)
可见该挠度函数满足下列边界条件:
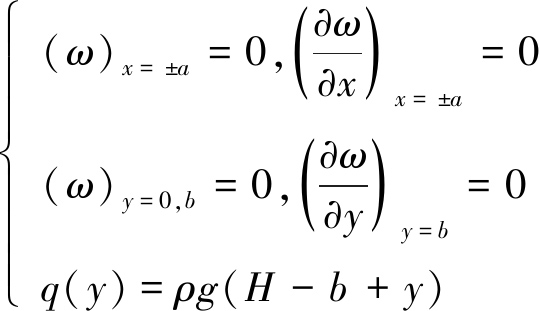
(4)
式中,H为人工坝体所受水头值,m;ρ为水密度,1 000 kg/m3;g为重力加速度,10 m/s2。
联立式(1),(3),(4)得
![]()
(5)
将式(5)代入式(3)得
![]()
(6)
现场人工坝体中的钢筋为11号工字钢,其弹性模量为200 GPa,泊松比按经验取0.3;混凝土等级为C30,其弹性模量为30 GPa,泊松比取0.2。
钢筋混凝土板可看作加筋混凝土复合材料,因此钢筋混凝土板结构弹性参数可利用复合材料的性质来确定[16-17]。
弹性模量的计算公式为
E1=Ex=Ecx+(Esx-Ecx)ρsx
(7)
E2=Ey=Ecy+(Esy-Ecy)ρsy
(8)
式中,E1为板的横向弹性模量;ρsx为x方向的配筋率;ρsx=Asx/Ax;Asx为钢筋的横截面积;Ax为钢筋混凝土板的横截面积;Ecx为混凝土横向弹性模量;Esx为钢筋横向弹性模量;E2为板的纵向弹性模量;ρsy为y方向的配筋率,ρsy=Asy/Ay,Asy为钢筋的横截面积,Ay为钢筋混凝土板的横截面积;Ecy为混凝土纵向弹性模量;Esy为钢筋纵向弹性模量。
泊松比的计算公式为
μ1=μcVc+μsVs
(9)
![]()
(10)
式中,μ1为板的纵向泊松比;μ2为板的横向泊松比;μs为钢筋的泊松比;μc为混凝土的泊松比;Vc为混凝土所占的体积比;Vs为钢筋所占的体积比。
剪切模量的计算公式为
![]()
(11)
式中,k为接触系数,k=0.4Vc-0.025;Gs为钢筋的剪切模量,矿用工字钢为低碳钢,按经验取值为80 GPa;Gc为混凝土的剪切模量,取值为12 GPa(根据《混凝土结构设计规范》[18]知,混凝土的剪切模量可取为其弹性模量的0.4倍)。
刚度计算公式为
![]()
(12)
![]()
(13)
![]()
(14)
在薄板弯曲问题中,法向应力σx,σy和切向剪应力τxy为主要应力,横向剪应力τzx和τzy为次要力,故对横向剪应力τzx和τzy不做计算。
挠度ω与应力间的关系式为

(15)
联立式(6)~(15),并代入相关参数,得到板的应力函数表达式为
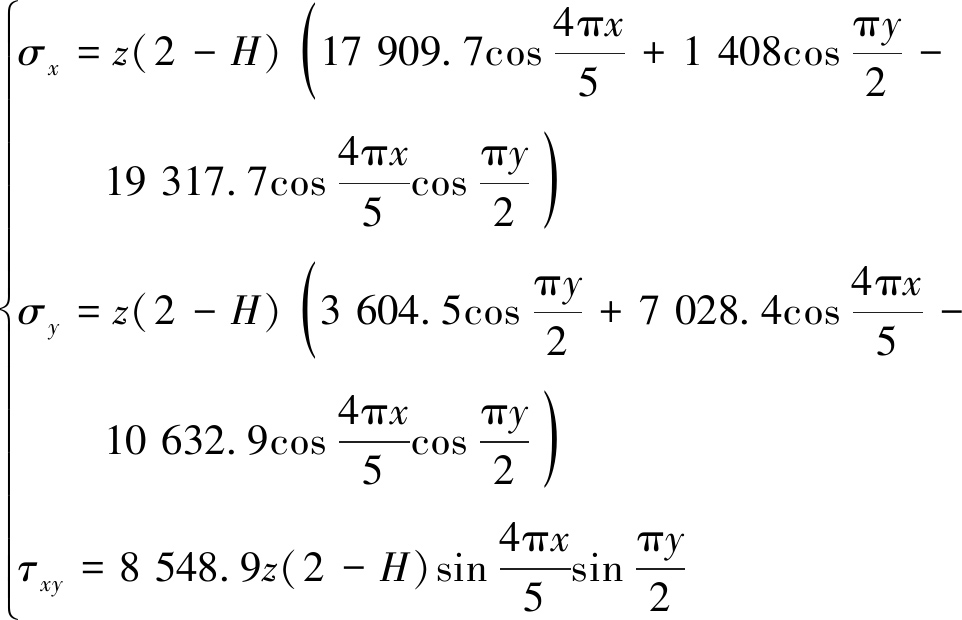
(16)
2.3 正交异性薄板在垂直载荷作用下的应力解
正交异形板的相容方程为
![]()
(17)
由式(17)可知,将应力函数Φ取为关于x和y的不超过3次幂的多项式,则应力分量与弹性常数无关,即应力分量和各向同性板中完全一样,此时纵向载荷作用下的薄板问题可看作平面应力问题,可利用应力变分法求出薄板内应力分量[19-20]。
应力变分方程为
![]()
(18)
变分法中的应力函数形式为
![]()
(19)
式中,Φ0为给定的应力分量应满足板的应力边界条件;Φm为给定的应力分量应满足板面力为0的应力边界条件;Am为互不依赖的m个系数。
令m=2,假设应力函数Φ的形式如下
![]()
(20)
经验证,σy,τyx满足y=0的应力边界条件:![]() 联立式(19),(20)得
联立式(19),(20)得

则可得出
![]()
(21)
![]()
(22)
![]()
(23)
将相关参数代入到式(21)~(23)得
σx=q(0.03y-0.04x2)
(24)
σy=-q(1+0.04y2)
(25)
τxy=0.07qxy
(26)
2.4 坝墙极限承载状态分析
将水压和垂直载荷分别作用下薄板内部产生的应力相加,得到在水压和垂直载荷共同作用下薄板内部的应力分布。
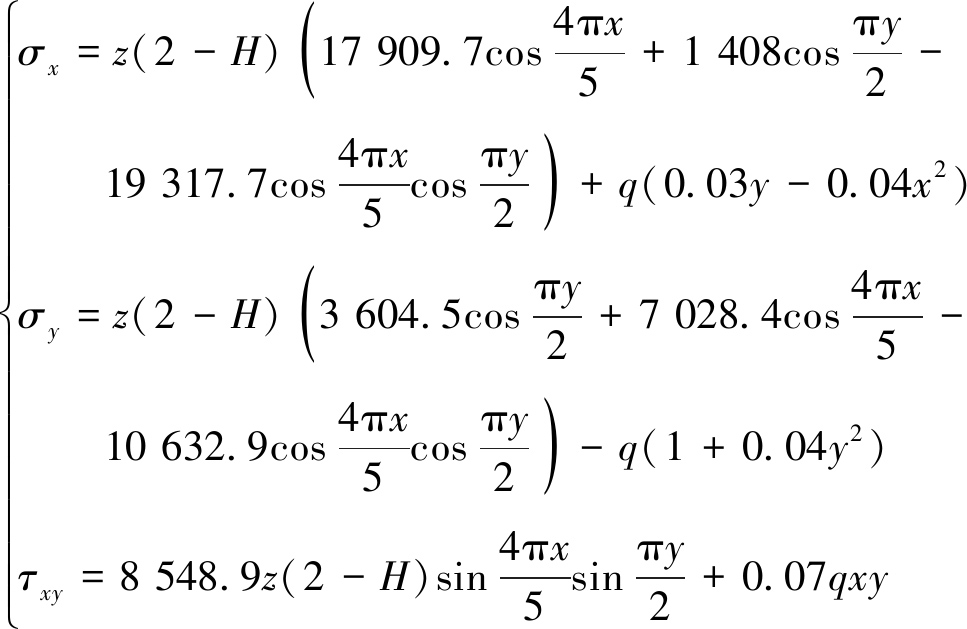
(27)
由式(27)可知,主要应力的极值在薄板表面z=±0.5处取得,因此应主要分析坝墙内外表面的极限应力状态。
库仑准则[21]是一种适用于岩石材料压剪破坏的强度准则,能体现受压下的剪切滑移破坏特性和反映受拉下的断裂破坏,因此笔者使用库仑准则来确定坝墙模型内外表面的安全应力状态。
库仑准则可表述为
![]()
(28)
其中,σ1,σ3分别为单元体的第一、第三主应力;c为黏结力;φ为内摩擦角;θ为岩石破断角,θ=π/4+φ/2。按照混凝土材料参数经验值,c取1.5 MPa,φ取40°。
![]()
(29)
f(x,y)为库仑函数;f=0表示煤岩处于临界破坏状态;f>0表示煤岩处于破坏状态,f < 0表示煤岩处于稳定状态。
利用MATLAB软件可分别绘制出不同上覆垂直载荷所对应的坝墙表面库仑函数f值分布,如图4所示。由图4可知,当垂直载荷为0 MPa时,简化后的现场坝墙表面中心处的库仑函数值最大,说明此时坝墙表面中心处最易发生破坏;当垂直载荷逐渐增大时,坝墙表面易破坏点位置由表面中心处逐渐下移到表面底边中点处。

图4 简化后的现场坝墙表面库仑函数值分布
Fig.4 Value-distribution of coulomb function on surface of dam wall
根据f值的大小,可得到坝墙表面易破坏点的位置,联立式(27)~(29)并代入易破坏点坐标,得到不同垂直载荷条件下的坝墙表面极限水头值。简化后的现场坝墙内表面和外表面分别对应的极限水头值随垂直载荷增加的变化规律如图5所示。

图5 坝墙内外表面极限水头值对比
Fig.5 Contrast of highest head of internal and external surface of dam wall
由图5可看出,简化后的现场坝墙外表面的极限水头值随着垂直载荷的增加而降低,内表面极限水头值呈先增大后减小的趋势。坝墙极限水头值应根据内外表面极限水头值间的较小者来确定,因此当垂直载荷为0时,简化后的现场坝墙极限水头值为80 m,稍小于现场坝体最大挡水高度(90 m)。这说明坝墙平面外的支撑墙结构对于提高坝体承载性能的作用不明显,支撑墙的设置是不必要的,所以可主要从坝墙骨架结构和坝墙厚度两方面对坝体结构进行优化。
3 基于极限承载能力的坝墙厚度优化
由上述分析可知,坝墙的横向和竖向等效配筋率分别仅为0.249%和0.332%,而在《混凝土结构设计规范》[18]中为避免结构发生脆性破坏而规定的受拉钢筋的最小配筋率为0.3%(由文献[18]中的相关计算方法得到),说明坝墙等效配筋率已接近规定的最小配筋率,现有坝墙骨架结构存在的优化空间已不大,因此下面从改变坝墙厚度的角度来对坝体结构进行优化。
3.1 不同厚度对坝墙极限水头值的影响
基于如图3所示的厚度为1 m的钢筋混凝土墙结构,将坝墙厚度等间隔依次减小(0.9,0.8,0.7,0.6,0.5 m),相应的坝墙厚度优化方案分别对应于方案1~5。根据上述计算方法,可得各方案对应坝墙的表面易破坏点位置和不同垂直载荷条件下的表面极限水头值。计算结果显示,各方案对应坝墙的表面易破坏点位置和内外表面极限水头值随垂直载荷增加的变化规律均与简化后的现场坝墙基本一致,各方案对应坝墙的内外表面极限水头值与垂直载荷间的变化规律如图6所示。

图6 坝墙内外表面极限水头值对比
Fig.6 Contrast of highest head of internal and external surface of dam wall
由图6可归纳出以下几点规律:① 随着坝墙上覆垂直载荷的增加,坝墙极限水头值会不断减小,且坝墙厚度越小,坝墙极限水头值的变化幅度越小。考虑到坝墙上覆垂直载荷随着上覆岩层残余变形量的变化会呈现出先上升后稳定的趋势,因此在上覆岩层垂直载荷达到稳定值之前,随着水库服务时间的增加,坝墙上覆垂直载荷会不断增大,坝墙极限水头值会不断减小。② 各方案对应坝墙表面的极限水头值变化曲线均存在一交点,该交点为坝墙易破坏面由外表面变为内表面的转折点,且坝墙厚度越小,转折点对应的垂直载荷越大,坝墙易破坏面变为内表面所需时间越长。③ 若坝墙上覆垂直载荷最终稳定值小于上述转折点对应的垂直载荷值,则坝墙稳定性受其外表面强度控制,且其极限水头值随垂直载荷增加的变化速率基本保持不变;若坝墙上覆垂直载荷最终稳定值超过上述转折点对应的垂直载荷值,则随着垂直载荷的增加,坝墙稳定性先受坝墙外表面强度控制,再受坝墙内表面强度控制,且其极限水头值随垂直载荷增加的变化速率会由小变大再变小。④ 水库储水水位的高低会影响坝墙内外表面发生破坏的先后次序。当储水水位高于转折点对应的极限水头值,则随着垂直载荷的增加,坝墙外表面先发生破坏,内表面后发生破坏;当储水水位低于转折点对应的极限水头值,而高于坝墙上覆垂直载荷稳定值对应的外表面极限水头值时,随着垂直载荷的增加,坝墙内外表面发生破坏的次序会与前者相反,即坝墙内表面先发生破坏,外表面后发生破坏。分析可知,在上述两种情况下,坝墙内外表面均会发生破坏,坝墙存在被贯穿的风险,且坝墙内外表面均发生破坏所需的时间会受储水水位的影响,储水水位越低,则坝墙内外表面均发生破坏所需的时间越长,即坝墙的长期稳定性越好;而当储水水位低于坝墙上覆垂直载荷稳定值对应的外表面极限水头值时,则随着垂直载荷的增加,坝墙只会有一个表面发生破坏,坝墙不存在被贯穿的风险。
由上述分析可知,在水库服务期间,受坝墙上覆垂直载荷变化的影响,不同时间段的坝墙极限水头值是不同的。所以,随着水库服务时间的推移,应根据坝墙极限水头值随垂直载荷的变化规律,灵活地调整水库储水水位,以避免坝墙发生破坏,甚至贯通的危险。
由于现场坝墙上覆垂直载荷测定困难,缺少相关实测数据,且难以直接计算,所以为了得到大柳塔矿地下水库挡水坝墙上覆垂直载荷的变化范围,利用FLAC3D数值分析软件对不同开采条件下的坝墙上覆垂直载荷稳定值进行了分析。
3.2 坝墙垂直载荷数值模拟
根据大柳塔矿地下水库所处煤层的实际赋存条件,建立如图7所示的简化地质模型(煤层上覆岩层部分未展示出)。

图7 数值模型示意
Fig.7 Numerical model diagram
数值模拟方案见表1,煤层埋深分别为100和200 m,采高分别为3,5,7 m,坝墙与采空区边界间的距离分别为5和10 m。
由现场实测数据可知,在巷道正常使用期间内,巷道顶板下沉量为2 cm左右[22],因此在模拟计算过程中,先对未加入坝墙的数值模型进行调整,使得模型中的巷道顶部下沉量为2 cm左右,随后基于该模型,加上坝墙,进行运算,从而得到坝体上覆垂直载荷稳定值。
在坝墙上覆垂直载荷模拟结果中,坝墙顶面所受的垂直载荷为非均匀的,出于计算需要,此处将坝墙垂直应力取为模拟结果的平均值。坝墙垂直载荷数值模拟结果见表2。
表1 数值模拟参数
Table 1 Numerical simulation parameters m
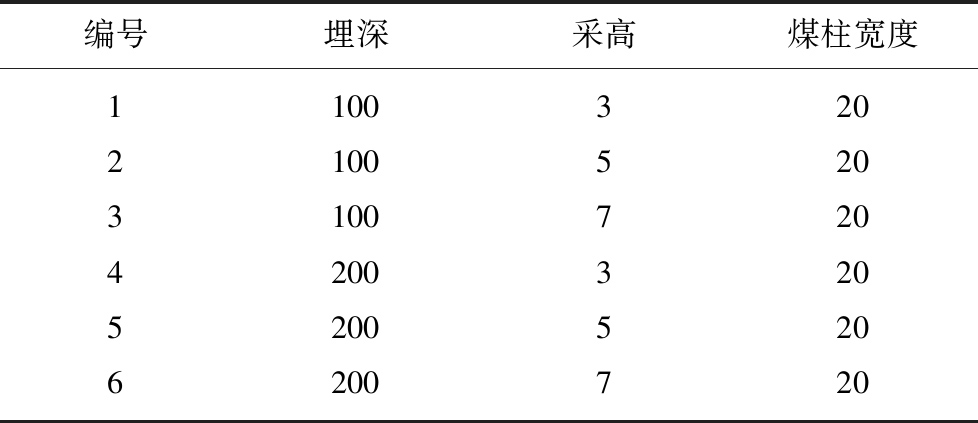
编号埋深采高煤柱宽度110032021005203100720420032052005206200720
表2 坝墙上覆垂直载荷数值模拟结果
Table 2 Numerical simulation results of vertical load on dam wall
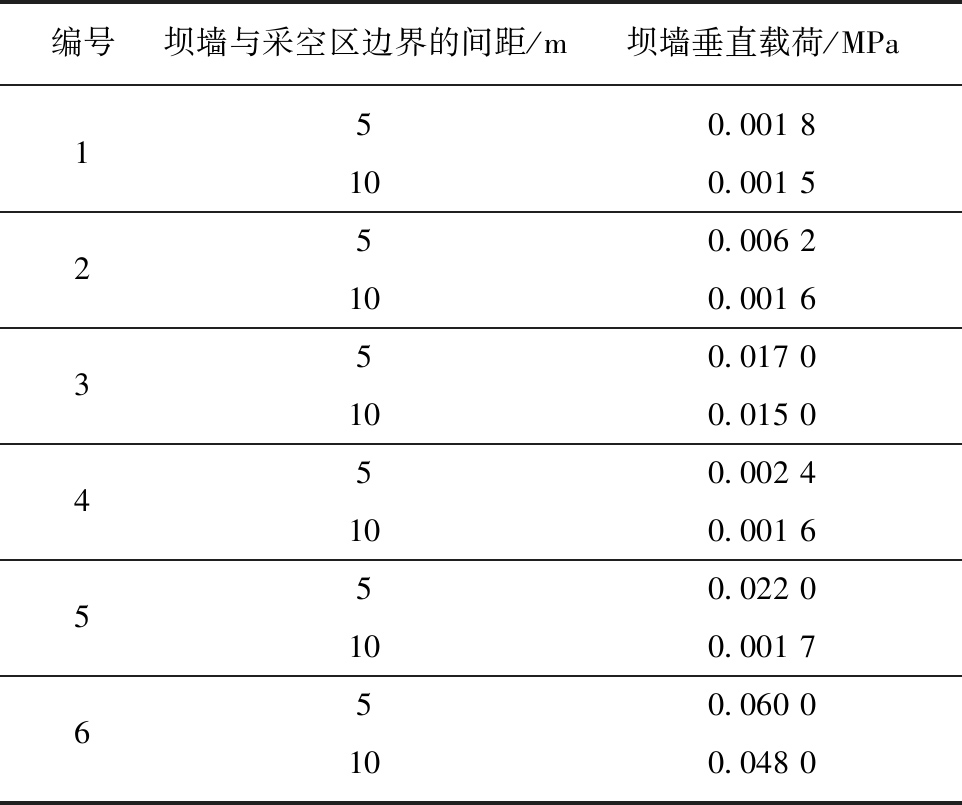
编号坝墙与采空区边界的间距/m坝墙垂直载荷/MPa150.001 8100.001 5250.006 2100.001 6350.017 0100.015 0450.002 4100.001 6550.022 0100.001 7650.060 0100.048 0
3.3 坝墙厚度优化结果
5种不同墙厚设计方案所对应的坝墙水头极限值随垂直载荷值的变化规律如图8所示。

图8 不同设计方案坝墙的极限水头值对比
Fig.8 Comparison of highest head of retaining walls with different design schemes
由图8可看出,在埋深为100~200 m,采高为3~7 m的开采条件下,当地下水库的日常储水水位处于15~19 m内时,方案4(墙厚0.6 m,横向配筋率ρx为0.249%,竖向配筋率ρy为0.332%)为较优的坝体结构设计方案;当地下水库的日常储水水位处于19~20 m内时,方案3(墙厚0.7 m,横向配筋率ρx为0.249%,竖向配筋率ρy为0.332%)为较优的坝体结构设计方案。据此,可将现场施工的“T”字形坝体优化为厚度较小的一字形墙体结构,从而节省坝体建设材料,提升坝体建设经济性。
4 结 论
(1)利用正交异性薄板模型,得到了坝墙主承载结构即工字钢混凝土墙在水压和上覆垂直载荷作用下的应力分布函数,基于库仑准则,得出坝墙即可满足承载力的要求,在其外侧增设支撑墙结构是没有必要的,在此基础上,考虑到坝墙骨架结构的等效配筋率已接近规范规定的最小值,所以可通过改变其厚度来进行坝体结构优化。
(2)通过坝墙的极限承载力分析得出随着上覆垂直载荷由0开始增加,坝墙表面易破坏点位置由中心处逐渐下移至底边中心处;在坝墙上覆垂直载荷达到稳定值之前,随着水库服务时间的增加,坝墙上覆垂直载荷会不断增大,坝墙极限水头值会不断减小。
(3)根据坝墙内外表面极限水头值的变化曲线得出随着垂直载荷的增加,坝墙易破坏面先为外表面,随后转变为内表面,且坝墙易破坏面由外表面变为内表面的转折点受坝墙厚度影响,坝墙厚度越小,转折点对应的垂直载荷越大;水库储水水位和转折点对应的极限水头值的相对大小会影响坝墙内外表面发生破坏的先后次序,且若储水水位高于坝墙上覆垂直载荷稳定时对应的外表面极限水头值,则随着垂直载荷的增加,坝墙会出现由内表面到外表面或由外表面到内表面的渐进破坏过程,从而使坝墙存在被贯穿的风险。
(4)在埋深为100~200 m,采高为3~7 m的开采条件下,大柳塔矿地下水库人工坝体可不设支撑墙结构,并在此基础上,可进一步根据地下水库的日常储水高度范围对坝墙厚度进行优化设计:当储水水位处于15~19 m内时,坝墙厚度可由原来的1 m减小为0.6 m;当储水水位处于19~20 m内时,坝墙厚度可减小为0.7 m,从而达到节省坝体建设材料,提高坝体建设经济性的优化效果。
[1] 范立民,马雄德,冀瑞君.西部生态脆弱矿区保水采煤研究与实践进展[J].煤炭学报,2015,40(8):1711-1717.
FAN Limin,MA Xiongde,JI Ruijun.Progress in engineering practice of water-preserved coal mining in western eco-environment frangible area[J].Journal of China Coal Society,2015,40(8):1711-1717.
[2] 陈苏社,黄庆享,薛刚,等.大柳塔煤矿地下水库建设与水资源利用技术[J].煤炭科学技术,2016,44(8):21-28.
CHEN Sunshe,HUANG Qingxiang,XUE Gang,et al.Technology of underground reservoir construction and water resource utilization in Daliuta Coal Mine[J].Coal Science and Technology,2016,44(8):21-28.
[3] 陈苏社,鞠金峰.大柳塔煤矿矿井水资源化利用技术[J].煤炭科学技术,2011,39(2):125-128.
CHEN Sunshe,JU Jinfeng.Utilization technology of mine water resources in Daliuta Mine[J].Coal Science and Technology,2011,39(2):125-128.
[4] 曹志国,何瑞敏,王兴峰.地下水受煤炭开采的影响及其储存利用技术[J].煤炭科学技术,2014,42(12):113-116.
CAO Zhiguo,HE Ruimin,WANG Xingfeng.Coal mining affected to underground water and underground water storage andutilization technology[J].Coal Science and Technology,2014,42(12):113-116.
[5] 缪协兴,王安,孙亚军,等.干旱半干旱矿区水资源保护性采煤基础与应用研究[J].岩石力学与工程学报,2009,28(2):217-227.
MIAO Xiexing,WANG An,SUN Yajun,et al.Research on basic theory of mining with water resources protection and its application to arid and semi-arid mining areas[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(2):217-227.
[6] 顾大钊.煤矿地下水库理论框架和技术体系[J].煤炭学报,2015,40(2):239-246.
GU Dazhao.Theory framework and technological system of coal mine underground reservoir[J].Journal of China Coal Society,2015,40(2):239-246.
[7] FAN Limin,MA Xiongde.A review on investigation of water-preserved coal mining in western China[J].International Journal of Coal Science & Technology,2018,5(4):411-416.
[8] 陈苏社.神东矿区井下采空区水库水资源循环利用关键技术研究[D].西安:西安科技大学,2016.
CHEN Sushe.Research on the key technology of water resources recycling utilization in the underground goaf reservoir in Shendong Mining Area[D].Xi’an:Xi’an University of Science and Technology,2016.
[9] 陈阳.煤矿地下水库挡水坝体防渗型式与渗控效果研究[D].北京:清华大学,2015.
CHEN Yang.Research on the seepage prevention and seepage control effect of coal mine underground reservoir water retaining dam[D].Beijing:Tsinghua University,2015.
[10] 顾大钊,颜永国,张勇,等.煤矿地下水库煤柱动力响应与稳定性分析[J].煤炭学报,2016,41(7):1589-1597.
GU Dazhao,YAN Yongguo,ZHANG Yong,et al.Experimental study and numerical simulation for dynamic response of coal pillars in coal mine underground reservoir[J].Journal of China Coal Society,2016,41(7):1589-1597.
[11] 白东尧,鞠金峰,许家林,等.李家壕煤矿地下水库人工坝体稳定性研究[J].煤炭学报,2017,42(7):1839-1845.
BAI Dongyao,JU Jinfeng,XU Jialin,et al.Stability analysis of mine underground reservoir artificial dam in Lijiahao Mine[J].Journal of China Coal Society,2017,42(7):1839-1845.
[12] 王悦帆.正交各向异性混凝土桥面板的动力分析[D].西安:西安建筑科技大学,2010.
WANG Yuefan.Dynamic analysis about the orthotropic bridge decks of reinforced concrete[D].Xi’an:Xi’an University of Architecture and Technology,2010.
[13] 林宏伟,石志飞.钢筋混凝土框架梁-剪力墙平面外连接节点的力学分析[J].建筑科学与工程学报,2007,24(3):56-60.
LIN Hongwei,SHI Zhifei.Mechanical analysis for non-planar reinforced concrete frame beam and shear-wall joint[J].Journal of Architecture and Civil Engineering,2007,24(3):56-60.
[14] 卜小明,严宗达.无拉力Winkler地基上自由边矩形薄板的弯曲[J].应用数学和力学,1989,10(5):419-426.
BU Xiaoming,YAN Zongda.Bending of rectangular thin plates with free edges laid on tensionless winkler foundation[J].Applied Mathematics and Mechanics,1989,10(5):419-426.
[15] 成祥生.应用板壳理论[M].济南:山东科学技术出版社,1989.
[16] 王福安.钢筋混凝土剪力墙平面外受弯等效宽度计算[D].北京:北京交通大学,2008.
WANG Fuan.The equivalent width of shear wall in bending at non-planar[D].Beijin:Beijing Jiaotong University,2008.
[17] 王耀先.复合材料结构设计[M].北京:化学工业出版社,2001.
[18] 中华人民共和国建设部.混凝土结构设计规范[M].北京:中国建筑工业出版社,2002.
[19] 徐芝纶.弹性力学简明教程(第四版)[M].北京:高等教育出版社,2013.
[20] 饶宏玲.采用弹性力学应力变分法求解基础置换砼块应力的一种方法[J].四川水力发电,1995,14(2):81-83.
RAO Hongling.A method to solve foundation replacement concrete block stress using elastic mechanics stress variational method[J].Sichuan Water Power,1995,14(2):81-83.
[21] 蔡美峰.岩石力学与工程(第四版)[M].北京:科学出版社,2013.
[22] 朱拴刚.特大煤巷断面锚杆支护技术的应用[J].内蒙古科技与经济,2010,14(5):95-96.
ZHU Shuangang.Application of bolt support technology in the section of ultra-large coal roadway[J].Inner Mongolia Science Technology & Economy,2010,14(5):95-96.
