费托合成(FTs)是将合成气(H2+CO)在催化剂作用下转化为烃类的重要过程,也是煤间接液化生产燃料和化学品的关键步骤。随着国际重要产油区政局的持续动荡和中国能源结构的逐步调整,对这一过程的基础研究和工业应用变得越来越广泛。费托合成是发生在催化剂表面的一系列聚合反应,其反应机理的复杂性和中间产物的多样性使得动力学的获得变得困难。经过数十年的发展,费托合成反应动力学研究在两个方向上均获得了较大的进展:一类是基于反应物组分消耗速率的集总动力学模型,另一类则是基于烃类产物生成速率的产物动力学模型[1-2]。笔者基于费托合成反应机理,建立适用于反应器设计和工艺优化的描述反应物CO转化的集总反应动力学模型。
1 概 述
费托合成反应集总动力学在预测反应速率方面准确度高,计算简单,因而在工程应用中有着重要作用。集总动力学形式一般表达为有效合成气的消耗速率r(CO+H2)或CO的消耗速率r(CO)。前者与水煤气变换(WGS)反应速率无关,是H2和CO发生费托合成的总反应速率,而r(CO)则是CO发生FTs反应和WGS反应的总反应速率[3],即
r(CO)=rFT+rWGS
(1)
基于CO消耗的反应动力学模型有两种形式,一种采用经验型幂律形式动力学方程,即
r(CO)=Pn(CO)Pm(H2)
(2)
其中,P为分压;上标n和m为反应级数。早期的动力学研究[4-5]大多集中在此领域,发现当CO转化率低于60%时,氢分压一级动力学模型能较好地预测转化率,同时水和CO2会抑制费托合成反应。另一种是通过假设不同的费托合成反应机理以及速率控制步骤,来推导LHHW(Langmuir-Hinshelwood-Hongen-Watson)型动力学方程[6],即
![]()
(3)
其中,k为动力学参数;上标a和b为反应级数;K为基元反应的平衡常数;下标i为跟动力学方程相关的反应物和产物。这类动力学模型简单明了,可清晰反映出反应物和产物分压对关键组分消耗的影响程度,通常能在比较宽的范围对CO或合成气转化率给出很好的预测,所以近年来的集总动力学研究大多为此类模型[6-7]。由于费托反应机理众多,且认识并不统一,所以基于不同机理会得到各异的动力学模型。从众多文献来看,费托反应体系中似乎没有单一的反应机理,很有可能是多种机理的共同作用,只是某种反应机理起着主要的作用。HUFF和SATTERFIELD[8-9]提出了分别基于碳化物机理(Carbide,M-CHx或M![]() CH2)、烯醇机理(Enolic,M
CH2)、烯醇机理(Enolic,M![]() CHOH)和CO插入机理(Direct Insertion,M
CHOH)和CO插入机理(Direct Insertion,M![]() CO)的3种动力学模型,压力0.445~1.480 MPa,氢碳比0.55~1.81。吉媛媛等[10-11]结合碳化物和甲酸盐机理,研究了Fe-Mn催化剂的CO转化动力学模型,认为CH2-s(s为活性中心)是生成烃类的“结构单元”,将CO生成CH2-s的某个基元反应假定为速率控制步骤,得到了7个动力学模型,压力1.5~3.0 MPa,氢碳比1.0~3.0。LEDAKOWICZ等[12]采用浆态床反应器研究了铁基催化剂的本征动力学,模型基于烯醇机理,假设CO和CO2在活性位上存在竞争吸附。高琳等[13]受计算量子化学研究结果的启发,提出了两种氢助解离机理,在CSTR中研究了Fe-Mn催化剂的动力学模型,氢碳比和压力最大值分别是2.0和2.5 MPa。MA等[6]通过分析83组动力学数据(压力1.3~2.5 MPa,氢碳比0.67~1.50),研究了26种FTs和WGS动力学模型,发现水对费托合成的抑制作用并不明显,而CO2在高CO转化率条件下对WGS的影响较大,研究得到了适用不同CO转化率范围的最优模型,但最优解是在特定温度(270 ℃)下得到的,适用范围有限。
CO)的3种动力学模型,压力0.445~1.480 MPa,氢碳比0.55~1.81。吉媛媛等[10-11]结合碳化物和甲酸盐机理,研究了Fe-Mn催化剂的CO转化动力学模型,认为CH2-s(s为活性中心)是生成烃类的“结构单元”,将CO生成CH2-s的某个基元反应假定为速率控制步骤,得到了7个动力学模型,压力1.5~3.0 MPa,氢碳比1.0~3.0。LEDAKOWICZ等[12]采用浆态床反应器研究了铁基催化剂的本征动力学,模型基于烯醇机理,假设CO和CO2在活性位上存在竞争吸附。高琳等[13]受计算量子化学研究结果的启发,提出了两种氢助解离机理,在CSTR中研究了Fe-Mn催化剂的动力学模型,氢碳比和压力最大值分别是2.0和2.5 MPa。MA等[6]通过分析83组动力学数据(压力1.3~2.5 MPa,氢碳比0.67~1.50),研究了26种FTs和WGS动力学模型,发现水对费托合成的抑制作用并不明显,而CO2在高CO转化率条件下对WGS的影响较大,研究得到了适用不同CO转化率范围的最优模型,但最优解是在特定温度(270 ℃)下得到的,适用范围有限。
可以看出,之前的动力学研究范围比较窄(氢碳比最高3.0,压力最高3.0 MPa),工业应用价值有限。本研究针对自主研发的工业费托合成铁催化剂CNFT-1(主要成分Fe-Cu-K-B-Si,堆密度0.8 g/cm3),采用广为接受的碳化物机理(烃产物通过CH2-s物种生成),在更为宽泛的条件下(氢碳比最高5.0,压力最高4.0 MPa)进行了动力学实验,获得更具有工业应用价值的的集总反应动力学模型。
2 动力学模型
笔者采用广为接受的碳化物机理,通过LHHW法推导反应速率表达式。参照文献[10-11,13]假设:
(1)烃生成反应发生在单一的表面活性中心(s),并且活性中心在催化剂表面均匀分布;
(2)反应达到稳定状态,中间体浓度(中间体占据活性位s的比例)保持不变,H2和CO与气相主体的浓度处于近似平衡,非稳定中间体浓度不随时间变化;
(3)氢气、水和一氧化碳为主要表面物种,中间体物种所占据的活性位忽略不计,催化剂上不会累积碳物种或氧物种;
(4)烃生成反应过程中只有一个速率控制步骤,速控步骤前生成的碳物种中间体处于近似稳态;
(5)费托反应基元步骤见表1,假设基元反应IV为速控步骤[7],其余基元反应均处于平衡状态。
根据假设(4),反应VI和VII达到平衡:
![]()
(4)
![]()
(5)
式中,K为基元反应的平衡常数;下标的数字代表此基元反应在表1中的序号;方括号[ ]代表此物种占据活性位s的比例。
表1 费托合成反应机理模型
Table 1 Mechanism model of FTs

No.Elementary stepsICO+sCOsIICOs+sCs+OsIIIH2+2s2HsIVCs+Hs→CHs+sVCHs+HsCH2s+sVIOs+H2H2OsVIIH2OsH2O+s
由式(4)和(5)可以得到
![]()
(6)
根据假设(4),反应I和II达到平衡:
![]()
(7)
![]()
(8)
由式(7)和(8)可以得到
![]()
(9)
由式(6)和(9)可以得到
![]()
(10)
根据假设(4),反应III达到平衡:
![]()
(11)
根据假设(3):
[s]+[Hs]+[COs]+[H2Os]=1
(12)
![]()
(13)
![]()
(14)
因为反应IV为速率控制步骤,由式(9),(11)和(14),CO消耗速率可表示为
r(CO)=K4[Cs][Hs]=
(mol/(kgcat·s))
动力学参数k,a,b和c对温度的依赖关系遵循Arrhenius定律:
![]()
(16)
![]()
(17)
![]()
(18)
![]()
(19)
式中,k0,a0,b0和c0分别为参考温度下的动力学常数;Ek为活化能;Ha,Hb和Hc为吸附热焓;R为热力学常数。
3 实验部分
反应动力学试验是在搅拌釜反应器(有效体积1.0 L,高径比H/D=2.5)中进行的,使用的H2和CO纯度分别为99.999%和99.9%,由气瓶供气,北京氦普北分气体工业有限公司生产。装置流程如下:原料气依次通过脱硫、脱氧及脱水后进入搅拌釜反应器,反应后的物料先后经过热分离罐(120 ℃)和冷分离罐(0 ℃)后,液相(合成水、轻油和蜡油)和气相(气体产物和未反应的原料气)得到分离。分离后的气相减至常压后进入气相色谱(GC,Agilent 789 0,配置1个FID和2个TCD)分析气体组成,最后由湿式气表计量后放空。试验过程如下:
(1)装填。搅拌釜中首先加入500 mL液体石蜡(密度0.84~0.89 g/cm3,沸点300~500 ℃,江苏永华化学科技有限公司生产)作为溶剂,然后倒入未还原的催化剂15.0 g。
(2)还原。设定装置系统压力2.0 MPa,H2流量350 mL/min,CO流量78 mL/min,搅拌转速400 r/min。首先以15 ℃/h的速率升温至120 ℃,恒温3 h;然后以10 ℃/h的速率升温至180 ℃,调整搅拌转速为800 r/min;最后以5 ℃/h的速率升温至还原温度260 ℃,持续24 h。
(3)反应。还原结束后,调整H2和CO流量为目标值,开始条件试验。
在进行动力学实验前,首先进行外扩散排除实验,确定空速范围和搅拌转速。根据外扩散阻力制约的判别标准[14-15],当搅拌转速超过400 r/min后(图1(a))以及空速>7 000 mL/(g·h)(图1(b))后,催化剂的CO转化不受外扩散阻力制约,相间和相内浓度梯度消失,相间传输限制排除,反应器内达到了理想混合,此时搅拌釜可以认为是全混流反应器[16-17]。
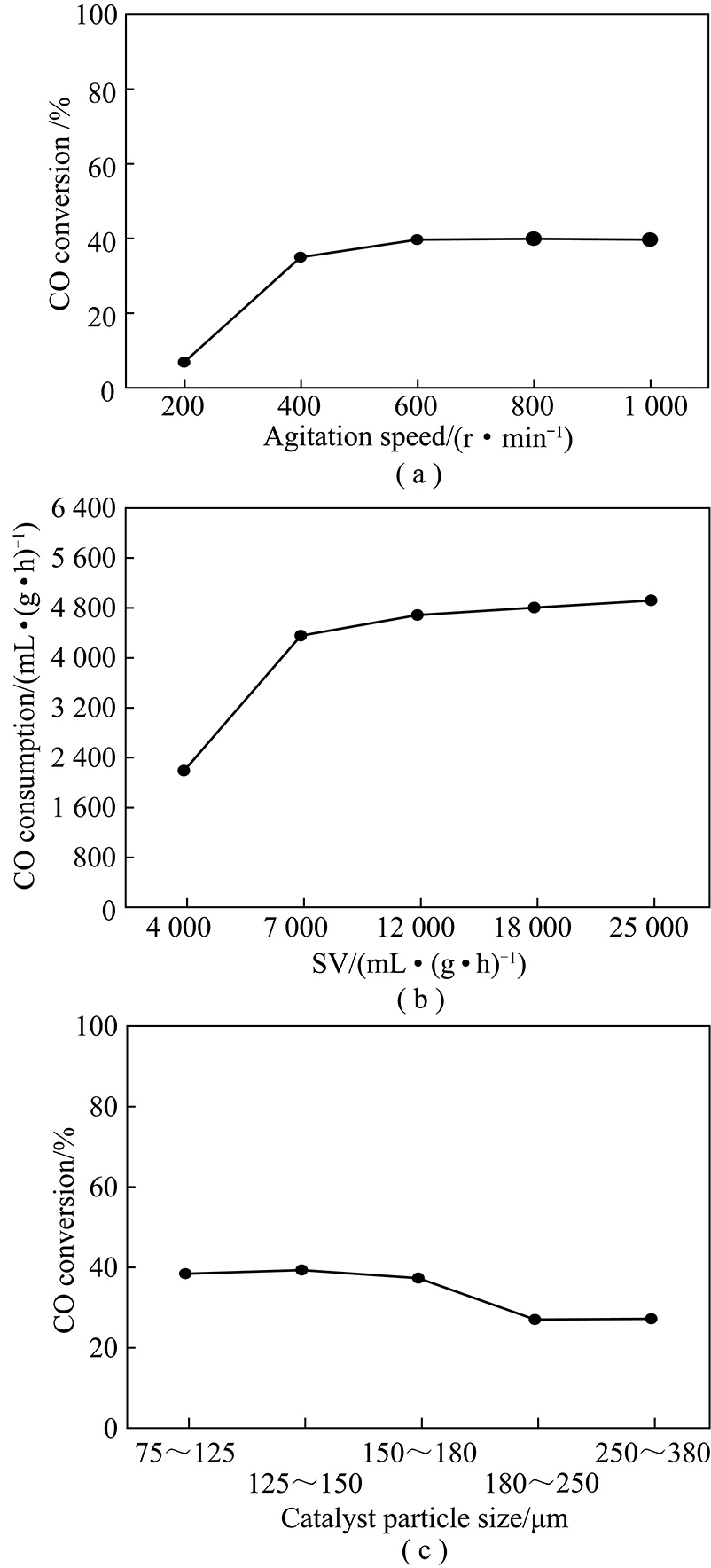
图1 CO转化率随搅拌转速、空速和催化剂粒径的变化趋势
Fig.1 Effect of agitation speed,space velocity and particle size on CO conversion
内扩散是通过设计实验来排除的,不同粒径催化剂对CO转化率的影响如图1(c)所示,可以看出:当催化剂粒径减小到150 μm时,CO转化率开始保持不变,即排除了内扩散。动力学实验中使用的催化剂粒径为50~120 μm,搅拌转速800 r/min,空速下限为8 000 mL/(g·h)。
在设计动力学实验时考虑温度(T)、原料气氢碳比(H2/CO)、压力(P)和空速(GHSV)4个因素,采用正交设计。安排实验时,以温度为首要因素,从低温向高温变化。考虑到原料气氢碳比对催化剂物相的影响[10-11],以H2/CO为次要因素。共有30个实验点,具体实验条件见表2。
表2 费托合成反应动力学实验条件
Table 2 Summary of experimental conditions
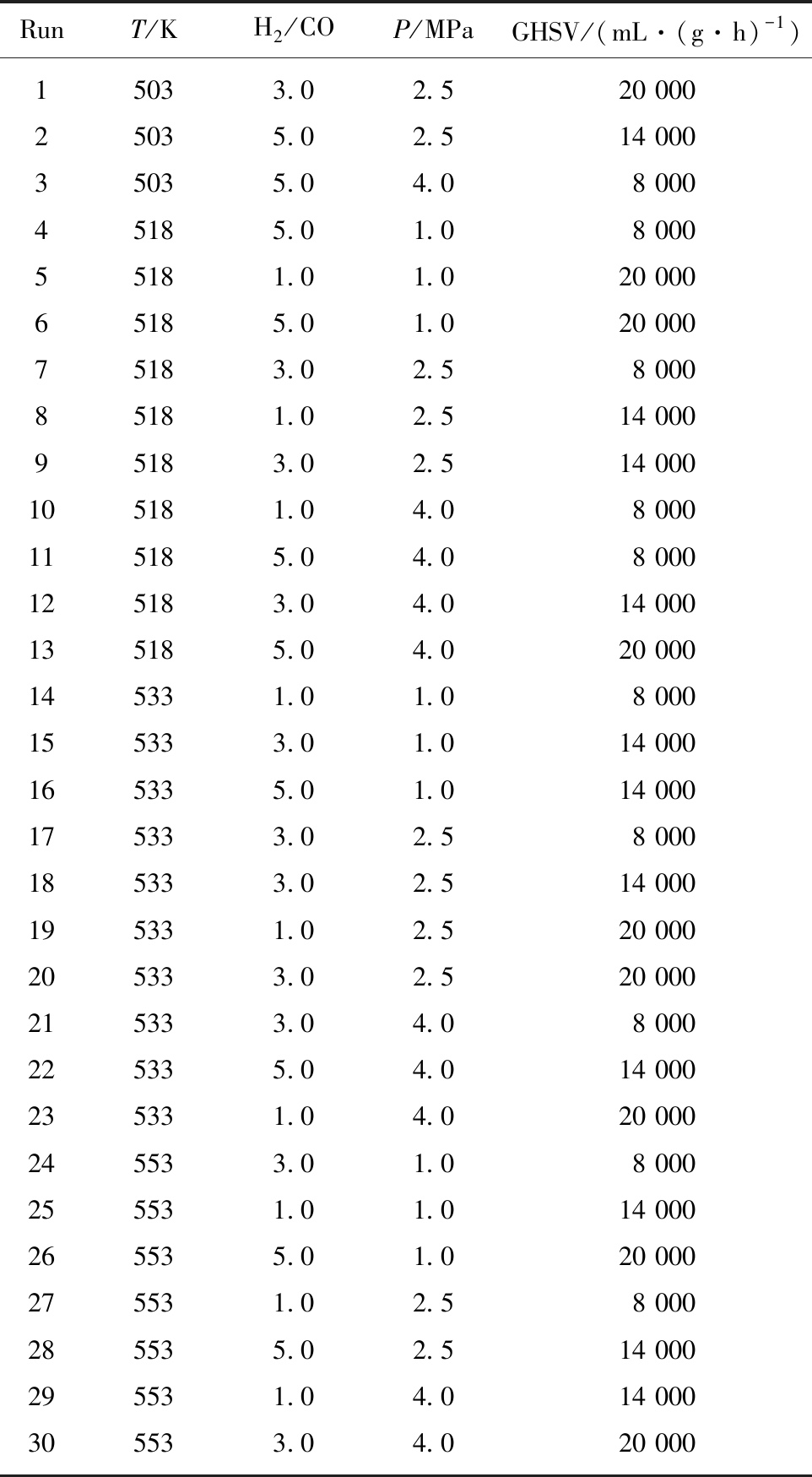
RunT/KH2/COP/MPa GHSV/(mL·(g·h)-1)15033.02.520 00025035.02.514 00035035.04.08 00045185.01.08 00055181.01.020 00065185.01.020 00075183.02.58 00085181.02.514 00095183.02.514 000105181.04.08 000115185.04.08 000125183.04.014 000135185.04.020 000145331.01.08 000155333.01.014 000165335.01.014 000175333.02.58 000185333.02.514 000195331.02.520 000205333.02.520 000215333.04.08 000225335.04.014 000235331.04.020 000245533.01.08 000255531.01.014 000265535.01.020 000275531.02.58 000285535.02.514 000295531.04.014 000305533.04.020 000
为确保反应是稳态操作,每次改变反应条件后,反应都运行24 h以上,并且每隔两个实验点就重复前一个反应条件,以检验两次反应结果是否有重复性。实验结果见表3(X代表转化率,S代表选择性,F代表反应器出口尾气量),可以看出:① CO转化率基本在动力学要求的范围内(20%~70%);② CO转化率和CO2选择性随反应条件的变化趋势基本符合费托合成反应基本规律,数据可靠合理。
4 结果与讨论
为估算动力学方程中的参数,首先以CO转化率的相对残差MARR(Mean Absolute Relative Residuals)建立目标函数,对目标函数最小化以获得最优模型参数:
表3 费托合成反应动力学实验结果
Table 3 Results of kinetics experiments

RunX(CO)/%S(CO2)/%F(CO)/(mL·min-1)F(CO2)/(mL·min-1)126.110.9297.211.4248.511.299.010.4367.013.537.210.2456.720.049.413.0512.514.8725.015.3634.014.1182.913.3760.421.065.120.8819.622.0467.225.1941.518.4169.822.21030.032.0232.431.91178.021.024.418.21248.019.7151.127.51349.716.0138.922.01438.036.6206.046.21537.522.0181.223.91646.022.5104.520.01770.028.749.733.31853.127.0135.741.51925.132.0620.666.62042.024.8241.143.32182.024.029.832.62271.026.056.235.82320.626.0658.444.42455.135.473.431.92527.234.0422.653.72641.025.0163.428.42770.041.299.495.72869.426.153.231.52958.044.3243.4148.83064.830.5145.982.0
![]()
(20)
其中,N为实验组数;m为CO转化率;下角exp代表试验值,cal代表计算值。模型中涉及的CO,H2,CO2和H2O在反应条件下是气相,且逸度系数在1.0±0.05[4],可以当作理想气体处理。
在动力学实验结果基础上,对数据进行非线性回归,得到CO转化率的相对残差分布如图2所示,残差分布比较均匀,MARR=8.7%,模型复相关指数R2=0.92,和其他FT反应动力学文献[6]中的数据水平相当。

图2 动力学模型相对残差分布
Fig.2 Relative residual distribution of model
对得到的动力学参数估计值进行F检验,取置信度α=0.05,计算模型Fc=73.3,大于其相应F值(F0.05=3.1)的10倍。即本动力学模型在置信度95%的区域内,F检验显著,且在统计意义上无差异。
费托反应动力学研究从早期的经验型幂律形式发展到现今广泛使用的基于反应机理和速率控制步骤的LHHW型,实验组数越来越多,而模型计算值与实验结果的误差越来越小。吉媛媛等[10-11]基于传统的碳化物机理,在固定床反应器中共进行了16组实验,得到的估算值与实验值相对误差小于25%;高琳等[13]将计算量子化学与两类反应机理相结合,在搅拌釜反应器中获得实验点20个,将误差缩小到20%;MA等[6]的动力学模型误差在10%以内,数据达83组。总的来看,动力学模型的精度越来越高,原因在于:① 反应基础理论的不断创新[18],这得益于谱学表征和计算机模拟技术的进步。比如在经典表面碳化物机理基础上提出的烷基化机理和碳烯插入机理,以及近年来提出的乙烯酮中间物种理论[19-20],还有烯烃吸附理论对产物偏离ASF(Anderson-Schulz-Flory)分布的较好解释。② 产生动力学模型的实验组数越来越多。动力学模型参数的求解都要依靠非线性拟合,更多的实验数据点能得到更准确的拟合结果。图3比较了动力学模型计算得到的CO消耗速率值和实验值的比较,可以看出:计算值和实验值吻合较好,两者之间的误差在15%以内(图4),模型可信度高。

图3 动力学模型预测值与实验值比较
Fig.3 Comparison of experiment and calculated results

图4 动力学模型计算得到的CO消耗速率与实验值比较
Fig.4 Parity plot of experiment and calculated reaction rates
动力学模型参数见表4,文献中报道的费托合成动力学结果表明:费托反应生成烃类的活化能Ek数值一般在55~142 kJ/mol[21-24]。本模型得到的Ek也落在此范围内,并与文献[11]得到的数值(101 kJ/mol)非常接近。参数a0和b0分别反映CO和H2在催化剂表面的吸附状况,比较a0和b0的数值可知:两者基本在一个数量级之内,而H2吸附热焓(ΔHb)小于CO吸附热焓(ΔHa),表明CO在催化剂表面为强吸附,H2相对为弱吸附,这一结果和诸多文献相符[10-11,13]。
表4 动力学模型参数
Table 4 Kinetics parameters of model

ParametersValuek0/(mol·(kg·s·MPa2/3)-1)0.15Ek/(kJ·mol-1)105.0a0/MPa-14.17Ha/(kJ·mol-1)102.6b0/MPa-0.54.10Hb/(kJ·mol-1)49.2c0/MPa-1-8.18Hc/(kJ·mol-1)2.0
5 结 论
(1)针对工业催化剂CNFT-1,基于碳化物机理,以次甲基生成基元反应为速率控制步骤,获得了CO转化集总动力学模型。
(2)以CO转化率相对残差MARR为目标函数建立模型并获得了最优模型参数,活化能Ek=105.0 kJ/mol,且F检验显著,说明获得的模型物理意义明确且统计意义无差异。
(3)在费托反应过程中,CO在催化剂表面为强吸附,H2相对为弱吸附。
(4)通过本动力学模型得到的CO消耗计算值和实验值相对误差<15%,可用于费托反应器设计和工艺优化。
[1] YANG R Y,ZHOU L P,GAO J H,et al.Effects of experimental operations on the Fischer-Tropsch product distribution[J].Catalysis Today,2017,298(1):77-88.
[2] FILOT I A W,ZIJLSTRA B,BROOS R J P,et al.Kinetic aspects of chain growth in Fischer-Tropsch synthesis[J].Faraday Discussions,2016,197:153-164.
[3] 孙启文.煤炭间接液化[M].北京:化学工业出版社,2012:39.
[4] ZIMMERMAN W H,BUKUR D B.Reaction kinetics over iron catalysis used for the Fischer-Tropsch Synthesis[J].Can.J.Chem.Eng.68(2),1990:292-301.
[5] BUB G,BAERNS M,BÜSSEMEIER B,et al.Prediction of the performance of catalytic fixed bed reactors for Fischer-Tropsch Synthesis[J].Chemical Engineering Science,1980,35(1):348-355.
[6] MA W P,JACOBS G,SPARKS D E,et al.Fischer-Tropsch synthesis and water gas shift kinetics for a precipitated iron catalyst[J].Catalysis Today,2016,275:49-58.
[7] VAN Der Laan G P,BEENACKERS A A C M.Intrinsic kinetics of the gas-solid Fischer-Tropsch and water gas shift reactions over a precipitated iron catalyst[J].Applied Catalysis A:General,2000,193(1):39-53.
[8] HUFF G A J,SATTERFLELD C N.Intrinsic kinetics of the Fisher-Tropsch synthesis on a reduced fused-magnetite catalyst[J].Ind.Eng.Chem.Process Des,1984:696-705.
[9] HUFF G A J,SATTERFLELD C N.Some kinetic design consideration in the Fisher-Tropsch synthesis on a reduced fused-magnetite catalyst[J].Ind.Eng.Chem.Process Des,1984:851-854.
[10] 吉媛媛,相宏伟,李永旺,等.超细粒子Fe-Mn工业催化剂F-T合成集总机理动力学(I)反应机理与动力学模型描述式[J].化工学报,2005,56(6):1020-1025.
JI Yuanyuan,XIANG Hongwei,LI Yongwang,et al.Lumped mechanism kinetics of Fischer-Tropsch synthesis over ultrafine particle Fe-Mn commercial catalyst(I) Reaction mechanism and kinetic model description[J].Journal of Chemical Industry and Engineering(China),2005,56(6):1020-1025.
[11] 吉媛媛,相宏伟,李永旺,等.超细粒子Fe-Mn工业催化剂F-T合成集总机理动力学(II)参数估算与模型筛选[J].化工学报,2005,56(6):1026-1030.
JI Yuanyuan,XIANG Hongwei,LI Yongwang,et al.Lumped mechanism kinetics of Fischer-Tropsch synthesis over ultrafine particle Fe-Mn commercial catalyst(II) evaluation of parameter and discrimination of model[J].Journal of Chemical Industry and Engineering(China),2005,56(6):1026-1030.
[12] LEDAKOWICZ S,NETTELHOFF H,KOKUUM R,et al.Kinetics of the Fisher-Tropsch Synthesis in the slurry phase on a potassium-promoted iron catalyst[J].Ind.Eng.Chem.Process Des.Dev,1985,24(4):1043-1049.
[13] 高琳,徐元源,李永旺.工业Fe-Mn催化剂上费托合成反应动力学的研究[J].燃料化学学报,2009,37(6):717-721.
GAO Lin,XU Yuanyuan,LI Yongwang.Study on lumped kinetics model for Fischer-Tropsch synthesis over an industrial Fe-Mn catalyst[J].Journal of Fuel Chemistry and Technology,2009,37(6):717-721.
[14] FROMENT G F,BISCHOFF K B,WILDE J D.Chemical reactor analysis and design,2nd edition[M].New York:John Wiley & Sons,Inc,1990:167.
[15] ZHAO L,ZHANG Y H,CUI P.Investigate the kinetics of coke solution loss reaction with an alkali metal as a catalyst based on the improved genetic algorithm[J].International Journal of Coal Science & Technology,2018,5(4):430-438.
[16] 陈诵英.催化反应工程基础[M].北京:化学工业出版社,2011:26-28.
[17] 田野,张立红,赵宜成,等.多相催化剂:基本原理与应用[M].北京:化学工业出版社,2018:148-151.
[18] 吴艳,赵鹏,毛学锋.煤液化条件下铁系催化剂的相变[J].煤炭学报,2018,43(5):1448-1454.
WU Yan,ZHAO Peng,MAO Xuefeng.Phase transformation of iron-based catalyst at coal liquefaction[J].Journal of China Coal Society,2018,43(5):1448-1454.
[19] 相宏伟,杨勇,李永旺.煤炭间接液化:从基础到工业化[J].中国科学:化学,2014,44(12):1876-1892.
XIANG Hongwei,YANG Yong,LI Yongwang.Indirect coal-to-liquids technology from fundamental research to commercialization[J].Scientia Sinica Chimica,2014,44(12):1876-1892.
[20] 温晓东,杨勇,相宏伟,等.费托合成铁基催化剂的设计基础:从理论走向实践[J].中国科学:化学,2017,47(11):1298-1311.
WEN Xiaodong,YANG Yong,XIANG Hongwei,et al.The design principle of iron-based catalysts for Fischer-Tropsch synthesis:From theory to practice[J].Scientia Sinica Chimica,2017,47(11):1298-1311.
[21] 滕波涛,常杰,刘颖,等.工业Fe-Mn催化剂上基于详细反应机理的F-T合成动力学模型.I.烯烃再吸附动力学研究[J].催化学报,2005,26(8):693-700.
TENG Botao,CHANG Jie,LIU Ying,et al.Detailed kinetics model of Fischer-Tropsch synthesis over an industrial Fe-Mn catalyst I.Kinetics study on olefin readsorption[J].Chinese Journal of Catalysis,2005,26(8):693-700.
[22] 滕波涛,常杰,王刚,等.工业Fe-Mn催化剂上基于详细反应机理的F-T合成动力学模型.Ⅱ.不同校正方法的动力学模型分析[J].催化学报,2005,26(8):701-706.
TENG Botao,CHANG Jie,WANG Gang,et al.Detailed kinetics model of Fischer-Tropsch Synthesis over an industrial Fe-Mn Catalyst I.Kinetics model analysis regressed by different correction methods[J].Chinese Journal of Catalysis,2005,26(8):701-706.
[23] YATES I C,SATTERFIELD C N.Effect of carbon dioxide on the kinetics of the Fischer-Tropsch synthesis on iron catalysts[J].Ind.Eng.Chem.Res.,1988,28(1):9-12.
[24] ZHOU L P,HAO X,GAO J H,et al.Studies and discriminations of the kinetic models for the iron-based Fischer-Tropsch catalytic reaction in a recycle slurry reactor[J].Energy & Fuels,2011,25(1):52-59.
