自主导航能力是煤矿井下移动机器人智能化程度评价的重要指标,国家煤矿安监局制定的《煤矿机器人重点研发目录》中,对38种煤矿机器人均提出了相应的自主导航功能需求[1]。随着计算机技术、传感器技术、机器人技术等的快速发展,已有一些具备自主导航能力的移动机器人相关研究成果及产品应用[2]。但针对煤矿井下这一特殊环境的移动机器人自主导航问题讨论较少,仍存在诸多关键问题亟待研究与解决。
煤矿井下移动机器人的自主导航就是要解决井下定位(我在哪?)[3]、导航地图创建(要去哪?)[4]以及基于地图的运动规划(怎么去?)[5]这3个关键技术问题,其中定位与地图创建存在相辅相成关系,即高精度的定位需要基于精确的地图,创建精确的地图需要基于高精度的定位,自主导航问题中的定位与地图构建被描述为同步定位与建图问题(simultaneous localization and mapping)[6]。目前移动机器人自主导航定位与建图问题中广泛使用的是基于二维激光雷达的方法,通过扫描匹配生成环境平面占据栅格地图,并基于该地图执行粒子滤波算法实现二维实时定位[7]。卡内基梅隆大学领域机器人中心,在2002—2006年的地面移动式土拨鼠(groundhog)机器人研发项目中,利用该方法对3个废弃地下矿井实现了地图创建,同时采用A*搜索策略实现了一定程度的自主探测功能,是首个真实地下环境中实现半自主导航的项目[8]。对于无人机等非地面移动式机器人,上述方法无法满足其三维空间下运动规划的要求。三维激光雷达可以高速精确的捕获环境中的距离信息,近年来随着无人车领域的大力推广得到了大量应用,同时也是煤矿井下三维地理信息系统(GIS)构建的主力传感器[9]。Clickmox公司与Inkonova公司使用四旋翼无人机平台,搭载三维激光雷达,可通过遥操作无人机扫描矿井下巷道环境,并离线处理获得高精度井下地图[10]。但激光数据类型单一,可视化的三维点云数据由于只具有距离信息与三维形貌,缺乏环境纹理,因此通过三维激光雷达构建环境数据后,处理时的环境信息标注与分类等工作还需耗费大量的人力、算力。面对煤矿井下移动机器人自主导航问题,其任务执行过程中的临场性、实时性应当处于更高的优先考虑级别。
移动机器人视觉导航是近年来的研究热点,内华达大学的自主机器人实验室,在2019年DARPA SubT地下挑战赛中,由无人机搭载单目相机,验证了Rovio视觉定位算法,并使用局部加全局的运动规划,完成了巡航任务[11]。视觉传感器种类众多,大致分为单目相机、多目相机、RGB-D相机以及新兴的事件相机(event camera)。其中RGB-D相机又被称为深度相机,在获取视觉数据的同时使用TOF(Time of Flight)或者结构光原理获得环境中的深度距离数据[12],因此省去了单双目相机的三角化处理步骤,节约了计算量。深度相机在地面开阔环境下由于强光照、观测物距离较远,会出现精度降低、数据失效等问题,而煤矿井下巷道环境较为狭窄,光照较暗,Kinect v1等结构光原理深度相机甚至可以在完全黑暗的环境下使用。同时,相对于三维激光雷达,视觉的信息更加丰富,移动机器人搭载视觉传感器任务执行后得到的结果更利于后续决策的制定与实施。
综上所述,本文提出一种煤矿井下移动机器人深度视觉自主导航方法。
1 深度视觉自主导航方法
该方法由机器人搭载RGB-D相机作为深度视觉数据采集传感器,通过地图创建与自主运行2个阶段实现自主导航任务。地图创建阶段通过对深度视觉数据的特征提取与匹配构建深度视觉数据关联ICP模型[13],利用图优化理论[14]构建与求解ICP-BA图模型的煤矿井下移动机器人深度视觉定位与建图问题。自主运行阶段使用Octomap[15]作为机器人导航地图,利用PNP原理[16]实时重定位。在此基础上,自主导航运动规划采用A*路径规划[17],Minimum-Snap[18]轨迹生成用于移动机器人的运动执行。算法流程如图1所示。

图1 煤矿井下移动机器人深度视觉自主导航流程
Fig.1 Process of the depth vision based mobile robot autonomous navigation method
2 深度视觉数据特征提取与匹配
传统RGB相机只能在一帧数据中获得一幅彩色图像,而RGB-D相机在采集彩色图像的同时,可以得到同尺寸的由16位整数记录的深度图。图2(a)所示为本文所使用Kinect v1相机所采集的一帧深度视觉数据,图2(b)为彩色图,图2(c)为深度图。通过深度图数据的读取,在彩色镜头标定后,可将单帧RGB-D深度视觉数据进行三维投影显示,如图2(d)所示。

图2 深度视觉传感器介绍
Fig.2 Introduction to depth vision sensor
深度视觉数据的图像处理是通过对采集到的视觉图像进行相应特征计算并构建数据关联,常用特征点法(Feature-based Methods)[19]与直接法(Direct-Methods)[20]。直接法基于光照不变假设,面对煤矿井下的特殊照明环境,特征点法通过选取合适的特征描述子,可以忽略光照变化的影响。另外,特征点法还具有计算量更少、更易获得良好重定位效果的优势。因此,本文采用特征点法对深度视觉数据中的连续两帧二维彩色图像进行图像处理。
世界坐标系是相机初始化成功后,与获取的第1帧图像固连的相机位姿定义的坐标系。图像特征点的提取与匹配就是找到三维世界坐标系下的环境特征,以及在不同图像平面坐标系下的投影表达及其共视关系。如图3所示,世界坐标系下的立方体,在k时刻与k+1时刻由相机捕获到图像,投影于其对应图像平面。图像平面中红点代表提取到的图像特征点,蓝色连线代表两帧图像特征点的匹配关系。

图3 图像特征点匹配模型
Fig.3 Image feature point matching model
图像的特征点由提取到的关键点与计算出的描述子两部分组成。最直观的特征点类型是角点,角点的关键点提取算法有Harris,Fast,GFTT等,这些基于角点的关键点提取算法具有计算速度快等优势,但当图像发生旋转、位移等变化时,角点的稳定性较差。后续的研究者设计出具有更加稳定局部特征的特征点类型,经典的方法有SIFT,SURF,KAZE,Orb等。描述子是将提取到的关键点进行编码计算并存储为一定的数据结构,广泛使用的描述子方法有Freak,Brief,Brisk等。图像特征的匹配就是根据计算出的描述子执行相似度计算,得分相近的描述子认为是同一环境特征在不同图像下的投影点,常用的匹配方法有Brute-Force(BF),FLANN等[21-23]。
图像特征点的提取与匹配方法众多,但对于不同的环境特点、计算机算力、实时性需求等客观因素,需要综合考量选择适宜的方案。针对煤矿井下的环境特点,本文设计如下实验:截取煤矿井下拍摄的视频中10组不同场景、相邻时刻图像(图4中前两列,图像分辨率为960×540),对5种图像特征提取与匹配方法(GFTT+BRISK+BF;GFTT+BRIEF+BF;ORB+BRIEF+BF;SIFT+SIFT+FLANN;SURF+SURF+FLANN)进行了综合比较。图4第3列展示的是本文实验中SURF+SURF+FLANN匹配结果:
为了更好的对比几种特征提取及匹配组合方法,上述图像特征提取与匹配程序增加了汉明距离粗匹配,与Ransanc剔除误匹配,同时未采用GPU加速及多线程技术,开发环境为:c++,opencv3.4.6(默认参数),运行环境为:Linux-64系统,CPU:I5-8 265U,RAM:8 G,其结果见表1。
表1对10组数据,5种方法统计了匹配关键点数量、耗时、准确度3个方面的评价结果。其中红色、蓝色、绿色标注数据,分别代表最多匹配关键点、最小耗时、最高准确度,“—”数据代表匹配失败。结果可见,SURF+SURF+FLANN方法在10组数据中均为匹配量最多,同时保持了较高的匹配准确度,但耗时严重;SIFT+SIFT+FLANN方法各项评价结果较差;ORB+BRIEF+BF方法在耗时方面具有绝对优势,但匹配成功率不足,关键点提取数量与准确度较差;GFTT+BRISK+BF与GFTT+BRIEF+BF匹配关键点数量与匹配准确度较为接近,但后者耗时远低于前者。
综上所述,在不考虑匹配耗时的情况下,SURF+SURF+FLANN与GFTT+BRIEF+BF方法综合效果较优。其中前者可以获得较多的稳定特征匹配数据,有利于获得完整的导航地图,因此适用于煤矿井下移动机器人深度视觉自主导航地图创建阶段中离线使用,而后者耗时方面的优势,更适用于自主运行阶段在线使用。
3 深度视觉图优化定位与建图
3.1 深度视觉匹配误差ICP模型
视觉图像平面下的特征提取与匹配解决了二维图像平面的数据关联问题,定义k时刻与k+1时刻得到的一组匹配深度视觉数据为
Fk=[Uk,Vk,Dk];Fk+1=[Uk+1,Vk+1,Dk+1]
(1)
其中,
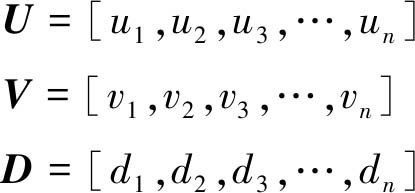
(2)
式中,F为不同时刻的一组经过匹配的深度数据集合;U,V为图像平面坐标系下的匹配数据二维坐标集;D为对应坐标下的深度数据集;n为一组匹配特征点的个数。
对k时刻与k+1时刻的F深度视觉匹配数据,在针孔相机模型下进行二维到三维变换,可以得到匹配特征点![]() 与
与![]() 在相机坐标下的三维表达:
在相机坐标下的三维表达:

图4 图像特征匹配结果
Fig.4 Results of the image feature extracting and matching
![]()
(3)
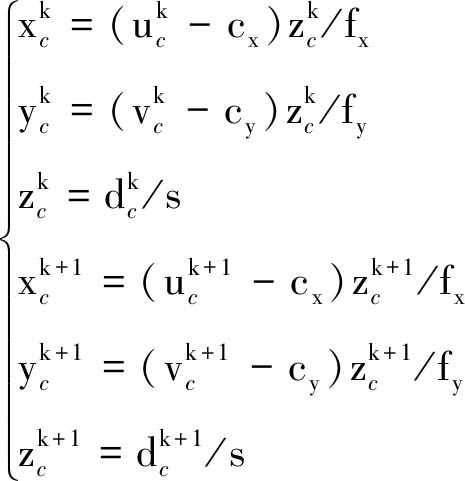
(4)
其中,cx,cy,fx,fy为相机内参,本文使用cam_calibration标定工具进行相机的内参标定;s为自定义深度缩放系数。至此一组深度视觉匹配数据被转换为三维到三维的ICP(Iterative Closest Points)模型,如图5所示,![]() 为k时刻与k+1时刻的相机坐标系原点,其经过变换后的对应相机坐标系下的深度视觉三维匹配数据为
为k时刻与k+1时刻的相机坐标系原点,其经过变换后的对应相机坐标系下的深度视觉三维匹配数据为![]()
设k时刻相机坐标系到世界坐标系的旋转与平移矩阵为![]() 可得
可得
![]()
(5)
表1 图像特征匹配结果统计
Table 1 Statistics of image feature matching results

关键点描述子匹配参数评估项组号组1组2组3组4组5组6组7组8组9组10数量2319171771291740—21GFTTBRISKBF耗时/ms299.45343.36 352.98346.10342.79362.25362.83352.97—353.19准确度0.910.660.880.820.940.6211—0.66数量1734237103222535769GFTTBRIEFBF耗时/ms37.5640.1639.8040.8847.7045.5941.0447.2748.7545.27准确度0.770.910.8610.950.720.88110.84数量7—367—37—7731ORBBRIEFBF耗时/ms28.51—23.5127.84—26.37—29.2826.5920.56准确度0.71—0.661—0.72—110.90数量941572821—8——30SIFTSIFTFLANN耗时/ms235.34233.17230.85236.68348.00—218.41——238.47准确度0.660.570.8810.81—1——0.83数量1 2751762965339314462281 511499335SURFSURFFLANN耗时/ms223.12164.40193.39209.25364.39238.84205.49301.69193.95195.27准确度0.830.700.770.640.820.770.910.970.950.84

图5 深度视觉匹配误差ICP模型
Fig.5 ICP-model of depth vision feature-matching error
其中,![]() 为相机坐标系下深度视觉匹配数据
为相机坐标系下深度视觉匹配数据![]() 在世界坐标系下的表达。理想情况下世界坐标系下的匹配深度视觉数据
在世界坐标系下的表达。理想情况下世界坐标系下的匹配深度视觉数据![]() 为同一路标点,存在如下关系:
为同一路标点,存在如下关系:
![]()
(6)
由于数据噪声、误匹配等因素会产生一定的误差,所以引入误差后的![]() 模型如下所示,其中误差模型e定义为
模型如下所示,其中误差模型e定义为
![]()
(7)
其中,![]() 为世界坐标系下,k+1时刻相机坐标系到k时刻相机坐标系的旋转与平移矩阵,即相机位姿的变换矩阵,该误差模型e为两帧深度视觉数据三维到三维的匹配误差ICP模型。
为世界坐标系下,k+1时刻相机坐标系到k时刻相机坐标系的旋转与平移矩阵,即相机位姿的变换矩阵,该误差模型e为两帧深度视觉数据三维到三维的匹配误差ICP模型。
3.2 深度视觉ICP-BA图模型构建与求解
煤矿井下移动机器人深度视觉自主导航地图构建阶段的定位与建图问题就是求解世界坐标系下,连续运动的相机位姿与环境中三维路标点坐标。如图6所示,红色圆点为环境中的路标点表示待求解的地图数据,蓝色相机图标代表不同时刻相机在世界坐标系的位姿,连续两帧相机位姿之间存在旋转R与平移t构成的变换矩阵。

图6 世界坐标下相机位姿变换
Fig.6 Camera pose translation in world frame
对于这一问题构建概率图模型如图7所示,其中节点类型有相机位姿与环境路标点两种,边为不同相机位姿下观测到不同路标节点的可视关系,同一相机位姿节点与多个路标节点相连表示当前位姿下相机观测到多个环境路标信息,同一路标节点与多个位姿节点相连表示关联的相机位姿状态下存在共视关系。
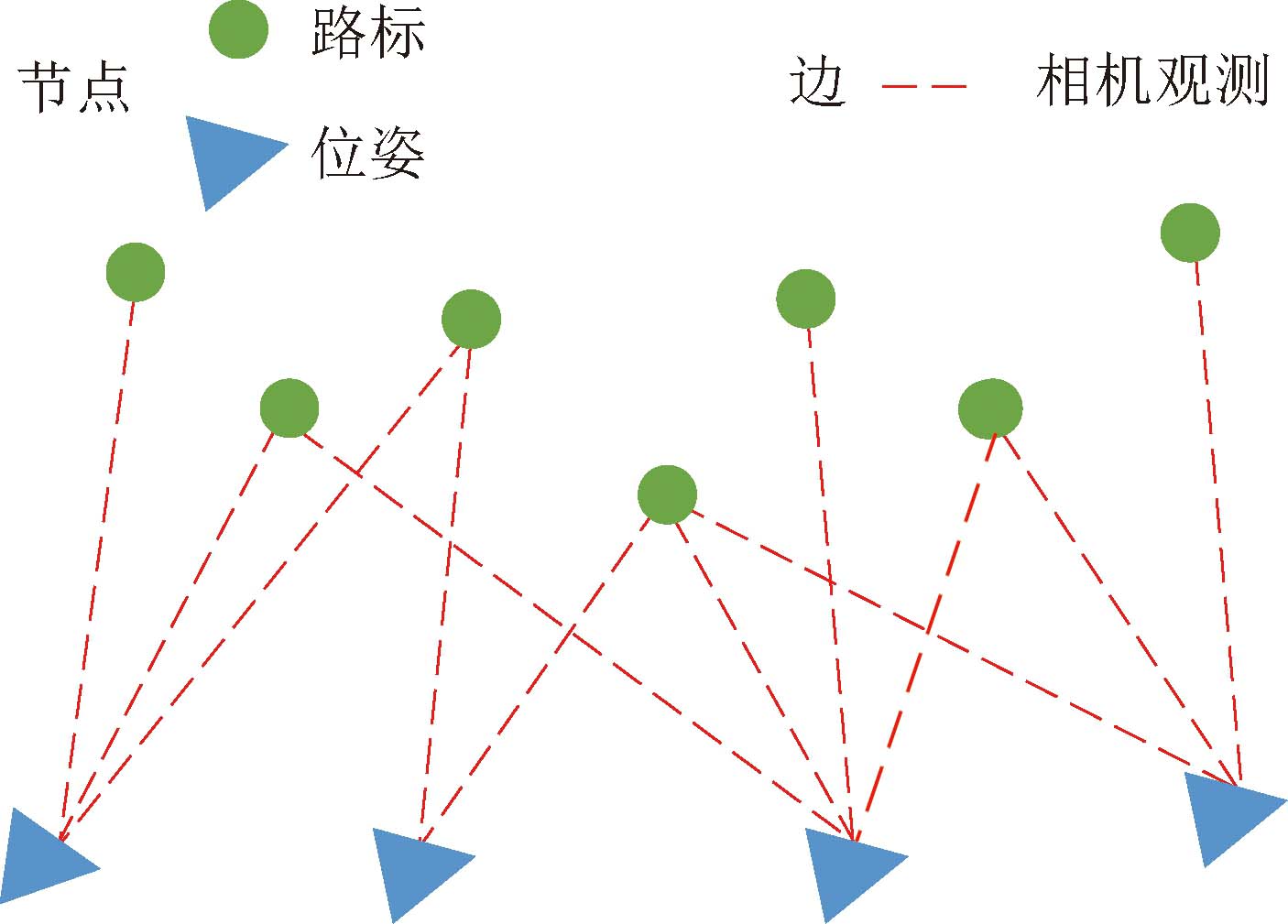
图7 定位与建图问题图模型
Fig.7 Graph of slam problem
按照机器人状态估计理论对深度视觉定位与建图问题概率图模型做如下数学定义:设k时刻状态为sk,其中状态由k时刻的相机位姿与观测到的路标信息组成。

(8)
式(8)为k时刻的状态定义,其中c为相机位姿状态,由位置![]() 与姿态四元数qw,qx,qy,qz表示,k时刻观测到的路标点集lk由i个路标点li组成。
与姿态四元数qw,qx,qy,qz表示,k时刻观测到的路标点集lk由i个路标点li组成。
定义整体定位与建图问题下的多个位姿与路标状态集为ξ,是由多次观测集γ得到,构建似然概率为
![]()
(9)

(10)
由贝叶斯法则得到的后验概率为
![]()
(11)
对于本文给出的煤矿井下深度视觉的概率图模型,系统状态变量最优估计即最大后验估计ξMAP,约等于求解最小似然概率PR(γ|ξ)的负对数![]() 该过程表达如下:
该过程表达如下:
![]()
(12)
假设观测条件概率分布服从如下高斯分布:
pr(γk|ξ)=Ν(μk,1)
(13)
则有
![]()
(14)
其中,γi-μi为2.1节构建的深度视觉数据三维到三维匹配误差ICP模型;‖‖2为二范数运算符。由此构建出煤矿井下移动机器人深度视觉自主导航地图构建阶段定位与建图问题的ICP-BA模型,使用非线性最小二乘形式的目标函数为
![]()
(15)
由于ICP误差模型是关于状态s的函数,式(15)可改写为E(s):
![]()
(16)
将k时刻ICP误差函数e(sk)在sk处一阶泰勒展开有:
e(sk+Δs)≐e(sk)+Jk(s)Δs
(17)
式中,Jk(s)为k时刻误差函数对k时刻状态量sk的雅克比矩阵。
将式(17)代入式(16),可得整体目标函数的泰勒近似展开式E(s+Δs)为
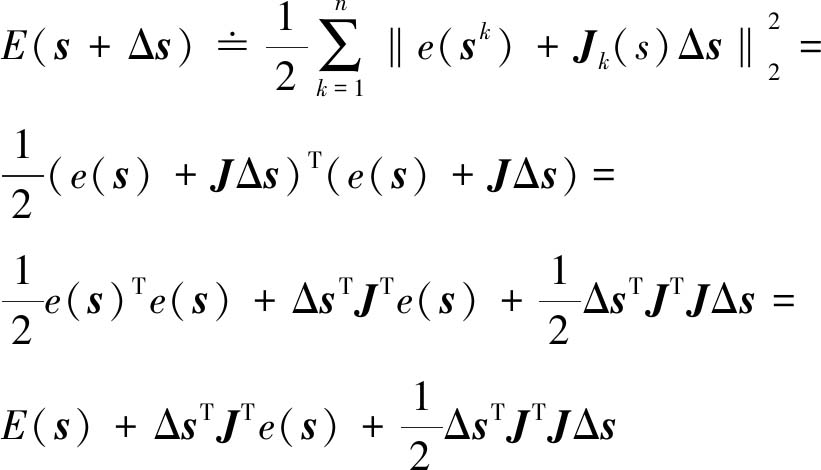
(18)
式中,J为不同时刻下的误差函数对其该时刻下状态变量的雅克比矩阵:
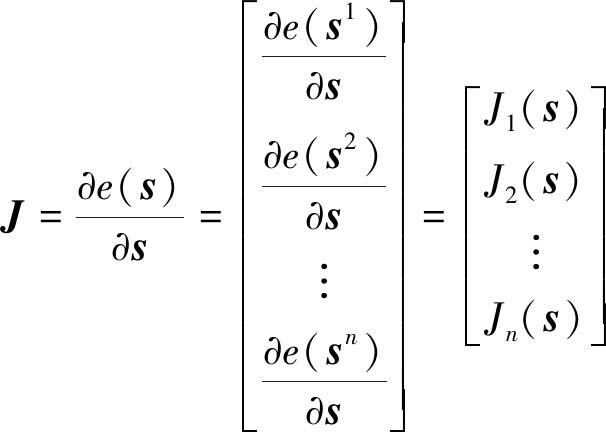
(19)
以图7为例,图中存在4个时刻下的相机观测到了7个环境路标,该图模型下的雅克比矩阵与误差函数矩阵为

(20)
其中

(21)
对整体目标函数式(18)迭代寻找下降方向使得目标函数最小,本文使用列文伯格-马夸尔特(LM)算法对这一问题进行求解。
令
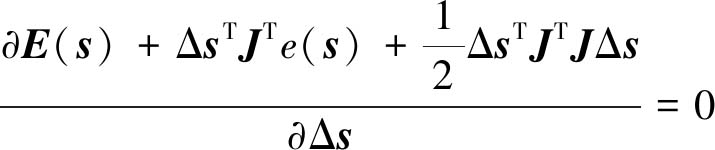
(22)
可得
(JTJ+αI)Δslm=-JTe(s),α≥0
(23)
其中,α为阻尼因子;I为单位矩阵;Δslm为LM算法下的状态迭代变化方向。通过对式(23)中阻尼因子α选取适当初值与更新策略,迭代求解状态变化方向Δslm,更新系统状态量s直到目标整体误差式(18)达到既定稳定状态。
通过上述方式最小化构建的整体目标函数,并采取滑动窗口策略,得到深度视觉定位与建图ICP-BA问题的解,即地图构建阶段相机的位姿估计与环境路标点。
图8(a)为实验室全景图,图8(b)为在该场景下使用上述方法得到位姿图与环境特征点集后,将关键帧中点云数据拼接优化处理得到的结果,包含104个关键位姿与1 789 336个三维环境点,其中关键帧选取策略为内点数大于阈值,且系统跟踪线程空闲时插入新的关键帧。

图8 实验室点云地图
Fig.8 Point-map of our laboratory
4 导航地图表达与重定位
4.1 Octomap地图结构
煤矿井下移动机器人深度视觉自主导航地图创建阶段构建的点云地图为无序存储数据类型,无法直接用于移动机器人的运动规划,同时大尺度环境下的点云地图数据过大,其载入与读取异常耗时,不利于地图数据的索引。因此在煤矿井下移动机器人深度视觉自主导航自主运行阶段需要对初始点云地图采用一定数据结构重分配,以满足运动规划算法执行的要求。
常见的移动机器人导航地图类型有Voxel hashing[24],TSDF(Truncated Signed Distance Functions)[25],ESDF(Euclidean Signed Distance Functions)[26]等,本文的导航地图使用基于三维占据栅格原理的Octomap,其数据存储为八叉树结构。如图9所示,一组三维空间下的Octomap类型地图将空间在xyz方向进行划分,每划分1次可得到1组8个叶子节点,通过n次递归划分可以得到不同分辨率下的树结构。图9中灰色方框代表该节点被部分概率占据,白色方框表示未被占据,最下层黑色方框表示完全占据。其中最下层表示的是最高分辨率下的叶子节点,假设三维地图原始数据覆盖为8.5 m×5.5 m×6.5 m,要想获得0.01 m×0.01 m×0.01 m分辨率的Octomap,需要在10 m×10 m×10 m的空间下进行10次上述递归划分。
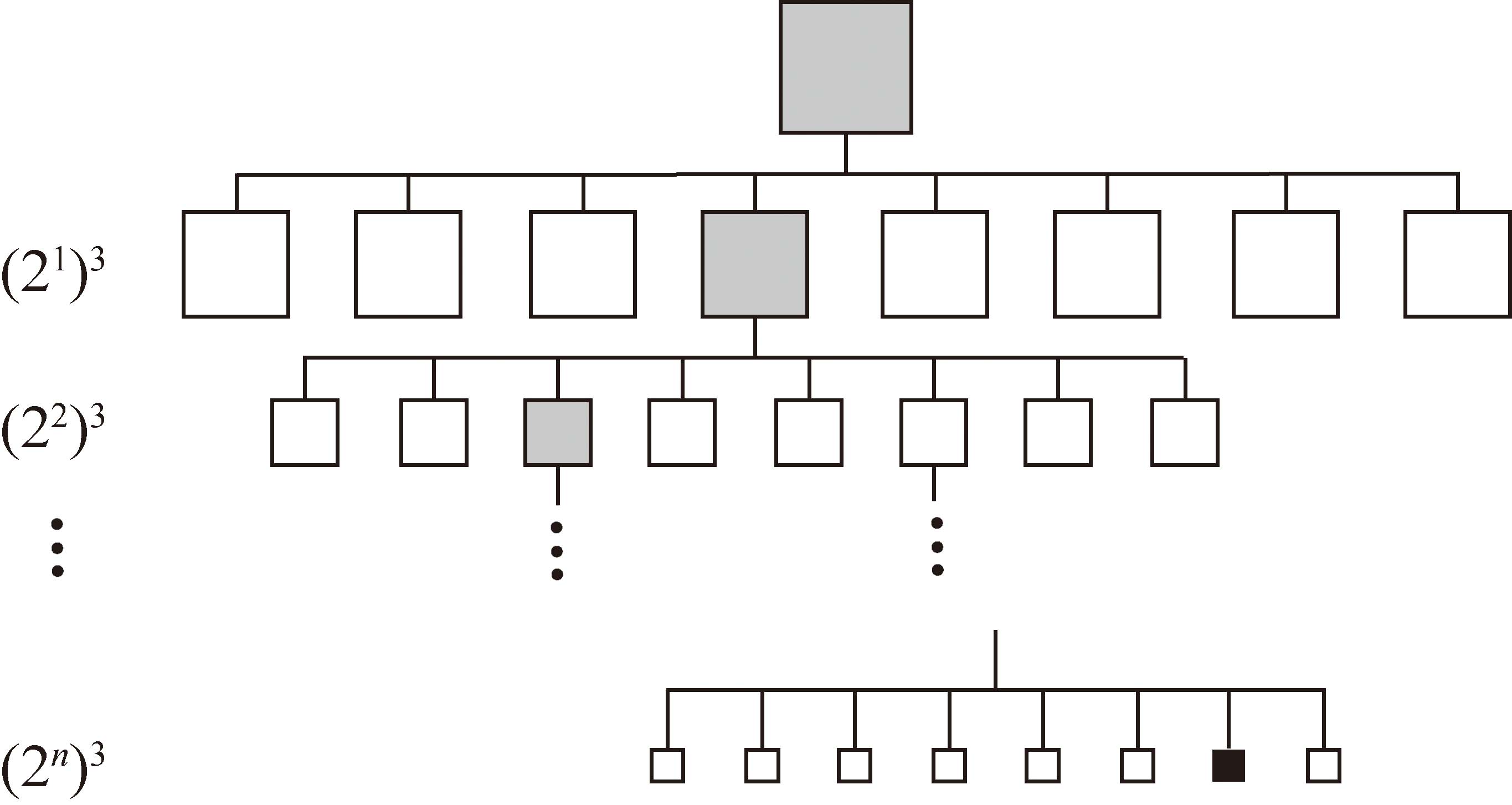
图9 八叉树数据结构
Fig.9 Octree data structure
本文对实验室建立原始点云地图经过八叉树数据结构存储后得到的Octomap,使用Octovis工具可查看空间划分情况,设置最高分辨率0.05 m时结果如图10所示。同时,实验室原始点云地图以.pcd格式存储大小57.3 MB,经过Octomap处理后以.bt格式存储后的地图大小仅为58.9 kB。

图10 实验室八叉树导航地图
Fig.10 Octomap of our laboratory
4.2 基于PNP的视觉重定位
煤矿井下移动机器人深度视觉自主导航的自主运行阶段需要基于视觉进行实时重定位,用于运动规划时的闭环反馈控制。
Dbow2(Bag-of-word Detector)是Zaragoza大学的Lopez等开发的开源软件库[27],被广泛运用于移动机器人导航领域的回环检测问题(Loop Closure Dection)。Dbow2可以通过相似度检测,快速寻找到与当前帧相似度最高的历史关键帧。本文自主运行阶段的重定位引入Dbow2作为单独线程实时运行,检测重定位时当前观测下对应的地图创建阶段历史关键帧,该帧间对应关系如图11所示。
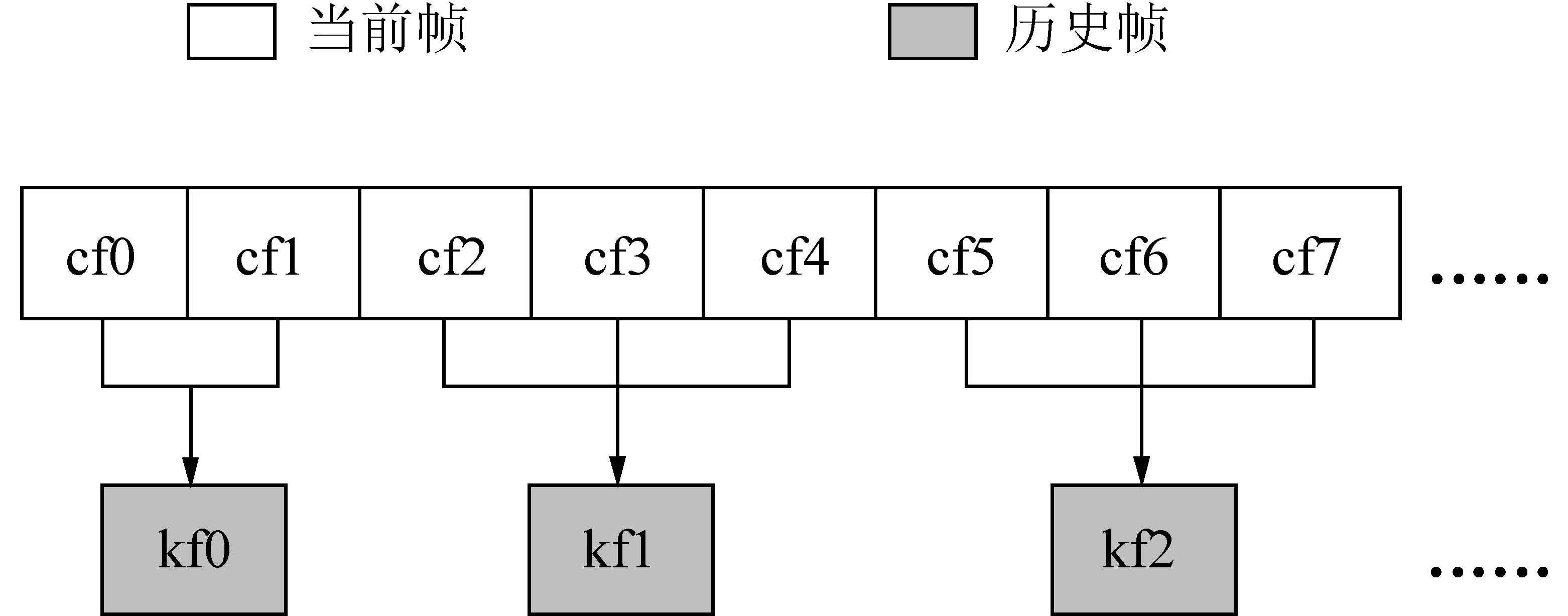
图11 重定位相似度检测帧间关系
Fig.11 Similarity detect inter-frame relationships between curr-ent frames and history key frames during relocalization process
历史关键帧中存有对应观测下的环境三维点云数据,重定位时当前观测为二维图像数据(本文重定位时不使用深度数据),通过Dbow2相似度检测出的历史关键帧与重定位当前帧关联,构建PNP模型,求解当前帧在地图中的相对位姿,即自主运行阶段的重定位。

图12 PNP问题模型
Fig.12 Model of the PNP problem
图12所示是一组历史关键帧的三维观测Pw在重定位当前帧的二维映射Fc。按照2.1节参数定义方式可构建该映射关系为
Fc=RcwTF′c+tcw=RcwPw+tcw
(24)
其中,矩阵T对应式(4),是历史关键帧按照针孔相机模型,在相机平面坐标系下,三维到二维的映射矩阵。F′为历史关键帧的二维观测。Rcw,tcw为待求解的重定位当前帧相机位姿。使用本文给出的图像特征提取与匹配方法可获得多组历史关键帧三维环境特征数据Pw与对应匹配二维特征数据Fc。当一组匹配点数小于10大于等于6时,使用DLT(Direct Linear Transform)算法线性求解初值,当获得大于10组匹配特征点时,使用EPNP(Efficient Perspective-N-Point)算法求解初值。构建重定位当前帧观测特征点真实值![]() 与理论值Fc的重投影误差模型,代入DLT/EPNP初值,使用非线性优化方法调整以得到精度更高结果,重投影误差最小二乘模型如下:
与理论值Fc的重投影误差模型,代入DLT/EPNP初值,使用非线性优化方法调整以得到精度更高结果,重投影误差最小二乘模型如下:
![]()
(25)
图13(a)为一张历史关键帧与重定位当前帧进行PNP重定位的结果,左上图为历史关键帧,左下图为重定位当前帧,左上图红色特征点与左下图黄色特征点匹配关系使用蓝线标注,通过PNP求解三维可视化位姿结果见右图红圈标注。使用该方法在实验室环境进行连续PNP重定位,得到连续状态下的相机位姿图,结果如图13(b)所示。

图13 实验室重定位结果
Fig.13 Result of relocalization in the lab
5 运动规划
5.1 A*路径规划
运动规划中的路径规划是指在导航地图中以一定的搜索策略找到一条从起点到终点无碰撞的连续路径。煤矿井下深度视觉移动机器人自主运行阶段的路径规划,就是在本文3.1节构建的Octomap导航地图中寻找一条无碰撞路径。煤矿井下移动机器人在任务执行时,时效性尤为重要,因此搜索策略应遵循路径最短原则。
A*算法是一种被广泛使用的高效最短路径规划方法,本文基于A*算法的搜索策略如图14所示。

图14 A*算法代价函数
Fig.14 Cost function of the A* arithmetic
在本文所使用的占据栅格导航地图中,除去障碍物所占据栅格外,共计6种栅格类型,分别为:起点、终点、当前节点、当前节点的子临区间节点、可行节点、障碍物节点。其中每一个当前节点对应周边的8个子临节点,代表移动机器人的运动方位。A*最短路径规划就是迭代的从起点开始,寻找每一时刻的子临节点中非障碍物、可行的、最优节点(离终点最近),直到终点。对这一过程中的第n时刻节点的定义代价函数为
argmin fi(n)=g(n)+ci(n)+hi(n)
(26)
其中,i代表1~8的子临区间序列,当考虑三维空间时,i取1~26;g(n),c(n),h(n)分别为起点到当前节点代价函数,当前节点到子临节点代价函数,子临节点到终点代价函数,具体定义如下:

(27)
式中所使用的dis代价函数为欧式距离。
![]()
(28)
从起点开始,使用式(27),(28)求解其子临节点的代价函数fi(n),并记录每次迭代后满足目标函数式(26)最小值的节点坐标,直到终点。连接从起点到终点的所有记录节点做为该目标函数下的最优路径规划结果。
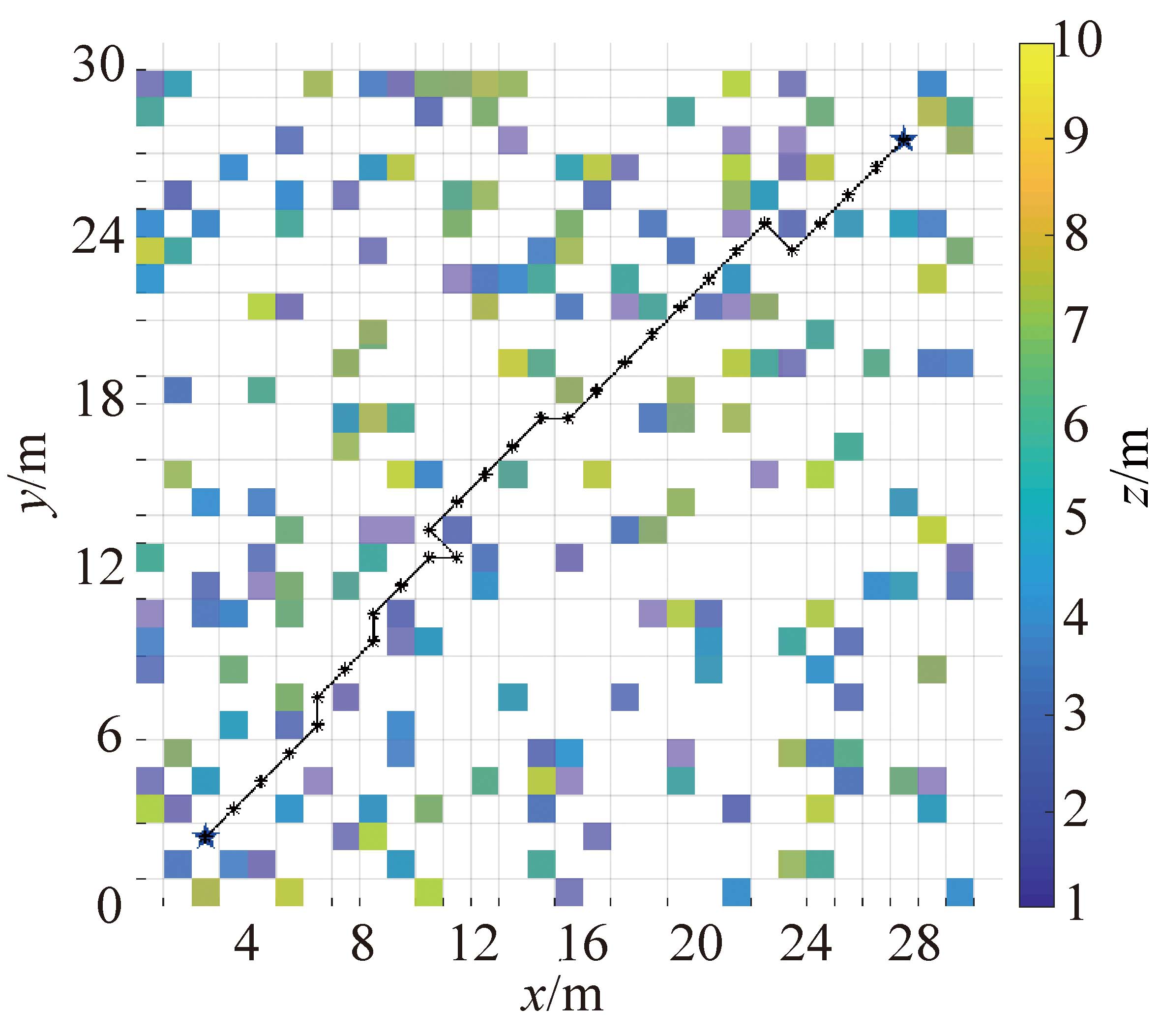
图15 A*算法路径规划结果
Fig.15 Result of the A* path planning
图15为在一张分辨率为1 m×1 m×1 m的随机导航地图(xy方向为30 m×30 m,障碍物占比20%,z方向为1~10随机数)中,使用上述A*路径规划方法得到的结果。图中黑线路径为使用欧式距离代价函数从起点迭代搜索至终点得到的最优路径,星号为设置的起点(3,3,3)与终点(28,28,28),彩色方格为障碍物,颜色代表该位置障碍物高度。
5.2 Minimum snap轨迹生成
路径规划的结果为一组导航地图中的坐标序列,不带有时间信息,因此无法直接产生速度、加速度等信息输入到控制器执行,同时路径规划的结果带有大量不光滑拐点,会产出巨大耗能与不稳定性,不利于移动机器人轨迹执行时的定位、控制。轨迹生成就是对路径规划加以约束,进行某种形式的优化,生成包含时间分配(time)、速度(velocity)、加速度(acceleration)、加加速度(jerk)等信息的轨迹并满足一定代价的控制需求。
最小化受力变化率的改变(Minimum snap)是一种移动机器人轨迹生成的代价指标,通过对整段轨迹加加速度变化率(snap)的约束,可生成一条光滑、连续的轨迹。Minimum snap指标下生成的轨迹节省能量,有利于移动机器人更长时间的运行。本文路径规划的结果为n-1个目标位,连同起点与终点,可将待生成轨迹分割为n段。
5.2.1 整体能量损失函数构建
移动机器人加加速度变化率(snap)是位置函数的4阶导数,为了构建该2次规划问题能量损失泛函,将每段轨迹任意方向的位置函数描述为7次8阶多项式,以满足方程半正定求解要求。设第l段轨迹任意方向位置函数Loc为
![]()
(29)
其中,p0~p7为多项式系数。则第l段轨迹任意方向的加加速度变化率函数方程为
![]()
(30)
第l段轨迹的Minimum snap最小化能量损失泛函定义为加加速度变化率函数的平方:
Jl(Tl)=![]() f(4)(Loc(t))2dt=[p0,…,pi,…,p7]·
f(4)(Loc(t))2dt=[p0,…,pi,…,p7]·

(31)
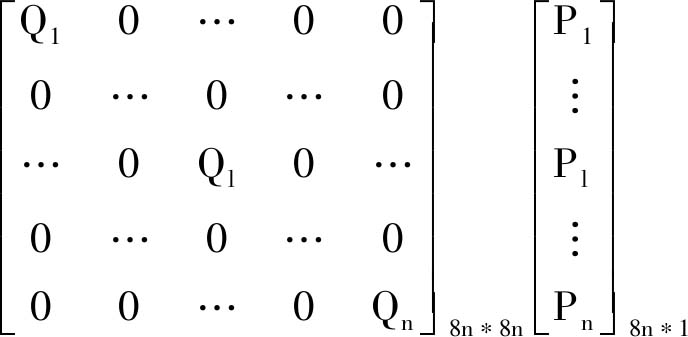
其中,Tl为第l段的时间分配变量;i,j为多项式系数上角标;PlT为第l段多项式系数行矩阵。将式(31)扩展至n段组成的任意方向整条轨迹有:
(32)
式(32)的整体能量损失目标函数为2次型,中间矩阵为8n*8n对称阵,因此该目标函数的最小化求解属于标准2次规划问题。本文对该2次规划问题通过构建等式约束的方法求解,具体包括连续性等式约束与光滑性等式约束。
5.2.2 连续性约束方程构建
轨迹连续性约束就是要构建每一段轨迹连接处,即第l段轨迹段尾,与l+1段轨迹的段首处,位置(Loc)、速度(Vel)、加速度(Acc)、加加速度(Jerk)相等,定义这些状态变量分别为
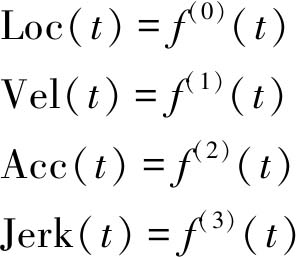
(33)
则第l段末尾时刻时间为Tl,第l+1段起始时刻时间为0,则任意方向连续性约束构建为
![]() ⟹
⟹

(34)
式中,k为导数阶数,从0到3分别代表位置、速度、加速度、加加速度;i,j分别为第l段末尾时刻与l+1段起始时刻的多项式系数。
5.2.3 光滑性约束方程构建
轨迹光滑性是要约束路径规划结果位置(起点、中间点、终点)的状态X满足轨迹多项式方程。其中X代表式(33)的4种状态,由此可得任意方向轨迹光滑性约束方程为
![]() ⟹
⟹

5.2.4 多项式求解与轨迹生成
联立式(32),(34),(35),分别对x,y,z方向求解目标函数式(32)能量泛函最小值情况下的每段轨迹系数P,将系数代入每段状态方程(33)中可求解出整段轨迹各个方向的状态量,具体求解实现使用matlab下的2次规划求解quadprog函数,其结果可视化如图16所示。
图16为在本文4.1节中所描述的随机三维导航地图(Octomap)中的轨迹位置规划结果。设定起始位置为[3 m,3 m,0 m],终止位置为[28 m,28 m,0 m],起始与终点的速度、加速度、加加速度均为0,设定整体规划时间25 s。结果显示,轨迹规划共计29段,其中在局部放大结果图16(c)中可看到,红色为生成的轨迹位置规划结果,黑色为原始路径规划结果。
通过构建最小化加加速度的变化率2次规划问题,并引入连续性与光滑性等式约束,得到的轨迹规划结果包括时间分配、速度、加速度、加加速度。结果数据的可视化如图17所示,图17(a)为最优每段轨迹执行时间分配,图17(b),(c),(d)分别为满足目标泛函的最优速度、加速度、加加速度规划结果,其中红线、蓝线分别代表x与y方向规划结果(z方向始终为0)。

图16 Minimum snap轨迹规划结果
Fig.16 Result of the Minimum snap trajectory planning

图17 轨迹规划结果
Fig.17 Result of the trajectory planning
6 结 论
(1)提出的煤矿井下移动机器人深度视觉自主导航方法,采用机器人搭载RGB-D相机作为深度视觉数据采集传感器,可实现地图创建与自主运行的自主导航任务。
(2)研究表明SURF+SURF+FLANN与GFTT+BRIEF+BF方法能够在煤矿井下获得良好匹配结果,前者适合地图创建阶段离线处理时使用,后者适合于自主运行阶段的重定位使用。建立了深度视觉ICP数据关联模型,构建与求解了深度视觉ICP-BA图模型,解决了煤矿井下移动机器人深度视觉定位与建图问题。
(3)使用了八叉树数据结构存储点云数据,将点云地图转为Octomap地图,用于移动机器人的运动规划。将实验室环境下得到的原始点云地图以最高分辨率0.05 m进行了转换,经过该处理后的地图所占存储空间下降了1 000倍左右,有效节省了内存空间,加快了运动规划索引效率。构建与求解了基于PNP模型的煤矿井下移动机器人自主运行阶段的重定位问题,通过对历史关键帧与当前帧的数据关联解算,得到了实验室环境下的连续帧PNP重定位结果。
(4)在Octomap导航地图与重定位的基础上进行了自主导航运动规划。采用了A*算法路径规划作为轨迹规划初值,设置了轨迹规划能量泛函为Minimum-Snap。在仿真随机Octomap地图上,引入了光滑性与连续性约束,求解出了可用于移动机器人运动执行的轨迹规划结果,该结果包含时间分配、速度规划、加速度规划、加加速度规划。
[1] 国家煤矿安全监察局.煤矿机器人重点研发目录[EB/OL].http://www.chinacoal-safety.gov.cn/gk/tzgg/201901/t20190109_223745.shtml,2019-01-02.
[2] 葛世荣,胡而已,裴文良.煤矿机器人体系及关键技术[J].煤炭学报,2020,45(1):455-463.
GE Shirong,HU Eryi,PEI Wenliang.Classification system and key technology of coal mine robot[J].Journal of China Coal Society,2020,45(1):455-463.
[3] KHAN S,AHMMED M K.Where am I? Autonomous navigation system of a mobile robot in an unknown environment[A].5th International Conference on Informatics,Electronics & Vision(ICIEV)[C].IEEE,2016.
[4] DURRANT-Whyte,HUGH.Where am I? A tutorial on mobile vehicle localization[J].Industrial Robot,21(2):11-16.
[5] PING Jiang,ZUREN Feng,YONG qiang.A Mosaic of Eyes[J].Robotics & Automation Magazine IEEE,2011,18(3):104-113.
[6] DURRANT-Whyte H,BAILEY T.Simultaneous localization and mapping:Part I[J].IEEE Robotics & Automation Magazine,2006,13(2):99-110.
[7] ABDELRASOUL Y,SAMAN A B S H M,SEBASTIAN P.A quantitative study of tuning ROS gmapping parameters and their effect on performing indoor 2D SLAM[A].2016,2nd IEEE International Symposium on Robotics and Manufacturing Automation(ROMA)[C].IEEE,2016:1-6.
[8] AARON Morris,DAVE Ferguson,ZACHARY Omohundro,et al.Recent developments in subterranean robotics[J].Journal of Field Robotics,2006,23(1):35-57.
[9] OLIVKA P,MIHOLA M,NOVAK P,et al.The design of 3D laser range finder for robot navigation and mapping in industrial environment with point clouds preprocessing[A].International workshop on modelling and simulation for autonomous systems[C].Springer,Cham,2016:371-383.
[10] CEURSTEMONT S.No GPS,No Pilot-No Problem[J].New Scientist,2017,236(3146):16.
[11] DANG T,MASCARICH F,KHATTAK S,et al.Field-hardened Robotic Autonomy for Subterranean Exploration[A].12th Conference on Field and Service Robotics (FSR) [C].2019:1452.
[12] HUANG A S,BACHRACH A,HENRY P,et al.Visual odometry and mapping for autonomous flight using an RGB-D Camera[A].IEEE International Symposium on Circuits & Systems[C].2017:235-252.
[13] RUSINKIEWICZ S,LEVOY M.Efficient variants of the ICP algorithm[A].In Proceedings Third International Conference on 3-D Digital Imaging and Modeling[C].2001:145-152.
[14] 梁明杰,闵华清,罗荣华.基于图优化的同时定位与地图创建综述[J].机器人,2013(4):118-130.
LIANG Mingjie,MIN Huaqing,LUO Ronghua.Graph-based SLAM:A Survey [J].Robot,2013(4):118-130.
[15] HORNUNG A,WURM K M,BENEWITZ M,et al.OctoMap:An efficient probabilistic 3D mapping framework based on octrees[J].Autonomous Robots,2013,34(3):189-206.
[16] LEPETIT V,MORENO-Noguer F,FUA P.Epnp:An accurate o(n) solution to the pnp problem[J].International Journal of Computer Vision,2009,81(2):155.
[17] DUCHON F,BABIEC A,KAJAN M,et al.Path planning with modified a star algorithm for a mobile robot[J].Procedia Engineering,2014,96:59-69.
[18] MELLINGER D,KUMAR V.Minimum snap trajectory generation and control for quadrotors[A].2011 IEEE International Conference on Robotics and Automation[C].IEEE,2011:2520-2525.
[19] MUR-Artal,RAUL,TARDOS,JUAN D.ORB-SLAM2:An open-source SLAM system for monocular,stereo,and RGB-D cameras[J].IEEE Transactions on Robotics,2017:1-8.
[20] ENGEL J,KOLTUN V,CREMERS D.Direct Sparse Odometry[J].IEEE Transactions on Pattern Analysis & Machine Intelligence,2017,40(3):611-625.
[21] 冯亦东,孙跃.基于SURF 特征提取和FLANN 搜索的图像匹配算法[J].图学学报,2015,36(4):650-654.
FENG Yidong, SUN Yue. Image matching algorithm based on SURF feature extraction and FLANN search[J].Journal of Graphics,2015,36(4):650-654.
[22] RUBLEE E,RABAUD V,KONOLIGE K,et al.ORB:An efficient alternative to SIFT or SURF[A].International conference on computer vision[C].2011:2564-2571.
[23] LIU Shanjun,WANG Han,HUANG Jianwei,et al.High-resolution remote sensing image-based extensive deformation-induced landslide displacement field monitoring method[J].International Journal of Coal Science & Technology,2015,2(3):170-177.
[24] NIEBNER M,ZOLLHOFER M,IZADI S,et al.Real-time 3D reconstruction at scale using voxel hashing[J].ACM Transactions on Graphics(ToG),2013,32(6):169.
[25] BYLOW E,STURM J,KERL C,et al.Real-time camera tracking and 3D reconstruction using signed distance functions[A].Robotics:Science and Systems(RSS) [C].2013:2-10.
[26] FRISKEN S F,PERRY R N,ROCKWOOD A P,et al.Adaptively sampled distance fields:A general representation of shape for computer graphics[A].Proceedings of the 27th annual conference on Computer graphics and interactive techniques[C].ACM Press/Addison-Wesley Publishing Co.,2000:249-254.
[27] GALVEZ-López D,TARDOS J D.Bags of binary words for fast place recognition in image sequences[J].IEEE Transactions on Robotics,2012,28(5):1188-1197.
