随着智能化装备和物联网技术的发展，矿山采、掘、运等安全生产过程逐渐趋向无人/少人化[1-3]，掘进机等装备位姿识别的精确性、实时性和可靠性，对煤矿井下安全生产管理、机器协同工作及智能化无人生产都具有重要意义。
文献[4-8]对掘进机位姿识别进行了研究。文献[4]提出了一种基于视觉的切割头姿态估计非接触测量方法，在掘进机上部署16点红外LED目标，通过建立单目视觉测量系统，处理LED目标图像并估计切割头的位置;文献[5]提出了一种基于掘进机位姿测量系统的自主标定方法，可代替传统人工对全站仪进行整平和设站;文献[6]基于机器视觉的掘进机机身实时监测系统，对掘进机机身位姿参数进行自动检测;文献[7]提出基于多传感器融合的悬臂式掘进机位姿检测方法;文献[8]提出了基于超宽带(UWB)测距技术的位姿检测方法，利用4个搭载UWB模块的移动基站机器人对机身节点进行测距，经过解算测距信息得到掘进机位姿参数。文献[9-11]对开放条件下的无源RFID系统定位识别算法、干扰对消设计方法、数据编码方法等进行了理论和技术研究。综合可知，矿井/隧道装备位姿识别基本上采用有源定位技术，通过实验仿真和设计的验证方案证明了各自有效性。在矿山工程应用中，基于无源RFID定位的位姿识别方法，尤其在抗多径干扰方面还鲜有相关研究。
目前国内外很多学者对开放环境下无源RFID定位识别方式和测距算法开展了研究。文献[12]在准确估计出移动目标反射波的TOA/DOA参数τi和θ的条件下，利用几何确定法精确求解移动目标位置;文献[13]提出一种残差加权多维标度算法，利用阅读器和标签之间的距离信息和标签之间的距离信息构建距离平方矩阵和内积矩阵，引入少量参考标签建立标签之间欧式距离和标签定位参数之间欧氏距离的线性关系以获取标签之间的距离信息;文献[14]建立待定位标签与阅读器、参考标签距离估计模型，将多径传播、高斯白噪声、相位差欧氏距离拟合引起的距离估计误差等效为正态分布，利用参考标签的相位差信息和位置信息计算出正态分布参量。随着无源RFID定位算法研究的深入，利用相位信息作为定位参数，从而获取距离信息的定位方法越来越受到学者们的青睐。文献[15]在使用无源RFID标签定位系统的基础上，选取相位差信息用于定位中的距离测量，证明了相位差对距离敏感，有助于准确定位;文献[16]研究了一种基于相位的复合测距系统，通过结合双频连续波(DFCW)和连续波(CW)的距离估计，在室内空间为反向散射射频标签提供相对准确和绝对的距离估计，但该种方法不适合动目标;文献[17]针对超高频915 MHz信号，提出“欠采样”条件下的双频副载波调幅的定位算法，但这种方法存在着测距精度和最大不模糊距离之间的矛盾，定位范围较小;文献[18-19]分别使用二次相差和参差频差方法获取测距信息，利用多频连续波改善距离模糊，但这两种多频连续波测距方法没有考虑最大化相位误差的容忍度问题，仿真表明测距精度可以达到分米级。
在空间受限的掘进作业环境下，电磁波频繁反射和散射会造成密集多径和大相位误差问题，现有的抗多径干扰和相位差测距算法不适合直接应用于复杂环境下采掘装备的位姿识别。因此，以掘进机为例，笔者提出一种基于相位信息的多频无源掘进机位姿识别算法，可以扩展应用到其他装备。采用无源宽带谐波标签，建立基于非线性二次谐波反向散射的抗干扰模型，以对抗密集多径干扰;基于距离的几何定位方法，提出CSMCW相位差测距方法，解决掘进工作面大相位误差条件下的距离模糊问题，以实现掘进机机身位姿姿态角的识别。
1 掘进机机身位姿识别系统模型
如图1所示，掘进机机身位姿识别模型由无源RFID的4个读写器S1～S4和A，B，C三个(或更多)无源谐波标签组成。随着工作面的推进，掘进工作面物理空间位置会发生改变，读写器S1～S4位置方便动态推进式部署，其中S1和S3沿顶部支护中线安装，S2和S4部署于两帮支护的两侧壁偏向于顶部支护位置。将A，B，C三个无源谐波黏附在掘进机机身上，选取在同一个水平面上且相互构成等腰直角三角形，其中A，B位于机身左侧，C位于机身右侧，且设AC=AB=2 m。
图1 无源RFID掘进机机身位姿识别模型
Fig.1 Model of passive RFID pose recognition for roadheader body
已知读写器S1～S4相对巷道坐标系的位置，一旦精确获得黏附在掘进机机身上A，B，C三个定位标签的坐标参数，利用掘进机机身姿态角公式计算，便可以确定掘进机机身当前的位姿。
2 谐波反向散射抗多径干扰
采用无源宽带谐波标签生成可利用的谐波信号来解决工作面上密集多径干扰问题[20]，建立的谐波反向散射抗多径模型如图2(a)所示。当下行链路信号以载波频率f0从发射机传到标签以后，利用无源标签中的非线性元件产生相应的二次谐波频率为2f0，接收天线只接收2f0频率的谐波信号，不再接收频率为f0的信号，即二次谐波频率2f0为从标签到接收天线链路的信号，下行、上行链路频率分集，在工作面密集多径场景下，如图2(b)所示，消除了传统反向散射中频率为f0的多径干扰信号。
图2 掘进工作面多径干扰场景
Fig.2 Dense multipath interference scene in heading face
3 CSMCW相位差测距方法
在空间受限的掘进工作面上，密集多径导致收发信号的相位差信息存在很大的测量误差;另外，矿井无线通信优质载波频率中心f一般位于916 MHz或2.4 GHz，波长λ=c/f，c为光速。可以求得相应载波信号波长λ约为几十厘米，掘进工作面测距范围为米级，射频信号从读写器发射，经无源谐波标签反向散射回到读写器，将经历多个载波整周期，会产生距离模糊问题。因此，掘进工作面上的位姿识别存在大相位误差条件下的距离模糊问题，为了不影响基于相位差信息测距、定位和识别过程的准确性，提出CSMCW相位差测距方法。
首先，为了最大化相位误差的容忍度，优化选取多频连续波频率。定义相位误差容忍值的阈值方程为
(1)
其中，fi为第i(1≤i≤K，K为多频连续波个数)个正弦波频率;N为自然数集合;ai至少有一个为非零值;f为所选的最优频率组合;Rmax为可测得的最远距离。最大相位误差阈值Φ为
(2)
通过式(1),(2)即可利用遗传算法优化选取K个相位误差容忍最大的最优频率序列，设最优频率组合为fmax=f1≥f2≥…≥fK=fmin，对于任意频率i，j∈[1,K]，令对应谐波的相位误差最大值为M，即
(3)
当a1=a2=…=aK=p时，p为≥1的整数
(4)
其中，当p=1时，
此时M值最小。
当a1，a2，…,aK为不全相等的整数时，从中任取2个值ak，as，满足ak≥as。
(5)
将式(4)，(5)的结论代入式(1)，得
(6)
将式(6)代入式(2)，即可确定最优频率组合下的最大相位误差阈值Φ为
(7)
然后，读写器S1～S4按时间顺序周期循环地连贯发射上述K个优化选取的多频连续波作为测距信号，掘进机上A，B，C三个无源谐波标签以时分复用和码分多址的方式对测距信号产生相应的二次谐波信号(频率分别为2f1，2f2,…,2fK)，谐波信号再反向散射回到读写器接收天线。对于任一个读写器来说，发射频率为fi的信号，就会收到2fi的谐波信号，经过2R的路程后收发信号会有一个相位差，建立视在相差函数
为
(8)
其中，
表示第i(1≤i≤K)个频率fi作用下应测得的相位差理论值;ni为第i个频率作用下的模糊数;R为读写器到谐波标签的真实距离，也是待精确测量的距离。但因为存在距离模糊问题，ni不能测得。
根据式(8)，得到读写器到谐波标签的真实距离R为
(9)
由于掘进工作面空间受限，密集多径干扰严重，实际测得的相位差φi和理论值之间会有误差，导致测距误差ei存在。因此，第i个频率作用下读写器到谐波标签的实际测量距离
可表示为
(10)
为了解决距离模糊问题，通过连贯发射多频连续波和有约束的最小均方误差的方法，使各个频率作用下的测量误差ei的平方和最小，即
(11)
同时，应满足0≤Ri≤Rmax，由式(10)可得
(12)
其中,φi∈[0,2π]，ni为≥0的整数，则得到式(11)的约束条件Ⅰ为
(13)
另外，由式(9)，(10)可推得测量距离Ri和真实距离R的关系式为
(14)
其中，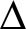
φi为相位差误差。则第i和第j个频率作用下的距离差可表示为
(15)
其中，Δφmax为最大相位差误差。将式(10)代入式(15)，则得到式(11)的约束条件Ⅱ为
(16)
比较测得的最大相位差误差Δφmax和式(7)得到的最大相位误差阈值Φ，如果Δφmax<Φ，式(16)改写为
(17)
此时，为求解ni和真实距离R，建立优化问题:
即可获得ni和真实距离R的无模糊估计值。
如果相位差误差很大，且Δφmax>Φ，式(17)将不成立，则放松阈值Φ为
Φm+1=Φmω
(18)
直至满足Δφmax< Φm+1为止。其中ω为松弛因子，取值大于1;Φm为第m次设置的阈值。用Φm+1替代式(17)中的Φ，则得
(19)
同理，为求解ni和真实距离R，建立优化问题:
即可获得ni和真实距离R的无模糊估计值。
4 基于CSMCW的位姿识别方法
4.1 机身无源标签坐标定位
以掘进机为例，为了准确有效地进行位姿识别，通过CSMCW相位差测距方法对掘进机机身上A，B，C三个无源谐波标签进行精确测距后，采用几何定位算法实现无源标签的精确定位。
已知读写器坐标分别为S1(x1,y1,z1)，S2(x2,y2,z2)，S3(x3,y3,z3)，S4(x4,y4,z4)，它们到A，B，C三个无源谐波标签的距离可以写成4个球面方程[12]:
(20)
求解方程组(20)可得到机身无源谐波标签的三维坐标，分别表示为A(xa,ya,za)，B(xb,yb,zb)，C(xc,yc,zc)。从而实现掘进机机身无源标签的精确定位。
4.2 机身姿态角计算
掘进过程中，掘进机机身位置偏移，会产生航向角、俯仰角、横滚角，由此可识别掘进机的位姿。
图3 掘进机机身位姿模型 Fig.3 Pose model of the roadheader body
以巷道横截面底线中心为坐标原点、巷道中线的方向为X轴、腰线方向为Z轴，建立掘进机机身位姿模型，分别给出如图3所示的航向角α(在XOY平面上掘进机与X轴夹角)、俯仰角β(在XOZ平面上掘进机与X轴夹角)，以及横滚角γ(在YOZ平面上掘进机与Y轴夹角)的姿态角计算公式
(21)
(22)
(23)
其中，(xa,ya,za)，(xb,yb,zb)和(xc,yc,zc)分别为无源标签A，B，C的三维坐标位置，3个无源标签被精确定位后，利用式(21)～(23)即可确定掘进机机身的具体位姿。
4.3 位姿识别流程
综合以上分析，给出了一种基于无源RFID的掘进机位姿识别方法，具体流程为:
(1)利用无源宽带谐波标签，建立谐波反向散射抗干扰模型;
(2)选用矿井无线通信优质载波频率(916 MHz和2.4 GHz)，利用式(1)和(2)通过遗传算法产生使得相位误差容忍度最大的最优频率组合;
(3)由式(2)和(6)，确定最优频率组合下的最大相位误差阈值Φ;
(4)依据二次谐波反向散射理论，收发信号产生一个相位差，建立视在相差函数，给出读写器到谐波标签真实距离和测量距离的关系式;
(5)应用连贯发射的多频连续波和最小均方误差方法，建立式(11)使各个频率作用下的测量误差ei的平方和最小，并推导得出相应的约束条件;
(6)在Δφmax<Φ和Δφmax>Φ两种不同条件下，分别利用式(11)和其相应的两个约束条件获得真实距离R的无模糊估计值，实现精确测距;
(7)采用几何定位算法求解掘进机身上3个无源标签的三维坐标A(xa,ya,za)，B(xb,yb,zb)和C(xc,yc,zc);
(8)基于掘进机机身位姿模型，依据无源标签的三维坐标位置，通过式(21)～(23)计算掘进机机身航向角、俯仰角和横滚角，继而确定掘进机机身的具体位姿。
5 性能评价
分别对谐波标签抗干扰性能、CSMCW相位差测距方法和掘进机位姿识别效果进行仿真测试。仿真实验场景示意如图4所示，实验场景尺寸为105 m×4 m×3 m。
图4 仿真场景示意
Fig.4 Schematic diagram of simulation scene
5.1 抗干扰性能评价
传统标签和谐波标签第i个散射体影响下的信干比(SIR)分别为
(24)
(25)
其中，Rtag和Ri为标签和第i个散射体相对于读写器的位置;
为标签的天线孔径;Gtag为标签的天线增益，σi为第i个反射体的雷达反射面积，发射信号波长为λ0，系数K由标签与其前端天线的阻抗匹配决定，当负载短路且天线阻抗为实数时，K的最大值为4。
设标签的有效天线孔径 等于雷达散射体面积σi，阅读器和标签天线是全向的，将标签放置在(10λ0,0)处。对于传统标签，K=4，Gtag=0 dB。图5为传统标签和谐波标签信干比等值线图。本文所采用的无源宽带谐波标签，与传统无源标签相比可以获得更大的信干比，具有更好的抗干扰性能。
图5 信干比等值线
Fig.5 SIR contours
5.2 测距仿真评价
以图4中读写器S2到标签A之间的距离为例，将本文提出的基于谐波反向散射抗干扰模型的CSMCW测距算法与二次相差测距算法[18]、参差频差测距算法[19]进行仿真测试与评价。仿真参数见表1，仿真中设置基本工作频率为900 MHz，且每种算法均产生5个频率。动态部署S2，分别取其与A间距离为d=50 m和100 m，当信噪比从-5～10 dB变化时，测距效果对比如图6所示;分别取信噪比为-5 dB和5 dB，当S2与A间距从0到100 m变化时，测距效果对比如图7所示。
由图6，7的测距效果对比可知:① 使用相同测距算法时，在相同信噪比情况下测量距离越短，测距误差越小;② 使用相同测距算法时，在相同测量距离情况下信噪比越高，测距误差越小;③ CSMCW测距算法相对于其它两种算法呈现最佳的测距效果。
因此，CSMCW测距算法可以精确测得S2与A的距离，同理，可以测得读写器S1，S3，S4到A的距离，利用式(20)，即可求得标签A得三维坐标A(xa,ya,za)。同样也可求得B(xb,yb,zb)，C(xc,yc,zc)，即实现掘进机机身无源标签的精确定位。
表1 仿真参数
Table 1 Simulation parameters
参数名称参数值相位误差阈值Φ/(°)20.8CSMCW松弛因子ω1.02优化产生频率数5二次相差频差5频差倍数5参差频差频差系数3,5,7,8,11读写器位置坐标S1(0,0,3),S2(1,2,2),S3(2,0,3),S4(1,-2,2)谐波标签位置坐标A(d,1,1.5),B(d+2,1,1.5),C(d,-1,1.5)多径数8直达路径密集多径到达时间/nsτ1=1 000其他路径到达时间/nsτ2=1 015 τ3=1 030τ4=1 045 τ5=1 065τ6=1 080 τ7=1 105
图6 不同信噪比时测距效果对比
Fig.6 Comparison of ranging effects at different SNRs
图7 不同距离时测距效果对比
Fig.7 Comparison of ranging effects at different distances
5.3 位姿识别效果评价
设掘进机沿着巷道坐标X轴方向前进时，航向角、俯仰角、横滚角均为0°。将A，B，C三维坐标数据分别代入式(11)～(13)中，可以得到系统在信噪比为-5 dB，距离d为0～100 m时的姿态角100次误差分布曲线，如图8所示。
图8 不同距离时的姿态角误差分布
Fig.8 Error distribution of attitude angle at different distances
由图8可知，距离为20 m时，航向角、俯仰角、横滚角误差精度约为0.6°;距离为50 m时，误差精度约为1.5°;距离为100 m时，误差精度约增加到2.3°。即信噪比一定时，位姿姿态角误差随距离增大呈增大趋势，这是由定位点误差随着距离的增加而变大导致的。
同时，可以得到系统在30 m和100 m距离、信噪比从-5～10 dB变化时的姿态角误差100次分布曲线图，如图9所示。由图9(a)可知，当信噪比为-5 dB时，航向角、俯仰角、横滚角误差精度约为1.5°以下;当信噪比为0 dB时，误差精度约为0.8°以下;当信噪比为10 dB时，误差精度约减小到0.1°以下;由图9(b)可知，当信噪比为-5 dB时，航向角、俯仰角、横滚角误差精度约为2.3°以下;当信噪比为0 dB时，误差精度约为1°以下;当信噪比为10 dB时，误差精度约减小到0.3°以下。即距离一定时，位姿姿态角误差随信噪比的增加呈减小趋势，这是由定位点误差随着信噪比的增加而减小导致的;同时对比图9(a)和(b)，也可以得到位姿姿态角误差随距离增大呈增大趋势。
图9 不同信噪比时的姿态角误差分布
Fig.9 Error distribution of attitude angle at different signal to noise ratios
6 结 论
(1)采用无源宽带谐波标签引入谐波信号，建立了基于非线性二次谐波反向散射的抗干扰模型，仿真结果表明，采用无源宽带谐波标签，与传统无源标签相比可以获得更大的信干比，具有较强的顽健性，能够有效抑制纳秒级密集多径干扰；
(2)通过基于距离的几何定位方法，提出CSMCW相位差测距算法，来解决大相位误差条件下的距离模糊问题。仿真结果表明，与其他测距算法相比，基于谐波反向散射抗干扰模型的CSMCW测距算法具有更强的鲁棒性，在低信噪比条件下定位测距可达到厘米级的分辨率。
(3)以掘进机为例，研究了基于CSMCW相位差测距的无源掘进机位姿识别方法。性能仿真分析表明，所提出的基于无源RFID的掘进机位姿识别方法具有较强的顽健性，能够满足动态作业环境下掘进机机身位姿识别的技术需求，并可以扩展到同类装备位姿识别应用。
[1] 王国法,赵国瑞,任怀伟.智慧煤矿与智能化开采关键核心技术分析[J].煤炭学报,2019,44(1):34-41.
WANG Guofa,ZHAO Guorui,REN Huaiwei.Analysis on key technologies of intelligent coal mine and intelligent mining[J].Journal of China Coal Society,2019,44(1):34-41.
[2] 胡青松,杨维,丁恩杰,等.煤矿应急救援通信技术的现状与趋势[J].通信学报,2019,40(5):163-177.
HU Qingsong,YANG Wei,DING Enjie,et al.State-of-the-art and trend of emergency rescue communication technologies for coal mine[J].Journal on Communications,2019,40(5):163-177.
[3] HARGRAVE Chad O,JAMES Craig A,RALSTON Jonathon C.Infrastructure-based localisation of automated coal mining equipment[J].International Journal of Coal Science & Technology,2017,4(3):252-261.
[4] YANG Wenjuan,ZHANG Xuhui,MA Hongwei,et al.Infrared LEDs-based pose estimation with underground camera model for boom-type roadheader in coal mining[J].IEEE Access,2019,7(3):33698-33712.
[5] 陈慎金,成龙,王鹏江,等.基于掘进机位姿测量系统的自主标定方法误差分析[J].煤炭学报,2018,43(9):2647-2652.
CHEN Shenjin,CHENG Long,WANG Pengjiang,et al.Error analysis of autonomous calibration strategy based on roadheader attitude measurement system[J].Journal of China Coal Society,2018,43(9):2647-2652.
[6] 杜雨馨,刘停,童敏明,等.基于机器视觉的悬臂式掘进机机身位姿检测系统[J].煤炭学报,2016,41(11):2897-2906.
DU Yuxin,LIU Ting,TONG Minming,et al.Pose measurement system of boom-type roadheader based on machine vision[J].Journal of China Coal Society,2016,41(11):2897-2906.
[7] 齐宏亮.掘进机器人位姿测控系统研究[D].阜新:辽宁工程技术大学,2012.
QI Hongliang.Research on estimating and control system of pose and position for robotic roadheaders[D].Fuxin:Liaoning Technical University,2012.
[8] 符世琛,李一鸣,宗凯,等.面向掘进机的超宽带位姿检测系统精度分析[J].仪器仪表学报,2017,38(8):1978-1986.
FU Shichen,LI Yiming,ZONG Kai,et al.Accuracy analysis of UWB pose detection system for roadheader[J].Chinese Journal of Scientific Instrument,2017,38(8):1978-1986.
[9] LIU Meng,WANG Hongjun,YANG Yang,et al.RFID 3-D indoor localization for tag and tag-free target based on interference[J].IEEE Transactions on Instrumentation and Measurement,2018,10(12):1-15.
[10] ZHANG Yunlei,MA Yongtao,MIAO Xinlong,et al.Multipath mitigation algorithm for multifrequency-based ranging via convex relaxation in passive UHF RFID[J].IEEE Internet of Things Journal,2019,6(2):744-752.
[11] SHANGGUAN Longfei,YANG Zheng,LIU Alex X,et al.STPP:Spatial-temporal phase profiling-based method for relative RFID tag localization[J].IEEE/ACM Transactions on Networking,2016,25(1):1-14.
[12] 张晓光,孙彦景,霍羽,等.基于TOA/DOA参数估计的隧道高分辨率无源移动目标定位[J].煤炭学报,2018,43(7):1965-1972.
ZHANG Xiaoguang,SUN Yanjing,HUO Yu,et al.Localization of high resolution passive mobile target based on TOA/DOA parameter estimation in tunnel[J].Journal of China Coal Society,2018,43(7):1965-1972.
[13] 王晶.基于多维标度的无源超高频RFID室内定位技术研究[D].天津:天津大学,2015.
WANG Jing.Indoor localization technology research based on multidimensional scaling for passive UHF RFID[D].Tianjin:Tianjin University,2015.
[14] 马永涛,苗新龙,高政,等.无源标签多径环境下基于凸优化的定位算法[J].天津大学学报(自然科学与工程技术版),2017,50(9):953-960.
MA Yongtao,MIAO Xinlong,GAO Zheng,et al.Localization algorithm based on convex relaxation in passive tag multipath environment[J].Journal of Tianjin University (Science and Technology),2017,50(9):953-960.
[15] LI Chenyang,MO Lingfei,XIE Xiujuan.Localization of passive UHF RFID tags on assembly line based on phase difference[A].Instrumentation and Measurement Technology Conference Proceedings[C].Taipei:IEEE,2016:1-6.
[16] ZHOU Chenming，GRIFFIN Joshua D.Phased-based composite ranging for backscatter RF tags:System analysis and measurements[J].IEEE Transactions on Antennas and Propagation,2018,669(8):4202-4212.
[17] 史伟光,刘开华,房静静,等.双频副载波调幅的UHF RFID定位方法[J].哈尔滨工业大学学报,2012,44(3):81-86.
SHI Weiguang,LIU Kaihua,FANG Jingjing,et al.UHF RFID location algorithm based on dual frequency subcarriers amplitude modulation[J].Journal of Harbin Institute of Technology,2012,44(3):81-86.
[18] 曹延伟,程翥,皇甫堪.多频连续波雷达两种测距算法研究[J].电子与信息学报,2005,27(5):789-792.
CAO Yanwei,CHENG Zhu,HUANGFU Kan.The research on two algorithms for muitiple frenqueney CW radar ranging[J].Journal of Electronics & Information Technology,2005,27(5):789-792.
[19] LI Xiaoping,WANG Wenjie,ZHANG Weile,et al.Phase-detection-based range estimation with robust Chinese remainder theorem[J].IEEE Transactions on Vehicular Technology,2016,65(12):10132-10137.
[20] CHEN Xianliang,CHEN Yong,ZHANG Hualei,et al.Long read range Class-3 UHF RFID system based on harmonic backscattering[J].Electronics Letters,2018,54(22):1262-1264.
