矿井通风是保障矿井安全健康运行的重要技术手段之一。在矿井生产过程中，必须源源不断地将地面新鲜空气输送到井下各作业地点，以供给人员呼吸，并稀释和排除井下各种有毒、有害的气体和矿尘。只有智能化地控制矿井风流，才能保证智能化采掘工作面的正常运行。
矿井通风智能化技术就是根据井下各个地点的温度、湿度、有害气体和矿尘浓度的变化实时保证供风质量，满足正常时期和灾变时期各用风地点按时按需供风，也是智能采矿不可或缺的重要组成部分。
但是，一般大中矿井的通风系统都是由几百条，甚至上千条风道组成的非线性流体网络，而且随着地面大气压和地温的变化、巷道的变形、掘进工作面和回采工作面的推进、通风设施的状态改变和各种车辆和设备的扰动，有许多风道的风阻和自然风压都是随时变动的，几十年来，尽管国内外有很多专家、学者致力于矿井通风理论、技术和应用方面的研究，在理论研究和软件开发方面取得了较大进展[1-2]。但是，目前的矿井通风控制还是靠人工或半人工完成，难以实现有效通风和按需供风，“一通三防”事故和瓦斯事故时有发生，发生灾变后也不能实时地、有效地控制风流以满足均压灭火、控灾、救灾和安全生产的需要，造成巨大的人员伤亡和经济损失。迄今为止，鲜有真正智能化或无人化矿井通风系统，从矿井通风方面讲已经造成了设备、技术和人力的很大浪费。
借助矿山物联网技术、自动化设备和智能软件系统的技术成果，实现矿井通风系统的全程自动化，将对矿井安全生产的减人提效起到致关重要的作用。笔者将介绍矿井通风智能化理论和技术研究成果，为实现矿井通风智能化和无人化提供借鉴。
1 风网结构及状态方程
风网结构和状态方程是智能化通风系统必不可少的基础。本文根据井巷空间结构和通风系统各风道间的拓扑关系，建立完整的通风网络拓扑图，而后把所有进风井口和回风井口虚拟为一个节点(编为一个节点号)，所有的巷道交叉点适当简化编为其他节点，原则上按照风流方向从始点到终点对风道进行编号，得到通风网络G。
假设通风网络G=(V,E)是一个无悬挂点的虚拟有向图,不失一般性可设G的基础图连通,V={v1,v2,…,vM}和E={e1,e2,…,eN}分别为G的节点集和风道集，并记|V|=M，|E|=N，即G有M个节点，N条风道，第k条风道可表示为ek=(vi,vj)，其中vi和vj分别为风道ek的始点号和终点号。
任意选择G的一个生成树，就可得到G的连支集及其对应的C=N-M+1个基本回路，不妨假设G的前C分支为连支(否则可对G的分支重新排序)，则可把基本回路矩阵表示为
B=(I,B2)=(B1,B2)=(Bij)C×N
(1)
记第j条风道的状态参数向量为
Tj=(Rj,hnj,Aj,Bj,Cj,qj,hj,hfj)T
(2)
其中，Rj,hnj,Aj,Bj,Cj,qj,hj和hfj分别为风道j的风阻、自然风压、风机特性曲线2次项系数量、风机特性曲线一次项系数、风机特性曲线常数项、风量、风压和风机风压。
记通风网络G的状态矩阵为
T=(T1,T2,…,TN)
(3)
则根据流体管网的平衡理论可知，风网状态参数一定满足下列方程组:
(4)
(5)
hj=Rj|qj|σj-1qj,σj≥1,(j=1,2,…,N)
(6)
(7)
其中，σj≥1为流态指数(对于紊流可取σj=2)。
方程(4)～(7)称为通风网络G的状态方程，它是矿井通风系统最基本的理论和计算模型，G的任何一组可行状态参数，必须满足这些方程组成的非线性方程组，这里要说明的是状态方程(1)～(7)看似稳定流动，事实上它们都是时态和瞬时的，特别是借助矿山物联网、4G/5G、流体力学分析技术可以计算出瞬时的自然风压或火风压、风机特性曲线2次项系数量等，较热传导、热辐射以及化学热力学的各种非稳定流动的仿真方法可行和可靠，因此在下列讨论中不再讨论瞬时问题和非稳定流动问题。
笔者将基于这些基本假设深入讨论通风智能化自然分风算法、按需分风计、风阻调节优化等基础理论，通风智能化关键技术、定点调节优化(包括按需调风优化、均压调节优化、风向调节优化)、联合调节优化、在线闭环调控、监控点优化布局、通风系统状态估计、需风量超前预测、风流方向智能控制、可靠性调节优化、通风系统初始化、通风系统故障诊断、智能调控风门风窗、通风智能软件系统等关键技术。
2 通风智能化基础理论
笔者认为，矿井通风智能化的理论核心问题是分风解算和优调优控模型及算法的收敛性问题，特别是自然分风和纯风阻调节算法及收敛性是通风系统智能化中首先要弄清楚和解决的2个核心问题，也是真正的数学问题。
2.1 自然分风计算理论
自然分风计算理论是实现通风自动化和智能化的基础理论，也是一切矿井通风仿真模拟计算和实时解算的核心理论，而实时解算又是矿井通风智能化的基础[2]。
自然分风计算是在各风道的风阻和自然风压以及各风机的特性曲线系数为常数时，求解各风道的风量和风压以及风机的工况点，对于状态方程(4)～(7)而言，就是在所有风道Rj，hnj，Aj，Bj和Cj已知的条件下，计算出所有风道的qj和hj。自1936年CROSS H提出了流体网络分析方法后，人们就开始研究用迭代方法和图论理论来分析和求解矿井自然分风问题。1951年，英国的斯考特(Scott)和恒斯雷(Honsley)，对哈德-克劳斯(Hard-Cross)进行了改进，提出了著名的斯考特-恒斯雷(Scott-Honsley)方法，同年，日本京都大学的平松良雄也提出了类似的方法，称为京大方法。但是，这些方法在理论上都没有证明其收敛性，更不能保证收敛到真实的系统状态，即“真收敛”。要实现矿井通风智能化就必须采用具有严格理论基础的模型和算法开发的软件系统，否则就不能保证计算能否收敛以及结果的正确性，也无法摆脱人工干预(包括算法选择、初值选择和结果的正确性评判等)，更无法实现矿井通风的智能化和无人化。
有关分风算法的收敛性问题，曾经有几位数学家进行过深入的研究[5-13]，但是文献[5-13]只给出了简单加压问题解的存在惟一性和收敛算法研究，文献[8]虽然给出了双树算法，但理论上并不完善。为此，笔者针对一般非线性管网方程组给出了完整的定解条件和全局收敛算法[10-11]，使得矿井通风网络的解算问题在理论上得到解决。
2.2 按需分风计算理论
针对状态方程(4)～(7)而言，按需分风解算问题就是在已知各风道自然风压和各风机的个体特性曲线系数或工况的条件下，固定部分风道的风阻、风量和风压，计算出“正确的”未知风阻、风量和风压，这也是通风系统状态估计和按需供风的计算基础，此问题不仅涉及到算法的收敛性，还涉及到状态方程(4)～(7)的定解条件，对于矿井通风智能化而言也是必备的基础理论问题。文献[10]的定理2.1给出了一般非线性管网方程组(4)～(7)存在惟一解的充分必要条件，文献[11]给出了包括矿井通风在内的非线性动力网络方程组的性质与解法，解决了矿井通风系统多态(包括层流、紊流等)流动的按需计算问题，不仅使得高速风流、低速风流、巷道风流、采空区风流和漏风通道风流可以混合解算，其解更符合实际，而且给出了算法的收敛性条件和定理(定理4.1)。为本文后面讨论的通风系统状态估计和智能调风控风奠定了基础。
2.3 风阻调节优化理论
对于状态方程(4)～(7)而言，风阻调节优化问题就是在所有风道
和Cj已知的条件下，固定需风风道集S1的
通过利用单纯的风阻调节方法，计算出可行的、并满足正常时期、发火时期和灾变时期需要的风阻调节量ΔRj和未知的qj(j∉S1)，并使风机功率消耗极小化。这也是矿井通风智能化中用到的基础理论之一。关于矿井通风系统纯风阻优化调节问题的研究，一般有线性规划法，最大通路法，非线性规划方法以及固定风量法等，可见文献[3,4,14-16]。其中，线性规划法和最大通路法对系统进行大量的简化[3,14]，计算结果只是在某种条件下的近似解。而固定风量法其实质就是定解问题[10-11]的特例，用这种方法求出的风阻可能为负值，使得方案不可行。非线性规划方法虽然没有对系统进行简化，但要计算出最优调节方案也是很困难的，事实上，只要没有经过严格理论证明的方法是很难得到最优解的。从一般的工程角度看，我们认为像文献[4]等给出的迭代算法已是不错的选择，其结果至少比一般的线性规划法和最大通路法为优，但文献[4]例6-1给出风机负压为3 286.028 Pa的调节方案就不是最优解，因为在需风条件不变的情况下，用笔者的方法可以得到风机负压为3 212.453 Pa的增阻调节方案。这也说明仅就风阻调节而言，用一般的方法和软件也很难得最优解，也就是说一般没有经过严格论证的方法用于通风自动化调节是不可靠的，这不仅是一个经济问题，更是一个安全问题。事实上，文献[10]在理论上已经比较彻底地解决了通风系统纯风阻优调算法的收敛性和可靠性问题。
3 通风智能化关键技术
矿井通风智能化的技术目标不仅是保证正常时期和灾变时期的按需供风和控风，而且要实现全程自动化和无人化通风，鉴于矿井通风的复杂性，还有很多关键问题需要解决。因此，尽管文献[3,16]等把风道的风压作为调节变量进行处理，表面上看可以解决优化调风问题，事实上，这种处理方法不仅在理论上没有证明可行性，在实践中也是不可行，因为当风压调节值的正负号和风流方向不一致，就无法得到可行的风阻值，而且不能总用辅扇调节。本节深入讨论和解决诸如定点调节优化、联合调节优化、状态估计等通风智能中的关键技术问题。
为了比较直观地论述智能通风的若干个关键技术及实现效果，我们以图1为例进行说明。其网络结构如图1所示，第13风道中的风机特性曲线分别为在此假设各风道的自然风压等于0，各风道的原始风阻向量为:R=(0.01,0.8,0.245,0.445,0.024 8,0.365,0.01,0.09,0.081,0.002 3,0.202 3,0.087 5,0.001)。
图1 矿井通风网络结构
Fig.1 Mine ventilation network structure
3.1 定点优化调节技术
定点调节优化问题是指对安装有调节风门或风窗的风道，在风门或风窗开度最大的基础上进行增阻调节，并最大限度地满足需风要求，使功率消耗最小。这也是最常用和最可行的调节技术，根据文献[15，17]，我们可以建立如下形式的定点调节优化模型:
(8)
(9)
(10)
hj=(Rj+ΔRj)|qj|σ-1qj,j∈S3
(11)
hj=Rj|qj|σj-1qj,j∉S3
(12)
(13)
ΔRj≥0，j∈S3
(14)
其中，σj≥1，Rj≥0为常数;Sf为风机风道集合；S1为需风风道集合；S2为控制风向风道集合，S3为可调风道集合;
为需风量
可以为0);δj为风向符号(δj=1为正向流动，δj=-1为反向流动);M1,M2为惩罚系统，一般取M1=105,M2=106;ΔRj为风阻调节量。
3.1.1 正常时期的按需调风
假设风道2和8为需风风道，需风量为20 m3/s和30 m3/s，风道8和9为可调风道，优化调节计算结果见表1。
由表9可知，用风道8和9的调节设施进行增阻调节，就可以满足风道2和8的按需供风。
3.1.2 灾变时期的均压调节
假设风道2和8为需风风道，需风量为20 m3/s和30 m3/s，风道10需要均压，风道5，8和9为可调风道，优化调节计算结果见表2。
由表2可知，用风道5,8和9的调节设施进行增阻调节，不仅可以满足风道2和8的正常供风，而且可以对风道10进行均压，这对灾变时期的实时灭火非常有用。
3.1.3 灾变时期的风向调节
假设风道2和8为需风风道，需风量为20 m3/s和30 m3/s，要求风道6和10的风向为正，风道5，8和9为可调风道，优化调节计算结果见表3。
表1 按需调风结果
Table 1 Results of on-demand flow regulation
序号风量/(m3·s-1)风压/Pa风阻增量/(kg·m-7)风机风压/Pa184.36071.165 4220.000319.999 8322.741126.703 14-2.741-3.344 0541.61742.953 06-18.876-130.047 0764.36041.421 6830.000274.159 40.214 62934.360288.376 60.163 2710-21.617-1.074 8118.38314.217 21242.743159.857 71384.3607.116 5567.937 9
表2 均压调节结果
Table 2 Pressure equalizing regulation results
序号风量/(m3·s-1)风压/Pa风阻增量/(kg·m-7)风机风压/Pa181.389 866.243220.000 0320.003312.903 740.79447.096 622.411520.000 0493.4461.208 776-7.096 8-18.383761.390 137.687830.000 0304.7270.248 49931.389 8486.7920.413 0410001129.999 6182.0651261.389 9329.7641381.389 86.624927.111 79
由表3可知，同样用风道5,8和9的调节设施进行增阻调节，不仅可以满足风道2和8的正常供风，而且可以按照要求改变风道6和10的风流方向，这对灾变时期的避灾、救灾和反风控制非常有用。
综上所述，利用本文建立的模型(8)～(14)，只需要在可调节的风道进行增阻调节，就可以解决正常时期的按需供风问题和灾变时期的均压和风向控制问题。
表3 风向控制调节结果
Table 3 Results of flow direction regulation
序号风量/(m3·s-1)风压/Pa风阻增量/(kg·m-7)风机风压/Pa179.426 563.085 7220.000 0319.998 0311.459 132.170 948.541 532.466 0510.559 7730.160 06.523 33660.899 10.295 1759.424 835.313 1830.000 0317.356 00.262 619929.425 2632.048 00.648 979109.440 6 0.204 9 1139.440 7314.692 01268.865 8414.968 01379.426 56.308 61 151.724 9
3.2 联合优化调节技术
虽然用模型(8)～(14)可以解决按需调风、均压调风或风向控制问题，但由表1～3可以看出，随着对风流要求的不断提高，风机的负压也逐渐加大，这也是因为固定了风机个体特性曲线，使其与增阻调节后与系统状态不再匹配的缘故。如果不固定主要通风机的个体特性曲线，选择最合适的风机运行曲线与之配合，就可以大幅度地降低功率消耗，这就是联合优化调节问题。文献[18]给出了同时对风道风阻和通风机转速等参数进行联合调节优化模型，或者把式(13)改为
(15)
其中，nj为风机j的转速;θj为风机j的动叶角度，所有形如X(θj)均为θj的二次函数(其系数可通过最小二乘拟合得到)。
当θj一定时，Aj(θj)，Bj(θj)和Cj(θj)为风机j转速为1时的个体特性曲线系数(可由流体机械的无因次压力曲线以及压力和转速的关系获得)。
一般情况下，nj和θj要满足上下界要求:
(16)
这样就可形成联合调节优化模型:
(17)
(18)
(19)
hj=(Rj+ΔRj)|qj|σ-1qj,j∈S3
(20)
hj=Rj|qj|σj-1qj,j∉S3
(21)
(22)
(23)
ΔRj≥0，j∈S3
(24)
当要求风流方向与j假设的始终点方向一致时取δj=1，否则取δj=-1。求解模型(17)～(24)可利用多层优化算法，文献[18]也给出了一个具体算例，限于文章篇幅，在此就不详细论述了。
3.3 在线闭环调控技术
由于投资的限制传感器个数不会太多，通风系统状态(各风道的风阻和自然风压)不容易准确识别，或者，灾变无法快速识别系统状态，但可以监测出用风点或灾变区的漏风量。这时，就需要在线闭环调节技术来满足特殊的调风需要。文献[19]给出了一个可行的闭环优调优控方法，其思想是借鉴人工的边调边测原理，用后台自动搜索各调节设施调节方向的方式进行，并尽可能地减少调节次数。
建立矿井通风系统在线闭环优调优控数学模型，该模型以各需风点的实测风量与其目标风量之差的平方和以及风机功耗最小为目标函数，以各风阻调节装置的调节参数为控制变量，以控制变量的可调节范围为约束;根据每次调节的目标风量，通过在线直接搜索方法确定每步各调节装置的调节量，通过实测需风点的供风量和风机工况实时计算目标函数值，并以目标函数值达到最小为控制策略，进行监测-目标和调节策略计算-发布命令-风阻调节装置调节-监测在线循环调控，直到满足容许误差或达到调节极限就完成了本次需风调节。
在线闭环优化调控数学模型，其目标函数为
MinF(Θ)=F(θ1,θ2,…,θn)=
(25)
其中，S1为用风风道集合;
为风道i的需风量(即目标风量);qi为风道i的实测风量;Sf，qfj和hfj分别为风机所在的风道集合、风机工况点的实测风量和风机风压;M≥0为常数。约束条件为
θi∈[di,Ui],i∈S3
(26)
其中，S3为风阻调节装置所在的风道集合;θi为第i个调节装置的调节参数，例如控制调节装置的步进电机的转动角度;di和Ui为调节参数θi的调节范围的下限和上限，Θ={θi|i∈S3}为调节参数向量;如果记
为一个将要执行的调节状态，则当Θ(t)满足式(26)时，则称状态Θ(t)“可行”，否则称状态Θ(t)“不可行”，在优化搜索时，每当搜索到“不可行”Θ(t)时，只需记目标函数值为“+
”，不执行真正的调节动作。
值得注意的是在实现过程中不仅要考虑到风流的稳定性，不能是风流大范围的忽高忽低变化，也要考虑尽量节省调节驱动电机的调节行程，上述方法充分利用了矿井通风系统的实际模型、物理模型、数学模型、物联网和通讯技术的各自优势，可以解决复杂环境下的各种应急风流控制问题。具体的在线闭环优调优控算法见文献[19]。
3.4 监控点优化布局技术
监控点优化布局问题是在满足矿井通风系统“可测”和“可控”的条件下，使得监测点(或传感器)和调控设施(调节风门或风窗)数量达到最小。
所谓“可测”就是指利用这些传感器数据能够估计出通风系统的状态参数，所谓“可控”就是指利用这些调节设施能够实现按需供风和按需控风。笔者在文献[20]中给出了监测点的布局模型和布局方法，其基本原理为通过建立完整的矿井通风系统网络拓扑结构图，进行全局通风阻力测定，获得通风系统初始状态;得到灵敏度矩阵;按照风道风阻的稳定性和重要性划分风道;按照风量的必测性、灵敏性和可测性划分风道;根据风道分类结果和灵敏度矩阵，对通风网络进行简化，得到G=(V,E)，对简化网络图G利用风量平衡定律(5)，寻找最优测风传感器布置方案。
测风传感器具体的布局方法见文献[20]中的步骤1～8，该文献不仅给出监测点布局实例，而且对灵敏度比较低低风速传感器还给出一个科学的安装方法。其优点是：① 利用普通的风速传感器及较少的安装数量，可实时获得每条风道较准确的风量，为通风系统在线分析状态识别和诊断提供了一个可行的解决方案；② 对于风速较低的风道，给出了长距低阻聚风风速传感器安装方法，提高了风速传感器测量量程和灵敏度。
控制点的布局原理同监测点，在此不一一论述。
3.5 通风系统状态估计方法
通风系统状态估计问题是指利用相应的监测传感器数据，通过软件处理、分析和计算，获得各风道的风阻、风量、风压、自然(火)风压，用于取代通风阻力测定和平差处理的，从而可以节省大量的人力和物力，并可自动提高工作效率。
对于任意一个矿井通风系统，先按照文献[20]对风道进行分类，并按照文献[21]中的方法布设温度传感器和气压传感器，以便计算各节点的气压和各风道的自然风压。然后，按照风道的分类和风速传感器的分布情况，分下列3种情况进行通风系统状态识别:
(1)在所有未知风阻的风道(例如含工作面巷道的所有用风风道)上都安装了风速传感器，可以测得其风量，如果满足文献[10]的定解条件，这时就变成了按需分风问题，可以实时求出未知风阻的惟一解(见本文的第2节)，从而可以解算出各风道的其他参数。
(2)不是所有未知风阻的风道上都安装了风速传感器，但用风速传器可以通过风网的风量平差计算获得所有风道的风量值，这是可以用文献[22]给出的风道参数多态自动识别方法计算出未知的风阻，从而可以解算出各风道的其他参数。
(3)如果情况(1)和情况(2)的条件均不满足，我们就可以利用文献[21]的通风系统状态识别方法加以解决。
该状态识别方法实际上是已知部分基础数据和部分实时监测数据(例如不变的巷道风阻、通风设施的状态风阻、监测到的风速或风量、风机工况、各测点的温度、湿度或密度等)实现待估数据(例如待估的经常变化的风道风阻、各构筑物异常状态、各风道的自然风压等)的最优反演，其核心技术就是通过求解下列非线性规划模型，获得各风道的风阻、风量和风压。
(27)
(28)
(29)
hj=Rj|qj|σ-1qj,σ≥1,(j=1,2,…,N)
(30)
(31)
Rj≥0,j∈S3
(32)
为常数，j∉S3
(33)
其中,S3为已知风阻的风道集合;
为风道i的监测风量;
风机j监测风压，其他符号同前。该模型的解法同纯风阻调节问题，在文献[21]中也给出了状态估计算例，说明了该方法的有效性。
3.6 需风量智能预测方法
从以上研究可知，无论矿井通风系统分风解算，还是优调优控，其目的就是保证矿井各用风地点的按时按需供风，要保证矿井各用风点的按时按需供风，提前知道各用风点的需风量是先决条件。
纵观现有的应用技术，无论是《煤矿安全规程》，还是工程技术人员，都是在假设作业人数、机电散热、环境温度以及有害气体(瓦斯)涌出量已知的条件下计算需风量的;即使通过安全监控系统和人员定位系统等物联网技术能够计算出各用风地点的瓦斯涌出量、煤尘产生量和人员个数，由于计算和调节过程需要耗费一定的时间，使所计算出的需风量已经处于滞后状态，中间也存在一个具有安全隐患的灰色时段，也形成了安全隐患。因此，实现需风量的超前预测也成了矿井通风智能化的一个关键技术。
虽然，曾有人提出用人工神经网络计算方法来预测瓦斯涌出量，把风流中的瓦斯体积分数作为预测参数，而由于瓦斯体积分数与实际供风量密切相关，实际供风量是随时变化的，因此该方法既不科学又无法实现，而且利用人工神经网络的另一个技术关键是输入参数的选择，已有方法并没有给出较科学的与合理的输入参数集合，直接导致这种方法实际上是无法实现的，也达不到应用目的。
笔者在文献[23]中提供一种矿井需风量的全息预测方法，建立了一个具有学习能力的全息人工神经网络预测模型，主要包括:除尘需风量全息预测模型、炮烟产生量全息预测模型、车辆废气排量全息预测模型、采掘工作面瓦斯涌出量全息预测模型和降温除湿舒适感需风量全息预测模型;获取与该工作面对应的各个全息预测模型的输入变量，并输入到对应的全息预测模型中，从而得到各个全息预测模型的输出变量;然后，得到该工作面在下一个控制时间段的需风量。其特点是根据满足矿井安全健康生产的瓦斯体积分数、粉尘质量浓度、炮烟浓度和舒适度要求，可以有效地预测用风点的实际需风量，解决了矿井通风系统正常时期按需供风和风流控制的需风量问题，为实时按需供风奠定了技术基础。由于该方法考虑的时空因素较多，必须借助于矿山4DGIS平台，其方法的合理性分析、具体的计算公式、机器学习模型和试验效果在文献[23]都有详细论述。
3.7 反风控制智能决策技术
虽然灾变时期的通风技术较多，例如防爆门的自动开启和复位，快速密闭，风流导向等。但可以不包括像瓦斯爆炸、火灾等事故的仿真和模拟技术，因为仿真和模拟技术只能进行推演、培训和系统设计参考，不能用于灾变现场。在这些技术中，笔者认为最核心的和最困难的当属灾变时期的风向和风量控制，像智能防爆门、自动密闭设施可归结为装备类，已有比较成熟的产品。
由前述可知，我们可以通过优化模型(8)～(14)给出控制风流方向的调节方案，但还没有给出确定反风风道的决策方法，下面就给出反风控制智能决策技术，思路和方法如下:
反风技术主要用于灾变时期，主要是避免“灾变风道”产生的乏风、污风、烟雾或高温风流流入有人场所、行人风道和人员撤离路线，确保这些风道在灾变时期流过的是“新鲜风流”或“无害风流”，我们把这些风道简称“限向风道”。如果灾变发生在回风区，只要规划好避灾路线和救灾路线即可;如果灾变发生在进风区或在用风区的非角联风道中，一般就需要全矿井反风;否则，就需要进行区域反风或局部反风。无论是哪种情况，以往都是由人工决定哪些风门关，哪些风门开，以及哪些主要扇风机需要反转，哪些主要扇风机可调节动叶角度，然后由人工付诸实施，无论从速度上，还是效率上都无法满足智能化采矿的需要。
在智能化或自动化通风系统中，有效地解决自动反风或风流方向智能决策问题还属于一个未解决的关键技术。在这里给出一个灾变时期的风流方向智能控制技术，其思路是:
(1)对于全矿井反风，无论是有反风风道反风(轴流式主要通风机或离心式主要通风机)、无反风风道反风(对互为备用双主要通风机)、主要通风机反转(轴流式主要通风机)，还是调整动页安装角(轴流式主要通风机)，只要做好反风预案，届时自动调用预案，改变通风系统和风机参数、切换有关风门开关状态，调用自然分风解算程序进行模拟即可。
(2)区域反风或局部反风，需要按下列步骤进行处理:① 按照实际风流方向，建立反风前的通风网络有向图G0=(V,E0)，其中节点集V同本文第1节的假设，风道的始终点可能要互换，因此，风道集记为E0;② 假设“灾变风道”为ez=(vi,vj)，从vj开始沿风流方向搜索到所有“限向风道”构成的风道子集Ex;③ 令式(8)中的S2=Ex，如果ez同时也是“限向风道”，且灾变发生在其进风侧(如工作面进风巷)，则取S2=Ex∪ez;设ek∈Ex，则当ek在Ex中与在E中同向时，取δj=-1，否则取δj=1;④ 把涉及到的有风门的风道均设为可调节风道，得到可调风道集S3，建立模型(8)～(14)，求解得到ΔRj(j∈S3);⑤ 当ΔRj较大(如ΔRj≥500 000)，则关闭该风门;否则，开启该风门并进行调节。
只需简单的数学力学推理就可以说明上述方法在灾变时期控制风流方向的有效性和可行性，不再详述。
3.8 可靠性优化调节技术
受到自然风压、火风压、行人、生产设备以及胶轮车和提升设备活塞风的扰动，矿井通风系统的运行状态都是动态的和不确定的，即使进行了实时优化和调控，也不能保证用风风道风流的稳定性，为了最大限度地减少各种随机因素对用风点供风量的扰动，有很多学者对通风系统的稳定性和可靠性进行了研究，但大多学者套搬了可靠性数学中的网络可靠性模型，事实上它们并不适用于流体网络，在此不作描述。笔者在文献[24]中提出了一个使用于矿井通风系统的和可行的可靠度计算和优化方法，基本思想为：
对于给定的通风系统图G=(V,E)和初始状态
其中R0和
分别为风阻和自然风压的均值向量(已定);
为固定风量向量;Q2,Hf为待定的风量和风机压力向量。然后按照前面纯风阻调节优化的方法，求得一个最经济的按需分风状态
在Ty下满足所有的平衡方程，不妨设Ty下各风机的压力分别是
然而在
和
取定的条件下，一般情况下，有许多个甚至无穷个ΔR≥0满足最经济的风阻调节方案。我们就从这许多个调节方案中，选择一个可靠度达到最大的风阻调节状态
按照文献[24]的思想，可以把通风可靠度优化归为下列规划问题进行求解:
(34)
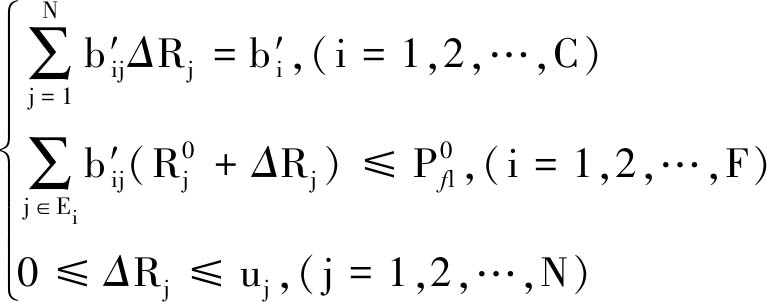
(35)
其中，S1为用风风道集合;Ei为第i台风机的一条从进风到回风的通路风道集合;Di(·)为风道i的随机扰动风量方差，
为与风阻有关的风量向量和初始风量向量。而且有其他符号的含义和求解规划式(34)～(35)的算法可参考文献[24]。由文献[24]中的算例，可以说明该类方法能够有效地提高用风风道的可靠性和稳定性。
3.9 通风系统初始化技术
矿井通风系统的初始化包括地质空间、井巷空间、采掘空间、风网结构和初始状态的初始化，初始化本身就是一项比较复杂的系统工程，也是建立智能化通风系统的基础工作。众所周知，无论是分风解算、系统优化、系统改造还是智能调风控风，都需要知道一个比较准确的通风系统初始状态，特别是各分支的风阻。如果已知的参数精度较低，甚至是错误数据，那么无论计算方法再先进、计算结果再精确、调节手段再智能也是徒劳的。如何获得比较可靠的通风系统初始状态参数就是“通风系统初始化技术”，实践证明最直接的初始化技术就是全局阻力测定，由于矿井通风网络是复杂多变的系统，测定时还有大量的随机扰动，既使消除了系统误差，随机误差也在所难免。为了消除这些扰动带来的不确定性，笔者认为将风道的风阻分解为原始风阻(固定部分)、局部风阻和扰动风阻3部分是非常必要的，而后经过反复(多天多时间段)测定和多次平差[25]，再通过统计分析，计算出每条风道的原始风阻、局部风阻和扰动风阻，就可获得通风系统当时的初始状态，笔者团队通过几十个矿井的阻力测定和数据处理实践也证明了该方法的可行性。
3.10 通风系统故障诊断技术
矿井通风智能化的实现也离不开故障诊断技术，但是有了前面的按需分风解算、状态估计等技术成果，再加上一轴温、振动等信号处理技术，只需在软件系统中加入一些基于诸如小波分解、EMD分解或VMD分解及相关性分析的故障诊断模块，就可解决矿井通风系统中通风设施、主要扇风机、监测传感器、风速超限、风量不足、内外部漏风等故障的诊断与识别问题，不再详述。
4 风门风窗智能调控技术
关于风门的自动开关控制，无论是气动、液动还是电动技术都已经比较成熟，目前的生产厂家也比较多。但是，关于高精度和高灵敏的智能调节风门和风窗研究的还比较少，事实上，无论是气动，还是液动都很难实现精细控制和敏捷控制，而采用伺服电机的电动控制又无法实现开环运行;更重要的是无论是调节风门，还是调节风窗，都要求调节范围或开度尽可能的大，只有这样才能提高调节装置的适用性，为了配合本文前几节的最优调节理论、模型和算法，实现通风系统智能调控，笔者所在团队在文献[26]中设计了一系列的智能调节风门风窗设计方案，这些设计方案包括多层推拉式调节风窗、百叶风窗式调节风门、卷帘式调节风门、多层推拉窗式调节风门、闸式卷帘风门、多层伸缩推拉门、密闭非伸缩推拉窗、密闭伸缩推拉窗中的一种或几种的组合。
在实施过程中，所有风门和风窗必须根据巷道尺寸进行定制，因此，在图2～5中我们只给出了部分设计方案的示意。由图2可以看出设计这种多层推拉式调节风窗，其目的通过多层叶片可以使风窗的开度(调节范围)极大化，而且随动扇个数(层数)越多开度越大，在此方案中，不仅用步进电机通过同步带可以精确地控制主动扇片的运动，而且还利用物位(开度)传感器实时返回风窗的开度，控制器不仅可以接受远程的控制命令驱动执行器，还负责采集和记录各种传感器和风窗的状态数据，并实时反馈到远程系统，这种多层推拉式调节风窗技术同样用于多层伸缩推拉门，在此不一一说明。图3～4给出的是百叶风窗式调节风门及其扩展形式，由图不难看出这种调节风门并不影响行人和胶带运输，而且也可以把调节范围做到极大化。图5给出的卷帘式调节风门及其变形，设计原理同其他调节风门。所有调节风窗风门中的部件名称已在图中标出，详细技术说明可参见文献[26]。
图2 多层推拉式调节风窗
Fig.2 Multi layer push-pull adjustable window
图3 百叶风窗式调节风门
Fig.3 Louvered regulating door
图4 多用途百叶风窗式调节风门
Fig.4 Louvered regulating door for multi-purpose
图5 卷帘式调节风门
Fig.5 Roller shutter regulating door
事实上，在上述每个方案中，我们设计的调控机构带有远程自动调节接口、就地遥控调节接口以及自动和手工调节切换装置，以便于各种情况下的应急处置。
有了这些调控装置，剩下的关键问题就是风道风阻增量和风门风窗调节装置调节参数的关系研究。这里假设所有调节装置均采用步进电机驱动，因此，不论哪种形式的风门和风窗，只需针对预安装调节风门或风窗的风道j建立电机转角(或叶片转角)与风阻增量的函数和逆函数关系，即可实现精准调控，可概括为
(36)
为了便于初始化，假设θj=0时，ΔRj=0，ΔRj随着θj的增大而增大，本文推荐使用下列形式的函数和逆函数:
(37)
(38)
其中，θj为步进电机的旋转角;ΔRj为θj对应的风阻增量;Sj为风道j的断面面积;
为θj=0时，由安装该风门或风窗在风道j产生的局部风阻值，对于百叶窗调节装置，可以在式(37)和(38)中用sin θj代替θj;aj,bj,cj为拟合参数，这些参数均可以在风门加工好后，在实验室用模拟风道或通过安装调试实验拟合获得。
通风智能的所有自动化装置和控制电路已由山东蓝光软件有限公司进行了研发和样机测试，由样机的实验结果可知，采用电机驱动不仅可以充分利用其细分特性和变速效果达到精密控制，甚至不需要行程、转角或开度传感器，也可以达到闭环的精准控制效果。其中的“矿用隔爆兼本质安全型步进电机控制箱”、“矿用隔爆型步进电机执行箱”和“矿用本安型物位传感器”等产品已通过《矿用产品安全标志认证》，这也是我国煤矿井下首套步进电机控制系统，目前已到了工业试验阶段。
最后，利用相关的传感器和物联网技术，通过电路板和嵌入式软件开发，把风门的开关控制和调节控制集成到一起，形成一套完整智能调控风门组合方案，如图6所示。由图6可以看出既可以解决风门的开关自动化问题，也可以解决风门的调节自动化问题;既可以实现单道风门的自动化，也可以实现双道风门的自动闭锁;不仅可以通过测速雷达和红外传感器识别车辆和行人，还可以与远程通风自动调控系统、人员和车辆定位系统、应急管理系统等联网，为实现通风系统的全局自动化和智能化奠定了硬件基础。
图6 智能调控风门的组合方案
Fig.6 Combination scheme of intelligent control damper
5 通风智能软件系统
在所有智能化系统中软件就是灵魂，矿井通风系统也不例外，笔者自发表第1篇关于矿井通风的论文[15]至今，经过30多年的理论研究和软件开发，终于取得了一些突破性进展，形成了完整的矿井通风智能化体系架构(图7)。由图7可以看出该体系由4个层次组成：第1层为矿山4DGIS平台，用于管理和矿井通风有关的气候、地形、地质、井巷、硐室及工作面的空间和属性数据;第2层为矿山物联网平台，为通风智能化提供基础网络、交换设备、精准感知器、控制装备和智能通风设施，在本层中之前还存在一个技术难题就是缺乏可用的宽量程、高灵敏的风速传感，目前该问题也得到了较好地解决[20,27];第3层为智能化通防软件，主要解决通风系统优化设计、模型建立、系统初始化、静态和半静态的数据处理、分风解算、机器学习等后台支持;第4层为通风智能调控系统，在前3层的基础上实时进行矿井通风的自动化智能化工作，是实现通风系统全程无人化的神经中枢。在山东蓝光软件有限公司的持续研发和成果转化过程中，开发了完整的矿山4DGIS平台和智能化通风软件，其功能涵盖了图7中的矿山4DGIS平台、智能化通防系统、通风智能调控系统3个层级中列出所有功能和矿山物联网平台中的数据采集和通风系统智能装备的调控部分，不仅可以与监测系统集成实现矿井通风系统的智能分析和4D可视化展现，而且得到了上百个煤矿的实际应用，取得了良好的效果。进一步的工作就是在完善的矿山物联网基础上，尽快部署矿井通风智能化调控系统，为矿山智能化提供基础保障。
图7 矿井通风智能化体系架构
Fig.7 Mine ventilation intelligent system architecture
6 结 论
(1)通过矿井通风系统风网结构、状态方程以及状态参数向量的定义，给出了矿井通风系统状态估计、分风解算、优化调节、风向控制和故障诊断等问题的表述基础。
(2)指出了矿井通风智能化的理论基础是自然分风计算、按需分风计算和风阻调节优化理论及算法的收敛性问题，并给出了解决思路。
(3)提出了定点优化调节、正常时期按需调风、灾变时期均压调节、灾变时期风向调节、风窗风机联合调节、在线闭环调节、监控点优化布局、通风系统状态估计、需风量智能预测、反风智能控制、可靠性优化调节、系统初始化和系统故障诊断等智能化通风关键技术和解决方法。
(4)发明了多层推拉式调节风窗、百叶风窗式调节风门、卷帘式调节风门、多层推拉窗式调节风门、闸式卷帘风门、多层伸缩推拉门、密闭非伸缩推拉窗、密闭伸缩推拉窗等多种自动调节装置，以适用于各种风道的安装和全断面调节。
(5)设计了包括矿山4DGIS平台、矿山物联网平台、智能化通防系统和智能调控系统4个层次的矿井通风智能化体系架构，定义和开发了成套的通风智能化软件系统。
[1] 卢新明.矿井通风智能化技术研究现状与发展方向{J].煤炭科学技术,2016,44(7):47-52.
LU Xinming,Study status and development orientation of mine ventilation intelligent technology[J].Coal Science and Technology,2016,44(7):47-52.
[2] 周福宝,魏连江,夏同强,等.矿井智能通风原理、关键技术及其初步实现[J/OL].煤炭学报:1-10[2020-06-19].https://doi.org/10.13225/j.cnki.jccs.ZN20.0338.
ZHOU Fubao,WEI Lianjiang,XIA Tongqiang,et al.Principle,key technology and preliminary realization of mine intelligent ventilation[J/OL].Journal of China Coal Society:1-10[2020-06-19].https://doi.org/10.13225/j.cnki.jccs.ZN20.0338.
[3] 陈开岩.矿井通风系统优化理论及应用[M].徐州:中国矿业大学出版社,2003:60-61.
[4] 王树刚.孙多斌.稳定流体管网理论[M].北京:煤炭工业出版社,2007:114-116.
[5] COLLINES M,COOPER L,HELGASON R,et al.Solving the pipe network analysis problem using optimization techniques[J].Management Science,1978,24(7):747-760.
[6] 王长钰.非线性管道网络中的线性逼近法的收敛性及推广[J].应用数学学报,1978,l(4):269-282.
WANG Changyu.Convergence and extension of the linear approximation method in nonlinear pipe network[J].Acta Mathematicae Applicatae Sinica,1978,l(4):269-282.
[7] 张建中.一类求解管道网络方程的迭代法及其推广[J].应用数学学报,1981,4(2):175-189.
ZHANG Jianzhong.An iterative method for solving the equation of pipe network and its extension[J].Acta Mathematicae Applicatae Sinica,1981,4(2):175-189.
[8] 黄翰文,聂义勇.矿井按需分风双树解算法[J].煤炭学报,1983(4):1-11.
HUANG Hanwen,NIE Yiyong.Bitree method for solution of mine air distribution[J].Journal of China Coal Society,1983(4):1-11.
[9] BHAMIDIPATI S,PROCARIONE J A.Nonlinear programming technique for analysis of mine ventilaion network[J].Mine Industry(Sec.A),1986(95):8-14.
[10] 卢新明.非线性管道网络中的数学规划问题及解法[J].应用数学学报,1989,12(3):281-291.
LU Xinming.Mathematical programming problem and solution nonlinear pipeline network[J].Acta Mathematicae Applicatae Sinica,1989,12(3):281-291.
[11] 卢新明.一类非线性动力网络方程组的性质与解法及其应用[J].系统工程学报,1991,6(2):99-107.
LU Xinming.The properties and solution of a class of nonlinear dynamical network equations and its application[J].Journal of systems engineering,1991,6(2):99-107.
[12] ALTMAN T,BOULOS P F.Convergence of Newton Method in Nonlinear Network Analysis[J].Mathematical and Computer Modelling(Oxford),1995,21(4):35-41.
[13] ALTMAN T,BOULOS P F.Solving Flow-Constrained Network:Inverse Problem[J].Journal of Hydraulic Engineering,1995,121(5):427-431.
[14] THOMAS A.MORLEY,WANG Y J.The Minimization of Venlilation Costs for controlled Flow Network[A].SME PrePrint,No.83-400.Annual Meeting[C].Vrah:1983.
[15] 卢新明.矿井通风系统最优调节问题的研究[J].煤炭学报,1985(1):56-64.
LU Xinming.Study on optimal regulation of mine ventilation system[J].Journal of China Coal Society,1985(1):56-64.
[16] 黄元平,李湖生.矿井通风网络优化调节问题的非线性规划解法[J].煤炭学报,1995,20(2):14-20.
HUANG Yuanping,LI Husheng.Solution of problems relevant to optimal control of mine ventilation network by non-linear programming technique[J].Journal of China Coal Society,1995,20(2):14-20.
[17] LU Xinming,The micro-computer assistant analysis for mine ventilation network[A].Proceedings of 5th US Mine Ventilation Symposium[C].1991:432-439.
[18] 卢新明,尹红.一种矿井通风系统的联合优调优控方法[P].中国专利:ZL201510256440.8:2016-05-25.
[19] 卢新明,尹红.一种矿井通风系统在线闭环优调优控方法[P].中国专利:ZL201510256743.X:2016-03-16.
[20] 卢新明,尹红.一种矿井全局精确测风的传感器优化布置方法[P].中国专利:ZL201710330660.X:2018-03-20.
[21] 卢新明,尹红.一种矿井通风系统状态识别方法[P].中国专利:ZL20140182176.3:2015-07-15.
[22] 卢新明,尹红.一种矿井通风系统风道参数的多态自动识别方法[P].中国专利:ZL201410542762.4:2015-05-27.
[23] 卢新明,尹红.矿井需风量的全息预测方法[P].中国专利:ZL201611051308.4:2017-11-21.
[24] 卢新明.矿井通风系统的可靠度及其优化[J].山东矿业学院学报,1987(4):29-37.
LU Xinming.Reliability of mine ventilation system and its optimization[J].Journal of of Shandong Mining Institute,1987(4):29-37.
[25] 卢新明.矿井通风网络测定平差新探[J].中国矿业学院学报,1988,17(3):78-84.
LU Xinming.A new approach to the adjustment of measurement of mine ventilation network[J].Journal of China University of Mining & Thenhnology,1988,17(3):78-84.
[26] 卢新明,尹红.一种矿井通风系统全局自动调节控制装置及方法[P].中国专利:ZL201410541885.6:2015-09-30.
[27] 王纪强,宁雅农,李振,等.二维风速风向传感器及系统[P].中国专利:ZL201810232305.3:2019-12-13.
[28] GB/T 34679—2017.智慧矿山信息系统通用技术规范[S].
