我国西北地区煤炭资源储量丰富,是重要的煤炭生产基地。近10余年来,随着西北地区侏罗纪煤炭资源的开采强度和规模的不断扩大,矿井顶板水害问题日益严重。因此,对煤层顶板含水层富水性进行合理有效的预测评价,不仅有利于全面掌握井田范围内顶板含水层区富水性分布情况,做出更加科学的风险预防决策,从而减轻甚至消除矿井突水隐患,而且对地下水资源保护有着重要意义[1-3]。
目前,针对煤层顶板含水层富水性评价方法主要分为3类,即物探法、抽(放)水试验法和多因素综合分析法[4-6]。其中,由于在物探和抽(放)水试验过程中存在工作量大,费用高,且控制范围有限等问题,使多因素综合分析法得到了国内外专家学者的青睐,并开展了大量的研究[7-10]。多因素综合分析法是借助现有的地质、构造、水文地质资料,综合煤层覆岩含水层岩性、构造等富水影响因素,利用一定的评价方法对含水层富水性进行预测分区[11-13]。
目前,含水层富水性预测的综合评价方法主要思路是首先建立富水性影响因素的指标体系,采用层次分析法,主成分分析法、灰色理论法及BP神经网络等方法确定各指标的影响程度(即权重)[14-18]。然而,现有的综合评价方法在评估过程中存在未能很好的解决数据的信息融合、各指标间的相互影响及主观模糊评判等不确定性因素,例如利用层次分析法将含水层富水性视为一个系统,使得定性与定量化评价相结合[14],但在评价过程中主要依靠专家打分进行各指标权重的赋值,主观性较强;主成分分析法有效的消除了样本中冗余的数据信息[15],但在其变量降维的过程中不得不付出使得评价指标值带有模糊性的代价;BP神经网络法为富水性预测问题提供了新的思路[16],对解决内部机制复杂的系统问题提供了参考,但由于机器学习需大量有效样本,当数据量不足时,易造成预测误差,使得评价结果出现较大偏差。
针对上述问题,笔者引入了能够全面客观反应事物确定性和不确定性的集对分析-可变模糊集耦合评价方法,实现了评价指标值与评价标准间关系的反映联系及评价指标值间的有机融合,有效地处理了各指标间的相互作用,从而提高了评估结果的稳定性和可靠性。基于此,笔者从岩性、构造2方面出发,依据实际水文地质条件,选取了4个评价指标,构建了预测评价模型,对金家渠井田主要充水含水层直罗组含水层富水性进行了预测分区,为井田顶板水害的防治提供了科学的依据。
1 研究区地质概况
研究区位于宁夏回族自治区灵武市盐池县宁东区南部(面积约为26.8 km2)。区内含煤地层全部被新生界地层所覆盖,属隐伏式煤田。区内地层由老至新发育有三叠系上统上田组(T3s),侏罗系中统延安组(J2y),直罗组(J2z),侏罗系上统安定组(J3a),古近系渐新统清水营组(E3q)和第四系(Qh)。井田内含煤地层为侏罗系中统延安组,含可采煤层10层(2,3,4,5,6,8,9,11,12和18煤),其中主要可采煤层为2,3,4和18煤层。煤层倾角变化较大,一般在10°~45°,断层附近局部可达45°~65°。
井田地处华北地台、鄂尔多斯盆地西缘褶皱冲断带的南北向逆冲构造带。井田内构造线总体走向为SN向,褶曲、断裂构造较发育。根据勘探和生产实际揭露,区内发现褶皱5条,依次为兔儿场背斜、金家渠背斜、尖儿庄背斜、尖儿庄向斜、杜窑沟背斜;发现断层49条,大型断裂有杜窑沟断层、金家渠断层和马柳断层(图1)。

图1 金家渠井田构造纲要及网格单元划分示意
Fig.1 Structure outline map of Jinjiaqu coal mine and schematic diagram of cell grid division
煤层上覆主要含水层为第四系孔隙潜水含水层、侏罗系中统直罗组砂岩孔隙裂隙承压水含水层和侏罗系中统延安组2~6煤间砂岩孔隙裂隙承压含水层(图2)。通过对研究区地质及水文地质条件分析可知,2煤上距直罗组底部分界线6.58~15.99 m,平均8.76 m。根据“三下”采煤规范[19]和经验公式计算研究区2煤导水裂缝带发育的最大高度为98.70 m,3煤导水裂缝带发育的最大高度为163.80 m,确定2,3煤开采时直接充水含水层为侏罗系中统直罗组砂岩孔隙承压水含水层。结合含隔水层剖面资料可知,导水裂缝带发育高度范围内均为含水层,各剖面垂向上均无连续稳定的隔水层,导水裂缝带一旦延伸到剥蚀面或上方赋水区域,直罗组上段含水层水将存在下渗中、下段的可能,因此经综合考虑,本文将直罗组作为富水性评价的对象,其厚度为96.62~572.77 m,平均厚度约380.81 m,与下伏延安组地层呈假整合接触。

图2 金家渠井田主要含、隔水层示意
Fig.2 Diagram of major aquifers and aquicludes
2 富水性控制因素
砂岩含水层富水性取决于含水层储水空间及其连通性,因此,砂岩的有效孔隙、裂隙发育情况直接影响到含水层富水性。前者受控于沉积及成岩作用,表现为岩石类型、岩层结构、砂岩层厚度等,后者受控于构造作用,表现为褶皱、断裂构造的发育情况。因此,在构造较为复杂的地区,含水层的富水性不仅取决于沉积因素,构造影响也较为明显[20-21],因此需要结合实际的水文地质情况,充分利用富水性的影响因素,建立并优化评价模型,做出合理的评价。
本文在分析井田地质、构造、水文地质资料的基础上,从岩性的角度出发,选取了砂岩等效厚度,砂岩岩性系数,砂泥互层数等3个评价因素,建立了岩性影响指数评价指标;从构造的角度出发,选取了断层交端点密度与断层规模密度2个评价指标对断层进行了定量评价,选取了煤层倾角变异系数评价指标对褶皱进行了定量表示,并利用Surfer软件绘制了各单一富水性因素评价专题图,如图3所示。
2.1 岩性及岩层结构
在含水层富水性评价过程中,岩性评价指标主要是对岩层赋水介质及含隔水性能优劣的评价。为了更加有效的评价富水性,本文综合了砂岩岩性系数(P),砂泥互层数(Nsm)及砂岩等效厚度(Meh)等3个评价因素,建立了岩性影响指数(Lid)。
(1)砂岩岩性系数(P)。砂岩岩性系数(P)是研究区内直罗组粗、中、细砂岩的累计厚度与直罗组整体厚度的比值。该比值越大,说明该区域内岩层砂岩占比越高,富水性越强。
(2)砂泥互层数(Nsm)。砂泥互层数(Nsm)是指直罗组内砂-泥岩互层交替出现的次数,其直接影响着含水层的渗透性,砂泥互层数越多,隔水性能越好。
(3)砂岩等效厚度(Meh)。砂岩厚度作为含水层富水性强弱评价的主要指标之一,其厚度越大富水性越强。本文考虑了粗、中、细砂岩的孔隙度及渗透性,引入了砂岩等效厚度(Meh),将砂岩孔隙度比值作为砂岩厚度换算的比例系数,乘以各类砂岩的真实厚度,计算公式为

图3 砂岩含水层单一富水性因素评价
Fig.3 Single factor evaluation of sandstone water yield zone
Meh=Mc+k1Mm+k2Mf
(1)
式中,Mc,Mm,Mf分别为粗砂岩、中砂岩、细砂岩的真实厚度,m;k1为中砂岩厚度换算等效系数;k2为细砂岩厚度换算等效系数。
按照覆压下岩石孔隙度和渗透率测定方法SY/T 6385—2019标准对研究区直罗组不同粒度砂岩孔隙度进行了测定(表1)。以粗砂岩为基准(约定为1),折算中、细砂岩的等效换算系数。粗砂岩,中砂岩,细砂岩的平均孔隙度分别为17.83%,14.38%,11.04%,计算可得k1=0.8,k2=0.6。
表1 直罗组砂岩孔隙度统计
Table 1 Porosity of different types of sandstones in Zhiluo Formation

岩性样本孔隙度/%第1组第2组第3组第4组平均值/%等效系数粗砂岩19.0016.9116.7218.6717.831.0中砂岩14.9215.2713.7314.8014.680.8细砂岩12.2013.518.0910.3711.040.6
上述3个指标中,砂岩岩性系数(P)和砂岩等效厚度与富水性存在正相关关系,砂泥互层数与富水性有负相关关系。综合考虑各指标的影响,建立了岩性影响指数(Lid),即
![]()
(2)
岩性影响指数(Lid)作为定量化评价岩性对含水层富水性的影响指标,建立了各影响因素之间的关系,便于分析计算。
2.2 构 造
地质构造对含水层富水性具有较为明显的控制作用[21],其影响可用断层、褶皱等构造控制的裂隙发育程度及导水通道等因素来表现。裂隙控制着地下水运动的方向、距离及赋水空间的大小。
2.2.1 断 层
从岩体完整性、断层的规模及断层的复杂程度3个方面出发,选取了断层交端点密度(DF)、断层规模密度(DS)2个评价指标,对断层进行定量评价。
采用200 m×200 m的正方形将研究区划分为867个网格单元,对下列指标进行统计,网格划分如图1所示。
(1)断层交端点密度(DF)。断层交端点密度指单位面积内断层交点数和端点数的总个数,计算过程见式(3)。由于断层交端点处岩体完整性差,因此单位面积内断层交、端点数越多,其砂岩渗透率和导水性能越好,富水性越好。
![]()
(3)
式中,DF为网格单元内断层交端点密度,个/km2;NI和NE分别为网格单元内断层的交点数和端点数,个;S为单位网格单元的面积,取0.04 km2。
(2)断层规模密度(DS)。断层规模密度指单位面积内所有断层的延展长度与其落差的乘积之和,计算过程见式(4)。该指标综合考虑了断层落差、断层延展长度,可以较全面地反映断层的规模。断层规模越大,发育越密集的地区,富水性越好。
![]()
(4)
式中,DS为断层规模密度;n为网格单元内断层的总条数;Hi为网格单元内第i条断层的落差,m;li为网格单元内第i条断层的延展长度,m。
2.2.2 褶 皱
采用煤层倾角变异系数(C)表征褶皱构造的复杂程度。当水平岩层的连续性和完整性遭到破坏时,煤层的倾角和产状会发生相应的变化,因此用煤层倾角的变化来表示构造的变化程度和分布情况。煤层倾角变异系数指单元内煤层底板倾角的标准差与倾角平均值的比值,在大量矿井地质工作的实践中证明,煤层倾角变异系数是反映构造,尤其是褶皱和小型断层发育情况的一个非常有效的指标,该指标值越大,表明构造越复杂。
![]()
(5)
式中,C为网格单元内煤层倾角变异系数值;m为网格单元内取值点的总个数;αi为煤层倾角,![]() 为m个煤层倾角的平均值,(°)。
为m个煤层倾角的平均值,(°)。
3 集对分析-可变模糊集耦合评价模型
3.1 集对分析
集对分析(Set Pair Analysis)是由赵克勤[22]提出的一种处理模糊、随机、中介和信息不完全所致不确定性的系统分析方法,其特点是对客观存在的种种不确定性给予评价,把不确定性与确定性作为1个同一度、差异度、对立度(简称“同、异、反”)系统,利用联系度进行辩证分析和数学处理。目前已成为处理不确定性系统问题中的研究热点,在水资源、水环境、物理与数学等众多领域得到了广泛的应用[23-24]。
在一定的问题背景下,建立集对A=(Q,W),A是由具有一定联系度的2个集合Q和W组成。2个集合之间的联系度通过定与不确定系统中同、异、反3个方面的特性的定量分析描述。联系度μ的表达式为
![]()
(6)
式中,S为两集合同一特性数;N为集合的总特性数;S/N为同一度,用a表示;R为对立特性数;R/N为对立度,用c表示;F=N-S-R,F/N为差异度,用b表示;其中a,b,c∈[0,1],且a+b+c=1;i为差异度系数,j为对立度系数。
3.2 可变模糊集理论
陈守煜[25]运用自然辩证法中关于运动的矛盾性原理,在模糊集合的基础上,建立了相对隶属度与相对隶属函数的概念,即可变模糊集合理论。其中相对隶属度和相对差异度作为2个量化指标,是可变模糊集理论的2个核心概念。具体定义为:设论域U上的一个模糊概念A,对于U中的任意元素u,u∈U,在相对隶属函数连续数轴上的任意一点,对具有吸引性质A的相对隶属度表示为μA(u),具有排斥性质Ac的相对隶属度表示为![]() 且
且![]() 定义DA(u)为u对A的相对差异度,其中
定义DA(u)为u对A的相对差异度,其中
![]()
(7)
3.3 集对分析-可变模糊集耦合评价法
本文引用集对分析理论与可变模糊集耦合评价方法,用集对分析的核心参数“联系度”作为可变模糊集的“差异度”,减少了信息的丢失,使评价结果更全面[26-27]。具体流程如图4所示。

图4 集对分析-可变模糊集耦合方法评价流程
Fig.4 Evaluation flow of Set Pair Analysis and Variable Fuzzy Set coupling method
(1)建立评价指标体系及等级标准。将各影响因素指标评价值构成的集合Q和各指标评价标准W构成一个集对A=(Q,W),其中
Q=(q11,q21,…,qm1,q12,q22,…,qn2…q1n,q2n,…,qmn)
W=(X01,X02,…,X0n,X11,X12,…,X1n,…,Xm1,
Xm2,…,Xmn)
式中,qmn为第n个指标下的第m个评价值;Xmn为第n个评价指标对应的评价标准的界限值。
(2)将集对分析中的差异度分为优异和劣异,将对立度细分为优反和劣反,得到多元联系度:
μ=a+(b1+b2)i+(c1+c2)j=
a+b1i++b2i-+c1j++c2j-
(8)
式中,a+b1+b2+c1+c2=1;i+∈[0,1];i-∈[-1,0];j+={0,1};j-=-1。
例如,假设共有5个评价等级,第3等级为最优等级。根据式(8)可知,当指标评价值qn位于第3等级的区范围内时,表明指标评价值具有同一性,此时a=1,b1=b2=c1=c2=0;当指标评价值qn位于相邻等级区间范围内,即第2,4等级内时,指标评价值可分为优异和劣异,趋向优越的一侧视为优异,其值记为b1,且qn越靠近第3评价等级,a越大,b1越小;远离优越的一侧视为劣异,其值记为b2,距离第3等级越远,a越小,b1越大;当指标评价值qn位于相隔等级区间范围内,即第1,5等级内时,指标评价值可分为优反和劣反,此时趋向优越的一侧视为优反,其值记为c1,且qn越靠近第3评价等级,a,b1越大,c1越小;远离优越的一侧视为劣反,其值记为c2,a,b2越小,c2越大。
煤层顶板砂岩含水层富水性评价模型为越小越优型,即指标评价值越小,富水性越弱。建立富水性影响因素指标评价值qn与评价等级k之间的单指标联系度μkn如下。本文结合模型实际情况及对分析理论中差异度系数和对立度系数的均分原则,取i+=0.5,i-=-0.5;同时参考系数特殊取值法,选取j+=0,j-=-1。计算公式为

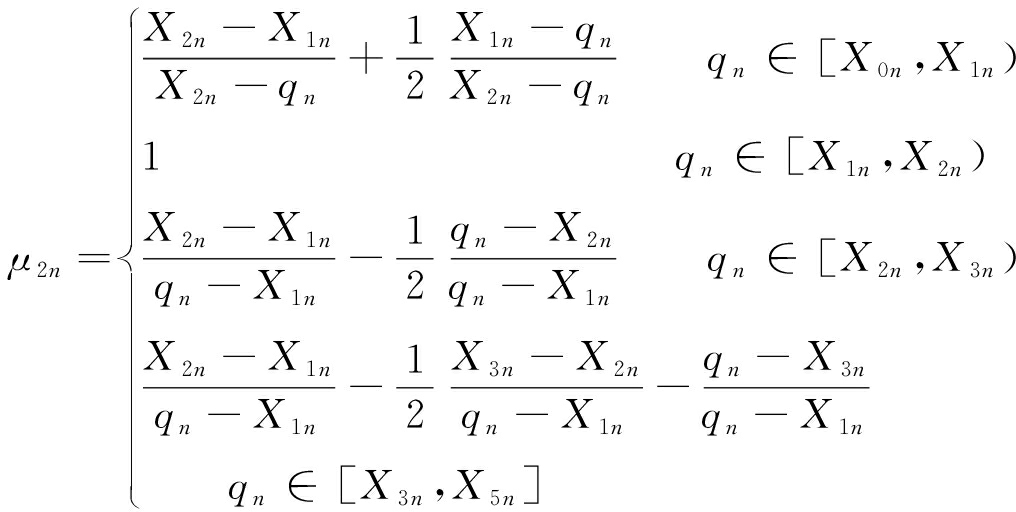

(9)


式中,μkn为第n个评价指标下的评价值与第k评价等级的联系度。
由计算可知,μkn越接近于1,表明指标评价值与评价等级k的一致性越高,两者之间“同”的关系更强,反之亦然。
(3)确定相对隶属度。利用上述已构建的可变模糊集相对差异度,由可变模糊集评价理论可知,对指标评价值隶属于模糊评价等级k的相对隶属度为
![]()
(10)
(4)确定指标权重。本文选用熵权系数法(Entropy Weight Method),对各个指标权重赋值,其基本思路是根据指标变异性的大小来确定客观权重,变异程度越大,熵值越小,权重也就越大。具体步骤如下:
① 为使数据之间更具有可比性及客观性,对各评价指标数据进行标准化处理,本文采用极差标准化公式
![]()
(11)
式中,q′mn为第n个评价指标对应的第m个评价标准的标值化结果值;qnmin,qnmax分别为第n个评价指标下的最小值与最大值。
② 求各指标的信息熵。根据信息论中信息熵的定义,一组数据的熵值为
![]()
(12)
![]()
(13)
式中,Hn为第n个指标的熵值;zmn为第n个指标下第m个项目的指标值的比重;ymn为第n个指标下第m个项目的指标值。
③ 确定各指标权重。
根据信息熵的计算公式,计算出各个指标的信息熵为H1,H2,…,Hk。通过信息熵计算各指标的权重:
![]()
(14)
式中,wn为第n个指标的权重。
(5)计算综合隶属度。

(15)
其中,α为优化准则参数,α=1为最小一乘方准则,α=2为最小二乘方准则;p为距离参数,p=1为海明距离,p=2为欧氏距离。α和p统称为可变模型参数,通常有4种组合:① α=1,p=1;② α=1,p=2;③ α=2,p=1;④ α=2,p=2。
(6)确定级别特征值及评价等级。4种参数组合下可变模糊识别模型之间的联系,是可变模糊识别方法的一个重要特点。对于各个评价指标均可通过可变模型参数的4种不同组合类型,计算得到4组综合隶属度向量,利用式(16),对4组综合隶属度向量进行归一化处理后,即可得到任一评价点下综合隶属度向量Vk:
![]()
(16)
最后,利用综合隶属度向量V与相应评价等级乘积的累加之和,求得4种模型参数下待评价含水层富水级别特征值H,分析级别特征值的稳定性,最终确定含水层富水性的等级。
![]()
(17)
4 金家渠井田直罗组砂岩含水层富水性评价
4.1 指标选取
本文选取了岩性影响指数、断层交端点密度、断层规模密度、煤层倾角变异系数共4个指标进行砂岩富水性预测,构建集对分析-可变模糊集耦合的富水性评价模型,其层次结构模型如图5所示。
4.2 评价指标取值标准
由于目前多因素融合方法确定的富水性等级只有相对意义,还没有通用的或者可供参考的富水性评价等级划分标准,因此笔者根据各项指标因子的物理含义及其对富水性的影响和作用,结合数据区间划分方法,采用了均分区间法对区间阈值进行赋值,各指标按富水性Ⅰ~Ⅴ级进行定量划分,指标越大,富水性相对越好,具体划分标准见表2。

图5 砂岩含水层富水性预测的层次结构模型
Fig.5 Hierarchy model for predicting Sandstone water yield zone of Sandstone Aquifer
表2 富水性评价指标取值标准
Table 2 Assessment Index of water yield zone

指标顺序指标类别评价等级富水性Ⅰ级富水性Ⅱ级富水性Ⅲ级富水性Ⅳ级富水性Ⅴ级1断层规模密度[0,0.001)[0.001,0.76)[0.76,1.52)[1.52,2.28)[2.28,3.04]2断层交端点密度[0,2)[2,4)[4,6)[6,8)[8,15]3煤层倾角变异系数[0,0.000 1)[0.000 1,0.36)[0.36,0.72)[0.72,1.08)[1.08,1.43]4岩性影响指数[0,50)[50,100)[100,150)[150,200)[200,250]
需要说明的是,对于反映构造发育程度的指标,多数网格数值为0,因此将0单独划分为1个区间,其他4个区间采用各指标非零最小值到最大值均分的原则进行划分[28]。
4.3 评价指标权重的确定
关于权重的确定常选取单一方法,其中主观赋权法重视各指标本身的含义,可以体现出决策者对不同指标的重视程度,但客观性较差;而客观赋权法具有较强的数学理论依据,但缺少决策者的参与和对实际情况的考虑。本文遵循客观科学性原则、全面性原则、定量与定性分析相结合的原则,将客观赋权法中的熵权系数法与主观的经验赋值法相结合,确定综合权重[29-31]。
含水层富水性的强弱受岩性和构造的共同影响。在工作面回采的过程中,断层密集区域的涌水量明显增加。由于研究区尚未有完整开采工作面,但与其水文地质条件相似的邻近宁东矿区金凤煤矿一采区3煤层工作面已回采结束,对采区有断层穿过和未有断层穿过且岩性相似的工作面的最大涌水量进行统计,二者最大涌水量分别为225 m3/h和152.1 m3/h。一般认为含水层富水性的强弱与工作面涌水量的大小呈正比关系,故此处岩性类指标和构造类指标的权重值分别是0.6和0.4。
针对构造类各指标利用熵权系数法进行权重的计算,具体评价指标权重值见表3。
表3 直罗组砂岩含水层富水性评价指标权重
Table 3 Weighted Prediction Index of Sandstone water yield zone of Zhiluo Formation

指标断层规模密度断层交端点密度煤层倾角变异系数岩性影响指数权重0.126 20.141 60.132 20.600 0
4.4 富水性评价结果及验证
结合采区钻孔、构造资料,绘制了各因素富水性评价专题图(图3)。在Surfer软件中栅格化后,提取各栅格点处评价值,构建各影响因素指标评价值与指标评价标准集合。
利用式(15)~(17)计算研究区顶板砂岩富水性在4种不同的可变模糊集模型参数下的归一化综合隶属度向量V和含水层富水性级别特征值H,得到4种模型参数下待评价含水层富水性影响等级变动范围,分析级别特征值的稳定性,并求得4种不同模型参数下的含水层富水性级别平均特征值![]() 最后,利用Surfer软件绘制平均特征值
最后,利用Surfer软件绘制平均特征值![]() 等值线图(图6)。由图6可知,富水性评价的平均特征值
等值线图(图6)。由图6可知,富水性评价的平均特征值![]() 主要集中于1~5级中的[2,4]区间。对于
主要集中于1~5级中的[2,4]区间。对于![]() 的数值,属于1~5级中的[2,3]区间,评价等级应为第3级,即富水性Ⅲ级;对于
的数值,属于1~5级中的[2,3]区间,评价等级应为第3级,即富水性Ⅲ级;对于![]() 的数值,属于1~5级中的[3,4]区间,评价等级应为第4级,即富水性Ⅳ级。
的数值,属于1~5级中的[3,4]区间,评价等级应为第4级,即富水性Ⅳ级。
根据《煤矿防治水细则》,含水层富水性依据钻孔单位涌水量q值进行等级划分,分为弱、中等、强和极强4个等级。研究区侏罗系直罗组砂岩含水层抽水试验钻孔Z1,Z7,Z8-1单位涌水量分别为0.069 6,0.067 8,0.021 1 L/(s·m),均小于0.1 L/(s·m),这3个钻孔均位于特征值2≤H<3的富水性Ⅲ级区域,因此富水性Ⅲ级区域对应弱富水区;Z6钻孔单位涌水量为0.149 L/(s·m),介于0.1~1 L/(s·m),110301工作面最大涌水量为590.4 m3/h,介于300~1 200 m3/h,目前正常涌水量为335.33 m3/h,介于180~600 m3/h,因此特征值3≤H<4的富水性Ⅳ级区域对应中等富水区。
富水性评价结果表明,研究区整体富水性较弱,大部分区域为富水性弱区,位于南部、东部及西部;富水性中等区域主要位于研究区中北部。
4.5 方法比较
集对分析-可变模糊集理论方法为一种综合集成的评价方法,其权重的确定建立在现有的综合评价方法之上。例如,本文所构建的基于集对分析-可变模糊集耦合法的直罗组含水层富水评价模型是建立在利用熵权系数法确定评价指标权重的基础之上。
为分析说明基于集对分析-可变模糊集耦合法的富水性评价模型与以往仅基于多元信息融合评价方法的富水性评价模型的不同之处,本文依据前文熵权系数法计算的权重,建立了基于熵权系数法的多源信息融合综合评价模型如下
E=0.132 2C+0.126 2DS+0.141 6DF+0.6Lid
(18)
式中,E为富水性指数;C,DF,DS,Lid为各指标标准化值。
根据式(20)计算研究区各网格单元的富水性指数,结合富水性指数频数直方图,确定了富水性分区阈值为0.2。利用已知单位涌水量的钻孔和工作面涌水情况,将富水性评价指数[0,0.2]定为弱富水性区,[0.2,1]为中等富水性区,并绘制了研究区直罗组砂岩含水层富水性指数等值线图如图7所示。由2种方法所得富水性评价结果对比可知,本文所建模型的评价结果与基于熵权系数法的多源信息融合综合评价模型结果有些差异。

图6 基于集对分析-可变模糊集耦合的研究区富水性分区
Fig.6 Zonation of water abundance based on Set Pair Analysis-Variable Fuzzy Set coupling method

图7 基于熵权系数法的多源信息融合富水性分区
Fig.7 Zonation of water abundance based on the Entropy Weight Method
为进一步对集对分析-可变模糊集耦合评价模型与基于熵权系数法的多源信息融合综合评价模型进行对比分析,本文将P1作为对照点,具体评价指标值见表4。
表4 P1点处富水性评价指标值
Table 4 Assessment index value of water yield in P1

评价指标名称断层规模密度断层交端点密度煤层倾角变异系数岩性影响指数指标值1.01200.010 176.872
由图6,7可知,P1点处集对分析-可变模糊集耦合评价模型评价结果为弱富水性区,基于熵权系数法的富水性评价模型评价结果为中等富水性区,造成此现象的原因主要有:
(1)在基于熵权法的富水性评价模型中,主要通过客观的计算各指标权重从而做出预测,但该方法忽视了评价指标与评价等级的互相影响,认为各指标独立,呈现出线性变化,即评价指标值越大,富水性越好。而分析表5中的相对隶属度结果可知,P1点处的各个指标值并非均呈现出明显的线性关系,其主要原因是考虑了各指标值间的影响,避免了部分评价指标值因较小而被忽略的可能性。
表5 P1位置处富水性评价指标相对隶属度计算结果
Table 5 Calculation results of the relative membership degree of water yield assessment index in P1

指标等级断层规模密度断层交端点密度煤层倾角变异系数岩性影响指数Ⅰ级1.001.000.261.00Ⅱ级1.000.881.000.88Ⅲ级0.870.750.880.76Ⅳ级0.750.690.750.69Ⅴ级0.690.770.690.65
(2)在集对分析-可变模糊集耦合评价中,利用4种参数组合计算了4类模型下的综合隶属度向量(表6),能较好的解决不易区分的相邻的两类差异和因数学模型而产生的误差,使得评价结果更为客观。
表6 P1位置处综合隶属度向量及富水性级别特征值计算结果
Table 6 Comprehensive membership vector and level eigenvalue calculation results in P1

模型参数归一化后的综合隶属度向量富水性级别特征值Hα=1,p=1[0.222 4,0.230 2,0.199 4,0.178 5,0.169 5]2.842 5(弱富水性区)α=1,p=2[0.225 8,0.228 3,0.197 8,0.179 1,0.168 9]2.895 2(弱富水性区)α=2,p=1[0.214 8,0.216 6,0.204 5,0.187 1,0.177 1]2.837 0(弱富水性区)α=2,p=2[0.217 1,0.217 8,0.203 5,0.186 8,0.174 8]2.884 3(弱富水性区)
5 结 论
(1)砂岩含水层富水性取决于含水层储水空间及其连通性,受控于沉积成岩作用和构造发育程度。研究区地处鄂尔多斯盆地西缘,构造相对复杂。在分析井田地质、构造、水文地质资料的基础上,从沉积控水角度,选取了砂岩岩性系数,砂泥互层数及砂岩等效厚度等评价因素,建立了岩性影响指数评价指标;从构造控水角度,选取了断层交端点密度、断层规模密度和煤层倾角变异系数3个评价指标,构建了砂岩含水层富水性评价的指标体系。
(2)基于研究区砂岩含水层岩性及构造特征,运用集对分析-可变模糊集耦合评价法建立顶板砂岩富水性评价模型,对直罗组砂岩含水层富水性进行了预测。划分了富水性相对等级及其分区,并与含水层抽水试验结果进行对比,确定出各分区富水性等级。富水性评价结果表明,研究区整体富水性较弱,大部分区域为富水性弱区,位于南部、东部及西部;富水性中等区域主要位于研究区中北部。
(3)对比分析表明,相较基于熵权系数法的多源信息融合评价法,基于集对分析-可变模糊集评价法所构建的含水层富水性评价模型能较好的处理数据与等级及数据间的相互影响和融合问题,评价结果更具科学性。
[1] 武强.我国矿井水防控与资源化利用的研究进展、问题和展望[J].煤炭学报,2014,39(5):795-805.
WU Qiang.Progress,problems and prospects of prevention and control technology of mine water and reutilization in China[J].Journal of China Coal Society,2014,39(5):795-805.
[2] 孙亚军,陈歌,徐智敏,等.我国煤矿区水环境现状及矿井水处理利用研究进展[J].煤炭学报,2020,45(1):304-316.
SUN Yajun,CHEN Ge,XU Zhimin,et al.Research progress of water environment,treatment and utilization in coal mining areas of China[J].Journal of China Coal Society,2020,45(1):304-316.
[3] 彭苏萍,毕银丽.黄河流域煤矿区生态环境修复关键技术与战略思考[J].煤炭学报,2020,45(4):1211-1221.
PENG Suping,BI Yinli.Strategic consideration and core technology about environmental ecological restoration in coal mine areas in the Yellow River basin of China[J].Journal of China Coal Society,2020,45(4):1211-1221.
[4] 施龙青,翟培合,魏久传,等.三维高密度电法技术在岩层富水性探测中的应用[J].山东科技大学学报(自然科学版),2008,27(6):1-4.
SHI Longqing,ZHAI Peihe,WEI Jiuchuan,et al.Application of 3D high density electrical technique in detecting the water enrichment of strata[J].Journal of Shandong University of Science and Technology(Natural Science),2008,27(6):1-4.
[5] 张强,雍自春,龙自阳,等.槽波地震探测技术在金家渠煤矿首采工作面断层探查中的应用[J].煤田地质与勘探,2018,46(S1):33-36.
ZHANG Qiang,YONG Zichun,LONG Ziyang,et al.Application of channel wave seismic technique in detection of faults in the first working of Jinjiaqu Colliery[J].Coal Geology & Exploration,2018,46(S1):33-36.
[6] 邱梅,施龙青,滕超,等.基于灰色关联-FDAHP法与物探成果相结合的奥灰富水性评价[J].岩石力学与工程学报,2016,35(S1):3203-3213.
QIU Mei,SHI Longqing,TENG Chao,et al.Water-richness evaluation of Ordovician limestone based on grey correlation analysis FDAHP and geophysical exploration[J].Chinese Journal of Rock Mechanics and Engineering,2016,35(S1):3203-3213.
[7] YIN Huiyong,SHI Yongli,NIU Huigong,et al.A GIS-based model of potential groundwater yield zonation for a sandstone aquifer in the Juye Coalfield,Shangdong,China[J].Journal of Hydrology,2018,557:434-447.
[8] 尹会永,魏久传,刘同彬,等.基于多源信息复合的煤层底板突水评价[J].山东科技大学学报(自然科学版),2008,27(2):6-9.
YIN Huiyong,WEI Jiuchuan,LIU Tongbin,et al.Evaluation of water inrush in seam floor based on multi-originated information complex[J].Journal of Shandong University of Science and Technology(Natural Science),2008,27(2):6-9.
[9] 曹庆奎,赵斐.基于模糊-支持向量机的煤层底板突水危险性评价[J].煤炭学报,2011,36(4):633-637.
CAO Qingkui,ZHAO Fei.Risk evaluation of water inrush from coal floor based on fuzzy support vector machine[J].Journal of China Coal Society,2011,36(4):633-637.
[10] 石守桥,魏久传,尹会永,等.济三煤矿煤层顶板砂岩含水层富水性预测[J].煤田地质与勘探,2017,45(5):104-108.
SHI Shouqiao,WEI Jiuchuan,YIN Huiyong,et al.Forecasting of water abundance of coal roof sandstone aquifer in Jining No.3 mine[J].Coal Geology & Exploration,2017,45(5):104-108.
[11] 黎良杰,钱鸣高,李树刚.断层突水机理分析[J].煤炭学报,1996,21(2):119-123.
LI Liangjie,QIAN Minggao,LI Shugang.Mechanism of water inrush through fault[J].Journal of China Coal Society,1996,21(2):119-123.
[12] 徐凤银,龙荣生,夏玉成,等.矿井地质构造定量评价及其预测[J].煤炭学报,1991,16(4):95-104.
XU Fengyin,LONG Rongsheng,XIA Yucheng,et al.Quantitative assessment and prediction of geological structures in coal mine[J].Journal of China Coal Society,1991,16(4):95-104.
[13] 韩德品,李丹,石亚丁,等.断层分层信息维及其在深部煤炭开采地质条件预测中的应用[J].煤炭学报,2010,35(8):1323-1330.
HAN Dengpin,LI Dan,SHI Yading,et al.Application of fault’s information dimensions among different coal seams in the prediction of deep coal resources exploitation[J].Journal of China Coal Society,2010,35(8):1323-1330.
[14] 王炳强,沈智慧,白喜庆,等.层次分析法(AHP)在矿山环境地质评价中的应用[J].中国煤田地质,2007,19(S2):57-59,76.
WANG Bingqiang,SHEN Zhihui,BAI Xiqing,et al.Application of AHP in mine environmental geological evaluation[J].Coal geology of China,2007,19(S2):57-59,76.
[15] 王颖,韩进,高卫富.基于主成分分析法的奥灰富水性评价[J].中国科技论文,2017,12(9):1011-1014.
WANG Ying,HAN Jin,GAO Weifu.Water-richness evaluation of ordovican limestone based on principal component analysis[J].China Sciencepaper,2017,12(9):1011-1014.
[16] 宫厚健,刘守强,曾一凡.基于BP神经网络的含水层富水性评价研究[J].煤炭技术,2018,37(9):181-182.
GONG Houjian,LIU Shouqiang,ZENG Yifan.evaluation research on water-richness of aquifer based on BP artificial neural network[J].Coal Technology,2018,37(9):181-182.
[17] FAN Limin,MA Liqiang,YU Yihe,et al.Water-conserving mining influencing factors identification and weight determination in northwest China[J].International Journal of Coal Science & Technology,2019,6(1):95-101.
[18] ONIFADE M,GENC B.Spontaneous combustion liability of coal and coal-shale:A review of prediction methods[J].International Journal of Coal Science & Technology,2019,6(2):151-168.
[19] 国家煤炭工业局.建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规程[S].北京:煤炭工业出版社,2000.
[20] 杨会峰,张翼龙,孟瑞芳.河套盆地构造控水研究及地下水系统划分[J].干旱区资源与环境,2017,31(3):177-184.
YANG Huifeng,ZHANG Yilong,MENG Ruifang.Study on water controlling mechanism of structures and dividing result of groundwater system in Hetao Basin,Inner Mongolia[J].Journal of Arid Land Resources and Environment,2017,31(3):177-184.
[21] 贺江辉.淮南煤田北部矿区构造控水机理研究[D].淮南:安徽理工大学,2015.
HE Jianghui.Study of structural control mechanism on groundwater in the north mining area of Huainan coal field[D].Huainan:Anhui University of Science and Technology,2015.
[22] 赵克勤.集对分析及其初步应用[M].杭州:浙江科学技术出版社,2000.
[23] 孟宪萌,胡和平.基于熵权的集对分析模型在水质综合评价中的应用[J].水利学报,2009,40(3):257-262.
MENG Xianmeng,HU Heping.Application of set pair analysis model based on entropy weight to comprehensive evaluation of water quality[J].Journal of Hydraulic Engineering,2009,40(3):257-262.
[24] 邱林,唐红强,陈海涛,等.集对分析法在地下水水质评价中的应用[J].节水灌溉,2007,32(1):13-15.
QIU Lin,TANG Hongqiang,CHEN Haitao,et al..Application of set pair analysis method in the evaluation of groundwater quality[J].Water Saving Irrigation,2007,32(1):13-15.
[25] 陈守煜.可变模糊集理论与模型及其应用[M].大连:大连理工大学出版社,2009.
[26] 李宗坤,李巍,葛巍,等.基于集对分析-可变模糊集耦合方法的溃坝环境影响评价[J].天津大学学报:自然科学与工程技术版,2019,52(3):49-56.
LI Zongkun,LI Wei,GE Wei,et al.Dam breach environmental impact evaluation based on set pair analysis-variable fuzzy set coupling model[J].Journal of Tianjin University(Science and Technology),2019,52(3):49-56.
[27] 吴开亚,金菊良,周玉良,等.流域水资源安全评价的集对分析与可变模糊集耦合模型[J].四川大学学报:工程科学版,2008,40(3):6-12.
WU Kaiya,JIN Juliang,ZHOU Yuliang,et al.Set pair analysis-variable fuzzy set assessment model for watershed water resources security[J].Journal of Sichuan University(Engineering Science Edition),2008,40(3):6-12.
[28] 陈秉正,韩春鹏.归纳式学习中连续型数据的区间划分问题[J].系统工程理论与实践,2001,21(4):1-7.
CHEN Bingzheng,HAN Chunpeng.Discretization for inductive learning from continuous sample data[J].Systems Engineering-Theory & Practice,2001,21(4):1-7.
[29] 魏久传,赵智超,谢道雷,等.基于岩性及结构特征的砂岩含水层富水性评价[J].山东科技大学学报(自然科学版),2020,39(3):13-23.
WEI Jiuchuan,ZHAO Zhichao,XIE Daolei,et al.Water-abundance evaluation of sandstone aquifer based on lithologic and structural characteristics[J].Journal of Shandong University of Science and Technology(Natural Science),2020,39(3):13-23.
[30] 侯恩科,纪卓辰,车晓阳,等.基于改进AHP和熵权法耦合的风化基岩富水性预测方法[J].煤炭学报,2019,44(10):3164-3173.
HOU Enke,JI Zhuochen,CHE Xiaoyang,et al.Water abundance prediction method of weathered bedrock based on improved AHP and the entropy weight method[J].Journal of China Coal Society,2019,40(10):3164-3173.
[31] 张晓亮.熵权耦合层次分析赋权在煤层底板突水评价中的应用[J].煤田地质与勘探,2017,45(3):91-95.
ZHANG Xiaoliang.Application of entropy weight method and analytic hierarchy process in evaluation of water inrush from coal seam floor[J].Coal Geology & Exploration,2017,45(3):91-95.
