陷落柱是灰岩岩溶空洞垮塌后被上覆煤系地层岩石充填后形成的一种特殊的隐伏垂向柱体状构造,广泛分布于华北型石炭、二叠纪煤田。近年来导水陷落柱导致的煤矿水害事故频发,给安全生产和人民生命财产带来的损失极为惨重。导水陷落柱的地球物理探测方法包括地震勘探、瞬变电磁法、直流电阻率法、大地电磁法、可控源音频大地电磁法、地质雷达等[1-2]。因为单一探查技术存在局限性,现有探测方法针对性不强、精度不高等原因,目前对小尺度大埋深导水陷落柱的精细探测尚难以实现。精细探测要求既要对陷落柱位置进行精确定位,又要对陷落柱富水性进行准确判断。2D或3D地面地震勘探作为煤矿采区采前构造勘探的首选技术手段,中国大部分煤矿都开展过相应探测工作[3]。矿井瞬变电磁法是目前煤矿水害探查最常用和有效的方法之一[4]。地震勘探空间分辨率高,瞬变电磁法对富水性敏感,2种方法的联合反演是实现导水陷落柱精细探测最有前景的方法之一。
联合反演是指在地球物理反演中联合应用多种地球物理观测资料,通过地质体的岩石物性和几何参数之间的相互关系共同反演得到同一地下地质-地球物理模型,多种类型的数据在反演中基于同一个目标函数和同一个计算过程[5]。因为一种方法观测数据的零空间可由另一种方法观测数据解出,并且不同类型观测数据受到的干扰因素不同,所以联合反演能够实现各种方法的优势互补,减少多解性,提高探测精度和分辨率[6-7]。联合反演根据是否基于相同地球物理场可以分为两大类,基于相同物性的联合反演和基于不同物性的联合反演。基于相同物性的联合反演主要包括不同电磁法观测数据的联合反演[8-9],以及不同地震方法之间的联合反演[10-11],而基于不同物性的联合反演又可以分为岩石物理法和几何结构法。岩石物理法基于物性参数之间的物理表达式或经验关系式(如加德纳公式和阿尔奇公式),几何结构法基于各类模型间存在的共同空间分布特征。在导水陷落柱探测中,电阻率主要受富水性控制,而富水性对岩层弹性参数影响较弱,所以弹性参数和电阻率参数之间难以存在惟一确定的对应关系,岩石物理法不适用于导水陷落柱探测。因为电阻率所反映的富水区域与陷落柱在几何形态上具有一致性,所以几何结构法在导水陷落柱探测方面具有一定的合理性。GALLARDO和MEJU在2003年提出了交叉梯度法[12],该方法是一种灵活有效的基于几何结构法的联合反演方法[13-14],所以本文采用交叉梯度联合反演方法进行陷落柱联合反演。
目前联合反演方法在矿井水害探测方面的相关研究和应用较少,并且在实现导水陷落柱精细探测方面传统的联合反演方法存在一定局限性。首先,在传统的联合反演方法中需要同时考虑多种方法的正演计算,为了控制计算成本,地震部分通常采用基于走时的初至波、反射波或透射波层析成像[15-17],非地震部分通常采用直流电阻率法、大地电磁法、可控源大地电磁法、磁法勘探和重力勘探等。以上方法虽然正演计算时间较少,但分辨率或探测深度相对较低,所以传统联合反演方法主要应用于大尺度目标体探测或浅地表成像,而导水陷落柱通常尺度小埋深大,传统联合反演方法难以满足探测要求,需进行地震多次覆盖反射波和矿井TEM等高精度方法的联合反演方法研究;其次,目前的联合反演方法主要应用于地面半空间探测,随着开采深度的增加以及下组煤的大规模开发,地面探测方法在探测精度和分辨率方面已经难以满足探测要求,矿井TEM为目前最常用和有效的方法之一,但受体积效应影响空间分辨率较低,所以有必要进行井下全空间条件下的联合反演方法研究。为了解决以上问题,实现导水陷落柱的精细探测,笔者提出基于矿井TEM和地震的单向交叉梯度联合反演方法,并通过理论模型对联合反演效果进行验证。
1 基于矿井TEM与地震波阻抗的单向交叉梯度联合反演算法
1.1 基于镜像模型的矿井Pseudo-2D TEM反演算法
井下全空间条件下瞬变电磁法存在双向探测问题,瞬变电磁场对顶板和底板方向的异常具有不可分性,所以直接采用全空间模型进行反演是不稳定的。在反演结果中巷道底板方向的异常可能反演到顶板方向,顶板方向的异常可能反演到底板方向。目前常规反演中全空间响应主要由半空间响应乘以全空间响应系数得到,用半空间模型来反映全空间地质情况必然存在一定的局限性。
针对全空间瞬变电磁反演问题,李飞等(2014)提出了基于镜像模型的1D瞬变电磁场全空间反演方法,并通过理论模型反演试算和工程实例证明了该方法的稳定性和有效性[18],将其拓展到2D情况。图1为基于镜像模型的全空间1D TEM模型示意,其中第1层中间位置为巷道位置,模型关于巷道镜像对称。ρ1,ρ2,…,ρnm为第1层到第nm层的电阻率,h1,h2,…,hnm为第1层到第nm层的厚度,第nm层的厚度无限大。为了方便进行Pseudo-2D反演计算,将第1层到第nm-1层的厚度设置为固定值,全空间1D镜像模型参数可以表示为
m=[ρ1,ρ2,…,ρnm]
(1)
观测数据表示为
d=[d1,d2,…,dnd]
(2)
定义f1D为全空间1D TEM正演算子,则基于镜像模型的1D全空间TEM正演公式为
d=f1D(m)
(3)
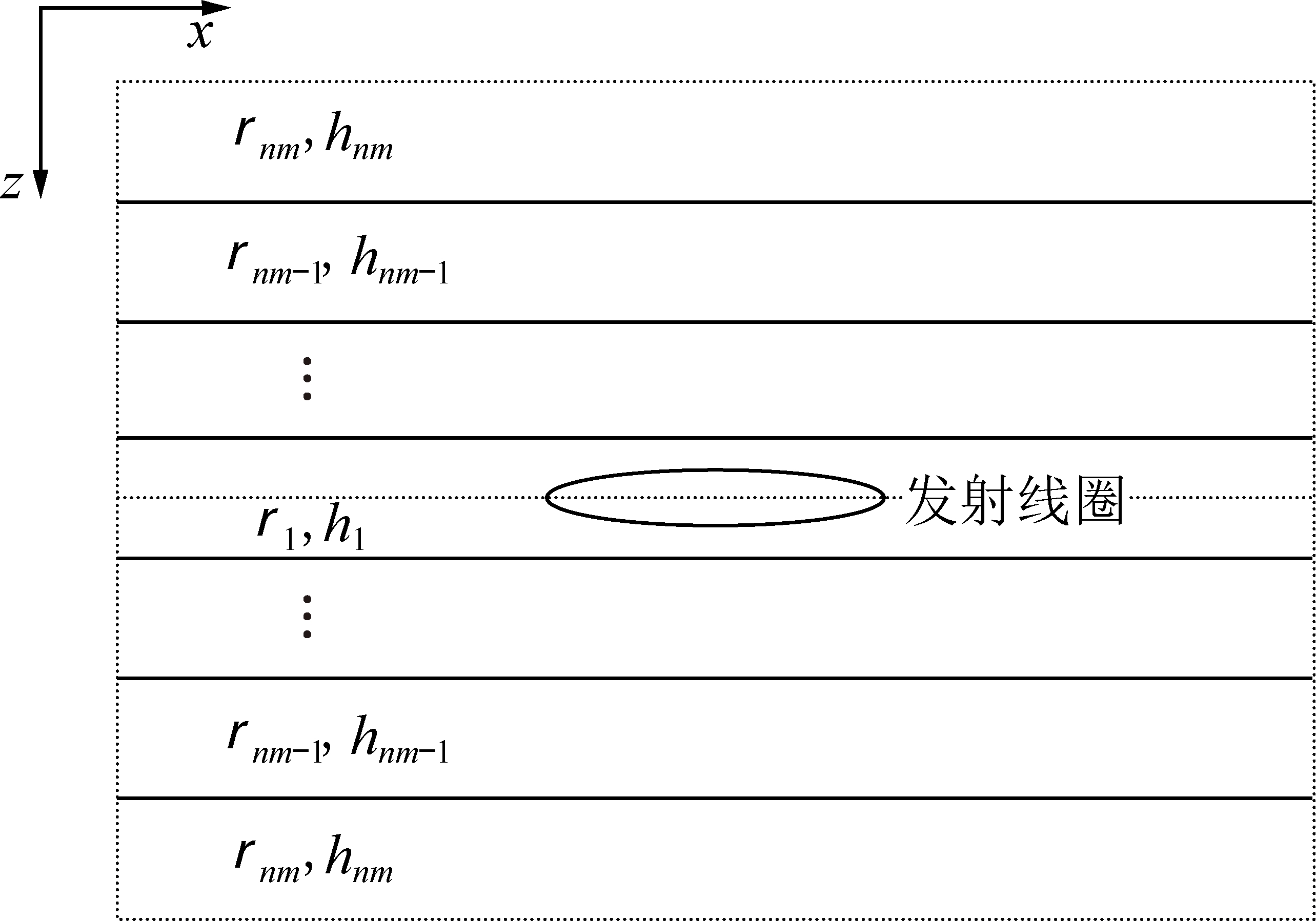
图1 基于镜像模型的全空间1D TEM模型示意
Fig.1 Model parameters in 1D whole space TEM inversion using mirror model
Pseudo-2D反演方法基于1D正演程序和2D电阻率模型,多位学者对此进行了研究。如SCHULTZ和RUPPEL(2005)开展了拟二维大地电磁反演算法研究[19],AUKEN和CHRISTIANSEN(2004)进行了拟二维电阻率法反演[20],SCHAMPER等(2012)提出了拟二维频率域电磁反演方法[21],OGUNBO(2015)等开展了拟二维TEM反演方法研究[22]。在以上研究中,拟二维反演方法均取得了良好的效果。基于镜像模型的Pseudo-2D TEM反演模型参数可以表示为
![]()
(4)
式中,m1,m2,…,mq为每个测点的层状镜像模型参数;q为测点总数。
基于镜像模型的Pseudo-2D TEM正演公式可以表示为
f(m)=[f1D(m1)T,f1D(m2)T,…,f1D(mq)T]
(5)
其中,f1D(m1)T,f1D(m2)T,…,f1D(mq)T为1D正演公式,全空间1D TEM正演算法见文献[23-24]。
Pseudo-2D TEM反演通过在x方向和z方向引入粗糙度矩阵将不同测点的1D模型联系起来,并在同一目标函数中考虑所有测点的观测数据:
Φ(m)=‖d-f(m)‖2+ωx‖Lxm‖2+
ωz‖Lzm‖2
(6)
式中,‖d-f(m)‖2为数据拟合项;‖Lxm‖2为x方向模型光滑项;‖Lzm‖2为z方向模型光滑项;ωx和ωz为加权算子。
基于最小二乘算法对式(6)求解可得
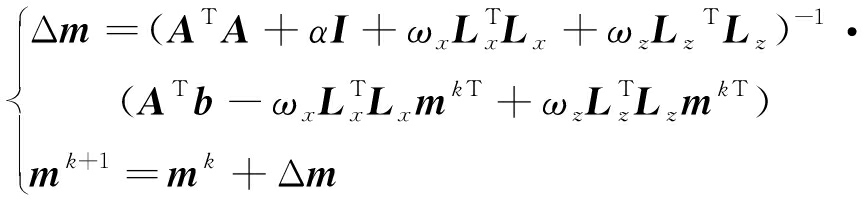
(7)
式中,Δm为第k次迭代的模型更新量;A为雅克比矩阵;I为单位矩阵;Lx和Lz为粗糙度矩阵;mk为第k次迭代的模型参数,mk+1为第k+1次迭代的模型参数;α为阻尼因子;ωx和ωz为加权算子。
基于交叉梯度的联合反演算法要求反演模型至少是2D的,基于镜像模型的矿井Pseudo-2D TEM反演算法实现了全空间2D TEM反演计算。同时,相对于传统2D TEM反演算法,基于镜像模型的矿井Pseudo-2D TEM反演算法可以大大节省计算时间,为联合反演建立了基础。
1.2 单向交叉梯度联合反演算法
传统基于交叉梯度联合反演算法目标函数为
Φ(mr,ms)=ωr‖dr-f(mr)‖2+ωs‖ds-
f(ms)‖2+ωxr‖Lxmr‖2+ωzr‖Lzmr‖2+
ωxs‖Lxms‖2+ωzs‖Lzms‖2+ωt‖t(mr,ms)‖2
(8)
式中,mr为电阻率模型参数;ms为地震模型参数;‖dr-f(mr)‖2为TEM数据拟合残差;‖ds-f(ms)‖2为地震数据拟合残差;‖Lxmr‖2为TEM模型在x方向的模型光滑项;‖Lzmr‖2为TEM模型在z方向的模型光滑项;‖Lxms‖2为地震模型在x方向的模型光滑项;‖Lzms‖2为地震在z方向的模型光滑项;‖t(mr,ms)‖2为交叉梯度项;ωr,ωs,ωxr,ωzr,ωxs,ωzs和ωt为各项的加权算子,ωr+ωs=1。
由式(8)可见,传统联合反演算法中同时包含了电法正演f(mr)和地震正演f(ms),所以需要大量的计算时间。为了控制计算成本,地震部分通常采用基于走时的初至波、反射波或透射波层析成像。然而导水陷落柱通常尺度小(最小可为几米),埋深大(几百米),基于走时的地震层析成像方法难以满足精度和分辨率要求。地震多次覆盖反射波方法探测精度和分辨率高,但正演计算成本高,难以适用传统联合反演算法。为了在联合反演算法中应用地震多次覆盖反射波数据,提出单向交叉梯度联合反演算法,在联合反演算法中去掉地震的正演过程f(ms),只在交叉梯度项中保留地震波阻抗模型参数。单向交叉梯度联合反演目标函数为
Φ(mr,m0s)=‖dr-f(mr)‖2+ωx‖Lxmr‖2+
ωz‖Lzmr‖2+ωt‖t(mr,m0s)‖2
(9)
式中,m0s为地震波阻抗模型参数;‖t(mr,m0s)‖2为交叉梯度项,交叉梯度项为
![]()
(10)
式中,![]() 为第k次迭代的电阻率模型参数;B为第k次迭代交叉梯度项tk的偏导数矩阵。
为第k次迭代的电阻率模型参数;B为第k次迭代交叉梯度项tk的偏导数矩阵。
因为在联合反演中,地震方法反演结果只对TEM方法反演过程进行了交叉梯度约束,而TEM反演结果不对地震方法反演过程进行交叉梯度约束,交叉梯度函数中m0s是一直不变的,所以称为单向交叉梯度联合反演算法。因为联合反演算法中不涉及地震反演过程,所以地震波阻抗反演可以通过商业软件完成。
基于最小二乘算法,可以得到式(9)的解为
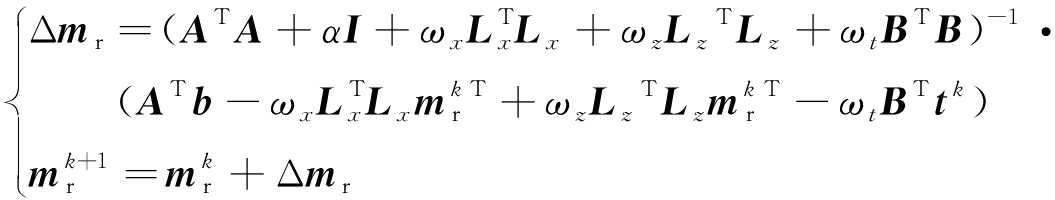
(11)
式中,Δmr为第k次迭代的模型更新量;A为雅克比矩阵;I为单位矩阵;Lx和Lz为粗糙度矩阵;![]() 为第k次迭代的模型参数;
为第k次迭代的模型参数;![]() 为第k+1次迭代的模型参数。
为第k+1次迭代的模型参数。
1.3 联合反演模型网格设置与地震波阻抗模型预处理
地震波阻抗反演模型和矿井TEM反演模型具有不同的特点。地震勘探范围相对较大,波阻抗反演模型分辨率相对较高,模型网格相对较小;矿井TEM探测范围相对较小,受体积效应影响,空间分辨率相对较低,模型网格相对较大。为了实现联合反演计算,选取探测方向TEM模型和地震模型的重叠区域作为联合反演区域。图2为进行底板水害探测时模型网格设置示意,黑色网格为地震波阻抗模型网格,蓝色网格为矿井TEM模型网格,联合反演区域为图中灰色部分。联合反演计算时只应用在联合反演区域内的地震波阻抗模型,TEM模型为关于巷道对称的镜像全空间模型。

图2 联合反演模型网格设置示意
Fig.2 Model grids of joint inversion
因为波阻抗模型网格较小,TEM模型网格较大,为了方便进行联合反演计算,首先需要进行两者之间的匹配转换。采用插值方法可以将原始波阻抗模型转换为与TEM模型具有相同网格大小的波阻抗模型(图3)。本文插值方法采用双三次插值,双三次插值算法原理见文献[25]。具体可以采用Matlab软件进行计算,代码为
m2=imresize(m1,[nx,nz],′bicubic′)
(12)
其中,m1为转换前模型;m2为转换后的模型;nx为转换后在x方向的网格数;nz为转换后在z方向的网格数;′bicubic′代表采用双三次插值方法。

图3 地震波阻抗模型插值转换示意
Fig.3 Interpolation of seismic impedance model
原始波阻抗模型采用双三次插值后,网格大小与TEM网格大小一致,理论上可以直接用于联合反演计算。但大量模拟试算表明:直接采用转换后的原始波阻抗模型进行联合反演计算效果并不好,分析原因为:① 转换后的原始波阻抗模型中存在大量次要结构变化,这些次要变化主要是由干扰(如绕射波和多次波)和网格的插值转换引入的;② 这些次要的结构变化超出了TEM的分辨率。所以,为了避免交叉梯度约束产生假异常,提高联合反演稳定性,对转换后的波阻抗模型进一步进行聚类分割处理。
聚类分割的作用是按照波阻抗值的大小,将波阻抗模型中的地层和异常构造进行分类,从而忽略地层和构造中的次要变化。本文聚类分割采用K-means算法。K-means算法是经典的基于均值划分的聚类方法,具有简洁和快速的优点,文献[26]给出了具体算法原理。通过Matlab函数库中的“K-means”函数可以实现聚类分割计算。图4为地震波阻抗模型插值转换和聚类分割示意。

图4 地震波阻抗模型插值转换和聚类分割示意
Fig.4 Interpolation and clustering segmentation of seismic impedance model
地震波阻抗模型进行插值转换和聚类分割后,即可进行联合反演计算。联合反演主要流程包括:① 设置联合反演参数,包括模型网格数量Nx和Nz、网格间距Δx和Δz、各项加权算子α,ωx,ωz和ωt等;② 计算矿井TEM全区视电阻率,建立联合反演初始模型;③ 进行地震波阻抗反演计算,并对波阻抗模型进行插值转换和聚类分割处理;④ 基于最小二乘算法进行联合反演迭代计算,当TEM数据拟合残差小于设定值εmin或迭代次数大于设定值nmax时,结束联合反演计算。
2 模型验证
2.1 含导水陷落柱模型
以华北型煤田含导水陷落柱为原型建立地质-地球物理模型。模型概化为5层地层和1个导水陷落柱(图5)。第1层为煤系地层的盖层——第四系地层,深度0~100 m。第2~4层为主要由砂岩、泥岩和煤层组成的煤系地层,深度分别为100~400,400~405和405~500 m,其中400~405 m为煤层。第5层为煤系地层的基底——奥陶系石灰岩,深度500~800 m。陷落柱位于模型的中心,发育于奥陶系灰岩顶界面以下50 m,向上发育至煤层底板以下30 m,深度435~550 m,直径50 m。
根据测井等资料统计,华北型煤田煤系地层中砂岩类岩石电阻率为30~120 Ω·m,煤层的电阻率较高为几欧姆米,灰岩类岩层根据不同的富水情况电阻率为几百到几千欧姆米,泥岩和第4系地层电阻率较低为0~60 Ω·m[27]。综合考虑华北型煤田地层的电性特征,第4系盖层电阻率设置为50 Ω·m,煤层电阻率设置为800 Ω·m,以砂岩和泥岩为主的其他煤系地层电阻率设置为100 Ω·m,奥陶系石灰岩地层具有一定富水性,电阻率设置为200 Ω·m,陷落柱为导水陷落柱,电阻率设置为1 Ω·m。综合考虑华北型煤田地层的弹性参数,设置模型的纵波速度、横波速度和密度[28-29]。含导水陷落柱地质-地球物理模型参数设置见表1。

图5 含导水陷落柱模型
Fig.5 Model with a water conducted karstic collapse column
表1 地质地球物理模型参数
Table 1 Parameters of geological and geophysical model
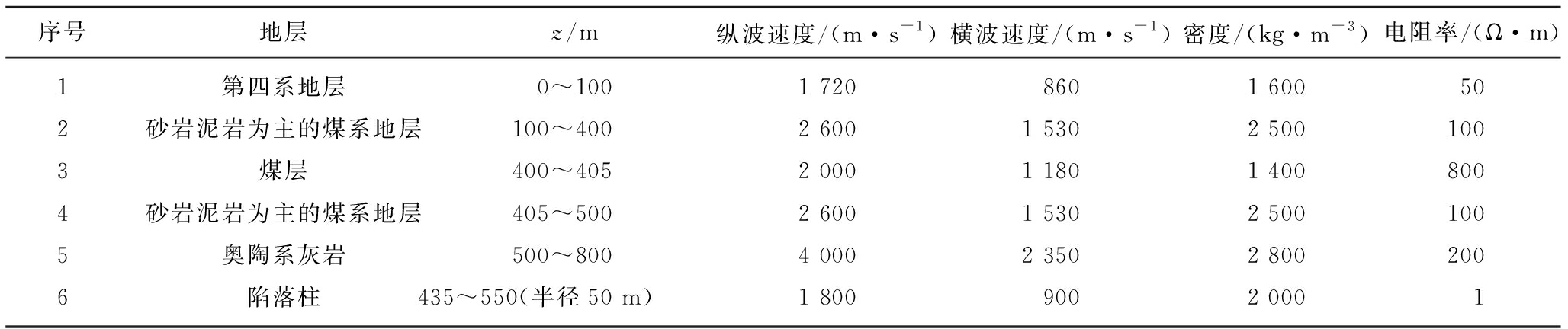
序号地层z/m纵波速度/(m·s-1)横波速度/(m·s-1)密度/(kg·m-3)电阻率/(Ω·m)1第四系地层0~1001 7208601 600502砂岩泥岩为主的煤系地层100~4002 6001 5302 5001003煤层400~4052 0001 1801 4008004砂岩泥岩为主的煤系地层405~5002 6001 5302 5001005奥陶系灰岩500~8004 0002 3502 8002006陷落柱435~550(半径50 m)1 8009002 0001
2.2 观测系统
地震勘探采用反射波多次覆盖观测系统(图6)。测线长度1 000 m,沿x轴方向布置。共设置19个炮点(标记为1~19号炮点),炮间距50 m。共设置101个检波点(标记为0~100号检波点),道间距10 m。每个炮点激发时101个检波点均接收。因为地面地震勘探一般是在煤层开采之前进行的,所以在3D地震正演中煤层为完整煤层。
矿井TEM探测在巷道中进行(图6),采用边长2 m的正方形发射和接收线圈,共设置15个测点(0~14号),测点间距10 m,测线长度140 m。因为巷道空腔对2次场的影响有限,在实际探测中数据处理一般不考虑巷道空腔的影响,所以3DTEM正演也没有考虑巷道空腔影响。采样时间设置为6.8~6 978 μs对数等分的30个采样时间点,对应25 Hz系统发射频率。

图6 地震勘探和矿井TEM观测系统
Fig.6 Observation system of mine TEM and seismic
2.3 正演结果
基于图6观测系统对图5含导水陷落柱模型分别进行了矿井TEM和地震勘探正演计算。矿井TEM和地震勘探正演均为3D正演,采用的正演算法均为有限差分方法。
图7为3D TEM正演结果,二次场强度已归一化为发射磁矩等于1 A·m2时强度值。由图7可见,靠近陷落柱的测点(5~9号测点,对应x=50~90 m范围)二次场强度显著增大,形成向上凸起的二次场异常形态。陷落柱对各测点二次场的影响是渐变的,陷落柱边界位置不存在二次场的突变,二次场异常范围大于实际陷落柱范围。
图8为3D地震正演结果。由图8可知,第四系盖层底界面反射波、煤层反射波、奥陶系灰岩顶界面反射波和陷落柱顶界面反射波相对清晰,但由于陷落柱尺寸小,陷落柱底界面反射波难以识别。

图7 3D TEM正演结果
Fig.7 3D TEM simulation result

图8 3D 地震正演结果
Fig.8 3D seismic simulation result
2.4 反演结果
在单独TEM反演中,模型网格数量为x×z=1.5×21,采用均匀模型网格Δx=Δz=10 m。深度方向最后一个网格Δz是无限大的,为了成图方便也设置为10 m。所以TEM模型的大小是x×z=150 m×210 m。其他反演参数设置包括:阻尼因子α=0.1,加权算子ωx=0.001,ωz=0.000 1,最小拟合残差εmin=10-3,最大迭代次数nmax=5。地震波阻抗反演在图8(b)叠后偏移剖面的基础上采用某商业软件完成,基于模型约束波阻抗反演方法,模型网格大小为Δx=5 m和Δz=0.2 m。在联合反演中ωt=0.05,其他参数与单独TEM反演中设置相同。
图9(a)为地震波阻抗反演结果。由图9(a)可知,陷落柱(上半部分)反映较清晰,形状与理论模型一致。煤系地层与奥陶系灰岩分界面位置与理论模型存在一定偏差,但分界面清晰。总体来说,地震波阻抗反演结果体现出了较高的空间分辨率,但仅根据波阻抗反演结果难以判断陷落柱的富水性。图9(b)为TEM反演结果,由图9(b)可知,反演结果对陷落柱反映明显,在陷落柱位置表现为低阻异常区,但是受体积效应影响难以确定陷落柱的边界。

图9 单独反演和联合反演结果
Fig.9 Inversion results of mine TEM and seismic impedance
图9(c)为联合反演结果,由图9(c)可知,联合反演结果同时重建了理论模型的形状和电性特征,相比单独TEM反演结果,显著提高了对陷落柱的分辨率。从单独TEM反演结果图9(b)来看,陷落柱位于煤层底板下20 m,从联合反演结果中可以准确确定陷落柱位于煤层底板下30 m,联合反演精度明显提高。矿井TEM和地震联合反演结果既具有较高的空间分辨率,又可以判断富水性,优于单独TEM反演结果和单独地震波阻抗反演结果。图9(d)为拟合残差随迭代次数变化情况,由图可见联合反演和单独TEM反演计算均具有较好的稳定性,联合反演拟合残差相对小于单独TEM反演拟合残差。
3 结 论
(1)采用基于镜像模型的矿井Pseudo-2D TEM反演方法和单向交叉梯度方法,可以实现矿井TEM和反射波多次覆盖地震数据的联合反演。为了方便进行联合反演计算并取得良好的联合反演效果,地震波阻抗模型需进行插值转换和聚类分割处理。
(2)联合反演能够同时重建理论模型的形状和电性特征,反演结果不仅具有较高的空间分辨率,而且能够反映陷落柱的富水性,优于单独TEM和单独地震方法反演结果。
(3)传统联合反演方法主要应用于大尺度目标体探测或浅地表成像,基于矿井TEM和地震的单向交叉梯度联合反演为大深度小尺度目标体的精细探测建立了理论和方法基础。当陷落柱埋深大尺度小,单一TEM方法难以取得良好探测效果时,如果具备2D或3D地震勘探数据,可以采用联合反演方法提高探测效果。本文通过理论模型试算验证了联合反演方法的有效性,实际应用中陷落柱大小、形状和电性特征相比理论模型更复杂,实际应用效果将在今后的研究中通过现场试验进行进一步的验证。
致谢 英得赛斯科技(北京)有限公司邱善武博士在地震反演方面提供了帮助,在此表示感谢。
[1] 程久龙,李飞,彭苏萍,等.矿井巷道地球物理方法超前探测研究进展与展望[J].煤炭学报,2014,39(8):1742-1750.
CHENG Jiulong,LI Fei,PENG Suping,et al.Research progress and development direction on advanced detection in mine roadway working face using geophysical methods[J].Journal of China Coal Society,2014,39(8):1742-1750.
[2] 薛国强,于景邨.瞬变电磁法在煤炭领域的研究与应用新进展[J].地球物理学进展,2017,32(1):319-326.
XUE Guoqiang,YU Jingcun.New development of TEM research and application in coal mine exploration[J].Progress in Geophysics,2017,32(1):319-326.
[3] 程建远,石显新.中国煤炭物探技术的现状与发展[J].地球物理学进展,2013,28(4):2024-2032.
CHENG Jianyuan,SHI Xianxin.Current status and development of coal geophysical technology in China[J].Progress in Geophysics,2013,28(4):2024-2032.
[4] 于景邨,苏本玉,薛国强,等.煤层顶板致灾水体井上下双磁源瞬变电磁响应及应用[J].煤炭学报,2019,44(8):2356-2360.
YU Jingcun,SU Benyu,XUE Guoqiang,et al.Transient electromagnetic response of double magnetic source in coal seam roof disaster caused by water and its application[J].Journal of China Coal Society,2019,44(8):2356-2360.
[5] MOORKAMP M,LELIVRE P G,LINDE N,et al.Integrated imaging of the earth:theory and applications[M].Wiley,2016.
[6] COLOMBO D,Stefano MD.Geophysical modeling via simultaneous joint inversion of seismic,gravity,and electromagnetic data:Application to prestack depth imaging[J].The Leading Edge,2007,26(3):326-331.
[7] HABER E,HOLTZMAN GAZIT M.Model fusion and joint inversion[J].Surveys in Geophysics,2013,34(5):675-695.
[8] VOZOFF K,JUPP D L B.Joint Inversion of Geophysical Data[J].Geophysical Journal of the Royal Astronomical Society,1975,42:977-991.
[9] CHENG Jiulong,LI Fei,PENG Suping,et al.Joint inversion of TEM and DC in roadway advanced detection based on particle swarm optimization[J].Journal of Applied Geophysics,2015,123:30-35.
[10] GRECHKA V,THEOPHANIS S,TSVANKIN I.Joint inversion of P and PS waves in orthorhombic media:Theory and a physical modeling study[J].Geophysics,1999,64(1):146-161.
[11] HORSPOOL N A,SAVAGE M K,BANNISTER S.Implications for intraplate volcanism and back-arc deformation in northwestern NEW Zealand,from joint inversion of receiver functions and surface waves[J].Geophysical Journal International,2006,166(3):1466-1483.
[12] GALLARDO L A,MEJU M A.Characterization of heterogeneous near-surface materials by joint 2Dinversion of dc resistivity and seismic data[J].Geophysical Research Letters,2003,30(13):1-4.
[13] MOORKAMP M,ROBERTS A W,JEGEN M,et al.Verification of velocity-resistivity relationships derived from structural joint inversion with borehole data[J].Geophysical Research Letters,2013,40(14):3596-3601.
[14] 李桐林,张镕哲,朴英哲,等.部分区域约束下的交叉梯度多重地球物理数据联合反演[J].地球物理学报,2016,59(8):2979-2988.
LI Tonglin,ZHANG Rongzhe,PU Yingzhe,et al.Multiple joint inversion of geophysical data with sub-region cross gradient constraints[J].Chinese Journal of Geophysics,2016,59(8):2979-2988.
[15] BENNINGTON N L,ZHANG H J,THURBER C H,et al.Joint inversion of seismic and magnetotelluric data in the Park field region of California using the normalized cross-gradient constraint[J].Pure and Applied Geophysics,2015,172(5):1033-1052.
[16] 高级,张海江,方洪健,等.一种高效的基于交叉梯度结构约束的三维地震走时与直流电阻率联合反演策略[J].地球物理学报,2017,60(9):3628-3641.
GAO Ji,ZHANG Haijiang,FANG Hongjian,et al.An efficient joint inversion strategy for 3D seismic travel time and DC resistivity data based on cross-gradient structure constraint[J].Chinese Journal of Geophysics,2017,60(9):3628-3641.
[17] 王月,张捷.地震走时和航空电磁联合反演三维速度和电阻率[J].地震研究,2018,41(1):22-31.
WANG Yue,ZHANG Jie.Joint seismic travel time and airborne electromagnetic inversion for 3D velocity and electrical resistivity[J].Journal of Seismological Research,2018,41(1):22-31.
[18] 李飞,谭强,刘德民,等.基于镜像模型的矿井瞬变电磁全空间反演研究[J].华北科技学院学报,2014,11(5):12-19.
LI Fei,TANG Qiang,LIU Demin,et al.Whole space inversion of mine transient electromagnetic method based on mirror model[J].Journal of North China Institute of Science and Technology,2014,11(5):12-19.
[19] SCHULTZ G,RUPPEL C.Inversion of inductive electromagnetic data in highly conductive terrains[J].Geophysics,2005,70(1):16-28.
[20] AUKEN E,CHRISTIANSEN A V.Layered and laterally constrained 2D inversion of resistivity data[J].Geophysics,2004,69:752-761.
[21] SCHAMPER C,REJIBA F,ROGER G.1D single-site and laterally constrained inversion of multi-frequency and multicompon-ent ground-based electromagnetic induction data;application to the investigation of a near-surface clayey overburden[J].Geophysics,2012,77(4):WB19-WB35.
[22] OGUNBO J N,ZHANG J.Joint seismic travel-time and TEM inversion for near surface imaging[A].SEG:84th Annual International Meeting[C].2014.
[23] 李貅.瞬变电磁测深的理论与应用[M].西安:陕西科学技术出版社,2002.
[24] KRIVOCHIEVA S,CHOUTEAU M.Whole-space modeling of a layered earth in time-domain electromagnetic measurements[J].Journal of Applied Geophysics,2002,50(4):375-391.
[25] 符祥,郭宝龙.图像插值技术综述[J].计算机工程与设计,2009,30(1):141-144.
FU Xiang,GUO Baolong.Overview of image interpolation technology[J].Computer Engineering and Design,2009,30(1):141-144.
[26] 孙吉贵,刘杰,赵连宇.聚类算法研究[J].软件学报,2008,19(1):48-61.
SUN Jigui,LIU Jie,ZHAO Lianyu.Clustering algorithms research[J].Journal of Software,2008,19(1):48-61.
[27] 李飞,程久龙,陈绍杰,等.基于时移高密度电法的覆岩精细探测方法研究[J].矿业科学学报,2019,4(1):1-7.
LI Fei,CHENG Jiulong,CHEN Shaojie,et al.Fine detection of overburden strata based on time lapse high density resistivity method[J].Journal of Mining Science and Technology,2019,4(1):1-7.
[28] 孟召平,张吉昌,JOACHIM Tiedemann.煤系岩石物理力学参数与声波速度之间的关系[J].地球物理学报,2006,49(5):1505-1510.
MENG Zhaoping,ZHANG Jichang,JOACHIM T.Relationship between physical and mechanical parameters and acoustic wave velocity of coal measures rocks[J].Chinese Journal of Geophysics,2006,49(5):1505-1510.
[29] 杨思通,程久龙.煤巷地震超前探测数值模拟及波场特征研究[J].煤炭学报,2010,35(10):1633-1637.
YANG Sitong,CHENG Jiulong.Numerical simulation of fore detecting with seismic in coal roadway and study of wave field characteristics[J].Journal of China Coal Society,2010,35(10):1633-1637.
