岩土体的细观特性是岩土介质宏观特征更加基本的属性,建立细观结构对宏观力学性质的定量反应分析理论已成为当前研究的热点问题。从细观力学角度着手研究岩土等碎散介质的变形和受力特性,是人们深入理解和认识岩土介质物理和力学特性的必由之路[1-5]。基于细观力学理论的PFC2D数值仿真试验技术,可以从细观角度揭示注浆过程中拉压应力场的分布、土颗粒的变形运动及其与浆液的耦合作用过程等注浆进程的发展动态,为软弱土、风化岩和破碎带等不良地质体的注浆加固分析研究开辟了一条新的途径[6-9]。
周健(2008,2010)等[10-11]基于颗粒流理论,通过调试PFC2D计算程序中的相关接触模型和力学参数,对砂土的应力应变关系及渗流特征进行了模拟;孙锋(2010)等[12]基于PFC2D内置的FISHTANK函数库和FISH语言,对致密土体在不同注浆压力和不同环境条件下劈裂缝的发生、发展规律进行细观模拟研究;蒋明镜(2014)等[13]运用PFC2D自定义的FISH语言和C++语言,通过建立N-S方程和Tait状态方程实现了弱可压缩流体的CFD-DEM耦合计算;郑刚(2015)等[14]通过PFC2D数值试验发现注浆压力是注浆过程中的决定性因素,注浆压力对浆液的扩散半径、土体的孔隙率及应力状态均有显著的影响。数值试验还表明浆液的扩散半径随注浆压力的增加先增后减,存在最优注浆压力;耿萍(2017)等[15]通过颗粒流软件验证了劈裂注浆是压密-劈裂-压密-劈裂的动态过程,现场注浆施工应针对实际地质情况,合理安排注浆孔以及注浆顺序等。
针对注浆过程中颗粒体的位移与渗透、压密和劈裂等作用方式的关系及其转变机理尚不明确,而劈裂注浆的力学机制也不十分清晰,同时考虑不同注浆深度、不同地质条件和不同浆液性质等细观参数变化条件下的注浆规律及效果分析也亟需加强研究。本文基于流固耦合的原理建立颗粒流数值模型,采用Itasca公司开发的PFC2D计算程序,从细观层面模拟研究了不同注浆条件下浆液的扩散和分布形态、颗粒体的位移及应力场的分布,并对不同渗透性质浆液、不同地质参数情形下的注浆效果进行了初步探索。
1 注浆细观模拟的基本理论
PFC2D将岩土介质看作离散颗粒的集合体,其求解思路是通过对软弱土或风化岩体的物理特征及接触关系进行概化,建立起反映实际工程问题的数值模型,从而将其映射到数学领域进行求解。PFC2D的计算优势[16-19]主要有:① 圆形颗粒的“叠合”特征宜于判断和描述,计算效率高;② 采用显式方法计算,内存消耗小;③ 内置的强大功能可同时对成千上万个颗粒进行动态计算;④ 颗粒彼此独立可以分离,能够实现大变形问题的模拟计算。
1.1 流动方程
在PFC2D数值模型中,浆液与颗粒体通过流固耦合的相互作用实现动态计算。颗粒体的孔隙间存在能承受水压的流体域(domain),通过假想的管道(pile)与四周连通,注浆过程中浆液通过连通的流体域和颗粒间的管道实现动态传播和扩散。浆液在管道内的流动假定遵从裂隙立方定理,其流量计算式为
![]()
(1)
其中,k为水力传导系数;a为管道孔径;p2-p1为管道连通的两相邻流体域的压力差;L为管道长度。当颗粒间接触力为拉力时管道孔径受力扩张,而当颗粒接触力为压力时管道孔径则收缩,管道孔径受颗粒接触力扩张和收缩的计算方法如下:
a=a0+mg(扩张)
(2)
![]() (收缩)
(收缩)
(3)
式中,m为缩放因子;g为两颗粒表面间的法向距离;F为法向接触力;a0为管道初始孔径;F0为管道孔径减小后的法向压力。
1.2 压力方程
储存在流体域中的流体压力在注浆过程中不断更新,以实现颗粒体与流体间的流固耦合作用。流体域内的流体压力大小主要取决于浆液流量,在特定的计算时步内流体压力增量的计算式为
![]()
(4)
式中,Δp为流体压力增量;Kd,Vd分别为浆液的体积模量和流体域的表观体积;∑q为进出该流体域的浆液流量;Δt为计算时间;ΔVd为表观体积增量。
1.3 求解方法
交替运用流量方程和压力方程,采用显示计算方法进行求解。由压力扰动ΔPp而流入某流体域的流量为
![]()
(5)
其中,N为与流体域连通的管道数量;R为该流体域周围颗粒的平均半径。流体域中的流体压力在更新过程中的压力响应为
![]()
(6)
当压力响应小于扰动压力时,系统能够保持稳定的动态计算。动态稳定计算的时间步长如下
![]()
(7)
2 计算模型及计算参数
本次数值试验共生成1 136个颗粒单元,颗粒粒径在3.5~5.0 mm均匀分布。为了保证颗粒体生成在指定的边界范围内,可以在模型四周设置墙体(wall)以防止颗粒逃逸,待不平衡力消除后将墙体删除。通过调用FISHTANK中的zap_dead_ends函数可以去除接触连接<2的颗粒,从而保证注浆过程中所有的管路都畅通。本试验模型的长和宽各为3 m,模型的四周由一排红色颗粒围成,代表不透水边界(图1)。图1(b)中黑色圆点代表流体域(domain),由域间的黑色线段构成颗粒间的缝隙通道。模型中粉红色的圆盘代表地层结构中的土体颗粒,连接圆颗粒间的红色线段则代表颗粒间的接触连接。

图1 二维颗粒流计算模型
Fig.1 Two-dimensional particle flow model
表1 颗粒细观参数
Table 1 Particle Meso-parameters

最大粒径Rmin/cm粒径比Rmax/Rmin法向接触刚度kn/(N·m-1)刚度比kn/ks摩擦因数fc孔隙率n法向黏结强度Fn/N切向黏结强度Fs/N5.01.35~1.475×10710.2~0.40.255×104~5×1065×104~5×106
颗粒流数值计算过程中,细观参数的合理选取是数值计算顺利开展的关键环节,本次数值试验前通过开展Darcy渗流试验、双轴压缩试验等模型试验得到了土体的孔隙率n、法向和切向接触刚度kn,ks及摩擦因数fc等力学参数(表1)。需要指出的是,模型介质的细观参数需要不断的校准和修改尝试才能重现岩土材料的宏观力学响应,如果细观参数与宏观响应结果不符则需反复调试,直到满足要求为止。细观参数的选取过程如图2所示。

图2 细观参数选取流程
Fig.2 Process of selecting meso-parameters
3 注浆效果细观分析
3.1 浆液-颗粒耦合作用下颗粒体位移
浆液-颗粒流固耦合作用体系中,颗粒体将随浆液的流动产生位移。颗粒的位移速度和大小可以从细观角度揭示注浆方式和注浆进程的变化,对进一步探索注浆机理具有重要意义。由图3,4可以看出,低压注浆条件下颗粒位置相对稳定,几乎不产生位移,而高压注浆条件下则颗粒相互挤压并向外膨胀,逐渐呈现出杂乱无序的特征。注浆压力对地层结构的改变和破坏作用十分显著。
3.2 不同深度注浆效果
不同深度条件下地层应力状态差别较大,为分析不同应力环境下土体渗透和劈裂注浆等作用方式的不同,通过改变n_bond(法向黏结强度Fn)和(s_bond切向黏结强度Fs)等力学参数对注浆效果进行了模拟测试。图5为注浆压力1 MPa作用下浆液的扩散情况,黏结强度参数分别取为5×104,5×105和5×106 N。由图5可以看出,低注浆压力条件下浆液基本以渗透的方式向外扩散,黏结强度最小的土体内出现了劈裂现象,黏结强度对浆液的扩散方式有一定影响。
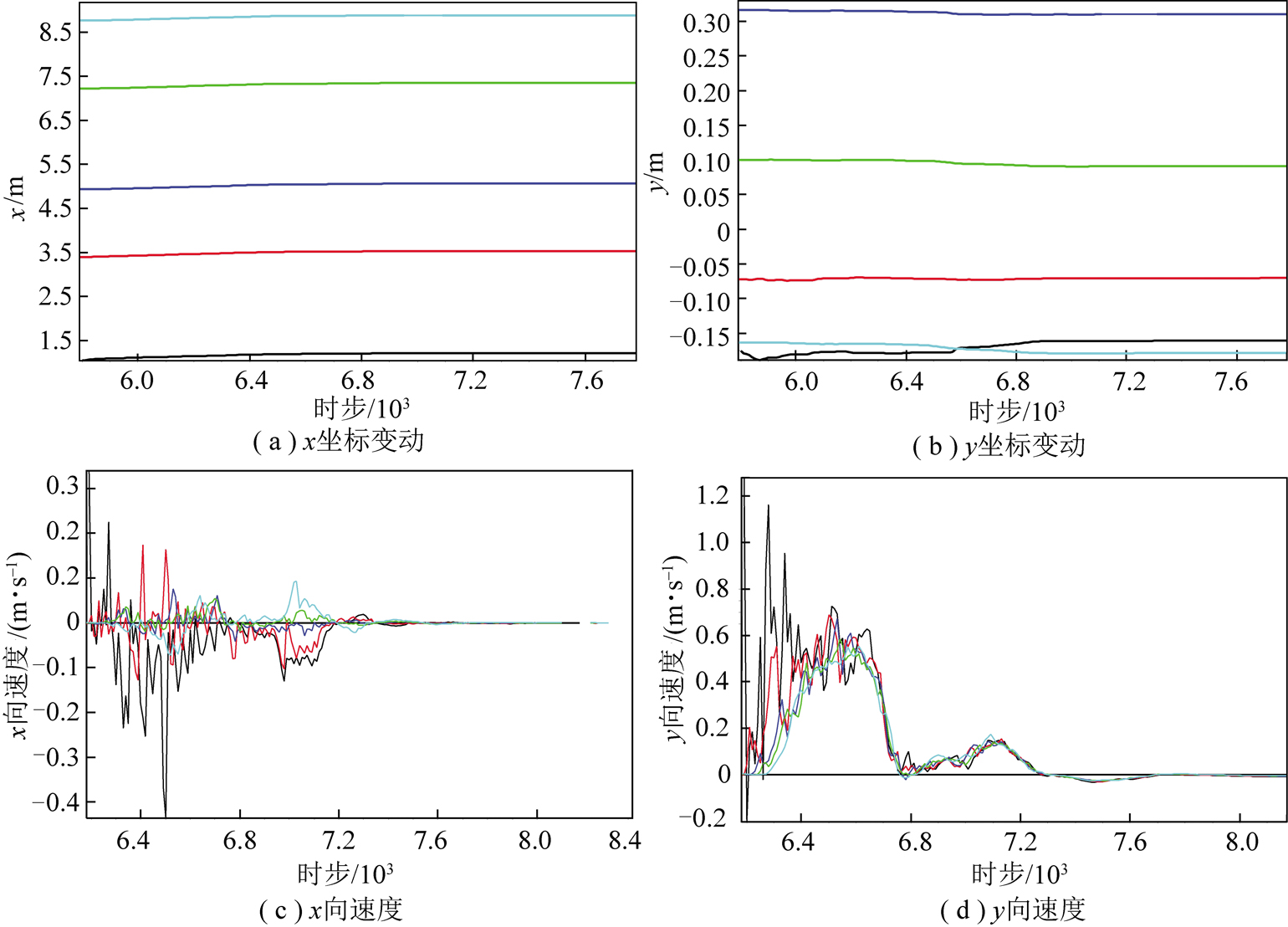
图3 1 MPa压力作用下颗粒位移情况
Fig.3 Particle displacement under 1 MPa pressure

图4 3 MPa压力作用下颗粒位移情况
Fig.4 Particle displacement under 3 MPa pressure

图5 p=1 MPa压力下浆液扩散情况
Fig.5 Diffusion of slurry under 1 MPa pressure
图6为2 MPa注浆压力作用下浆液的扩散情况,由图中可以看出浆液基本以劈裂灌注方式为主,随黏结强度增加,劈裂缝数目逐渐减少,劈裂效果变差。风化岩体或破碎带等不良地质体注浆加固工程中,黏结强度的适度降低可表征岩体的风化破坏程度,图5,6的模拟结果可为风化岩体注浆设计和施工提供规律性指导。

图6 p=2 MPa压力下浆液扩散情况
Fig.6 Diffusion of slurry under 2 MPa pressure
3.3 孔隙率变化
图7为监测半径0.5,1和1.5 m范围内土体孔隙率的变化趋势线,注浆压力分别为1,2和3 MPa。由图中可以看出低注浆压力条件下土体孔隙率增加仅2.3%~7.0%,而高注浆压力作用下产生劈裂缝,大大拓展土体应力空间,孔隙率增幅达23.5%~33.3%。

图7 土体内部孔隙率变化
Fig.7 Changes of internal porosity in soils
3.4 弹塑性应力状态分析
数值计算表明钻孔周围土体应力场呈环向和径向放射状分布(图8),黑色和青色线条分别代表压应力场和拉应力场。根据弹塑性应力状态特征和柱形扩孔理论,可将钻孔周围土体分为塑性流动区、塑性软化区和弹性区3种应力状态[23-24]。假定所模拟土体为服从Mohr-Coulomb强度准则(式(8))的理想弹塑性体,则土体塑性流动区、塑性软化区和弹性区的径向应力和环向应力(式(9)~(11))分别为
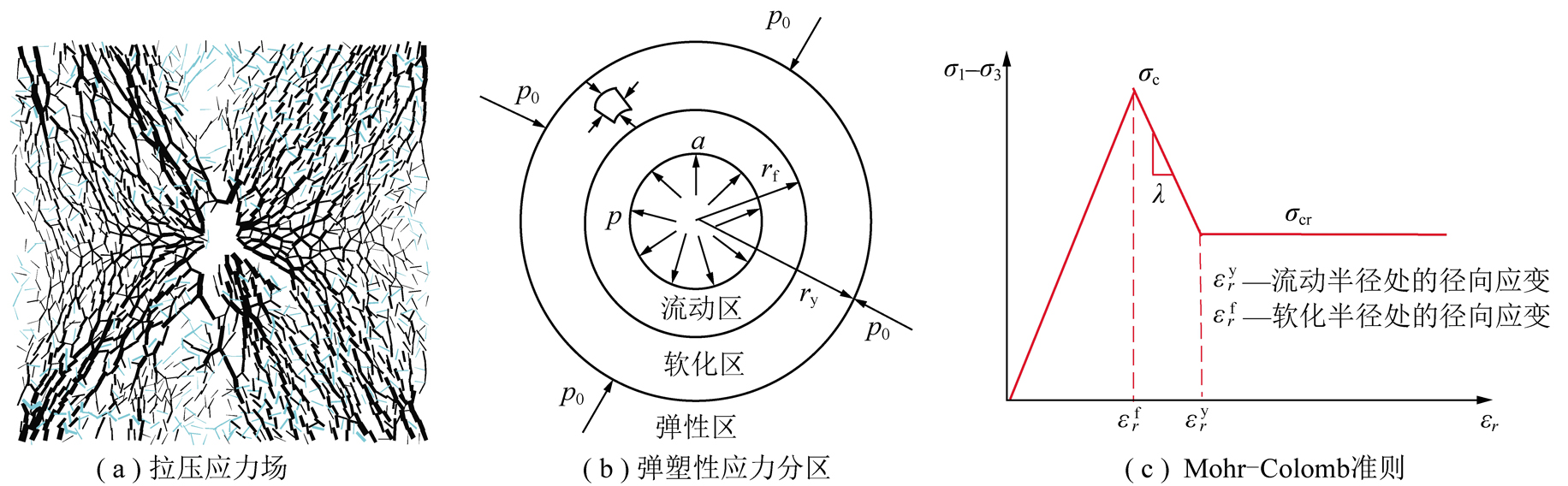
图8 注浆孔应力状态分析
Fig.8 Stress analysis of grouting holes
σr=Mσθ+σ0,M=(1+sin φ)/(1-sin φ) (8)
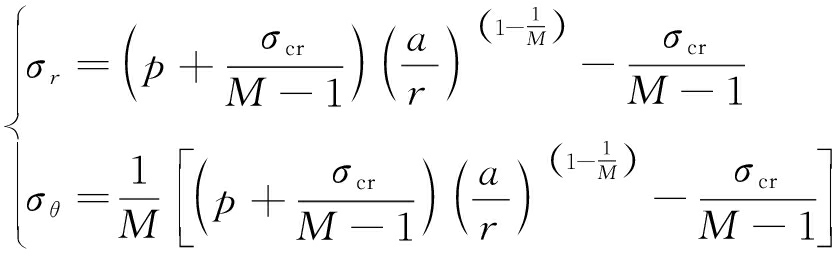
(9)
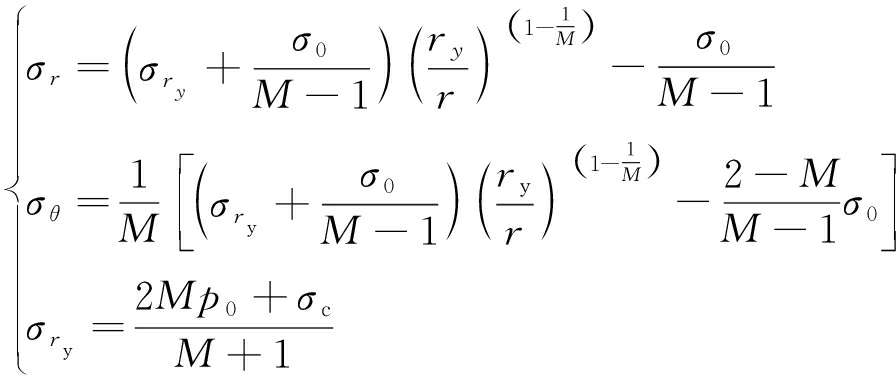
(10)

(11)
其中,p为钻孔内的注浆压力;σcr和σc分别为土的残余强度和峰值强度;ry,rf分别为软化区和塑性流动区半径;σry为弹塑性交界面上的径向应力;p0为无限远处静止土压力。式(9)~(11)表明在注浆压力p作用下,土体环向受拉而径向受压,土体产生拉裂破坏而后出现劈裂缝,浆液由渗透方式向劈裂方式转变。
4 浆液性质及地层参数对注浆效果的影响
浆液的渗透性质和土体粒径、级配及摩擦因数等地质条件对注浆效果有一定影响,为检测不同浆液黏度或不同地质条件等因素对扩散形态、方式的作用及影响,通过调节命令流中的perm,fric等相关参数开展了模拟测试试验。
4.1 不同渗透性质浆液
图9分别为注浆压力1,2和3 MPa条件下浆液在土体中的扩散情况,水力传导系数设置为perm=0.1。由图9可以看出低压时浆液的流动扩散速度较慢,基本以压密形式与地基土相互作用,浆液扩散范围十分有限;高压条件下产生较密集的劈裂缝,能够取得理想的劈裂注浆效果。

图9 水力传导系数perm=0.1浆液扩散形态
Fig.9 Hydraulic conductivity perm=1 slurry diffusion pattern
图10为水力传导系数perm=1.0条件下浆液在土体中的扩散情况,由于浆液渗透性能提高10倍,浆液流速大幅提高,浆液不会在注浆通道上积聚并起压,使得劈裂缝数量明显减少。这些计算结果与文献[25-28]中的结果相符,对注浆施工具有一定指导意义。

图10 水力传导系数perm=1浆液扩散形态
Fig.10 Hydraulic conductivity perm=1 slurry diffusion pattern
4.2 最大最小粒径比的影响
图11为不同粒径比条件下浆液的扩散情况,由图11可以看出粒径比小的土体级配不良,结构不密实易被注浆压力启劈;颗粒粒径比大的土体结构密实,能够抵抗注浆压力对地层的破坏作用,浆液以渗透扩散形式为主。

图11 p=1 MPa压力下浆液扩散情况
Fig.11 Slurry Diffusion at Pressure p=1 MPa
4.3 摩擦因数的影响
由图12可以看出,颗粒间的摩擦因数对浆液扩散范围的影响并不明显。这是因为在劈裂注浆过程中,注浆压力一旦将土层劈开产生裂缝,土颗粒在压力作用下就将相互分离,颗粒间的摩擦因数便无法对注浆效果施加影响。

图12 不同摩擦因数下土体的劈裂注浆效果
Fig.12 Grouting effect of soil under different friction coefficients
5 数值模拟与模型试验结果对比分析
图13分别给出了不同实验室条件所得到的注浆结石体形态,试验条件请见表2。图13(a)为砂料渗透注浆模型试验结果,注浆压力由空气压缩机提供,为30~60 kPa,注浆时长15 s,结石体基本呈椭球形;图13(b)为深厚冲积层劈裂注浆浆脉分布情况,注浆压力2.5 MPa,劈裂缝宽度0.3~2.0 cm,扩散半径约0.5 m,注浆结果及规律与本文PFC数值计算基本相符。

图13 数值试验与室内试验对比
Fig.13 Comparison of numerical and laboratory tests
表2 模型试验条件
Table 2 Model test conditions

渗透注浆试验水灰比砂料性质注浆压力/kPa扩散半径/cm劈裂注浆试验水灰比注浆压力/MPa注浆管间距/m注浆时长/min0.8∶1中粗砂30~60 15 0.6~0.72.5 0.8 20
6 结 论
(1)数值计算表明,注浆压力对地层结构的改变和破坏作用十分显著,黏结强度增加劈裂效果逐渐变差,孔隙率随注浆压力提高则显著增大。
(2)基于Mohr-Colomb准则的弹塑性理论对钻孔周围土体的应力场进行理论推导,指出环向受拉径向受压的力学机制是劈裂注浆作用方式出现的根本原因。
(3)浆液黏度增加有利于提高劈裂-压密注浆的注浆效果,摩擦因数增加则对注浆效果影响不大。实验室试验对比分析表明,PFC2D模拟注浆过程是可行的。
[1] JIANG M J,SHEN Z F,WANG J F.A novel three-dimensional contact model for granulates incorporating rolling and twisting resistances[J].Computers and Geotechnics,2015,65:147-163.
[2] DUAN Hongfei,JIANG Zhenquan,ZHU Shuyun.New composite grouting materials:Modified urea-formaldehyde resin with cement[J].International Journal of Mining Science and Technology,2012(22):195-200.
[3] 蒋明镜.现代土力学研究的新视野——宏微观土力学[J].岩土工程学报,2019,41(2):195-254.
JIANG Mingjing.New paradigm for modern soil mechanics:Geomechanics from micro to macro[J].Journal of Geotechnical Engineering,2019,41(2):195-254.
[4] 尹振宇.土体微观力学解析模型:进展及发展[J].岩土工程学报,2013,35(6):993-1009.
YIN Zhenyu.Micromechanics-based analytical model for soils:Review and development[J].Journal of Geotechnical Engineering,2013,35(6):993-1009.
[5] CHANG C S,YIN Z-Y.Micromechanical modeling for behavior of silty sand with influence of fine content[J].International Journal of Solids and Structures,2011,48(19):2655-2667.
[6] ZHAO G S,ZHOU G Q,ZHONG G R.Analysis of stratum grouting influence on shaft lining stress with the methods of simulation and in site measurements[J].Procedia Earth and Planetary Science,2009(1):497-502.
[7] STILLE H,GUSTAFSON G,H SSLER L.Application of new theories and technology for grouting of dams and foundations on rock[J].Geotechnical and Geological Engineering,2012,30(3):603-624.
SSLER L.Application of new theories and technology for grouting of dams and foundations on rock[J].Geotechnical and Geological Engineering,2012,30(3):603-624.
[8] HERNQVIS L,FRANSSON Å,GUSTAFSON G,et al.Analyses of the grouting results for a section of the APSE tunnel at äspö Hard ROCK Laboratory[J].International Journal of Rock Mechanics and Mining Sciences,2009,46(3):439-449.
[9] FRANSSON Å.Non-parametric method for transmissivity distributions along boreholes[J].Ground Water,2001,40(2):201-204.
[10] 周健,池永.砂土力学性质的细观模拟[J].岩土力学,2003,24(6):901-906.
ZHOU Jian,CHI Yong.Microscopic simulation of mechanical properties of sand[J].Geotechnical Mechanics,2003,24(6):901-906.
[11] 周健,张刚,孔戈.渗流的颗粒流细观模拟[J].岩土力学,2006,37(1):28-32.
ZHOU Jian,ZHANG Gang,KONG Ge.Microscopic simulation of particle flow in seepage[J].Geotechnical Mechanics,2006,37(1):28-32.
[12] 孙锋,张顶立,陈铁林,等.土体劈裂注浆过程的细观模拟研究[J].岩土工程学报,2010,32(3):474-480.
SUN Feng,ZHANG Dingli,CHEN Tielin,et al.Microscopic simulation of soil splitting grouting process[J].Journal of Geotechnical Engineering,2010,32(3):474-480.
[13] 蒋明镜,张望城.一种考虑流体状态方程的土体CFD-DEM耦合数值方法[J].岩土工程学报,2014,36(5):793-801.
JIANG Mingjing,ZHANG Wangcheng.Coupled CFD-DEM method for soils incorporating equation of state for liquid[J].Journal of Geotechnical Engineering,2014,36(5):793-801.
[14] 郑刚,张晓双.劈裂注浆过程的二维颗粒流的模拟研究[J].厦门大学学报(自然科学版),2015,54(6):905-912.
ZHENG Gang,ZHANG Xiaoshuang.Meso-mechanical simulation of fracture grouting using particle flow code in two dimensions[J].Journal of Xiamen University(Natural Science),2015,54(6):905-912.
[15] 耿萍,卢志楷,丁梯,等.基于颗粒流的围岩注浆动态过程模拟研究[J].铁道工程学报,2017(3):34-40.
GENG Ping,LU Zhikai,DING Ti,et al.Research on the dynamic process simulation of rock grouting based on particle flow[J].Journal of Railway Engineering Society,2017(3):34-40.
[16] 廖雄华,周健,徐建平,等.粘性土室内平面应变试验的颗粒流模拟[J].水利学报,2002(12):11-16.
LIAO Xionghua,ZHOU Jian,XU Jianping,et al.Particle flow simulation of indoor plane strain test of cohesive soil[J].Journal of Water Resources,2002(12):11-16.
[17] 蒋应军,任皎龙,徐寅善.级配碎石力学性能的颗粒流数值模拟方法[J].同济大学学报(自然科学版),2011,39(5):699-704.
JIANG Yingjun,REN Jiaolong,XU Yinshan.A numerical simulation method for mechanical properties of Graded Macadam[J].Journal of Tongji University(Natural Science Edition),2011,39(5):699-704.
[18] CUNDALLPE,HARTRG.Numerical modeling of discontinue[J].Engineering Computations,1992,9(2):101-113.
[18] 张连震.地铁穿越砂层注浆扩散与加固机制及工程应用[D].济南:山东大学,2017.
ZHANG Lianzhen.Study on penetration and reinforcement mechanism of grouting in sand layer disclosed by subway tunnel and its application[D].Ji’nan:Shandong University,2017.
[19] 周健,池永,池毓蔚,等.颗粒流方法及PFC2D程序[J].岩土力学,2000,21(3):271-274.
ZHOU Jian,CHI Yong,CHI Yuwei,et al.Particle flow method and PFC2D program[J].Geotechnical Mechanics,2000,21(3):271-274.
[21] Itasca CONSULTING Group.PFC2D user’s manual(version3.1)[M].Minneapolis,Minnesota:Itasca Consulting Group,Inc,2004.
[22] Itasca Consulting Group Inc.PFC2D(particle flow code in 2D) theory and background[R].Minnesota,USA:Itasca Consulting Group Inc.,2008.
[23] 徐芝纶.弹性力学简明教程[M].北京:高等教育出版社,2005.
[24] 邹金锋,李亮,杨小礼,等.土体劈裂灌浆力学机理分析[J].岩土力学,2006,27(4):625-629.
ZOU Jinfeng,LI Liang,YANG Xiaoli,et al.Mechanism analysis of fracture grouting in soil[J].Rock and Soil Mechanics,2006,27(4):625-629.
[25] 李鹏,张庆松,王倩,等.隧道泥质断层多序注浆动态劈裂扩散规律[J].中国公路学报,2018,31(10):328-338.
LI Peng,ZHANG Qingsong,WANG Qian,et al.Dynamic fracturing diffusion law considering the influence of multiple sequence grouting in argillaceous fault[J].China Journal of Highway Transportation,2018,31(10):328-338.
[26] 李术才,张伟杰,张庆松,等.富水断裂带优势劈裂注浆机制及注浆控制方法研究[J].岩土力学,2014,35(3):744-752.
LI Shucai,ZHANG Weijie,ZHANG Qingsong,et al.Research on advantage-fracture grouting mechanism and controlled grouting method in water-rich fault zone[J].Rock and Soil Mechanics,2014,35(3):744-752.
[27] 朱明听,张庆松,李术才,等.土体劈裂注浆加固主控因素模拟试验[J].浙江大学学报(工学版),2018,52(11):2058-2067.
ZHU Mingting,ZHANG Qingsong,LI Shucai,et al.Simulation test for main control factors of soil splitting grouting reinforcement[J].Journal of Zhejiang University(Engineering Science),2018,52(11):2058-2067.
[28] 程盼,邹金锋,李亮.冲积层中劈裂注浆现场模型试验[J].地球科学-中国地质大学学报,2013,38(3):649-655.
CHENG Pan,ZOU Jinfeng,LI Liang.Field model test of splitting grouting in alluvium[J].Journal of Geosciences of China University of Geosciences,2013,38(3):649-655.
