从生产数据中挖掘煤层气井产量与排采工艺之间的内涵关系，对于指导生产具有重要意义。煤层气井生产数据具有数据量大、信息种类多等特征，生产参数与产量之间的关系复杂[1]。以煤层气的解吸、扩散、渗流等机理为基础，建立煤层气井流体流动的理论模型[2-4]，并用数值模拟的方法进行产量预测是广泛采用的方法。但理论分析常常需要基于假设建立模型，理论计算结果往往难以匹配不同生产井的数据。为此，一些学者建立了基于统计学的人工智能算法模型，用于预测煤层气井的流体流动规律[5-14]，取得了较好的效果，但在一些方面仍有待改进。例如，神经网络算法需要大量数据支撑，才可以保证运算的准确率;支持向量机可以弥补神经网络算法的缺陷，但经典的支持向量机只可以进行二分类运算，而在实际的工程应用中，往往要解决多分类问题的数据挖掘[15]。为了避免上述方法的缺陷，出现了一对多支持向量机、一对一支持向量机以及随机森林等新型算法。其中，随机森林算法具有分类速度快、改善过度拟合、有效处理高维大样本数据、预估某个特征在分类中具有的重要性以及具有较强的抗噪音能力等特点，可以大大降低计算量，还能保持较高的精确度[15-17]。为此，笔者依托沁水盆地郑村区块的煤层气井，利用随机森林算法，对地质参数、排采工艺参数与产量数据进行相关性分析，进而建立了基于随机森林算法的煤层气井产量模型。用于预测煤层气井的日产气量。

1 随机森林算法原理与模型

随机森林由Breiman提出，是一种个体学习器全部为决策树的同质集成学习器[18]。随机森林模型由多棵决策树模型组成，在进行预测时，由多棵决策树进行联合预测，精度较高[19]。决策树的形成来源于对已经训练过的样本集(假设共有n个样本)进行随机抽取k个样本，每次随机抽样的结果为一棵决策树模型Ti(X,Qk)，i=1,2,…,k。其中，X为自变量，Qk为因变量。随机森林算法具有随机抽样、建立多棵决策树的特点，多棵决策树组合形成回归估计rn(X,Dn)为

(1)

其中，Dn为总数据集;X(X1, X2,…, Xi,…,Xk,k<n)为Dn中被抽取的自变量随机参数;EQ为与X有关的期望，其中rn(X,Q,Dn)为

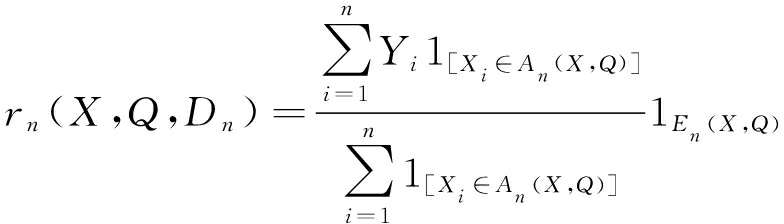
(2)

其中，1[·]为指标函数，当下标条件符合时1[·]=1，否则1[·]=0;Yi为在学习样本中与Xi相对应的因变量;An(X,Q)为一个包含X的随机单元分区;En(X,Q)为判定条件:

(3)

联立式(1)和(2)即可得到随机森林对因变量Q的回归估计:

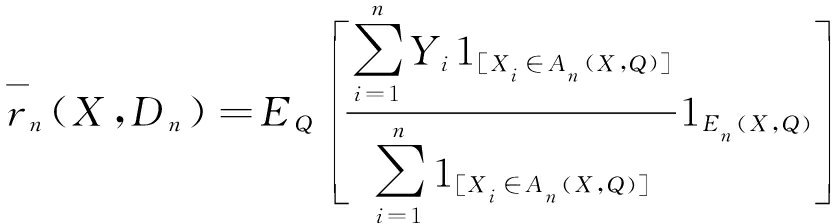
(4)

计算时可通过增加训练集Dn的数量，提高模型的预测精度[20]。当对新的数据进行分类预测时，采用多数投票法对新数据进行最终分类的输出，得到泛化误差PE*为

Q)=j)<0)

(5)

随机森林算法所使用的决策树模型是运用于分类以及回归的一种树结构。决策树由节点和有向边组成，一棵决策树包含一个根节点、若干内部节点和若干叶节点。根节点包含样本全集，内部节点对应于一个属性测试，每个节点包括的样本集合根据属性测试的结果被划分到子节点中。最终叶节点对应为决策结果，根节点到每个叶节点的路径对应了一个判定测试路径。

根据随机森林算法对分类树和回归树的定义[21]，将分类树、回归树的计算原理及流程总结如图1，2所示。图1分类树的最后一层为分类标签，其他节点可以认为是某个特征属性。按照特征判定标准逐步进行判定，直到最后一步得到分类结果。如图2所示的回归树中所有节点均为某一个待回归属性。按照特征判定标准逐步运行之后，即可得到回归值。

随机森林算法的回归精度由回归树的误差函数e(A)来体现:

(6)

式中，NA为节点A处的样本数;Bi为节点A处的第i个样本;为节点A处的样本均值。

2 排采工艺参数分析与历史产量拟合

2.1 模型主要参数

影响煤层气产能的参数包含地质参数、工程措施和排采工艺参数。煤储层地质参数分为动态参数和静态参数两个部分。静态地质参数由煤层的本质属性决定，如:煤层埋深、煤层厚度、地应力等;动态地质参数在排采过程中发生动态变化，如储层压力、渗透率等。排采工艺参数多为动态参数，主要受人为调控，如井底流压、套压、动液面深度、冲次、冲程等。

郑村区块主要开采山西组3号煤层和太原组15号煤层。以15号煤层为研究对象，煤层埋藏深度418～804 m，平均576 m，埋深呈北深南浅趋势变化。煤厚在1.5～8.8 m，平均厚度3.7 m。平均含气量为18.89 m3/t，属于煤层气富集区[22]。15号煤层煤岩类型以光亮煤为主，结构为碎裂、原生结构。孔隙以微孔、小孔为主;割理较发育，外生裂隙为煤层气的主要渗流通道。主裂隙长度主要为0.5～6.0 cm，密度约为11～25条/(5 cm)，高度为0.5～6.0 cm，裂隙连通性中等。煤储层渗透率为0.89×10-15 m2,综合分析表明15号煤层整体渗透性差，属于低渗储层，煤层顶板以灰岩为主，底板以泥岩为主，封闭性好[23]。

煤层气井在选址、钻井、水力压裂等前期工作均已完成的前提下，排采工艺参数成为影响煤层气井日产气量的主要因素。本文的重点在于研究排采工艺参数对煤层气井日产气量的动态影响规律。常见的煤层气井排采工艺参数包括生产套压、井底流压、动液面高度、冲次、冲程。因此在建模过程中，重点挖掘排采工艺参数与日产气量的内涵关系。选取8口15号煤层生产井，生产时间约为2 000～3 000 d，生产数据每日记录1次，将每天的生产数据为一个样本数据点，即每口井可以提取2 000个以上的数据样本点。

2.2 排采工艺参数的重要性分析

随机森林中有ntree棵决策树，那么特征变量xi的重要性计算公式为

(7)

Gain(xi,v)=GI(v)-wLGI(vL)-wRGI(vR)

(8)

(9)

其中，为特征变量xi的重要性，相当于算法结果中的IncMSE;Gain(xi,v)为xi在节点v的基尼信息增益;GI(v)为节点v的Gini指数定义;Sxi为xi在ntree棵树中所有节点分割结合;vL，vR分别为节点v的左右子节点;wL，wR为分配给左侧和右侧子节点的样本比例;为节点v中类别c所占的样本比例;C为有C个样本类别。

以A358井为例，将套压、流压、动液面、冲程、冲次、煤层埋深、日产气等参数与产量数据输入至R语言中，使用随机森林算法进行相关性(重要性)挖掘。将日产气量作为因变量，将套压、流压、动液面、冲程、冲次、煤层埋深作为自变量，得到重要性指标(IncMSE与IncNodePurity)如图3所示。图3中IncMSE为自变量重要性，即increase in MSE(均方误差的增量)。若特征变量xi对因变量(日产气量)相关性越高，则xi的IncMSE值越大。即说明xi对因变量(日产气量)越重要。IncNodePurity为节点纯度的增加，节点纯度表示节点对应的样本数据集中各类别数据所占的比例情况，若数据集中的所有数据均为同类，则数据集合为完全纯洁、纯度最高[24]。IncNodePurity数值代表模型精度，IncNodePurity数值越大，样本集合的不确定性越小，模型精度越高。由图3可知，自变量的重要性顺序为:流压>套压>动液面>冲次>冲程>埋深。

根据以往研究成果和本文随机森林算法得到的IncMSE与IncNodePurity，选用煤层埋深、生产套压、井底流压、动液面高度、冲次5个参数作为随机森林模型的自变量。同一口井的煤层深度变化不大，因此煤层埋深与日产气量的相关性不明显。但是不同埋深的煤储层应力分布、渗透率、孔隙度差异较大，导致其产量发生变化[25-26]。对不同埋深的生产井数据进行机器学习时，煤层埋深的影响将会增高。

2.3 排采数据预处理

排采原始数据中常常会包含有噪声、不完整的数据，此类数据对机器学习的准确性有影响，需对数据进行预处理，包括缺失值处理和异常数据处理两个方面。

2.3.1 缺失值处理

缺失值产生的主要原因是:在施工过程中未测量、虽测量但未记录。本文使用填补法补全数据，补全规则如下:

(1)套压列:空缺值补充为0。套压值空缺的原因一般为气井投产早期阶段煤层气未解吸，无数据记录，套压为0。

(2)流压、动液面列的数据在2014年11月之前，采用工人手动记录，经常每隔3～7 d才记录1次，故数据存在较多空缺值。在早期无产气时，由于排水作用，流压、动液面呈现降低的趋势，笔者将人工记录的数据作为端点数据，对空缺数据采用线性插值的方法补全。

(3)日产气列空缺值补充为0。因为日产气、日产水值空缺，一般为当天无产气、产水。

(4)冲次列的空缺值补充为0或借前1天数据，原因:冲次数据空缺一般因为停井，所以冲次数据补为0;也有时是由于工作人员未记录，所以采用前1天数据。

2.3.2 异常数据处理

异常数据是指那些明显偏离其他数据样本的数据“跳点”。人为因素，设备因素以及环境因素是造成排采数据出现异常点的主要原因。人为因素如记录数据错误、记录缺失等。设备因素如电路故障、抽油机故障、抽油杆断脱、卡泵等，此类因素无法预知且对煤层气日产量影响大。环境因素如遭雷击、因其他煤层气井压裂施工而停井、因环保问题而停井等[27]。考虑到煤层气排采过程中不确定性因素造成产量异常不能用于排采规律分析，本文将此类异常数据剔除。对于人为因素造成的记录缺失，则进行缺失值补全。

以A358井为例，异常数据预处理前后的套压、井底流压等参数如图4所示。

2.4 煤层气历史产量的拟合分析

随机森林算法可以解释若干自变量对因变量的影响。假设因变量存在n个样本，影响因变量的自变量为f个。在随机森林运算过程中，算法采用Bootstrap重抽样方法，随机抽取因变量的部分样本值，并从f个自变量中随机选取指定个数的变量，以此确定决策树节点[20]。在随机森林运算过程中，由于决策树的构建方法为随机抽样，所以算法构建出的每棵决策树可能互不相同，通常会随机生成几百甚至几千棵决策树。算法会从中选择重复度最高的决策树作为最终的运算结果。由决策树T构成组合模型，通过求ntree棵决策树的平均值形成随机森林模型的预测值。

以A358井为例，按如下步骤建立煤层气产量模型:

(1)运用Bootstrap法则，从2 440条生产数据中重复抽取数据，产生机器学习数据集，据此构建关于日产气量的回归树。而每次抽取学习部分的数据时，未被抽取的数据作为袋外数据，组成对日产气量的测试数据集。

(2)构建日产气量回归树时，在每棵树的分节点处从5个自变量:储层埋深、生产套压、井底流压、动液面高度、冲次中随机选取mtry种数据作为备选分枝变量，然后根据分枝优度准则在其中确定最优分枝。

(3)生成ntree棵日产气回归树，对煤层气井历史产气量进行拟合分析，建立了基于随机森林算法的煤层气井产气量模型(建模流程如图5所示)，拟合效果通过袋外数据预测的准确度来评价。

在随机森林算法建模过程中需要确定2个重要参数:mtry与ntree。mtry为树节点在预选时，所用的变量个数，若此数值太小会导致随机森林算法过于拟合，致使算法精度降低，太大会导致模型计算速度降低。ntree太小会导致训练不充分，太大会增加模型的运算量。在R程序中，一般的随机森林算法默认为mtry=1，ntree=500。为了提高计算精度，需要优先确定最优的mtry,ntree的数值。

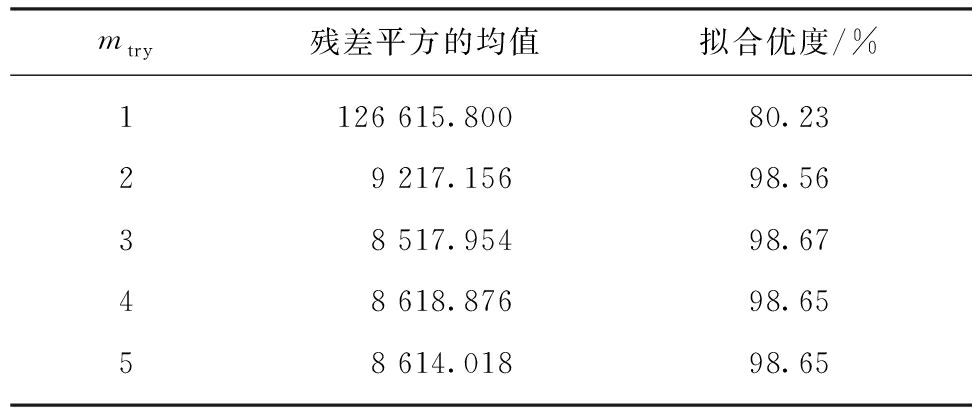
mtry选定的依据为:当随机森林算法模型计算得出的残余误差平方的均值越小、拟合优度越高时，此mtry数值为最优数值。表1显示了A358井数据使用随机森林算法，通过尝试不同的mtry值，进行残差平方均值与拟合优度计算。本模型中mtry的最优数值为3。

mtry数值确定后，再确定ntree的数值。设置ntree数量为1 000，A358井数据经过模型计算，得到模型误差与ntree的关系如图6所示。ntree的值越大，模型计算误差越小，当ntree>200，模型计算误差接近下界。依据ntree的数量不可过大或过小，且计算误差需要平稳较低的原则，故本模型中ntree的数值选定为400。

通过R语言中predict()函数，使用所建立的randomForest.model，带入作为模型自变量的排采工艺参数数据，即可进行对历史日产气量的拟合。

计算得到A358煤层气井的日产气量如图7所示。通过对比模型计算值与实际日产气量值，2 440个计算样本的平均误差为3.33%，其中84.3%的样本数据误差低于5%，可见本文基于随机森林算法建立的煤层气产量模型对实际生产数据的回归效果很好。

3 基于随机森林算法的日产气量预测

基于随机森林算法建立的煤层气产量模型，还可用于预测煤层气井未来的日产气量。将煤层埋深、生产套压、井底流压、动液面深度、冲次等自变量数值输入模型，计算得到A358井未来60 d的产气量。由表2可知:模型的预测值与实际产量的相对误差平均为2.19%;较高误差出现在第9天，为17.51%，95%的预测值与实际产量的误差小于5%。

除了A358煤层气井之外，本文对15号煤层的其他煤层气井(A345，A378，A339，A359，A374，A337，A354)也进行了日产气量的预测，以便进一步验证模型的适用性。煤层气井目标储层均为15号煤层，但产气量存在显著的差异。依据煤层气井日产气量的分类标准[28]，表3中A339,A374井为高产井，A358，A345，A378，A359， A354井为中产井，A337井为低产井。

依据随机森林构建流程(图5)，8口井模型计算的日产气量结果见表3。分析发现，A337井的降套压规律与其余7口井有差异。8口煤层气井见气之后，套压均呈现下降趋势。其中:A337井的套压下降过程中还伴随着反复的上下波动;A337和A345井的井底流压下降趋势为阶梯型;其余井的下降趋势为连续型。A337，A345井的产量低于其余井。可见井底流压和套压的控制对煤层气井产量影响较大，这与文献[29]的结论是一致的。

本文模型对15号煤层的不同产能煤层气井进行了60 d范围的日产气量预测，并将预测值与实际产气量进行了对比。对比表3中的相关数据，发现本文模型计算得到产量预测值中95%的计算值与实际产量的误差低于10%。由此可见在掌握煤层气井地质条件和生产数据的条件下，利用随机森林算法建立的煤层气产量模型，可实现对煤层气井产能的合理评价和预测。

基于气水两相流的理论模型，CLARKSON C R 和SEIDLE J 对煤层气井产量进行了预测[2-3]，其中CLARKSON C R将模型预测的煤层气井产量与实际产量进行了对比[2]，如图8所示，该模型研究了井底流压下降对产量的影响，计算结果反映了排采过程中日产气量和日产水量的变化趋势。

与以往模型不同，本文利用随机森林算法计算分析了地质参数和常见的排采工艺参数(井底流压、套压、动液面高度、冲次、冲程等)的重要性指标，在此基础上回归得到了基于随机森林算法的煤层气产量模型。模型综合考虑了多项排采工艺参数和历史产气量的动态变化对煤层气井当前日产气量的影响，具有较高的拟合及预测精度，为现有煤层气井的产能评估和预测提供了借鉴。

4 结 论

(1)对沁水盆地郑村区块太原组15号煤层的煤层气井地质参数、生产数据与产量数据的内涵关系进行了数据挖掘，计算得到了地质参数和排采工艺参数对产气量影响的重要性指标。研究显示井底流压和生产套压的变化对煤层气井产气量的影响较大。

(2)模型综合考虑了多个排采工艺参数和历史产气量的动态变化对煤层气井后续日产气量的影响，依据随机森林算法的分枝优度准则，可计算得到不同排采方案下的煤层气井日产气量，为现有煤层气井的产能评估和预测提供了一种新的方法。

(3)利用随机森林算法的煤层气产量模型，计算得到了沁水盆地郑村区块8口不同产能类型的煤层气井日产气量，模型拟合及预测精度较好，日产气量预测值中95%以上的数据与实际产量数据(测试样本)的误差小于5%。因此基于随机森林算法的煤层气产量模型具有较高的拟合及预测精度。

参考文献

[1] 李亚林.基于机器学习方法研究煤层气单井产量主控因素及产量预测[D].北京:中国石油大学,2017.

LI Yalin.Study on main control factors and production rediction of single well production of coalbed methane based on machine learning[D].Beijing:China University of Petroleum,2017.

[2] CLARKSON C R,QANBARI F.A semi-analytical method for forecasting wells completed in low permeability,undersaturated CBM reservoirs[J].Journal of Natural Gas Science and Engineering,2016,30:19-27.

[3] SEIDLE J P.Coal well decline behavior and drainage areas:Theory and practice[A].SPE Gas Technology Symposium[C].Calgary,2002.

[4] SUN Zheng,SHI Juntai,WU Keliu,et al.A fully-coupled gas-water two phase productivity equations for low-permeability CBM wells[J].Journal of Petroleum Science and Engineering,2018,166:611-620.

[5] 李贵红,张泓,崔永君,等.基于多元逐步回归分析的煤储层含气量预测模型——以沁水盆地为例[J].煤田地质与勘探,2005，33(3):22-25.

LI Guihong,ZHANG Hong,CUI Yongjun,et al.A predictive model of gas content in coal reservoirs based on multiple stepwise regression analysis:a case study from Qinshui Basin[J].Coal Geology & Exploration,2005,33(3):22-25.

[6] 胡亚斐,张遂安,吴峙颖.基于地质多元统计分析的煤层气含量建模方法——以沁水盆地南部某区块3号煤层为例[J].煤田地质与勘探,2013,41(2):33-36.

HU Yafei,ZHANG Suian,WU Zhiying.The gas content modeling method based on geological statistical analysis:With seam No.3 in southern Qinshui basin as an example[J].Coal Geology & Exploration,2013,41(2):33-36.

[7] 陈凤,申东日,陈义俊,等.模糊小波网络在煤与瓦斯突出预测中的应用[J].煤矿安全,2006(10):51-54.

CHEN Feng,SHEN Dongri,CHEN Yijun,et al.Application of waveletfuzzy net in prediction of coal and gas outburst[J].Safety in Coal Mines,2006(10):51-54.

[8] 郝吉生,袁崇孚.模糊神经网络技术在煤与瓦斯突出预测中的应用[J].煤炭学报,1999,24(6):624-627.

HAO Jisheng,YUAN Chongfu.The applying of fuzzy network techniques in prediction of coal and gas outbursts[J].Journal of China Coal Society,1999,24(6):624-627.

[9] 吴财芳,曾勇.基于遗传神经网络的瓦斯含量预测研究[J].地学前缘,2003,10(1):219-224.

WU Caifang,ZENG Yong.The genetic neural networks and gas content forecast[J].Earth Science Frontiers,2003,10(1):219-224.

[10] 吕玉民,汤达祯,李治平,等.煤层气井动态产能拟合与预测模型[J].煤炭学报,2011,36(9):1481-1485.

LÜ Yumin,TANG Dazhen,LI Zhiping,et al.Fitting and predicting models for coalbed methane wells dynamic productivity[J].Journal of China Coal Society,2011,36(9):1481-1485.

[11] 孟召平,田永东,雷旸.煤层含气量预测的BP神经网络模型与应用[J].中国矿业大学学报,2008,37(4):456-461.

MENG Zhaoping,TIAN Yongdong,LEI Yang.Prediction models of coal bed gas content based on BP neural networks and its applications[J].Journal of China University of Mining &Technology,2008,37(4):456-461.

[12] 苗玉,杨建华,卢伟.基于灰色支持向量机的煤层气单井采气参数预测[J].计算机应用,2016,36(S2):108-111,138.

MIAO Yu,YANG Jianhua,LU Wei.Coal-bed methane well’s parameter prediction based on grey support vector machine[J].Journal of Computer Applications,2016,36(S2):108-111,138.

[13] 李艳芳,程建远,王成.基于支持向量机的地震属性优选及煤层气预测[J].煤田地质与勘探,2012,40(6):75-78.

LI Yanfang,CHENG Jianyuan,WANG Cheng.Seismic attribute optimization based on support vector machine and coalbed methane prediction[J].Coal Geology & Exploration,2012,40(6):75-78.

[14] 颜爱华.煤层瓦斯含量多源数据分析及其预测研究[D].北京:中国矿业大学(北京),2010.

YAN Aihua.Study on multisource data analysis and prediction of gas content[D].Beijing:China University of Mining & Technology(Beijing),2010.

[15] 孙健,李琪,陈明强,等.基于机器学习的油气水层随钻识别模型优选[J].西安石油大学学报(自然科学版),2019,34(5):79-85,90.

SUN Jian,LI Qi,CHEN Mingqiang,et al.Optimization of model for identification of oil/gas and water layers while drilling based on machine learning[J].Journal of Xi’an Shiyou University (Natural Science Edition),2019,34(5):79-85,90.

[16] 温廷新,张波.露天煤矿边坡稳定性的随机森林预测模型[J].科技导报,2014,32(Z1):105-109.

WEN Tingxin,ZHANG Bo.Prediction model for open-pit coal mine slope stability based on random forest[J].Science & Technology Review,2014,32(Z1):105-109.

[17] 方匡南,吴见彬,朱建平,等.随机森林方法研究综述[J].统计与信息论坛,2011,26(3):32-38.

FANG Kuangnan,WU Jianbin,ZHU Jianping,et al.A review of technologies on random forests[J].Statistics & Information Forum,2011,26(3):32-38.

[18] LEO Breiman.Random forests[J].Machine learning.2001,45:5-32.

[19] 李欣海.随机森林模型在分类与回归分析中的应用[J].应用昆虫学报,2013,50(4):1190-1197.

LI Xinhai.Using“random forest”for classification and regression[J].Chinese Journal of Applied Entomology,2013,50(4):1190-1197.

[20] BIAU Gerard.Analysis of Random Forests Model[J].Journal of Machine Learning Research,2012,13:1063-1095.

[21] 张松林.CART-分类与回归树方法介绍[J].火山地质与矿产,1997,18(1):67-75.

ZHANG Songlin.An introduction to the methodology of CART—classification and regression trees[J].Volcanology & Mineral resources,1997,18(1):67-75.

[22] 肖七林,张曼婷,刘颖,等.沁水盆地南部煤层气地球化学特征及影响因素[J].地质科技情报,2017,36(5):118-124.

XIAO Qilin,ZHANG Manting,LIU Ying,et al.Geochemical characteristics of coalbed gas and influencing factors in the south of Qinshui Basin[J].Geological Science and Technology Information,2017,36(5):118-124.

[23] 李梦溪,崔新瑞,王立龙,等.郑村井区15号煤煤层气开发实践与认识[J].中国煤层气,2013,10(6):18-23,27.

LI Mengxi,CUI Xinrui,WANG Lilong,et al.Practice and cognition for CBM development in No.15 coal seam of Zhengcun Wellblock[J].China Coalbed Methane,2013,10(6):18-23,27.

[24] 屈俊峰,朱莉,胡斌.两种决策树的事前修剪算法[J].计算机应用,2006,26(3):670-672.

QU Junfeng,ZHU Li,HU Bin.Two algorithms of prepruning decision tree[J].Computer Applications,2006,26(3):670-672.

[25] 秦勇,申建.论深部煤层气基本地质问题[J].石油学报,2016,37(1):125-136.

QIN Yong,SHEN Jian.On the fundamental issues of deep coalbed methane geology[J].Acta Petrolei Sinica,2016,37(1):125-136.

[26] 叶建平，张守仁，凌标灿，等.煤层气物性参数随埋深变化规律研究[J].煤炭科学技术,2014,42(6):35-39.

YE Jianping,ZHANG Shouren,LING Biaocan,et al.Study on Variation law of coalbed methane physical property parameters with seam depth[J].Coal Science and Technology,2014,42(6):35-39.

[27] 王林,马飞英,刘全稳,等.基于产生式系统的煤层气井排采异常识别技术[J].煤田地质与勘探,2017,45(3):72-76.

WANG Lin,MA Feiying,LIU Quanwen,et al.Abnormal drainage identification of coalbed methane well based on production system[J].Coal Geology & Exploraytion,2017,45(3):72-76.

[28] 赵贤正,杨延辉,陈龙伟,等.高阶煤储层固-流耦合控产机理与产量模式[J].石油学报,2015,36(9):1029-1034.

ZHAO Xianzheng,YANG Yanhui,CHEN Longwei,et al.Porduction controlling mechanism and mode of solid-fluid coupling of high rank coal reservoirs[J].Acta Petrolei Sinica,2015,36(9):1029-1034.

[29] 胡秋嘉,毛崇昊,石斌,等.沁水盆地南部高煤阶煤层气井“变速排采-低恒套压”管控方法[J].煤炭学报,2019,44(6):1795-1803.

HU Qiujia,MAO Chonghao,SHI Bin,et al.“Variable speed drainagelow casing pressure”control method of high rank CBM wells in South Qinshui Basin[J].Journal of China Coal Society,2019,44(6):1795-1803.

A gas production model of vertical coalbed methane well based on random forest algorithm

ZHU Qingzhong1,HU Qiujia1,DU Haiwei1,FAN Bin1,ZHU Jie2,ZHANG Bin1,ZHAO Yuhan2,LIU Bin1,TANG Jun2

(1.PetroChina Huabei Oilfield Company,Renqiu 062550,China; 2.School of Mechanics & Civil Engineering,China University of Mining and Technology (Beijing),Beijing 100083,China)

Abstract:The evaluation and prediction of coal bed methane (CBM) is the critical basis of CBM exploitation schemes.Random Forest algorithm performs well in the evaluation and prediction of CBM,which has the advantages of small computation and high accuracy.The production of CBM is controlled by the geological parameters,engineering measures and extraction process parameters.The geological parameters of coal reservoir are divided into dynamic parameters and static parameters.The static geological parameters,such as the buried depth of the coal seam,the thickness of the coal seam,and the ground stress,are determined by the essential properties of the coal seam.Dynamic geological parameters,such as reservoir pressure and permeability,change dynamically in the process of pump and production.Mainly controlled by human operation,the pumping process parameters are mostly dynamic parameters,including bottomhole pressure,casing pressure,dynamic liquid level,pumping speed and stroke,which play an important role on CBM production,when the coalbed methane well enters the production stage after site selection,drilling and hydraulic fracturing stages.According to random forest algorithm,we analyzed how geological parameters and drainage parameters affect the gas production and ranked the parameters impacting on the gas production of coalbed methane well:flow pressure>casing pressure>dynamic liquid level>stroke>buried depth.The production data of coalbed methane wells in the latest 60 days were used as the test sample of gas production prediction,and the historical production data were used as the learning sample.The learning sample data were input into the R Programming Language after processing the missing values and abnormal production data,and Random Forest algorithm was used to fit and analyze the CBM production data.The production model of CBM wells was established by considering the effects of the process parameters and the dynamic changes of historical gas production on the subsequent daily gas production of CBM.Based on the branching goodness criterion of Random Forest algorithm,the model predicted the daily gas production of coalbed methane wells under different pumping schemes.After comparing the predicted value with the test sample,we found that the error between more than 95% of the predicted daily gas volume and the actual production data (test samples) is less than 5%,which means the production model of CBM vertical wells based on Random Forest algorithm has high fitting and prediction accuracy,providing a new method for CBM well productivity evaluation and prediction.

Key words:coalbed methane well;gas yield model;random forest algorithm;history matching;yield prediction

中图分类号:P618.11

文献标志码:A

文章编号:0253-9993(2020)08-2846-10

朱庆忠，胡秋嘉，杜海为,等.基于随机森林算法的煤层气直井产气量模型[J].煤炭学报,2020,45(8):2846-2855.

ZHU Qingzhong,HU Qiujia,DU Haiwei,et al.A gas production model of vertical coalbed methane well based on random forest algorithm[J].Journal of China Coal Society,2020,45(8):2846-2855.

收稿日期:2020-02-15

修回日期:2020-05-22

责任编辑:常明然

DOI:10.13225/j.cnki.jccs.2020.0205

基金项目:国家科技重大专项资助项目(2017ZX05064)

作者简介:朱庆忠(1966—)，男，河北景县人，教授级高级工程师，博士。Tel:0317-2752796，E-mail:cyy_zqz@petrochina.com.cn