内排土场是近水平、缓倾斜煤层露天开采的必然产物[1],也是治理煤自燃、扬尘与控制边坡稳定的最佳措施,其空间利用最大化是实现从技术可行的“容量”层次提升到经济合理的“成本效益”层次[2]。虽然我国露天煤矿横采内排开采技术已经广泛应用[3-6],但由于地层产状自身的倾斜性,导致内排土场工作线布置难于求解,若规划不合理,排土空间严重滞后,露天煤矿生产费用大幅增加[7-13]。因此,确定内排空间利用最大化的露天煤矿排土线布置方法成为解决该问题的关键。
近年来,国内外专家学者对内排土场规划及内排方案优化展开大量研究,如肖双双等[7]以剥离费用最小为目标,基于剥、采、排布置时空关系,提出了内排土场动态调整约束条件,构建了露天矿内排长远规划模型;丁小华等[14]以哈尔乌素露天煤矿内排土场为研究对象,优化原有端帮内排方案,提出避免剥离物运距“舍近求远”的最优方案。但针对内排空间利用最大化的露天煤矿排土线布置方法研究较少,广泛基于Auto CAD、3Dmine等绘图软件进行试绘,当内排土场基底为水平或近水平时,快捷、准确求出其布置方向;当内排土场基底为缓倾斜或倾斜时,试绘工作量大,且难于求出精确解。因此,迫切需要提出一种新的计算方法,用于解决内排空间利用最大化的露天煤矿排土线布置难题,为横采内排追踪开采技术在工程实践上的应用提供理论基础。
笔者以追踪距离50 m作为内排空间利用最大化的依据,应用3Dmine软件,在建立内排空间利用最大化的工程条件基础上,推导了露天煤矿排土线布置的数学表达式,理论上揭示了采场工作线布置及边坡角、内排土场边坡角、基底倾角对排土线布置的影响规律,并以某露天煤矿为工程示例,优化设计内排土场工作线布置,以期为类似工程实践提供借鉴。
1 建立内排空间利用最大化的工程条件
根据《煤炭工业露天矿设计规范》(GB50197—2015)[15]可知,内排土场最下一个排土台阶的坡底线与最下部采煤台阶坡底线的安全距离,应不小于50 m,即横采内排追踪距离为50 m,当最下台阶均能满足该条件,即可实现内排空间最大化。众所周知,当煤层为水平时,内排土场基底倾角为0°,采场工作线与内排工作线平行布置,且追踪距离为50 m,即可实现内排空间最大化,如图1(a)所示。当煤层为倾斜时,排土工作布置与采场工作线布置平行,会导致大量内排空间滞后(图1(b)),因此,需要将内排土场工作线布置进行优化,使其弥补平行布置内排空间滞后的不足,强化内排,建立内排空间最大化的工程条件,为推导露天煤矿排土线布置方法提供计算模型,如图1(c)所示。

图1 内排空间利用最大化的工程条件
Fig.1 Engineering conditions for maximizing the utilization of internal waste dump space
2 基于内排空间利用最大化的露天煤矿排土线布置方法
基于以上倾斜煤层露天矿内排空间利用最大化工程条件及已构建的采场、内排土场、端帮和基底空间几何模型,假设露天煤矿采场工作帮边坡角为βc;内排土场边坡角为βp;基底倾角为α;采场工作线布置方向为θc(采场工作线与端帮夹角);内排土场工作线布置方向为θp(排土工作线与端帮夹角)。
2.1 排土线布置优化
2.1.1 采场工作线横向布置,排土线布置优化
我国多数露天煤矿将采场工作线横向布置,为了内排空间利用最大化,内排土场工作线必然斜向布置,如图2所示。将露天煤矿划分两个计算区域,分别为Ⅰ区、Ⅱ区,Ⅰ区内的内排土场工作线布置可通过3Dmine中扩展台阶功能简单快捷求解,Ⅱ区内的排土线需要反复绘制,绘图工作量大,因此建立空间几何形态进行具体分析,推导采场工作线横向布置,排土线布置的表达式,计算模型侧视及空间几何形态如图3所示。

图2 计算区域分区示意及计算模型俯视
Fig.2 Calculation area partition schematic and top view of model

图3 计算模型侧视及空间几何形态
Fig.3 Lateral view of calculation model and space geometric shape
(1)绘制计算模型空间几何形态流程。第1个排土台阶在内排土场基底处尖灭点为O′,内排土场与端帮最下台阶交点为O,连接O′ O,长度为L0,以点O′,O分别作采场工作帮、端帮的垂线,平面交点为B,OB长度为L3,以点B向下作垂线与基底交点为B′,BB′长度为H,连接OB′,OB′长度为L,O′B′长度为L1,∠BO′B′为采场工作帮边坡角βc,∠BOB′为内排土场基底倾角α;以点O作内排土场工作线的平行线,以点O′作内排土场工作线的垂线,在平面交点为C,连接OC,O′C,长度分别为L4,L″2,以点C作垂线与基底交点为C′,与点O′同一标高为点C″,CC′长度为H1,C′C″长度为H2,连接OC′,OC′长度为L5,连接O′C′,O′C′长度为L2,O′C″长度L′2,∠CO′C″为内排土场边坡角βp,∠CO′C′为βs,∠C′O′C″为βj;以点C,C′分别作垂线与OB,OB′的交点为A,连接OA长度为l3,过点O′作垂直于端帮的竖直面,与基底交线为O′D′,与CA交点为点D,O′D′在水平面投影为O′D″,长度为Ld,∠D′O′D″为基底倾角α。
(2)内排空间利用最大化的露天煤矿排土线布置表达式推导。假设尖灭点O′与Ⅱ区端帮最下一个台阶坡底线标高的高差为H,则有

(1)
在三角形C′O′C″,D′O′D″与C″O′D″中根据三角函数关系可知

(2)
化简式(2)可得
![]()
(3)
在三角形BO′B′,BOB′与OO′B′中根据三角函数关系可知

(4)
在三角形CO′C″,COO′中根据三角函数关系可知

(5)
联立式(4),(5)可得
![]()
(6)
在三角形AOA′,OAC中根据三角函数关系可知

(7)
在三角形CO′C″与C′O′C″中根据三角函数关系并与式(1),(2)联立可得
![]()
(8)
由于θp1与θp互为余角,因此:
θp1+θp=90°
(9)
综合式(3),(6)~(9),内排土场工作线布置方向θp的表达式为
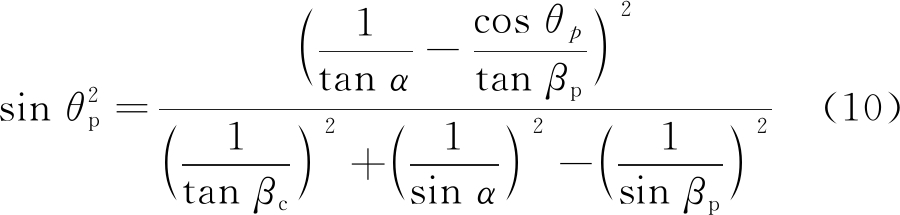
分析式(10)可知,当θp=0°时,α=βp,即横采内排开采程序实现内排空间利用最大化的充要条件为:基底倾角α小于内排土场边坡角βp。
2.1.2 采场工作线斜向布置,排土线布置优化
为了进一步研究采场工作线布置方向θc对内排土场工作线布置方向θp的影响,揭示采场工作线斜向布置时内排土场工作线布置方向θp与基底倾角α、采场工作帮边坡角βc、内排土场边坡角βp的关系,构建内排空间利用最大化的工程条件(图4),建立空间几何形态模型(图5),计算原理、作图流程及求解过程与采场工作线横向布置相同,只需将模型采场端向内排土场侧移动,形成公共边O′D。

图4 计算区域分区示意及计算模型俯视
Fig.4 Calculation area partition schematic and top view of model

图5 计算模型侧视及空间几何形态
Fig.5 Lateral view of calculation model and space geometric shape
假设第1个排土台阶在基底尖灭点O′与点D高差为H,则有

(11)
在三角形A′O′A″,D2O′D″1与A″O′D″1中根据三角函数关系可知

(12)
化简式(12)可得
cos θc=tan βg/tan α
(13)
在三角形AOA′,AOD中根据三角函数关系可得

(14)
由于![]() 结合式(14)可得
结合式(14)可得

(15)
在三角形ADO′中根据三角函数关系可知
![]()
(16)
联立式(11),(15),(16)可得

(17)
由于采场与内排土场具有相同的形态参数,只是数值不同,因此采取同样的原理与方法可求解出
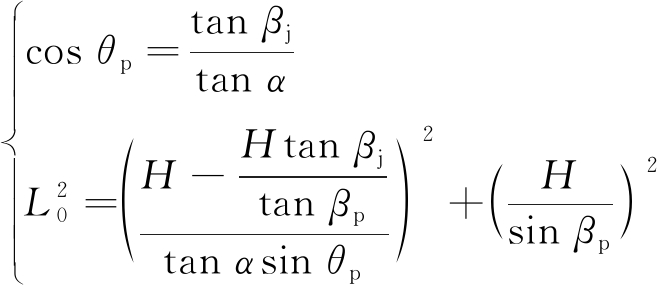
(18)
联立式(13),(17),(18),可得内排土场工作线布置方向θp的表达式为
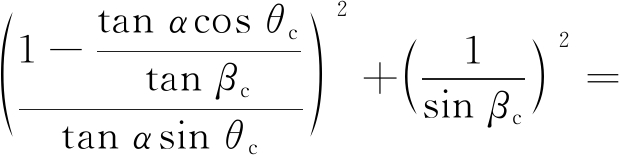

(19)
当θc=90°时,式(19)可化简为

(20)
综上分析可知,当θc=90°时,式(10)与式(20)具有一致性。
2.2 露天煤矿排土线布置影响因素分析
由于式(19)为隐函数,不能直接看出内排空间利用最大化的露天煤矿排土线布置方向θp与其他因素的相关性,笔者基于MATLAB与Origin软件,采用控制变量法对单一因素进行研究,揭示基底倾角α、采场工作帮边坡角βc、内排土场边坡角βp、采场工作线布置方向θc对内排土场工作线布置方向θp的影响规律,分析结果如图6所示。
分析图6可知,内排空间利用最大化的露天煤矿排土线布置方向θp与基底倾角α、采场工作帮边坡角βc呈负相关,与内排土场边坡角βp、采场工作线布置方向θc呈正相关。

图6 内排土场工作线布置方向θp与其他因素的关系曲线
Fig.6 Curve of relationship between θp and other factors
3 工程示例
某露天煤矿开采境界内可采原储量为 945.06 Mt,开采工艺为:松散土层剥离采用轮斗-胶带连续工艺,上部岩石剥离及采煤均用单斗-卡车间断工艺;原煤产量18.0 Mt/a,平均剥采比6.0 m3/t,年剥离量约为108 Mm3;采场工作帮边坡角约为16.1°,内排土场边坡角约为15.5°,内排基底倾角约为13.5°。笔者以该露天煤矿横采区为工程示例,根据该矿《2019—2023年剥采工程进度计划》可知,2023年横采区南帮、东帮、北帮均到界,由于征地及外排费用较大等原因,剥离物料全部排弃至东内排场,且采场工作线与南端帮垂直布置。因此,优化露天煤矿东内排土场工作线布置方向,充分利用内排空间对实现该矿安全经济高效生产具有重要意义。
基于以上分析,将采场工作帮边坡角、内排土场边坡角等已知参数代入式(10)或(20)中,求解内排土场工作线布置方向θp为
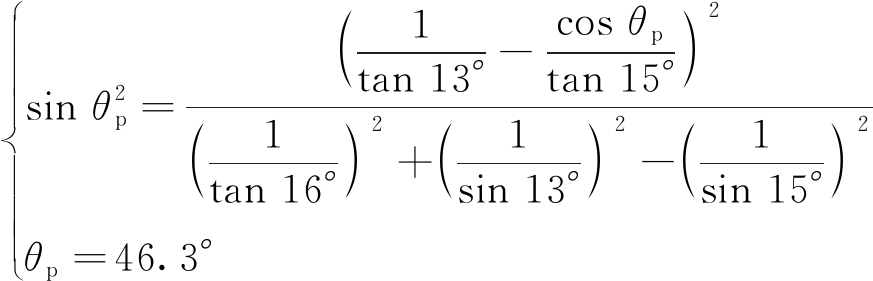
将内排土场工作线布置方向θp=46.3°求解后,应用3Dmine软件,简洁精确绘出露天煤矿横采区剥采工程平面图,如图7所示。

图7 2023年某露天煤矿横采区剥采工程进度计划示意
Fig.7 Stripping project schedule in 2023 of the horizontal mining area of an open-pit coal mine
针对2种方案进行内排量对比计算可知,内排空间利用最大化的方案②比方案①多利用约为15.1 Mm3内排空间,经济效益显著。计算结果如图8所示。

图8 2种方案内排空间利用量计算
Fig.8 Computation of utilization of internal waste dump based on two schemes
4 结 论
(1)兼顾基底倾角、采场工作帮边坡角、内排土场边坡角、采场工作线布置方向等相关因素,建立了内排空间利用最大化的露天煤矿排土线布置表达式,可与3Dmine软件结合,弥补常用方法设计排土线布置试绘工作量大的不足,为横采内排追踪开采技术在工程实践上的应用提供理论基础。
(2)横采内排开采程序实现内排空间利用最大化的充要条件为:基底倾角α小于内排土场边坡角βp;内排土场工作线布置方向θp与基底倾角α、采场工作帮边坡角βc呈负相关,与内排土场边坡角βp、采场工作线布置方向θc呈正相关。
(3)工程示例表明,某露天煤矿横采区2023年计划采场工作线方向θc=90°,内排土场工作线布置方向θp=46.3°才能实现内排空间利用最大化。
[1] 王东,李广贺,曹兰柱,等.软弱基底内排土场支挡煤柱的力学效应[J].煤炭学报,2019,44(3):934-941.
WANG Dong,LI Guanghe,CAO Lanzhu,et al.Mechanical effect of supporting and retaining coal pillar on internal waste dump with weak basement[J].Journal of China Coal Society,2019,44(3):934-941.
[2] 黄甫.内排条件下露天矿长远排土规划研究[D].徐州:中国矿业大学,2017.
HUANG Pu.Long-term planning of internal dumping in surface coal mining[D].Xuzhou:China University of Mining & Technology,2017.
[3] 周伟,韩流,才庆祥.内排土场对端帮边坡稳定性影响研究[J].采矿与安全工程学报,2015,32(4):671-676.
ZHOU Wei,HAN Liu,CAI Qingxiang.Influence of inner dump on end-slope stability[J].Journal of Mining & Safety Engineering,2015,32(4):671-676.
[4] 尚涛,才庆祥,刘勇,等.露天矿分区过渡期间合理开拓运输系统选择[J].中国矿业大学学报,2004,29(4):50-54.
SHANG Tao,CAI Qingxiang,LIU Yong,et al.Optimal selection of pit haulage systemin transition period for mining-in-areas[J].Journal of China University of Mining & Technology,2004,29(4):50-54.
[5] 赵红泽,张瑞新,刘云,等.改进模糊层次分析法的露天矿开采程序优化[J].辽宁工程技术大学学报(自然科学版),2014,33(2):145-151.
ZHAO Hongze,ZHANG Ruixin,LIU Yun,et al.Optimization of mining sequence based on improved fuzzy analytic hierarchy process in surface mines[J].Journal of Liaoning Technical University(Natural Science),2014,33(2):145-151.
[6] 白润才,白文政,刘光伟,等.倾斜煤层窄长形露天矿横采内排分期境界优化[J].煤炭学报,2017,42(10):2601-2608.
BAI Runcai,BAI Wenzheng,LIU Guangwei,et al.Installment boundary optimization of cross exploitation and inner dumping in the inclined coal seam narrow elongated open-pit mine [J].Journal of China Coal Society,2017,42(10):2601-2608.
[7] 肖双双,黄甫,李克民,等.露天矿内排长远规划模型及其求解方法[J].煤炭学报,2018,43(4):951-958.
XIAO Shuangshuang,HUANG Pu,LI Kemin,et al.Long-term planning model of internal dumping in surface coal mining and its solution method[J].Journal of China Coal Society,2018,43(4):951-958.
[8] MOSELHI O,ALSHIBANI A.Optimization of earthmoving operations in heavy civil engineering projects[J].Journal of Construction Engineering and Management.2009,135(10):948-954.
[9] MUNIAPPEN Kesavan,GENC Bekir.Dynamic simulation of an ope-ncast coal mine:A case study[J].International Journal of Coal Science & Technology,2020,7(1):164-181.
[10] OZDEMIR Burak,KUMRAL Mustafa.A system-wide approach to minimize the operational cost of bench production in open-cast mining operations[J].International Journal of Coal Science & Technology,2019,6(1):84-94.
[11] LONG N Q,BUCZEK M M,HIEN L P,et al.Accuracy assessment of mine walls’ surface models derived from terrestrial laser scanning[J].International Journal of Coal Science & Technology,2018,5(3):328-338.
[12] NOLAN A,KECOJEVIC V.Selection of overburden surface mining method in West Virginia by analytical hierarchy process[J].International Journal of Coal Science & Technology,2014,1(3):306-314.
[13] XIAO Shuangshuang,DONG Guowei,WANG Hongsheng.Dynamic capacity balance between stripping and mining of a dragline stripping system[J].International Journal of Coal Science & Technology,2020,7(2):380-387.
[14] 张亮,丁小华,曹智勇.近水平单一煤层露天矿端帮内排方案优化研究[J].煤炭科学技术,2017,45(4):45-49.
ZHANG Liang,DING Xiaohua,CAO Zhiyong.Study on optimization of internal dumpling of end wall for nearly horizontal open-pit coal mine with single coal seam[J].Coal Science and Technology,2017,45(4):45-49.
[15] GB50197—2015.煤炭工业露天矿设计规范[S].
