矿井通风系统在生产中无法避免风门开关或破损、巷道冒落或变形、底臌或片帮等现象,这种现象会引起系统等效风阻发生持久或永久性变化,称为矿井通风系统阻变型故障[1]。故障发生地点所对应矿井通风网络分支所在的位置称为故障位置,对应故障位置发生等效风阻变化的大小称为故障量。矿井通风系统阻变型故障诊断的目的为准确识别阻变型故障位置及其故障量。
在工程应用中,针对不同领域有许多不同故障诊断方法,如支持向量机,贝叶斯,遗传算法,神经网络,模糊逻辑学,深度学习等[2-11]。目前,在水管网、 管网、电网及天然气管网等方面有较多的相关研究。有相关学者利用贝叶斯分类器对水管网的泄漏位置进行了诊断研究[10];文献[12]针对城市给水管网故障诊断,提出了实时故障诊断方法,利用人工神经网络技术诊断故障位置、故障程度和故障影响范围;文献[13]针对电网中的信息畸变、保护断路器不正确动作等异常信息,提出了通过训练最大熵隐马尔科夫模型对电网故障数据所隐藏的异常模式进行挖掘,从而实现电网的故障诊断;文献[14]利用随机矩阵谱理论,建立成品油管道管网模型,提出集中式管道管网故障诊断模糊决策方法和基于图论模型的管道管网故障诊断方法,用于成品油管道管网的故障诊断;文献[15]利用支持向量机对水管网局部堵塞频率进行了故障诊断研究;文献[16]利用变分模式分解和模糊相关分类方法对天然气管网的小泄漏进行诊断了研究;文献[17]利用贝叶斯网络模型针对天然气管网失效概率进行了研究;文献[18]利用粒子群优化支持向量机参数,基于特征熵对管道泄漏进行了定位研究;文献[19]提出了一种基于信度规则库模型的无线传感器网络故障诊断方法,并利用协方差矩阵自适应进化策略(CMA-ES)对无线传感器网络故障模型的初始参数进行优化。目前,对于矿井通风系统故障诊断方面的研究包括:凌六一等[20]针对矿井通风机机械故障,利用收集的故障样本,提出了结合BP神经网络和D-S证据理论对各证据相结合的矿井通风机机械故障诊断的方法;黄雷[21]针对矿井局部通风故障诊断,收集了矿井历史局部故障实例,基于Web技术开发了矿井局部通风故障诊断专家系统;龚晓燕等[22]收集了矿井局部通风系统故障样本,并利用遗传算法和神经网络将故障进行分类,对局部通风系统的故障类别和位置进行了诊断研究;赵丹等[23-24]利用专家系统理论技术及矿井通风监控系统建立了矿井通风智能诊断专家信息库,用以解决通风系统故障诊断存在主观判断和误判断的问题,并确定出矿井通风系统流体网络中的分支风量与分支风阻之间的数学关系,从而通过监测到的异常风速值间接求出故障分支的位置;笔者等[1]定义了矿井通风系统阻变型故障诊断,以各矿井通风流体网络每条分支的风量作为特征,以矿井通风仿真系统[25-26]仿真模拟的阻变型故障实例作为样本,利用支持向量机分类方法对阻变型故障进行了分类和回归研究;胡青伟[27]构建了矿井通风系统异常诊断指标体系,并实现对矿井通风系统的异常状态诊断,建立了矿井通风系统异常影响范围库,利用矿井通风在线监测数据和BP神经网络方法实现矿井通风系统异常原因识别的技术。
目前在矿井通风系统故障诊断方面的研究主要集中在机械故障、矿井通风系统稳定性及异常诊断等方面,而对矿井通风系统阻变型故障诊断方面的研究较少,且这些故障诊断方法中难以避免故障训练样本的收集。因此,在矿井通风系统阻变型故障诊断方法中存在几个亟待解决的问题:① 需要建立专家系统或收集故障样本,在诊断过程中离不开样本的参与;② 故障位置诊断和故障量诊断无法同时进行,在进行故障诊断之前需要分别建立故障位置诊断和故障量诊断模型;③ 难以实现矿井通风系统阻变型故障实时在线诊断。基于此,笔者基于CMA-ES进化算法[28],提出一种无监督学习的故障诊断方法,建立分类与回归一体化的数学模型,实现矿井通风系统阻变型无监督故障诊断。此方法在诊断过程中无需故障样本参与训练,避免因样本数据噪声产生的误差或出现欠拟合及过拟合的现象,同时可达到矿井通风系统阻变型故障实时诊断的目的。
1 故障诊断模型及求解方法
1.1 问题描述
在矿井通风系统阻变型故障诊断对应的通风系统流体网络中,将故障位置对应的分支称为故障分支;将为故障诊断提供数据的分支称为观测点。设V为矿井通风系统流体网络中m个节点的集合,E为矿井通风系统流体网络中n条分支的集合,则矿井通风系统流体网络为G=(V, E),其中V={v1,v2,v3,…,vm},E={e1,e2,e3,…,en}。设矿井通风系统中未发生阻变型故障的通风系统流体网络观测点的原始风阻集合对应的向量为R0;发生阻变型故障后的观测点风量集合对应的向量为Q′;风压集合对应的向量为H′;矿井通风系统流体网络中故障分支编号为ex;故障量大小为Δrx,N·s2/m8,其中x∈(1,2,3,…,n),表示故障位置对应分支编号索引。矿井通风系统阻变型故障诊断的目标为:在已知正常情况下,各观测点的风阻R0=(r01,r02,r03,…,r0n)及故障时所监测到的观测点风量Q′=(q′1,q′2,q′3,…,q′n)和风压H′=(h′1,h′2,h′3,…,h′n),求出x及Δrx。其中,风阻单位为N·s2/m8,风量单位为m2/s,风压的单位为Pa。
对于任何正常运行或出现阻变型故障的矿井通风系统,均满足:
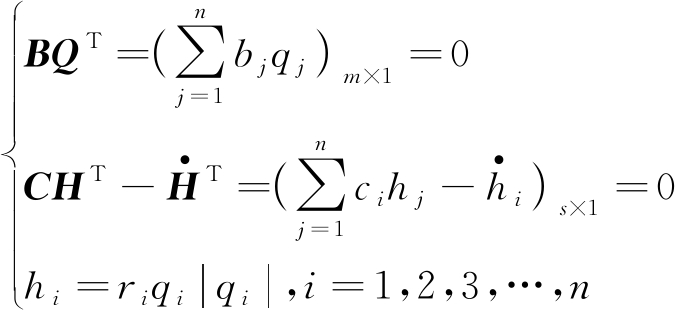
(1)
其中,B为节点和分支所组成的关联矩阵;Q和H分别为分支风量集合和风压集合所对应的向量;![]() 为回路附加阻力矩阵;C=(cij)s×n为通风网络的回路矩阵;s为回路总数,其中
为回路附加阻力矩阵;C=(cij)s×n为通风网络的回路矩阵;s为回路总数,其中
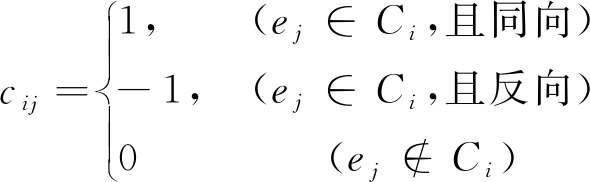
(2)
由式(1)可知,任何分支的等效风阻发生变化会引起整个系统各分支对应的风量及风压发生变化。反之,当监控到系统中分支风量和风压发生变化时,系统对应的流体网络中至少有一条分支的等效风阻发生变化,且常见为一条分支的等效风阻发生变化[1]。
在笛卡尔坐标系中,假设p=(p1,p2,…,pz),q=(q1,q2,…,qz)为欧几里得空间中的两点,则点p和点q之间的欧式距离表达式为
d(p,q)=d(q,p)=
![]()
(3)
根据欧式距离的定义,将矿井通风系统阻变型故障后的风量(风压)向量与预设等效风阻所求的风量(风压)向量作为欧几里得空间中的两点,则矿井通风系统阻变型故障诊断问题可转化为求故障前后风量(风压)向量的欧式距离问题。若所求得的欧式距离大,则说明预设的等效风阻与实际发生的故障位置和故障量不符合,反之若求得的欧式距离越小,则说明所预设的故障位置和故障量越接近实际阻变型故障发生的情况。
1.2 无监督学习故障诊断数学模型
矿井通风系统阻变型故障诊断实际为求解欧式距离问题,而距离小方可得到准确的故障位置和故障量,因此,矿井通风系统阻变型故障诊断模型为求解故障前后故障分支风量(风压)欧式距离最小的优化问题。流体网络中观测点的风量(风压)与等效风阻之间的关系符合平衡定律:
(q′1,q′2,…,q′x,…,q′nq,h′1,…,h′x,…;h′nh)=f(Rx)
(4)
Rx=(r01,r02,…,r0x+Δrx,…,r0n)
(5)
式中,nq∈[0,n]为监测风量的观测点数,nh∈[0,n]为监测风压的观测点数;r0i为编号i的分支原始风阻,N·s2/m8,i=1,2,3,…,n;q′x为故障后分支ex的风量,m2/s;h′x为故障后分支ex的风压,Pa。
设待求解的向量为x=(x,Δrx),其中x为故障位置,属于分类问题;Δrx为故障量,N·s2/m8,属于回归问题,利用式(6)作为矿井通风系统阻变型故障诊断无监督学习模型的目标函数,求得的最优解既包括分类结果,也包括回归结果,实现矿井通风系统阻变型故障诊断的分类与回归一体化。
![]()
(6)
式中,α+β=1为自定义调节参数;0<x≤n;lx≤Δrx≤ux,lx和ux分别为故障分支ex对应等效风阻变化下限和上限,![]() 为CMA-ES进化迭代过程中的风量解;q′i为故障后分支ei的风量,
为CMA-ES进化迭代过程中的风量解;q′i为故障后分支ei的风量,![]() 为CMA-ES进化迭代过程中的风压解;h′i为故障后分支ei的风压,Pa。
为CMA-ES进化迭代过程中的风压解;h′i为故障后分支ei的风压,Pa。
1.3 故障诊断模型的求解
矿井通风系统阻变型故障诊断为一个求最小欧式距离的优化问题,优化求解方法有很多,其中CMA-ES算法是一种最成功的无导数全局优化算法,被归为一种进化策略算法[29]。因此,笔者所提的阻变型故障诊断模型求解方法为CMA-ES,下面介绍求解的关键流程。
(1)随机产生新解。通过对多变量正态分布进行抽样,生成新种群,每次迭代从![]() 中产生λ个新解,mt为正态分布的均值,σt∈
中产生λ个新解,mt为正态分布的均值,σt∈ +为步长,Ct=BD2BT为协方差矩阵,B为正交矩阵,D为对角矩阵。采样搜索点的基本方程为
+为步长,Ct=BD2BT为协方差矩阵,B为正交矩阵,D为对角矩阵。采样搜索点的基本方程为
xi=mt+σtyi
(7)
其中,t为迭代次数;i=1,2,3,…,λ,yi=BDN(0,I);I为单位矩阵。
(2)求解目标函数值。利用式(6)和式(7)求解各个解对应的目标函数值f(xi:λ),其中i=1,2,3,…,λ,并对其进行从小到大排序操作:
f(x1:λ)≤f(x2:λ)≤…≤f(xλ:λ)
(8)
(3)更新均值参数。设μ为被选择解的个数,ωi为重组的正权系数,则均值参数的更新如下:
![]()
(9)
其中,ω1≥…≥ωμ>0。
(4)更新协方差矩阵。构造进化路径公式为
![]()
(10)
其中,c为协方差矩阵秩,称为累积更新学习率,![]() 则协方差矩阵的更新如下:
则协方差矩阵的更新如下:
![]()
(11)
(5)更新步长参数。根据式(12)和(13)对步长参数进行更新。
![]()
(12)
![]()
(13)
其中,s0=0;cσ为学习速率的累加步长控制参数;dσ为更新步长的阻尼参数。
(6)终止判断。判断是否达到设定的最大迭代代数,如果达到则终止,输出x,否则根据式(7)~(13)继续迭代计算,直至达到终止条件终止。
2 模拟仿真试验
为了验证所提的矿井通风系统阻变型故障诊断无监督学习模型的可行性和求解方法的有效性。本文使用文献[1]的矿井通风系统及其数据,其网络图如图1所示,利用网络解算迭代,模拟矿井通风系统阻变型故障,并使用CMA-ES对数学模型进行求解。
为了证明CMA-ES方法对矿井通风系统阻变型故障诊断的适用性和泛化性,阻变型故障模拟覆盖除风井分支外的整个矿井通风网络,即所有试验的故障分支的集和为矿井通风中除风井分支外的所有分支。在进行试验之前需要对每条故障分支的风阻上下限进行估算,以避免网络解算过程中出现无法找到风机工况点的现象。根据文献[1]所提供的分支编号及对应的风阻,通过对每条故障分支的风阻不断进行增值和降值操作,最终得到各故障分支的风阻变化上下限见表1,其中风井变化范围为[0,0],x为故障分支编号索引,即故障位置,lx和ux分别为各故障分支的等效风阻变化下限和上限,N·s2/m8。
模拟仿真试验过程中,每次试验选择一条分支作为故障分支,并在故障分支对应的等效风阻变化范围内随机产生一个浮点数作为故障量。如当x=3,故障分支为e3,l3=-0.003 N·s2/m8,u3=3.0 N·s2/m8,在-0.003与3.000之间随机取浮点数0.349 6作为故障量,即:Δr3=0.349 6 N·s2/m8。利用r03=r03+Δr3=0.03+0.349 6=0.379 6 N·s2/m8替换原始风阻,并进行矿井通风网络解算可得到一组风量集合向量Q′和一组风压集合向量H′,模拟产生了故障位置和故障量对应的监控风量和监控风压。初始化n=100,及各故障分支对应的风阻变化上、下限,使用式(7)~(13)进行迭代求最优解,当达到终止条件时,将输出的x和Δr与模拟产生的故障位置和故障量进行比较,若输出的故障位置与模拟产生的故障位置一致,表明故障位置诊断结果正确,否则故障位置诊断失败;若输出的故障量与模拟产生的故障量误差较大,表明故障量诊断结果不可靠,反之,误差越小说明故障量诊断结果越可靠。
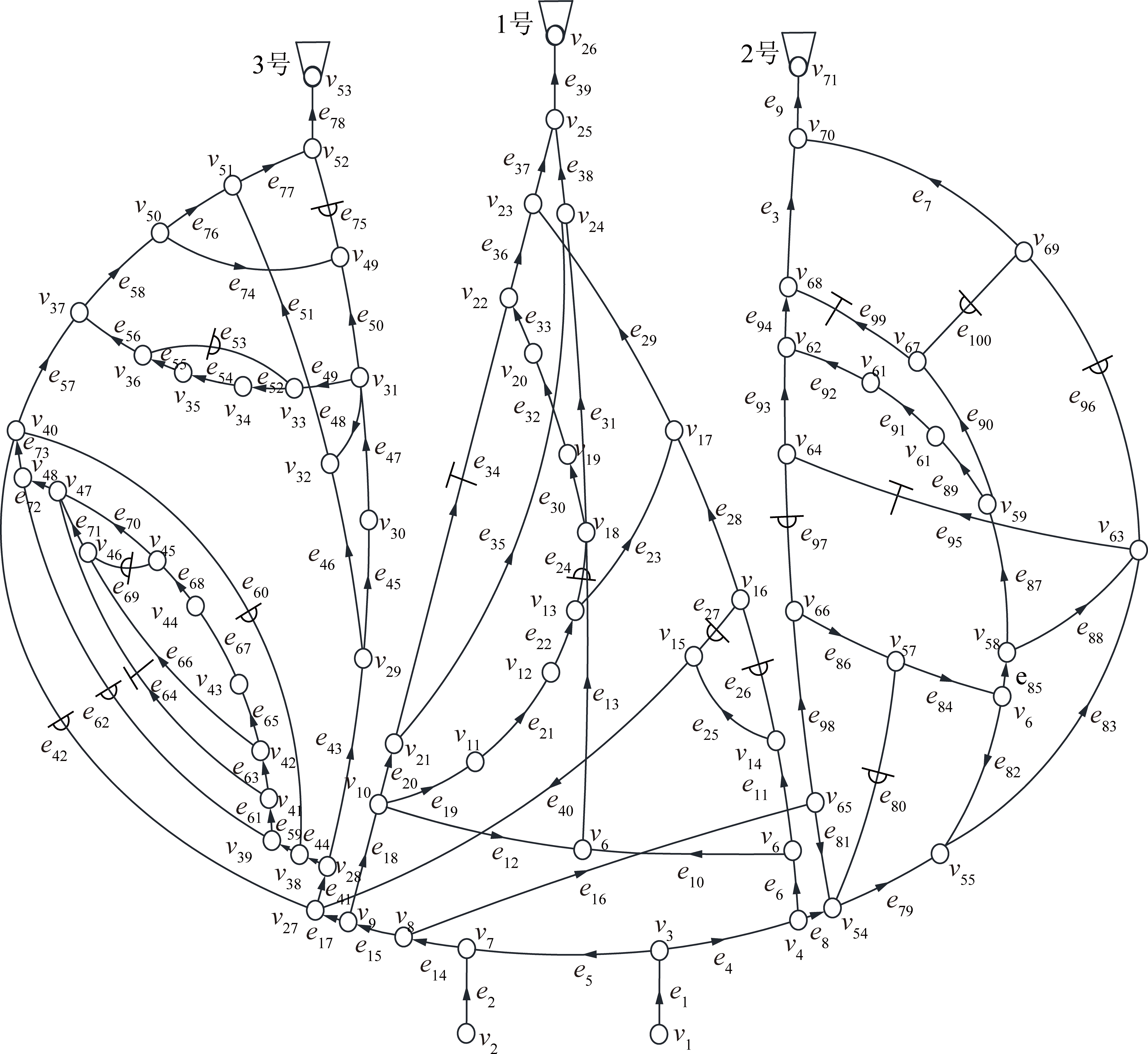
图1 试验矿井通风系统流体网络
Fig.1 Test mine ventilation system fluid network diagram
表1 故障分支等效风阻变化范围
Table 1 Equivalent wind resistance variation range for fault branches
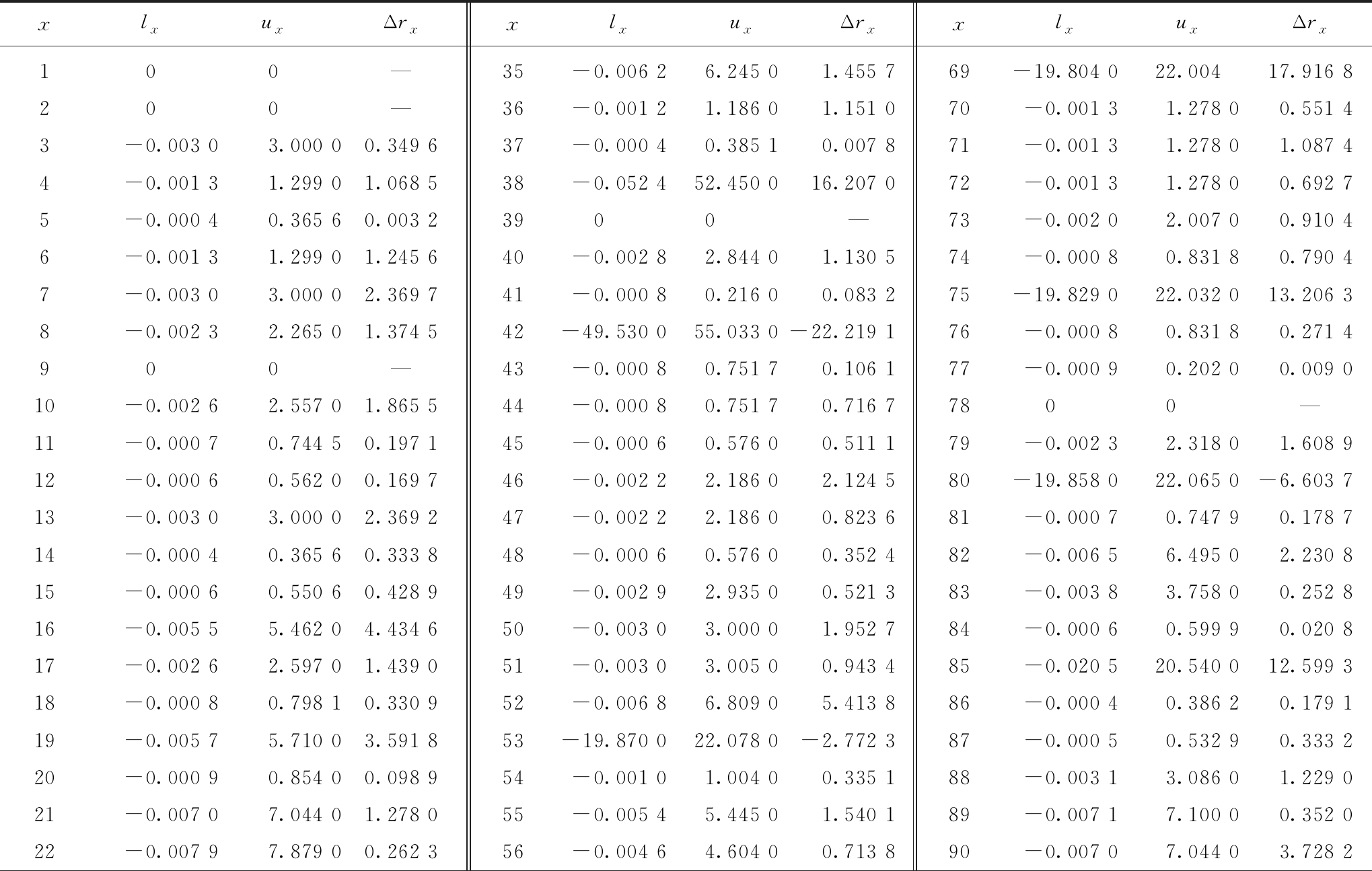
xlxuxΔrxxlxuxΔrxxlxuxΔrx100—35-0.006 26.245 01.455 769-19.804 022.00417.916 8200—36-0.001 21.186 01.151 070-0.001 31.278 00.551 43-0.003 03.000 00.349 637-0.000 40.385 10.007 871-0.001 31.278 01.087 44-0.001 31.299 01.068 538-0.052 452.450 016.207 072-0.001 31.278 00.692 75-0.000 40.365 60.003 23900—73-0.002 02.007 00.910 46-0.001 31.299 01.245 640-0.002 82.844 01.130 574-0.000 80.831 80.790 47-0.003 03.000 02.369 741-0.000 80.216 00.083 275-19.829 022.032 013.206 38-0.002 32.265 01.374 542-49.530 055.033 0-22.219 176-0.000 80.831 80.271 4900—43-0.000 80.751 70.106 177-0.000 90.202 00.009 010-0.002 62.557 01.865 544-0.000 80.751 70.716 77800—11-0.000 70.744 50.197 145-0.000 60.576 00.511 179-0.002 32.318 01.608 912-0.000 60.562 00.169 746-0.002 22.186 02.124 580-19.858 022.065 0-6.603 713-0.003 03.000 02.369 247-0.002 22.186 00.823 681-0.000 70.747 90.178 714-0.000 40.365 60.333 848-0.000 60.576 00.352 482-0.006 56.495 02.230 815-0.000 60.550 60.428 949-0.002 92.935 00.521 383-0.003 83.758 00.252 816-0.005 55.462 04.434 650-0.003 03.000 01.952 784-0.000 60.599 90.020 817-0.002 62.597 01.439 051-0.003 03.005 00.943 485-0.020 520.540 012.599 318-0.000 80.798 10.330 952-0.006 86.809 05.413 886-0.000 40.386 20.179 119-0.005 75.710 03.591 853-19.870 022.078 0-2.772 387-0.000 50.532 90.333 220-0.000 90.854 00.098 954-0.001 01.004 00.335 188-0.003 13.086 01.229 021-0.007 07.044 01.278 055-0.005 45.445 01.540 189-0.007 17.100 00.352 022-0.007 97.879 00.262 356-0.004 64.604 00.713 890-0.007 07.044 03.728 2
续 表

xlxuxΔrxxlxuxΔrxxlxuxΔrx23-0.001 21.186 00.377 557-0.008 38.318 00.946 791-0.006 36.344 06.072 624-198.008 0220.009 0-77.296 458-0.000 80.751 70.311 392-0.013 713.690 03.148 125-0.000 40.374 40.168 059-0.000 80.751 70.523 093-0.001 31.320 00.253 726-29.706 033.007 08.797 860-49.521 055.023 011.355 194-0.062 862.790 025.784 327-29.706 033.007 029.083 961-0.000 80.751 70.091 195-0.012 612.590 06.319 928-0.000 60.595 00.089 162-49.542 055.047 038.275 196-19.902 022.113 0-1.389 929-0.000 30.306 80.078 363-0.001 51.514 00.428 397-99.070 0110.080 080.773 730-0.004 64.577 02.930 264-19.812 022.014 0-4.242 498-0.005 05.000 04.473 431-0.003 43.421 01.265 165-0.000 40.396 60.310 499-19.870 022.078 017.546 332-0.000 70.680 90.610 366-0.003 13.091 01.409 6100-19.800 022.000 09.546 533-0.003 43.365 01.779 367-0.001 01.032 00.906 534-0.052 952.850 024.804 368-9.904 011.004 0-4.554 6
针对不同的nq和nh大小,分别进行多次模拟试验,以分析风量特征、风压特征及风量-风压复合特征下的矿井通风系统阻变型无监督学习故障诊断性能及故障诊断模型的工程应用适用性。因此,针对所有的分支监控数据,设计4组模拟试验:① nq=100,nh=0;② nq=0,nh=100;③ nq=100,nh=100;④ 随机给定nq和nh,并随机选择风量和风压监测的位置。每组试验过程中,分别以每条分支作为故障分支,模拟产生故障量,进行最优求解,并以故障位置诊断准确度和故障量误差大小作为故障诊断的评价指标。
3 结果分析
根据表1给定的故障分支编号及其对应的等效风阻变化下限和上限,除风井对应的分支外,每次不重复的以其中一条分支作为故障分支进行一次故障模拟,模拟得到的故障分支和故障量见表1,其中故障量Δrx的单位为N·s2/m8。所有故障分支的模拟故障量均在设定的等效风阻变化上下限范围内,符合试验设定条件。
根据表1提供的故障位置和故障量,进行矿井通风网络解算得到发生阻变型故障情况下的风量(风压),利用所提出的阻变型故障诊断模型进行故障诊断,得到的故障位置和故障量诊断结果如图2所示。图中左侧为故障位置诊断结果与故障位置模拟结果的对比,右侧为故障量诊断结果与故障量模拟结果对比。其中在故障位置结果图中,若“模拟位置”与“预测位置”重合在一个坐标点上,说明故障位置的诊断结果与模拟结果一致,否则认为故障位置诊断失败,这种情况下的故障量诊断也被认定为失败;剔除故障量诊断失败的结果,得到图中右侧的故障量诊断结果,横坐标为模拟的故障量,纵坐标为预测的故障量,黑色的圆点离红色虚线的垂直距离越小,说明故障量诊断的结果越好,故障量诊断误差越小。如图3所示为故障量成功诊断情况下的误差分析,其中横坐标为试验序号,左侧纵坐标对应诊断和模拟故障量的相对误差,右侧纵坐标对应诊断和模拟故障量的绝对误差。
根据图2,3可得到,以风量为故障诊断的特征时(nq=100,nh=0),故障位置和故障量诊断性能均不如以风压作为故障诊断特征(nq=0,nh=100)进行故障诊断得出的诊断性能好,而以风量-风压同时作为故障诊断特征(nq=100,nh=100)时,故障诊断的性能最佳,在图中表现为“模拟位置”和“预测位置”坐标重合点数更多,故障量诊断误差更小;相对误差呈现为上下波动少,与发生故障的故障量大小无关,故障诊断的绝对误差较其他更为平稳;相对误差整体比分别以风量或风压单独作为故障诊断特征时小,且相对误差在±5%内的试验次数最多。
通过对各故障分支发生故障进行统计分析得出表2,其中EMA表示平均绝对误差,EMS表示均方误差。① 当风量作为故障诊断的特征,并以所有分支作为观测点时,即nq=100,nh=0。故障位置诊断的准确率为86.71%,故障量诊断的平均绝对误差为0.432 3 N·s2/m8,均方误差为4.439 9 N2·s4/m16,R2为0.977 5。② 当风压作为故障诊断的特征,并以所有分支作为观测点时,即nq=0,nh=100。故障位置诊断的准确率为94.74%,故障量诊断的平均绝对误差为0.224 7 N·s2/m8,均方误差为1.052 7 N2·s4/m16,R2为0.995 1。③ 当风量-风压同时作为故障诊断的特征,并以所有分支作为观测点时,即nq=100,nh=100。故障位置诊断的准确率为96.55%,故障量诊断的平均绝对误差为0.118 4 N·s2/m8,均方误差为0.158 7 N2·s4/m16,R2为0.999 1。
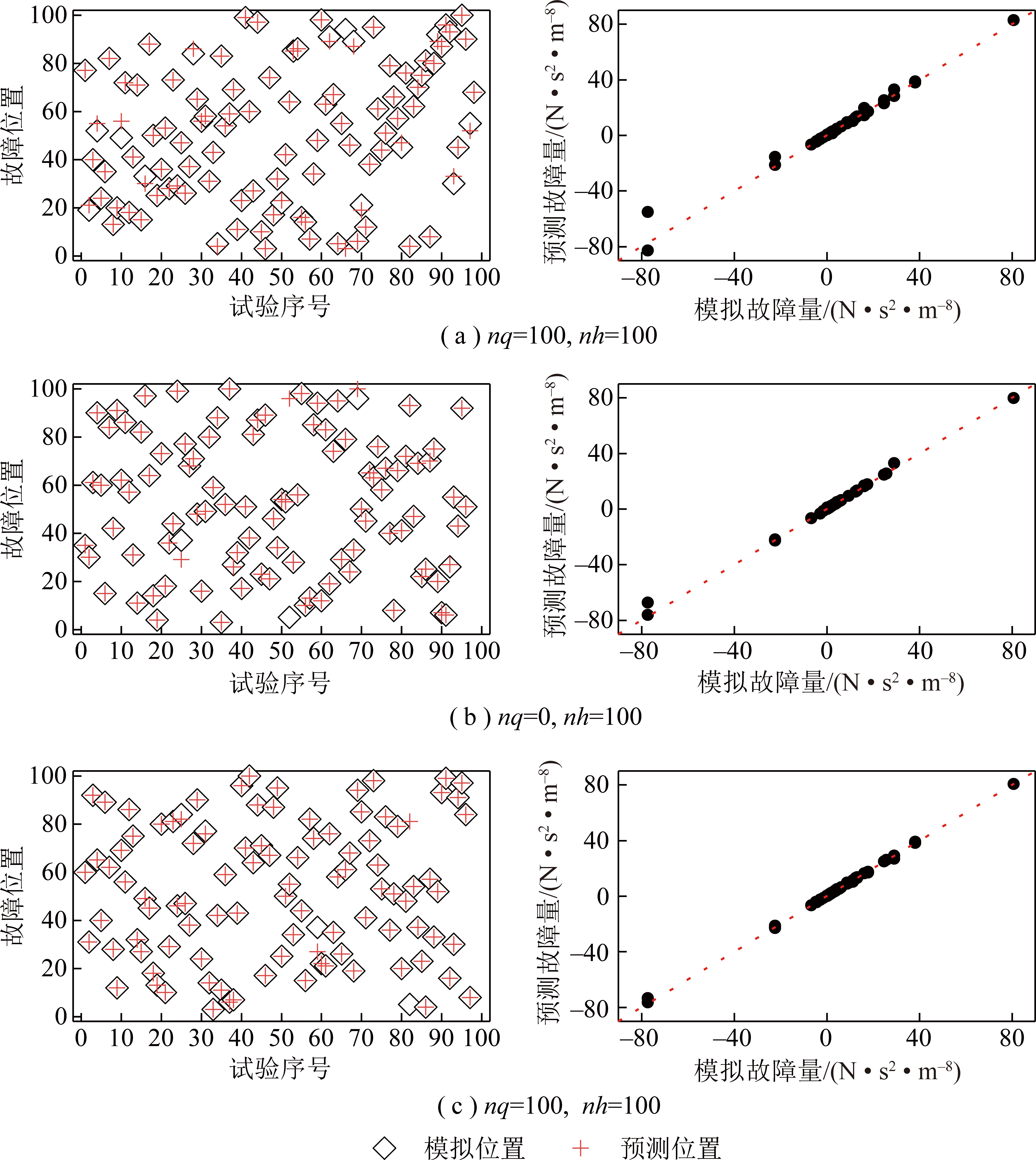
图2 故障位置和故障量诊断结果
Fig.2 Results of fault location and amount of fault diagnosis
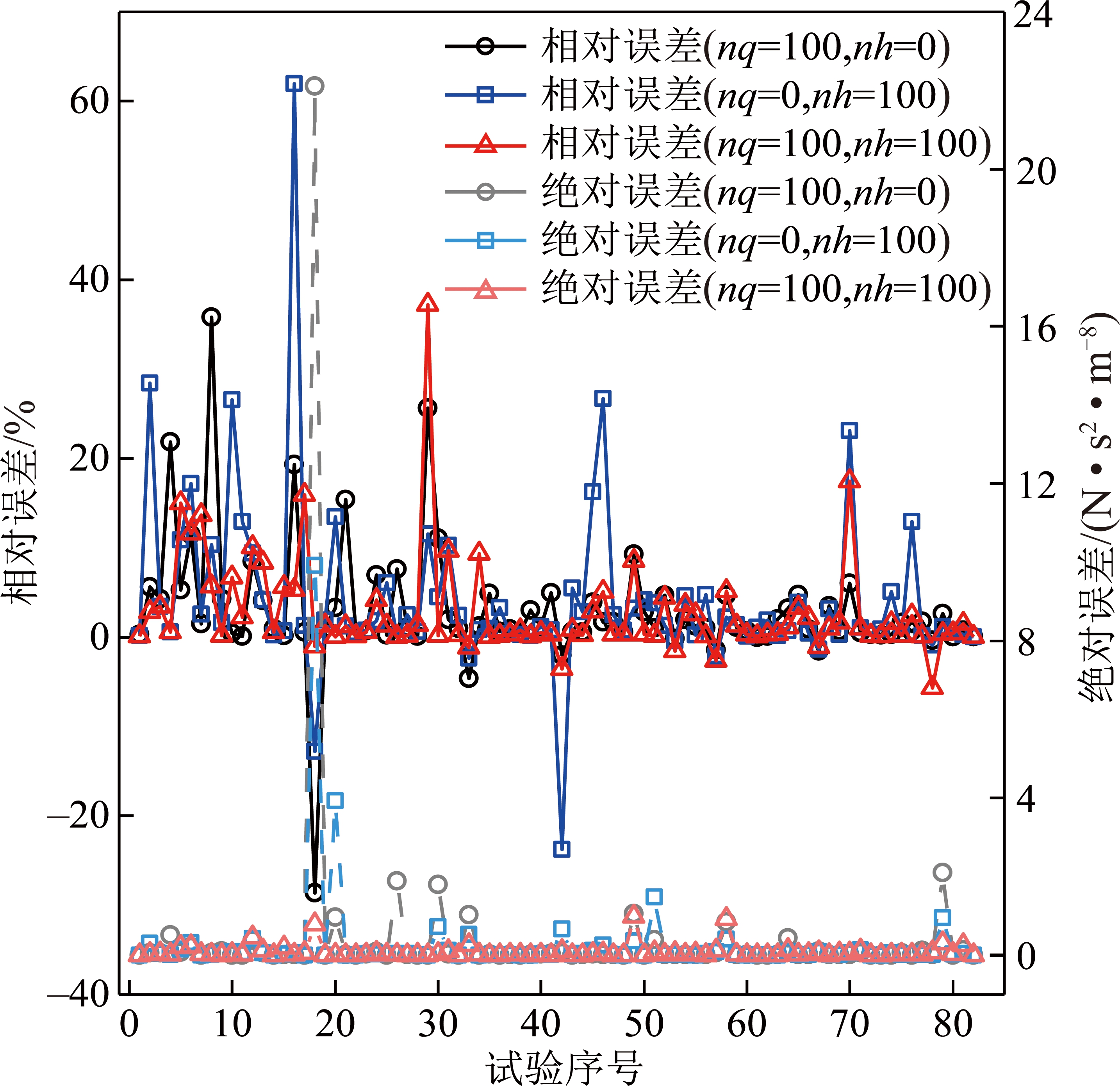
图3 故障量诊断误差
Fig.3 Error in fault diagnosis
不同观测点比例下的故障位置诊断准确率如图4所示,其中横坐标表示在进行故障诊断时,选择的观测点数占所有分支总数的比例,纵坐标表示不同观测点比例下的故障位置诊断准确率。由故障诊断结果可知,即使观测点比例小于50%,故障位置诊断的准确率均超过80%,高于文献[1]中使用支持向量机及所有观测点进行故障位置诊断的准确率(78.11%)。当选择部分观测点进行故障位置诊断时,也可达到选择所有观测点进行故障位置诊断的准确率,且观测点比例大小与故障诊断的准确率无直接影响关系。整体故障位置诊断结果呈现出的趋势为:风量-风压混合特征下的故障诊断优于风压单一特征的故障诊断,而风量单一特征下的故障诊断性能相对不佳,但是其具有一定的稳定性,即使20%以下的观测点也可达到nq=100下的故障位置诊断准确率。
表2 试验结果统计
Table 2 Test result statistics

试验方案准确率/%EMA/(N·s2·m-8)EMS/(N2·s4·m-16)R2nq=100,nh=086.710.432 34.439 90.977 5nq=0,nh=10094.740.224 71.052 70.995 1nq=100,nh=10096.550.118 40.158 70.999 1
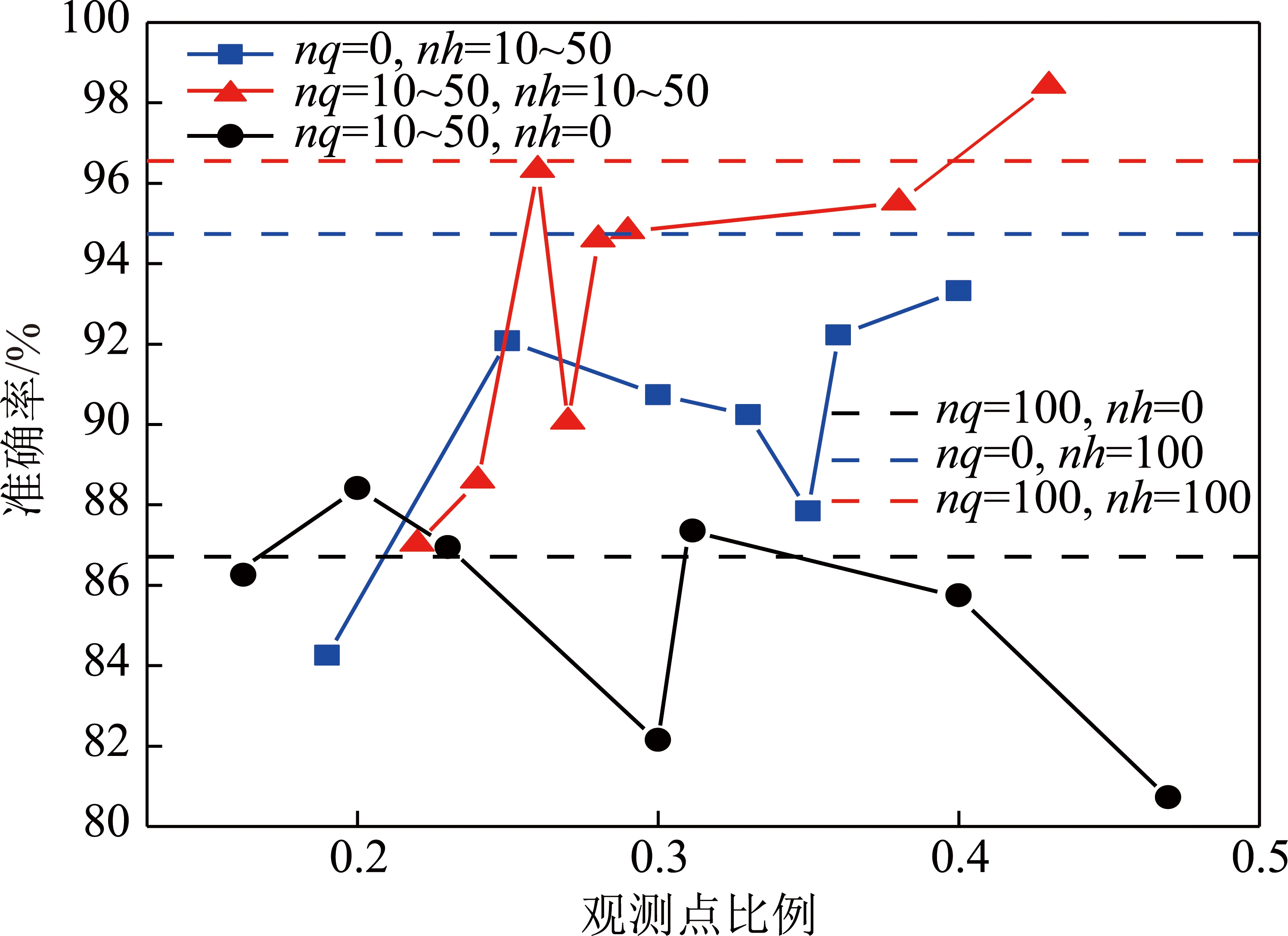
图4 不同观测点比例下的故障位置诊断结果
Fig.4 Results of fault location diagnosis at different observation point ratios
上述试验结果证明矿井通风系统阻变型故障位置诊断和故障量预测,风量-风压混合特征下的故障诊断试验结果均最优,全部分支的风量和风压监测下,故障位置准确率达到96.55%,故障量诊断的平均绝对误差为0.118 4 N·s2/m8,均方误差为0.158 7 N2·s4/m16,R2为0.999 1,而低于50%观测点比例下故障位置诊断准确率也可达到甚至超过96.55%。选择不同数量的风量分支和风压分支进行故障位置和故障量模拟和故障诊断试验,其结果见表3。当观测点比例超过50%,低于65%时,故障位置诊断的准确率超过97%,故障量诊断R2值超过0.99,平均绝对误差低于0.32 N·s2/m8,均方误差低于1.89 N2·s4/m16。结果表明,本文所提的方法可用于矿井通风系统阻变型故障诊断。
表3 不同风量和风压观测点数故障诊断结果
Table 3 Results of fault diagnosis for different air volume and wind pressure observation points
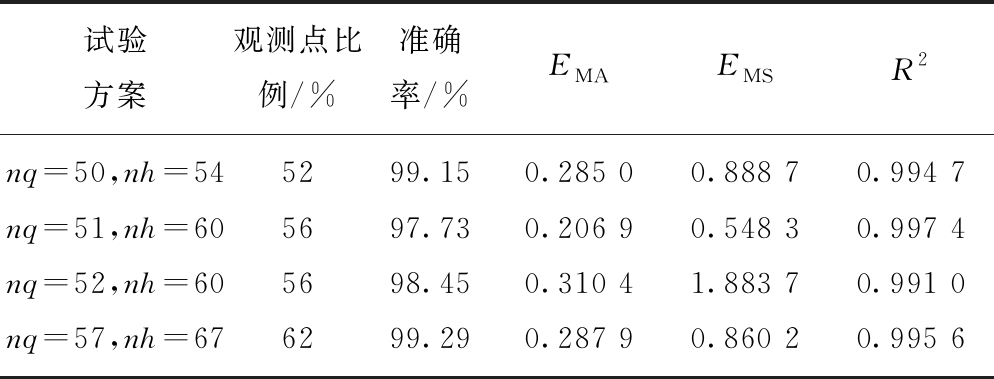
注:EMA单位为N·s2/m8;EMS单位为N2·s4/m16。
试验方案观测点比例/%准确率/%EMAEMSR2nq=50,nh=545299.150.285 00.888 70.994 7nq=51,nh=605697.730.206 90.548 30.997 4nq=52,nh=605698.450.310 41.883 70.991 0nq=57,nh=676299.290.287 90.860 20.995 6
课题组在金川集团二矿进行实际应用试验。通过打开关闭状态下的风门和停机运行状态下的风机机站方式进行故障模拟,利用金川二矿矿井通风系统获取的矿井通风网络图,分支数为1 006条,节点数为870个,经过节点映射网络等技术后,矿井通风网络图分支数为178条,节点数为106个。利用观测点位置优化计算得到观测点数为总分支数的10%,但在复杂的井下环境中,其中3个观测点不具备人工测试数据的条件,共得到15观测点。本次共进行了5个阻变型故障工业试验,其中4个风门打开试验位置分别为:850水平材料车场风门、850水平通主斜坡道风门、1050水平措施道与回风道联络巷风门、1350水平充填回风道风门;1个风机停机试验位置为:850水平西翼风机站。5个故障点的故障诊断准确率均达100%。
综上述,本文所提出的无监督学习阻变型故障诊断模型可使用风量或风压单一特征进行矿井通风系统阻变型故障诊断,要获得更高的故障诊断准确率,需使用风量-风压复合特征进行故障诊断,即使选择部分观测点对应的巷道进行风量(风压)监控也具有较高的故障诊断准确率。
4 结 论
(1)使用CMA-ES对建立的分类与回归一体化的矿井通风系统阻变型故障诊断数学模型进行求解,可实现无需样本参与训练的无监督学习故障诊断,进而实现矿井通风系统阻变型故障的实时诊断。
(2)风量-风压复合特征比风量或风压单一特征下的矿井通风系统阻变型故障诊断可获得更高准确率的故障位置诊断和更低误差的故障量诊断。在实际应用中,结合风速和压差传感器同时配备使用可实现更为精准的阻变型故障诊断。
(3)在本文试验条件下,使用部分观测点条件下的风量-风压复合特征矿井通风阻变型故障诊断,故障位置诊断的准确率最高可达到99.29%,故障量诊断的R2值超过0.99,其故障诊断的性能优于风量或风压单一特征下的阻变型故障诊断。
(4)观测点比例大小与故障位置诊断准确率及故障量诊断误差无直接影响关系,但是与观测点的合理选配(传感器布置位置优化选定)有关,合理的观测点选配方案可实现在少量观测点数的情况下达到100%准确率的效果,此问题另文介绍。
[1] 刘剑,郭欣,邓立军,等.基于风量特征的矿井通风系统阻变型单故障源诊断[J].煤炭学报,2018,43(1):143-149.
LIU Jian,GUO Xin,DENG Lijun,et al.Resistance variant single fault source diagnosis of mine ventilation system based on air volume characteristic[J].Journal of China Coal Society,2018,43(1):143-149.
[2] YAN X A,JIA M P.A novel optimized SVM classification algorithm with multi-domain feature and its application to fault diagnosis of rolling bearing[J].Neurocomputing,2018,313:47-64.
[3] MOHAMMED M A,GHANI M K A,ARUNKUMAR N,et al.Genetic case-based reasoning for improved mobile phone faults diagnosis[J].Computers & Electrical Engineering,2018,71:212-222.
[4] ZHAO H T,LAI Z H.Neighborhood preserving neural network for fault detection[J].Neural Networks,2019,109:6-18.
[5] SONG L,WANG H,CHEN P.Step-by-step fuzzy diagnosis method for equipment based on symptom extraction and trivalent logic fuzzy diagnosis theory[J].IEEE Transactions on Fuzzy Systems,2018,26(6):3467-3478.
[6] TRABELSI M,BOUSSAK M,GOSSA M.PWM-Switching pattern-based diagnosis scheme for single and multiple open-switch damages in VSI-fed induction motor drives[J].ISA transactions,2012,51(2):333-344.
[7] GUO D F,ZHONG M Y,JI H Q,et al.A hybrid feature model and deep learning based fault diagnosis for unmanned aerial vehicel sensors[J].Neurocomputing,2018,319:155-163.
[8] HELBING G,RITTER M.Deep learning for fault detection in wind turbines[J].Renewable & Sustainable Energy Reviews,2018,98:189-198.
[9] ZHANG Y Y,LI X Y,GAO L,et al.A new subset based deep feature learning method for intelligent fault diagnosis of bearing[J].Expert Systems with Applications,2018,110:125-142.
[10] SOLDEVILA A,FERNANDEZ-CANTI R M,BLESA J,et al.Leak localization in water distribution networks using Bayesian classifiers[J].Journal of Process Control,2017,55:1-9.
[11] YI Xin,REN Lifeng,MA Li,et al.Effects of seasonal air temperature variation on airflow and surrounding rock temperature of mines[J].International Journal of Coal Science & Technology,2019,6(3):388-398.
[12] 梁建文,肖笛,赵新华,等.给水管网故障实时诊断方法[J].水利学报,2001,32(12):40-47.
LIANG Jianwen,XIAO Di,ZHAO Xinhua,et al.On-line fault diagnosis of water distribution systems[J].Journal of Hydraulic Engineering,2001,32(12):40-47.
[13] 胡江,赵冬梅,张旭,等.基于最大熵隐马尔科夫模型的电网故障诊断方法[J].电网技术,2019,43(9):3368-3375.
HU Jiang,ZHAO Dongmei,ZHANG Xu,et al.A power grid fault diagnostic method based on maximum entropy hidden markov model[J].Power System Technology,2019,43(9):3368-3375.
[14] 胡旭光.基于随机矩阵谱理论的成品油管道管网故障诊断方法研究[D].沈阳:东北大学,2017.
HU Xuguang.Research on products oil pipeline network fault diagnosis based on spectral theory of random matrix[D].Shenyang:Northeastern University,2017.
[15] KIM D S,SHIN S,CHOI G B,et al.Diagnosis of partial blockage in water pipeline using support vector machine with fault-characteristic peaks in frequency domain[J].Canadian Journal of Civil Engineering,2017,44(9):707-714.
[16] XIAO Q Y,LI J,BAI Z L,et al.A small leak detection method based on VMD adaptive de-noising and ambiguity correlation classification intended for natural gas pipelines[J].Sensors,2016,16(12):16.
[17] WANG W H,SHEN K L,WANG B B,et al.Failure probability analysis of the urban buried gas pipelines using Bayesian networks[J].Process Safety and Environmental Protection,2017,111:678-686.
[18] NI L,JIANG J C,PAN Y,et al.Leak location of pipelines based on characteristic entropy[J].Journal of Loss Prevention in the Process Industries,2014,30:24-36.
[19] HE W,QIAO P L,ZHOU Z J,et al.A new belief-rule-based method for fault diagnosis of wireless sensor network[J].IEEE Access,2018,6:9404-9419.
[20] 凌六一,黄友锐.基于多传感器信息融合的矿井通风机故障诊断[J].煤炭科学技术,2008,36(6):72-74.
LENG Liuyi,HUANG Yourui.Fault diagnosis of mine ventilator base on multi sensor information integration[J].Coal Science and Technology,2008,36(6):72-74.
[21] 黄雷.基于Web的矿井局部通风故障诊断专家系统[D].西安:西安科技大学,2008.
HUANG Lei.Fault diagnosis expert system of local ventilation in coal mine based on web[D].Xi’an:Xi’an University of Science and Technology,2008.
[22] 龚晓燕,孙晓辉.基于遗传算法的矿井局部通风故障诊断神经网络模型[J].煤矿安全,2008,39(5):35-38.
GONG Xiaoyan,SUN Xiaohui.Neural network model for fault diagnosis of mine local ventilation based on genetic algorithm[J].Safety in Coal Mines,2008,39(5):35-38.
[23] 赵丹,刘剑,潘竞涛.基于网络分析的矿井通风智能诊断专家系统[J].安全与环境学报,2011,11(4):206-210.
ZHAO Dan,LIU Jian,PAN Jingtao.A renovated network-based intelligent diagnosis mining-ventilation expertise system[J].Journal of Safety and Environment,2011,11(4):206-210.
[24] 赵丹,潘竞涛.改进灵敏度矩阵的矿井通风故障源诊断及传感器布置研究[J].中国安全科学学报,2011,21(2):78-84.
ZHAO Dan,PAN Jingtao.Fault source diagnosis for mine ventilation based on improved sensitivity matrix and its wind speed[J].China Safety Science Journal,2011,21(2):78-84.
[25] 贾进章,刘剑,耿晓伟.矿井通风仿真系统数学模型[J].辽宁工程技术大学学报,2003,22(S1):88-90.
JIA Jinzhang,LIU Jian,GENG Xiaowei.Mathematical model of mine ventilation simulation system[J].Journal of Liaoning Technical University,2003,22(S1):88-90.
[26] ZHOU Lihong,YUAN Liming,THOMAS Rick.Iannacchione Anthony.Determination of velocity correction factors for real-time air velocity monitoring in underground mines[J].International Journal of Coal Science & Technology,2017,4(4):322-332.
[27] 胡青伟.大平煤矿通风系统异常诊断研究[D].徐州:中国矿业大学,2019.
HU Qingwei.Research on abnormal diagnosis of ventilation system in Daping coal mine[D].Xuzhou:China University of Mining and Technology,2019.
[28] HANSEN N,OSTERMEIER A.Completely derandomized self-adaptation in evolution strategies[J].Evolutionary Computation,2001,9(2):159-195.
[29] HANSEN N.The CMA evolution strategy:A comparing review[M].Springer:Towards a New Evolutionary Computation,2006:75-102.
