射流破煤技术是煤层增渗与瓦斯强化抽采技术的重要组成部分，根据射流载体的不同，可以分为水力化射流和气体射流两种类型。水力化射流的研究历史悠久，有代表性的包括高压水射流[1-3]、磨料水射流[4-5]和空化水射流[6-7]等。卢义玉等[4]认为水射流破煤主要借助于冲击效应、剥蚀效应以及震动效应等冲击荷载作用。李根生等[8]研究发现水射流作用下，煤体的破坏可分成若干阶段，在每个阶段由于压缩剪切作用形成破碎核，在破碎核侧面形成拉应力区产生径向拉伸裂纹。顾北方等[9]通过对高压水射流割缝煤体损伤演化规律进行研究，提出水射流破煤可分为冲击破坏、剪切破坏和拉伸破坏3个阶段。CHENG[10]对具有不同长度裂纹的岩石相似材料在单轴压缩载荷作用下的力学性能和破坏特征、损伤空间发展规律以及损伤演化特征进行了实验研究，结果表明，随着裂纹长度的增加，主要破坏模式由剪切破坏转变为拉伸破坏。
考虑到水力化射流技术可能存在的水封抑制瓦斯解析[11]和降低煤体渗透率[12-13]的缺陷，即因毛细管效应而在煤层孔隙通道中产生封堵效应，从而降低煤层的抽采率;裂隙煤体内煤泥浆液颗粒逐渐扩散并沉积，裂隙不断被充填，导致裂隙煤体渗透率的不断下降。一些学者提出了气体射流破煤增渗的技术方向，包括磨料气射流[14]和高压气射流[15]等。关于气体射流破煤机理，刘勇等[15]认为高压气体射流冲击煤体时，以准静态载荷和动态载荷作用于煤体，并以应力波加载的方式在煤体内形成贯穿裂纹导致煤体破裂。赵旭等[16]开展了高压氮气冲击致裂试验，认为煤体在气射流的冲击作用下形成初始裂缝，在准静态应力场作用下促使裂纹得到进一步扩展。需要指出的是，气射流破煤是高压气体自喷嘴加速，在空气中自由发展，最终破煤成坑的连续综合过程。与水射流不同的是，由于气体本身的黏滞性、可压缩性和三维运动特征，气体压力、速度、温度和密度等基本物理属性在整个连续过程中必然会有明显变化，其变化规律也直接决定了本身能量较低的气体射流的最终破煤效果，而以往的研究主要集中在气射流破煤成坑阶段，对于其连续过程机理研究处于相对空白的状态。
因此，笔者基于空气动力学与岩石力学等理论，详细分析了气射流破煤“加速-发展-冲击”的连续综合过程，理论推导不同阶段的数学模型并以此为基础提出气射流破煤的判别准则，并初步分析气射流破煤能力与成坑特征。
1 气射流破煤连续过程机理
1.1 气射流加速
为使高压气射流冲击作用于煤体壁面有更高的滞止压力，将更多的静压能转变为动能，则需要气射流拥有更高的速度。从空气动力学[17]角度出发，在不可压缩流体的假设下，借助流体的连续方程m=ρSV可知，气体流经管路截面的收缩引起气流加速，管路截面扩张引起气流减速，通常通过喷嘴实现气体的加速。由于不可压缩流体可视为亚声速可压缩流体的一种极限情况，因此认为亚声速气流遵循相同规律。但超声速气体的流动特点相反，假设气体在喷嘴中的流动为一维定常等熵流动，对流体的的连续性方程取对数微分有
(1)
式中，ρ为流体的密度，kg/m3；S为流体截面积，m2；V为流体的流动速度，m/s。
对量热完全气体，其动量方程有
(2)
式中，k为绝热系数；Ma为马赫数；p为气体的压力，MPa。
气体能量方程的微分形式可写成
(3)
式中，T为气体的温度，K。
对气体的状态方程p=ρRT进行微分处理得
(4)
式(1)～(4)即为考虑喷嘴截面积变化时的一维定常等熵流动的基本方程组，若将喷嘴截面积的变化率dS/S视为独立自变量，则可以求出各气动参数与喷嘴截面积变化率之间的关系。结合马赫数Ma的微分形式:
(5)
联立式(1)～(5)，可得到气体参数(流速)微分变量与喷嘴截面积变化率之间的关系式为
(6)
对亚声速流(Ma<1)而言，dV和dS异号，其物理意义为速度的变化和截面积的变化的方向相反，即在缩放形喷嘴的收缩段(dS<0)内，亚声速气流降压升速;在喷嘴的扩张段内(dS>0)内，亚声速气流增压减速。而对超声速流(Ma>1)来说，在喷嘴收缩段内，超声速气流增压降速;扩张段内，气流降压增速。考虑到dV不会趋于无穷大，当Ma=1即1-(Ma)2=0时，必有dS=0。满足dS=0的截面只能是喷嘴最大截面或者最小截面处，但是亚声速气流只有经过收缩段才能加速到声速，超声速气流也只有在收缩段中才能减速至声速，因此在喷嘴的最小截面处亚声速气流能够达到的最大速度就是声速，同样，超声速气流在喷嘴的最小截面处能实现的最小速度也是声速。
基于以上分析可以得出，单纯的截面收缩并不能使亚声速气流加速至超声速，即借助目前普通的圆锥收缩性喷嘴，气流速度最大只能达到声速。要想使气体实现超声速流动，必须采用收缩-扩张形喷嘴，即拉瓦尔喷嘴。在相同外界参数条件下，通过缩放型喷嘴可实现气流速度自亚声速至超声速的跃迁。缩放形喷嘴通常由收敛段、喉部、扩张段3部分组成，其结构如图1所示。
图1 缩放型喷嘴结构示意
Fig.1 Schematic diagram of scaled nozzle structure
1.2 气射流发展
气体射流自喷嘴喷出至环境介质之中，直至冲击某一壁面为止，射流沿其发展特性可分为典型3区，即自由射流区、冲击区和壁面射流区[18-19]，其分区如图2所示。
图2 气射流发展分区示意
Fig.2 Schematic diagram of air jet development zones
在自由射流区，射流外边界与周围空气介质间存在剪切-驱动等相互作用，剪切应力的存在会导致湍流现象的产生，引起射流速度在轴向的衰减，同时加剧射流对周围空气流体的卷吸，引起射流总流量的增加，造成射流断面沿径向的不断扩张;在冲击区，射流发展开始受到壁面限制，轴向速度急剧下降，但射流作用于壁面的静压力开始上升，显现出很大的压力梯度，迫使射流流线产生快速弯曲，射流由原先的轴向流动转换为近壁面流动，该区域的特征是滞止点的存在和射流流线的径向弯曲;在壁面射流区，射流总体呈现沿径向向外的运动，射流速度沿壁面向外快速上升直至最大值，由于存在与壁面和空气介质间的剪切等相互作用，在距滞止点较远距离后，射流速度开始衰减直至为零。
1.3 气射流冲击
与理想弹塑性材料破裂过程的弹塑性破裂理论[20]和锻造挤压理论[21]不同，由于煤体是裂隙孔隙双重介质特性的脆性材料，当射流以一定的动能瞬时冲击煤体时，接触的瞬间射流速度迅速减小，逆压力梯度显现，生成爆破冲击波，并对煤体施加能量极强的冲击压缩作用力，对煤体壁面造成破坏形成塑性压缩破碎区。气爆冲击作用下在煤岩体内部生成应力波，应力入射波和自由面反射波拉伸作用下对煤岩体造成一定程度的损伤破坏，煤岩体内部粒子发生错位，介质单元发生切向拉伸和径向压缩，并进一步产生径向初始裂纹。
与黏度较高的液态水不同，当高压气射流连续冲击作用于波动破坏形成的破碎区和初始裂纹时，粘性较低的气体会快速充满这些裂纹空间，产生作用于裂纹内壁的准静态压力分布(图3)，压力可以近似等同于射流作用下的滞止压力[22]，准静态压力作用时间取决于高压气源的补充和裂纹尖端应力场的影响。准静态压力促使初始裂纹扩展、延伸、沟通，在煤体内部生成交叉裂纹网。当作用于裂纹内气体的拉伸应力超过煤岩体的抗拉强度极限时，发生失效破坏，煤体颗粒被剥离，产生以射流轴线为圆心的塑性破坏区，形成冲蚀坑。进入这些裂纹的高压气体经膨胀后压力逐渐降低，当压力降低至不足以支撑裂纹进一步扩展后，裂纹止裂。
图3 裂纹内压力示意
Fig.3 Schematic diagram of pressure inside crack
由于气体准静态压力作用的时间要远大于波动作用的时间，一般认为在气射流冲击破岩阶段，准静态压力破坏占主体，且拉伸破坏应是气射流破煤成坑的主要作用机制。
1.4 连续过程机理
综上，气射流破煤是高压气体自喷嘴加速，经空气介质中发展，直至冲击破煤的连续综合过程。通过缩放型喷嘴可实现超声速跃迁加速;之后向空气介质中喷出，在剪切作用下其轴向速度不断衰减，在卷吸作用下径向断面持续扩张;当射流接触到煤体表面后，冲击区内射流轴向速度急剧下降而静压力急速上升，形成破碎核与延展裂纹;黏度较低的气体渗入裂纹空间并在裂纹尖端产生拉应力，当其超过煤体的抗拉强度极限时，煤体发生失效破坏，形成塑性破碎坑。
2 连续过程数学模型与射流破煤准则
2.1 加速阶段数学模型
由空气动力学相关理论可知，当高压气体流经参数已知的缩放型喷嘴，其加速后的气体状态取决于喷嘴参数以及进口气流压力、温度和出口外界背压。当喷嘴任一截面面积与喉部面积比值确定后，可通过式(7)求得加速后气体能达到的马赫数[17]:
(7)
式中，S为喷嘴任一截面面积;St为喷嘴喉部面积;k为绝热系数，对空气取值为1.4。
在研究空气动力学问题时，为使复杂问题得到简化，引入一个假想的参考状态，即空气自某一真实状态经过绝能等熵过程，速度减少至0的状态，称为该真实状态下所对应的滞止状态。在滞止状态下，假定高压气体在喷嘴中的流动过程是一维定常等熵绝热流动，即流动中的气体与外界不存在热量、功的交换，没有流量的加入或引出，不计高压气体与喷嘴管壁间的摩擦作用。对缩放型喷嘴而言，超声速气流在喷嘴中的流动情况可由滞止状态下的气流参数表示：
(8)
式中，P为气体压力;P*为滞止状态下气体压力;ρ为气体密度;ρ*为滞止状态下气体密度;T为气体热力学温度;T*为滞止状态下气体热力学温度。
马赫数的含义为
(9)
其中，a为该状态下对应的当地空气声速，可由
求得，R为气体常数，对空气取值为287.06 J/(kg·K)，T为气体热力学温度。联立式(7)，(8)，(9)，可得在确定喷嘴进口总压、总温和喷嘴出口外界背压条件下，喷嘴出口截面的气流速度U0为
(10)
式中，Mamax为给定喷嘴参数条件下出口端所能达到的最大马赫数。
2.2 发展阶段数学模型
气射流发展阶段的影响因素包括喷嘴半径b0、喷嘴-平板距离H、入射角度θ和射流初速度U0等。为便于分析，在射流流场中建立直角坐标系(x，y)，用于分析自由射流区和冲击区，坐标系(x1，y1)用于分析冲击区和壁面射流区，如图4所示。
图4 气射流发展阶段示意
Fig.4 Schematic diagram of air jet development stage
定义射流轴向压力为Pm，滞止点处压力值为Ps，壁面压力为Pw，Um为射流速度，Um1为任意截面x1方向上Um的最大值，bu代表自由射流区段内流体截面速度为1/2Um的径向长度尺寸。根据1.2节分析可知，自滞止点开始，随x1的增大而增大，直至最大值，之后由于湍流混合周围空气介质而导致速度降低，在距射流轴线较远Um1处趋于0。在自由射流区段内，射流轴向速度Umf和径向长度bf的关系式为
Umf，bf=f1，2(M0，ρ，x)
(11)
式中，
即喷嘴截面动量通量。
冲击区内，射流速度Um、断面长度尺寸bu及压力分布Pm存在有
Um，bu=f3，4(M0，ρ，x，H)
(12)
Pm=f5(M0，ρ，x，H)
(13)
运用量纲分析，参考类似领域相关研究结论[23]，对射流发展过程中各参数进行分析，建立如下方程:
(14)
(15)
(16)
对于自由射流区存在有
(17)
联立式(14),(17)可得
(18)
对射流冲击区压力进行分析，结合式(16)，可得在滞止点处压力值为
(19)
联立式(16),(19)可得
(20)
射流冲击作用于煤体，距射流轴线x1处壁面压力分布情况有
(21)
联立式(19)和(21)，冲击区内壁面压力与滞止点处压力存在以下关系:
(22)
根据BELTAOS和RAJARATNAM[24]的研究结论，式(22)可写成
(23)
射流作用于煤体壁面的压力分布情况直接关系到射流破煤的可行性，对冲击区内射流速度和射流压力进行分析:
(24)
(25)
运用连续性方程:
(26)
当y取0即在射流轴线方向上时，有
(27)
对式(27)做积分处理有
(28)
结合式(14)，射流轴向速度分布可写成
(29)
(30)
结合动量守恒定律，滞止点处压力值可表达为
(31)
式中，
取0.13[23]。
冲击区内，假设射流冲击产生的湍流现象及气体粘性效应可忽略不计，有
(32)
联立式(19)和式(23)，可得到沿壁面x1方向上的速度分布情况为
(33)
2.3 冲击阶段数学模型
对于表面有射流作用的煤体，破碎核及延展裂纹内的应力集中由射流滞止压力和诱导应力共同构成，煤体破坏准则可定义为
P′+σt≥St
(34)
其中，P′为作用于裂纹内的法向压力;σt为射流冲击作用下产生和发展的诱导拉应力。P′可理解为射流的滞止压力值，诱导压力σt取决于射流冲击的特征和裂隙的几何形状。
图5 气射流冲击壁面压力分布
Fig.5 Distribution of gas jet impact wall pressure
现考虑一无限大平板受高压气射流垂直冲击(图5)，壁面作用有沿壁面法向P′=P′(x，y)的压力分布，柱坐标系下的应力分布情况可表示为
其中，v为射流速度;r为到Z轴的径向距离。方程表征由于法向压力的存在而引起的物体任意一点处的压力情况，当P′已知时，法向压力产生的的应力情况可通过积分求得。射流冲击作用于平板壁面时，设在平板表面有一点Q，x和y分别指向Q点的切线方向，在Z=0处利用叠加原理，有
在式(36)中，将σr，σθ拆分为含Z的局部项和不含Z的非局部项，局部项可表达为
(37)
对式(38)分析发现，Z值很小时，除在点Q附近外，等式右边数值都很小。由于点Q附近压力分布不明显，近似认为压力和Q点处相等，在这种情况下，认为σr，σθ不受θ的影响，对式(37)进行积分处理，可得
(38)
对式(38)在半径很小的圆内进行积分(L取为a)，有
(39)
当Z趋向于0时，有
(40)
对非局部相有
(cos θ2-sin θ2)ldldθ
(41)
考虑到非局部相数值较局部相数值要小的多，且在趋向轴线方向时逐渐消失，一般只考虑局部项。将局部应力破坏准则和局部项相结合，建立基于煤体的拉伸破坏准则下射流压力与材料泊松比和煤体抗拉强度间关系式:
(42)
2.4 气射流破煤能力与破碎坑特征判识准则
结合气射流破煤连续过程的数学模型，当射流冲击作用于煤体的射流压力大于煤体临界破坏压力时，会有冲蚀孔洞的形成。因此，联立式(8)，(10)，(31)，(42)，可得气射流能否破煤的判识准则:
(43)
其中，k对空气取1.4，R对空气取287.06 J/(kg·K)，其余相关参数定义与式(8)一样。定义气体的滞止参数与静参数之比
(44)
对式(43)化简后有
(45)
当煤体粒子被射流冲蚀剥离后，射流冲击距离逐渐增大，滞止点处压力值逐渐减小，当压力小于煤岩体临界破坏压力时，射流不足以对煤体造成破坏。在喷嘴几何参数、气体状态参数及煤体力学参数已知，且射流初始冲击距离确定的前提下，射流冲蚀形成孔洞的轴向深度可由下式求得
(46)
其中，k对空气取1.4，R对空气取287.06 J/(kg·K)，其余相关参数定义与式(8)一样。对式(46)化简后有
(47)
考虑到射流冲击作用于煤体存在径向压力分布，当压力大于临界破坏压力时，可计算得出对应冲击距离下冲蚀孔洞的半径为
x=7.7×103Tρb0(1-2v)(d0.4-1)×
(48)
式中，
为射流冲击作用下壁面临界破坏压力;
为冲击距离h条件下的滞止点处压力值。
3 气射流破煤规律理论计算
由于气体本身的低密度特性决定了气射流冲击能量相较水射流小，为初步分析气射流破煤能力与成坑规律，根据2.4节推导的数学模型对其破煤规律进行理论计算。选取喷嘴进口气流总压分别为4，8，12 和16 MPa，温度均为300 K,出口外界背压均为101 325 Pa的4种工况条件。认为高压气体在喷嘴内做绝能等熵流动，计算4种工况条件下气射流的马赫数、出口温度、密度和流速，结果见表1。
表1 不同工况条件下射流参数
Table 1 Jet parameters under different working conditions
工况条件4 MPa/300 K8 MPa/300 K12 MPa/300 K16 MPa/300 K马赫数3.043.523.824.03出口温度/K104.9686.1076.6870.63ρ/(kg·m-3)16.0326.3135.1443.16U0/(m·s-1)626.03655.60669.88678.89
选取3种不同强度的煤体与1种岩体，结合2.4节中推导的气射流破煤准则，依照其抗拉强度和泊松比，计算得出各煤岩体临界破坏压力，见表2。
表2 煤岩体力学参数及临界破坏压力[25]
Table 2 Mechanical parameters of coal and rock mass and critical failure pressure[25]
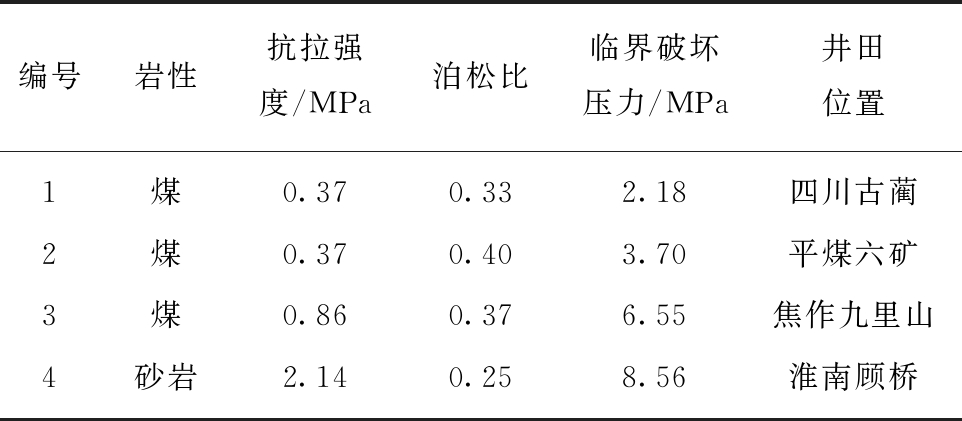
编号岩性抗拉强度/MPa泊松比临界破坏压力/MPa井田位置1煤0.370.332.18四川古蔺2煤0.370.403.70平煤六矿3煤0.860.376.55焦作九里山4砂岩2.140.258.56淮南顾桥
考虑自由射流区内存在速度近似保持和喷嘴出口处速度U0不变的势流核，长度自喷嘴沿轴向延伸6D～7D(D为喷嘴出口直径)[26]，结合式(45)，为保证射流得到充分发展，选取初始冲击距离为30 mm，计算不同工况条件下滞止点处压力与冲击距离间的关系，计算结果如图6所示。
分析图6可知:在同一喷嘴入口压力条件下，随着冲击距离的不断增大，滞止点处压力值不断减小;喷嘴出口直径越大，冲击作用于滞止点处压力值越大。对不同喷嘴入口压力而言，随着喷嘴入口压力的提高，射流冲击作用于滞止点处压力值增大。同时结合四种不同强度煤岩体的临界破坏压力进行对比分析，认为随着喷嘴入口压力和喷嘴直径的增加，射流冲击破煤岩效果不断提升，当喷嘴入口压力取16 MPa、喷嘴直径取4 mm时，气射流可对强度较大的砂岩造成冲蚀破坏。
为直观考察气射流冲击煤岩体形成冲蚀孔洞的特征，选取初始冲击距离为30 mm，喷嘴出口截面直径 4 mm，根据式(47)，(48)，计算不同喷嘴入口压力条件下的破碎孔洞形状，其结果如图7所示。随着煤岩体强度的提升，射流冲击破煤岩效果开始下降。对同一种煤岩体而言，随着喷嘴入口压力的提升，射流冲击形成的冲蚀孔洞深度和径向长度都不断增大，但孔洞轴向深度的增加量要远大于径向长度的增加量。分析认为，当喷嘴入口压力提高时，射流冲击动能增大，作用于裂纹内的气体滞止压力变大，体现在冲蚀孔洞轴向和径向破碎范围的扩大;但由于壁面压力自轴线向外衰减速度较快，造成孔洞径向长度增加量要远小于轴向深度增加量。进一步观察发现，随着喷嘴入口压力的提升，射流冲击同一煤岩体形成的冲蚀孔洞形状由最初的锥形渐变为橄榄球形。分析认为，在初始冲击距离条件下，喷嘴入口压力较大的气射流还未得到充分发展，即射流断面还未实现最大程度的扩张;随着冲蚀的进行，冲击距离不断增大，射流由不充分发展转变为充分发展，滞止点压力开始减小，破煤范围不断缩小;以上综合过程导致了橄榄球形孔洞的形成。
图6 不同射流条件下破煤岩能力曲线
Fig.6 Gas jet breaking capacity curves on coal and rock under different jet flow conditions
图7 不同射流条件下冲蚀孔洞特征
Fig.7 Characteristics of broken holes under different jet flow conditions
4 结 论
(1)气射流破煤是高压气体自喷嘴加速，经空气介质中发展，直至冲击破煤的连续综合过程，不同阶段的特征与控制机理均不同。高压气体通过缩放型喷嘴可实现超声速流动，射流发展流经空气介质后对煤体进行冲击，形成破碎核及延展裂纹，煤体粒子被冲蚀剥离形成破碎坑。
(2)通过建立气射流冲击破煤全过程的数学模型，理论推导得出了气射流破煤能力与破碎坑特征的判识准则，为进一步的理论研究与现场工艺设计奠定了基础。
(3)通过计算不同工况条件下射流冲击作用于滞止点处的压力值，以及与不同强度煤岩体临界破坏压力进行比较，结果表明:随着冲击距离的增大，滞止点处压力值不断减小;在低压力入口条件下，气射流可对强度较小的煤体造成冲蚀破坏，当入口压力达到16 MPa时，可实现对砂岩的冲蚀破坏。
(4)基于理论计算，初步分析了射流冲击作用下破碎坑的形成特征。对同一煤体而言，随着射流压力的提高，破碎坑轴向深度和径向长度都不断增大，但轴向深度增加量要远大于径向长度增加量;破碎坑形状由最初的锥形渐变为橄榄球形。
[1] 李晓红,卢义玉,赵瑜,等.高压脉冲水射流提高松软煤层透气性的研究[J].煤炭学报,2008,33(12):1386-1390.
LI Xiaohong,LU Yiyu,ZHAO Yu,et al.Study on improving the permeability of soft coal seam with high pressure pulsed water jet[J].Journal of China Coal Society,2008,33(12):1386-1390.
[2] 李晓红,卢义玉,向文英.水射流理论及在矿业工程中的应用[M].重庆:重庆大学出版社,2007.
[3] 司鹄,王丹丹,李晓红.高压水射流破岩应力波效应的数值模拟[J].重庆大学学报,2008(8):942-945,950.
SI Hu,WANG Dandan,LI Xiaohong.Stress wave effect in numerical simulation on rock breaking under high-pressure water jet[J].Journal of Chongqing University,2008(8):942-945,950.
[4] 卢义玉,沈晓莹,汤积仁,等.磨料水射流钻头破岩过程的力学分析[J].中国矿业大学学报,2012,41(4):531-535.
LU Yiyu,SHEN Xiaoying,TANG Jiren,et al.Mechanical analysis of rock breaking by an abrasive water jet bit[J].Journal of China University of Mining & Technology,2012,41(4):531-535.
[5] 王明波.磨料水射流结构特性与破岩机理研究[D].东营:中国石油大学,2007.
WANG Mingbo.Abrasive water jet flow property and rock-breaking mechanism[D].Dongying:China University of Petroleum,2007.
[6] 卢义玉,冯欣艳,李晓红,等.高压空化水射流破碎岩石的试验分析[J].重庆大学学报(自然科学版),2006,29(5):88-91，103.
LU Yiyu,FENG Xinyan,LI Xiaohong,et al.Experiments on breaking rock with high-pressure cavitating water jets[J].Journal of Chongqing University (Natural Science Edition),2006,29(5):88-91,103.
[7] ZHOU Wei,HE Kai,CAI Jiannan,et al.Simulation and experimental study on cavitating water jet nozzle[J].IOP Conference Series:Earth and Environmental Science,2017,51:012006.
[8] 李根生,廖华林,黄中伟,等.超高压水射流作用下岩石损伤破碎机理[J].机械工程学报,2009,45(10):284-293.
LI Gensheng,LIAO Hualin,HUANG Zhongwei,et al.Rock damage mechanisms under ultra-high pressure water jet impact[J].Journal of Mechanical Engineering,2009,45(10):284-293.
[9] 顾北方.高压水射流割缝煤体损伤演化规律研究与应用[D].北京：中国矿业大学(北京),2016.
GU Beifang.Coal damage and evolution law under influence of high pressure water hydraulic cutting and their application[D].Beijing:China University of Mining and Technology (Beijing),2016.
[10] CHENG Xiaoyu.Damage and failure characteristics of rock similar materials with pre-existing cracks[J].International Journal of Coal Science & Technology,2019,6(4):505-517.
[11] 张国华,梁冰,毕业武.水锁对含瓦斯煤体的瓦斯解吸的影响[J].煤炭学报,2012,37(2):253-258.
ZHANG Guohua,LIANG Bing,BI Yewu.Impact of water lock on gas desorption of coal with gas[J].Journal of China Coal Society,2012,37(2):253-258.
[12] 刘勇,何岸,魏建平,等.水射流卸压增透堵孔诱因及解堵新方法[J].煤炭学报,2016,41(8):1963-1967.
LIU Yong,HE An,WEI Jianping,et al.Plugging factor and new plugging method to hydraulic relieving stress[J].Journal of China Coal Society,2016,41(8):1963-1967.
[13] 魏建平,姚邦华,刘勇,等.裂隙煤体注浆浆液扩散规律及变质量渗流模型研究[J].煤炭学报,2020,45(1):204-212.
WEI Jianping,YAO Banghua,LIU Yong,et al.Grouting fluid diffusion law and variable mass seepage model for fractured coal[J].Journal of China Coal Society,2020,45(1):204-212.
[14] 刘勇,张慧栋,魏建平，等.基于拉法尔喷嘴的磨料气体射流加速规律研究[J].中国安全生产科学技术,2018,14(11):26-32.
LIU Yong,ZHANG Huidong,WEI Jianping,et al.Study on acceleration laws of abrasive gas jet based on Laval nozzle[J].Journal of Safety Science and Technology,2018,14(11):26-32.
[15] 刘勇,何岸,魏建平,等.高压气体射流破煤应力波效应分析[J].煤炭学报,2016,41(7):1694-1700.
LIU Yong,HE An,WEI Jianping,et al.Analysis of stress wave effect during coal breakage process by high pressure gas jet[J].Journal of China Coal Society,2016,41(7):1694-1700.
[16] 赵旭.高压氮气冲击致裂煤岩体裂隙发育规律研究[D].徐州:中国矿业大学,2017.
ZHAO Xu.Study on fissure development law of high pressure nitrogen impacting fracture for coal and rock mass[D].Xuzhou:China University of Mining and Technology,2017.
[17] 陈浮,权晓波,宋彦萍.空气动力学基础[M].哈尔滨:哈尔滨工业大学出版社,2015.
[18] SIMIONESCU 
tefan-Mugur,T
NASE Nicoleta-Octavia,BROBOAN Diana,et al.Impinging air jets on flat surfaces at low reynolds numbers[J].Energy Procedia,2017,112:194-203.
[19] TUMMERS Mark,JACOBSE Jeroen,VOORBROOD Sebastiaan.Turbulent flow in the near field of a round impinging jet[J].International Journal of Heat and Mass Transfer,2011,54:4939-4948.
[20] BITTER J G A.A study of erosion phenomena part I[J].Wear,1963,6(1):5-21.
[21] LEVY A V,BUQIAN W.Erosion of hard material coating systems[J].Wear,1988,121(3):325-346.
[22] KALIAZINE Andrei,ESLAMIAN Morteza,TRAN Honghi.On the failure of a brittle material by high velocity gas jet impact[J].International Journal of Impact Engineering,2010,37:131-140.
[23] BELTAOS S,RAJARATNAM N.Impingement of axisymmetric developing jets[J].Journal of Hydraulic Research,1977,15(4):311-326.
[24] BELTAOS S,RAJARATNAM N.Plane turbulent impinging jets[J].Journal of Hydraulic Research,1973,11(1):29-59.
[25] 巫修平.碎软低渗煤层顶板水平井分段压裂裂缝扩展规律及机制研究[D].北京:煤炭科学研究总院,2017.
WU Xiuping.Research on control mechanism of fracture propagation of multistage hydraulic fracturing horizontal well in roof of broken soft and low permeable coal seam[D].Beijing:China Coal Research Institute,2017.
[26] 陈庆光,徐忠,张永建.湍流冲击射流流动与传热的数值研究进展[J].力学进展,2002,32(1):92-108.
CHEN Qingguang,XU Zhong,ZHANG Yongjian.Advances in numerical studies of turbulent impinging jet flow and heat transfer[J].Advances in Mechanics,2002,32(1):92-108.
06