煤炭作为世界上分布最广、最丰富的资源，已成为世界能源结构的主导能源之一。然而，煤矿工作环境的复杂性给煤矿开采带来了很大的困难，煤矿的安全问题近年来受到越来越广泛的关注[1]。为解决煤矿生产事故和人员伤亡问题，同时实现井下安全生产自动化，实施无人工作面智能化采煤具有重要意义，其中采煤机位置和姿态的确定是实现井下自动化的关键技术之一。鉴于井下煤矿环境的特殊性，无线定位[2]、蓝牙定位[3]、卫星定位[4]、天文定位[5]等方式都依赖外部可靠的信息源，同时这些定位方式都无法测量采煤机的实时姿态，因此其在井下的应用都受到了极大的限制。基于惯性导航系统(SINS)的采煤机定位定姿技术是一种既不依赖于外部信息源又不向外辐射能量的自主导航系统[6-7]。SINS是指将陀螺仪和加速度计捷联组成的惯性测量单元直接固定在运载体上，利用陀螺仪和加速度计实时测量采煤机的角速度和加速度，并基于牛顿三大定律计算采煤机的姿态、速度、位置。高自主性及安全性的特点使得惯性导航系统能够满足于井下煤矿环境的采煤机定位，并受到了广泛的关注[8-9]。
采煤机初始姿态角的确定作为导航定位的前提，后续导航的性能很大程度上取决于初始姿态矩阵的精确程度[10-11]。采煤机初始对准主要包括2个连续的阶段:粗对准和精对准。所谓粗对准，顾名思义，即在没有任何先验知识的情况下短时间内获得粗略的初始姿态矩阵。经短时间的粗对准后，初始姿态误差角可以限制在几度以内[12-13]。相对于粗对准，精对准是在粗对准的基础上，通过构建线性失准角误差方程，并利用卡尔曼滤波技术不断修正粗对准获得的初始姿态矩阵，进而获得更加精确的初始姿态角。因此，粗对准作为精对准的前提，高性能的粗对准可以有效地提高精对准的精度和收敛速度[14-15]。
惯性导航粗对准主要包括解析法和优化法。解析法是在运载体对地静止环境下执行，即运载体相对地面没有明显的角运动和线运动，同时初始对准的所在地理位置精确已知，利用陀螺仪和加速度计敏感载体系下的地球自转角速度和重力加速度，同时结合导航系下的地球自转角速度和重力加速度，最终确定出初始姿态旋转矩阵。然而解析法需要载体长时间保持静止状态，同时这种方法收敛速度慢且精度低，因此限制了其在井下采煤机初始对准的应用[16-17]。近年来，基于优化的动基座粗对准方法(OBA)得到了广泛的关注，OBA方法利用姿态分解技术，将采煤机的实时姿态矩阵分解为2个时变矩阵和1个常值矩阵，利用陀螺仪和加速度计获得多个时刻且不共线的观测矢量，最终采用优化算法确定出采煤机的初始姿态矩阵[18-20]。OBA算法不仅可以在晃动的载体上进行初始对准，而且该方法具有一定的抗干扰能力，因此OBA方法可以运用于采煤机截割煤壁环境下的初始对准。然而，由于采煤机的工况环境比较恶劣，干扰较多，采煤机截割煤壁时会产生剧烈的震动，固联在采煤机机身的SINS容易受到震动的影响，震动会使得加速度计敏感到高频噪声值，这些高频噪声会累积到OBA算法中，最终造成OBA算法的性能严重下降。虽然设计低通滤波器可以有效地抑制加速度计敏感到的高频噪声，但是对于不同的机动条件及环境，低通滤波器的参数选择是一个繁琐的过程，过低的截止频率有可能滤除有用的信息，而过高的截止频率又会降低对准性能，因此合理的低通滤波器参数是提高井下采煤机初始对准的一项关键指标。针对上述问题，笔者建立了采煤机动力学模型，通过仿真分析的手段获得采煤机截割煤壁时机身运动信息，并运用傅里叶变换将时域运动信号转换到频域，从而获得低通滤波器的截止频率。之后，采用等纹波逼近法构建低通滤波器模型，并将所建立的低通滤波器引入到OBA方法中，从而有效地抑制震动所产生的高频噪声。最后搭建采煤机截割煤壁模拟实验台验证所提出方法的有效性。
1 采煤机OBA算法原理
1.1 采煤机动态对准原理
如图1所示，其中b系为采煤机的机体坐标系，n系为地理坐标系，i系为惯性坐标系。采煤机动态对准的目标是利用SINS确定出采煤机机体坐标系b系相对于地理坐标系n系的姿态变换矩阵
由姿态变换矩阵的链式传导法则，对t时刻的姿态阵作如下分解
(1)
式中，
为初始姿态矩阵;
为载体系的变化;
为载体系的变化。
图1 采煤机机身坐标系
Fig.1 Coordinate of the shearer fuselage
对方程
为采煤机在地理坐标系下的速度;vb(t)为采煤机在载体坐标系下的速度)两端求导同时结合微分方程
可以将地理坐标系下的惯性导航比力方程转换到采煤机机体坐标系下
(2)
式中，vn为惯导速度;
为加速度计输出的比力;
为载体坐标系下的地球自转角速度分量;
为载体坐标系相对于惯性坐标系的角速度。
方程(2)两端乘以姿态阵
并结合方程(1)可以推导出
(3)
当获得了多个不同时刻且不共线的向量α和β，就可以通过优化的手段确定出初始姿态角
1.2 数值解算算法
为了将式(3)应用于导航计算机中，需要对式(3)进行离散化，在时间段[0,tm]中对式(3)两端进行积分，同时由于是一个常值矩阵，由此得到下式
(4)
考虑到地球自转角速度
相对于采煤机的机体角速度
来说是一个小量，因此α可以写为
(5)
对α中第1项
进行分部积分
(6)
将式(6)代入式(5)并整理得
(7)
对式(4)，(7)进行离散化，得
(8)
式中，Ts为采样时间;I3为3×3的单位矩阵;为采煤机的角速度在载体坐标系下的投影;
为地理坐标系的旋转角速度。
由于采煤机工况环境较为恶劣，割煤所产生的剧烈震动会降低加速度计的性能，剧烈震动会使得加速度计敏感到高频噪声并输出异常值。由式(8)可知，当加速度计的输出
受到干扰时，干扰所产生的误差会随着时间累积在α(tm)中，这将极大地降低动态对准的性能，倘若不能有效的处理这一固有缺陷，那么就无法顺利完成基于优化的采煤机动态对准。在采煤机实际工况中，震动的干扰往往属于高频噪声，采煤机截割煤壁时机身的晃动频率一般属于低频信息，因此可以采取频率分离的手段，通过选择合理的截止频率设计一种低通滤波器来抑制震动所产生的高频噪声。相对的，对于低通滤波器而言，截止频率是关键指标之一，因此接下来的主要目标是确定出低通滤波器的截止频率，进而可以采用频率分离的手段完成基于优化的采煤机动态对准。
2 基于采煤机动力学模型的频域去噪技术
2.1 采煤机动力学模型
井下采煤机工作条件恶劣，工况复杂，在建立截割状态的采煤机动力学模型时，对采煤机的运行工况和结构作适当的简化[22]。
(1)采煤机的滚筒和机身质量分布均匀，忽略其弹性并转化为集中质量。
(2)忽略采煤机下面刮板输送机的弹性阻尼，并视摇臂、滑靴的阻尼为黏性阻尼。
(3)作用于滚筒上的载荷按文献[23]所给的曲线变化。
根据采煤机的结构特点，采煤机的运动可以认为是具有阻尼的多自由度受迫振动。采用质量块法，将滚筒采煤机简化为如下5个部分:前后滚筒、前后摇臂与采煤机机身，同时将滚筒和机身视为刚体，采煤机滑靴与摇臂建模为弹簧阻尼系统首先考虑垂直平面Z方向的运动情况，对图2(a)进行动力学建模，取左右滚筒和采煤机机身的平衡位置起的位移Z1，Z2，Z3作为广义坐标，利用牛顿-拉格朗日方程获得采煤机在机体垂直平面Z轴方向的系统动能、系统弹性势能、系统的耗散能。
(9)
(10)
(11)
式中，T为系统动能;U为系统弹性势能;D为系统耗散能;Z1，Z2，Z3分别为采煤机前后滚筒和机身的位移;m1，m2，m3分别为采煤机前后滚筒和机身的质量;k1，k2为前后摇臂的连接刚度;c1，c2 为前后摇臂的连接阻尼;k3，k4为前后导向滑靴的连接刚度;c3，c4为前后导向滑靴的连接阻尼。
图2 采煤机动力学模型
Fig.2 Dynamic model of the shearer
将式(9)～(11)代入拉格朗日动力学方程(12)，由此得到采煤机沿着机体Z轴的动力学模型(13)，即
(12)
式中，Fi为受到的力;xi为位移。
(13)
为了方便MATLAB求解，将式(13)改写为状态方程的形式，可得
(14)
式中，M为质量矩阵;C为阻尼矩阵;K为弹性系数矩阵;F为由Fi组成的矢量。
X和Y方向的动力学方程可以通过同样的手段获得，因此将这两个方向的建模过程省略。图2中，F′Z，FZ，F′X，FX，F′Y，FY分别为采煤机左滚筒和右滚筒的受力沿着Z，X，Y轴的投影;Y1，Y2为左右滚筒的Y轴方向的位移;c5～c12为采煤机的等效阻尼;k5～k12为采煤机的等效刚度。
2.2 采煤机动力学模型求解
为了获得采煤机截割煤壁时机身的运动状态，需要对非线性微分方程(14)进行求解，然而在方程(14)中，广义力F是一个时变函数，无法获得方程(14)的解析解。为了获得非线性微分方程(14)的解，采用降阶的方式，将方程(14)转化为6个一阶微分方程，同时利用MATLAB提供的基于Runge-Kutta变步长算法的Ode45函数求解非线性微分方程(14)，将MG150/345-WDK型采煤机的有关参数代入微分方程，该类型采煤机的具体参数如下:采煤机机身质量m3为15 300 kg，前滚筒质量m1和后滚筒质量m2为2 430 kg，采煤机前摇臂和后摇臂在Z方向的阻尼c1,c2分别为690.7 N/(m/s),采煤机前摇臂和后摇臂在Z方向的刚度k1,k2分别为149 000 N/(m/s)，采煤机前后导向滑靴在Z方向的连接阻尼c3，c4为90 N/(m/s),采煤机前后导向滑靴在Z方向的连接刚度k3，k4为300 000 N/m。通过数值模拟的方式，分析采煤机截割煤壁时的动力学特征，图3，4为采煤机截割煤壁时机身的运动加速度幅值曲线和频率曲线。
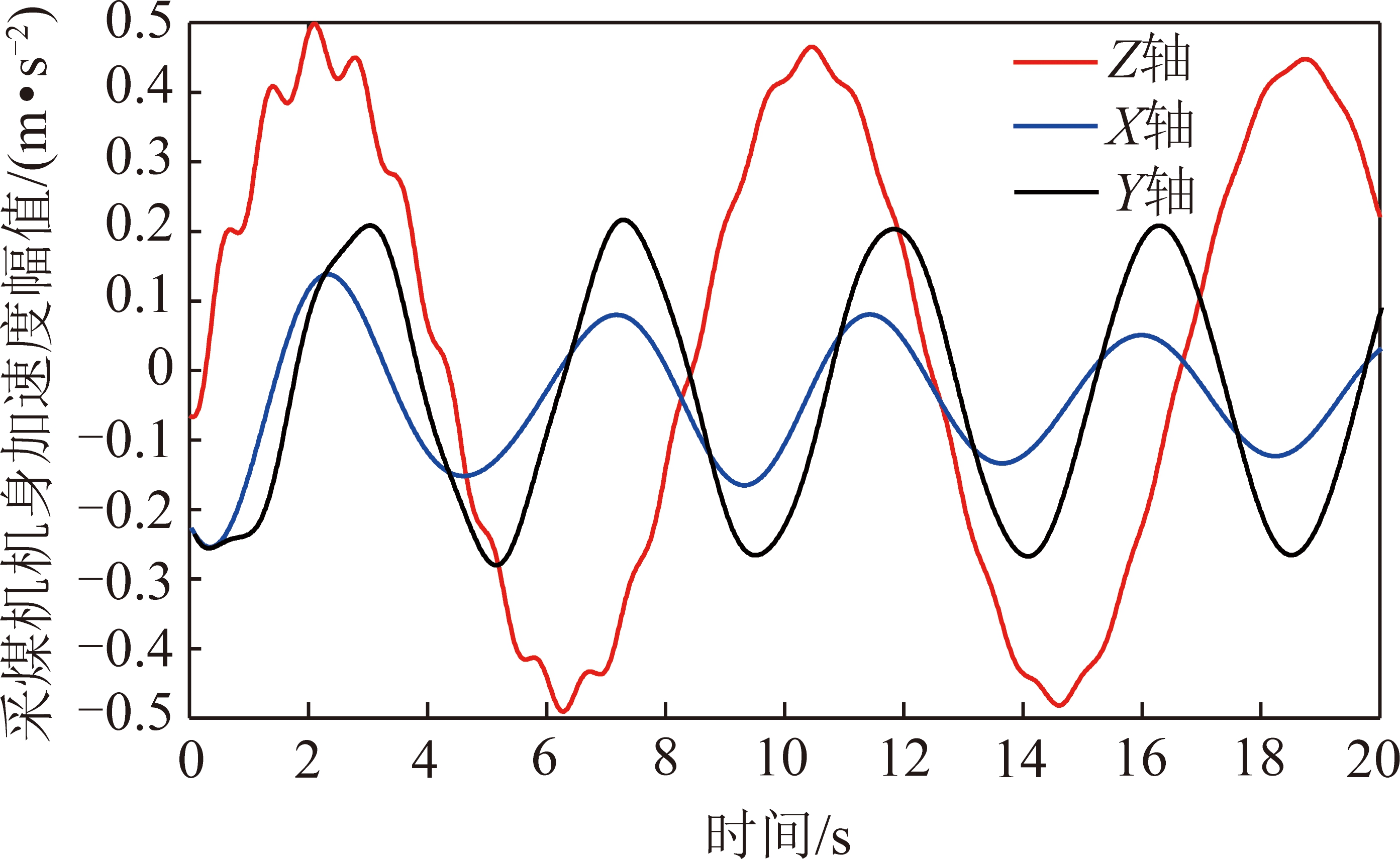
图3 采煤机机身加速度时域曲线
Fig.3 Time domain curves of the acceleration for shearer fuselage
图4 采煤机机身加速度频域曲线
Fig.4 Frequency domain curves of the acceleration for shearer fuselage
由图3可知，采煤机机身的加速度呈现周期性的波动，采煤机机身X，Y，Z轴的加速度最大幅值分别为0.20，0.27，0.49 m/s2，采用傅里叶变换将时域加速度信号转换到频域后，得到了采煤机截割煤壁时机身运动频谱图，从图4可以看出采煤机在截割煤壁时机身的加速度信号主要位于0～2 Hz的低频段，属于低频信息。然而当采煤机截割煤壁时，剧烈的震动会导致加速度计敏感到高频噪声。因此如果设计一个理想的低通滤波器，能够抑制由于采煤机震动引发的高频噪声，并且保留有用的低频信息，那么这种做法可以提高OBA对准的精度和对准时间。2.2节通过动力学建模的方式确定出采煤机截割煤壁时机身振动频率位于0～2 Hz的低频段，在实际中，采煤机的动力学参数和仿真所采用的参数存在一定的差异，因此在设计数字滤波器时将截止频率设置为5 Hz。
2.3 基于采煤机振动频率的滤波器设计
工程中常用的数字滤波器分为2种，一种是有限长单位冲激响应(FIR)滤波器，另一种是无限冲激响应(IIR)滤波器。FIR滤波器虽然计算量略大一些，但是其具备线性相位及稳定性的优点在数字信号处理领域发挥着巨大的作用。常用的FIR滤波器设计手段包括窗函数法，频率采样法，最佳逼近法等。其中等纹波最佳逼近法是一种优化设计方法，所设计的FIR滤波器的幅频响应在通带和阻带是等波纹的，这种方法相较于窗函数法和频率采样法，滤波器阶数相同时，该方法设计的滤波器最大逼近误差最小，滤波器性能最高，因此笔者采用等纹波最佳逼近法设计FIR滤波器。
FIR滤波器具有线性相位的条件是滤波器系数h(n)为实序列，并且序列h(n)关于(N-1)/2偶对称，若要设计线性相位滤波器，定义加权误差函数E(ω)为
E(ω)=W(ω)[Hd(ω)-Hg(ω)]
(15)
其中，W(ω)为误差加权函数;Hd(ω)为理想的幅度特性函数;Hg(ω)为实际设计的滤波器幅度特性函数。等纹波最佳逼近基于切比雪夫逼近，在通带和阻带内满足误差极大值最小化准则，采用Remez多重交换迭代算法求解滤波器的系数h(n)，W(ω)的取值越大，那么相应的频率段逼近精度越高，在Remez多重交换迭代算法中W(ω)是已知的函数。
采用最佳逼近法并利用Remez多重交换迭代算法设计所需要的FIR滤波器，FIR滤波器指标如下:采样频率为100 Hz，通带截止频率为5 Hz，阻带起始频率为10 Hz，通带最大衰减为1 dB，阻带最小衰减为40 dB，滤波器的阶数为31阶，则所设计的幅度曲线如图5所示。
图5 FIR滤波器幅度特性曲线
Fig.5 Amplitude characteristic curve of FIR filter
3 实 验
为验证所提出的方法的有效性和优越性，搭建了采煤机截割煤壁SINS初始对准实验，实验平台如图6所示。实验系统包括光纤捷联惯导，MG150/345-WDK型号采煤机，导航计算机以及供电装置。光纤捷联惯导固定在采煤机机身中央并采用专用的防爆电源供电，光纤捷联惯导包括三轴加速度计和三轴陀螺仪，其中加速度计和陀螺仪以100 Hz的采样频率采集采煤机的角速度和加速度信号，陀螺仪和加速度计的零偏分别为0.01°/h和10-4g。
图6 采煤机初始对准实验平台
Fig.6 Experimental platform for initial alignment of shearer
光纤捷联惯导固定在采煤机上预热10 min左右，待惯导启动稳定后，首先采煤机保持静止10 min左右，之后操作人员启动采煤机进行280 s的截割煤壁实验，将上述总计880 s的陀螺仪和加速度计数据保存进行事后分析。首先采用传统的粗对准外加卡尔曼滤波精对准对前10 min的数据进行预处理，所得到的初始姿态角作为初始对准的参考值。接着利用后280 s的数据进行姿态跟踪，所得到的实时姿态曲线如图7所示，图7反应出了采煤机截割煤壁时机身的晃动情况，将此姿态跟踪的结果作为评估运动对准性能的指标。
图7 采煤机机身实时姿态角
Fig.7 Real-time attitude angle of shearer fuselage
图8 采煤机机身加速度频域曲线
Fig.8 Frequency domain curve of the acceleration for shearer fuselage
首先将采煤机截割煤壁时机身的加速度信号进行傅里叶变换，变换后的频域曲线如图8所示。对比图4，8，在采煤机动力学建模的过程中，对采煤机的运行工况及结构做了适当的简化，因此图4，8在数值上存在着一些差异，但是从图8中可以明显的看出采煤机机身的晃动频率位于低频段，这和动力学建模所得到的结论一致。此外，从图8中可以看出，采煤机截割煤壁时，机身的晃动会造成加速度传感器敏感到高频噪声值，这些高频噪声值虽然数值不大，但是会累加到动态OBA对准算法中，从而造成OBA算法精度以及收敛速度下降。因此，接下来对传统的动基座对准算法和所提出的基于频域分离算子的采煤机动基座SINS初始对准算法进行对比，从而验证所提出算法的有效性和合理性。
图9，10是传统的OBA算法和经过滤波器补偿后横滚角和俯仰角的实时误差跟踪曲线，由于俯仰角和横滚角的可观测性较强，因此经数字滤波器补偿后和未补偿的OBA算法都取得了较好的效果，实时跟踪误差均小于1°，但是所提出的算法跟踪精度更高，稳态后误差小于0.1°，而传统的OBA算法的俯仰角和横滚角的误差会随着时间发散。
图9 俯仰角误差曲线
Fig.9 Error curves of pitch angle
图10 横滚角误差曲线
Fig.10 Error curves of roll angle
图11 航向角误差曲线
Fig.11 Error curves of heading angle
图11是航向角的误差跟踪曲线，由于航向角的可观测性较差，因此相对于横滚角和俯仰角而言，两种算法的收敛速度和精度都有所下降。从图11可以看出，所提出的算法获得的对准结果不仅精度更高，而且收敛速度更快，其原因是数字滤波器过滤了采煤机截割煤壁时的高频振动噪声，这些高频噪声会累积在传统的OBA算法中，由此导致传统的OBA算法收敛速度慢以及精度低等问题，因此所提出的算法适用于井下采煤机快速对准。
4 结 论
(1)研究了采煤机截割煤壁时SINS运动对准问题。针对采煤机动基座初始对准收敛速度慢及精度低等问题，提出了1种基于频域分离算子的采煤机动基座SINS初始对准算法，该方法可以有效地抑制高频震动干扰。
(2)所提出的算法具有更快的收敛速度以及更高的精度，俯仰角和横滚角的稳态误差小于0.1°，航向角稳态误差小于0.7°，满足后续精对准的要求，因此所提出的算法对于井下采煤机SINS初始对准问题具有广泛的应用前景。
[1] ZHENG Yi,LI Ying,MAGESH Thiruvengadam,et al.DPM dispersion inside a single straight entry using dynamic mesh model[J].International Journal of Coal Science & Technology,2017,4(3):234-244.
[2] LUO Chengming,LI Wei,FAN Mengbao,et al.A collaborative positioning algorithm for mobile target using multisensor data integration in enclosed environments[J].Computer Communications,2014,44:26-35.
[3] 张浩,赵千川.蓝牙手机室内定位系统[J].计算机应用,2011,31(11):3152-3156.
ZHANG Hao,ZHAO Qianchuan.Indoor positioning system for bluetooth cell phone[J].Journal of Computer Applications,2011,31(11):3152-3156.
[4] TANG Yonggang,WU Xuanxin,WU Meiping,et al.INS/GPS integration:Global observability analysis[J].IEEE Transactions on Vehicular Technology,2009,58(3):1129-1142.
[5] 刘美莹,王虎,汶德胜,等.空间目标天文定位方法及观测分析[J].光子学报,2014,43(11):159-166.
LIU Meiying,WANG Hu,WEN Desheng,et al.Celestial positionning method and observation analysis for space object[J].Acta Photonica Sinica,2014,43(11):159-166.
[6] 樊启高,李威,王禹桥,等.一种采用捷联惯导的采煤机动态定位方法[J].煤炭学报,2011,36(10):1758-1761.
FAN Qigao,LI Wei,WANG Yuqiao,et al.A shearer dynamic positioning method using strap down inertial navigation[J].Journal of China Coal Society,2011,36(10):1758-1761.
[7] 马宏伟,张璞,毛清华,等.基于捷联惯导和里程计的井下机器人定位方法研究[J].工矿自动化,2019,45(4):35-42.
MA Hongwei,ZHANG Pu,MAO Qinghua,et al.Research on positioning method of underground bobot based on strapdown inertial navigation and odometer[J].Industry and Mine Automation,2019,45(4):35-42.
[8] 乔春光,王学文,谢嘉成,等.基于采煤机运行轨迹的刮板输送机竖直面形态解算方法[J].工程设计学报,2018,25(5):495-502.
QIAO Chunguang,WANG Xuewen,XIE Jiacheng,et al.Vertical plane shape calculation method of scraper conveyor based on running track of shearer[J].Chinese Journal of Engineering Design,2018,25(5):495-502.
[9] 杨海,李威,罗成名,等.基于捷联惯导的采煤机定位定姿技术实验研究[J].煤炭学报,2014,39(12):2550-2556.
YANG Hai，LI Wei，LUO Chengming,et al.Experimental study on position and attitude technique for shearer using SINS measurement[J].Journal of China Coal Society,2014,39(12):2550-2556.
[10] 崔潇,秦永元,严恭敏,等.基于矩阵卡尔曼滤波的捷联惯导初始对准算法[J].中国惯性技术学报,2018,26(5):585-590.
CUI Xiao，QIN Yongyuan，YAN Gongmin,et al.Initial alignment algorithm for SINS based on state matrix Kalman filter[J].Journal of Chinese Inertial Technology,2018,26(5):585-590.
[11] 孟东,缪玲娟,邵海俊,等.简化七阶CQKF及其在SINS大失准角初始对准中的应用[J].宇航学报,2018,39(8):905-912.
MENG Dong，MIAO Lingjuan，SHAO Haijun,et al.A seventh-degree simplified CQKF and its application in SINS initial alignment of misalignment angle[J].Journal of Astronautics,2018,39(8):905-912.
[12] 王律化,石志勇,宋金龙,等.行进间粗对准误差分析方法[J].探测与控制学报,2018,40(5):35-40.
WANG Lühua,SHI Zhiyong,SONG Jinlong,et al.Error analysis of moving base coarse alignment[J].Journal of Detection & Control,2018,40(5):35-40.
[13] 陈光武,程鉴皓,李少远,等.基于改进小波降噪的MEMS间接粗对准方法研究[J].大连理工大学学报,2019(3):323-330.
CHEN Guangwu,CHENG Jianhao,LI Shaoyuan,et al.Research on indirect coarse alignment method of MEMS based on improved wavelet denosing[J].Journal of Dalian University of Technology,2019(3):323-330.
[14] 严恭敏,秦永元.捷联惯导系统静基座初始对准精度分析及仿真[J].计算机仿真,2006(10):36-40,60.
YAN Gongmin,QIN Yongyuan.Initial alignment accuracy analysis and simulation of strapdown inertial navigation system on a stationary base[J].Computer Simulation,2006(10):36-40,60.
[15] CHANG Lubin,HE Hongyang,QIN Fangjun.In-Motion initial alignment for odometer-aided strapdown inertial navigation system based on attitude estimation[J].IEEE Sensors Journal,2017,17(3):766-773.
[16] LI Wanli,WU Wenqi,WANG Jinling,et al.A fast SINS initial alignment scheme for underwater vehicle applications[J].Journal of Navigation,2013,66(2):181-198.
[17] YUAN Dongyu,MA Xiaochuan,LIU Yu,et al.Dynamic initial coarse alignment of SINS for AUV using the velocity loci and pressure sensor[J].Iet Science Measurement & Technology,2016,10(8):926-933.
[18] 朱兵,许江宁,吴苗,等.水下动基座初始对准中的鲁棒自适应UKF方法[J].仪器仪表学报,2018,39(2):73-80.
ZHU Bing,XU Jiangning,WU Miao,et al.Robust adaptive UKF approach for underwater moving base initial alignment[J].Chinese Journal of Scientific Instrument,2018,39(2):73-80.
[19] 严恭敏,翁浚,白亮,等.基于惯性参考系的动基座初始对准与定位导航[J].系统工程与电子技术,2011,33(3):618-621.
YAN Gongmin,WENG Jun,BAI Liang,et al.Initial in-motion alignment and position determination based on inertial reference frame[J].Systems Engineering and Electronics,2011,33(3):618-621.
[20] CHANG Lubin,LI Jingshu,LI Kailong.Optimization-based alignment for strapdown inertial navigation system comparison and extension[J].IEEE Transactions on Aerospace & Electronic Systems,2014,52(4):1697-1713.
[21] MORTARI Daniele.Euler-q algorithm for attitude determination from vector observations[J].Journal of Guidance,Control,and Dynamics,1998,21(2):328-334.
[22] 杨海.SINS/WSN组合定位下采煤机精确位姿感知理论及技术研究[D].徐州:中国矿业大学,2016.
YANG Hai.Research on accurate position and pose perception theory and technology for shearer with SINS/WSN integrated localization[D].Xuzhou:China University of Mining and Technology,2016.
[23] 姜鹏.MG400/930-WD型滚筒采煤机动力学特性研究[D].阜新:辽宁工程技术大学,2015.
JIANG Peng.Research on dynamic characteristics of MG400/930-WD type drum shearer[D].Fuxin:Liaoning Technical University,2015.
06