煤层开采引起上覆岩层产生移动,由此发生了一系列力学现象,研究开采引起的覆岩运移规律是发展开采技术的基础[1]。然而,由于现场研究费用高、难度大及监测设备受限等因素,物理模型试验是研究覆岩变形破断规律、顶板来压特征的主要手段[2]。目前,物理模型试验中位移测试多采用近景摄影、全站仪、百分表等,应力应变监测多采用应变片、压力传感器等手段,由于测试精度低、操作多为点式测量等原因,这些测试手段难以连续、实时进行整场测量。
光纤传感技术由于其可以实现长距离、高精度、分布式测量等诸多优点,被广泛应用于各种工况下的结构健康检测。其中布里渊光时域分布式光纤传感技术(BOTDA)优点突出,精度高,实现分布式测试,可测量绝对温度和应变[3]。光纤布拉格光栅(FBG)是应用最为广泛的光纤传感技术之一,现已被广泛应用于电力、矿业和建筑等多个领域[4]。BOTDA/FBG联合应用于实验室、现场的研究已逐步成熟。柴敬等综合利用光纤光栅和分布式光纤传感技术对采动覆岩变形进行联合监测,形成了顶板来压规律、覆岩垮落形态、物理相似模型温/湿度场的检测等一系列的研究成果[5-8]。施斌和张丹对煤层采动过程中覆岩变形与破坏的发育规律进行了监测和分析,揭示覆岩变形与破坏的发育特征[9]。张丁丁等研究松散层沉降光纤光栅监测的应变传递规律并在工程中应用[10]。吴冰,朱鸿鹄等利用光纤光栅对冻土含冰量进行监测,得出部分规律[11]。
数字图像相关(Digital Image Correlation,DIC)技术是一种基于非接触式图像的光学方法,利用数字图像获取结构体全场位移和应变响应,相关学者已将其应用于岩石力学试验中[12-13]。朱鸿鹄在砂土质地基模型试验中,基于FBG,BOTDA 和粒子图像测速(Particle Image Velocimetry,PIV)结合技术获得了土体的应变,其中PIV 与DIC 原理相同。2 种方法在具体数值有较大的差异,在小变形条件下,FBG 读数的稳定性明显好于PIV[14-15]。对于光纤传感技术与DIC 测量精度的研究,鲜有相关文献报道。
笔者将BOTDA,FBG 和DIC 技术应用于物理相似模拟试验中,用BOTDA 以及FBG 传感器进行结构内部应变测试,用DIC 进行表面应变实时监测,研究不同原理测试方法在获得数据上的关系,建立对应换算比例。分析不同光测方法对同一对象观测的应变值差异较大的原因。
1 光测方法原理
1.1 BOTDA 应变
BOTDA 为利用光纤作为传感元件,当被测光纤受到外力或温度变化时,光纤中受激布里渊散射光的频率将发生变化,通过转换就能获得光纤沿线的应变信息。布里渊频移变化量与温度和应变变化[16]为
其中,Δε 为应变变化量;ΔVB 为布里渊频移量,MHz;C1 为温度灵敏度系数,MHz/℃;ΔT 为温度变化量,℃;C2 为应变灵敏度系数,103 GHz。该方法基于光的散射原理,测量布里渊散射光的频率变化。
1.2 FBG 应变
利用光纤材料特性,在纤芯形成空间相位光栅,即FBG,应变与温度的变化都能够引起的反射光波长变化[17]为
其中,ΔλBi 为光纤光栅中心波长的变化量,nm;λBi(i=1,2)为光栅初始中心波长,nm;KT 为温度灵敏度系数,对于室温下,一般取值0.794;Δε,ΔT 为光栅应变、温度变化量;Kε 为应变灵敏度系数,对于典型石英光纤,取值0.78。依据公式可以方便求出外界应变Δε 的值。该方法基于光纤耦合模式理论,测量反射光的波长变化。
上述2 种方法在温度变化较小的情况下(如5 ℃),可忽略温度的影响。
1.3 DIC 应变测量原理
DIC 技术是使用工业相机获取物体表面的散斑图像,基于算法进行图像分析以定量提取被测结构体表面的三维坐标、位移场及应变场等变形信息。DIC通过求取变形图像前后子区中心点的位移差来获取测量点Pi(i=1,2,3)的位移,如图1所示。
DIC 应变计算本质上是对位移的求导,子区测量点在空间中的变化可用梯度矩阵F[18]表示:

其中,共有6 个未知数,ui,vi 为测量点Pi 的横向和竖向位移分量,F11,F12,F21,F22 为梯度矩阵F 的各元素分量。因此,至少需要3 个测量点的变形信息,采用最小二乘法计算变形张量,拉伸张量U 表示为
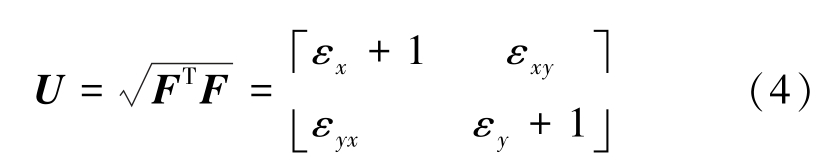
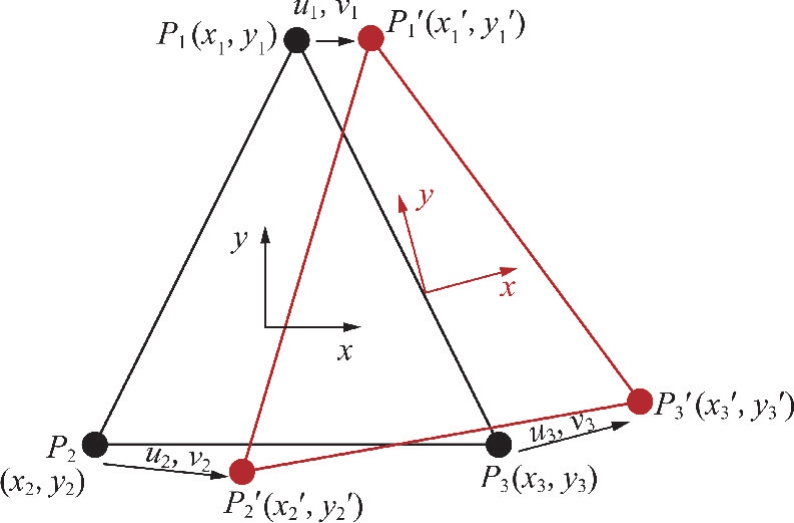
图1 数字图像相关应变计算原理
Fig.1 Calculation principle of digital image correlation strain
由式(4)中可以得出被测物体x 和y 方向的应变。
BOTDA,FBG 测试方法是以光为载体、光纤为媒介对外界信号进行感知和传输,本质上是一种“线应变”。DIC 应变测量通过至少3 个测量点的位移数据求出应变,本质上是“面应变”。
2 测试数据差异性
2.1 应变范围
对于掺锗石英光纤,BOTDA 应变灵敏度系数C2通过标定实验得出,其值为48 GHz;FBG 应变灵敏度系数Kε=0.78。本次试验,BOTDA 与FBG 所测应变表示为
对于直径为2 mm 的单模紧套光纤进行分布式光纤应变监测时,ΔVB 在0~480 MHz;对于典型的聚烯乙酯封装的FBG 传感器,ΔλBi 范围在0~8 nm。由此可得,FBG 传感器(1 550 nm)最大监测应变为6.617×10-3;BOTDA 最大测试应变为10-2。
图2为不同地质条件下模拟煤矿上覆岩层变形破断时,由BOTDA 和FBG 监测出的最大应变值,横坐标为物理模型模拟开挖工作面的推进距离,数据点来自文献的研究成果[6,8,19-21]。引入高采比k(k=h/m)表述上覆岩层的位置,h 为光纤的埋设位置,m 代表煤层的采高,即从0~30 倍的高采比进行统计。由图2可知,当覆岩产生破断时,BOTDA/FBG 测得应变离散程度高,但是总体上,随着高采比k 的增大,测得的应变相对要小些,这符合覆岩变形的基本规律;BOTDA 测得的应变大致为0~7×10-3,平均应变3.656×10-3;FBG 监测结果分布在0~5×10-3,平均应变2.352×10-3。试验测试结果在量级上与理论值基本一致。
DIC 为基于连续变形假设的光测方法,其监测应变的测试范围为5×10-5~20,获取应变场的大范围数据,因此,从理论上讲,BOTDA,FBG 和DIC 测试结果在量级上可能存在1~2.86×103 倍的差异。
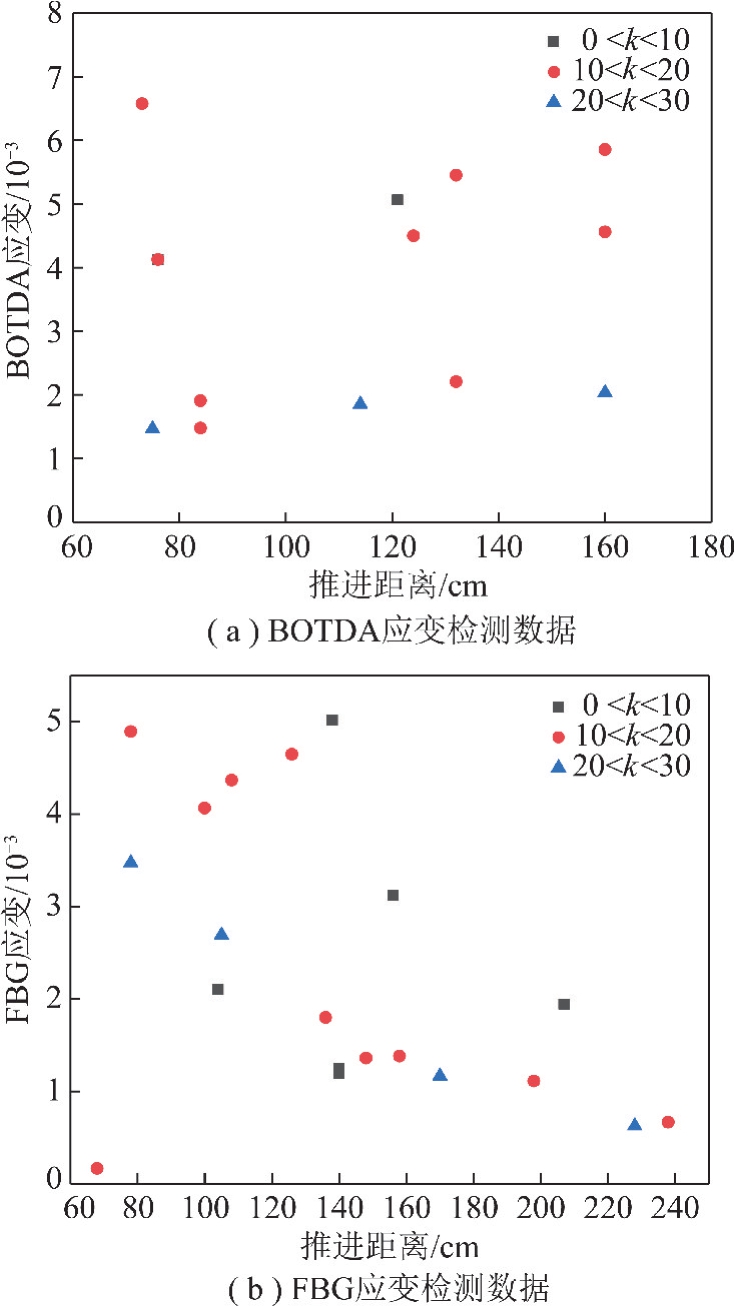
图2 模型覆岩破断时的光纤测试数据
Fig.2 Optical data of model overburden breaking
2.2 监测应变差异性
根据1.3 节,DIC 的应变测试本质是基于连续变形对位移的求导,测点位于均匀变形区域时,应变测试数据接近实际应值;测点位于裂隙及其附近非均匀变形区域时,应变测试数据有差异。图3为DIC 测量裂隙周围变形示意,测点1 位于裂隙上,其所在的正方形子区涵盖了裂隙区域以及应变局部化带内的非均匀变形区域,DIC 无法有效计算裂隙上的位移数据,测点1 的位移值必定与实际位移值相差较大[22]。测点2 布置在应变局部化带边界上,其所在子区涵盖了应变局部化带内的非均匀变形区域和应变局部化带外的均匀变形区域,DIC 不可能同时准确获取非均匀变形区域和均匀变形区域的位移值,因此测点2 的位移值必然与实际位移值相差较大,这与前人的研究成果一致[23]。测点3 位于应变局部化带之外,子区包含应变局部化带外的均匀变形区域,测点3 的位移值与实际位移值相吻合。

图3 DIC 测量裂隙周围变形示意
Fig.3 Diagram of deformation around fracture measured by DIC
DIC 的应变测量可以等效于在模型表面一定大小的应变片,在此称作虚拟应变片,虚拟应变片的边长LVSG 为
其中,Lw 为正六边形半径上除应变测点之外的测点数;Lst 为子区间距;Lsu 为子区大小;α 为测试系统放大倍率。为了保证DIC 的测量精度,最终确定Lw 为3;Lst 为5 pixel;Lsu 为34 pixel;α 为1.8 pixel/mm,由式(7)求得LVSG 为24.44 mm。此外,本次试验中DIC测量系统位移分辨率为0.01 pixel,DIC 测量系统的精度为0.006 mm。
对于GOM-ARAMIS 软件,其虚拟应变片为正六边形,虚拟应变片面积为1 552.15 mm2;BOTDA 解调仪空间分辨率设置为50 mm,对于直径为2 mm 光纤,其与岩层的接触面积为100 mm2,也就是说光纤在某点的应变实际为光纤与岩层接触面积上所有应变的平均值。由此得出,当DIC 测点位于均匀变形区域时,DIC 与BOTDA 的应变测试结果比值为15.52。
3 相似物理模型试验
3.1 模型概况
试验以某矿为研究背景,选用河砂、粉煤灰、石膏、大白粉作为相似材料。选取几何相似比为1 ∶150,制作相似模型,模拟开挖的煤层编号为1-2 煤,煤层厚度m = 1.3 cm,关键层位于煤层上方h=19 cm 处。模型两侧边界煤柱30 cm,开切眼10 cm,模拟工作面开挖步距为3 cm,从保护煤柱向右侧推进,累计开挖77 次,共推进240 cm。采用光纤监测关键层变形破坏,由光纤埋设位置得k=15.8。
3.2 监测系统布置
模型共布置有3 种光测传感监测系统,BOTDA,FBG 和DIC 技术的监测系统如图4所示,各测量系统均在每次开挖结束后采集数据。
埋设3 支FBG 应变传感器,编号为 FBG01(λB1=1 535.58 nm),FBG02(λB2=1 555.73 nm),此外还有1 支温度补偿传感器FBG03,采用竖直埋设的方法,监测结果中数据为正表明岩层处于受拉状态,数据为负表明岩层处于受压状态。一根直径2 mm的单模紧套光纤,埋设于关键层最中间位置,埋设光纤直径小于2 mm 时岩层位移变化误差小于5%,对岩层变形影响小[24]。DIC 监测系统由两个CCD 数字摄像机组成,分辨率为600 万像素。
3.3 试验覆岩变形破坏过程
工作面自保护煤柱推进至25 cm 时,直接顶垮落,垮落高度1.1 cm,垮落长度22 cm;推进至37 cm,工作面初次来压,垮落高度4.5 cm,垮落长度34 cm;推进至58 cm,顶板上部10.5 cm 处出现离层,张开度0.8 cm,长度达到21 cm,工作面第1 次周期来压;推进至76 cm,顶板上部9.6 cm 处出现新的离层,张开度为0.3 cm,长度达到25.5 cm;工作面推进至115 cm,采空区中部离层裂隙被压闭合,上覆岩层20~39.6 cm 处新的离层裂隙进一步发育,如图5(a)所示;推进至121 cm,覆岩变形至上表面,地表出现明显下沉,裂隙带被压实,此时裂隙带高度在33.5 cm;推进至178 cm 时,顶板垮落高度5.6 cm,长度172 cm;推进至220 cm,工作面上部岩层14.5 cm处产生离层,张开度0.5 cm,长度27 cm;推进至240 cm,垮落带高度达到8 cm,裂隙带高度为36.5 cm,覆岩变形如图5(b)所示,回采结束,模型顶部下沉量为0.9 cm,岩层左侧垮落角54°,右侧垮落角为56°。

图4 物理模型光测监测系统布置
Fig.4 Layout of optical monitoring system for physical model

图5 物理模型试验覆岩变形及对应DIC 应变云图
Fig.5 Deformation of overburden in physical model test and corresponding DIC strain nephogram
4 试验结果与分析
4.1 均匀变形区域的应变对比
工作面推进至22 cm 时,由BOTDA 与DIC 获得的关键层应变监测结果如图6所示,此时工作面覆岩区域为均匀连续变形,DIC 测试的平均应变(3.704×10-4)与BOTDA 测试的平均应变(2.22×10-5)比值为16.70,与理论计算值15.52,较为接近。
为了能够准确评价DIC 测量的精度,利用工作面推进至220 cm 时全站仪测点的观测值,与DIC 的测试结果进行对比如图7所示,DIC 与全站仪所测结果整体变化趋势一致,误差为8.3%。说明试验选取的DIC 子区大小、以及子区间距的参数可行,保证了DIC 测量精度对试验观测的需要。
4.2 FBG 监测应变
在工作面推进过程中,FBG 传感器测试的应变变化如图8所示,横坐标为模型长度。FBG01 距离模型边界130 cm,应变变化曲线如图8(a)所示,当工作面推进至76 cm 时,受到覆岩运移影响,岩层弯曲下沉,FBG01 应变值开始变化;推进至100 cm 时,工作面基本位于FBG01 传感器下方,FBG01 的应变为-1.63×10-4;当推进至133 cm 时,传感器位置的岩层形成悬臂梁结构,应变迅速达到最大2.573×10-3;此后随着工作面推进,岩层破断、垮落和逐渐被压实,应变又变为负值并趋于稳定。FBG02 距离模型边界190 cm,应变变化曲线如图8(b),工作面推进至157 cm 时,应变值为-1.29×10-4;当推进至175 cm时,应变迅速达到最大2.768×10-3,此后随着工作面推进,FBG02 应变值减小至负值最后逐渐稳定。
4.3 DIC 监测应变
图9为工作面推进过程中,FBG01,FBG02 所在位置的DIC 测试应变曲线。图9(a)中,当工作面推进106 cm 之前,DIC 所测得应变基本为0,在此期间,FBG01 所在位置并未发生离层裂隙。此后应变开始阶段性增大,当工作面推进至112 cm 时,应变为2.242×10-2;推进至124 cm 时,应变为3.248×10-2;推进至136 cm 时应变达到最大值6.076×10-2。上覆岩层中出现离层,并逐渐变小直至稳定。

图6 BOTDA 与DIC 应变对比
Fig.6 Comparison of strain between BOTDA and DIC

图7 全站仪和DIC 测量结果对比
Fig.7 Comparison of total station and DIC results
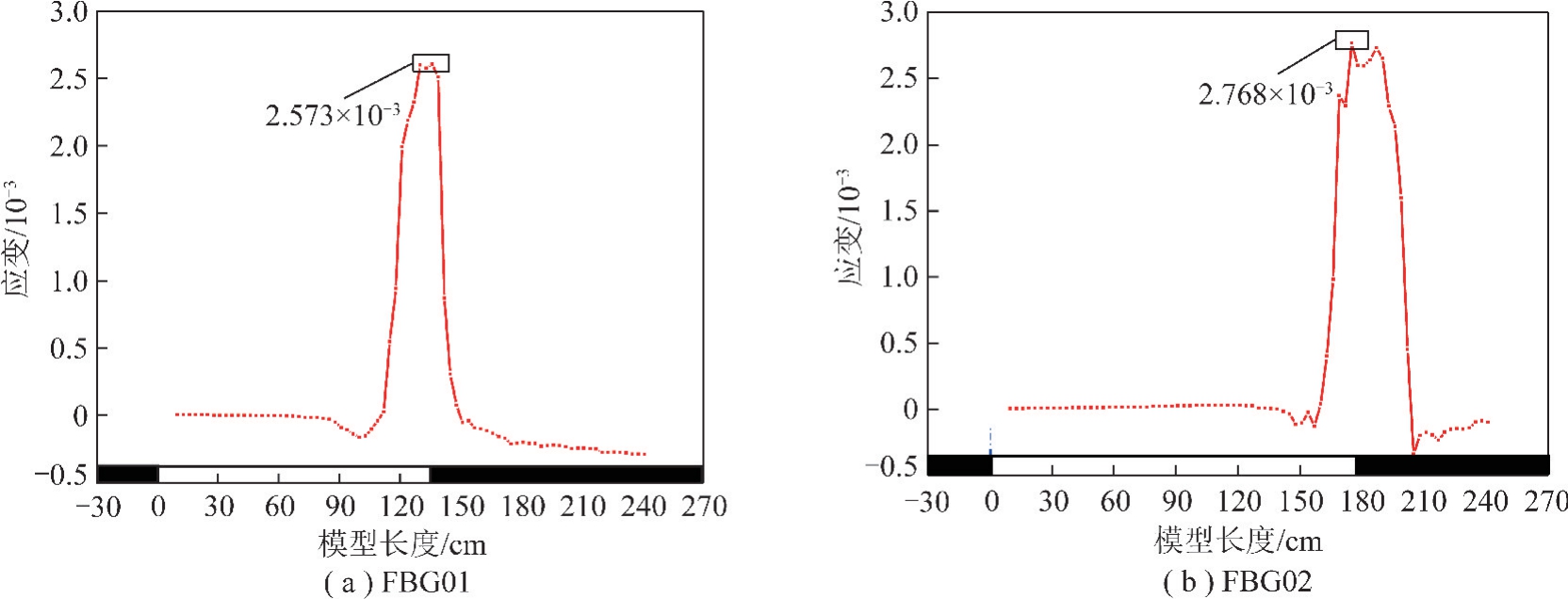
图8 物理模型FBG 监测应变
Fig.8 FBG monitoring strain of physical model
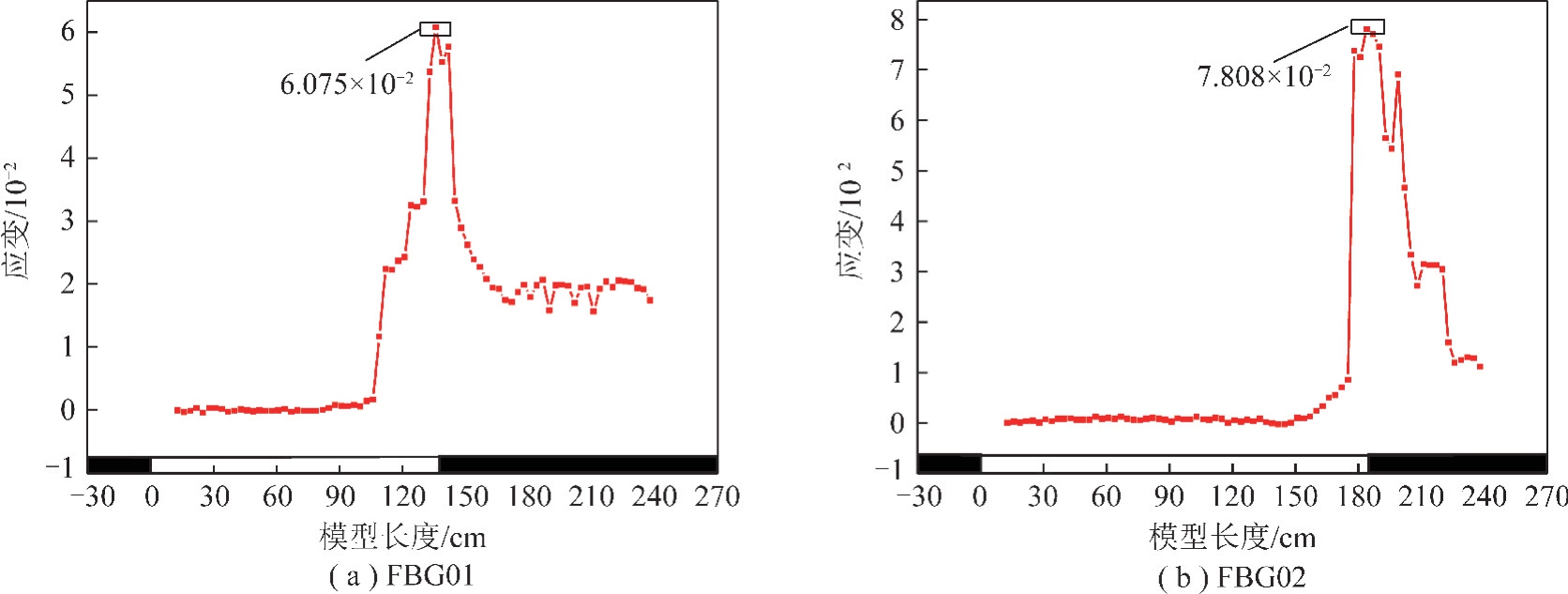
图9 物理模型FBG 位置处DIC 监测应变
Fig.9 DIC monitoring strain at FBG location of physical model
图9(b)中,工作面推进至157 cm 之前,DIC 测点应变基本为0,此后随工作面推进,应变逐步增加,推进至175 cm 时,应变增加至8.531×10-3,然后开始急剧增大,推进至184 cm 时,应变达到最大7.808×10-2,从199 cm 开始,应变开始阶段性下降,最终稳定在10-2 左右。
引入离层位置偏差量ηF,ηD 来衡量FBG 与DIC对离层位置判定的准确程度,计算公式为
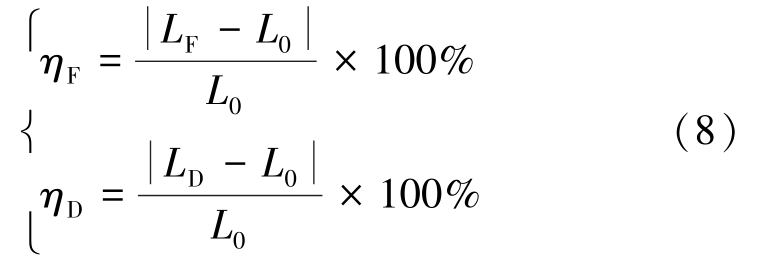
式中,LF 为FBG 应变最大值所确定的离层距离左侧煤柱的距离,cm;L0 为模型实测离层位置,cm;LD 为DIC 应变最大值所确定的离层距离左侧煤柱的距离,cm。
对于FBG01 应变最大值出现时,真实离层位置距离左侧煤柱131 cm,此时偏差ηF01 为1.52%,ηD01为3.82%。同理,对于FBG02 真实离层位置距离左侧煤柱177 cm,计算得ηF02 为1.13%,偏差ηD02 为3.95%。
FBG01 测得最大应变2.573×10-3,DIC 测得应变为6.076×10-2,DIC 测试值与FBG 测试值比值为23.6。FBG02 测试应变,DIC 测试值与FBG 测试值比值为28.2。DIC 与FBG 获得的“测点应变”有较大的差异,但是,FBG 和DIC 监测的应变曲线可以较好地显示测点附近离层裂隙的发育情况,应变最大值出现位置基本相同,FBG 测得结果更好。在应变曲线峰前,DIC 与FBG 测试应变均快速增长至最大,说明岩层变形的突发性。在应变曲线峰后阶段,DIC 更好地反映了上覆岩层的变形,有一个逐步稳定的发展过程,而不是出现负值。其原因主要是光纤和岩层之间的不完全接触造成的;还有其他一些因素可能导致这种差异。
4.4 BOTDA 监测“线应变”
工作面推进过程中,布置在关键层中的BOTDA监测的沿线应变曲线如图10所示。图10(a)中,当工作面推进至70 cm 时,关键层岩层发生弯曲,围岩应力重新分布,岩层内部光纤受到拉应力的作用,产生正应变,出现微小凸峰,应变值达到1.58×10-4,出现1 号凸峰。当工作面推进至85 cm 时,关键层内光纤受到的拉应力进一步增大,应变值达到3.01×10-4。图10(b)中,推进至121 cm 时,工作面第5 次周期来压,关键层破断,顶板结构失稳,发生回转,岩层破坏特征为拉破坏,在靠近左侧煤柱和工作面后方形成破断线,在破断线附近的光纤拉应力增大,呈现双凸峰(2 号,3 号)趋势。
工作面从121~175 cm 推进过程中,2 号凸峰应变达到10-3,基本不变;3 号凸峰的应变值最大达到1.083×10-3,随工作面推进至175 cm 时降低为8.13×10-4,其原因是关键层位置裂隙闭合,岩层内部弹性能释放。在此后推进过程中,3 号凸峰位置几乎不变,其峰值逐渐趋于稳定。图10(c)中,工作面推进至190 cm 时第10 次周期来压,曲线在双凸峰状的基础上出现新的凸峰(4 号),位置在190 cm 处,应变值7.68×10-4。随着工作面继续向前推进,4 号凸峰位置逐步向右移动,峰值1.7×10-3;图10(d)中,推进至223 cm 时,4 号凸峰应变增大至1.745×10-3;推进至240 cm 时,应变值降为1.323×10-3。
BOTDA 测试的应变曲线中2 号凸峰出现位置基本保持不变,峰值稳定在9×10-4 左右,表明此处岩层变形小,围岩应力趋于稳定。3 号凸峰峰值稳定在7×10-4 左右,位置也基本不变,说明随着工作面推进,应力也趋于稳定。4 号凸峰峰值随工作面推进距离的增加先增大,之后又逐渐降低,表明了岩层内弹性能的变化由积聚到逐渐释放的动态变化过程。
4.5 DIC 监测“线应变”
图11为工作面推进过程中,沿光纤埋设位置的DIC 测线应变测试结果。图11(a)中,工作面推进至55 cm 时,伴随着工作面顶板的下沉而发生微小变形,推进至70 cm 时,应变增大到1.461×10-2。图11(b)中,工作面从121~175 cm 推进过程中,曲线呈现双凸峰状,3 号凸峰位置右移及峰值增大,最大峰值为0.121;之后图11(c),(d)中,工作面从190 cm 推进至240 cm 时,曲线在双凸峰状的基础上同样出现新的凸峰(4 号),最大峰值为6.8×10-2。
对比图10和图11,凸峰出现位置,以及整体趋势,BOTDA 和DIC 应变曲线基本一致,BOTDA和DIC 的应变曲线随着工作面推进,曲线由单凸峰到双凸峰的“马鞍形”,再到3 个凸峰。在整个覆岩变形破断过程中,2 号凸峰位置变化不大,3号凸峰位置先逐渐向右移动,之后稳定在150 cm左右,4 号凸峰也呈现先向右移动,再逐渐稳定状态。BOTDA 应变曲线和DIC 应变曲线都呈规律性地先上升后下降,最后趋于稳定。总之,BOTDA应变峰值位置与DIC 应变曲线中应变峰值位置相近,他们均较好的反映出来破坏现象,以及发生破坏的位置, 也说明了岩层内外部变形的同步性。

图10 物理模型BOTDA 监测应变
Fig.10 BOTDA monitoring strain of physical model

图11 物理模型DIC 监测应变
Fig.11 DIC monitoring strain of physical model
同理,引入破断范围偏差来衡量BOTDA 与DIC对破断线范围判定的准确程度,如工作面推进175 cm 时,真实破断范围为183 cm,BOTDA 偏差为3.25%,DIC 所测偏差为1.62%。比较工作面过程中破断范围偏差,DIC 测得破断范围更精确。
2 号凸峰在工作面推进过程中相对稳定,DIC 监测的2 号凸峰从22 cm 移动到19 cm,平均应变为6.7×10-2;BOTDA 监测的2 号凸峰从16 cm 移动到27 cm,平均应变9.09×10-4,DIC 与BOTDA 监测的平均应变比值为74;3 号凸峰应变先增大后减小,DIC与BOTDA 监测的平均应变比值最小为69,最大为133;4 号凸峰DIC 与BOTDA 监测的平均应变比值最小为27,最大为41。综上,在工作面推进过程中,DIC与BOTDA 监测的平均应变比值在27~133,平均应变差异较大。
4.6 应变差异原因
BOTDA 与DIC 结果有差异的原因有以下几点:从试验角度分析,试验物理模型为平面应力状态,模型面没有得到有效约束控制;不完善的检测条件影响了照片的质量,图像处理过程造成了误差,图像失真无法完全消除,计算误差会累积。从光纤传感技术角度,岩层垮落导致光纤和岩层之间的不完全接触,出现滑移、脱落现象;砂土脆性材料,对传感器的接触面积以及应变的有效传递产生影响;光纤应变测量高度依赖于BOTDA 的空间分辨率,本次试验BOTDA 空间分辨率为50 mm;光纤以及外护套具有一定的直径,使模型岩层变形产生一定误差。从数字图像相关技术测试角度分析,岩层的真实变形场可能异常复杂,从而导致变形后的子区形状难以描述,无法有效估计形函数误差;缺乏完备的散斑质量评价标准与优化的理论模型;不同变形条件下,缺乏优化计算参数的选择的标准方法;子区大小、间距这些参数的选择与设置也会影响应变检测。所有这些因素都可能给测量带来不确定性,不同光测方法虽然在具体数值有一定的差异,但总体趋势一致。需要在进一步的研究中分析影响因素,并逐步消除。
BOTDA 测试方法本质上是一种“线应变”,DIC是“面应变”,研究两种不同的光测方法的融合机制,用BOTDA 以及FBG 传感器进行结构内部应变测试,DIC 进行表面应变监测,进行大试样或者大范围的岩石力学试验观测。
5 结 论
(1)BOTDA 测试方法本质上是一种“线应变”,DIC 本质上是“面应变”。BOTDA 和FBG 的测试应变量级相同;对于本次试验中DIC 测试参数的设置,一方面满足相似模型监测精度要求,另一方面,在均匀连续变形区域DIC 与BOTDA 监测的应变比值为15.52~16.70,在非均匀变形区域监测的应变比值为27~133。
(2)相对实际离层出现位置而言,FBG 和DIC 测得结果有存在一定偏差,最大偏差为3.95%。对比2个测点,FBG 测试结果更准确。
(3)BOTDA 和DIC 均可以判断关键层破断范围,在此次试验中DIC 测试的破断范围偏差值更小,测试结果更好。
(4)BOTDA,FBG 和DIC 监测应变在数值上存在差异性,且测试精度各有优劣,但总体的应变曲线基本趋势一致,反映了岩层内外部变形的同步性。3 种光测传感技术联合可以用于监测分析覆岩关键层运移规律,揭示不同开挖状态的破坏形态。进一步的研究将建立他们之间的量化关系。
[1] 钱鸣高,许家林.煤炭开采与岩层运动[J].煤炭学报,2019,44(4):973-984.QIAN Minggao, XU Jialin.Behaviors of strata movement in coal mining[J].Journal of China Coal Society,2019,44(4):973-984.
[2] 娄金福,高富强,李建忠,等.采场模型试验应力(压力)测量系统研制及应用[J].煤炭学报,2019,44(S1):31-40.LOU Jinfu,GAO Fuqiang,LI Jianzhong,et al.Research and application of stress(pressure)measurement system for physical modeling[J].Journal of China Coal Society,2019,44(S1):31-40.
[3] 吴海颖,朱鸿鹄,朱宝,等.基于分布式光纤传感的地下管线监测研究综述[J].浙江大学学报(工学版),2019,53(6):44-57.WU Haiying,ZHU Honghu,ZHU Bao,et al.Review of underground pipeline monitoring research based on distributed fiber optic sensing[J].Journal of Zhejiang University(Engineering Science),2019,53(6):44-57.
[4] 娄建华,刘军,王洁,等.DSP 光纤光栅解调系统研究[J].西安科技大学学报,2012,32(1):91-94,120.LOU Jianhua,LIU Jun,WANG Jie,et al.Research on DSP fiber Bragg grating demodulation system[J].Journal of Xi’an University of Science and Technology,2012,32(1):91-94,120.
[5] 柴敬,袁强,李毅,等.采场覆岩变形的分布式光纤检测试验研究[J].岩石力学与工程学报,2016,35(S2):3589-3596.CHAI Jing,YUAN Qiang,LI Yi,et al.Experimental study on overlying strata deformation based on distributed optical fiber sensing[J].Chinese Journal of Rock Mechanics and Engineering,2016,35(S2):3589-3596.
[6] 柴敬,孙亚运,钱云云,等.基于FBG-BOTDA 联合感测的岩层运动试验研究[J].西安科技大学学报,2016,36(1):1-7.CHAI Jing,SUN Yayun,QIAN Yunyun,et al.Strata movement testing based on FBG-BOTDA combined sensing technology in similar model[J].Journal of Xi’an University of Science and Technology,2016,36(1):1-7.
[7] CHAI J,LIU Q,LIU J,et al.Optical fiber sensors based on novel polyimide for humidity monitoring of building materials[J].Optical Fiber Technology,2018,41:40-47.
[8] 柴敬,王帅,袁强,等.采场覆岩离层演化的光纤光栅检测实验研究[J].西安科技大学学报,2015,35(2):144-151.CHAI Jing,WANG Shuai,YUAN Qiang,et al.Experimental study on the separation evolution of overlying strata above the stope by FBG sensing[J].Journal of Xi’an University of Science and Technology,2015,35(2):144-151.
[9] 张丹,张平松,施斌,等.采场覆岩变形与破坏的分布式光纤监测与分析[J].岩土工程学报,2014,37(5):925-957.ZHANG Dan,ZHANG Pingsong,SHI Bin,et al.Monitoring and analysis of overburden deformation and failure using distributed fiber optic sensing[J].Chinese Journal of Geotechnical Engineering,2015,37(5):952-957.
[10] 张丁丁,柴敬,李毅,等.松散层沉降光纤光栅监测的应变传递及其工程应用[J].岩石力学与工程学报,2015,34(S1):3289-3297.ZHANG Dingding,CHAI Jing,LI Yi,et al.Strain transfer function of embedded fiber bragg grating sensors for uncosolidated layer settlement deformation detector and its application[J].Chinese Journal of Rock Mechanics and Geotechnical Engineering, 2015,34(S1):3289-3297.
[11] 吴冰,朱鸿鹄,曹鼎峰,等.基于光纤光栅的冻土含冰量监测可行性试验研究[J].岩土工程学报,2019,41(12):2323-2330.WU Bing,ZHU Honghu,CAO Dingfeng,et al.Feasibility study on FBG-based monitoring method for ice content in frozen soil[J].Chinese Journal of Geotechnical Engineering,2019,41 (12):2323-2330.
[12] 潘红宇,葛迪,张天军,等.应变率对岩石裂隙扩展规律的影响[J].煤炭学报,2018,43(3):675-683.PAN Hongyu,GE Di,ZHANG Tianjun,et al.Influence of strain rate on the rock fracture propagation law[J].Journal of Chinese Coal Society,2018,43(3):675-683.
[13] 何满潮,王炀,刘冬桥,等.基于二维数字图像相关技术的块系花岗岩超低摩擦效应实验研究[J].煤炭学报,2018,43(10):2732-2740.HE Manchao,WANG Yang,LIU Dongqiao,et al.Experimental study on ultra-low friction effect of granite block based on two-dimensional digital image correlation technique[J].Journal of Chinese Coal Society,2018,43(10):2732-2740.
[14] ZHANG C C,ZHU H H,SHI B.Role of the interface between distributed fibre optic strain sensor and soil in ground deformation measurement[J].Scientific Reports,2016,6:36469.
[15] 李飞,朱鸿鹄,张诚成,等.地基变形光纤光栅监测可行性的试验研究[J].浙江大学学报(工学版),2017,51(1):204-211.LI Fei,ZHU Honghu,ZHANG Chengcheng,et al.Experimental study on feasibility of fiber Bragg grating-based foundation dformation monitoring[J].Journal of Zhejiang University (Engineering Science),2017,51(1):204-211.
[16] KISHIDA K,LI C S,LIN S,et al.Pulse pre-pump method to achieve cmorder spatial resolution in Brillouin distributed measuring technique[J].Technical Report of IEICE,OFT,2004,47:15-20.
[17] 王静,李术才,隋青美,等.基于相似材料的光纤应变传感器在分区破裂模型试验中的研究[J].煤炭学报,2012,37(9):1570-1575.WANG Jing,LI Shucai,SUI Qingmei,et al.Study of FBG strain sensors based on similar materiel in zonal disintegration model test[J].Journal of China Coal Society,2012,37(9):1570-1575.
[18] YONG S,ZEREN G,QINGCHUAN Z,et al.Spatial uncertainty of measurement errors in digital image correlation[J].Optics and Lasers in Engineering,2018,110:113-121.
[19] 柴敬,袁强,张丁丁,等.基于光纤Bragg 光栅的采动支承压力分布试验研究[J].西安科技大学学报,2016,36(2):163-170.CHAI Jing,YUAN Qiang,ZHANG Dingding,et al.Experimental study on mining-induced abutment pressure distribution pattern based on FBG sensor[J].Journal of Xi’an University of Science and Technology,2016,36(2):163-170.
[20] 柴敬,袁强,王帅,等.长壁工作面覆岩采动“横三区”光纤光栅检测与表征[J].中国矿业大学学报,2015,44(6):971-976.CHAI Jing,YUAN Qiang,WANG Shuai,et al.Detection and representation of mining induced three horizontal zones based on fiber bragg grating sensing technology[J].Journal of China University of Mining & Technology,2015,44(6):971-976.
[21] 柴敬,汪志力,刘文岗,等.采场上覆关键层运移的模拟实验检测[J].煤炭学报,2015,40(1):35-41.CHAI Jing,WANG Zhili,LIU Wengang,et al.Monitoring movement laws of overlying key strata for coal mining in similar model[J].Journal of China Coal Society,2015,40(1):35-41.
[22] XU X,SU Y,ZHANG Q.Theoretical estimation of systematic errors in local deformation measurements using digital image correlation[J].Optics and Lasers in Engineering,2017,88:265-279.
[23] 王学滨,杜亚志,潘一山.基于DIC 粗-细搜索方法的单轴压缩砂样的应变分布及应变梯度的实验研究[J].岩土工程学报,2012,34(11):2050-2057.WANG Xuebin,DU Yazhi,PAN Yishan.Experimental studies on strain distribution and gradients for sand specimens under uniaxial compression based on digital image correlation coarse-fine search method[J].Chinese Journal of Geotechnical Engineering,2012,34(11):2050-2057.
[24] 袁强.采动覆岩变形的分布式光纤检测与表征模拟试验研究[D].西安:西安科技大学,2017:24-35.YUAN Qiang.Experimental study on detection and representation of mining-induced overburden deformation with distributed optical fiber sensing[D].Xi’ an:Xi’ an University of Science and Technology,2017:24-35.
