地下煤层开采势必引起上覆岩层和地表的移动变形,为认识特定地质采矿条件下地表移动变形规律,最直接、有效的手段是建立地面岩移观测站。通过分析定期观测数据,可以定量确定地表移动变形量的大小、角量参数和预计参数,为后续开采沉陷预计、开采损害评价等提供技术依据和参数[1-3]。开采引起的地表移动包括垂直下沉和水平移动两个分量,由两点间的下沉差可计算出地表倾斜,由两点间的倾斜差可计算出地表曲率,由两点间的水平移动差可计算出地表变形。
如果下沉和水平移动分别用函数W(x)=FW(x),U(x)=FU(x)表示,则倾斜,曲率,水平变形3个变形分量又可分别表示为T(x)= dW(x)/dx,K(x)=dW2(x)/dx2,ε(x)=dU(x)/dx。
由此可知,不论是基于观测数据还是预计模型,都可以得到并绘制出下沉、倾斜、曲率、水平移动和水平变形5 条移动变形曲线或5 类移动变形等值线;观测数据分析的目的是为了认识采动地表移动变形规律并确定移动参数与预计参数,而预计的目的是事先预知开采可能产生的地表移动变形、评估采动可能造成的地表损害程度,以便科学、有效地指导地下开采设计与优化,减小开采损害。按照现行规范[4],只要预计的地表倾斜、曲率和水平变形3 个值中的一个指标达到某一限值即可确定该建筑物的损坏等级[5]。如何客观、科学地预计地表移动变形并评价煤矿区地表建筑物采动损坏程度,早已引起研究者和煤炭生产企业的重视;预计方法也从传统的静态预计,发展到基于时间函数[6-7]、采动充分性[8]的动态过程预计;而在损坏程度评价方法上,研究者们通过引入物元模型[9]、模糊综合评判[10]、层次分析法[11]等,开展了建筑物采动损坏程度的多元判据研究与综合评价[12-13];也对采动区建筑物地基、基础协同作用[14]、露天矿开采引起的周边建筑物损害区位特征进行了分析[15];针对建筑物采动损坏评价研究的迫切性以及临界变形值确定和损坏等级划分研究现状,文献[16]归纳分析了基于模糊数学、物元模型、神经网络、聚类分析、熵权法、点数法等多种理论方法的优缺点,详细介绍了脆弱性曲线、分类回归树等国际上采动建筑物损坏评价研究的新进展;国外学者将建筑结构与地基土视为相互作用系统,引入Winkler 模型[17-19]和相对刚度系数[20]以表达建筑结构与地基土之间的作用关系;2020年KAHIA 等利用人工神经网络模型,通过分析不同建筑物长度、建筑物均布载荷、地基极限承载力、建筑物刚度、Winkler 地基弹性模量、地表曲率半径的18 900 种可能组合,建立了从弹性条件到弹塑性条件下的挠度传递比的原型模型[21],以期从理论上建立建筑结构与地基相互作用关系,阐述建筑结构损坏产生的力学机理。
除了底面积小的高耸建筑物对倾斜变形敏感外,一般建筑物均对水平变形敏感,通常以水平变形为主要指标来界定其损坏等级。我国现行规范对于长度小于20 m 的砖混结构建筑物,其损坏等级划分指标相同,并未考虑建筑物长度影响。实际上,采动建筑物的损坏既与地表不均匀移动变形有关,也受建筑物的结构长度及其抵抗变形能力影响。笔者试图对采动地表移动变形、建筑物损坏特征以及建筑结构与地基相互作用进行分析,进而探讨建筑物结构长度、水平变形与采动损坏等级间的关系。
1 地表倾斜变形
下沉主断面上水平地表A,B 两点间距为l,采动地表沉陷后A,B 点分别移动到A′和B′,如图1所示。A,B 两点之间的下沉差为ΔW,水平移动差为ΔU,A,B 两点在A′和B′连线上由下沉和水平移动产生的实时位形上的变形为
其中,由A′和B′两点间下沉差引起的实时位形上的变形为
图1 地表水平时的变形
Fig.1 Deformation for horizontal surface
当A,B 两点之间初始距离为l=10 m,两点间的下沉差ΔW=0.3 m,两点间的水平移动差为ΔU=0.1 m,则不均匀下沉和水平移动引起的变形为εA′B′=10.44 mm/m,其中非均匀下沉引起的变形为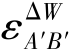
=0.45 mm/m。如果按初始位形计算,地表水平移动引起的变形值为εAB=ΔU/l=10 mm/m。需要注意的是
和εA′B′ 是沿实时位形A′B′方向上的变形,而εAB 是沿初始位形AB 方向上的变形[22]。
当初始地表为斜面时,如图2所示。 A,B 两点之间的初始高差为hAB,两点之间水平距离仍为l,则A,B 两点之间的斜距为
。受采动影响后A 点移动到A′,B 点移动到B′,两点之间的下沉差为ΔW,水平移动差为ΔU,A,B 两点在A′和B′连线上由下沉和水平移动产生的实时位形上的变形为
图2 地表倾斜时的变形分析
Fig.2 Deformation for inclined surface
当hAB=0 时,式(3)可以归化式(1),表明地表水平时非均匀下沉和移动引起的变形是地表倾斜时的一个特例。当两点间不存在非均匀水平移动,则倾斜地表非均匀下沉引起的两点间的变形为
以初始水平距离l=10 m 为例,两点间的下沉差和初始高差对变形的影响如图3所示。由图3可知,随着下沉差和初始高差的增大,由此产生的变形也随之增 大;当ΔW = 170 mm,hAB = 0.5 m 时,εA′B′ =1 mm/m。英国煤炭局在其沉陷工程师手册中,建议对地形产生的变形应予以改正[23]。
图3 不均匀下沉和地形起伏的影响
Fig.3 Surface deformation caused by uneven subsidence and topography
2 地表曲率变形
当地面A,B,C 号点受采动影响,B 点移动至B′点,C 点移动至C′点,如图4所示。 A′,B′点的倾斜TA-B 和B′,C′点的倾斜TB-C 分别为
式中,ΔWB-A,ΔWC-B 分别为B,A 点及C,B 点间的下沉差;lA-B,lB-C 分别为A,B 点间及B,C 点间的水平距离;α,β 分别为A,B 点及B,C 点间的倾斜角度。
由于下沉差ΔW 远小于两点间的水平距离,tan α≈α,tan β≈β,故有
其中,θ 为相邻3 点的倾斜差。假设测点间距相等,由式(7)可得地表曲率KA-B-C 为
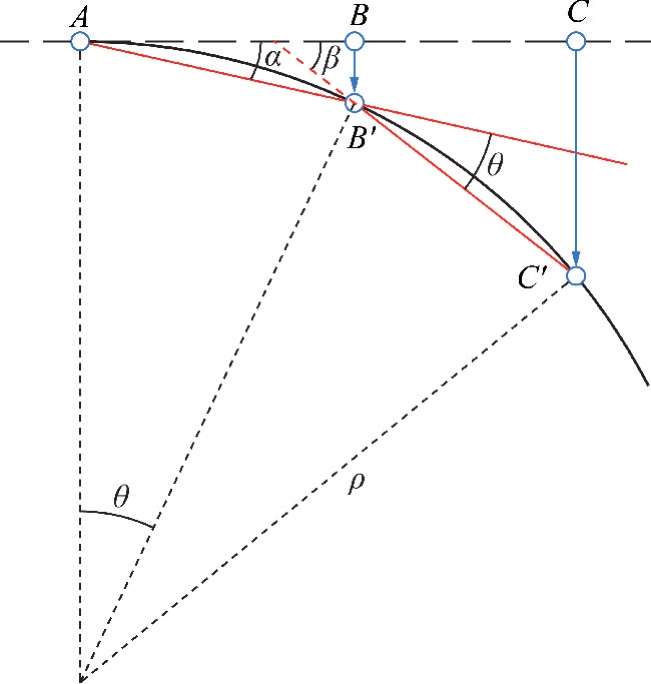
图4 地表曲率分析
Fig.4 Analysis of curvature
由图4可知
由于曲率半径ρ 远大于两点间的距离l,两点之间的距离l 又远大于两点间的下沉差,以弦长代替弧长,从而有
实际观测站布设中,由于地形及地物等影响,无法保证测段长度等间距;当测点间距不等,通过两相邻测段长度取平均来计算曲率,可能会导致计算出的曲率偏小,从而掩盖了最大曲率的影响,如图5所示。当B 点缺失,由A 点直接到C 点使得地表曲率将从1/ρ′减小到1/ρ。英国的研究结果认为,实地观测的测段长度取采深的1/20 适宜,水平变形的计算应选与该点相连的短边[24]。综合考虑监测效率、工作量和实际可操作性等因素,我国采用的监测点间距随采深的变化见表1[1]。
图5 测段过长的影响
Fig.5 Impact by longer distance
表1 测点间距的建议值
Table 1 Suggested distance between monuments m
开采深度 <50 50～100 100～200 200～300 >300测点间距 5 10 15 20 25
研究表明,曲率半径ρ 越小,地表的变形就越大,从而导致地面建筑物损害越大。英国和西班牙等国学者研究认为,地表曲率与变形的关系可表示为
其中,ε 为变形; a 为系数。英国煤炭局根据实地观测数据,研究得出系数a = 0.024 [23],由此可根据实测的曲率来预计水平变形。SANMIQUEL 等[24]根据西班牙2008—2016年的16 个下沉剖面上的观测数据,开采深度500～600 m,开采的宽深比在0.7～1.5,回归分析确定的系数上限a=0.018、下限a=0.012。但如果按照中国的概率积分预计方法,曲率和水平变形之间关系可用表示为
其中,b 为水平移动系数; r 为主要影响半径。比较式(11)和式(12),只有当θ/l=a/b2r2 时,两者计算的变形才相等。
3 曲率变形与建筑结构损坏特征
地表曲率是由地表不均沉陷引起的,假设柔性建筑物长度为L,含基础的建筑物高度为H,地表差异沉陷产生的曲率为1/ρ,由图6可知,该建筑结构的最大挠度Δ0 和挠度比Δ0/L 分别为
图6 曲率引起的建筑物变形
Fig.6 Building strain by curvature
在凸曲率作用下,建筑结构顶部产生的伸长量e和拉伸变形ε 分别为
式(15)和式(16)表明,正曲率影响下建筑结构的最大伸长量与建筑物的长度、高度成正比,与地表曲率半径成反比;而最大拉伸变形与建筑物高度成正比,与地表曲率半径成反比,与建筑物长度无关。同理,式(15)和式(16)以挠度比表示可分别改写为
采动地表曲率对建筑物的影响十分复杂,国外相关学者均对采动建筑物地基受力分布进行了研究。1983年RAUSCH 采用地基系数理论研究给出了凸凹曲率条件下基础完全嵌入地基的反力分布,如图7所示。KRATZSCH 认为当基础下为厚软岩层,在凸曲率区采动引起的附加地基反力,将使采后不均匀地基反力分布变得平缓,而在凹曲率区因叠加影响则会增大,如图8所示[25]。开采引起地表不均匀沉陷是必然发生的,而位于沉陷区地表的建筑物如何抵抗或适应采动变形,与建筑结构的刚度、强度以及地表土的性质密切相关;DECK[26]据此推测建筑物结构变形与地表变形存在如下关系:①当建筑结构强度高、刚度大时,结构无变形,挠度Δ=0,建筑物切入地表,如图9(a)所示;②建筑结构强度高、刚度大,虽然结构无变形,切入地表但结构底部与地表分离,如图9(b)所示;③对于柔性建筑物,适应地表变形,建筑物的挠度等于地表不均匀沉陷的最大挠度,如图9(c)所示;④建筑物和地表均产生相应变形,建筑物切入地表,但建筑物挠度小于地表挠度,如图9(d)所示;⑤建筑物与地表均产生相应变形,建筑物切入地表但底部与地表分离,建筑物挠度小于地表挠度,如图9(e)所示。
图7 地基反力示意[25]
Fig.7 Foundation reaction[25]
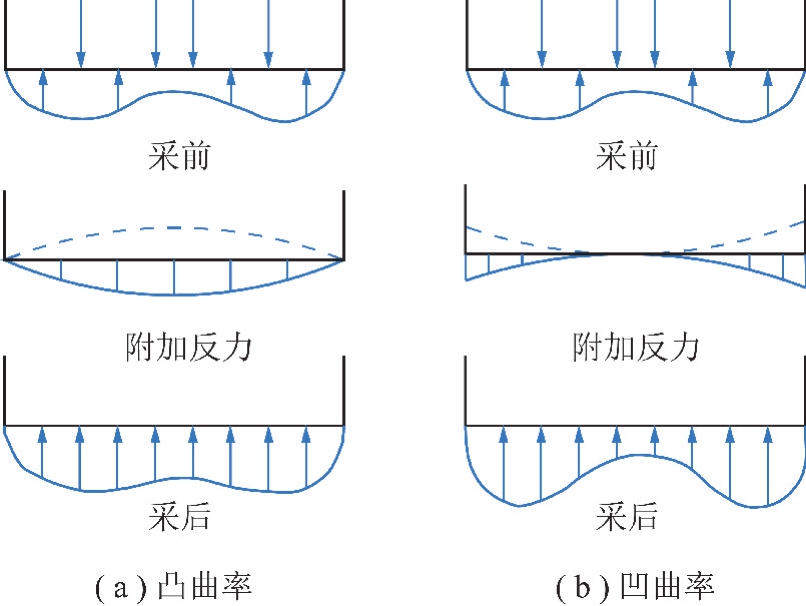
图8 厚软岩层地基反力分布[25]
Fig.8 Distribution of subgrade reaction[25]
图9 地表与结构的变形关系[26]
Fig.9 Interaction of soil and building[26]
BOSCARDIN 和BURLAND 把建筑物简化为简支梁,分别分析了在凸曲率和凹曲率状态下的弯曲破坏和剪切破坏,如图10所示[27-28]。在凸曲率影响下,建筑物顶部的弯曲变形产生拉伸裂缝,剪切变形引起倒八字裂缝,如图10(a)所示;而在凹曲率影响下,建筑物底部的弯曲变形产生拉伸裂缝,剪切变形引起正八字裂缝,如图10(b)所示。对砖石、砖混结构建筑物,一般不会出现单一的弯曲变形或剪切变形,通常受弯曲变形与剪切变形的耦合影响,在建筑结构砖石连接处等薄弱部位出现八字形和竖向裂缝。
4 地表建筑物采动损坏程度
4.1 评价模型
图10 建筑结构的弯曲破坏与剪切破坏
Fig.10 Tensile and shearing damge to building
国内外地表建筑物采动损坏程度评价模型和方法都是基于大量的现场实践和实测,经综合处理分析而建立的。我国采用倾斜、曲率和水平变形作为损坏等级划分指标,现行规范对于长度或变形缝区段内长度≤20 m 的砖混结构建筑物,给出的损坏等级划分标准如图11所示。由图11可知,只要地表水平变形、倾斜、曲率中任一值达到某一损坏分级值时,就可确定该建筑物的损坏等级;即使建筑物长度>20 m,也参照同等标准确定损坏等级而不考虑建筑物的长度影响。由于矿区采动影响建筑物一般为平房或低层建筑物,而底面积小的高层建筑物对倾斜变形敏感,且随着开采深度的增加地表曲率变形值减小,实际应用中通常以地表水平变形值作为建筑物损坏程度评价的界定指标。
图11 砖混结构建筑物损坏等级
Fig.11 Damage classification for masonry
英国则采用建筑物结构长度和长度变化作为损坏等级的划分指标,结构长度变化e <0.03 m 为很轻微或可忽略的损坏,0.03～0.06 m 为轻微损坏,0.06～0.12 m 为明显损坏,0.12～0.18 m 为严重损坏,结构物长度变化>0.18 m 为很严重损坏。由于英国采动房屋一般为2 层,房屋高度H=6.75 m,将建筑物结构长度变化0.03,0.06,0.12 和0.18 m 分别代入式(17),计算可得相应的建筑物挠度比分别为1 ∶1 800,1 ∶900,1 ∶450 和1 ∶300。利用式(18)可得建筑损坏等级划分模型见式(19),依据该模型所画的示意图如12(a)所示。
由图12(a)可知,建筑物的损坏程度与建筑物长度有关,建筑物越长其抵抗采动变形能力越低,同等量级的采动地表变形导致的建筑物损坏会随建筑物长度增加而加重。与我国现行的采动损坏等级划分标准(图11)相比,其优点是考虑了采动建筑物结构的长度,即使变形缝区段长度<20 m,也可体现出结构长度的影响,这也在实际应用中客观解释了同一变形条件下区段长度小的建筑物损坏轻微、区段长度大的建筑物损坏严重。
图12 考虑砖混结构建筑物长度的采动损坏分级[24]
Fig.12 Classification of mining damage considering the length of masonry[24]
我国建筑地基基础设计规范规定,对于一般砖墙承重结构,包括有内框架的建筑物长高比<10、有圈梁、天然地基或条形基础,当挠度比达到1 ∶150 时,分隔墙及承重砖墙将出现相当多的裂缝,可能发生结构破坏。对于一般钢筋混凝土框架结构,当挠度比达到1 ∶500 时,建筑物开始出现裂缝;当挠度比达到1 ∶300 时,分隔墙或外墙产生裂缝等非结构性破坏;当挠度比达到1 ∶150 时,将发生严重变形和结构性破坏[29]。
我国现行规范和指南中,单体长度或变形缝区段内长度≤20 m 的砖混结构建筑物,I,II,III,IV 级损坏对应的水平变形分级指标分别为2,4 和6 mm/m;参考建筑地基基础设计规范,结合我国乡村振兴和新农村建设实际,选取的2 层砖混结构建筑物长度为20 m、高度为6 m;由式(18)计算可得建筑结构伸长量的分级值e 分别为0.04,0.08 和0.12 m。为进一步细分I 级和IV 级损坏,按等比例条件选取ε=1,8 mm/m,同理可得对应的伸长量分级值e 分别为0.02,0.16 m。由式(17)计算可得建筑结构伸长量分级值0.02,0.04,0.08,0.12 和0.16 m 对应的建筑结构挠度比Δ0/L 分级值1 ∶2 400,1 ∶1 200,1 ∶600,1 ∶400 和1 ∶300,以及对应的水平变形分级值1,2,4,6 和8 mm/m。
以单体结构长度20 m 的建筑物伸长量分级值为基准,建立随结构长度变化的损坏评价指标为
其中,εi 为第i 级损坏的水平变形分级值;ei 为建筑结构伸长量分级值,e1 =0.02 m,e2 =0.04 m,e3 =0.08 m,e4=0.12 m,e5=0.16 m;L 为建筑物的结构长度,m。依赖建筑物结构长度变化的损坏程度分等定级指标体系如图12(b)所示。
对比图11和图12(b),可知本文建议的建筑物损坏分类指标具有如下优势:
(1)地表建筑物采动损坏程度分等定级指标定量化,针对每个受影响的建筑物个体。当预计的地表水平变形ε≤20 mm/L 时,损坏等级为I1 级,损坏程度为极轻微,结构处理措施为不修;当20 mm/L<ε≤40 mm/L 时,损坏等级为I2 级,损坏程度为轻微,结构处理措施为简单维修;当40 mm/L<ε≤80 mm/L时,损坏等级为II 级,损坏程度为轻度,结构处理措施为小修;当80 mm/L<ε≤120 mm/L 时,损坏等级为III 级,损坏程度为中度,结构处理措施为中修;当120 mm/L<ε≤160 mm/L 时,损坏等级为IV1 级,损坏程度为严重,结构处理措施为大修;当ε>160 mm/L 时,损坏等级为IV2 级,损坏程度为极严重,结构处理措施为拆建。
(2)兼顾并有条件地继承了现行规范的评价指标。当建筑结构长度L=20 m 时,现行规范中I,II,III,IV 级损坏对应的水平变形分级值与本文中的I2,II,III,IV1 级损坏的分级值完全相等,分别是2,4 和6 mm/m;同时增加了I1 级损坏的水平变形分级值1 mm/m 和IV2 级损坏的水平变形分级值8 mm/m,从而明确区分了极轻微、轻微以及严重、极严重的损坏状态,消除了现行标准I,IV 级损坏评价的模糊性。
(3)充分考虑了结构长度这一建筑物采动损坏敏感性指标:当建筑物结构长度L>20 m 时,随着长度增加,抵抗变形能力降低,同等水平变形条件下损坏程度增大;当建筑物结构长度L<20 m 时,随着长度减小,抵抗变形能力增加,同等水平变形条件下损坏程度减小;表明本文给出的随结构长度和地表变形值变化的采动建筑物损坏程度定量评价结果更具合理性。
4.2 实验验证
某矿二采区开采深度480 m、采厚4.8 m、煤层倾角2°～4°;布置有4 个编号为221,223,225 和227 的长壁开采工作面,走向长分别为610,680,720 和720 m;工作面宽度分别为152,140,146 和142 m,工作面间护巷煤柱宽度为15 m;该采区东部有一村庄,建筑物以2000年新建的砖石、砖混平房为主,有少量2 层砖混结构;房屋长度多在10～20 m,少数达到25 m。根据该矿的观测资料,确定下沉系数0.72、水平移动系数0.3、主要影响角正切2.0;预计的地表最大移动变形值分别为下沉3 456 mm、 水平移动1 037 mm、倾斜14.4 mm/m、曲率0.04 mm/m2、水平变形6.57 mm/m。工作面与村庄的位置关系及预计的地表变形等值如图13所示。
图13 村庄与开采工作面的位置关系及预计的水平变形
Fig.13 Prediction of horizontal strain and the relative position between working face and village
图14分别为按现行规范和本文建议的分类标准确定的建筑物损坏等级分布图。对比发现,两者的分类评价结果都体现了地表变形越大、损坏程度越严重的特点,但本文方法因兼顾了建筑物结构长度,同等地表变形条件下、结构长度越长损坏程度越重、结构长度越短损坏程度越轻,使得地表建筑物采动损坏程度评价结果更符合实际。
图14 损坏等级划分结果对比
Fig.14 Comparisons of classification of building damage
采动地表建筑物的损坏程度既与地表移动变形值密切相关,也与工作面、地表建筑的相对位置关系有关。当建筑物位于工作面正上方,工作面推进方向垂直于建筑物长轴时有利;当建筑物位于采空区边界外,工作面边界平行于建筑物长轴时有利[30];由此可知图13中村庄建筑物所处位置和房屋长轴方向相对于开采工作面呈最不利态势。
5 结 论
(1)无论地表水平与否,采动后的地表倾斜将引起实时位形上的变形,该变形随下沉差和地面坡度的增加而增大;当两点间水平距离为10 m,高差为0.5 m,下沉差为170 mm 时,其实时位形上的变形将达到1 mm/m;针对地表非均匀沉陷,建立了沉陷后倾角、点间距与曲率半径的表达关系,分析了点间距对曲率计算值的影响,给出了处理建议。
(2)基于建筑物结构长度、含基础高度以及表曲率半径,建立了建筑结构最大挠度和挠度比表达式,分析了凸曲率作用下建筑结构顶部伸长量和拉伸变形的关系;通过分析建筑物与基础的作用关系,分析了地基反力分布、地表与结构变形关系以及建筑结构破坏特征。
(3)在兼顾和继承现行规范的基础上,提出了顾及建筑物结构长度和地表变形的损坏程度评价模型和指标体系;进一步给出了极轻微/轻微、严重/极严重的划分指标,消除了现行规范损坏等级确定的模糊性;对比试验分析表明,本文的评价结果既能体现地表变形大、建筑物损坏程度重的特点,也能反映同等地表变形条件下建筑物损坏程度随结构长度的变化,结构长度越长、损坏程度越重,反之亦然。
[1] 中国矿业学院,阜新矿业学院,焦作矿业学院.煤矿岩层与地表移动[M].北京:煤炭工业出版社,1981.
[2] 何国清,杨伦,凌赓娣,等.矿山开采沉陷学[M].徐州:中国矿业大学,1990.
[3] 崔希民,邓喀中.煤矿开采沉陷预计理论与方法研究评述[J].煤炭科学技术,2017,45(1):160-169.CUI Ximin,DENG Kazhong.Research review of prediction theory and meth9d for coal mining subsidence[J].Coal Science and Technology,2017,45(1):160-169.
[4] 国家安全监管总局,国家煤矿安监局,国家能源局,等.建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规范[S].北京:煤炭工业出版社,2017.
[5] 胡炳南,张华兴,申宝宏.建筑物、水体、铁路及主要井巷煤柱留设与压煤开采指南[M].北京:煤炭工业出版社,2017.
[6] 彭小沾,崔希民,臧永强,等.时间函数与地表动态移动变形规律[J].北京科技大学学报,2004,26(4):341-344.PENG Xiaozhan,CUI Ximin,ZANG Yongqiang,et al.Time function and prediction of progressive surface movements and deformations[J].Journal of University of Science and Technology Beijing,2004,26(4):341-344.
[7] 张兵,崔希民,赵玉玲,等.开采沉陷倾向主断面动态预计模型与算法[J/OL].煤炭学报:1-11[2021-02-01].http:/ /doi:10,13225/j.cnki.jccs.2019.1814.ZHANG Bing,CUI Ximin,ZHAO Yuling,et al.Prediction model and algorithm for dynamic subsidence of inclined main section[J].Journal of China Coal Society:1-11[2021-02-01].http:/ /doi:10,13225/j.cnki.jccs.2019.1814.
[8] 李全生,郭俊廷,戴华阳.基于采动充分性的地表动态下沉预计方法[J].煤炭学报,2020,45(1):160-167.LI Quansheng,GUO Junting,DAI Huayang.Surface dynamic subsidence prediction method based on mining sufficiency degree[J].Journal of China Coal Society,2020,45(1):160-167.
[9] 刘立民,刘汉龙,陈爱道,等.建筑物塌陷损坏评价的物元模型及其应用[J].防灾减灾工程学报,2003,23(2):94-99.LIU Limin,LIU Hanlong,CHEN Aidao,et al.Matter-element evaluation method and application to damage buildings caused by ground subsidence[J].Journal of Disaster Prevention and Mitigation Engineering,2003,23(2):94-99.
[10] 胡炳南.建筑物采动破坏程度的模糊综合评判[J].煤矿开采,1993(3):23-27.HU Bingnan.Fuzzy evaluation of mining induced damage of buildings[J].Coal Mining Technology,1993(3):23-27.
[11] 何荣,王斌.基于层次分析法的矿区建筑物损害程度模糊评价[J].河南理工大学学报(自然科学版),2017,26(1):32-37.HE Rong,WANG Bin.Fuzzy evaluation of damage degree of buildings based on analytic hierarchy process[J].Journal of Henan Polytechnic University(Natural Science),2017,26(1):32-37.
[12] 魏威,李夕兵.地采诱发建筑物损害识别的多元判别分析模型[J].中南大学学报(自然科学版),2013,44(8):3335-3343.WEI Wei,LI Xibing.Identification of building damage induced by underground mining using multivariate discriminant analysis model[J].Journal of Central South University(Science and Technology),2013,44(8):3335-3343.
[13] 刘潇鹏,郭广礼,徐良骥,等.采动区建筑物损害综合评价技术研究[J].中国矿业,2019,28(4):168-172.LIU Xiaopeng, GUO Guangli, XU Liangji, et al.Research on the comprehensive evaluation of building damage in mining area[J].China Mining Magazine,2019,28(4):168-172.
[14] 邓喀中,郭广礼,谭志祥.采动区建筑物地基、基础协同作用特性研究[J].煤炭学报,2001,26(6):601-605.DENG Kazhong,GUO Guangli,TAN Zhixiang.Study on the properties of coordination of the base and foundation of the building above mining subsidence areas[J].Journal of China Coal Society,2001,26(6):601-605.
[15] 高安琪,王金安,李飞,等.西露天矿周边建筑物损害区位特征分析[J/OL].煤炭学报:1-11[2021-02-01].http:/ /doi:10,13225/j.cnki.jccs.2019.1628.GAO Anqi,WANG Jin’an,LI Fei,et al.The locational characteristics of buildings damage around the West Open-pit Mine[J/OL].Journal of China Coal Society:1-11[2021-02-01].http:/ /doi:10,13225/j.cnki.jccs.2019.1628.
[16] 崔希民,张兵,彭超.建筑物采动损害评价研究现状与进展[J].煤炭学报,2015,40(8):1718-1728.CUI Ximin,ZHANG Bing,PENG Chao.Current status and progress on the estimation of mining-induced building damage[J].Journal of China Coal Society,2015,40(8):1718-1728.
[17] DECK O,SINGH A.Analytical model for the prediction of building deflections induced by ground movements[J].International Journal for Numerical and Analytical Methods in Geomechanics,2012,36:62-84.
[18] BASMAJI B,DECK O,HEIB Ma.Analytical model to predict building deflections induced by ground movements[J].European Journal of Environmental and Civil Engineering,2019,23(3):409-431.
[19] VESIC A B.Beams on elastic subgrade and Winkler’s hypothesis[A].Proceedings of the 5th International Conference on Soil Mechanics and Foundation Engineering[C].Paris:1963:845-850.
[20] SON M,CORDING E.Evaluation of building stiffness for building response analysis to excavation-induced ground movements[J].Journal of Geotechnical and Geoenvironmental Engineering,2007;133:995-1002.
[21] KAHIA E E,DECK O,KHOURI M,et al.A new simplified metamodel to evaluate the transmission of ground movements to structures integrating the elastoplastic soil behavior[J].Structures,2020,23:324-334.
[22] CUI Ximin,MIAO Xiexing,WANG Jinan,et al.Improved prediction of differential subsidence caused by underground mining[J].International Journal of Rock Mechanics and Mining Science,2000,37(4):615-627.
[23] National Coal Board Mining Department.Subsidence engineer’s handbook[M].London:National Coal Board Mining Department,1975.
[24] SANMIQUEL L,BASCOMPTA M,VINTRO C,et al.Subsidence management system for underground mining[J].Minerals,2018,8(6):243.
[25] KRATZSCH H.Mining subsidence engineering [M].Berlin:Springer,1983.
[26] DECK O,HEIB M A.HOMAND F.Taking the soil-structure interaction into account in assessing the loading of a structure in a mining subsidence area[J].Engineering Structures,2003,25:435-448.
[27] BOSCARDING M D,CORDING E J.Building response to excavation induced settlement[J].Journal of Geotechnical Engineering,1987,115(1):1-21.
[28] BURLAND J B,WROTH C P.Settlement of buildings and associated damage[A].Proceedings of the Conference on “Settlements of Structures[C].London:1974:611-654.
[29] GB 50007—2011,建筑地基基础设计规范[S].北京:中国建筑工业出版社,2011.
[30] 煤炭科学研究院北京开采研究所.煤矿地表移动与覆岩破坏规律及其应用[M].北京:煤炭工业出版社,1981.
