-非对称X”型→临界贯通式“非对称
-非对称X”型→开口非贯通式“非对称
-非对称X”型。针对研究一侧采空基本顶板结构破断的3类力学模型，从模型特征、破断影响因素、初次破断位置、煤柱侧破断形态、实体煤侧破断位置、整体断裂位态及工程指导意义共7个方面，总结对比了“三边固支+简支模型”(第1类)、“三边弹性基础+考虑煤柱宽度和支撑能力的单一塑化模型”(第2类)与建立的“三边弹塑性基础+考虑煤柱宽度和支撑能力的双重塑化模型”(第3类)的重要区别。采矿理论与工程
摘 要:为了研究一侧采空条件下基本顶板结构的破断规律，构建考虑煤柱宽度及承载能力与实体煤弹塑性变形的基本顶板结构力学模型，全面计算探究了侧方采空条件下基本顶板在煤柱区及实体煤区的断裂位置、顺序及形态等。结论如下：① 煤柱区基本顶的破断形态有3类且随着基本顶厚度h、弹性模量E及弹性煤体基础系数kt增大，而煤柱宽度Lm与煤柱基础系数ksm、煤体塑化范围Lts与塑化程度ξs及跨度L减小时的破断形态变化规律为“单一连续长弧形”→“临界对接双长弧形”→“分隔式双短弧形”；② Lm及ksm主要影响煤柱区基本顶的破断位态；Lm及ksm增大，实体煤区主弯矩减小；③ 实体煤区基本顶破断位态有5类且随着h,E及ξs增大，而Lts,kt及L减小时的断裂模式演变规律为：“长边与短边断裂线均处于塑化煤体区”→“长边断裂线处于塑化煤体区而短边处于煤体弹塑性分界区”→“长边断裂线位于塑化煤体区而短边断裂线位于弹性煤体区”→“长边断裂线位于煤体弹塑性分界区而短边断裂线位于弹性煤体区”→“长边与短边断裂线均处于弹性煤体区”，存在长边与短边断裂线同时位于煤体弹塑性分界区的情况；④ h,E及Lts较大而L及kt较小时，破断顺序为：中部(靠近煤柱侧)→长边(3类位置)→短边(3类位置)→煤柱侧(3类位置)；⑤ 整体破断形态分为3类且随着h,E及kt增大，而Lm,ksm,Lts，ξs及L减小时，整体破断形态的变化模式为：闭合贯通式“非对称-非对称X”型→临界贯通式“非对称-非对称X”型→开口非贯通式“非对称-非对称X”型。针对研究一侧采空基本顶板结构破断的3类力学模型，从模型特征、破断影响因素、初次破断位置、煤柱侧破断形态、实体煤侧破断位置、整体断裂位态及工程指导意义共7个方面，总结对比了“三边固支+简支模型”(第1类)、“三边弹性基础+考虑煤柱宽度和支撑能力的单一塑化模型”(第2类)与建立的“三边弹塑性基础+考虑煤柱宽度和支撑能力的双重塑化模型”(第3类)的重要区别。
移动阅读
CHEN Dongdong，WU Yiyi，XIE Shengrong,et al.Study on the first fracture of the main roof plate structure with one side goaf and elastic-plastic foundation boundary[J].Journal of China Coal Society,2021,46(10):3090-3105.
Abstract:In order to study the fracture rule of the main roof plate structure under the condition of one side goaf,the mechanical model of the main roof plate structure considering the width and bearing capacity of the coal pillar and the elastic-plastic deformation of the solid coal was established.This paper comprehensively calculated and explored the fracture position,sequence and shape of the main roof above the coal pillar area and solid coal area under the condition of one side goaf.The conclusions are as follows.① There are three types of fracture modes of the main roof above the coal pillar area,and with the increase of the thickness h,the elastic modulus E of the main roof and the elastic coal foundation coefficient kt,while with the decrease of the coal pillar width Lm,the coal pillar foundation coefficient ksm,the range of plastic zone Lts,the plasticization degree ξs,and the span L,the change rule of the fracture modes are as follows：“single continuous long arc”→“critical butt joint double long arc”→“separated double short arc”.② The Lm and ksm mainly affected the fracture state of the main roof above the pillar area.With the increase of Lm and ksm,the main bending moment decreased above the solid coal area.③ There are five types of fracture states of main roof above the solid coal area.With the increase of h,E and ξs,while Lts,kt and L decrease，the change rules of main roof plate fracture modes are as follows：“the long edge and short edge fracture line are above the plasticized coal area”→“the long edge fracture line is above the plasticized coal area while the short edge fracture line is above the elastic-plastic boundary area”→“the long edge fracture line is above the plasticized coal area while the short edge fracture line is above the elastic coal area”→“the long edge fracture line is above the elastic-plastic boundary area of coal while the short edge fracture line is above the elastic coal area”→“the long edge and the short edge fracture line are both above the elastic coal area”.There is a case that the fracture line of the long edge and the short edge are both located above the elasto-plastic boundary zone of the coal at the same time.④ The h，E and Lts are larger while L and kt are smaller,the main roof fracture order is as follows:middle part (near the coal pillar side) → long side (three types of location) → short side (three types of location) → coal pillar side (three types of location).⑤ The overall fracture patterns of the main roof can be divided into three types，with the increase of h,E and kt,while the decrease of Lm，ksm，Lts，ξs and L,the change modes of the overall fracture morphology are as follows：closed asymmetric “-X” type → critical through asymmetric “-X” type → open type asymmetric “-X” type.Aiming at the three kinds of mechanical models of main roof plate structure fracture with one side goaf,the important differences among the “trilateral fixed + simply supported model” (the first category),“trilateral elastic foundation + considering the width and supporting capacity of coal pillar model” (single plasticization model,the second category) and the “trilateral elastic-plastic foundation + considering the width and supporting capacity of coal pillar” (double plasticization model,the third category) established in this paper are summarized and compared from seven aspects,including model characteristics,fracture influencing factors,initial fracture position,pillar side fracture shape,solid coal side fracture position,overall fracture position and engineering guiding significance.The model in this paper obtains many new conclusions that the traditional models can not get,which effectively makes up for the defects and deficiencies of the traditional models,and has important value in improving the theoretical understanding level and practical guidance of plate fracture in mining engineering.
一侧采空条件下，采场基本顶板结构在实体煤区与煤柱区上覆的实际破断位态及变化模式(位置、顺序、形态等)对采场顶板灾害预警、沿空巷道位置选择、停采工作面合理位置确定[1-2]及近距离煤层的遗留煤柱覆岩结构特征与失稳条件[3-4]研究等方面具有重要理论意义和实际价值。
一直以来，科技工作者主要从理论计算、相似模拟、数值计算及现场实测等方面研究覆岩的破断规律，如固支边、简支边及考虑煤体基础可变形条件下的顶板梁[1,5]及板[6-14]的破断扰动规律，其中理论研究是量化分析并解决采矿工程问题的重要方法之一。
理论研究的关键是力学模型的载体及边界条件，通常根据研究问题的需要及计算的难易程度来决定构建力学模型的类别。而对于基本顶板结构破断规律的研究，尤其是对一侧采空条件下基本顶板结构力学模型的研究主要有“实体煤侧固支+煤柱侧简支梁模型”、“三边固支+一侧简支板模型”[1,11]及“三边弹性基础边界+一侧煤柱支撑板模型”[15-17]，该类研究所得结论不断推进了对一侧采空条件下基本顶在实体煤和煤柱侧破断规律的深入认识，在理论和实践指导上均有进步意义。
然而，梁模型无法研究全区域的破断位态，所以局限性较大；对于传统的固支板模型，由于基本顶下伏的支撑基础——煤体的刚度小于基本顶的刚度数倍，远无法严格满足固支边界，所以无法研究基本顶深入煤体及煤柱破断的实际特征，缺陷较大；而对于“三边弹性基础边界+一侧煤柱支撑的板模型”在传统模型基础上有本质性进步，且丰富发展了对一侧采空基本顶板破断规律的认识，但是依旧有一定缺陷，因为未考虑实体煤区必然发生塑化，特别是大范围塑化条件下，不能忽略煤体塑化范围和程度的影响，而煤体塑化必然显著影响基本顶在煤柱区及实体煤区的破断位置、破断顺序及形态等。
笔者针对采矿工程中广泛存在的工作面一侧采空问题，构建同时考虑实体煤塑化程度和塑化范围、煤柱宽度及塑化程度的一侧采空条件下基本顶板结构破断力学模型，研究基本顶长边区域及短边区深入煤体断裂位置的分区属性(弹性区、塑性区、弹塑性分界区)及非对称性和非同区性，研究煤柱区域基本顶的破断模式及影响因素，这对弥补传统模型的缺陷和不足，提高对一侧采空条件下基本顶板结构破断规律的认识深度等，具有重要意义。
一侧采空条件下的长壁开采工作面，开采区域周边的三侧为实体煤、一侧为煤柱，其中，三侧实体煤区的基本顶由下伏直接顶和煤层支撑，采空侧的基本顶主要由煤柱支撑。如图1所示，传统模型为了简化计算，假设实体煤侧为基本顶的固支边界或者弹性基础边界，煤柱侧为基本顶的简支边界，然而实体煤的塑性区范围及塑化程度、煤柱的宽度及塑化程度(双塑化)必然对一侧采空条件下基本顶在长边实体煤区、短边实体煤区及煤柱区的破断模式产生直接相互影响，但是传统模型无法研究该问题。所以构建考虑煤体弹塑性变形的一侧采空条件下(考虑煤柱宽度及塑化程度)基本顶板结构力学模型，即双塑化模型(实体煤塑化与煤柱塑化)可以更符合实际的研究开采全区域的基本顶破断位态、演变模式及影响因素等。
图1 边界条件对比示意
Fig.1 Comparison of boundary conditions
根据弹性薄板力学假设[18]：
(1)
式中，h为板厚度，m；l为板短边长度，m。
一般条件下长壁开采工作面均满足式(1)，即符合弹性薄板假设[1,19]。
如图2所示，建立考虑三侧实体煤弹塑性变形且考虑煤柱宽度和塑化程度(支撑系数)的弹-塑性基础边界一侧采空基本顶板结构初次破断力学模型。其中，区域边界W1W2W3W4为不受/基本不受开采扰
图2 弹塑性基础边界一侧采空基本顶板模型
Fig.2 Main roof structure model with elastic plastic foundation boundary and one side goaf
动影响的边界，那么该边界各截面的挠度和转角均为0。设边W1W2距离O点距离为yt，边W2W3距离O点长度为xt。
区域A1A2A3A4为已开采区，工作面倾向长度为2x0，走向宽度为2y0，基本顶承担载荷为q。
矩形圈T1T2T3T4为实体煤的弹塑性分界边，长边塑性区宽度为Ltsc，短边塑性区宽度为Ltsd，也可简化设长边与短边区域的煤体塑性区宽度为Lts；实体煤侧起始边界区的支撑基础系数为ks0，弹性区煤体基础系数为kt，满足kt>ks0≥0，ks为塑性区煤体基础系数(kt>ks>ks0)，且ks经路径Lts正相关增长到kt，符合塑性区煤体塑化程度随塑化深度的基本变化规律(煤体深处，塑化程度越小)。
区域W1Wm1Wm2W4为煤柱支撑区，煤柱支撑区的宽度设为Lm，煤柱支撑基础系数设为ksm，且kt>ksm≥0。基本顶在已经开采区Ωo、煤体塑化区Ωs、弹性煤体区Ωt、煤柱区Ωm的挠度偏微分方程如式(2)～(5)，见表1。
表1 各分区挠度方程
Table 1 Deflection equation of each zone
所属分区各分区挠度偏微分方程Ωo区,挠度函数设为ωs0(x,y)∂4ωs0(x,y)∂x4+2∂4ωs0(x,y)∂x2∂y2+∂4ωs0(x,y)∂y4=1Dq(2)Ωs区,挠度函数设为ωss(x,y) ∂4ωss(x,y)∂x4+2∂4ωss(x,y)∂x2∂y2+∂4ωss(x,y)∂y4=-ksωss(x,y)D(3)Ωt区,挠度函数设为ωst(x,y) ∂4ωst(x,y)∂x4+2∂4ωst(x,y)∂x2∂y2+∂4ωst(x,y)∂y4=-ktωst(x,y)D(4)Ωm区,挠度函数设为ωsm(x,y) ∂4ωsm(x,y)∂x4+2∂4ωsm(x,y)∂x2∂y2+∂4ωsm(x,y)∂y4=-ksmωsm(x,y)D(5)
为便于表达实体煤与煤柱的塑化程度，设煤柱的塑化程度为ξm，实体煤的塑化程度为ξs，其表达式如式(6)所示。
(6)
式中，ξm为煤柱的塑化程度；ξs为实体煤塑化程度。
(7)
式中，E为弹性模量，GPa；h为基本顶厚度，m；μ为泊松比。
2.2.1 开采区与实体煤区的连续条件
区域A1A2A3A4为已开采区，该矩形的3边(A1A2，A2A3，A3A4)为开采区域与实体煤壁分界边，该分界边满足连续条件(截面的剪力、挠度、弯矩及转角均连续)，如式(8)，(9)所示。
(8)
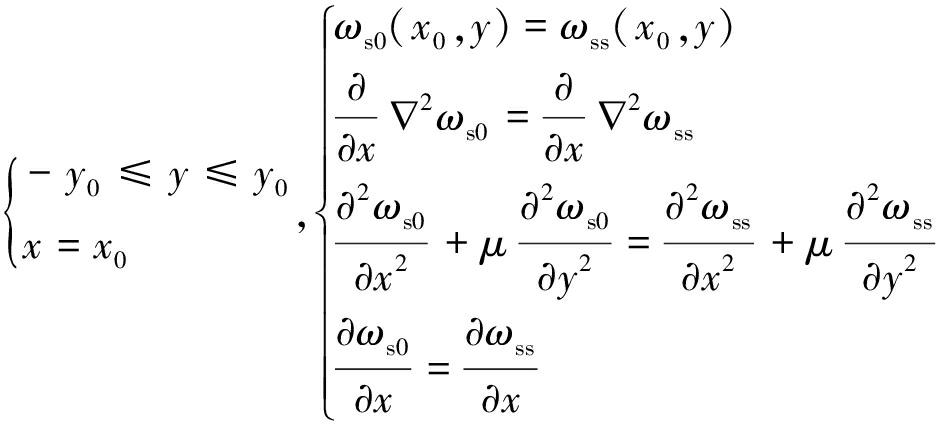
(9)
2.2.2 实体煤弹性区与塑性区的连续条件
边T1T2，T3T4与T2T3为实体煤的塑性区与弹性区的分界边，满足连续条件，如式(10)，(11)所示。
(10)
(11)
2.2.3 煤柱区与开采区、塑性区、弹性区连续条件
边A4A1为开采区与煤柱的分界边，边A1T1,A4T4为煤柱与塑性实体煤的分界边，满足连续条件，如式(12)～(14)所示。
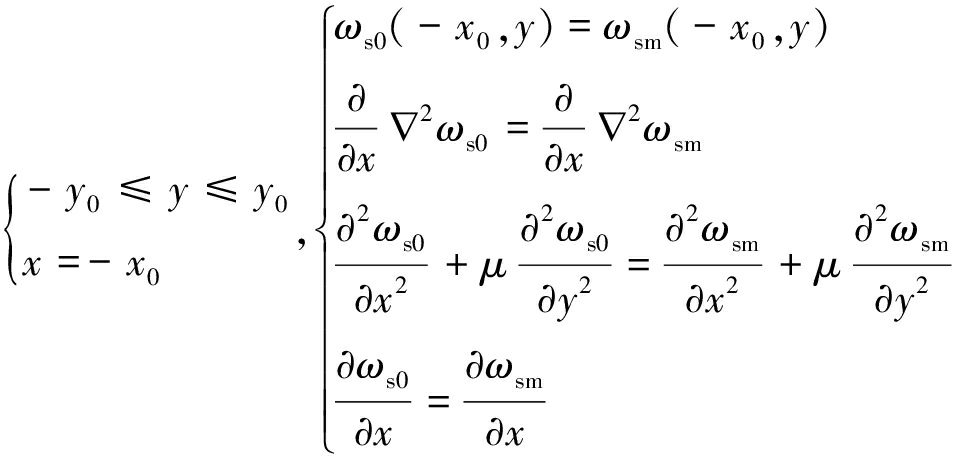
(12)
(13)
(14)
2.2.4 模型外边界条件
(1)弹性煤体区的外边界条件。由于该模型考虑了实体煤的塑性变形和弹性变形，其中弹性区的外边界(Wm1W2,Wm2W3,W2W4)需要考虑是否受到采动的影响，当所取该外边界距离开采区较远时(一般该距离取3～5倍开采区长边长度[1,19])，该边界不受或者基本不受采动影响，此时确定的边界条件对于模型求解有利且精确，不受采动影响的边界任意截面挠度和转角均为0。
(2)煤柱区外边界条件。煤柱的邻空侧W1W4边与采空侧的破断块体为铰接关系，所以W1W4边可近似假设为简支边，该点区别于传统模型不考虑煤柱宽度(即煤柱整体为简支边)，这样方可通过模型研究煤柱宽度及塑化程度对基本顶破断规律的影响。而煤柱区外边界W1Wm1与W4Wm2不受开采扰动影响，任意截面挠度和转角均为0。
要全面研究考虑煤体弹塑性变形及煤柱宽度和塑化程度(支撑系数)条件下的基本顶板结构全区域的应力状态、实体煤区基本顶断裂线与煤体弹塑性分界线的关系、煤柱区断裂位态等均需要得出在满足2.2 节所述各类边界条件时的偏微分方程(2)～(5)的解，显然该计算十分复杂且难以获得精确解。基于采矿工程问题的复杂性及工程尺度的要求(精确解非必须)，确定以有限差分的近似计算解法[18-20]完成上述边界条件下的偏微分方程组的求解，可满足工程尺度的要求。
基本顶在煤柱区、开采区、塑性煤体区及弹性煤体区的偏微分方程(2)～(5)，需要通过差分法(节点代号如图3所示，Q为中心节点，节点编号用纵横轴交点编号β与γ表示，节点间距Δx=Δy)转化为差分方程。式(15)～(18)为偏微分方程(2)～(5)转化后的差分方程。
图3 节点编号
Fig.3 Node number
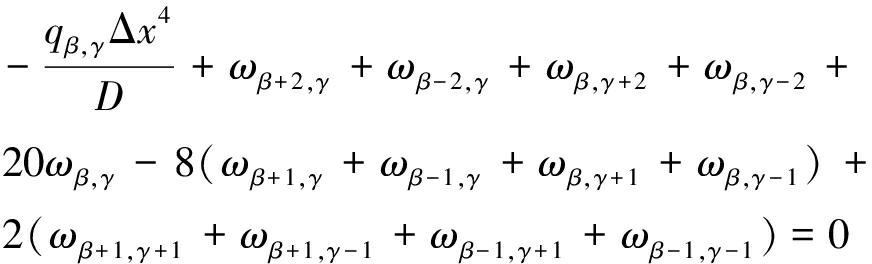
(15)
(16)
(17)
(18)
基本顶在煤柱区、开采区、塑性煤体区及弹性煤体区的偏微分方程与外边界条件方程转化为差分方程后，各个分区的基本顶挠度(任一节点的)可通过具有13个挠度未知节点的差分方程来表达，各个节点的挠度之间均满足各区域的挠度差分方程，所以可以组建未知节点挠度的差分方程组，加之边界条件差分方程，便求解出全区域任一节点的挠度解，可通过Matlab软件开展辅助计算。
(19)
(20)
由于弯矩分量可以通过各个节点的挠度解进行计算(式(19))，可见首先求出挠度解至关重要，节点挠度解代入弯矩分量方程得出节点的弯矩，再由节点弯矩代入主弯矩差分方程(式(20))得到基本顶全区域的主弯矩分布特征图，基于主弯矩的数值大小及位置与弯矩极限进行对比方可判定基本顶是否发生破断以及破断的顺序、位置及形态等。同时，构建的方程可研究基本顶的尺寸、厚度、弹性模量、煤柱宽度和支撑系数等变化时的量化关系，所以该模型可以深入全面的研究弹塑性基础边界一侧采空条件下基本顶的破断模式及变化规律。
由表达弹塑性基础边界与一侧采空(考虑煤柱宽度和塑化程度)条件下的基本顶板结构各区域挠度方程可知，基本顶破断规律由煤体塑化程度、塑化范围、基本顶厚度、弹性模量、开采区域跨度(长宽比、基本顶抗拉强度等)、弹性煤体的基础系数、煤柱宽度及塑化程度等决定，要研究清楚该规律首先需要明确弹塑性基础边界一侧采空条件下基本顶全区域的应力状态，得到各个区域的主弯矩极值大小及位置特征，进而可判断基本顶的破断模式。
图4为本文模型得到的基本顶全区域主弯矩分布特征云图(图4只是展示了基本顶厚度h改变时的云图基本特征，其他因素也会产生此类特征，后续内容采用控制变量法研究各种因素对破断规律的影响，以此为基础详细展示模型得到的新结论)，其中工作面推进跨度及倾向长度分别为42 m及126 m；表征基本顶参数的E,h，μ，q分别为32 GPa，(2.2,6.2,8.2 m)，0.24,0.35 MPa；表征实体煤浅部塑化程度的参数ks0、实体煤深部弹性区基础系数kt、煤体塑性区深度Lts分别为0,1.6 GN/m3,3 m；煤柱宽度为5 m，支撑系数为0.4 GN/m3(0.25kt)。
由图4可得如下基本结论：
(1)开采区周边基本顶破断模式。实体煤侧与煤柱侧的基本顶主弯矩分布特征及断裂圈位态差异显著。
如图4(a)，(c)所示，在开采区域的两侧长边及短边深入实体煤区的主弯矩均为负值(上侧面先断)，且为主弯矩极值区，并设长边区域的绝对值最大主弯矩为Msc(非长边中线上，距离煤壁的长度为Lsc)；实体煤短边绝对值最大主弯矩为Msd(距离煤壁的长度为Lsd)；中部区的主弯矩为正值(下侧面先断)，绝对值最大主弯矩设为Msz(非开采区中心点，中部偏煤柱侧)。
煤柱区域的基本顶主弯矩主要表现为3类：一是图4(a),(b)中①，煤柱中部为基本顶的主弯矩极值区且为负值(上侧面先断)，设该区域绝对值最大主弯矩为Msm(短边煤柱的中垂线上，距离煤柱内壁的长度为Lsm)，煤柱侧基本顶破断线为“单一连续长弧形”，整体破断圈为闭合贯通式 “非对称”型；二是图4(a),(b)中②，煤柱区中部不存在主弯矩极值区，取而代之的为两侧对称分布的短弧形主弯矩迹线(对应区的上侧面先断)，煤柱区基本顶破断线为“分隔式双短弧形”，整体破断圈为开口非贯通式“非对称” 型；三是图4(a),(b)中③，处于上述2者之间的类型，即此时煤柱区中部的断裂线为1条与2条的临界状态，煤柱区基本顶破断线为“临界对接双长弧形”，整体破断圈为临界贯通式 “非对称” 型。
图4 弹-塑性基础边界一侧采空模型基本特征
Fig.4 Basic characteristics of the model with one side goaf and elastic-plastic foundation boundary
(2)开采区中部的破断模式。如图4所示，不论开采区周边基本顶的断裂圈是闭合贯通式还是开口非贯通式，开采区上覆的基本顶均为非对称“X”型破断形态(基本顶的下侧面先断)，且煤柱侧基本顶破断线的分叉段 “>”均延展贯穿到煤柱区域，且采空侧破断线的分叉起点偏向煤柱侧。
(3)总体破断模式。如图4(b)所示，弹塑性基础边界一侧采空条件下，基本顶有3类破断模式，闭合贯通式的“非对称-非对称X”型、临界贯通式“非对称-非对称X”及开口非贯通式“非对称-非对称 X” 型。
图4展示了基本顶的弯矩云图特征、断裂圈特征及主弯矩极值位置特征等，下面采用控制变量法具体研究煤体塑化程度及塑化范围、基本顶厚度及弹性模量、开采区域跨度(长宽比、基本顶抗拉强度等)、弹性煤体的基础系数等指标影响下的一侧采空基本顶板结构破断规律并与传统模型结论进行对比，说明本文模型的进步意义。
由表达基本顶全区域的偏微分方程可知，弹塑性煤体(塑化程度ξs和塑化范围Lts)与一侧采空(煤柱宽度Lm与塑化程度ξm)模型中的参数ξs,Lts,Lm及ξm为影响其破断模式的直接影响因素。
图5为煤体塑化范围Lts对基本顶破断模式的影响规律(后文曲线的分区编号顺序均为从左向右依次编号，序号的编号无特定含义)。煤体塑化范围Lts会改变基本顶的破断顺序及位置，且可决定在煤柱区的破断形态。
图5 煤体塑化范围Lts对基本顶板结构破断模式的影响
Fig.5 Influence of coal plasticization range Lts on the fracture mode of main roof structure
(1)破断顺序方面。如图5(a)的(i)区，Lts较小时，Msc>Msz>Msd，基本顶破断顺序为：长边→开采区中部→实体煤侧短边(其中长边与开采区中部的起断位置均靠近煤柱侧，下同，不在赘述)，而煤柱区中部不破断；Lts较大时，如图5 (a)的(ii)区，破断顺序为开采区中部→长边→实体煤侧短边→煤柱区中部；存在长边与开采区中部同时破断的情况如Lts=Lts0时。
(2)破断位置及形态方面。如图5(b)～(d)所示，塑化范围增大时，实体煤区基本顶断裂线深入煤体的距离均增大，而煤柱区断裂线更靠近煤柱内壁，即断裂位置整体向实体煤区转移。
从整体的断裂圈形态及区位特征角度看，图5中主要展示了以下7类基本顶的破断模式。
模式1，煤体塑化范围Lts较小时，如图5(b)的①区，基本顶在煤柱区中部不发生破断，而是在煤柱中部的两侧破断扩展，所以煤柱区基本顶的破断形态为“分隔式双短弧形”，长边与短边实体煤侧基本顶的破断线均在塑化煤体区上覆，整体破断形态为开口非贯通式“非对称-非对称X”型，如图5(c)，(d)的①所示。
模式2，如图5(b)的②区，Lts<Lsc<Lsd，实体煤侧基本顶断裂线均处于弹性煤体区上覆，煤柱侧断裂线为“单一连续长弧形”，整体破断形态为闭合贯通式“非对称-非对称X”型，如图5(c)，(d)的②所示。
模式3，如图5(b)的③区，Lsc<Lts<Lsd，实体煤短边侧基本顶断裂线处于弹性煤体区上覆，而实体煤长边侧的破断线处于塑化煤体区上覆，煤柱侧断裂线为“单一连续长弧形”，整体破断形态为闭合贯通式“非对称-非对称X”型，如图5(c)，(d)的③所示。
模式4，如图5(b)的④区，Lsc<Lsd<Lts，长边及实体煤短边的基本顶断裂线均处于塑化煤体区上覆，整体破断形态为闭合贯通式“非对称-非对称 X”型，如图5(c)，(d)的④所示。
模式5，如图5(b)，Lts=Lts0时(或附近区域)，煤柱区基本顶破断线为“临界对接双长弧形”，断裂圈在弹性煤体区，如图5(c)，(d)的“①与②过渡区”所示。
模式6，如图5(b)，Lts=Lsc-ts时，实体煤短边区基本顶断裂线在弹性煤体区，而长边区深入煤体的破断线与煤体的弹塑性分界线重合，如图5(c)，(d)的“②与③过渡区”所示。
模式7，如图5(b)，Lts=Lsd-ts时，实体煤短边深入煤体区的破断线与煤体的弹塑性分界线重合，而长边破断线处于塑化煤体区，如图5(c)，(d)的“③与④过渡区”所示。
由下文的研究可知，其他参数配合改变时，会存在开采区域长边与实体煤短边破断线同时处于煤体弹塑性分界区的情况。
由于煤体塑化程度ξs=(kt-ks0)/kt，ks0增大即代表煤体塑化程度减小。如图6所示，煤体塑化程度既可改变基本顶的破断顺序，也可改变基本顶在实体煤区的破断位置(包括实体煤区基本顶破断线距离煤壁距离、处于实体煤的哪类分区)，以及在煤柱区的破断位置及形态等。
图6 破断规律的ks0影响曲线
Fig.6 Influence curves of ks0 on fracture rule
(1)破断顺序方面。煤体塑化程度ξs增大，基本顶相对悬顶面积增大，即受载面积增大，则实体煤区及煤柱区的主弯矩数值均增大。ξs较大时，Msc>Msz>Msd>Msm，破断顺序为“长边→中部→实体煤短边→煤柱区”；ξs较小时，Msd<Msc<Msz，基本顶在煤柱区中部不发生破断，而是在煤柱中部的两侧破断扩展，所以此时煤柱区基本顶的破断形态为“分隔式双短弧形”。
(2)破断位置方面。煤体塑化程度ξs减小时，长边与短边实体煤区基本顶的破断位置深入煤体的距离显著减小，而深入煤柱区的破断位置显著增大直至煤柱中部不发生破断，即ξs减小，煤柱区破断线的变化模式为“单一连续长弧形”→“临界对接双长弧形”→“分隔式双短弧形”。
如图6的①区，煤体的塑化程度较大时，Lts<Lsc<Lsd，长边与实体煤短边破断线均处于煤体的弹性区，整体破断形态为闭合贯通式“非对称-非对称 X”型。
如图6的②及③区，随ξs减小，Lsc<Lts<Lsd，实体煤短边侧基本顶断裂线处于弹性煤体区上覆，而实体煤长边侧的破断线处于塑化煤体区上覆，整体破断形态为闭合贯通式“非对称-非对称 X”型或者开口非贯通式“非对称-非对称”型。
如图6的④区，随ξs减小，Lsc<Lsd<Lts，实体煤长边与实体煤短边侧基本顶断裂线均处于塑性煤体区上覆，整体破断形态为开口非贯通式“非对称-非对称X”型。
随ξs减小，基本顶整体破断形态的变化模式为：闭合式“非对称-非对称 X”型→临界贯通式“非对称-非对称X”型→开口非贯通式“非对称-非对称X”型。
如图7所示，支撑基本顶的煤柱宽度Lm主要改变基本顶的断裂形态，特别是煤柱区的断裂形态(及煤柱区的主弯矩)，对实体煤区基本顶断裂线的区位特征(处于煤体的弹性区或塑性区等)影响小。
图7 破断规律的Lm影响曲线
Fig.7 Influence curves of Lm on fracture rule
(1)破断位置方面。随着Lm减小，煤柱区的主弯矩显著减小，而实体煤区的主弯矩增大，但增长幅度小(且工作面的长宽比x0/y0越大，Lm对实体煤区主弯矩影响越小，反之越大)，这是因为，煤柱宽度减小则承担载荷的能力减小，那么悬顶区的基本顶载荷更多的需要长边与短边实体煤来支撑，相应的出现了煤柱区主弯矩减小而实体煤区主弯矩增大的情况。
(2)破断形态方面。随着Lm减小，煤柱侧基本顶的断裂线距离煤柱内壁的距离显著减小(减小幅度降低)，破断线的形态变化模式为：“单一连续长弧形”→“临界对接双长弧形”→“分隔式双短弧形”。
随Lm减小，基本顶整体破断形态的变化模式为：闭合式“非对称-非对称 X”型→临界贯通式“非对称-非对称X”型→开口非贯通式“非对称-非对称”型。
如图8所示，煤柱支撑系数ksm主要改变基本顶的断裂形态，特别是煤柱区的断裂形态(及煤柱区的主弯矩)，对实体煤区基本顶断裂线的区位特征影响甚小(对实体煤区的主弯矩影响也小)。ksm减小意味着煤柱承担载荷的能力减小，所以煤柱区的主弯矩显著减小，总载荷基本不变，所以实体煤区的主弯矩会小幅度增大。
图8 破断规律的ksm影响曲线
Fig.8 Influence curves of ksm on fracture rule
随着ksm减小，煤柱侧基本顶的断裂线距离煤柱内壁的距离增大，破断线的形态变化模式为：“单一连续长弧形”→“临界对接双长弧形”→“分隔式双短弧形”。
随着ksm减小，基本顶整体破断形态的变化模式为：闭合式“非对称-非对称 X”型→临界贯通式“非对称-非对称X”型→开口非贯通式“非对称-非对称”型。
由上述分析可知，煤体的塑化程度和范围，煤柱的宽度和塑化程度直接影响了弹塑性基础边界一侧采空条件下基本顶板的全区域破断形态、破断线的区位特征及破断顺序等。
下面分析该模型的间接影响因素(与煤体塑化参数和煤柱参数非直接相关的因素)，即基本顶的厚度、弹性模量、实体煤的弹性基础系数及推进跨度(长宽比)。
如图9所示，改变弹性区煤体基础系数kt，煤柱区及实体煤区的基本顶破断位态、破断顺序等有显著变化。
图9 破断规律的kt影响曲线
Fig.9 Influence curves of kt on fracture rule
(1)破断顺序方面。kt增大时，实体煤长边与短边区域基本顶主弯矩均增大而中部区域及煤柱区的主弯矩减小。
如图9(a)的(i)区，kt较小时，Msz>Msc>Msd>Msm，破断顺序为中部→长边→实体煤侧短边→煤柱侧；kt较大时，如(ii)及(iii)区，破断顺序为开采区长边→中部→实体煤侧短边→煤柱区中部(或煤柱中部区域不破断而中部区两侧形成短弧形破断形态)；存在长边与开采区中部同时破断的情况。
(2)破断位置及形态方面。如图9(b)所示，随着kt增大，实体煤区基本顶断裂圈深入煤体距离显著减小，断裂位置区位变化模式：长边与实体煤短边均位于弹性煤体区→长边位于塑性煤体区而短边位于弹性煤体区→长边与实体煤短边均位于塑性煤体区。
随着kt增大，煤柱区断裂线深入煤柱距离显著增大，直至煤柱中部区域无破断线，破断线的形态变化模式为：“单一连续长弧形”→“临界对接双长弧形”→“分隔式双短弧形”。
随着kt增大，基本顶整体破断形态的变化模式为：闭合式“非对称-非对称 X”型→临界贯通式“非对称-非对称X”型→开口非贯通式“非对称-非对称”型。
如图10所示，基本顶的厚度h对煤柱区及实体煤区的基本顶破断位态、破断顺序等有重要影响。
图10 破断规律的h影响曲线
Fig.10 Influence curves of h on fracture rule
(1)破断顺序方面。h减小时，长边、实体煤短边与煤柱区的主弯矩均增大而开采区中部的主弯矩减小。
h较大时，Msz>Msc>Msd>Msm(或无)，破断顺序为：中部→长边→实体煤侧短边→煤柱区中部(或无极值区，即煤柱中部区域不破断而中部区两侧形成短弧形破断形态)；h较小时，破断顺序为长边→中部→实体煤侧短边→煤柱区中部；存在长边与开采区中部同时破断的情况。
(2)破断位置及形态方面。随着h减小，实体煤区及煤柱区的基本顶断裂圈深入煤体距离显著减小，破断线区位特征的变化模式：长边与实体煤短边断裂线均位于弹性煤体区→长边断裂线位于塑性煤体区而短边断裂线位于弹性煤体区→长边与实体煤短边断裂线均位于塑性煤体区。
随h增大，基本顶在煤柱区断裂线深入煤柱距离显著增大，直至煤柱中部区域无破断线，破断线的形态变化模式为：“单一连续长弧形”→“临界对接双长弧形”→“分隔式双短弧形”。
随h增大，基本顶整体破断形态的变化模式为：闭合贯通式“非对称-非对称X”型→临界贯通式“非对称 -非对称X”型→开口非贯通式“非对称-非对称”型。
弹性模量E与h的影响规律基本相同。
对于长壁工作面，推进跨度L改变，表示基本顶悬顶的长宽比改变，同时跨度越大表示基本顶的强度也越大，悬顶跨度改变(长宽比改变)，可以显著影响主弯矩大小及断裂圈深入煤体距离。
随着L增大，基本顶断裂圈深入实体煤区距离显著减小，长边与实体煤短边区基本顶断裂线均由位于弹性煤体区逐步向塑性煤体区转移。
随着L减小，煤柱区断裂线深入煤柱距离增大，直至煤柱中部区域无破断线，破断线的形态变化模式为：“单一连续长弧形” → “临界对接双长弧形”→“分隔式双短弧形”。
随着L增大，整体破断形态的变化模式为：闭合贯通式“非对称-非对称”型→临界贯通式“非对称-非对称X”型→开口非贯通式“非对称-非对称 X”型。
由于板结构模型可以研究开采全区域顶板的破断位态特征及各特征区域之间的相互关系，比岩梁模型有无可替代的优势，所以采用板结构模型研究问题至关重要，特别是侧方采空条件下，是无法采用梁模型进行研究的。
当前，针对一侧采空条件下基本顶板的破断问题主要有3类模型，第1类(第1阶段)是传统的“实体煤侧三边固支+煤柱侧简支模型”；第2类(第2阶段)是“实体煤侧三边弹性基础边界+考虑煤柱参数”的单一塑化模型；第3类(第3阶段)是本文建立的“实体煤侧三边弹塑性基础边界+考虑煤柱参数”的双塑化模型。
图11从模型特征、影响因素、初次破断位置、煤柱侧破断位置、实体煤侧破断位置及整体断裂位态及指导意义方面，全面对比了模型的区别，得到了传统模型得不到的诸多新结论。
由图11可知，本文的一侧采空基本顶板结构模型考虑的因素及所得结论相对于传统模型均更加全面，下面几个方面简要说明本文模型的指导意义。
图11 一侧采空基本板结构模型对比
Fig.11 Comparison of main roof plate structure models with one side goaf
(1)煤柱区域基本顶破断模式方面。煤柱的宽度及塑化程度，基本顶的h,E，煤体的塑化程度及范围等均会显著影响煤柱区基本顶的破断模式，且破断模式差异显著，所以不可忽略这些因素对煤柱区基本顶破断模式的影响，否则所得结论与实际差距巨大。
对于近距离煤层开采，明晰遗留煤柱上覆岩块的破断位态，方可构建符合工程实际的力学模型，从而研究煤柱与顶板的联合稳定性及失稳条件等，才能有效评估煤柱及覆岩区对下伏开采对象的影响程度和范围等。
(2)实体煤区域破断模式方面。开采区域长边基本顶深入煤体破断，且断裂线可能处于实体煤的塑性区、弹性区或者弹塑性分界区，不同分区基本顶的稳定程度不同。基于3类深入煤体的断裂位置，可有效指导大面积来压预警。
实体煤短边区域基本顶的断裂线位置有3类，弹性、塑性或弹塑性煤体分界区，沿空掘巷阶段，基本顶的断裂位置对巷道应力分布及稳定性影响大，所以对指导沿空煤巷位置选择意义显著。
可见本文的力学模型在传统模型基础上更进一步，弥补了传统模型的缺陷和不足，对理论认识和实践发展均有推进作用。
现从一个方面(煤柱区基本顶断裂位置角度)列举实例进行说明。
如图12所示，2层近水平煤层的平均间距约为20 m，2号煤层平均厚度2.1 m、抗压强度14 MPa，埋深440～460 m，基本顶为细砂岩平均厚度7.4 m、抗压强度82 MPa，2号层的12106工作面与12108工作面已经采空稳定，区段煤柱宽度10 m(图12中x1与x2的和为10 m)。下伏3号煤层开采区段巷道布置位置受到上覆遗留煤柱的影响，采动过程中明晰遗留煤柱区上覆覆岩结构特征，才能构建合适模型并得出其稳定条件，进而有效指导下伏工作面的布置和开采，预防强矿压产生。
在3号层13102工作面的回风巷可以钻孔窥视2号层区段煤柱上覆基本顶的断裂情况(图12中的xh为10 m,yh为20 m)。钻孔窥视得到，区段煤柱上覆基本顶只有一条而非两条断裂线，其中断裂线距离12106面煤柱壁的距离x1约为4.1 m，与本文模型计算结果一致。该类型属于本文模型提出的区段煤柱区基本顶的破断类型为“分隔式双短弧形”，即煤柱区上覆无12108工作面开采导致的基本顶新断裂线，由于12106工作面先开采，所以该断裂线是12106工作面开采导致的破断线，而12108工作面开采时，煤柱区无新的贯通式断裂线产生，验证了本文模型计算结果的合适性。
图12 窥视示意
Fig.12 Peep result diagram
由文献[1]的理论公式“(8-5)”计算得到工作面短边区域煤体塑性区宽度约为2.3 m，即煤体弹塑性分界线的距离为2.3 m，本文力学模型计算得到基本顶深入煤体断裂线距离约为4.3 m(钻孔窥视得到的实际断裂线位置x1约为4.1 m，两者接近)，即断裂线距离明显大于煤体的弹塑性分界线距离，且断裂线处于弹性煤体区而非煤体的弹塑性分界线，这属于本文模型得到基本顶断裂线所处分区的类型之一，这也证明了本文模型计算结果的合适性。
(1)煤柱区基本顶的破断形态有3类，且随着基本顶厚度h、弹性模量E及弹性煤体基础系数kt增大，而煤柱宽度Lm及煤柱基础系数ksm、实体煤塑化范围Lts及塑化程度ξs及跨度L减小时的破断模式及演变规律为“单一连续长弧形”→“临界对接双长弧形”→“分隔式双短弧形”。
(2)Lm及ksm主要影响煤柱区基本顶的破断位态，对实体煤区主弯矩大小有影响，但影响程度小。
(3)实体煤区基本顶破断位态有5类且随着h,E及ξs增大，而Lts,kt及L减小时的断裂模式及演变规律为：“长边与短边断裂线均处于塑化煤体区”→“长边断裂线处于塑化煤体区而短边处于弹塑性分界区”→“长边断裂线位于塑化区而短边断裂线位于弹性区”→“长边断裂线位于弹塑性分界区而短边断裂线位于弹性煤体区”→“长边与短边断裂线均处于弹性煤体区”，存在长边与短边破断线同时位于煤体弹塑性分界区的情况。
(4)整体破断形态分为3类且随着h,E及kt增大，而Lm,ksm,Lts，ξs及L减小时，整体破断模式及变化规律为：闭合式“非对称-非对称X”型→临界贯通式“非对称-非对称X”型→开口非贯通式“非对称-非对称X”型。h,E及Lts较大而L及kt较小时，破断顺序为偏向煤柱侧中部→长边深入实体煤区(弹性区、弹塑性分界区、塑性区)→实体煤短边(弹性区、弹塑性分界、塑性区)→煤柱侧(煤柱侧中部区，中部临界或中部区的两侧破断)。
鉴于采矿工程问题的复杂性，本文的模型依旧无法全面反映工程的全部问题。但在解决一侧采空基本顶板结构破断规律的模型方面，本文在传统的“3边固支+煤柱侧简支”(第1类)、“三边弹性基础+考虑煤柱宽度和支撑能力”(第2类)的基础上，更全面的考虑了影响一侧采空基本顶破断的其他实质性因素，弥补了传统模型的缺陷及不足，有利于指导实践。
[1] 钱鸣高,石平五,许家林.矿山压力与岩层控制[M].徐州:中国矿业大学出版社,2013.
[2] 黄庆享,杜君武,刘寅超.浅埋煤层群工作面合理区段煤柱留设研究[J].西安科技大学学报,2016,36(1):19-23.
HUANG Qingxiang,DU Junwu,LIU Yinchao.Study on section coal pillar of group mining in shallow buried coal seams[J].Journal of Xi’an University of Science and Technology,2016,36(1):19-23.
[3] 冯国瑞,白锦文,史旭东,等.遗留煤柱群链式失稳的关键柱理论及其应用展望[J].煤炭学报,2021,46(1):164-179.
FENG Guorui,BAI Jinwen,SHI Xudong,et al.Key pillar theory in the chain failure of residual coal pillars and its application prospect[J].Journal of China Coal Society,2021,46(1):164-179.
[4] 鞠金峰,许家林,朱卫兵.关键层结构提前滑落失稳对浅埋近距离煤层出煤柱压架灾害的影响[J].煤炭学报,2015,40(9):2033-2039.
JU Jinfeng,XU Jialin,ZHU Weibing.Influence of overlying key strata structure pre-sliding on support failure disaster while mining in the lower coal seam cut across below the upper adjacent coal pillar under shallow cover[J].Journal of China Coal Society,2015,40(9):2033-2039.
[5] 潘岳,顾士坦,杨光林.裂纹发生初始阶段的坚硬顶板内力变化和“反弹”特性分析[J].岩土工程学报,2015,35(7):860-869.
PAN Yue,GU Shitan,YANG Guanglin.Variation of internal force and rebound property of hard roof at initial stage of cracking[J]. Chinese Journal of Geotechnical Engineering,2015,35(7):860-869.
[6] 何富连,何文瑞,陈冬冬,等.考虑煤体弹-塑性变形的基本顶板初次破断结构特征[J].煤炭学报,2020,45(8):2704-2717.
HE Fulian,HE Wenrui,CHEN Dongdong,et al.First fracture structure characteristics of main roof plate considering elastic-plastic deformation of coal[J].Journal of China Coal Society,2020,45(8):2704-2717.
[7] 谢生荣,陈冬冬,曾俊超,等.考虑两侧煤柱与弹性煤体基础的基本顶板初次破断特征[J].煤炭学报,2019,44(1):115-126.
XIE Shengrong,CHEN Dongdong,ZENG Junchao,et al.First fracturing characteristics of main roof plate structure considering coal pillars and elastic coal foundation on both sides of stope[J].Journal of China Coal Society,2019,44(1):115-126.
[8] 陈冬冬,何富连,谢生荣,等.弹性基础边界基本顶板结构周期破断与全区域反弹时空关系[J].岩石力学与工程学报,2019,38(6):1172-1187.
CHEN Dongdong,HE Fulian,XIE Shengrong,et al.Time-space relationship between periodic fracture of plate structure of main roof and rebound in whole region with elastic foundation boundary[J]. Chinese Journal of Rock Mechanics and Enginering,2019,38(6):1172-1187.
[9] 陈冬冬,谢生荣,何富连,等.长边两侧采空(煤柱)弹性基础边界基本顶薄板初次破断[J].煤炭学报,2018,43(12):3273-3285.
CHEN Dongdong,XIE Shengrong,HE Fulian,et al.First fracturing of thin plate of main roof with elastic foundation boundary on both sides of the long side of goaf(coal pillars)[J].Journal of China Coal Society,2018,43(12):3273-3285.
[10] 王红胜,张东升,李树刚,等.基于基本顶关键岩块B断裂线位置的窄煤柱合理宽度的确定[J].采矿与安全工程学报,2014,31(1):10-16.
WANG Hongsheng,ZHANG Dongsheng,LI Shugang,et al.Rational width of narrow coal pillar based on the fracture line location of key rock B in main roof[J].Journal of Mining & Safety Engineering,2014,31(1):10-16.
[11] 何富连,赵计生,姚志昌.采场岩层控制论[M].北京:冶金工业出版,2009.
[12] 王金安,张基伟,高小明,等.大倾角厚煤层长壁综放开采基本顶破断模式及演化过程(I)——初次破断[J].煤炭学报,2015,40(6):1353-1360.
WANG Jin’an,ZHANG Jiwei,GAO Xiaoming,et al.Fracture mode and evolution of main roof stratum above longwall fully mechanized top coal caving in steeply inclined thick coal seam(I)—Initial fracture[J].Journal of China Coal Society,2015,40(6):1353-1360.
[13] 李肖音,高峰,钟卫平.基于板模型的采场顶板破断机理分析[J].采矿与安全工程学报,2008,25(2):180-183.
LI Xiaoyin,GAO Feng,ZHONG Weiping.Analysis of fracturing mechanism of stope roof based on plate model[J].Journal of Mining & Safety Engineering,2008,25(2):180-183.
[14] 王红卫,陈忠辉,杜泽超,等.弹性薄板理论在地下采场顶板变化规律研究中的应用[J].岩石力学与工程学报,2006,25(S2):3769-3774.
WANG Hongwei,CHEN Zhonghui,DU Zechao,et al.Application ofelastic thin plate theory to change rule of roof in underground stope[J].Chinese Journal of Rock Mechanics and Enginering,2006,25(S2):3769-3774.
[15] 陈冬冬,谢生荣,何富连,等.长边采空(煤柱)弹性基础边界基本顶薄板破断规律[J].采矿与安全工程学报,2018,35(6):1191-1199.
CHEN Dongdong,XIE Shengrong,HE Fulian,et al.Fracture rule of main roof thin plate with the elastic foundation boundary and long side coal pillar[J].Journal of Mining & Safety Engineering,2018,35(6):1191-1199.
[16] 蒋金泉,张培鹏,秦广鹏,等.一侧采空高位硬厚关键层破断规律与微震能量分布[J].采矿与安全工程学报,2015,32(4):523-529.
JIANG Jinquan,ZHANG Peipeng,QIN Guangpeng,et al.Fracture laws of one-side mined high-position hard thick key strata and microseismic energy distribution[J].Journal of Mining & Safety Engineering,2015,32(4):523-529.
[17] 陈冬冬,何富连,谢生荣,等.一侧采空(煤柱)弹性基础边界基本顶薄板初次破断[J].煤炭学报,2017,42(10):2528-2536.
CHEN Dongdong,HE Fulian,XIE Shengrong,et al.First fracture of the thin plate of main roof with three sides elastic foundation boundary and one side coal pillar[J].Journal of China Coal Society,2017,42(10):2528-2536.
[18] 徐芝纶.弹性力学[M].北京:高等教育出版社,2006.
[19] 谢生荣,陈冬冬,曾俊超,等.基本顶板结构初次破断与全区域反弹时空关系[J].煤炭学报,2019,44(9):2650-2663.
XIE Shengrong,CHEN Dongdong,ZENG Junchao,et al.Space-time relationship between the first fracture of main roof structure and whole regional rebound[J].Journal of China Coal Society,2019,44(9):2650-2663.
[20] 王汉权,成蓉华.微分方程数值方法——有限差分法[M].北京:科学出版社,2020.