移动阅读
移动阅读
收稿日期:2020
0531
修回日期:20200922
GAO Wei，CUI Shuang，XIAO Ting,et al.Crack initiation of rock based on the minimum plastic zone radius criterion[J].Journal of China Coal Society,2021,46(10):3193-3202.
岩石是一种典型的地质体，其中含有大量裂隙、节理及微裂纹。国内外大量工程实践和研究表明，岩石工程的失稳破坏大多与自身的裂纹起裂扩展有关，岩石的变形破坏过程实质是内部裂纹不断产生、演化和扩展的过程[1]。岩石中多裂纹的起裂及其贯通破坏机制研究是岩石断裂力学研究的重点课题之一，同时也对裂隙岩体工程稳定性、边坡滑坡预防及构造地震产生机制及预测预报等研究具有重要的理论和实际意义[2]。因此，研究岩石中多裂纹的起裂规律对岩体工程的稳定性具有重要的理论意义和工程价值。
目前，研究者对岩石中多裂纹的起裂规律已进行了大量研究，主要研究方法有理论计算、室内试验和数值模拟。
在理论计算方面，许多学者从能量、应力和应变等角度分别建立了不同的断裂准则。席婧仪[3]采用最大周向拉应力准则和应变能密度因子准则分别计算了受拉和受压多裂纹的起裂角。刘红岩[4]将T应力引入到传统断裂力学的最大周向拉应力准则，提出了考虑T应力的修正最大周向应力准则，研究了岩石压剪裂纹的起裂机理。刘洋等[5]用最大周向拉应力准则计算了单一裂纹在单轴压缩荷载作用下的应力强度因子及其扩展趋势，认为断裂角只与裂纹和载荷有关。李宏福等[6]以受单向压缩的中心斜裂纹为研究对象，基于修正的最大周向拉应力准则分析了裂纹间的摩擦因数、闭合度对主裂纹尖端应力强度因子及裂纹起裂角的影响。尽管目前裂纹起裂理论计算方面已经有了较多研究成果，但大部分研究均为弹性断裂的研究，考虑裂尖塑性区影响的研究尚不多。
研究多裂纹起裂常用的试验方法有CT扫描、压缩断裂试验、光弹性试验、数字图像相关方法和声发射等。郭奇峰等[7]采用声发射与表面应变监测等手段，采用最大畸变能理论对单轴压缩条件下裂隙花岗岩的裂纹起裂荷载、起裂角以及裂纹扩展路径进行试验与计算。CAO等[8]基于含三条预置裂纹的类岩石材料单轴压缩试验，研究了多裂纹的起裂、压密、扩展和贯通机制。徐丽海[9]以岩石裂纹系统为研究对象，利用类岩石材料物理试验和数字图像相关方法相结合的手段研究了类岩石材料中不同尺寸及布置形式的单裂纹、双裂纹的起裂及扩展规律。李存宝等[10]为研究页岩在破坏过程中的起裂机制，对具有不同层理倾角的页岩岩样进行了不同围压下的常规三轴压缩实验，研究了层理倾角对起裂荷载和裂纹损伤应力的影响。尽管目前裂纹起裂试验研究方面已经有了较多成果，但大部分研究均为裂纹弹性扩展的研究，关于裂纹尖端塑性区影响的研究尚不多。
数值模拟研究方面，杨庆和刘元俊[11]采用颗粒流软件PFC2D实现了含不同岩桥倾角的预制双裂纹石膏材料在单轴压缩作用下裂纹扩展贯通的过程。李铮等[12]采用近场动力学方法模拟了单轴压缩状态下，含预制裂纹的类岩石材料裂纹起裂和连接问题。孙翔等[13]基于有限元与离散元混合方法分别对初始裂纹倾角为45°的单裂纹以及岩桥为90°的双裂纹岩石试样在单轴压缩作用下，裂纹的扩展过程进行了模拟。周小平等[14]基于扩展有限元法，建立了单轴压缩作用下类岩石材料多裂纹扩展过程和扩展路径的数值模拟方法。但数值模拟方法的输入参数难以获取，且输入参数如何与岩石的宏观力学性质更好对应还需要进一步研究。同时，考虑裂尖塑性区影响的研究也不多。
尽管目前多裂纹起裂领域已有了较多研究成果，但大部分研究没有考虑裂尖塑性区对裂纹起裂的影响，仅仅通过物理试验和数值模拟再现多裂纹起裂扩展及断裂过程。实际上，裂纹尖端塑性区的存在是材料抵抗断裂的重要因素，与裂纹的断裂扩展角有密切关系，裂纹起裂角取决于裂纹面处的应力，遵循塑性核区域的局部最小值或全局最小值[15]。因此，裂尖塑性区对裂纹的起裂影响很大。为了考虑裂尖塑性区的影响，基于摩尔-库伦强度准则推导了裂尖塑性区半径公式，并考虑硬化对其进行了修正，然后基于最小塑性区半径准则得到了裂纹的起裂角和起裂荷载。最后，计算了共线三裂纹试样中心裂纹长度与外裂纹长度比值、裂纹倾角和裂纹间距对起裂荷载的影响，进而分析了岩石中多裂纹的起裂规律。
裂纹尖端及其坐标表示如图1所示。
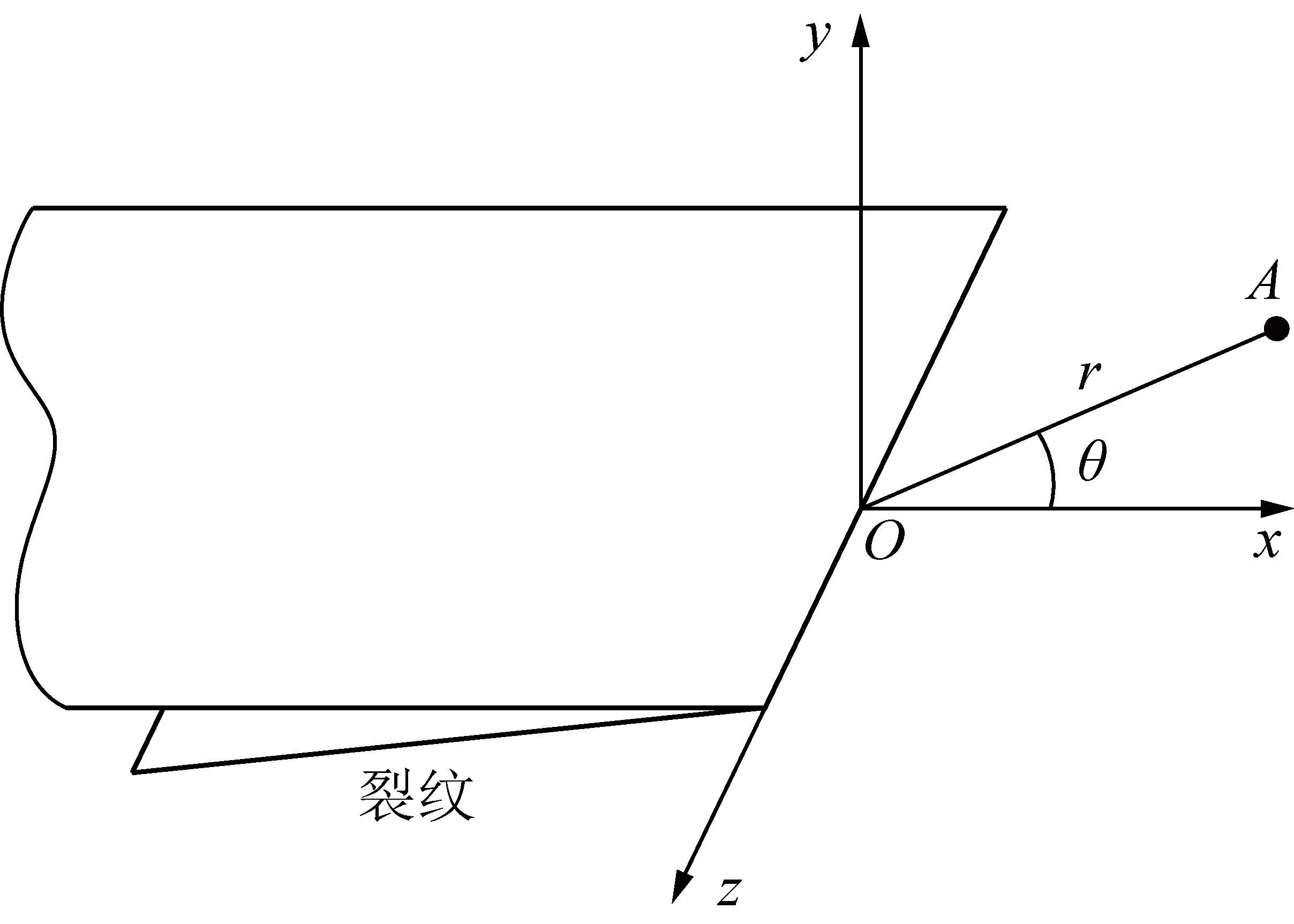
图1 裂纹尖端及其坐标表示
Fig.1 Crack tip and its coordinate representation
由断裂力学[16]可知，裂纹尖端处的主应力为
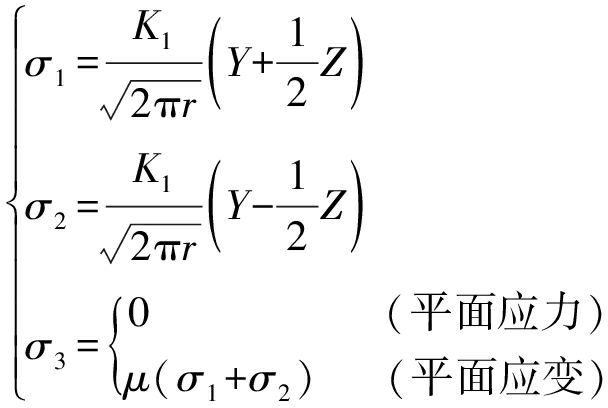
(1)
其中，Y,Z分别为
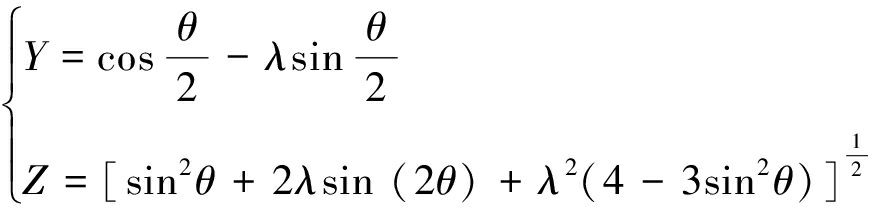
(2)
式中，σ1,σ2和σ3分别为大主应力、中主应力和小主应力；r为图1中A点到坐标原点的距离；θ为图1中OA与x轴的夹角；μ为泊松比;λ=KⅡ/KⅠ，KⅠ,KⅡ分别为Ⅰ型,Ⅱ型裂纹的应力强度因子。
摩尔-库伦强度准则是岩土工程领域使用最普遍的岩土力学准则，可以比较准确地反映应力水平较低的岩土强度特征。该准则假设，岩石内一点的破坏主要决定于大主应力和小主应力，与中间主应力无关。摩尔-库伦强度准则[17]可以表示为
σ1-ασ3=σt
(3)
其中，σt为材料抗拉强度；α=σt/σc为材料抗拉强度与抗压强度的比值,即硬化系数。将式(1)代入式(3)，可以得到塑性区半径公式为
(4)
平面应变状态下κ=1-2αμ;平面应力状态下κ=1。
实际岩石工程中岩石常处于受压状态，其内部裂纹在压缩作用下可能闭合，而受压闭合裂纹由于闭合裂纹面的物质相互不可侵入，使得裂纹面之间只能产生滑动[18]。因此，通常情况下可以认为裂纹的Ⅰ型奇异消失。为了简化计算，假设KⅠ=0，从而式(4)化简为
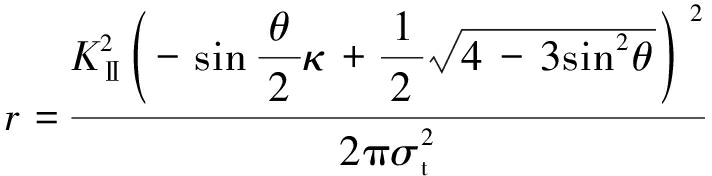
(5)
前述推导的裂纹尖端塑性区半径是基于K场可一直延续到弹塑性边界(无过渡区)的假设，简单地将K场中小于R处的应力由K场解换为σ3。因此，1.1节给出的塑性区尺寸解无法满足总体静力平衡条件。
针对此问题，IRWIN[19]提出了“应力松弛修正”的概念，但该修正理念把仅适用于裂纹尖端小范围的应力场近似公式应用于整个裂纹面，使修正后裂纹面上的内力与外力不平衡，且没有考虑到塑性区内材料的硬化。基于这些不足，甘卫平等[20]提出了考虑硬化的纯Ⅰ型裂纹尖端塑性区修正模型，本文基于其基本思想，对基于摩尔-库伦强度准则的裂纹尖端塑性区尺寸进行修正，如图2所示，图2中，a为裂纹的半长，也就是裂纹中部到裂纹尖端的距离;rys+rx为塑性区长度R；rys为当应力到达屈服应力
时，线弹性分析所对应的塑性区长度;rx为修正后的塑性区长度与线弹性分析塑性区长度的差值。
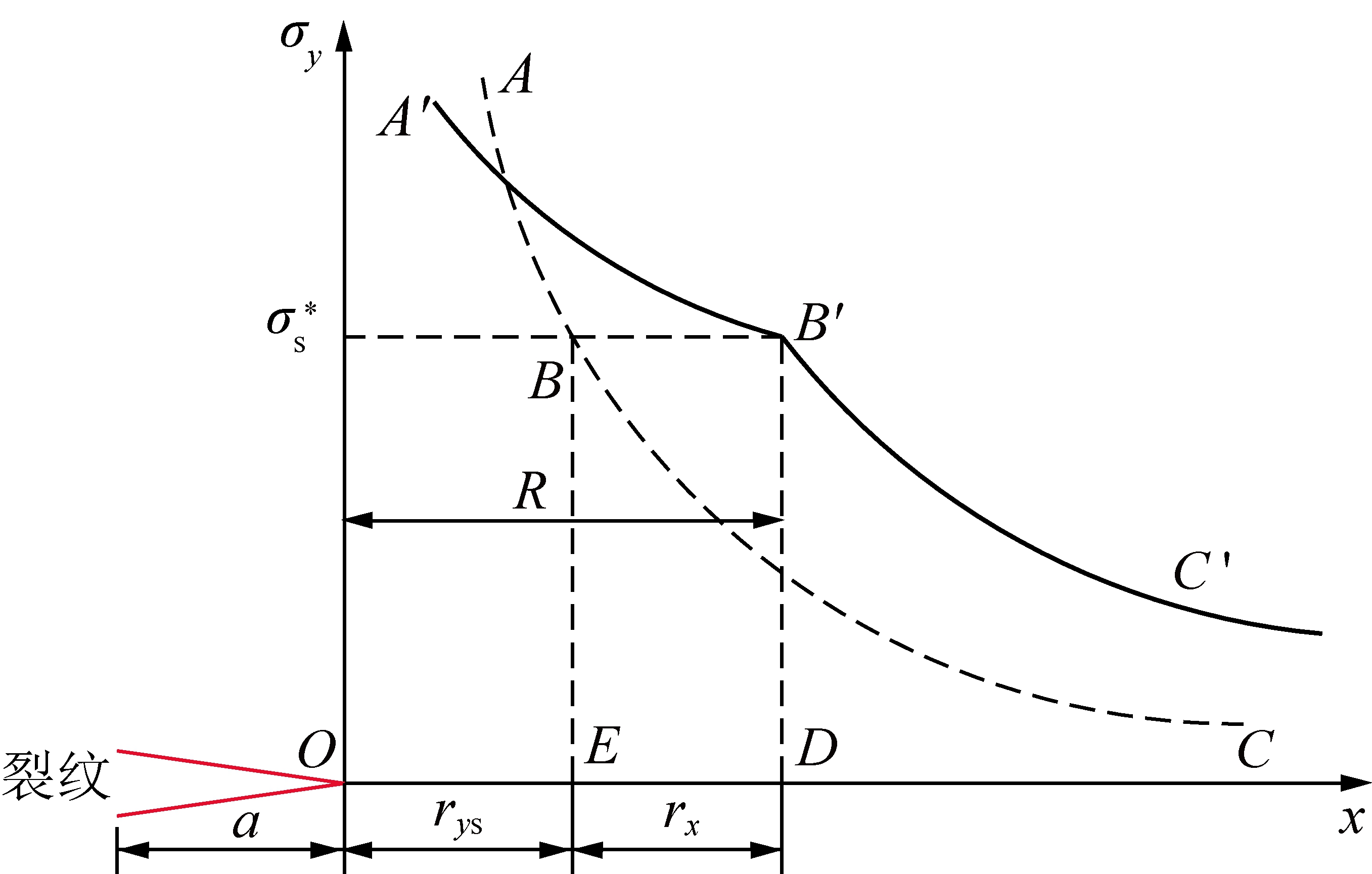
图2 考虑硬化的塑性区修正模型 Fig 2 Plastic zone correction model considering hardening
图2中，曲线A′B′代表材料硬化时的应力分布σy，可表达为
(6)
式中，为有效屈服应力极限，平面应力状态时取
平面应变状态时取
为屈服应力极限;R为θ=0时的塑性区尺寸;n为硬化指数，硬化指数一般取值在0～1[21]。
曲线ABC代表弹性区的应力场分布，可表达为
(7)
虚线ABC表示K场下应力σy沿裂纹延长线的分布曲线，此曲线下的面积为S1。假定当裂纹尖端达到有效屈服应力后，经应力松弛，弹性区的应力场往前平移rx。曲线A′B′代表材料硬化时的应力分布，B′C′段近似为BC段的平移，曲线A′B′C′下的面积为S2。S1为弹性阶段下净截面的内力，S2物理含义为屈服阶段下净截面的内力，根据力学原理，稳定材料的内力与外力保持平衡，因此，S1与外力平衡且S2也与外力平衡，故S1=S2，即曲线A′B′C′下的面积等于ABC下的面积。由于BC段和B′C′段均代表弹性应力场的变化规律，因此，2段曲线下的面积可近似看作相等，故有:
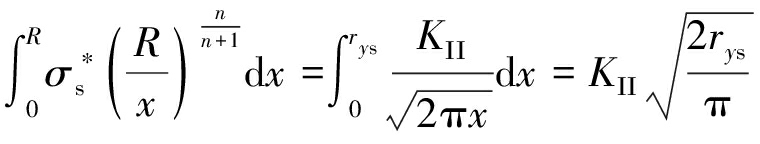
(8)
如图2中B点所示，假定x=rys是
的点，令θ=0，将式(5)代入式(8)可得:
(9)
(10)
同理，当θ≠0，考虑材料硬化的塑性区半径是未考虑材料硬化的塑性区半径的2/(1+n)倍，考虑材料硬化的塑性区半径rp公式为
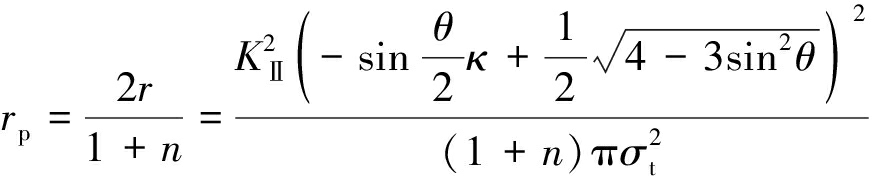
(11)
从物理概念来说，裂纹尖端塑性区是一个高度紧张的区域，裂纹尖端必须通过这个高应变区域传播，才能到达核外的弹性加载区。最小塑性区半径准则[22]认为裂纹沿着裂纹尖端到塑性区边界的最小半径方向起裂，在此方向上，产生新裂纹面所需的塑性功最小，也就是所需的断裂能最小。为了考虑裂纹尖端塑性区的影响，这里基于最小塑性区半径准则求解裂纹的起裂角及起裂荷载。
以对称布置三共线裂纹为例来计算起裂角和起裂荷载，设一无限大平板，中心有3条对称布置的共线裂纹，板受与裂纹线成β角的单向均布压力σ作用，如图3所示，a′，b′，c′为裂纹尖端a,b,c的对称点。目前的大部分研究是以排列形式较简单的单裂纹或双裂纹为研究对象，分析这些裂纹形式下的扩展规律，而对于不等长多裂纹扩展规律的研究还较少。本文以对称布置的三共线裂纹为研究对象，可以简化模型的计算量，所需研究的裂纹尖端数由6个简化为3个。
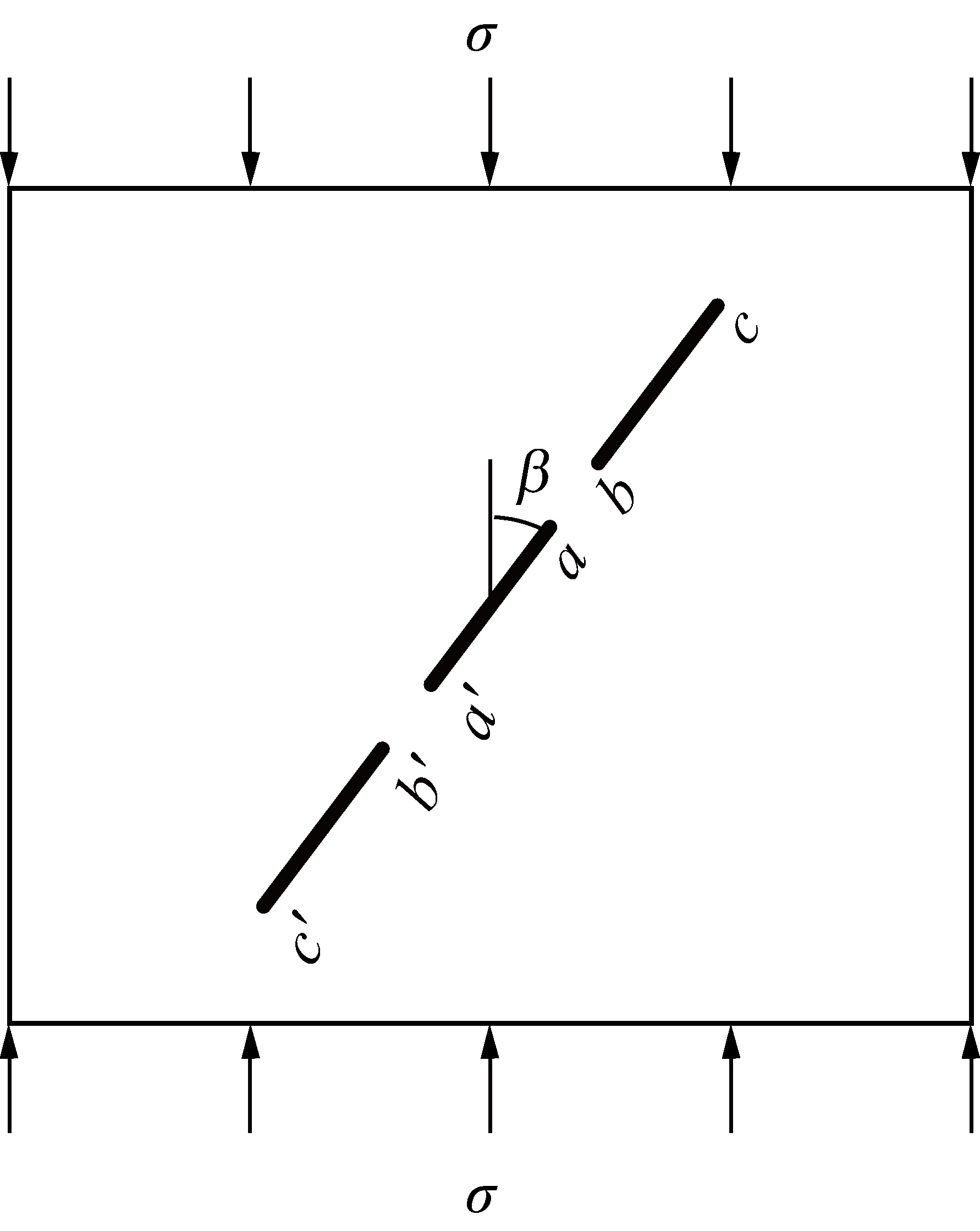
图3 含对称布置的三共线裂纹受单轴压缩作用
Fig.3 Model of three collinear cracks with symmetrical arrangement under uniaxial compression
裂纹沿塑性区半径rp最小的方向起裂[22]，有:
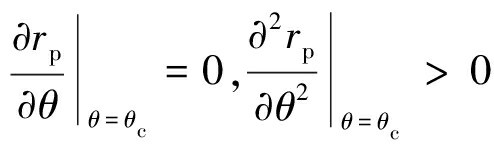
(12)
其中，θc为起裂角。在单向应力状态下，将式(11)代入式(12)，可得
(13)
(14)
对于受压裂纹，三共线裂纹起裂角θc判据均为式(13)和式(14)。其中，平面应力状态下κ=1;平面应变状态下κ=1-2αμ。
根据最小塑性区半径准则，起裂方向上塑性区半径rp达到临界值rc时开裂，即
rp>rc
(15)
对于纯Ⅱ型裂纹(KⅠ=0)，本文采用文献[23]的方法来计算临界值rc，为
rc=rⅡc
(16)
基于文献[23]，断裂准则可写为
(17)
其中
c22=1+ζ(1-cos θc)+3cos2θc
(18)
式中，平面应力状态下μ*=0;平面应变状态下μ*=μ;KΙc为Ⅰ型断裂韧度;KⅡc为Ⅱ型断裂韧度。
目前对于平面多裂纹应力强度因子计算问题，主要有3种解析解法:权函数法、边界配置法和复变函数法。相对而言，复变函数法更灵活，适用范围更广，该法可求解任意分布的多裂纹应力强度因子。因此，本文采用文献[24]中的复变函数法计算裂纹尖端的应力强度因子，其中，中心裂纹尖端的应力强度因子为
(19)
外裂纹内尖端的应力强度因子为
(20)
外裂纹外尖端的应力强度因子为
(21)
其中，
为椭圆第1类完全积分;
为椭圆第2类完全积分[25];椭圆模
为裂纹面闭合度;β为裂纹倾角(裂纹面与轴向力的夹角);f为摩擦因数;a,b,c分别为中心裂纹尖端、外裂纹内尖端和外裂纹外尖端到坐标原点的距离。
将式(19)代入式(17)可得中心裂纹起裂荷载为
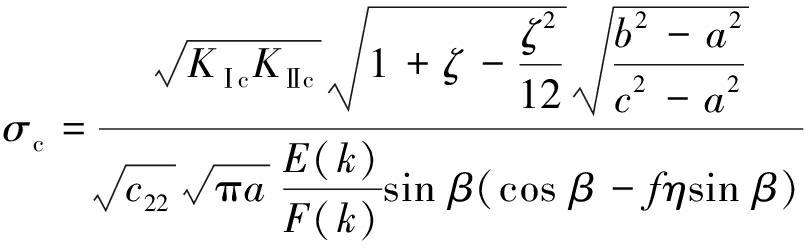
(22)
将式(20)代入式(17)可得外裂纹内尖端起裂荷载为
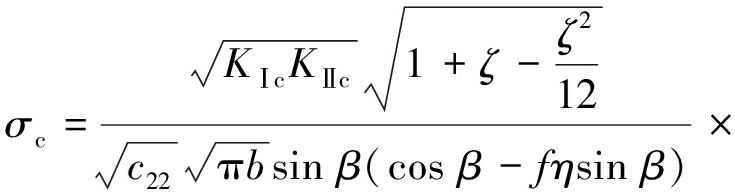
(23)
将式(21)代入式(17)可得外裂纹外尖端起裂荷载为
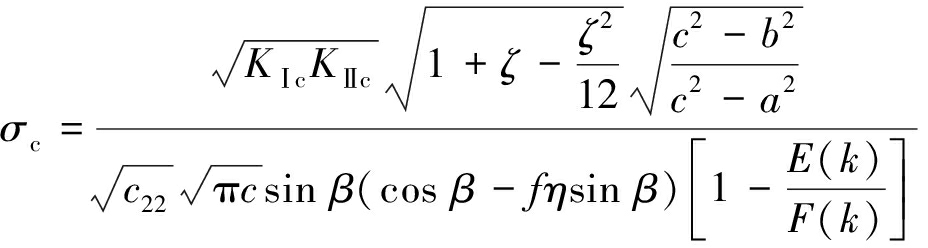
(24)
通过裂纹起裂角可以反映裂纹将沿哪个方向扩展，研究裂纹起裂角对裂纹扩展路径的预测具有重要意义。知道了裂纹扩展路径就可以采取有效的止裂措施防止裂纹破坏，同时对地震、滑坡、岩爆、塌方等自然灾害的预测预报具有重要意义[26]。而且，计算裂纹起裂角是计算起裂荷载的理论前提。因此，研究岩石裂纹起裂角具有重要的理论和工程意义。
以对称布置的三共线受压裂纹为例，如图3所示。裂纹起裂角判据为式(13)和式(14)。将式(13)化简为
3sin2θc-2κ2cos θc+2κ2-4=0
(25)
平面应力状态下κ=1，求解式(25)和(14)得θc=70.43°。平面应变状态下κ=1-2αμ，式(25)可表示为
3sin2θc-2(1-2αμ)2cos θc+
2(1-2αμ)2-4=0
(26)
由以上分析可以发现，平面应力状态下，受压裂纹的起裂角为定值，而平面应变状态下受压裂纹的起裂角与硬化系数α和泊松比μ有关。为研究平面应变状态下受压裂纹的起裂角与硬化系数的之间关系，令泊松比μ=0.3，硬化系数α分别取0,0.1,0.2,0.3和0.4，代入式(26)和式(14)分别计算不同硬化系数α对应的起裂角，其结果如图4所示。同理，令硬化系数α=0.3，泊松比μ分别取0,0.1,0.2,0.3和0.4，代入式(26)分别计算不同泊松比μ对应的起裂角，其结果与上相同。起裂角与泊松比的关系图和起裂角与硬化系数的关系图一致，所以用一个图表示，如图4所示。
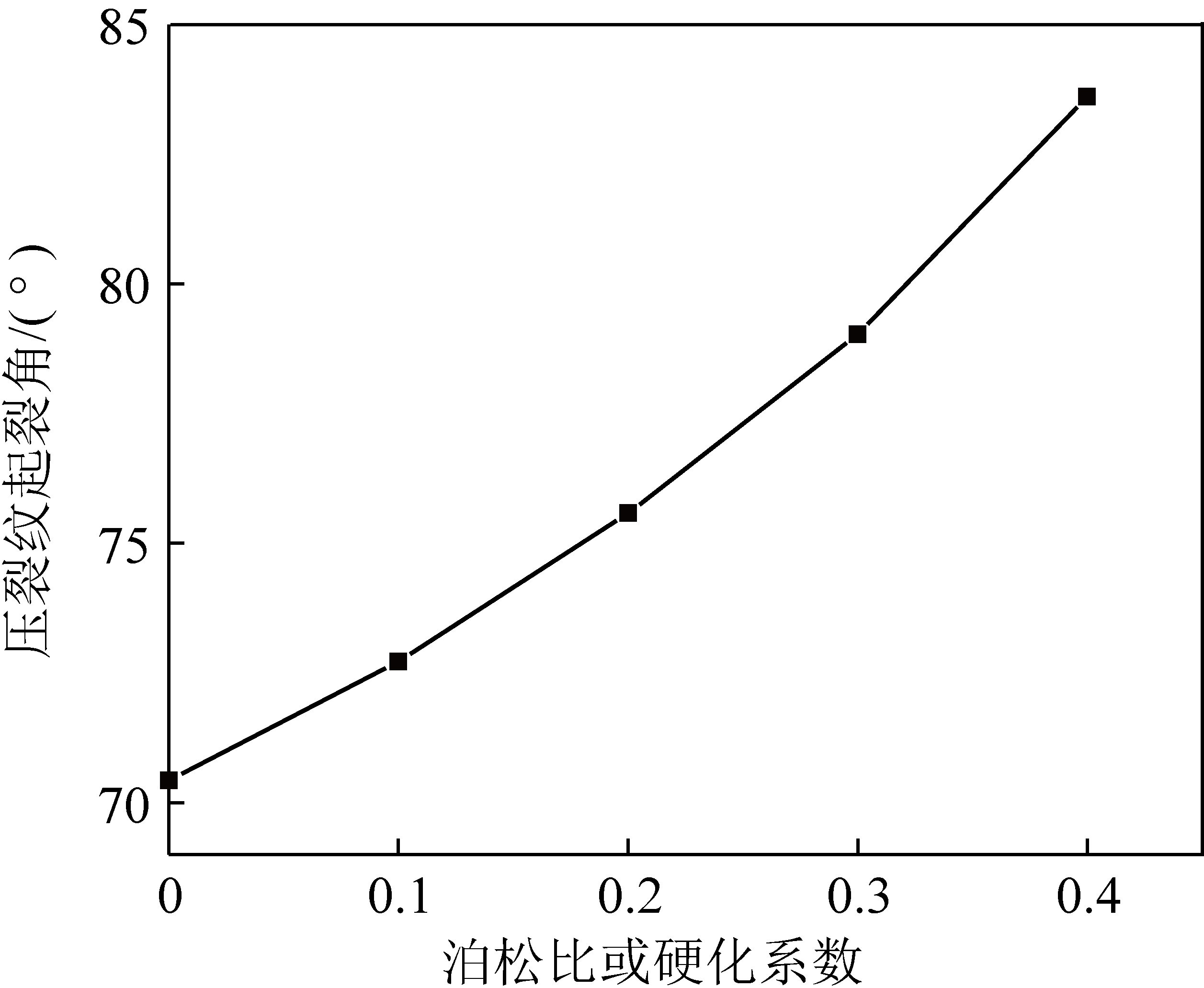
图4 平面应变状态下受压裂纹的起裂角与泊松比或 硬化系数的关系
Fig.4 Relationship between crack initiation angle and Poisson’s ratio and hardening coefficient under plane strain
由图4可知，平面应变状态下受压裂纹的起裂角随硬化系数和泊松比的增大而增大。
岩石裂纹起裂荷载会对裂纹扩展造成严重影响，从而诱发一系列工程灾害。开展岩石多裂纹起裂机理研究，获取复杂裂隙状态下的岩石裂纹起裂荷载对研究地下工程围岩的潜在破坏模式、止裂控制理论，分析岩体孕灾机理，实现地下工程的安全、稳定建设和运行具有重要的理论价值和工程意义[27]。
以对称布置的三共线受压裂纹为例，如图3所示。裂纹在不同压应力下，裂纹闭合度η不同。因此，这里对2种特殊受压裂纹进行分析:张开型裂纹(η=0)及完全闭合裂纹(η=1)。
如图3所示，设压应力σ=10 MPa，裂纹面摩擦因数f=0.5，裂纹面与轴向力的夹角(裂纹倾角)β=π/4，外裂纹长度取定值10 mm，即c-b=10;裂纹间距取定值10 mm，即b-a=10。令中心裂纹长度为2a=t(c-b)，t分别为0.5,1.0,1.5,2.0,2.5和3.0。设材料硬化指数n=0，硬化系数α=0.2，泊松比μ=0.3。Ⅰ型断裂韧度KIC=0.52 MN/m3/2，Ⅱ型断裂韧度KⅡc=0.52 MN/m3/2。将硬化系数α=0.2，泊松比μ=0.3代入式(25)计算受压裂纹起裂角，然后将起裂角代入式(22)～(24)，分别计算不同中心裂纹长度与外裂纹长度比值t的张开型裂纹(η=0)和完全闭合型裂纹(η=1)的起裂荷载，其结果如图5,6所示。
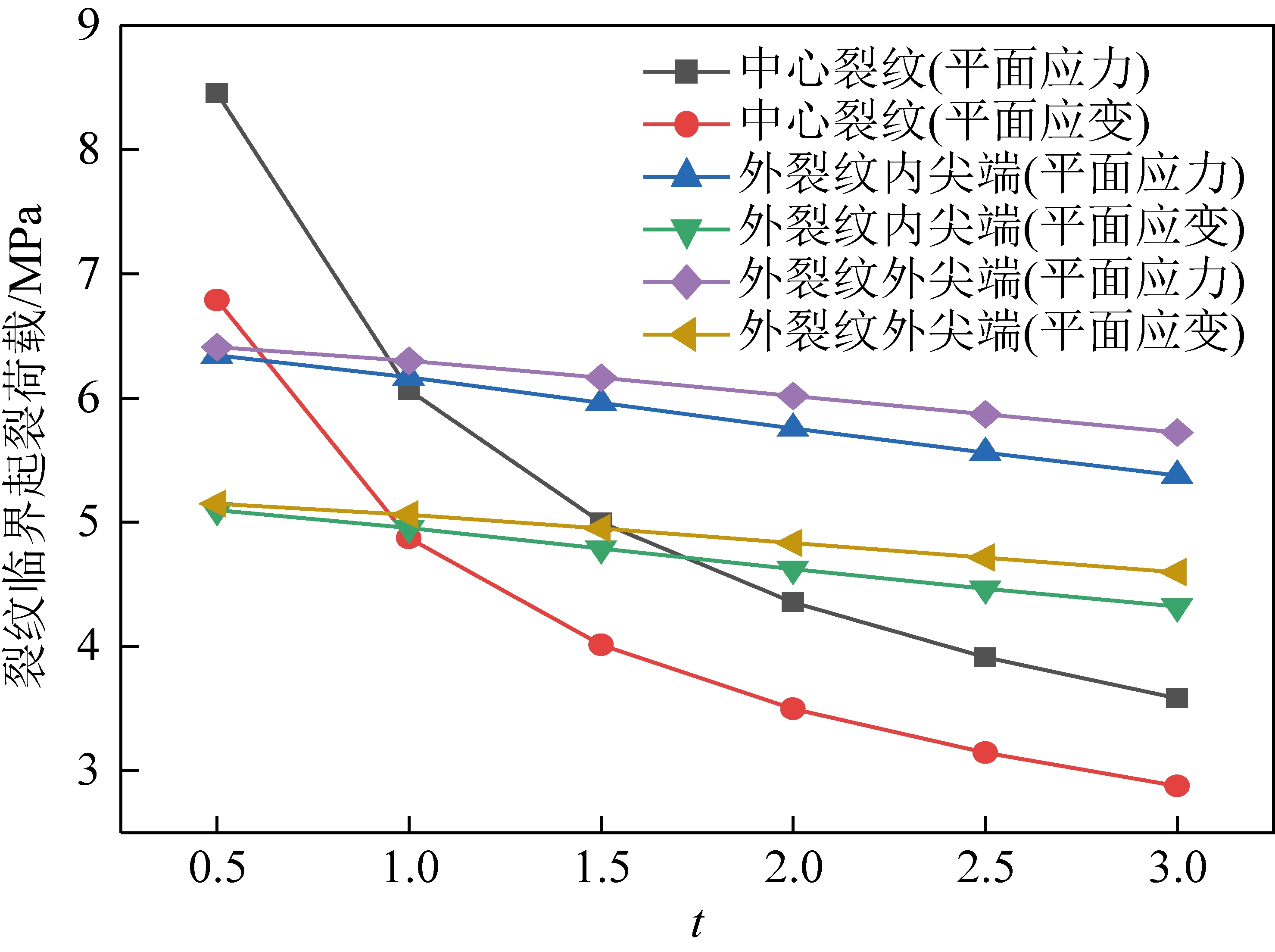
图5 单轴压缩下裂纹起裂荷载随t值的变化曲线图(η=0)
Fig.5 Curves of crack initiation load with value t under uniaxial compression(η=0)
由图5和图6可知，各裂纹起裂荷载均随t增加而逐渐减小。当t>1时，相同t值下中心裂纹的起裂荷载始终小于外裂纹尖端的起裂荷载，且外裂纹外尖端的起裂荷载最大，说明中心裂纹最易起裂，外裂纹外尖端最难起裂。
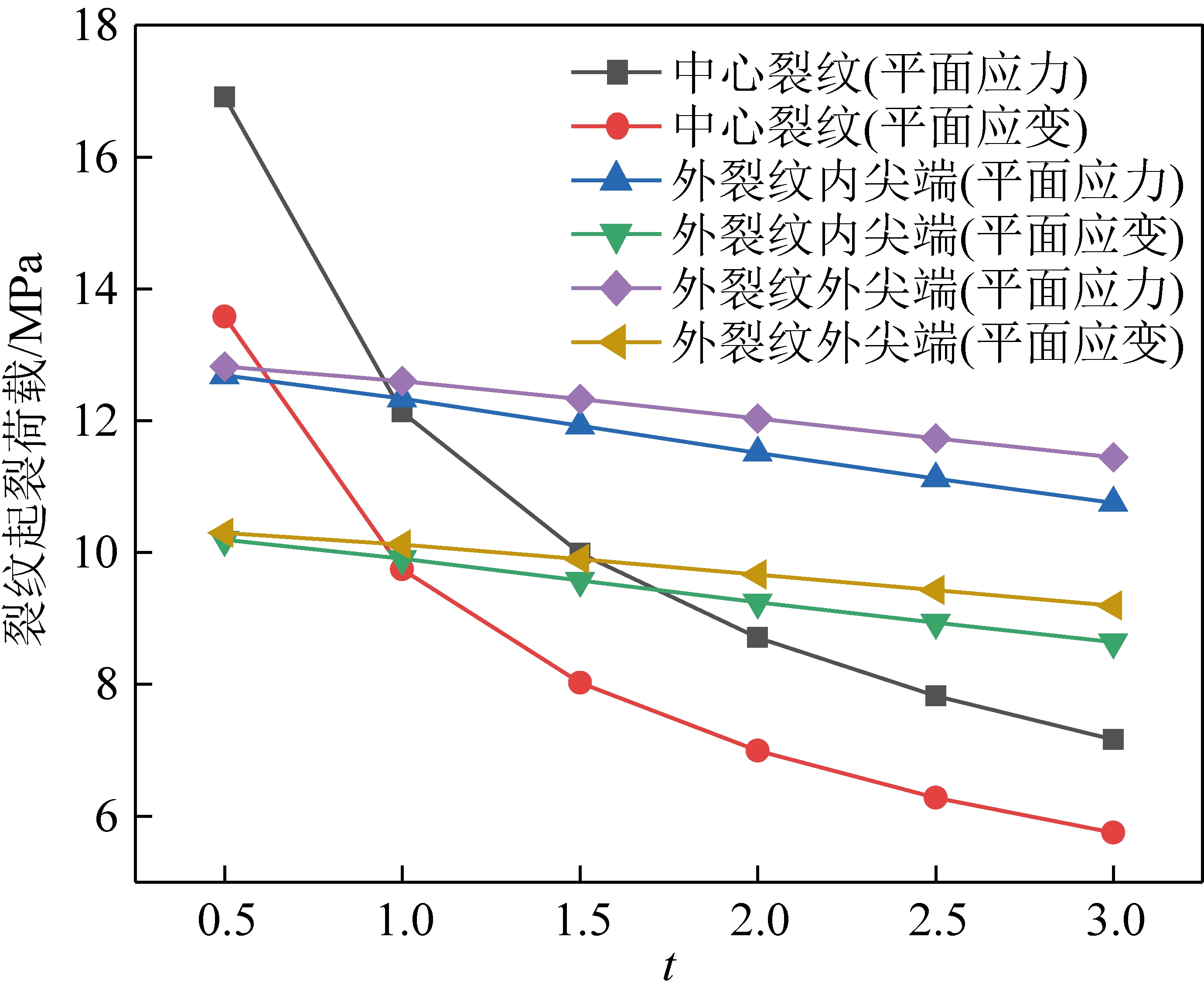
图6 单轴压缩下裂纹起裂荷载随t值的变化曲线(η=1)
Fig.6 Curve of crack initiation load with value t under uniaxial compression(η=1)
相同条件下，平面应力状态下的起裂荷载大于平面应变状态下的起裂荷载，这是因为平面应力状态下塑性区较大，使裂纹扩展阻力增加，提高了岩石的断裂韧性。裂纹面完全闭合时，所需的起裂荷载比裂纹面张开的起裂荷载大，这是因为随着裂纹闭合度的增加，裂纹面接触面积增大，裂纹面克服摩擦力做功越大，裂纹发生相对滑动越困难，因此所需的起裂荷载越大。
中心裂纹与外裂纹内、外尖端的起裂荷载对裂纹长度比t的灵敏度不同，当t从0.5增加到3.0时，中心裂纹的起裂荷载减小57.6%，外裂纹内尖端减小15.2%，外裂纹外尖端减小10.7%。可见，中心裂纹对裂纹长度比t最敏感，外裂纹内尖端次之，外裂纹外尖端最不敏感。
设a=5，b=15，c=25，其他条件与4.1节相同，裂纹倾角β分别取10°,20°,30°,40°,45°,50°,60°,70°和80°。计算不同裂纹倾角β下张开型受压裂纹(η=0)和闭合型受压裂纹(η=1)的起裂荷载，计算结果如图7,8所示。
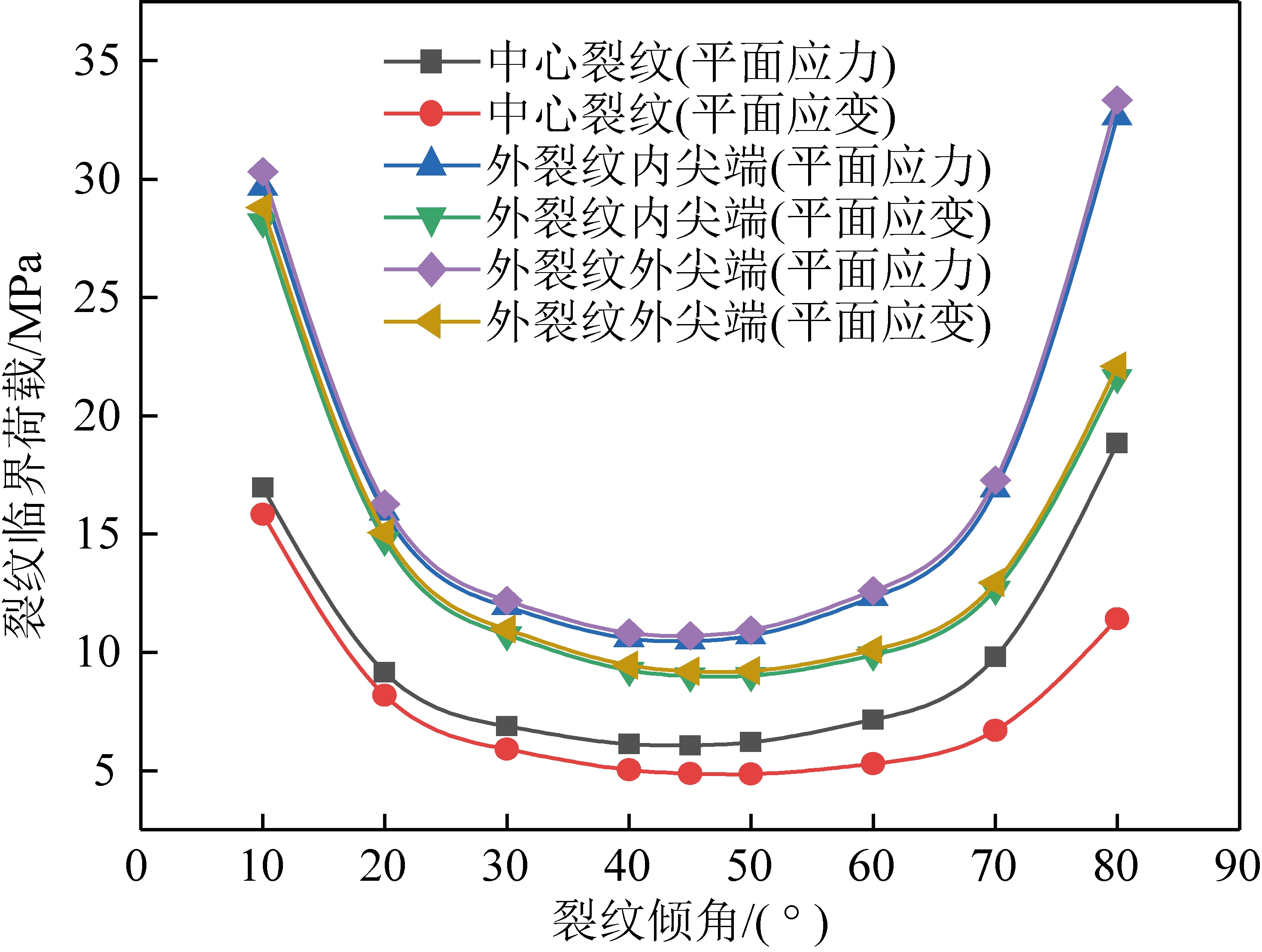
图7 单轴压缩下裂纹起裂荷载随裂纹倾角β的 变化曲线图(η=0)
Fig.7 Curves of crack initiation load with crack inclination β under uniaxial compression(η=0)
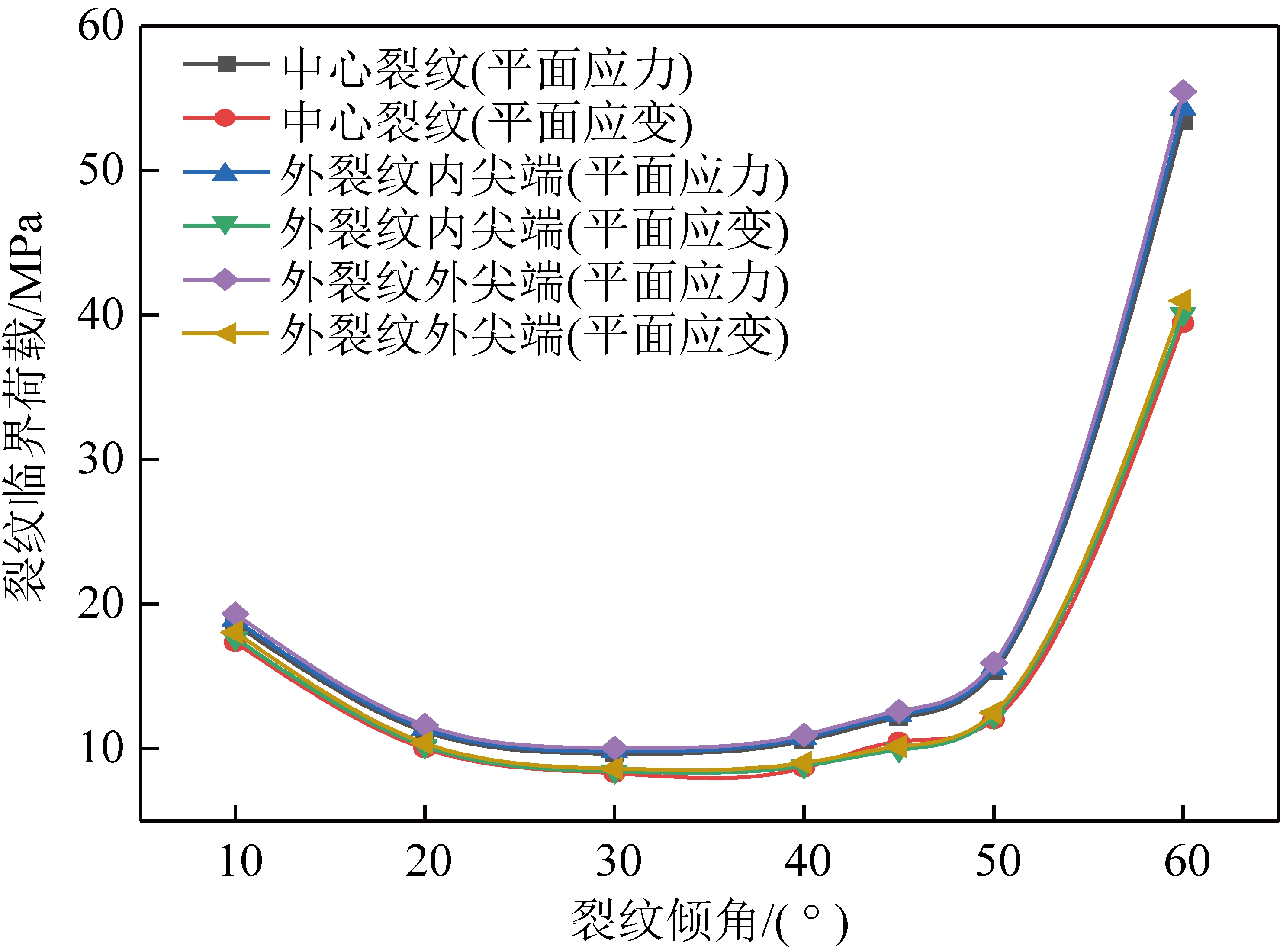
图8 单轴压缩下裂纹起裂荷载随裂纹倾角β的变化 曲线图(η=1)
Fig.8 Curves of crack initiation load with crack inclination β under uniaxial compression(η=1)
从图7，8可知，受压状态下，裂纹起裂荷载先随着裂纹倾角增加而减小，后随裂纹倾角增加而增加。受压状态下，裂纹面闭合度不同，裂纹起裂荷载也不同，完全闭合裂纹的起裂荷载远大于张开型裂纹。
从力学角度解释，单轴受压状态下，裂纹的起裂受Ⅱ型应力强度因子控制，Ⅱ型应力强度因子随裂纹倾角先增大后减小。对于张开型受压裂纹，由图7可知，裂纹起裂荷载在裂纹倾角为45°时取最小值。对于完全闭合裂纹，裂纹起裂荷载最小值对应的裂纹倾角与裂纹面上的摩擦因数有关。对于本文选取的摩擦因数f=0.5，在裂纹倾角31.7°时，所需起裂荷载最小。
设中心裂纹与外裂纹的裂纹间距s′分别取2,4,6,8,10,14和20 mm，其他条件与4.1节相同。计算不同裂纹间距下张开型裂纹(η=0)和完全闭合型裂纹(η=1)的起裂荷载，计算结果如图9,10所示。
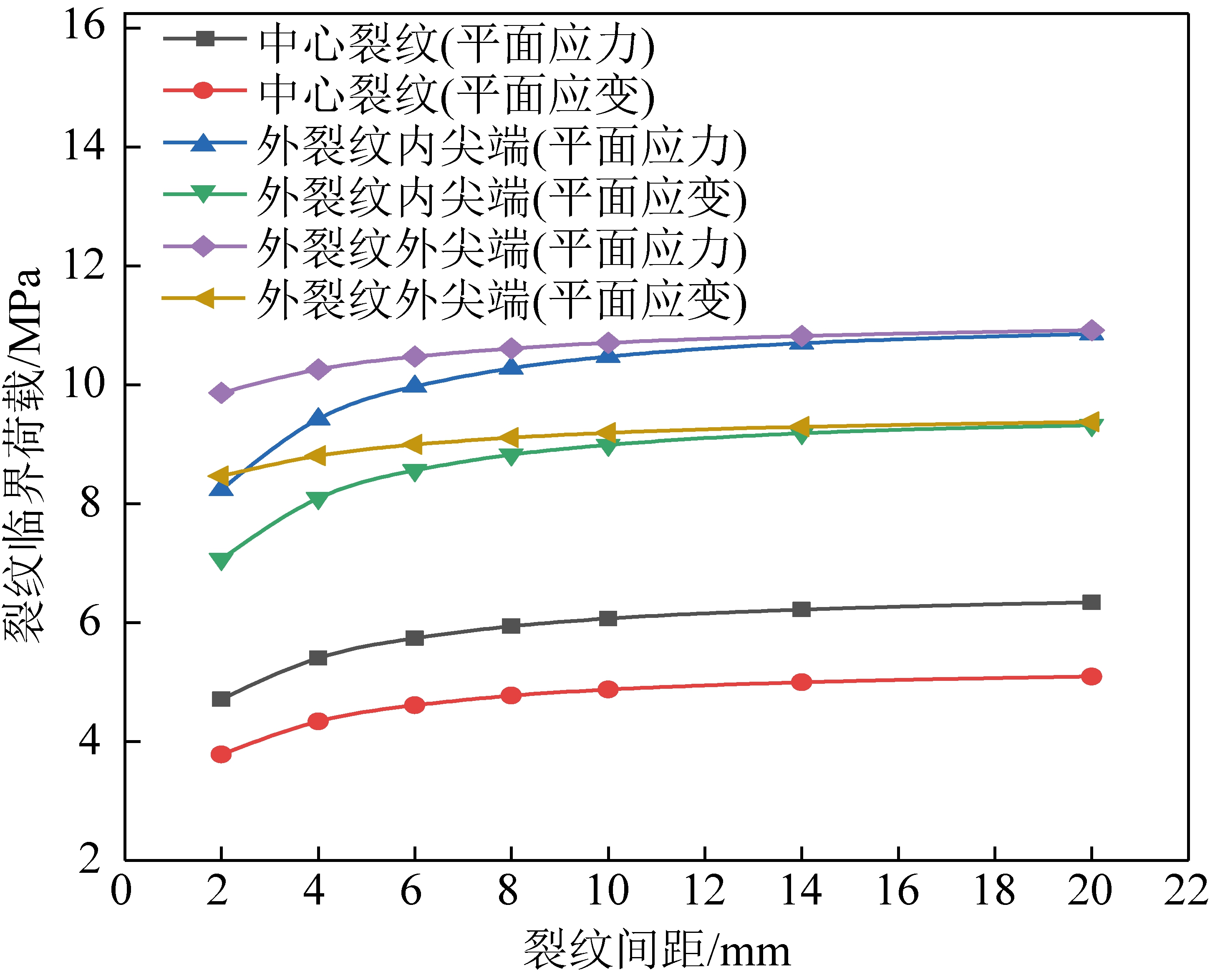
图9 单轴压缩下裂纹起裂荷载随裂纹间距s′的变化 曲线(η=0)
Fig.9 Curves of crack initiation load with crack spacing s′ under uniaxial compression(η=0)
图10 单轴压缩下裂纹起裂荷载随裂纹间距s′的变化 曲线(η=1)
Fig.10 Curves of crack initiation load with crack spacing s′ under uniaxial compression(η=1)
对比图9和10可知，受压状态下张开型裂纹(η=0)和完全闭合型裂纹(η=1)的起裂荷载随裂纹间距变化规律相同:随着裂纹间距的增加，裂纹起裂荷载逐渐增加。这说明，裂纹间距越大，裂纹越难起裂。
中心裂纹与外裂纹内、外尖端的起裂荷载对裂纹间距s′的灵敏度不同，当s′从2 mm增加到20 mm时，中心裂纹的起裂荷载增加34.7%，外裂纹内尖端增加31.9%，外裂纹外尖端增加10.7%。可见，中心裂纹对裂纹间距s′最敏感，外裂纹内尖端次之，外裂纹外尖端最不敏感。
为了验证理论计算的合理性，选择文献[3]中试件7和试件10的开裂试验数据作为算例，来计算分析裂纹的起裂荷载。
该试验采用相似材料模型实验，试件由水、泥、砂混合人工制备而成，在制作试件过程中采用厚度0.5 mm的薄不锈钢片预制裂纹，试验在3 000 kN超高刚性伺服试验机设备上完成，单轴压缩试验过程中采用位移控制方式，加载速率为0.2 mm/min。试验过程中，采用FASRCAM SA1.1高速摄影机对试件的整个加载过程进行图像信息采集得到裂纹起裂情况。
含三共线预制裂纹的试件7和试件10的试验模型如图11所示。
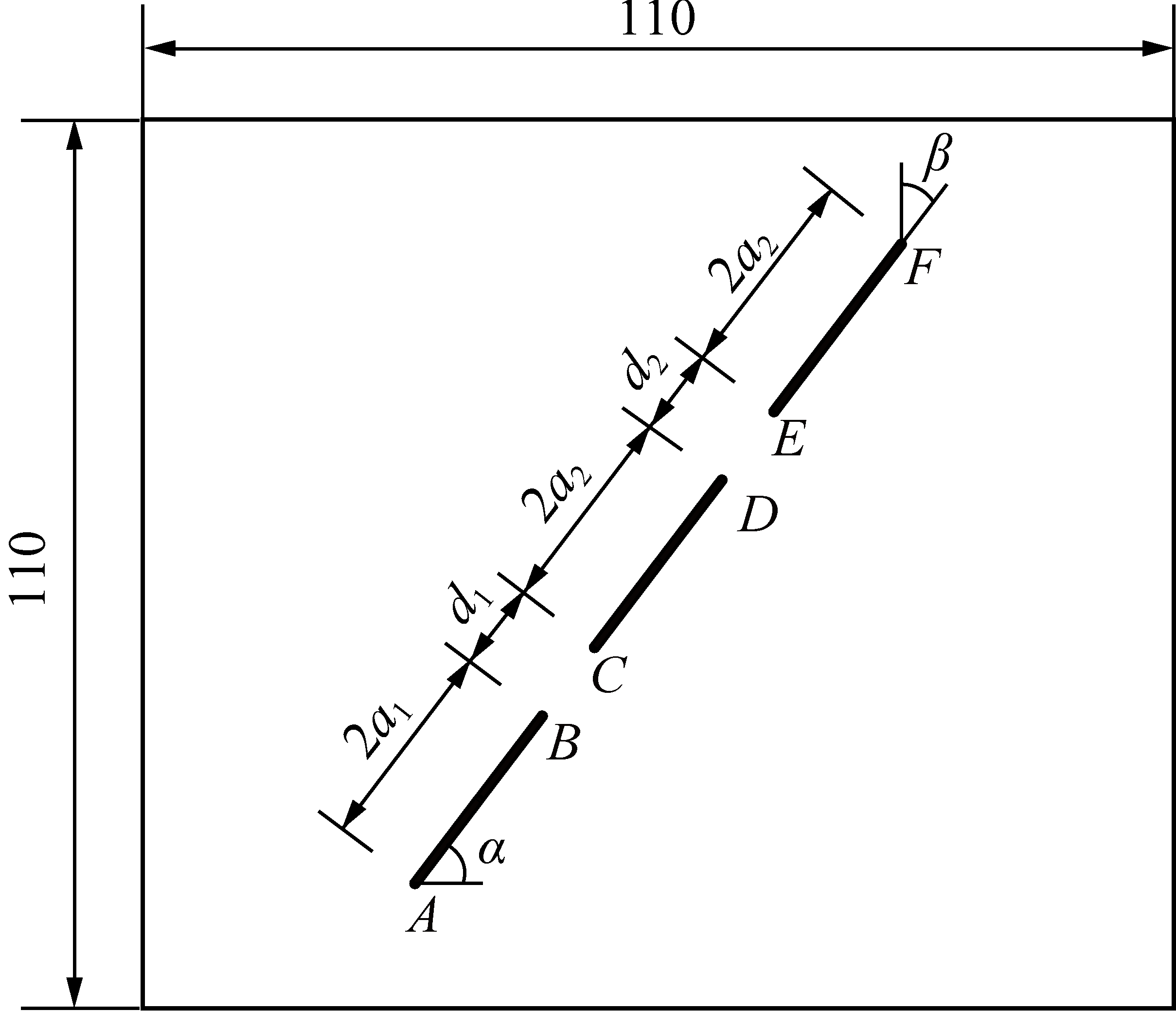
图11 模型示意[3]
Fig.11 Model diagram[3]
图11中裂纹面与受力方向的夹角β=π/4，裂纹角α=π/4，主裂纹半长a1=18 mm，次裂纹半长a2=12 mm。试件7:d1=d2=18 mm。试件10:d1=d2=12 mm，其中，d1为裂纹尖端B到C之间的距离;d2为裂纹尖端D到E之间的距离。通过高速摄影机拍得的最终破坏形态如图12,13所示，通过伺服试验机直接测得的起裂荷载和峰值强度见表1。
图12 试件7最终破坏形态 Fig 12 Final failure form of specimen 7
图13 试件10最终破坏形态 Fig 13 Final failure form of specimen 10
表1 起裂荷载和峰值强度
Table 1 Crack initiation load and peak strength
参数试件7试件10起裂荷载试验值/MPa25.123.6峰值强度试验值/MPa46.744.8
从试件7和试件10的破坏形态可发现B端、C端、D端和E端发育的次生剪切裂纹贯通了岩桥，2个岩桥均发生剪切破坏。A端和F端发育的翼裂纹在应力作用下沿加载方向朝试件端部扩展。岩桥的贯通剪切破坏和翼裂纹扩展造成试件7和试件10的破坏。
要计算裂纹起裂荷载还需知道裂纹的断裂韧度、裂纹面摩擦因数和裂纹面闭合度等相关参数，由于该文献中没有测量数据，本文以常见的参数取值范围为标准，参考文献[28]假设断裂韧度KⅠc=KⅡc=2 MN/m3/2，裂纹面摩擦因数f=0.5，裂纹面闭合度η=1，裂纹断裂选择最小塑性区半径准则。
由于裂纹受压闭合，Ⅰ型应力分量的奇异性不复存在，预置裂纹尖端应力强度因子KⅠ=0，按平面应力状态求解裂纹起裂角θc=70.43°。对于试件10，计算得到各裂纹尖端起裂荷载为:A端PA=26.24 MPa，B端PB=25.56 MPa，C端PC=26.97 MPa，D端PD=28.56 MPa，E端PE=29.03 MPa，F端PF=29.57 MPa。由于B端所需起裂荷载最小，B端最先起裂，所以将PB作为起裂荷载。同理可以计算试件7的起裂荷载，详见表2。由表2可知，理论计算得到的起裂荷载与试验中测得的起裂荷载相对偏差都在10%以下，两者比较吻合，从而可以证明理论计算的合理性。同时试件7的裂纹间距大于试件10的裂纹间距，试件7的裂纹起裂荷载大于试件10的裂纹起裂荷载，从而，间接证明了4.3节中随着裂纹间距的增加，裂纹起裂荷载逐渐增加的结论。
表2 起裂荷载试验值和理论计算值
Table 2 Test and theoretical values of crack initiation load
参数试件7试件10起裂荷载试验值/MPa25.123.6起裂荷载理论计算值/MPa27.3225.56相对偏差/%8.88.3
虽然理论计算得到的裂纹起裂荷载和试验的结果较为相符，但仍有一定的差别，这是因为参考文献[3]中无断裂韧度、摩擦因数、闭合度实测值，本文根据参考文献[28]取值，与实际参数可能有一定偏差。
(1)平面应力状态下受压裂纹的起裂角为定值70.43°，平面应变状态下受压裂纹的起裂角随硬化系数和泊松比的增大而增大。
(2)受压裂纹起裂荷载与中心裂纹长度与外裂纹长度的比值t成反比，与裂纹间距s′成正比，随裂纹倾角β的增加，先减小后增大，且受压裂纹的极值点与裂纹面的摩擦效应有关。
(3)中心裂纹对裂纹长度比t和裂纹间距s′最敏感，外裂纹内尖端次之，外裂纹外尖端对裂纹长度比t和裂纹间距s′最不敏感。
(4)受压裂纹的起裂荷载与裂纹面的摩擦因数和闭合度有关，相同条件下，张开型受压裂纹起裂荷载小于完全闭合型受压裂纹的起裂荷载。平面应力状态下的起裂荷载大于平面应变状态下的起裂荷载。
本文工作仅仅是初步理论研究，其应用于复杂的实际工程尚需进行更多工作，这也是以后要进行的研究方向。另外，本文研究主要针对裂纹的二维应力状态进行，更加复杂的三维应力状态分析也将是以后的研究工作。
[1] XUE Junhua,WANG Hanpeng,ZHOU Wei,et al.Experimental research on overlying strata movement and fracture evolution in pillarless stress-relief mining[J].International Journal of Coal Science & Technology,2015,2(1):38-45.
[2] 李克钢,王庭,秦庆词,等.主、次裂隙对岩石变形破坏机制的影响研究[J].中国安全生产科学技术,2019,15(2):181-186.
LI Kegang,WANG Ting,QIN Qingci,et al.Study on the influence of primary and secondary fractures on rock deformation and failure mechanism[J].Journal of Safety Science and Technology,2019,15(2):181-186.
[3] 席婧仪.水泥基脆性材料不等长裂纹相互作用与扩展规律研究[D].北京:中国矿业大学(北京),2015.
XI Jingyi.Study on the interaction and propagation of unequal length cracks in cement-based brittle materials[D].Beijing:China University of Mining and Technology(Beijing),2015.
[4] 刘红岩.考虑T应力的岩石压剪裂纹起裂机理[J].岩土工程学报,2019,41(7):1296-1302.
LIU Hongyan.Fracture initiation mechanism of rock compression shear crack considering T stress[J].Chinese Journal of Geotechnical Engineering,2019,41(7):1296-1302.
[5] 刘洋,何沛田,赵明阶.基于损伤断裂理论的岩石破坏机理研究[J].地下空间与工程学报,2006(6):1076-1080.
LIU Yang,HE Peitian,ZHAO Mingjie.Study on rock failure mechanism based on damage fracture theory[J].Chinese Journal of Underground Space and Engineering,2006(6):1076-1080.
[6] 李宏福,邢闯锋,李欣.单轴压缩下岩体斜裂纹断裂特性研究[J].水利与建筑工程学报,2014,12(3):1-4.
LI Hongfu,XING Chuangfeng,LI Xin.Fracture characteristics of oblique cracks in rock mass under uniaxial compression[J].Journal of Water Resources and Architectural Engineering,2014,12(3):1-4.
[7] 郭奇峰,武旭,蔡美峰,等.预制裂隙花岗岩的裂纹起裂机理试验研究[J].煤炭学报,2019,44(S2):476-483.
GUO Qifeng,WU Xu,CAI Meifeng,et al.Experimental study on crack initiation mechanism of prefabricated fractured granite[J]. Journal of China Coal Society,2019,44(S2):476-483.
[8] CAO P,LIU T,PU C,et al.Crack propagation and coalescence of brittle rock-like specimens with pre-existing cracks in compression[J].Engineering Geology,2015,187:113-121.
[9] 徐丽海.基于DIC类岩石材料裂纹扩展试验与数值模拟研究[D].贵阳:贵州大学,2018.
XU Lihai.Research on crack growth test and numerical simulation of rock materials based on DIC[D].Guiyang:Guizhou University,2018.
[10] 李存宝,谢和平,谢凌志.页岩起裂应力和裂纹损伤应力的试验及理论[J].煤炭学报,2017,42(4):969-976.
LI Cunbao,XIE Heping,XIE Lingzhi.Experiment and theory of shale initiation stress and crack damage stress[J].Journal of China Coal Society,2017,42(4):969-976.
[11] 杨庆,刘元俊.岩石类材料裂纹扩展贯通的颗粒流模拟[J].岩石力学与工程学报,2012,31(S1):3123-3129.
YANG Qing,LIU Yuanjun.Particle flow simulation of crack propagation and penetration in rock materials[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(S1):3123-3129.
[12] 李铮,郭德平,周小平,等.模拟岩石中裂纹扩展连接的近场动力学方法[J].岩土力学,2019,40(12):4711-4721.
LI Zheng,GUO Deping,ZHOU Xiaoping,et al.Near field dynamic method for simulating crack growth and connection in rock[J]. Rock and Soil Mechanics,2019,40(12):4711-4721.
[13] 孙翔,刘传奇,薛世峰.有限元与离散元混合法在裂纹扩展中的应用[J].中国石油大学学报(自然科学版),2013,37(3):126-130,136.
SUN Xiang,LIU Chuanqi,XUE Shifeng.Application of mixed finite element and discrete element method in crack propagation[J]. Journal of China University of Petroleum (Edition of Natural Science),2013,37(3):126-130,136.
[14] 周小平,杨海清,董捷.压应力状态下多裂纹扩展过程数值模拟[J].岩土工程学报,2010,32(2):192-197.
ZHOU Xiaoping,YANG Haiqing,DONG Jie.Numerical simulation of multiple crack growth under compressive stress[J].Chinese Journal of Geotechnical Engineering,2010,32(2):192-197.
[15] 赵程,田加深,松田浩,等.单轴压缩下基于全局应变场分析的岩石裂纹扩展及其损伤演化特性研究[J].岩石力学与工程学报,2015,34(4):763-769.
ZHAO Cheng,TIAN Jiashen,SONG Tianhao,et al.Study on crack growth and damage evolution of rock based on global strain field analysis under uniaxial compression[J].Chinese Journal of Rock Mechanics and Engineering,2015,34(4):763-769.
[16] 郦正能,关志东,张纪奎,等.应用断裂力学[M].北京:北京航空航天大学出版社,2012.
LI Zhengneng,GUAN Zhidong,ZHANG Jikui,et al.Applied fracture mechanics[M].Beijing:Beihang University Press,2012.
[17] 俞茂宏,彭一江.强度理论百年总结[J].力学进展,2004(4):529-560.
YU Maohong,PENG Yijiang.A century’s summary of strength theory[J].Advances in Mechanics,2004(4):529-560.
[18] 董晗.单轴压缩下岩石斜裂纹扩展规律研究[D].重庆:重庆大学,2016.
DONG Han.Study on the law of oblique crack propagation in rock under uniaxial compression[D].Chongqing:Chongqing University,2016.
[19] IRWIN G R.Fracture,encyclopaedia of physics[M].Berlin:Springer Berlin Heidelberg,1958:551-589.
[20] 甘卫平,王慧敏,韩德光.裂纹尖端塑性区修正公式的改进[J].轻合金加工技术,2001(2):15-18.
GAN Weiping,WANG Huimin,HAN Deguang.Improvement of the modified formula of the plastic zone at the crack tip[J]. Light Alloy Fabrication Technology,2001(2):15-18.
[21] LI Huigui,LI Huamin.Mechanical properties and acoustic emission characteristics of thick hard roof sandstone in Shendong coal field[J].International Journal of Coal Science & Technology,2017,4(2):147-158.
[22] KHAN S M A,KHRAISHEH M K.A new criterion for mixed mode fracture initiation based on the crack tip plastic core region[J]. International Journal of Plasticity,2004,20(1):55-84.
[23] 任利,朱哲明,谢凌志,等.复合型裂纹断裂的新准则[J].固体力学学报,2013,34(1):31-37.
REN Li,ZHU Zheming,XIE Lingzhi,et al.New criteria for composite crack fracture[J].Chinese Journal of Solid Mechanics,2013,34(1):31-37.
[24] ZHU Z.An Alternative form of propagation criterion for two collinear cracks under compression[J].Mathematics and Mechanics of Solids,2009,14(8):727-746.
[25] 刘培杰,宋明辉.椭圆函数与模函数[M].哈尔滨:哈尔滨工业大学出版社,2012.
[26] DOU Linming,MU Zonglong,LI Zhenlei,et al.Research progress of monitoring,forecasting,and prevention of rockburst in underground coal mining in China[J].International Journal of Coal Science & Technology,2014,1(3):278-288.
[27] 武旭,王帆,席迅,等.正交型交叉裂隙岩石强度特征与破裂机理试验研究[J].煤炭学报,2020,45(7):2681-2690.
WU Xu,WANG Fan,XI Xun,et al.Experimental study on the strength characteristics and fracture mechanism of orthogonal cross-fractured rocks[J].Journal of China Coal Society,2020,45(7):2681-2690.
[28] 熊飞,靖洪文,苏海健,等.尖端相交裂隙砂岩强度与破裂演化特征试验研究[J].煤炭学报,2017,42(4):886-895.
XIONG Fei,JING Hongwen,SU Haijian,et al.Experimental study on the strength and fracture evolution characteristics of sandstone with tip intersecting fractures[J].Journal of China Coal Society,2017,42(4):886-895.