
移动阅读

移动阅读
TANG Shibin,SUN Kang,ZHANG Yongliang,et al. Fracture growth of Brazilian disk with open/closed cracks[J]. Journal of China Coal Society,2021,46(11):3459-3469.
天然岩体中包含不同类型的不连续性结构面,如裂隙、节理、层理、断层和剪切带等。这些不连续结构面在外荷载的作用下极易引起裂纹的起裂、扩展、贯通以及断层的滑移等,显著影响岩体的稳定性。荷载作用下裂纹扩展过程不仅与裂隙的性质(例如长度、位置和方向)有关,也与载荷的类型、大小和方向有关。在岩体工程中,岩体的失稳破坏与裂纹的发育、扩展及贯通密切相关。因此,裂纹扩展的机理及特性的研究具有重要的工程意义。为了便于叙述和理解,笔者将岩石中含有的初始裂隙、节理、层理、断层等统称为“裂隙”,而将裂隙在力的作用下扩展所形成破裂称为“裂纹”。
巴西圆盘作为岩石力学试验中重要的试样,除了可以测试包含中心裂纹的岩石试样的静态和动态断裂韧性以外,还可以用来研究岩石中裂纹的起裂、扩展和贯通过程及特征。目前,有关含初始裂隙巴西圆盘的裂纹扩展研究,主要包括针对天然岩石或相似材料试样的研究。在含初始裂隙的巴西圆盘试样中,由于岩石和类似岩石的材料抗拉强度较低[1],裂纹起裂和扩展过程比较迅速,通常起裂方向遵循(近似)平行于最大压缩载荷的方向[2]。AL-SHAYEA等[3]试验研究了在拉剪混合模式下,荷载和温度对含不同倾角裂隙的脆性石灰岩巴西圆盘试样的裂纹起裂及扩展特性的影响。GHAZVINIAN等[4]开展了石膏材料预制巴西圆盘的试验研究,探讨了裂隙倾角和长度对脆性材料断裂过程的影响。ALIHA等[5]通过具有相同裂隙长径比的巴西圆盘试验发现,裂纹扩展不受圆盘尺寸的影响。HAERI等[6]使用混凝土预制初始裂隙的巴西圆盘,研究了不同裂隙倾角对裂纹扩展的影响。SHARAFISAF等[7]通过数字图像识别方法(DIC)对含张开裂隙和填充裂隙的巴西圆盘最大主应变和最大剪切应变进行测量,研究裂隙倾角及填充材料对巴西圆盘裂纹扩展影响。
除了试验方法,越来越多的数值模拟方法也应用到岩石等脆性材料的裂纹扩展研究中,如有限元方法(FEM)、不连续位移方法(DDM)、离散元方法(DEM)、相场法(PFM)等。EFTEKHARI等[8]和DONG等[9]对含闭合裂隙的岩石试样进行了裂纹扩展的模拟研究,通过在断裂准则中引入非奇异应力(也称为T-应力)对裂纹扩展的影响,得到了满意的结果,但T-应力计算较复杂,尤其是闭合裂隙间的T-应力计算。HAERI等[6]使用不连续位移法模拟了含闭合裂隙的巴西圆盘的裂纹扩展,但基于传统断裂方法模拟得到的裂纹扩展轨迹呈现出锯齿状,与试验结果不符。SARFARAZI等[7]利用PFD2D对多组含不同倾角平行非闭合裂隙的巴西圆盘进行模拟,裂纹的扩展和贯通很好地说明了裂纹的产生以及扩展路径。ZHOU等[10]通过相场法对平行裂隙数量及裂隙间隔对裂纹扩展影响进行研究,但使用相场法计算得到的裂纹扩展,其裂纹面之间并没有产生物理分离,只是数学分离。
由于含闭合裂隙试样制备比较困难,大部分试验方法针对张开裂隙进行研究。目前有关压剪应力状态下闭合型裂隙的数值研究较少,部分结果[6,11]表明,计算得到的闭合裂纹扩展路径呈锯齿状,而相对均匀的准脆性材料试验[4,6]却表明,即使是闭合裂隙,裂纹扩展轨迹也呈现出路径光滑的特征。因此,为了研究不同类型裂隙对巴西圆盘裂纹扩展行为特征的影响规律,需要研究能同时计算张开和闭合裂隙的断裂准则。笔者在自主研发的岩石断裂模拟FACT(Failure Analysis and Computing Toolkit)系统中集成了MTS准则和改进的断裂模拟方法,并开展了含不同类型裂隙的巴西圆盘裂纹扩展过程研究,从而分析裂纹的起裂、扩展及贯通规律,其中FACT系统实现了几何模型构建、网格划分、裂纹扩展模拟以及后处理显示等全过程的处理。
天然岩体中包含了大量的初始裂隙,如图1所示。这些裂隙在荷载作用下产生的扩展、贯通等,导致岩体工程灾变。正如前文所述,巴西圆是岩石力学参数测量中非常重要的一种方法,不仅用于抗拉强度的测试,还可以研究岩石的裂纹扩展特性,如图2的试验结果所示。

图1 含裂隙的天然岩体
Fig.1 Natural rock masses with flaws

图2 含有初始裂隙的巴西圆盘试验结果[6]
Fig.2 Experimental results of different Brazilian disc tests with initial fault[6]
天然裂隙有的处于张开状态,有的处于闭合状态。因此,笔者重点研究含张开裂隙(图3(a))和闭合裂隙(图3(b))巴西圆盘裂纹扩展规律及机理。此外,各种天然材料由于风蚀、搬运和沉积作用下填充原有的张开裂隙,产生了含填充材料的裂隙(图1(b))(以下称为“填充裂隙”)。因此,笔者也对含填充裂隙的巴西圆盘(图3(c))进行有关研究。

图3 3种数值模型
Fig.3 Three types of numerical models
计算所需材料参数及裂纹宽度和长度均取自文献[12],巴西圆盘材料参数见表1,填充裂隙材料参数见表2。计算模型的加载方式采用竖向位移加载,加载平台与巴西圆盘之间摩擦因数为1.0,初始裂隙面之间无摩擦,裂隙倾角β=45°,其他具体尺寸如图3所示。值得注意的是,模型中加载平台与巴西圆盘之间为接触条件,且裂纹面之间也可能处于接触状态,此时采用罚函数方法进行接触迭代计算,当接触的侵入量小于某个预设值后便停止迭代,认为其接触计算满足要求。
表1 数值模型所用的力学参数[12]
Table 1 Mechanical properties of numerical model

弹性模量/GPa泊松比单轴抗压强度/MPa抗拉强度/MPa密度/(kg·m-3)1.375±0.0250.285±0.0156.35±0.052.38±0.051 500
表2 填充材料的力学性质参数[12]
Table 2 Mechanical properties of filled material

弹性模量/GPa泊松比单轴抗压强度/MPa抗拉强度/MPa密度/(kg·m-3)1.13±0.020.2±0.011.28±0.10.3±0.050.9
目前有关岩石裂纹扩展的判据主要有:① 最大周向应力准则[13](MTS准则);② 最大能量释放率准则[14](G准则);③ 应变能密度因子准则[15](S准则)。还有诸如压剪断裂理论[16]、双参数符合应力理论[17]、最小J2准则[18]等。其中,MTS准则形式简单,其运用至今仍较为普遍,尤其针对岩石这类抗拉强度较低的材料,MTS准则更接近于裂纹扩展的实际情况。
在线弹性断裂力学中,二维复合型裂纹在局部坐标系(图4(a))下的应力为

(1)
式中,KⅠ和KⅡ分别为Ⅰ型和Ⅱ型应力强度因子;θ为裂纹的倾角;σrr为径向应力;σθθ为周向应力;τrθ为剪应力;r为距离裂纹尖端的半径。
MTS准则判断裂纹扩展方向的断裂准则公式为
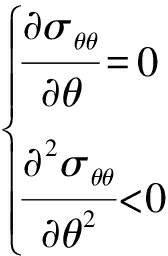
(2)
将式(2)代入式(1)可得到裂纹扩展角度θc为
(3)
基于MTS准则,笔者针对含不同类型初始裂隙的巴西圆盘进行了裂纹扩展研究。由式(3)可以看出,θc的计算与裂纹尖端的应力强度因子KⅠ和KⅡ密切相关。目前有限元数值计算中强度因子计算方法主要包括J-积分法和位移法等,而通过J-积分法衍生出M-积分和区域等效积分法。和区域等效积分类似,相互积分法可以通过面积分(体积分)计算平面(三维)问题的强度因子;此外,相比于位移法,相互积分法计算强度因子所需单元数少,计算精度更高。因此,笔者采用相互积分法对裂纹尖端的应力强度因子进行计算。由于裂纹尖端附近为应力集中区域,因此单元划分采用1/4节点奇异单元(图4(b))。

图4 裂纹尖端局部坐标系及裂纹尖端单元类型
Fig.4 Local coordinate system at crack tip and the type of the crack tip elements
在进行裂纹扩展计算时,随着位移荷载的增加,裂纹尖端发生扩展,θc由式(3)计算得到。如图5所示(θ1,θ2,θ3为当前裂纹扩展方向与上一次裂纹方向之间的夹角),在θc方向增加裂纹扩展长度Δa,得到

图5 裂纹扩展路径模拟示意
Fig.5 Diagram of crack propagation path simulation
新的裂纹尖端。然后基于新的裂纹尖端重新构建有限元模型,再进行加载计算。重复以上过程,直至获得整个裂纹扩展轨迹。笔者根据上述方法,编制相关的有限元计算程序,并且开展了如下的研究工作。
断裂力学方法最初被应用于材料力学领域,其荷载形式主要以拉伸为主。但对于含初始闭合裂隙的巴西圆盘采用压缩加载方式时,不同Δa得到的裂隙扩展路径呈现出锯齿状。
为了进一步分析不同荷载形式对裂纹扩展路径的影响作用,首先使用提出的断裂模拟方法对含闭合裂隙的方板(图6(a))进行单轴拉伸断裂模拟,方板尺寸为80 mm×80 mm,初始裂隙长度为3 mm,材料参数见表1,取Δa分别为1.0,2.0和3.0 mm。由图6(b)可以看出,不同Δa下,计算得到的裂纹扩展路径基本相同。裂纹扩展路径逐步转向垂直于最大拉应力的方向,且整个扩展轨迹并未出现锯齿状现象。也即表明,传统的断裂准则能够很好地模拟拉伸荷载引起的裂纹扩展,即使是Δa较大时也不会引起较大的偏差。尽管图7所示的巴西圆盘产生的裂纹扩展亦是拉伸开裂,但其承受的压缩荷载,裂纹扩展路径表现出与拉伸荷载不同的特点。

图6 含闭合裂隙的模型示意及裂纹扩展路径模拟
Fig.6 Plate model with closed fault and numerical modeling results of fracture growth path

图7 MTS准则计算得到的裂纹扩展路径
Fig.7 Fracture growth path modeled by MTS criterion
为了更仔细地分析裂纹扩展轨迹变化特征及规律,对其扩展角度以及应力强度因子变化进行了分析。从图8(a),(b)中张开裂隙的强度因子和扩展角度的变化规律中可以看出,当Δa较大时(Δa=1.0 mm),KⅠ始终保持正值,而KⅡ则随着裂纹扩展出现正负震荡。由式(3)可知,θc受KⅡ的正负震荡影响,也出现正负变化,进而产生锯齿状裂纹扩展路径。当Δa较小时(Δa=0.5 mm),计算得到张开裂隙的KⅡ逐渐趋近于0,裂纹扩展只受控于KⅠ的变化,而KⅠ在整个裂纹扩展过程中始终保持为正数,因而得到裂纹扩展的方向始终偏向最大主应力方向。从图8(c),(d)中闭合裂纹的强度因子和扩展角度的变化规律中可以看出,当Δa较大时,KⅡ的正负震荡导致裂纹扩展路径呈现锯齿状。即使是Δa减小到0.5 mm,在裂纹扩展初期亦出现KⅡ的正负震荡。当然,如果继续减小Δa,KⅡ的正负震荡特性也会减弱,但问题在于,数值计算无法实现太小Δa的裂纹扩展模拟。进一步减小Δa将导致网格划分、强度因子计算、计算耗时等一系列的计算难题。
综上所述,传统断裂准则模拟拉伸荷载引起的裂纹扩展表现良好,但在模拟压缩荷载诱发的裂纹扩展方面却往往出现偏差或错误。完全依靠减小裂纹扩展路径的方法无法做到快速、有效的裂纹扩展路径的模拟,针对多裂纹的扩展模拟更难以实现。由于工程岩体主要是处于自重、构造应力等压缩荷载作用,因此需要寻求更为有效的断裂模拟方法。

图8 MTS准则计算获得的强度因子和扩展角度变化
Fig.8 SIFs and fracture growth angle modeled by MTS Criterion
传统断裂模拟方法需要计算强度因子KⅠ和KⅡ,因此,裂纹扩展路径的计算精度与KⅠ和KⅡ的计算结果密切相关。压缩荷载作用下计算得到的KⅡ正负震荡是导致裂纹扩展路径锯齿状的根本原因。事实上,由式(1)~(3)建立的MTS准则只考虑了裂纹尖端应力场泰勒级数展开式的奇异项,忽略了展开式中的常数项(非奇异应力,亦称为T-应力)以及高阶的O(r1/2)项。尽管高阶项可以忽略,但常数项对岩石的裂纹扩展有着明显的影响。笔者[19-22]曾探讨了T-应力对裂纹扩展的影响作用,结果表明,当考虑T-应力时,修正的断裂准则对裂纹扩展路径的捕捉比传统的MTS准则有较大的改善,模拟得到的裂纹扩展路径呈现光滑特征[9]。进一步地,笔者也提出了计算岩石类材料在压缩应力状态下T-应力的数值求解方法[22]。尽管考虑了T-应力的断裂准则能够很好地模拟压缩作用下张开、闭合裂纹扩展,但其计算较繁琐,不仅要计算强度因子KⅠ和KⅡ,还要计算T-应力,当裂纹面闭合后,还存在沿着和垂直裂纹面2个方向的T-应力计算。事实上,裂纹的扩展主要取决于裂纹尖端附近的局部应力场,该应力场可以通过数值计算获得,裂纹尖端可以采用高精度的单元类型(如图4所示的奇异单元)以及加密局部网格,可以获得更高的计算精度。裂纹扩展是其尖端的应力状态达到了破坏条件的宏观表现。通过对裂纹尖端应力的计算,可以获得其局部坐标系下σθθ,σrr,τrθ等应力的分布。基于此,笔者尝试建立基于局部应力状态分析的改进断裂准则及相关的裂纹扩展模拟方法。根据式(2)可知,∂σθθ/∂θ=0实际上等价于τrθ= 0。因此,获得裂纹的起裂角度就是需要找出裂纹尖端附近τrθ= 0的方向。传统的断裂模拟方法是通过求得裂纹尖端的KⅠ和KⅡ,然后代入式(1)中的τrθ= 0进行计算,这就必然会遇到压缩荷载作用下计算的KⅡ正负震荡的问题,导致裂纹扩展路径锯齿状(图8(b),(d))。笔者利用τrθ= 0进行起裂角度计算的原理,首先通过高精度的数值计算获得局部坐标系下的应力分布,再依据τrθ数据获得τrθ=0的方向,这也即拉破裂的扩展方向,且当σθ≥σt时,产生拉破裂。此外,依据|τrθ|取得最大值的方向为剪切破裂方向,且|τrθmax|≥τcr时产生剪切破裂(τcr为材料的抗剪强度)。
(1)对于张拉断裂,其扩展方向判断条件为:① 当周向应力σθθ达到材料的抗拉强度σt时才能扩展;② 对应扩展角θc所在平面的剪切应力τrθ为0,即
(4)
式中,σt为材料的抗拉强度;σθ为θ方向的周向应力。
(2)对于剪切断裂,其扩展方向判断条件为:① 剪切应力τrθ的正负号只代表方向的不同,因此取|τrθ|作为判断剪切裂纹是否产生的阈值;② 剪切破裂的方向为|τrθ|取最大值的方向;③|τrθ|达到抗剪强度τcr时剪切裂纹扩展,即
|τrθ,max|=τcr
(5)
与MTS准则不同,改进的断裂准则不需计算裂纹尖端的应力强度因子甚至是T-应力,只需以裂纹尖端为极坐标原点建立局部坐标系,通过判断距离裂纹尖端半径为r点的应力(图4)是否达到扩展条件,从而进行扩展角度的计算。通过提高裂纹尖端的单元密集程度以及采用高精度单元,可以获得更为精确的应力分布。该方法易于实现自动化的裂纹扩展计算。具体的计算步骤为:① 建立数值模型并进行单元划分,然后施加初始荷载进行加载求解,获得模型中的应力场分布;② 利用式(4)和式(5)判断裂纹是否满足裂纹扩展条件。如果不满足扩展条件,则需要增加荷载,直到满足裂纹扩展条件;③ 使用差值方法计算张开裂纹扩展角度θT或者剪切裂纹扩展角度θS;④ 沿着不同扩展方向θT或者θS,裂纹的长度增加Δa,得到新的裂纹尖端位置,并进行该区域的网格局部自动重划分;⑤ 判断裂纹是否扩展至失稳位置或者是否满足计算终止条件。若不满足则根据新的裂纹尖端位置,重新计算包含新生裂纹的模型中应力分布,重复第②~④步,直到满足终止条件为止,停止计算。
从上述的裂纹扩展模拟方法中可以看出,该法不需要计算KⅠ,KⅡ以及T-应力等数据,避免了这些数据计算不准的难题(尤其是闭合接触裂缝的计算更容易计算不准),显著简化了计算的易操作性和提高了计算精度。此外,通过裂纹尖端区域的局部网格自动重划分方法,裂纹单步的扩展长度并不受网格大小的限制,解决了裂纹扩展的网格依赖性问题(当然,网格的疏密会对应力场的计算精度有重要的影响,需要保证应力场的计算精度)。
采用改进的断裂模拟方法开展了图3所示的张开和闭合裂纹扩展的研究,其结果如图9所示。从裂纹的扩展路径中可以看出,2种类型的初始裂隙均沿着光滑的路径扩展,且当Δa=0.5,1.0,2.0 mm时,3种Δa情况下的裂纹扩展路径基本重合。计算结果与图2所示的试验结果吻合。但从图7可以看出,传统的断裂模拟方法显然在大步长时不适宜,即使是小步长,对于闭合裂纹扩展计算仍有偏差。图10进一步对比了小步长情况下,MTS准则和改进的断裂模拟方法获得的张开裂纹扩展路径。可以看出,笔者提出的方法与小步长的MTS准则计算路径一致,从而印证了改进断裂模拟方法计算张开裂纹扩展路径的准确性。

图9 改进的断裂模拟方法计算的张开和闭合裂纹扩展
Fig.9 Fracture growth path of both open and closed fault modelled by the improved fracture criterion

图10 MTS准则和改进的断裂模拟方法模拟 张开裂纹扩展路径对比
Fig.10 Comparison of fracture growth path between MTS criterion and improved fracture criterion
基于上述结果可以看出:
(1)当裂纹扩展步长较小时,MTS断裂准则能够较为精确地模拟张开裂纹扩展路径,但闭合裂纹扩展模拟则存在问题;当步长放大后,MTS准则的模拟结果与实际情况有较大偏差。然而,笔者提出的断裂模拟方法却能够很好地模拟此类裂纹扩展,且不受小步长的限制。
(2)当裂纹面处于接触状态时,MTS断裂准则不能很好地模拟裂纹的扩展路径,而笔者改进的断裂模拟方法却能获得较好的计算结果,且步长放大后裂纹扩展路径模拟仍具有较高的计算精度。也即笔者提出的断裂模拟方法,可以在一定程度上增大扩展步长却并不影响计算精度。以图9和图10为例,改进的断裂模拟方法计算整个断裂过程时,Δa=0.5,1.0,2.0 mm的计算步数分别为需32,16,8步,而MTS准则只有在Δa=0.5 mm才能得到较好计算结果,但其计算步数为32步。可见改进的断裂模拟方法大幅提高了裂纹扩展的计算效率。
图11和图12为改进的断裂模拟方法得到的图3中张开和闭合裂纹扩展过程。从图11,12可以看出,张开裂隙在整个扩展过程中,裂纹面一直处于分离状态。而闭合裂隙在裂纹扩展初期,初始裂隙面一直处于闭合状态,但当裂纹扩展到一定程度后,初始裂纹面分离,也即由接触状态变为分离状态。图13分析了初始闭合裂隙在整个裂纹扩展过程中的接触与分离状态。结果表明,在裂纹扩展的初期,初始裂隙面始终处于闭合状态(图13中以橙色表示);但当裂纹扩展一定长度后,接触面出现了部分分离(如图中黄色所示)、部分接触的状态(如第3~6步所示)。最终裂隙面出现了全分离状态。因此,运用笔者提出的数值模拟方法不仅能够方便、快速、精确地模拟裂纹扩展过程,还能获得该过程中的接触状态变化,从而获得裂纹扩展的内在机理。

图11 改进的断裂模拟方法计算的张开裂纹扩展应力变化
Fig.11 Stress evolution during fracture growth in the open fault calculated by the improved fracture simulation method

图12 改进的断裂模拟方法计算的闭合裂纹扩展应力变化
Fig.12 Stress evolution during fracture growth in the closed fault calculated by the improved fracture simulation method
图14为初始闭合裂隙的裂纹扩展角度变化(与裂纹方向的夹角,如图5所示)。由图14可以看出,扩展角度θc逐渐趋向45°(也即沿着竖直的加载方向),并未出现如图8所示的角度正负震荡变化现象。从扩展角度的斜率变化可以看出(也即图14中tan θ),从起裂阶段扩展方向的斜率变化不大,裂纹扩展路径的弯曲程度较小;但从第1~4步,裂纹扩展路径的斜率变化较大;而在第4步之后斜率变化均匀,逐渐趋近于1,也即裂纹的扩展轨迹逐渐平行于竖直中心轴线。
图15为运用改进的断裂模拟方法计算得到的含填充裂隙的巴西圆盘裂纹扩展路径及应力分布云图。在整个裂纹扩展的过程中,填充物与初始裂隙之间接触状态由完全接触逐渐变为部分接触,该计算结果与SHARAFISAF[7]的试验结果吻合。上述结果也表明,笔者提出的岩石断裂模拟方法在张开、闭合、填充裂纹扩展方面都有较好的模拟效果。

图13 初始裂隙裂纹面接触状态变化
Fig.13 Variety of contact state of initial crack surface

图14 改进的断裂准则计算闭合型裂纹扩展角度和斜率
Fig.14 Fracture growth angle and its gradient in the closed crack specimen modeled by the improved fracture criterion
2.4.1 裂纹起裂角度
根据经典的线弹性断裂力学理论,MTS准则采用式(3)计算裂纹的起裂角,计算得到-θ0随KⅡ/KⅠ的变化如图16所示,由断裂力学可知,当KⅠ=0时为纯Ⅱ型裂纹,此时KⅡ/KⅠ→∞时, 相应的起裂角度-θ0则趋近于常数70.53°,且这个起裂角度和初始裂隙的角度变化无关。然而,BOBET等[23]在试验中发现随着初始裂隙倾角的增大,裂纹的起裂角度逐渐增大,即使是纯Ⅱ型裂纹扩展,其起裂角度仍随着裂隙倾角而变化。因此,采用经典的断裂准则并不能体现出裂隙初始倾角对起裂角度的影响作用。对含不同倾角闭合裂隙的巴西圆盘,采用改进的断裂模拟方法进行起裂角度的计算,结果如图17所示,可以看出,该方法获得的起裂角随初始裂隙倾角的增大而增大,符合相应的试验结果[6],这也验证了笔者方法较传统断裂准则更能精确模拟裂纹的扩展路径。

图15 改进的断裂准则计算填充型裂纹扩展 轨迹及最大主应力变化
Fig.15 Propagation path and contour of max principal stress of filled crack with improved fracture criterion

图16 起裂角度-θ0与KⅡ/KⅠ的关系
Fig.16 Relationship between initial propagation angle -θ0and KⅡ/KⅠ

图17 不同倾角裂隙下起裂角度变化
Fig.17 Variation of crack initiation angle of in specimens with different initial inclination angles
2.4.2 裂纹扩展轨迹
由图7可知,对于初始张开和闭合裂隙,当扩展步长Δa取0.5 mm和1.0 mm时,MTS准则计算得到裂纹扩展轨迹差别较大,其中Δa=1.0 mm时均得到锯齿状裂纹扩展路径;而当Δa=0.5 mm时,张开裂隙计算得到光滑的裂纹曲线,但闭合裂隙仍存在局部锯齿状扩展轨迹。与MTS准则计算得到裂纹扩展轨迹不同,运用改进的断裂模拟方法计算得到不同类型初始裂隙的裂纹扩展轨迹均为光滑曲线,且同一类型初始裂隙、不同扩展步长Δa的裂纹扩展轨迹几乎重合,裂纹最终扩展至加载点。
2.4.3 巴西圆盘裂纹扩展特征
以初始张开型裂隙为例,SHARAFISAF等[7]在含张开裂隙的巴西圆盘试验中发现,一旦达到峰值荷载,裂纹快速扩展,试样的最终破坏为张拉裂纹的破裂模式。运用改进的断裂模拟方法,从位移加载量——裂纹尖端单元最大张拉应力曲线(图18)可以看出,裂纹尖端的张拉应力达到抗拉强度之前(裂纹未扩展),随着位移加载量逐渐增加,裂纹尖端的最大拉应力逐渐变大,2者是线性相关的;一旦最大拉应力到达抗拉强度,即使竖向位移加载量不变化,随着裂纹不断扩展,裂纹尖端的最大拉应力会一直增加,直到最终破裂,这说明在对含初始张开型裂隙的巴西圆盘中,裂纹一旦起裂,其扩展是一种失稳扩展,与SHARAFISAF等[7]试验结果相符。

图18 改进的断裂准则计算裂尖单元最大张拉应力变化
Fig.18 Variation of the maximum tensile stress of crack tip element with Improved Fracture Criterion
(1)对含张开型和闭合型裂隙的巴西圆盘,采用传统断裂准则计算时,扩展步长Δa对扩展路径的影响较大,无论Δa大还是小,均会产生锯齿状裂纹扩展路径。而采用改进的断裂模拟方法,Δa对计算结果影响较小,且不同Δa计算得到的裂纹扩展路径均为光滑曲线。
(2)采用传统断裂准则计算得到Ⅱ型应力强度因子KⅡ的正负变化是导致裂纹扩展角度产生正负震荡变化的根本原因,进而产生锯齿状裂纹扩展路径。通过对比闭合和张开裂隙的接触状态变化可以发现,KⅡ的正负变化是初始裂隙面的接触所致。
(3)传统断裂准则解决拉伸问题具有很好的效果,但是处理压缩荷载下裂纹的扩展问题,尤其是闭合裂隙,会出现锯齿状裂纹。而改进的断裂准则,不仅解决了上述问题,且能够同时考虑张拉和剪切裂纹的扩展,受扩展步长Δa影响较小,提高了计算效率和准确性。
[1] BIENIAWSKI Z T. Mechanism of brittle fracture of rock:Part Ⅱ-experimental studies[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts. Pergamon,1967,4(4):407-423.
[2] HOEK E,BIENIAWSKI Z T. Brittle fracture propagation in rock under compression[J]. International Journal of Fracture,1965,1(3):137-155.
[3] AL-SHAYEA N A. Crack propagation trajectories for rocks under mi-xed mode I-II fracture[J]. Engineering Geology,2005,81(1):84-97.
[4] GHAZVINIAN A,NEJATI H R,SARFARAZI V,et al. Mixed mode
crack propagation in low brittle rock-like materials[J]. Arabian Journal of Geosciences,2013,6(11):4435-4444.
[5] ALIHA M R M,AYATOLLAHI M R,SMITH D J,et al. Geometry and size effects on fracture trajectory in a limestone rock under mixed mode loading[J]. Engineering Fracture Mechanics,2010,77(11):2200-2212.
[6] HAERI H,SHAHRIAR K,MARJI M F,et al. Experimental and numerical study of crack propagation and coalescence in pre-cracked rock-like disks[J]. International Journal of Rock Mechanics and Mining Sciences,2014,67:20-28.
[7] SHARAFISAFA M,SHEN L,ZHENG Y,et al. The effect of flaw filling material on the compressive behaviour of 3D printed rock-like discs[J]. International Journal of Rock Mechanics and Mining Sciences,2019,117:105-117.
[8] EFTEKHARI M,BAGHBANAN A,MOHTARAMI E,et al. Determination of crack initiation and propagation in two disc shaped specimens using the improved maximum tangential stress criterion[J]. Journal of Theoretical and Applied Mechanics,2017,55(2):469-480.
[9] DONG Z,TANG S B. Numerical study of near-wellbore hydraulic fracture propagation[J]. Theoretical and Applied Fracture Mechanics,2019,103:102274.
[10] ZHOU S. Fracture propagation in brazilian discs with multiple pre-existing notches by using a phase field method[J]. Periodica Polytechnica Civil Engineering,2018,62(3):700-708.
[11] LIU F,BORJA R I. A contact algorithm for frictional crack propagation with the extended finite element method[J]. International Journal for Numerical Methods in Engineering,2008,76(10):1489-1512.
[12] SHARAFISAFA M,SHEN L,XU Q. Characterisation of mechanical behaviour of 3D printed rock-like material with digital image correlation[J]. International Journal of Rock Mechanics and Mining Sciences,2018,112:122-138.
[13] ERDOGAN F,SIH G C. On the crack extension in plates under plane loading and transverse shear[J]. Journal of Basic Engineering,ASME,1963,85(4):519-525.
[14] SIH G C. Strain-energy-density factor applied to mixed mode crack problems[J]. International Journal of Fracture,1974,10(3):305-321.
[15] PALANISWAMY K. Crack propagation under general in-plane loading[D]. California Boulevard:California Institute of Technology,1972.
[16] 于骁中,陶振宇,谯常忻,等.岩石、混凝土断裂力学在国内的进展[J]. 水利学报,1984(9):1-10.
YU Xiaozhong,TAO Zhenyu,TONG Changxin,et al. Advances in fracture mechanics of rocks and concrete in China [J]. Journal of Hydraulic Engineering,1984(9):1-10.
[17] 许斌,江见鲸. 混凝土Ⅰ-Ⅱ复合型断裂判据研究[J]. 工程力学,1995(2):13-21.
XU Bin,JIANG Jianjing. Study on the Ⅰ-Ⅱ composite fracture criterion of concrete [J]. Engineering Mechanics,1995(2):13-21.
[18] 赵艳华,徐世烺. Ⅰ-Ⅱ复合型裂纹脆性断裂的最小J2准则[J]. 工程力学,2002(4):98-102.
ZHAO Yanhua,XU Shihuan. Minimum J2 criterion for brittle fracture of Ⅰ-Ⅱ composite cracks[J]. Engineering Mechanics,2002(4):98-102.
[19] TANG S B,BAO CY,LIU H Y. Brittle fracture of rock under combined tensile and compressive loading conditions[J]. Canadian Geotechnical Journal,2017,54(1):88-101.
[20] TANG S B. The effect of T-stress on the fracture of brittle rock under compression[J]. International Journal of Rock Mechanics & Mining Sciences,2015,79:86-98.
[21] 唐世斌,黄润秋,唐春安. T应力对岩石裂纹扩展路径及起裂强度的影响研究[J].岩土力学,2016,37(6):1521-1529.
TANG Shibin,HUANG Runqiu,TANG Chun’an. Study on the effect of T stress on the crack propagation path and crack initiation strength of rock[J]. Rock and Soil Mechanics,2016,37(6):1521-1529.
[22] TANG S B,DONG Z,HUANG R Q. Determination of T-stress using finite element analysis[J]. Science China Technological Sciences,2017,60:1211-1220.
[23] BOBET A. The initiation of secondary cracks in compression[J]. Engineering Fracture Mechanics,2000,66(2):187-219.