
移动阅读

移动阅读
GUO Changfang,WU Xiang,YANG Zhen,et al. Intelligent inversion method of electromagnetic wave CT detection within working face under the constraint of multi-source information fusion[J]. Journal of China Coal Society,2021,46(11):3623-3635.
工作面地质异常的精准预测是实现煤矿智能精准开采的重要基础和前提,对于推动煤炭资源的安全高效开采具有重要意义[1-2]。煤矿工作面电磁波CT(Computerized Tomography)技术作为一种非接触式探测方法,具有施工便捷、效率高、分辨能力强、成本较低、无破坏性等优点,已成为目前煤矿工作面内地质异常探测的主要方法之一[3]。
煤矿工作面电磁波层析成像技术来自于医学上常用的CT技术,属于图像重构技术的应用之一。在利用电磁波CT技术对工作面内地质异常进行层析反演计算时,需要求解的是一个病态矩阵方程。针对该矩阵方程的求解方法,最为经典的是GORDEN[4]提出的代数重建算法(ART)、GILBERT[5]提出的联合迭代重建算法(SIRT)及其优化算法[6-7]。然而这些常见的层析反演算法大都采用单一的初始模型,通过反复向改进的邻近解集移动,直到满足允许条件以求得最终解。其反演结果很大程度上取决于单一初始模型的选择,而且容易陷入局部最优解。随着计算机计算能力的提高以及人工智能技术的快速发展,先进的智能计算方法已经被广泛应用于各种复杂模型问题求解过程中。
自1960年以来,蒙特卡洛法、BP神经网络、遗传算法、粒子群等智能算法通过模仿生物的生存和进化规则而逐步发展起来,并为复杂多维度问题的处理提供了新的思路和方法。由于这些算法对初始模型的依赖程度较低,其强大的全局搜索能力和特殊的进化搜索机制引起了各领域学者的广泛关注[8-9]。1985年以来,这些智能算法开始应用于地球物理反演问题中,特别是在地震反演领域取得较多的进展[10-11]。随后,智能计算方法也逐渐在大地电磁反演领域得到推广和应用。然而智能算法在工作面电磁波CT层析反演领域的应用和研究较少。针对目标函数极值的求解,蒙特卡洛法在样本数量比较少的情况下,会朝着局部最优解方向收敛,但在求解参数维度较大的情况下缺乏实用性[12]。神经网络算法在实际应用过程中难以解决多参量的优化求解问题。遗传算法是一种具有高效、并行、全局搜索能力的智能算法,在进化搜索的过程中,能够通过之前积累的进化知识自主调整进化方向,求得目标函数的最优解。遗传算法作为一种实用、高效、鲁棒性强的优化算法,由于其本身的开放特性,具有较好的改进潜能,发展非常迅速,是目前应用较为广泛的智能寻优搜索算法[13-15]。因此,笔者将遗传算法及其优化算法引入工作面电磁波CT地质异常反演重构过程,对于工作面内地质异常的精准识别具有重要意义。
工作面掘进和回采期间时刻都在揭露地质信息,地质数据的产生在时间和空间上是持续发展和动态变化的过程。在工作面电磁波CT层析反演的过程中,如果能够充分结合工作面在掘进及回采过程中揭露的掘进数据、钻探数据以及回采数据等多源先验地质信息作为约束,对于提高工作面内地质异常反演的精准性具有重要意义[16]。笔者建立了基于多种群自适应遗传算法和多源数据约束的地质异常层析反演模型,通过函数测试和数值模拟对提出方法的可行性和有效性进行了验证,并成功应用于工程探测资料处理,为工作面内地质异常的精准反演和预测提供了一种新思路。
电磁波CT探测方法主要是利用不同介质对电磁波吸收能力的差异,根据采集到电磁波信号的强度对传播区域内的异常介质进行预测。电磁波在同一介质中传播的过程中,其辐射强度的高低主要与发射功率以及天线的组合形式有关。因此,在选择天线的形式时需要综合考虑探测所需的最佳匹配形式,从而使得辐射的能量达到最大化。在井下探测时,受到工作面现场施工条件的限制,通常考虑方向因子较简单的天线,因此选择磁偶极子天线激发产生电磁波,如图1所示。

图1 磁偶极子天线辐射场
Fig.1 Radiation field of magnetic dipole antenna
如图1所示,当电磁波辐射源在各向同性、均匀的介质中传播时,若观测点P到辐射源点A的距离为r(观测点在辐射场内),则点P处的电磁波场强E为
(1)
其中,E为传播介质中距离发射点r位置的实测场强,μV;E0为电磁波发射端产生的初始场强,μV;β为传播介质的吸收系数, dB/m;R为发射点距接收点之间的距离,m;sin θ为方向性因子;θ为发射端天线轴与电磁波采集点方向之间的夹角。对于工作面电磁波CT探测的现场空间条件下,θ的数值可近似为90°,则场强E的计算公式变为
(2)
在煤矿工作面进行电磁波CT探测时,接收机采集到的场强值都是H(dB)。因此,式(2)经过分贝转换[17]可得
H=H0-βr-ln r
(3)
式中,H为实测记录的场强值,dB;H0为发射初始场强值,dB。
电磁波层析反演计算时,首先将煤矿工作面目标探测区域进行网格离散,假设共划分成B个网格。其中,每个网格称为一个像素,并用xj代表第j个网格的真实吸收系数,j=1,2,3,…,B。
假设射线的总条数为N,则从发射端穿过探测区域到达接收端的任一条射线yi(i=1,2,3,…,N),在第j个网格的截距为dij,则在第i条射线路径上有
(4)
由式(3)可知
Hi=H0-yi-ln ri
(5)
即
(6)
式中,Hi为第i条射线采集到的电磁波场强数据;ri为第i条射线的长度。
工作面电磁波CT探测过程是在多个发射点发射电磁波,其中针对每一个发射点激发产生的电磁波在多个接收点进行数据采集,则式(4)可进一步推广为
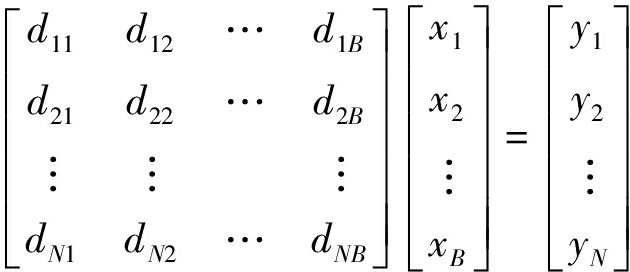
(7)
即
D×X=Y
(8)
式中,D为A×B阶系数矩阵,即每条射线通过每个网格的截距,其中射线条数为N,网格数目为B;X为B×1阶吸收系数矩阵;Y为A×1阶实测常数矩阵。
由于煤矿井下工作面现场探测条件的限制,射线的条数一般远小于网格的数目,因此需要求解的是一个具有病态特征的稀疏矩阵的解。由于方程(7)没有唯一解,而目前常见的ART,SIRT等传统层析反演算法大多依赖于问题的线性化形式,采用单一的初始模型,通过反复向改进的邻近解集移动,反演的结果很大程度上取决于初始值的选择。针对该问题,将式(7)矩阵求解问题转化为一个泛函极值求解问题,并建立目标函数反演模型,进而通过具有较强全局搜索能力的智能算法对目标函数进行求解。
在电磁波层析反演过程中,目标函数的定义为观测数据与理论数据之间的差值。首先,根据式(5)得出电磁波在传播过程中场强的实测损耗值;然后,对探测范围内介质网格赋予随机的初始吸收系数,进而根据式(4),计算得到电磁波在传播过程中场强的理论损耗值;最后,通过智能算法反复更新每个网格的吸收系数值,直到目标函数值取得最小或迭代次数达到设定上限时,即满足停止条件,输出当前时刻每个网格的吸收系数数值作为反演结果。具体目标函数定义为
(9)
因此,地质异常层析反演模型可定义为:求X′∈C,使得
f(X′)=min f(X)
(10)
其中,![]() 为目标函数f(X)达到最小值时,得到的每个网格对应反演的吸收系数矩阵,C={(x1,x2,…,xj,…,xB)|Lu≤xj≤Ll,j=1,2,…,B}; Lu和Ll分别为变量变化的上、下限。
为目标函数f(X)达到最小值时,得到的每个网格对应反演的吸收系数矩阵,C={(x1,x2,…,xj,…,xB)|Lu≤xj≤Ll,j=1,2,…,B}; Lu和Ll分别为变量变化的上、下限。
基本遗传算法(Single Genetic Algorithm,SGA)是一种借鉴生物进化过程中适者生存的自然选择规律,从而演变形成的一种具有较强全局搜索能力的智能算法。SGA作为一种全局优化的随机搜索智能算法,其搜索性能的优劣主要决定于带有概率性质的交叉算子和变异算子[18]。由于SGA往往采用单一固定的遗传参数,因此遗传参数的选择尤为重要。应用SGA解决不同的具体问题时,不同行业的学者提出了不同遗传参数的取值方法[19],但到目前为止,仍然没有一个统一的参数选择规则。当面对一个新的优化问题时,需要经过大量的测试才能从中选择出最优的结果。然而这不仅需要消耗大量的时间,而且得到的结果也并非全局最优解。
因此,利用SGA智能算法对建立的电磁波层析反演目标函数模型求解时,为了尽可能避免早熟收敛现象的出现,笔者在SGA的基础上,通过引入多种群协同进化算子以及自适应调整算子对其进行优化,在保证种群多样性的同时(全局搜索性能),尽可能提高搜索的精准性(局部搜索性能),以获得更加精确的层析反演结果。
2.2.1 多种群遗传算法
多种群遗传算法(Multiple Population Genetic Algorithm,MPGA)是在SGA的基础上,通过具有不同遗传参数的多个种群协同进化搜索的方式,使得每个种群朝着不同方向进化,从而具有更大范围和更加精细化的进化搜索能力。同时,通过移民算子实现了多个种群协同进化过程中优质信息的交流,而且最终获得的结果是由多个种群协同进化综合搜索所得。MPGA通过多个具有不同遗传参数的种群协同进化搜索,使得SGA的全局搜索性能得到一定提高。
2.2.2 自适应遗传算法
交叉概率Pc和变异概率Pm的选择是影响SGA进化搜索性能的关键指标。Pc的取值越大,越容易产生新个体。但是如果Pc的取值过大时,种群中的个体特别是高质量的个体越容易被破坏,从而导致结果难以收敛。如果Pc的取值过小时,新个体就越不容易产生,从而使得整个搜索进化过程变得更加缓慢,甚至停滞不前。另一方面,对于变异概率Pm的取值来讲,如果Pm的取值太小,就不容易产生新的个体基因组合结构。但是,如果Pm的取值太大,那么遗传算法就等同于一种随机搜索算法。经过多年理论和实践发现,SGA在进化到不同的阶段需要不同的参数设置[20-21]。自适应遗传算法(Adaptive Genetic Algorithm,AGA)能够使得种群在进化过程中对应交叉概率Pc和变异概率Pm的取值随着适应度值的不同而自适应的发生变化。对于适应度值较大的个体(距离目标函数最优解较近的个体),选择较低的Pc和Pm取值,从而使得该个体得以保护,并进入下一代中;而对于那些适应度值较小的个体(距离目标函数最优解较远的个体),往往选择较高的Pc和Pm取值,从而使得这些个体更容易被破坏并产生新的个体。
因此,AGA能够很好地解决SGA交叉概率Pc和变异概率Pm取值问题,在SGA搜索进化过程中,能够时刻保持种群的多样性,同时也有利于保证种群的收敛性能,进一步提高了SGA的局部搜索能力。
2.2.3 多种群自适应遗传算法
MPGA智能算法具有较强的全面搜索能力,而AGA智能算法能够实时有效的调整种群的进化方向,因此将这2种思想进行整合,通过设计多种群自适应遗传算法(Multi-population Adaptive Genetic Algorithm,MAGA)能够显著提高SGA的搜索性能。另一方面,通过设置精英个体(所有种群中适应度值最高的个体)并将其单独保留,不参与遗传操作,防止其结构被破坏,保证了算法的全局收敛能力。其具体实现流程如图2所示。

图2 多种群自适应遗传算法进化流程
Fig.2 Evolutionary flow chart of MAGA
(1)参数初始化,其中,MP为种群的数量;NP为种群中个体的数量;Nmax为种群最大遗传代数;Ggap为代沟;K为种群二进制编码位数;Pc1为多种群交叉概率上限;Pc2为多种群交叉概率下限;Pm1为多种群变异概率上限;Pm2为多种群变异概率下限;Ngen为当前进化代数。
(2)初始化多个种群Porigin(Ngen=0),则
Porigin={Pop(Ngen,1),Pop(Ngen,2),…, Pop(Ngen,p),…,Pop(Ngen,MP)}
(11)
其中,Pop(Ngen,p)为在第Ngen代进化过程中第p个种群。
Pop(Ngen,p)={P(Ngen,p,1),P(Ngen,p,2),…, P(Ngen,p,n),…,P(Ngen,p,NP)}
(12)
其中,P(Ngen,p,n)为在第Ngen代进化过程中第p个种群中第n个个体。

(13)
其中,xj(Ngen,p,n)为在第Ngen代进化过程中第p个种群中第n个个体中第j个变量。
(3)个体评价,计算每个种群中每个个体的适应度值F(Ngen, p, n),其中,F(Ngen, p, n)为进化到第Ngen代时,第p个种群中第n个个体的适应度值。
Ngen=1,2,3,…,Naxg;p=1,2,3,…,MP;n=1,2,3,…,NP。
(4)根据设置的Ggap进行选择操作。
(5)交叉操作。其中,第p个种群在第Ngen代进化过程中,交叉概率Pc(Ngen,p)的自适应变化范围为[Pc2(p),Pc1(p)],则
Pc1(p)=Pc2+(Pc1-Pc2)δ
(14)
Pc2(p)=Pc1(p)-0.3
(15)
各种群交叉概率定义为

(16)
其中,δ为0~1的随机数;Fc(Ngen,p)为第Ngen代进化过程中第p个种群中要进行交叉操作的2个个体中较大的适应度值;Favg(Ngen,p)为第Ngen代进化过程中第p个种群的平均适应度值;Fmax(Ngen,p)为第Ngen代进化过程中第p个种群中最大适应度值。
(6)变异操作。所有种群中第p个种群在第Ngen代进化过程中,变异概率Pm(Ngen,p)的自适应变化范围为[Pm2(p),Pm1(p)],则
Pm1(p)=Pm2+(Pm1-Pm2)δ
(17)
Pm2(p)=Pm1(p)/10
(18)
各种群变异概率定义为

(19)
其中,Fm(Ngen,p)为第Ngen代进化过程中第p个种群中变异个体的适应度值。
(7)移民算子。不同种群之间都互相独立,主要通过移民算子实现种群间的信息互换。具体的互换规则为:将目标种群中质量最差的个体替换为源种群中质量最好的个体。
(8)人工选择操作。每一代进化结束后,由人工算子选择出每个种群中的最优个体,然后通过对比选择出所有种群中最优个体进行单独存储。由于精英个体不进行选择、交叉和变异等遗传操作,以确保不同群体在进化过程中产生的最优个体不被破坏或丢失。
(9)判断是否达到终止条件。如果未达到,则返回到第(3)步;如果达到,输出结果。
为了测试MAGA智能算法的进化搜索能力,首先通过一个典型的含有多个极值的一元函数g(x)为例进行测试,如图3所示。分别通过SGA和MAGA在[1,2]内寻找以下目标函数的最小值:
(20)
由图3可以看出,该目标函数含有多个极小值。为了求得该目标函数g(x)的全局最小值,并检验MAGA的搜索性能,分别通过SGA,MPGA,AGA和MAGA按照表1中的参数设置,进行重复50次重复搜索计算,得到的进化过程和进化结果如图4和表2所示。

图3 目标函数分布示意
Fig.3 Distribution diagram of objective function
由图4和表2可以看出,上述4种不同寻优算法经过50次重复计算发现,SGA算法出现16次早熟收敛现象,平均寻优结果最高为-0.792;MPGA和AGA算法分别出现5次和3次早熟收敛现象,AGA出现3次早熟收敛现象;而MAGA未出现早熟收敛现象,平均寻优结果最低为-0.869。
表1 参数设置
Table 1 Parameters setting

SGA参数设置MPGA参数设置参数数值参数数值种群中个体的数量NP10种群的数量MP5种群最大遗传代数Nmax20种群中个体的数量NP10代沟Ggap0.9种群最大遗传代数Nmax20交叉概率Pc0.9代沟Ggap0.9变异概率Pm0.01交叉概率Pc0.9变量的二进制编码位数K20变异概率Pm0.01变量的维数Nvar1变量的二进制编码位数K20变量变化的下限Ll1变量的维数Nvar1变量变化的上限Lu2变量变化的下限Ll1变量变化的上限Lu2AGA参数设置MAGA参数设置参数数值参数数值种群中个体的数量NP10种群的数量MP5种群最大遗传代数Nmax20种群中个体的数量NP10代沟Ggap0.90种群最大遗传代数Nmax20多种群交叉概率上限Pc10.95代沟Ggap0.90多种群交叉概率下限Pc20.75多种群交叉概率上限Pc10.95多种群变异概率上限Pm10.1多种群交叉概率下限Pc20.75多种群变异概率下限Pm20.001多种群变异概率上限Pm10.10变量的二进制编码位数K20多种群变异概率下限Pm20.001变量的维数Nvar1变量的二进制编码位数K20变量变化的下限Ll1变量的维数Nvar1变量变化的上限Lu2变量变化的下限Ll1变量变化的上限Lu2

图4 SGA,MPGA,AGA和MAGA智能算法50次 重复进化搜索结果
Fig.4 Search results of SGA,MPGA,AGA and MAGA intelligent algorithms with 50 times of repeated evolution
表2 50次重复计算平均寻优结果
Table 2 Average optimization results of 50 repeated calculations

算法SGAMPGAAGAMAGA平均寻优结果-0.792-0.851-0.856-0.869
因此,通过对具有多极值特征的一元函数g(x)的求解可知,在SGA算法的基础上,MAGA算法通过多种群协同进化算子和遗传参数自适应调节算子能够更稳定的搜索到更为精确的全局最优解,有效提高了SGA算法的全局和局部搜索能力。
为了进一步提高工作面内地质异常反演预测的精准性,在MAGA层析反演智能算法的基础上提出了范围约束、就近约束和平均值约束3种约束模型,使得巷道、钻探以及回采揭露的先验约束数据融入到MAGA智能算法的层析反演搜索计算过程中。
在煤矿工作面已揭露区域内,对采用MAGA智能算法进行层析反演计算得到的每个网格的吸收系数值进行约束处理。其中,在无地质异常揭露的区域内,若x′j小于当前通过反演得到的所有网格的平均吸收系数值xavg,则x′j并不发生改变;若该区域中x′j大于xavg,则通过在变量的下限Ll与xavg之间随机产生一个数值来代替x′j。
对于在有地质异常揭露的区域内,若x′j大于xavg,则x′j并不发生改变;若x′j小于xavg,则通过在变量的上限Lu与xavg之间随机产生一个数值来代替x′j。
在范围约束条件下,基于MAGA智能算法的层析反演数学模型为

(21)
(22)
其中,f为目标函数;x′j为探测区域第j个网格对应的反演吸收系数值;xavg为探测区域所有网格对应反演的层析反演吸收系数平均值;δ为0~1的随机数;Q1为正常区域(无异常构造揭露区域)内大于xavg的网格序号集合;Q2为异常区域(有异常构造揭露区域)内小于xavg的网格序号集合。
在煤矿工作面已揭露区域范围内,对采用MAGA智能算法进行层析反演计算得到的每个网格的吸收系数值x′j进行约束处理。其中,在无地质异常揭露的区域内,若x′j小于xavg,则x′j并不改变;若x′j大于xavg,则x′j替换为距离该网格最近的反演吸收系数值小于xavg的网格所对应反演的吸收系数值xc。
对于有地质异常揭露的区域内,若x′j>xavg,则x′j并不发生改变;若x′j<xavg,则将x′j替换为距离该网格最近的反演吸收系数大于xavg的网格所对应反演的吸收系数值xd。对于满足要求同时具有相同最近距离的网格,通过取多个网格对应吸收系数的平均值对其进行替代。
在就近约束条件下,基于MAGA智能算法的层析反演数学模型如式(23)所示:

(23)
其中,Q3为反演区域内小于当前所有网格对应反演的平均吸收系数值xavg的网格序号集合;Q4为反演区域内大于当前所有网格对应反演的平均吸收系数值xavg的网格序号集合。
在煤矿工作面已揭露区域范围内,对采用MAGA智能算法进行层析反演计算所得到的每个网格的吸收系数值x′j进行约束处理。其中,在无地质异常揭露的区域内,若小于xavg,则x′j并不改变;若x′j大于xavg,则该网格的吸收系数值x′j用xavg进行替代。
在地质异常揭露的区域内,若x′j大于xavg,则x′j并不发生改变;若x′j小于xavg,则该网格的反演吸收系数值x′j用xavg进行替代。
在平均值约束条件下,基于MAGA智能算法的层析反演数学模型为

(24)
将上述3种约束模型融入到MAGA智能算法的层析反演进化过程中,以控制其进化方向,进一步提高工作面内地质异常层析反演的精准性。其中已揭露的多源先验约束数据主要有巷道揭露数据、钻探揭露数据以及回采过程中揭露数据。
为了进一步验证基于多源数据约束的MAGA智能算法在煤矿工作面内部地质异常层析反演应用中的性能和效果,根据煤矿工作面狭长的特点,建立长600 m和宽200 m的工作面模型,如图5所示。在该工作面模型中存在2处常见的地质异常区域,由于通过电磁波CT技术对工作面地质异常进行反演计算的基础是煤层与地质异常介质对电磁波吸收能力存在一定的相对差异,同时为了更加直观地验证本文提出预测方法的可行性,将异常区域的电磁波吸收系数设置为β1=1.0 dB/m,其余正常区域的电磁波吸收系数设置为β2=0.5 dB/m。
以电磁波CT探测方法为基础,利用MAGA智能算法并分别结合范围约束、就近约束和平均值约束3种约束模型,对该工作面模型内的异常区域进行层析反演,最终通过工作面模型区域内的电磁波吸收系数拟合分布结果,进而推断出异常区域的分布情况。

图5 模型构造分布示意
Fig.5 Distribution diagram of model construction
在观测系统布置中,发射点之间的间距为30 m,对应接收点的间距为10 m,射线总数量N=420条。在层析反演计算之前,首先对探测区域进行网格离散化处理,每个网格的尺寸为10 m×10 m,探测区域共计划分成B=1 200个网格,网格的吸收系数值即为需要反演求解的目标。其中,MAGA智能算法在反演过程中参数设置见表3。
将巷道、钻探以及回采过程中揭露的多源地质数据通过建立的约束模型融入到MAGA智能算法反演计算过程中,其中多源先验约束信息分布如图6所示。其中,钻探间距为50 m,正常钻孔深度为150 m,两巷接替进行,对于揭露构造的区域增加钻孔密度,如图6(b)所示。巷道揭露数据主要体现在巷道两帮及开切眼周边的网格吸收系数值;钻探及回采揭露数据主要体现在所遍历的网格吸收系数值。
表3 工作面层析反演模型多种群自适应遗传算法参数设置
Table 3 Parameters setting of MAGA for tomographic inversion model

参数数值种群的数量MP5种群中个体的数量NP10种群最大遗传代数Nmax500代沟Ggap0.90多种群交叉概率上限Pc10.95多种群交叉概率下限Pc20.75多种群变异概率上限Pm10.10多种群变异概率下限Pm20.001变量的二进制编码位数K20网格数量B1 200变量变化的下限Lu0.20变量变化的上限Ll1.30
经过500代的进化搜索,在MAGA智能算法的基础上,通过3种不同约束模型分别得到的目标函数f的进化过程如图7所示,最终的收敛结果见表4。

图6 工作面掘进及回采过程中揭露多源先验约束信息分布示意
Fig.6 Distribution diagram of multi-source prior information revealed in the process of working face excavation and mining

图7 MAGA智能算法在不同约束模型条件下随揭露先验数据增加反演得到的目标函数f进化曲线
Fig.7 Evolution curves of objective function f obtained by MAGA based on different constraint models with the increase of exposed prior data
表4 MAGA智能算法在不同约束模型条件下随揭露先验数据 增加反演得到的目标函数f收敛结果(Ngen=500)
Table 4 Convergence results of objective function f obtained by MAGA based on different constraint models with the increase of exposed prior data (Ngen=500) dB/m

约束信息目标函数f范围约束就近约束平均值约束无约束6.014巷道揭露先验数据5.6225.4045.480增加钻孔揭露先验数据5.4225.9844.581增加回采至115 m揭露先验数据6.0566.1234.189增加回采至375 m揭露先验数据8.1036.5493.632增加回采至600 m揭露先验数据11.0808.2722.998
从上结果中可以发现,无约束条件下MAGA智能算法经过500代的搜索进化最终的目标函数收敛于6.014 dB/m。随着揭露先验约束数据的增加,范围约束和就近约束模型对约束区域网格吸收系数的更新将会产生较大幅度的改变,范围约束和就近约束模型对应反演的最终目标函数值整体呈上升趋势,并高于无约束条件下MAGA智能算法对应的收敛结果,最终数值分别为11.08 dB/m(范围约束)和8.272 dB/m(就近约束)。
而平均值约束模型对应反演的最终目标函数值随着约束数据的增加逐渐降低,始终低于无约束条件下MAGA智能算法对应的收敛结果,最终收敛数值为2.998 dB/m。因此,在平均值约束模型下,MAGA智能算法对地质异常反演目标函数最优解的搜索性能更好。
经过500代的搜索进化,基于MAGA智能算法和平均值约束的反演模型随着外部揭露多源地质数据的增加,得到的层析成像结果如图8所示。
从基于平均值约束的MAGA智能算反演得到的层析成像结果中可以发现,随着外部揭露多源地质信息的增加,层析成像结果中异常区的范围更加集中,轮廓也更加明显,与模型设置的异常区范围也越来越吻合。因此,通过综合考虑工作面层析反演算法本身的优化以及对周围揭露多源地质信息的充分利用,有效提高了工作面内地质异常层析反演的精准性,为工作面的透明化建设奠定了基础。

图8 基于平均值约束的MAGA智能算法随揭露先验约束数据增加反演得到的层析成像结果
Fig.8 Tomography results obtained by MAGA based on mean constrained model with the increase of exposed prior data
为了验证所提出方法的可行性,以山西大同矿区8208工作面探测为例,对工作面内的地质异常体进行反演和预测。该工作面煤层结构复杂,厚度不稳定,煤厚为4.29~9.44 m,含有1~4层夹矸,夹矸厚度为0.10~0.40 m,煤层大致走向南北,倾向东,倾角为2°~10°。煤层整体赋存形式为背、向斜组成的褶曲构造。该工作面的走向长1 000 m,倾向宽150 m,在工作面的两巷共揭露了7条断层和3个陷落柱,其分布如图9所示。
本次电磁波CT勘探采用WKT-E型坑透仪,发射点间距为50 m,接收点间距为10 m。观测射线呈扇形分布,每个发射点对应的射线覆盖扇形区角度为37°,共计418条射线,如图10所示。

图9 8208工作面地质概况示意
Fig.9 Geological sketch map of 8208 working face

图10 8208工作面探测观测系统
Fig.10 Layout of the observing systems for 8208 working face
在对8208工作面采集到的电磁波CT数据进行层析反演之前,首先对工作面探测区域进行网格离散化处理。为了保证每条射线都能分布在网格的内部,定义每个网格的尺寸为10.3 m×10.3 m,网格数量共计为1 470个。
在工作面两巷和钻孔揭露的先验数据基础上,基于平均值约束和MAGA智能算法经过500代的搜索进化,目标函数值最终收敛于2.605 dB/m,如图11所示,最终得到的层析反演结果如图12所示。
由图12可以看出,共包含2处异常区,左侧异常区域主要分布在距离开切眼180~320 m,右侧异常区主要分布在距离开切眼745~930 m,与周围揭露构造较为吻合。从层析成像反演结果中可以看出,异常区的成像效果较为明显。从左右两侧异常区的分布中可初步判断,2处异常区附近揭露的地质构造很大可能贯穿了整个工作面。因此,工作面在从左往右回采过程中,当回采至距离开切眼180 m附近时,异常构造将会对回采工作产生较大的影响,建议在320 m附近重新开切眼,继续进行工作面的回采,最终建议终采线设置在745 m附近。

图11 基于巷道和钻孔揭露先验数据约束的MAGA 智能算法反演得到的目标函数值进化曲线
Fig.11 Evolution curves obtained by MAGA based on the prior data of roadways and boreholes

图12 8208工作面层析成像结果
Fig.12 Tomographic result of 8208 working face
8208工作面在回采过程中,从开切眼位置(0 m)回采至185 m位置时,受构造影响,煤层变薄,回采工作被迫停止,并在325 m的位置重新开切眼,与MAGA智能算法层析反演推断结果基本一致。
(1)将工作面内地质异常反演过程中的矩阵求解问题转换为泛函极值问题,并建立了基于智能算法求解的电磁波反演目标函数模型,为工作面内地质异常的反演提供了一种新思路。
(2)设计了多种群协同进化算子和遗传参数自适应调节算子对SGA进行优化,并建立了基于多种群自适应遗传算法的地质异常反演模型。通过函数测试发现MAGA智能算法有效增强了SGA的全局和局部搜索能力,保证了种群的多样性,提高了目标函数搜索的准确性。
(3)提出了范围约束、就近约束和平均值约束3种电磁波层析反演先验数据约束模型,建立了基于多源先验数据约束的MAGA智能算法反演模型;通过数值模拟和工程应用揭示了平均值约束模型能够充分利用先验约束数据,在反演计算过程中有效调整MAGA智能算法的进化方向,进一步提高了工作面地质异常层析反演的精准性。
[1] 王存飞,荣耀. 透明工作面的概念、架构与关键技术[J]. 煤炭科学技术,2019,47(7):156-163.
WANG Cunfei,RONG Yao. Concept,architecture and key technologies for transparent longwall face[J]. Coal Science and Technology,2019,47(7):156-163.
[2] 李爽,薛广哲,方新秋,等. 煤矿智能化安全保障体系及关键技术[J]. 煤炭学报,2020,45(6):2320-2330
LI Shuang,XUE Guangzhe,FANG Xinqiu,et al. Coal mine intelligent safety system and key technologies[J]. Journal of China Coal Society,2020,45(6):2320-2330.
[3] 张辉,潘冬明,刘朋,等. 模拟分析初始场强对坑透反演结果的影响[J]. 地球物理学进展,2016,31(6):2788-2795.
ZHANG Hui,PAN Dongming,LIU Peng,et al. Simulation and analysis of the influence of initial field intensity on the inversion results[J]. Progress in Geophysics,2016,31(6):2788-2795.
[4] GORDON R,BENDER R,HERMAN G T. Algebraic reconstruction techniques(ART) for three-dimensional electron microscopy and X-ray photography[J]. Journal of Theoretical Biology,1970,29(3):471-481.
[5] GILBERT P. Iterative methods for the three-dimensional reconstruction of an object from projections[J]. Journal of Theoretical Biology,1972,36(1):105-117.
[6] EGGERMONT P P B,HERMAN G T,LENT A. Iterative algorithms for large partitioned linear systems with applications to image reconstruction[J]. Linear Algebra and its Applications,1981,40:37-67.
[7] CENSOR Y. Parallel application of block-iterative methods in med-ical imaging and radiation therapy[J]. Mathematical Programming,1988,42(1):307-325.
[8] 唐彤彤,杨维,邵小桃. 基于PSO-GA的Kriging插值法建立透地通信分层地层媒质模型[J]. 煤炭学报,2016,41(11):2913-2920.
TANG Tongtong,YANG Wei,SHAO Xiaotao. Establishment of a layered stratum model for though-the-earth communication based on the Kriging interpolation method with PSO-GA[J]. Journal of China Coal Society,2016,41(11):2913-2920.
[9] 程久龙,赵家宏,董毅,等. 基于LBA-BP的矿井瞬变电磁法岩层富水性的定量预测研究[J]. 煤炭学报,2020,45(1):330-337.
CHENG Jiulong,ZHAO Jiahong,DONG Yi,et al. Quantitative prediction of water abundance in rock mass by transient electro-magnetic method with LBA-BP neural network [J]. Journal of China Coal Society,2020,45(1):330-337.
[10] 方中于,王丽萍,杜家元,等. 基于混合智能优化算法的非线性AVO反演[J]. 石油地球物理勘探,2017,52(4):797-804,626-627.
FANG Zhongyu,WANG Liping,DU Jiayuan,et al. Nonlinear AVO inversion based on hybrid intelligent optimization algorithm [J]. Oil Geophysical Prospecting,2017,52(4):797-804,626-627.
[11] SOUPIOS P,AKCA I,MPOGIATZIS P,et al. Applications of hybrid genetic algorithms in seismic tomography[J]. Journal of Applied Geophysics,2011,75(3):479-489.
[12] 王家映. 地球物理资料非线性反演方法讲座(二) 蒙特卡洛法[J]. 工程地球物理学报,2007,4(2):81-85.
WANG Jiaying. Lecture on non-linear inverse methods in geophysics(二) Monte Carlo Method[J]. Chinese Journal of Engineering Geophysics,2007,4(2):81-85.
[13] RAMACHANDRAN S,JAYALAL M L,RIYAS A,et al. Application of genetic algorithm for optimization of control rods positioning in a fast breeder reactor core[J]. Nuclear Engineering and Design,2020,343(4-5):420-435.
[14] BOGGI S,FANO W G. Numerical response and causality study of the magnetic permeability-frequency function of NiZn ferrites using Genetic Algorithm[J]. Journal of Magnetism and Magnetic Materials,2020,500.
[15] 程珩,胡茂欣,权龙. 改进遗传算法在环锤式破碎机动平衡中的应用[J]. 煤炭学报,2013,38(9):1686-1691.
CHENG Heng,HU Maoxin,QUAN Long. Application of improved genetic algorithms in dynamic balancing of wreath hammer crusher[J]. Journal of China Coal Society,2013,38(9):1686-1691.
[16] 程建远,朱梦博,王云宏,等. 煤炭智能精准开采工作面地质模型梯级构建及其关键技术[J]. 煤炭学报,2019,44(8):2285-2295.
CHENG Jianyuan,ZHU Mengbo,WANG Yunhong,et al. Cascade construction of geological model of longwall panel for intelligent precision coal mining and its key technology[J]. Journal of China Coal Society,2019,44(8):2285-2295.
[17] 于治会. 分贝及其应用[J]. 电子机械工程,2002,18(6):4-7.
YU Zhihui. The decibel and its applications[J]. Electro-mechanical Engineering,2002,18(6):4-7.
[18] KARAFOTLAS G,HOOGENDOORN M,EIBEN A E. Parameter control in evolutionary algorithms:Trends and challenges[J]. IEEE Trans Evol Comput,2015,19(2):167-187.
[19] GREFENSTETTE J J. Optimization of control parameters for genetic algorithms[J]. IEEE Transactions on Systems,Man,and Cybernetics,1986,16(1):122-128.
[20] CERVANTES J,STEPGENS C R. Limitations of existing mutation rate heuristics and how a rank GA overcomes them[J]. IEEE Trans Evol Comput,2009,13(2):369-397.
[21] SRINIVAS M,PATNAIK L M. Adaptive probabilities of crossover and mutation in genetic algorithms[J]. IEEE Transactions on Systems,Man,and Cybernetics,1994,24(4):656-667.