移动阅读
采矿理论与工程
移动阅读
收稿日期:2021
0110
修回日期:20210308
HAN Jun，MA Shuangwen，ZHANG Ming,et al. Design and engineering practice of rebar bolt for large deformation roadway[J]. Journal of China Coal Society,2021,46(12):3745-3755.
随着浅埋深能源储量的枯竭，深部地下开采已成为国家能源安全及经济可持续发展的关键。目前国内地下煤炭主采层深度为地下600～800 m，最大开采煤层为地下1 500 m[1-2]。随着开采煤层向深部发展，地下煤矿巷道围岩地应力增加，造成巷道围岩软化及大变形，甚至诱发冒顶、冲击地压等多种井下灾害，严重威胁工程安全和资源有效开采。
锚杆支护由于岩层控制效果好、成本低等特点已在我国地下煤矿巷道支护大规模应用，是目前巷道围岩主要的岩石控制手段。据统计，我国煤矿地下巷道每年安装螺纹钢锚杆超过1.7亿根[1]，是人员和设备安全及整个采矿作业的最终保障。
进入深部开采后，针对高地应力、强采动扰动、巷道围岩大变形、围岩软化破碎等情况，国内外学者研发了多种锚网支护技术和支护材料。在基础理论研究领域，LI[3-4]提出，在高地应力条件下，应提高锚杆的承载能力，适应围岩大的变形，在支护结构破坏前尽量吸收较多能量。在支护材料方面，研发了可加长锚杆[5-6]、让压锚杆[7]等新深部巷道支护材料；康红普院士团队[8]强调在高地应力和深部巷道围岩大变形支护中，使用高强锚杆、锚索、拱形棚、高强度钢网和高预紧力；何满潮院士团队[9-10]研发了软岩巷道和复杂地质条件的支护新材料恒阻大变形锚杆，极大地提高了锚固系统的吸能能力。在巷道支护设计方面，多种支护元素联合支护与耦合技术取得了长足进展，例如锚索/锚杆优化布置加全长注浆加高预紧力的方案[11]及软岩巷道全断面可缩性支护方案[12]等。新支护材料的引入也为巷道支护工程提供了更丰富的手段，例如使用泡沫混凝土回填、可伸缩U型钢棚架、预应力锚索等控制深部软岩巷道底臌[13],以及采用加长锚杆+刚性螺纹钢锚杆+喷射混凝土支护围岩大变形巷道，并在高地应力区域允许围岩有一定的初始变形[14]。
上述研究为深部巷道新的地质条件下锚杆支护提供了新理论、新材料、新技术等。然而，作为锚网支护最基本的支护元素，即螺纹钢锚杆本身，鲜有针对深部资源开采巷道围岩大变形进行优化。锚固力学载荷传递基础理论显示，螺纹钢的螺纹是锚杆与周围介质载荷传递的承担者，它与周围介质的相互作用是锚固性能的关键[15-16]，所以，针对深部巷道围岩大变形条件下螺纹优化设计具有重要研究意义；而且，螺纹设计优化不增加支护成本，不改变支护设备及工艺，是易推广、易见成效的技术革新。
针对深部地下煤矿巷道围岩大变形工矿条件，本项研究回顾螺纹的设计的发展，理论分析螺纹几何参数在锚固系统中的作用，基于锚固力学的载荷传递机理，设计开发适用于围岩大变形的螺纹钢锚杆，并进一步通过实验室实验和工矿现场试验进行效果检验。
锚杆在矿业大规模应用始于20世纪90年代。目前，国内地下煤矿回采巷道基本使用3种锚杆，如图1所示。顶板锚杆多采用φ22 mm左旋螺纹钢锚杆，煤柱帮采用φ17～20 mm右旋螺纹钢锚杆，部分煤矿在采煤帮采用玻璃钢锚杆避免火花。
图1 我国煤矿常用锚杆
Fig.1 Bolts commonly used in coal mines in China
螺纹钢锚杆的锚固力来自于它的螺纹，没有螺纹的圆钢几乎没有轴向承载能力。研究证明[16-18]，不同螺纹的锚杆其载荷传递能力不同，即螺纹不同锚固性能不同。影响锚固性能的重要螺纹参数包括肋宽w、肋高h、半径r、肋坡角α、间距L、剪涨滑移破坏时螺纹承载角i及肋在杆体的螺旋上升角(图2)。
图2 螺纹重要几何参数
Fig.2 Geometric parameter of bolt
目前矿用螺纹钢锚杆的螺纹参数是从土木行业钢筋螺纹参数引入的。混凝土行业钢筋螺纹几何的研究有超过百年的历史[19]。20世纪40年代文献[20-22]成为ASTM制定当时钢混结构中钢筋螺纹标准的主要依据。20世纪80年代螺纹参数研究趋于完成[23-24]。进入20世纪90年代后，虽然钢筋螺纹优化研究仍有一些不错的进展，例如文献[25-27]，但混凝土行业钢筋螺纹几何优化已基本趋向完善。经过1个多世纪的发展，目前混凝土用φ20 mm钢筋的螺纹几何参数基本为肋间距约12 mm、肋高1～2 mm、肋坡角45°～70°。该几何参数亦是目前国内外多个国家和地区建筑用钢筋螺纹几何的行业标准，包括美国的ASTM、英联邦的BS和我国的GB标准。
20世纪90年代,锚杆开始在地下巷道广泛应用，最初，矿用锚杆就是土木行业的钢筋。由于锚杆安装过程中需要搅拌药卷锚固剂，为了使顶锚杆和帮锚杆都能搅拌均匀，逐渐演化出左旋锚杆和右旋锚杆，并为锚固剂流淌顺畅去掉了钢筋的纵筋；但是，这些变革与载荷传递并没有直接关系，即影响锚固性能的螺纹几何参数并未改变。
地下巷道锚杆与地面混凝土结构钢筋在支护要求、应用环境、破坏方式等多个方面存在很大差异。首先，混凝土结构一般只允许弹性变形，而锚杆锚固体塑性变形是常态，甚至部分失效也是允许的；其次，地面土木结构没有地应力，而地下锚固体受地应力的作用，地应力既影响围岩变形又影响锚杆产生的锚固应力；最后，地面钢混结构在钢筋受轴力时破坏方式一般为混凝土劈裂，而锚杆安装在的围岩内，其受轴力的破坏方式只能为拔出破坏。表1总结混凝土钢筋与矿用锚杆各种差异及对系统载荷传递的影响。
表1 地面混凝土钢筋与井下锚杆差异对比
Table 1 Difference comparison between ground concrete reinforcement and underground anchor rod
差异钢筋锚杆分析变形范围弹性塑性钢筋螺纹应增加峰值;锚杆应增加残余强度地应力无有2种锚固结构的初始应力状态不同锚固剂环无有钢混为2介质结构,锚杆锚固体是3介质结构内部连接有无钢筋载荷传递主体依靠内部连接;锚杆杆体只有通过螺纹周围介质有限无穷大导致2种结构在支护元受轴力的破坏方式不同主要破坏方式混凝土劈裂锚杆拔出/破断力学模型不同
由于2种支护元素存在多方面差异，因此，历经百年优化的钢筋螺纹参数，并不是地下矿用锚杆螺纹的优化设计。例如，地面土木结构一般要求变形量不超过弹性范围且附加安全系数，因此螺纹设计中重点考虑锚固力峰值；而深部巷道围岩大变形条件下，锚固段塑性形变不可避免，因此增加锚杆锚固段残余强度、提高锚固段吸能能力比增加锚固力峰值更重要。
由于锚杆大规模应用较晚，针对矿用锚杆的螺纹优化研究不多。早期较为重要的研究包括澳大利亚学者FABJANCZYK和TARRANT在1992年的试验研究[28]，通过不同肋高锚杆试样的拉拔试验，认为锚固力与钻孔直径、锚杆直径、肋几何以及锚固剂力学参数有关，也是“三径”的早期研究。
肋间距优化是锚杆螺纹优化研究的重点。1996年BLUMEL开启了锚杆肋间距优化研究[29]，通过锚杆拉拔试验，得到了加大肋间距可以提高锚杆载荷传递能力的结论。进入2000年后，AZIZ等[30-31]通过75 mm和115 mm锚固段长度拉拔试验，发现当锚杆的肋间距为37.5 mm时锚固效果最佳。国内方面，林健等[32-33]通过11,22,33和44 mm肋间距锚杆拉拔试验，认为肋间距为33 mm时锚固性能最佳；吴涛[34]、赵象卓[35]等分别对左旋和右旋2种国内常用锚杆不同肋间距(12,24,36和48 mm)的拉拔力和吸能能力进行试验研究，得到肋间距为24 mm时吸能效果最佳。
上述实验室拉拔试验结果显示，提高锚杆螺纹肋间距可以增强锚固段载荷传递能力及锚固段吸能能力。但是，上述研究也存在不足，首先是基础理论研究不足；另外，各试验研究的结果也不一致。基于载荷传递机理，通过破坏方式与破坏过程分析，研发适用于深部开采围岩大变形条件下的螺纹钢锚杆是本研究的目标。
锚固结构体由锚杆、锚固剂、围岩、锚杆-锚固剂交界面以及锚固剂-围岩交界面5个元素组成。各元素之间通过相互作用，即载荷传递，将载荷从不稳定的元素转移到稳定元素，最终形成稳定锚固结构体，是锚杆支护的目的[36-37]。
锚杆系统内载荷传递的能力，即承载能力，决定该锚杆的锚固效果。锚杆的承载能力一般以锚固段应力、应变(或位移)曲线衡量，锚杆锚固性能是锚固力峰值、残余强度、锚固段吸能能力的综合表现。综合近年锚固性能要素研究方面的科研成果，可以认为影响锚杆锚固性能的关键要素为锚杆螺纹几何、三径、锚固剂和围岩强度等。例如，康红普等[38]认为影响锚固力的因素包括锚杆直径、锚杆外形、锚固剂的力学性能以及围岩的强度和完整性；AZIZ等[39]报道了影响锚固性能的因素包括钻孔直径、锚固剂环厚度、安装时间、手套效应和超拌(搅拌时间>凝胶时间)等。
锚固失效是锚固结构体一个或多个元素破坏失效。锚杆受轴力条件下，锚固结构体5个元素中2个交界面是较为脆弱的部分。锚杆-锚固剂交界面比锚固剂-围岩交界面面积小，如果2个交界面抗剪强度近似，则锚杆-锚固剂交界面更易发生破坏；围岩较软易破碎，则锚固剂-围岩交界面容易发生破坏。
锚固破坏失效的破坏方式分析和破坏过程分析方法是载荷传递机理分析的主要手段。该方法在20世纪70年代被土木界用于钢混结构承载的本构研究[40]，20世纪90年代被加拿大学者[41]引入到矿用锚索本构关系研究，认为锚索锚固破坏是由于锚固剂环切向应力大于材料抗拉强度，并建立了相应力学模型“黏结强度模型(BSM)”
在针对螺纹钢锚杆载荷传递和锚固破坏研究中，CAO等[16,42]通过试验观测与理论分析，认为锚杆-锚固剂交界面主要存在2种破坏模式，即平行剪切破坏和剪涨滑移破坏(图3，其中，R为锚杆外径，l为嵌入锚固剂长度)。平行剪切破坏是最大肋高组成的圆柱面产生直剪破坏；而剪涨滑移破坏则是锚杆横肋压坏部分锚固剂组成一个锥形头，并在轴力作用下撑涨周围介质的轴向滑移。
图3 平行剪切破坏和剪涨滑移破坏[42]
Fig.3 Parallel shear failure and dilational slip failure[42]
2种破坏同时发生时，螺纹几何产生的锚固力峰值最大，锚固段抗破坏效果最好。针对莫尔-库仑材料，可以推导出单个肋间距锚固段最大锚固力峰值的螺纹几何参数[42]满足：
(1)
(2)
其中，参数L，h，r为锚杆外形参数，mm，如图2所示；φ和c为锚固剂内摩擦角和黏聚力；p为作用于锚杆表面的平均法向应力。可以看到，螺纹参数的优化与锚固剂强度、地应力相关；而剪涨滑移的残余强度还与围岩强度有关。
式(1)，(2)给出了单位锚固段针对锚固力峰值的最佳螺纹几何参数表达式。围岩变形使锚固力超出峰值后，锚固段进入残余强度阶段。在围岩变形量大情况下，提高锚固力残余强度是有效的岩层控制手段。
对平行直剪破坏方式，锚固段残余强度即为破坏圆柱面的残余抗剪强度，表达为柱面平均法向应力与滑动摩擦因数的乘积，而圆柱面平均法向应力与地应力有关。对剪涨滑移破坏，在锚固力达到峰值后，锚杆螺纹连同残留锚固剂(图2深色三角部分)形成锥体，在轴力作用下挤压和摩擦周边介质产生的阻力即是锚固段残余强度，因此，研究锥形头在岩土介质中的阻力是分析锚固段残余强度的关键。
锥形结构在岩土介质中滑移是岩土力学和锚固力学一个重要研究内容。GAUDREAU等[43]在BRUNSWICK矿山进行了锥形锚杆现场试验，并将锥形结构的载荷-位移曲线分为弹性阶段、屈服点和塑性阶段。KILIC等[44]试验研究圆锥几何参数对锚固效果的影响，发现锚固强度取决于周边介质的抗剪强度和抗压强度。CAI等[45]通过试验研究锥形结构阻力，设计开发了适用于岩爆矿山支护的锥形锚杆，也是工程实践中肋间距最大的锚杆。恒阻大变形锚杆的恒阻器也是锥形结构在钢套筒中扩张-滑移产生恒定阻力[9]。LIANG等[46]采用解析与数值计算方法，开发了锥形结构受轴力的力学模型。在动载条件下，ST-PIERRE等[47]基于锥形锚杆锚固体落锤试验，采用集中质量方法，建立了一个锥形锚杆动载力学模型。
综合考虑上述研究成果，锥形结构剪涨滑移阻力可分为2部分：一是滑移面摩擦力；二是锥形结构撑涨周边介质的阻力，2者叠加即为一个锚杆螺纹剪涨滑移破坏条件下的锚固力残余强度，如图4所示。
图4 锥形结构剪涨滑移阻力[46]
Fig.4 Shear slip resistance of conical structure[46]
与平行剪切破坏相比，剪涨滑移破坏后的残余锚固力强度除摩擦阻力外，还有锥形头扩张周边介质的阻力；后者造成周边介质变形，介质变形产生的应力与初始地应力进行叠加，进一步提高了锥形头的摩擦阻力。因此，一般情况下剪涨滑移破坏的锚固力残余强度大于平行直剪破坏。因此，通过控制锚固段破坏方式的方法，对矿用锚杆螺纹进行优化设计，增加锚固力残余强度,提高锚固段在整个破坏过程中的吸能能力，是针对深部资源开采巷道围岩大变形锚杆螺纹优化研究的理论依据与分析手段。
锚杆半径是杆体承载能力参数，目前矿用锚杆一般为φ18～22 mm。在杆体直径优化方面，如果杆体屈服强度大于锚固力峰值，进一步提高杆体直径并不能有效提升锚固效果，且增高了材料成本(锚杆按质量计价)及劳动强度。因此，只有在锚杆杆体破断较多的矿井，才有必要考虑提高杆体直径。
目前在混凝土行业GB标准和矿用锚杆行业标准中，规定螺纹在锚杆杆体的上升角不大于45°，但ASTM和BS中没有明确规定。有上升角的锚杆轴向承载后，会产生一个使杆体旋转的扭矩，上升角不同则扭矩的大小不同；但锚杆的轴向转动刚度非常大，不同上升角产生的轴向扭矩对锚杆轴向应力状态的影响可以忽略不计。因此，理论上螺纹上升角对锚杆轴向承载没有影响。
螺纹上升角在锚杆安装过程中有非常重要的作用。巷道锚杆安装一般使用树脂药卷锚固剂，左旋锚杆在搅拌锚固剂时螺纹逆着锚固剂流淌方向，防止阻碍锚固剂流速过快造成深部锚杆段锚固剂不足。右旋锚杆则相反，其螺纹加速锚固剂流淌，适用于安装阻力大情况，例如煤帮支护的水平钻孔等。
螺纹上升角不同也会造成锚杆机的安装阻力、转速、扭矩、进速等不同，但其大小和方向只在锚杆安装过程中发挥作用，一旦锚固剂顺利流淌并充满整个钻孔，上升角不再影响后续锚固体的载荷传递及锚固效果。
锚固力由螺纹承载，因此，螺纹肋宽应与其最大承载量相匹配。为保障螺纹的承载能力，煤炭科学研究院设计了大螺纹宽度的锚杆，降低螺纹承载时的应力集中。但是，增加肋宽的同时也降低了螺纹滑移的位移量，因此，螺纹宽度优化应综合考虑其承载能力和锚固段的总吸能。
螺纹的肋坡角是螺纹几何优化研究的重要内容。20世纪70年代前，学术界普遍认为螺纹肋坡角的法向即为钢筋对周围介质作用的最大主应力方向。20世纪70年代钢混黏聚力基础理论研究取得了突破性进展[40,48]，认识到螺纹几何的肋坡角(图2中α)并非承载角，而包含临近介质在内的锥形角(图2，3中i)才是螺纹的承载角，其法向方向是周围介质最大主应力方向逐渐成为学术界共识。
承载角后续研究[42,44,46]发现，在螺纹肋坡角较小情况下，其角度变化对锚固性能依然有一定影响。综合相关研究，可以认为：在肋坡角较大情况下，例如>45°，锚固破坏首先是周围介质的压破坏，然后螺纹与残留介质组合生成一个较小的承载角，并参与后续锚固力峰后阶段的力学行为；在肋坡角较小情况下，例如<30°，由于钢-树脂黏结强度小于树脂本身的抗剪强度，因此螺纹与周边介质的破坏面就是钢-树脂交界面，此时的螺纹肋坡角等于后续剪涨滑移的承载角。
目前，钢筋及矿用锚杆行业标准都规定肋坡角>45°，实践中钢筋和锚杆螺纹肋坡角都>70°，所以，锚杆螺纹肋坡角不是锚固段峰后阶段的承载角。在锚杆螺纹几何优化中，肋间距与肋高需要相互匹配，在肋高2 mm时，15°肋坡角的肋宽已经>15 mm，因此，螺纹优化中无法选取非常小的肋坡角设计。
在固定肋间距条件下，早期锚杆肋高研究[28]结果显示一定程度增加肋高可提升锚固力。后续研究[16,42]提出了肋高与肋间距匹配的原则。在平行直剪破坏条件下，增加肋高不改变锚固段的破坏方式，锚固力提升仅是破坏圆柱面半径增加造成的；在剪涨滑移破坏方式下，增大肋高能提高周围介质的径向位移量，可以明显提高锚固段的残余强度。因此，在肋高和肋间距匹配情况下，增加肋高可以提高锚固段的吸能能力。
增加肋高会对锚固工艺产生影响，锚杆直径不变情况下，增加肋高需增加钻孔直径，锚固剂用量及锚杆机的安装阻力需相应增加。目前，钢混结构国标及矿用锚杆行业标准规定螺纹钢肋高为1～2 mm。
锚杆螺纹肋间距优化是螺纹几何的重点研究内容，国内外学者采用实验室拉拔试验方法对肋间距进行参数优化研究，但优化结果并不一致，文献[29-35]试验研究得到的最佳肋间距分别是54.8,37.5,33.0,48.0和24.0 mm。后续研究发现[49]，实验室拉拔试样不同，则锚固力也不同。上述各个肋间距研究结果的差异，是由于研究者使用的锚杆、锚固剂、套筒、三径等不同造成的。
实验室拉拔试样使用的套筒是对现场围岩的模拟，因此在实验室拉拔试验中应选用与现场围岩径向刚度相同的套筒，以增加试验结果的可靠性。对于工矿现场来说，由于各工矿现场地质条件差异较大，而锚固力与地应力、围岩条件、围岩力学属性等相关，即使选用相同锚杆、锚固剂和三径，锚固力也不同。因此，并不存在一个适合所有矿井的最佳肋间距，而只有某个特点地质条件下的最佳肋间距。
增加螺纹肋间距可以增加锚固段残余强度及系统吸能能力。在肋间距12 mm情况下，横肋产生锚固力的最大位移量是12 mm，增大肋间距可以增加残余锚固力的位移量。值得注意的是，理论上，2个相邻横肋之间是没有锚固力的，因此，肋间距优化应综合考虑承载点的密集程度与峰后残余强度持续的位移量，前者控制围岩的初始变形，后者控制围岩的持续变形。
基于前期研究成果，考虑螺纹几何对锚固性能的影响，采用增加锚固段残余强度的方法，本项研究开发出一种适合深部资源开采巷道围岩大变形条件的螺纹钢锚杆，如图5所示，螺纹参数见表2。
表2 围岩大变形锚杆外形参数
Table 2 Shape parameters of rock bolt with large deformation
直径/mm肋高/mm顶肋宽/mm底肋宽/mm肋间距/mm肋坡角/(°)2021.53.65060
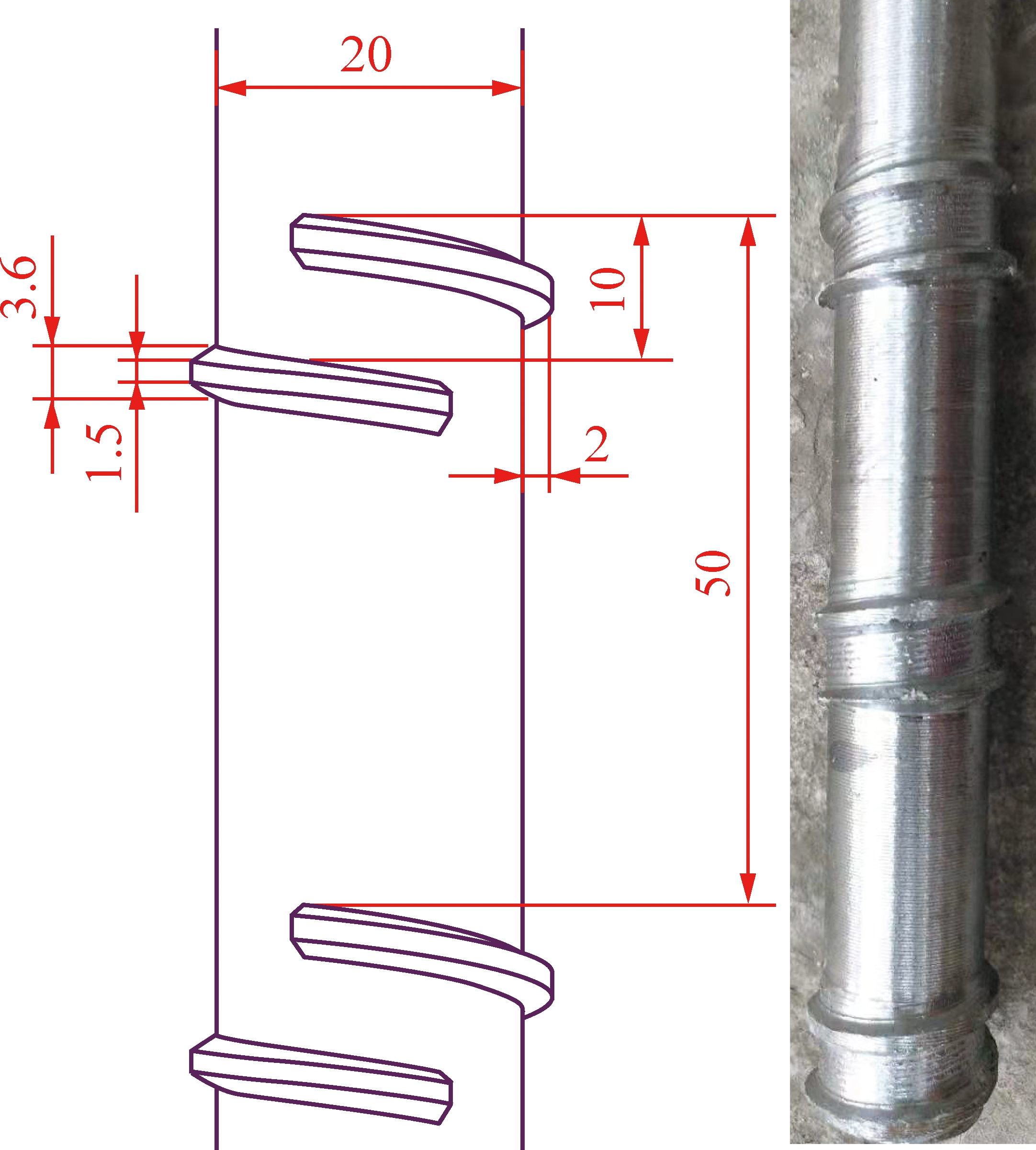
图5 围岩大变形锚杆示意
Fig.5 Schematic diagram of rock bolt with large deformation
杆体直径设计为20 mm，与目前矿用锚杆类似。在锚杆杆体破断较多的矿井应选用更大直径锚杆或其他支护措施。由于在拉拔试验中未观测到横肋破坏的现象，故新锚杆肋宽设计为1.5 mm，与左旋锚杆类似。新锚杆肋坡角设计为60°，符合目前矿用锚杆螺纹参数标准，且由于破坏方式为剪涨滑移，该角度大小不影响锚固段的残余强度。为增加锚固段峰后残余强度的大小，螺纹肋高设计为2 mm，是目前矿用锚杆螺纹设计行业标准的最大值。
围岩大变形锚杆的关键特征是肋间距50 mm，与肋间距12 mm锚杆相比，显著增加了残余锚固力的位移量。大肋间距锚杆的锚固性能在多项研究中得到了验证[29-35]，是极为可靠的设计。具体数字50 mm并无特殊意义，即与40～60 mm具有相同意义，只是由于前期肋间距研究范围都是12～50 mm。进一步明显增大肋间距，例如100 mm以上，理论上，可以进一步增加锚固段的吸能能力，但是，横肋减少导致整根锚杆产生锚固力的节点变少，对早期围岩控制及离层控制不利。在离层区域，采用全长锚固并增密锚杆应力点，是离层控制的有效手段，故50 mm肋间距是提高锚固段吸能能力与兼顾离层控制的折中设计。
与12 mm螺纹钢锚杆相比，新设计锚杆横肋数量较少，在锚杆安装过程中锚固剂流速变快，因此，新锚杆螺纹设计为左旋，使螺纹在锚固剂搅拌过程中阻碍锚固剂流淌；且在横肋重叠区域设计了1个10 mm的开口，进一步降低锚固剂流速。该开口设计并不改变锚杆的锚固性能，仅为配合目前国内常用锚杆机及锚固剂。新设计锚杆配套锚固剂为细料石粉填充剂树脂药卷锚固剂，锚固方式为全长锚固；在使用粗料填充剂的矿井应进行现场测试确定新锚杆的安装设备和工艺。
新设计锚杆对制造材料无要求，可使用矿井常用500或600号钢材，也可由高延展钢、或高吸能钢制造。新锚杆也可以与其他锚杆技术并行使用，例如加长锚杆、可伸长锚杆等；新锚杆也不影响联合支护设计，例如锚网与注浆、棚架等联合支护。
为研究围岩大变形锚杆的承载能力，对围岩大变形锚杆和常规左旋螺纹钢锚杆做了对比测试，左旋锚杆螺纹参数见表3。
表3 左旋锚杆外形参数
Table 3 Shape parameters of left spiral rock bolt
直径/mm肋高/mm顶肋宽/mm底肋宽/mm肋间距/mm肋坡角/(°)21.01.53.61265
锚固试样的锚固剂采用矿用树脂锚固剂(CKa2335)。针对典型深部软岩回采巷道，巷道顶板弹性模量设为20.0 GP，泊松比0.20的砂岩，平均水平地应力设为16 MPa，计算得到该地质条件的锚固段径向刚度与铝套筒类似；故选用内径为32 mm(模拟钻孔直径)和壁厚5.8 mm的6061铝管制作套筒，尽量保证锚固试样在锚杆受轴力作用下的径向形变与在该类顶板中一致。测试结果如图6(a)所示。
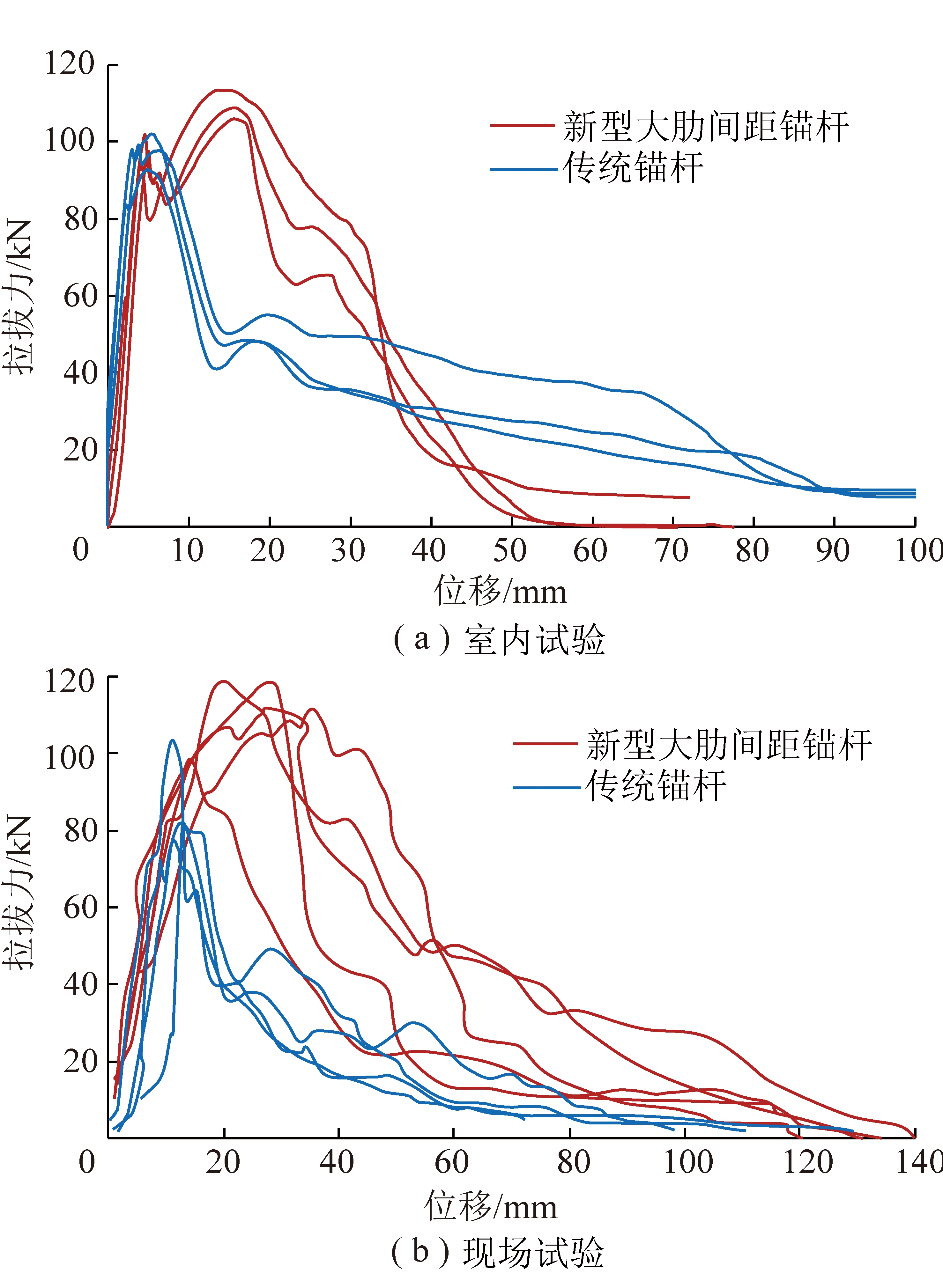
图6 室内和现场拉拔试验曲线
Fig.6 Pullout test curves in laboratory and field
同时，在钱家营煤矿2822工作面回风巷顶板进行了现场拉拔试验。该工作面埋深约700 m，地应力σ1，σ2和σ3分别为32.2,19.3和16.7 MPa。巷道主要支护形式为锚杆(索)网支护，但由于巷道收敛量较大，又采用了U型棚作为2次补强支护。钻孔平均直径31.8 mm，试验锚杆锚固长度200 mm。试验结果如图6(b)所示。
实验室和现场数据分析可知，围岩大变形锚杆拉拔力平均峰值分别为113.0 kN和118.0 kN，比左旋锚杆提高了13%和16%。从能量吸收的角度看，新锚杆在实验室和现场的平均吸能为3 169 J和3 351 J，较左旋锚杆提高了15%和55%。结果表明，在试验条件下，围岩大变形锚杆的锚固性能优于矿用的左旋锚杆。
新设计锚杆锚固性能现场测试地点选取在开滦(集团)有限责任公司钱家营矿业分公司(简称钱家营矿，下同)。近年矿井年产量约6.0 Mt，第1生产水平为-600 m水平，第2生产水平为-850 m水平，均属复合结构中厚煤层。地应力测试结果显示，钱家营地应力是以水平应力为主导，-850 m水平最大主应力36.04～36.85 MPa，高于其他煤矿区一般水平。平均主应力与垂直应力比值为1.61～1.68，最大主应力与最小主应力比值1.93～2.64，即最大水平主应力与最小水平主应力相差较大，最大主应力方位129°。
回采巷道采用金属拱型支架支护或锚杆支护，锚杆支护采用锚网、钢带、锚索联合支护，锚杆包括φ20 mm右旋锚杆和21.7 mm左旋锚杆，间排距700～1 000 mm，补强支护使用φ17.8 mm锚索，长度8 000 mm，锚杆(索)预紧力无具体要求，支护参数如图7所示。
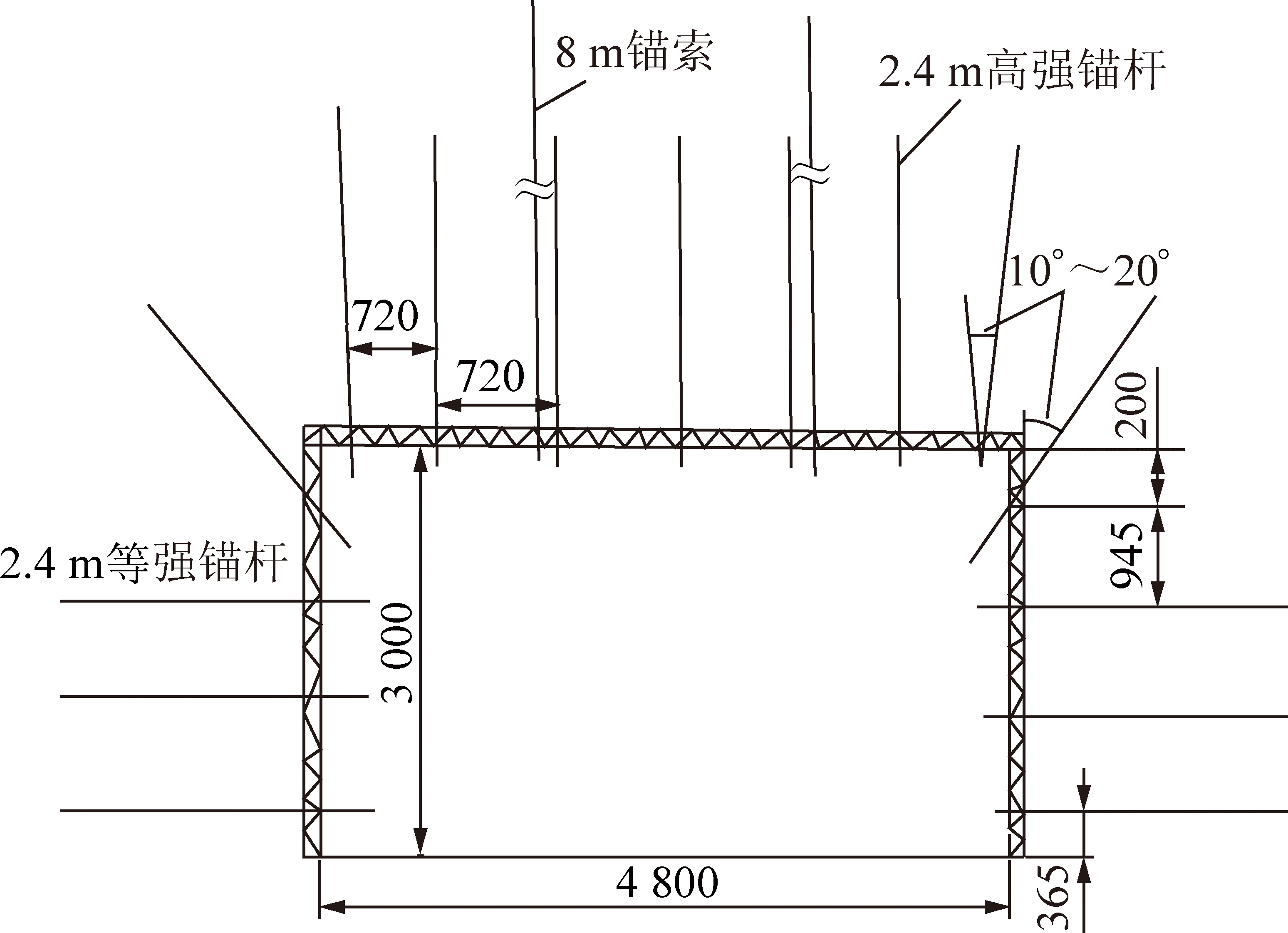
图7 锚杆支护参数示意
Fig.7 Schematic diagram of bolt support parameters
随着开采深度的不断增加，钱家营矿巷道支护带来诸多难题。棚架支护在巷道掘进较短时间即可能出现U型钢棚子大变形，在井下变形量大的位置测得两帮收敛量达1.7 m，顶底板移近量为0.7 m；锚杆支护出现部分锚杆破断失效情况，补强支护与巷道返修工作量日益增大，严重影响安全生产和经济效益，亟需针对围岩大变形的支护新材料、新技术。
选取钱家营煤矿2173回风巷进行井工试验，为类似地质条件回采巷道锚杆支护方案优化提供现场应用依据。试验巷道分3段，试验段1采用钱家营矿原有的端头锚固支护方式作为对照试验段；试验段2使用原有锚杆但采用全长锚固方式，锚固剂型号换用MSZ2850中速锚固剂；试验段3使用新型锚杆全长锚固支护，锚固剂为MSZ2850中速锚固剂。主要测试全长锚固方式及新型锚杆与原支护方案的差异，其他支护材料例如钢网、锚索、托盘、及间排距等参数,包括锚杆安装设备及操作工艺等与原支护相同。
试验检测量包括巷道两帮及顶底板收敛量(十字交叉方法)、锚杆破断或失效(现场统计)顶板离层及锚杆内力检测，测试时段从掘进工作面推进50 m至回采工作面超前支护抵达，约7个月，监测方案布置如图8所示。
图8 监测断面位置示意
Fig.8 Schematic diagram of monitoring section position
通过十字交叉测得3个监测断面的最大两帮收敛量和顶底板移近量见表4。结果显示，钱家营现有锚杆将端头锚固方式更改为全长锚固方式可以减少巷道变形，采用新型锚杆全长锚固方式后则可明显降低巷道围岩变形量。
表4 巷道变形监测结果
Table 4 Roadway deformation monitoring result mm
监测断面顶底板移近量两帮收敛量14471 13023818643298801
现场统计获得锚杆破断或失效数据见表5，结果显示新锚杆全长锚固可减少锚杆破断失效。
表5 试验巷道锚杆(索)失效统计
Table 5 Statistics of rock bolt failure in roadway 个
失效方式试验巷道1试验巷道2试验巷道3锚杆断裂754锚杆托盘脱落受损1274锚索托盘脱落受损111
顶板下沉量如图9所示，整体下沉量变化大小依次为：试验巷道1>试验巷道2>试验巷道3，且试验巷道1距顶板1.5 m处出现离层。因此，全锚锚固方式更有利于对顶板离层的控制，且围岩大变形锚杆支护方式顶板下沉量最小，进一步说明围岩大变形锚杆相对现有的锚杆支护方式效果较好。
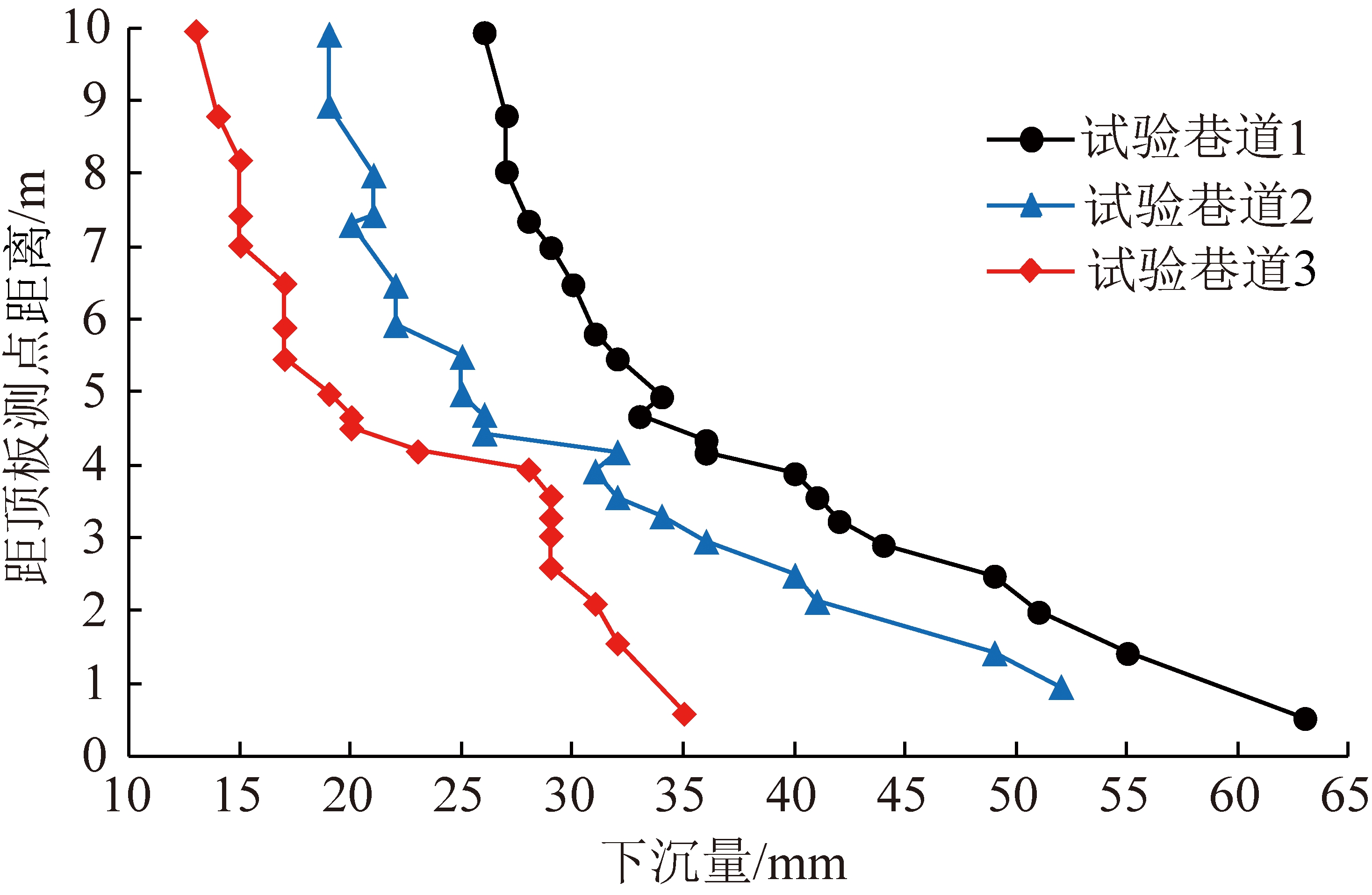
图9 顶板下沉量变化曲线
Fig.9 Roof subsidence change curves
顶板和巷帮锚杆受力如图10所示，顶锚杆受力受采动影响较明显，而巷帮无明显规律。从顶板锚杆受力曲线可以看出，试验巷道1,2受力无明显区别，都表现出较大的承载力，而试验巷道3受力依然处于锚杆的弹性阶段，具有较好的持久支护能力。
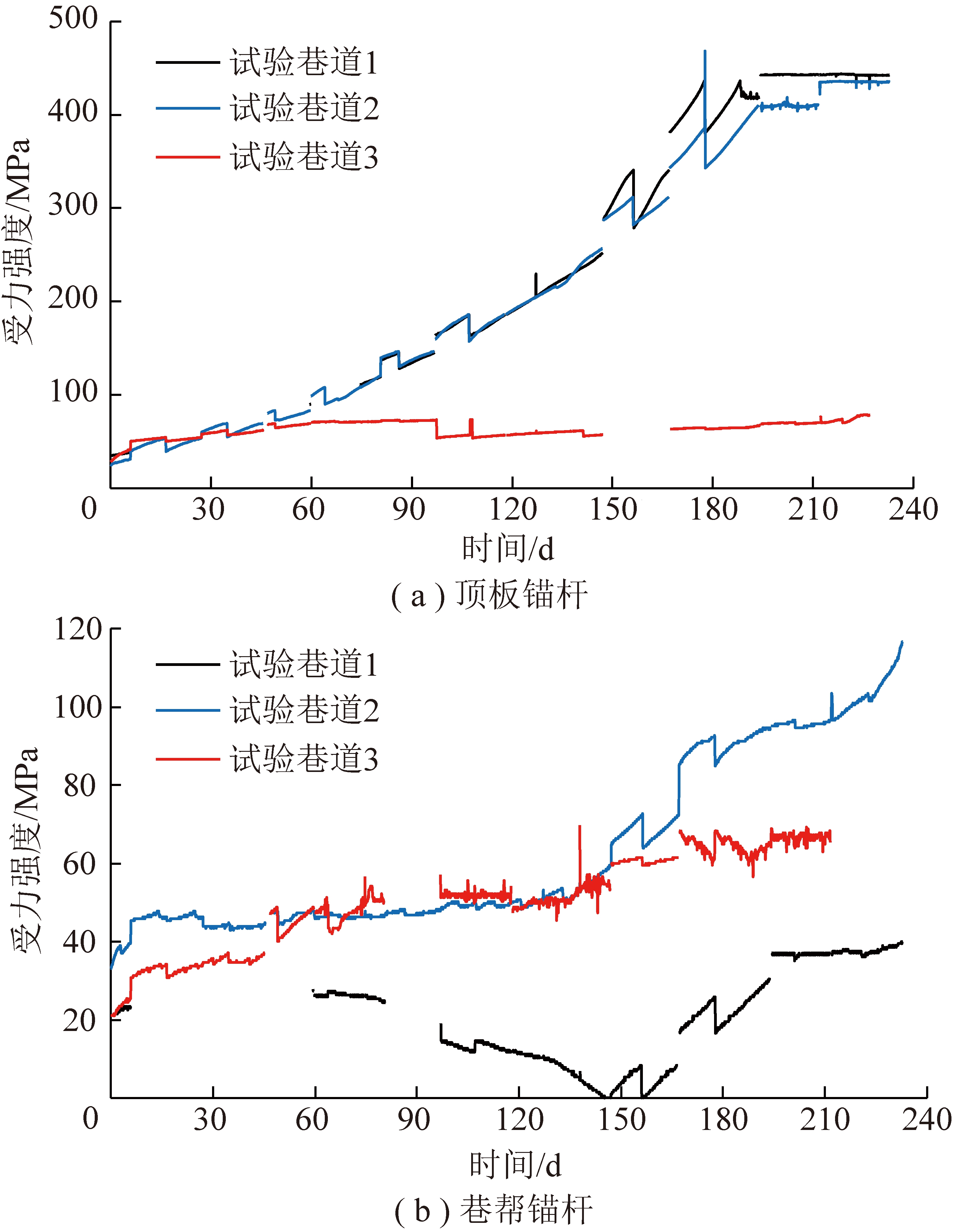
图10 顶板和巷帮锚杆受力变化曲线
Fig.10 Stress variation curves of roof and roadway side bolt
通过对比3种锚杆支护方案的巷道变形、锚杆破断、顶板离层和锚杆内力，综合分析，可以得出围岩大变形锚杆支护更有利于深部巷道围岩的控制这一结论。
(1)通过分析螺纹各参数对锚固性能的影响，明确了锚杆肋间距对提升锚杆锚固性能有重要作用；通过提高锚杆肋间距可控制锚固段发生剪涨滑移破坏，进而提高系统残余强度和吸能能力，并以此为依据，设计了一种适用于巷道围岩大变形的新型大肋间距锚杆。
(2)通过在实验室使用铝套筒模拟现场顶板围岩条件开展拉拔测试，结果表明，新型大肋间距锚杆锚固力可达113 kN，吸能能力为3169 J，较传统左旋锚杆分别提高了13%和15%；现场顶板拉拔测试表明，新型大肋间距锚杆锚固力为118 kN，吸能能力为3 351 J，较传统左旋锚杆分别提高了16%和55%。
(3)现场深部回采巷道支护工程应用表明，与传统矿用常规支护方式相比，使用全长锚固新型大肋间距锚杆支护有效减少了锚杆(索)破断失效现象；顶底板和两帮表面变形量减小了33.3%和29.1%；锚杆受力也依然处于弹性阶段，具有强的承载性能。
[1] 康红普. 我国煤矿巷道锚杆支护技术发展60年及展望[J]. 中国矿业大学学报,2016,45(6):1071-1081.
KANG Hongpu. Sixty years development and prospects of rock bolting technology for underground coal mine roadways in China[J]. Journal of China University of Mining & Technology,2016，45(6):1071-1081.
[2] 何满潮,郭鹏飞. “一带一路”中的岩石力学与工程问题及对策探讨[J]. 绍兴文理学院学报(自然科学),2018,38(2):1-9.
HE Manchao,GUO Pengfei. On problems of rock mechanics and engineering in the belt and road and their countermeasures[J]. Journal of Shaoxing University(Natural Science),2018,38(2):1-9.
[3] LI C C. A practical problem with threaded rebar bolts in reinforcing largely deformed rock masses[J]. Rock Mechanics and Rock Engineering,2007,40(5):519-524.
[4] LI C C. Field observations of rock bolts in high stress rock masses[J]. Rock Mechanics and Rock Engineering,2010,43(4):491-496.
[5] 刘洪涛,王飞,蒋力帅,等. 顶板可接长锚杆耦合支护系统性能研究[J]. 采矿与安全工程学报,2014,31(3):366-372.
LIU Hongtao,WANG Fei,JIANG Lishuai,et al. On the performance of lengthened bolt coupling support system in roadway roof[J]. Journal of Mining & Safety Engineering,2014,31(3):366-372.
[6] 刘洪涛,王飞,王广辉,等. 大变形巷道顶板可接长锚杆支护系统性能研究[J]. 煤炭学报,2014,39(4):600-607.
LIU Hongtao,WANG Fei,WANG Guanghui,et al. Research on lengthening bolt roof support system performance in largely deformed roadway[J]. Journal of China Coal Society,2014,39(4):600-607.
[7] 马念杰,赵希栋,赵志强,等. 深部采动巷道顶板稳定性分析与控制[J]. 煤炭学报,2015,40(10):2287-2295.
MA Nianjie,ZHAO Xidong,ZHAO Zhiqiang,et al. Stability analysis and control technology of mine roadway roof in deep mining[J]. Journal of China Coal Society,2015,40(10):2287-2295.
[8] 康红普,林健,吴拥政. 全断面高预应力强力锚索支护技术及其在动压巷道中的应用[J]. 煤炭学报,2009,34(9):1153-1159.
KANG Hongpu,LIN Jian,WU Yongzheng. High pretensioned stress and intensive cable bolting technology set in full section and application in entry affected by dynamic pressure[J]. Journal of China Coal Society,2009,34(9):1153-1159.
[9] HE Manchao,GONG Weili,WANG Jiong,et al. Development of a novel energy-absorbing bolt with extraordinarily large elongation and constant resistance[J]. International Journal of Rock Mechanics and Mining Sciences,2014,67:29-42.
[10] 郭志飚,王炯,张跃林,等. 清水矿深部软岩巷道破坏机理及恒阻大变形控制对策[J]. 采矿与安全工程学报,2014,31(6):945-949.
GUO Zhibiao,WANG Jiong,ZHANG Yuelin,et al. Failure mechanism and constant resistance large deformation control measures of deep soft rock in Qingshui Coal Mine[J]. Journal of Mining & Safety Engineering,2014,31(6):945-949.
[11] 荆升国. 高应力破碎软岩巷道棚-索协同支护围岩控制机理研究[D]. 徐州:中国矿业大学,2009:99-101.
JING Shengguo. Study on control mechanism of cooperating support of frame and anchor cable in soft fragmentized supporting rock roadway with high stress[D]. Xuzhou:China University of Mining and Technology,2009:99-101.
[12] 高明仕,赵一超,李明,等. 软岩巷道顶,帮,底全支全让O型控制力学模型及工程实践[J]. 岩土力学,2014,35(8):2307-2313.
GAO Mingshi,ZHAO Yichao,LI Ming,et al. Roof and support and bottom yielding support with whole section and O-shape control principle for soft rock roadway and engineering practice[J]. Rock and Soil Mechanics,2014,35(8):2307-2313.
[13] 郑朋强,陈卫忠,谭贤君,等. 软岩大变形巷道底臌破坏机与支护技术研究[J]. 岩石力学与工程学报,2015,34(S1):3143-3150.
ZHENG Pengqiang,CHEN Weizhong,TAN Xianjun,et al. Study of failure mechanism of floor heave and supporting technology in soft rock of large deformation roadway[J]. Chinese Journal of Rock Mechanics and Engineering,2015,34(S1):3143-3150.
[14] 王卫军,袁超,余伟健,等. 深部大变形巷道变形巷道围岩稳定性控制方法研究[J]. 煤炭学报,2016,41(12):2921-2931.
WANG Weijun,YUAN Chao,YU Weijian,et al. Stability control method of surrounding rock in deep roadway with large deformation[J]. Journal of China Coal Society,2016,41(12):2921-2931.
[15] CAO C,NEMCIK J,AZIZ N,et al. A study of rock bolting failuremodes[J]. International Journal of Mining Science & Technology,2013,23(1):79-88.
[16] CAO C,NEMCIK J,AZIZ N,et al. Analytical study of steel bolt profile and its influence on bolt loadtransfer[J]. International Journal of Rock Mechanics & Mining Sciences,2013,60:188-195.
[17] AYDAN O. Thestabilisation of rock engineering structures by rock bolts[D]. Nagoga:Nagoya University,1989:52-73.
[18] AZIZ N,JALALIFAR H,REMENNIKOV A,et al. Optimisation of the bolt profile configuration for load transfer enhancement[A]. Coal 2008:Coal Operators’Conference [C]. Wollongong:University of Wollongong,2008:125-131.
[19] ABRAMS D A. Tests of bond between concrete and steel[D]. Urbana:University of Illinois,1913:71.
[20] CLARK A P. Comparative bond efficiency of deformed concrete reinforcingbars[J]. Aci Journal Proceedings,1946,43(4):381-400.
[21] CLARK A P. Bond of concrete reinforcingbars[J]. Aci Journal Proceedings,1949,46(11):161-184.
[22] ASTM. A615/A615M-09 Standard specification for deformed and plain billet-steel for concrete reinforcement[S]. West Conshohocken:ASTM International,2004.
[23] GOTO Y,OTSUKA K. Experimental studies on cracks formed in concrete around deformed tension bars[J]. Contemporary Sociology,1980,294:85-100.
[24] MURATA J,KAWAI A. Studies on bond strength of deformed bar by pullouttest[J]. Journal of Japanese Society of Civil Engineering,1984,1:113-122.
[25] DARWIN D,GRAHAM E K. Effect of deformation height and spacing on bond strength of reinforcingbars[J]. Aci Materials Journal,1993,90(6):646-657.
[26] CAIRNS J,JONES K. Influence of rib geometry on strength of lapped joints:An experimental and analyticalstudy[J]. Magazine of Concrete Research,1995,47:253-262.
[27] DYBE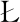
P,FURTAK K. The influence of high-strength concrete-rebars bond conditions on the mechanism of its failure[J]. Magazine of Concrete Research,2017,69(4):163-174.
[28] FABJANCZYK M W,TARRANT G C. Load transfer mechanisms in reinforcing tendons[A]. Proceedings of the 11th International Conference on Ground Control in Mining[C]. Morgantown:University of West Virginia,1992:1-8.
[29] BLUMEL M. Performance of grouted rock bolts in squeezing rock[A]. Proceedings of EUROCK’96,Predictions and Performance in Rock Mechanics and Rock Engineering[C]. Rotterdam:Balkema,1996:885-891.
[30] AZIZ N,WEBB B. Study of load transfer capacity of bolts using short encapsulation push test[A]. Coal 2003:Coal Operator’s Conference[C]. Wollongong:University of Wollongong,2003:72-80.
[31] AZIZ N,JALALIFAR H,CONCALVES J. Bolt surface configura-tions and load transfer mechanism[A]. Coal 2006:Coal Operators’Conference[C]. Wollongong:University of Wollongong,2006:236-244.
[32] 林健,任硕,杨景贺. 树脂全长锚固锚杆外形尺寸优化实验室研究[J]. 煤炭学报,2014,39(6):1009-1015
LIN Jian,REN Shuo,YANG Jinghe. Laboratory research of resin full-length anchoring bolts dimension optimization[J]. Journal of China Coal Society,2014,39(6):1009-1015.
[33] 林健,任硕. 树脂全长锚固锚杆外形尺寸优化数值模拟研究[J]. 采矿与安全工程学报,2015,32(2):273-278.
LIN Jian,REN Shuo. Numerical simulation optimization research of bolt profile configuration with resin full-length anchoring[J]. Journal of Mining and Safety Engineering,2015,32(2):273-278.
[34] 吴涛,CAO Chen,赵象卓,等. 不同肋间距锚杆锚固性能实验室试验研究[J]. 煤炭学报,2017,42(10):2545-2553.
WU Tao,CAO Chen,ZHAO Xiangzhuo,et al. Laboratory study on anchorage performance in different rib spacings of bolt[J]. Journal of China Coal Society,2017,42(10):2545-2553.
[35] 赵象卓,张宏伟,CAO Chen,等. 不同围岩条件下锚杆肋间距与锚固力优化研究[J]. 岩土力学,2018,39(4):1263-1270，1280.
ZHAO Xiangzhuo,ZHANG Hongwei,CAO Chen,et al. Optimization of bolt rib spacing and anchoring force under different conditions of surrounding rock[J]. Rock and Soil Mechanics,2018,39(4):1263-1270，1280.
[36] WINDSOR C R,THOMPSON A G. Rock Reinforcement-technol-ogy,testing,design and evaluation[J]. Excavation Support & Monitoring,1993,4:451-484.
[37] 官山月,马念杰. 树脂锚杆锚固失效的力学分析[J]. 采矿与安全工程学报,1997 (Z1):204-206.
GUAN Shanyue,MA Nianjie. Mechanical analysis of anchorage failure of resin anchorage rod[J]. Journal of Mining & Safety Engineering,1997 (Z1):204-206.
[38] 康红普,崔千里,胡滨,等. 树脂锚杆锚固性能及影响因素分析[J]. 煤炭学报,2014,39(1):1-10.
KANG Hongpu,CUI Qianli,HU Bin,et al. Analysis on anchorage performances and affecting factors of resin bolts[J]. Journal of China Coal Society,2014,39(1):1-10.
[39] AZIZ N,CRAIG P,MIRZAGHORBANALI A,et al. Factors influencing the quality of encapsulation in rockbolting[J]. Rock Mechanics and Rock Engineering,2016,49(8):1-15.
[40] TEPFERS R. Cracking of concrete cover along anchored deformed reinforcing bars[J]. Magazine of Concrete Research,1979,31:3-12.
[41] YAZICI S,KAISER P K. Bond strength of grouted cablebolts[J]. International Journal of Rock Mechanics and Mining Science & Geomechanics Abstracts,1992,29(3):279-292.
[42] CAO C,REN T,COOK C,et al. Analytical approach inoptimising selection of rebar bolts in preventing rock bolting failure[J]. International Journal of Rock Mechanics & Mining Sciences,2014,72:16-25.
[43] GAUDREAU D M,AUBERTIN S,SIMON R. Performance assessment of tendon support systems submitted to dynamicloading[A]. Ground Support in Mining and Underground Construction[C]. Balkema:Taylor & Francis Group plc,2004:299-312.
[44] KILIC A,YASAR E,CELIK A G. Effect of grout properties on the pull-out load capacity of fully grouted rock bolt[J]. Tunnelling and underground space technology,2002,17(4):355-362.
[45] CAI M,CHAMPAIGNE D. Influence of bolt-grout bonding on
MCBconebolt performance[J]. International Journal of Rock Mechanics & Mining Sciences,2012,49:165-175.
[46] LIANG Y,HE M,CAO C. A mechanical model forconebolts[J]. Computer & Geotechnics,2017,83:142-151.
[47] ST-PIERRE L,HASSANI F P,RADZISZEWSKI P H,et al. Development of a dynamic model for a conebolt[J]. International Journal of Rock Mechanics & Mining Sciences,2009,46(1):107-114.
[48] LUTZ L A,GERGELY P. The mechanics of bond and slip of deformed bars in concrete[J]. Aci Journal,1967,64(11):711-721.
[49] 韩军,张明,CAO Chen,等. 套筒刚度对左旋锚杆锚固力的影响研究[J]. 采矿与安全工程学报,2020,37(5):890-897.
HAN Jun,ZHANG Ming,CAO Chen,et al. The influence of sleeve stiffness on anchoring force of left spiral bolt[J]. Journal of Mining & Safety Engineering,2020,37(5):890-897.