
移动阅读

移动阅读
GUO Jianqiang,YANG Qiandong,LU Xuefeng,et al. Research on generalized unified strength theory of rock (mass) failure[J]. Journal of China Coal Society,2021,46(12):3869-3882.
在高地应力、高地温、高岩溶水压及强施工扰动的共同作用下,深部围岩会出现大变形(扩容)、巷道底臌(破坏)、高能级岩爆及分区破裂化等工程灾害[1-4]。由于浅部岩体力学理论没有考虑深部岩体真实应力环境和工程扰动状态,因此迫切需要发展适用于高应变能环境下岩体力学的新理论。扩容既与深地空间的有效利用密切相关(比如,扩容可导致深埋盐岩油气储库由于容积减小而失效),又是地震发生的先兆[5]。自Bridgman首次发现岩石存在扩容现象以来[6],国内外学者已提出了很多扩容准则[7-11],但这些扩容准则仅能体现出偏量弹性应变能(而非弹性应变能)是岩石扩容的内在机理[12],即已有扩容准则的数学表达式表征的物理涵义与扩容的内在机理不一致。
强度准则选择对更好地发挥材料的强度潜力、减轻结构自重及节约能源均具有十分重要的作用,且结构的破坏防控在很多情况下依赖于所选择的强度理论[13-14]。尽管国内外已提出了上百个强度准则,但这些强度准则同样仅能反映出偏量弹性应变能(而非弹性应变能)是岩石屈服或破坏的内在机理[15-22],即当前强度准则的数学表达式表征的物理涵义与屈服或破坏的内在机理同样也不一致。
国内外研究均指出弹性应变能突然释放是岩爆发生的内在机理[23-26],但当前岩爆判据的数学表达式所体现的物理含义与岩爆发生的内在机理并不统一[18,27],这很可能是已有岩爆判据精度与适用性不高的重要原因之一。
针对深地环境下变形能高度积聚或震源释放的应变能是否会导致深部岩体发生扩容、屈服或破坏及岩爆等问题,扩容准则、强度准则及岩爆判据发展相对较为滞后。一方面,这些准则所表征物理含义本质上仍以1773年Coulomb提出的最大剪应力(或材料单元体上的剪应力与正应力组合达到某一极限值时)为基础,未全面考虑物质能量状态,而能量转化是物质物理过程的本质属性[15-16];另一方面,这些准则在应用广度上有待提高。比如,强度准则的计算表明岩体未破坏,这既未阐明当前应力水平下是否扩容,又未揭示地震释放应变能或支护结构劣化后是否扩容、破坏抑或是岩爆;同理,若计算结果表明未扩容或无岩爆活动,这也未阐明地震释放应变能或支护结构劣化后是否扩容、破坏抑或是岩爆。由此可见,建立扩容准则、强度准则及岩爆判据的统一数学表达式,并使其能够反映地震释放应变能与支护结构影响就显得很有必要。为便于阐述,作如下定义:本文后面广义统一强度理论或稳定性判别准则是扩容准则、强度准则及岩爆判据的统一表达式的总称。
深地空间原位试验与监测难度相对较大,其设计与稳定性计算主要依赖于所选择的判别准则。基于可释放应变能是材料扩容、屈服或破坏的根本原因[12,16],以现有强度准则为基础,建立能反映深部岩体赋存环境高能级、大体量工程灾害的强度理论;然后利用强度理论对国内外经典扩容应力、真三轴强度及一些重大深部岩石工程岩爆进行计算,并与地球物理研究中普遍适用的Byerlee定律进行比较;最后利用该理论对地震作用下深部岩体稳定性进行研究。
物质物理过程须遵守能量守恒定律[15-16],即
U=Ud+Ur
(1)
Ur=Ue+Urx=(UeJ2+UeI2)+Urx
(2)
式中,U为材料单位体积的总输入能量;Ud为材料单位体积的耗散能,满足热力学熵增原理,反映了材料的强度不断劣化[15-16];Ur为单位体积的可释放应变能,使材料发生破坏;Ue为与材料应力状态有关的单位体积的弹性应变能,可全部释放;Urx为除弹性应变能之外,由其他因素引起的单位体积的可释放应变能总称,比如,震源释放应变能等;UeJ2,UeI2分别为偏量弹性应变能与张量弹性应变能[17-19]。
(1)三轴压缩条件下材料单位体积的总能量U[15]计算公式为
U=![]() σ1dε1+
σ1dε1+![]() σ2dε2+
σ2dε2+![]() σ3dε3
σ3dε3
(3)
式中,σi(i=1,2,3)分别为最大主应力、中间主应力及最小主应力;ε1,ε2,ε3分别为与主应力相对应的主应变。
式(3)为一般式,既适用于各向同性材料,也适用于各向异性材料,即ε2≠ε3,ε2=-ν2ε1,ε3=-ν3ε1时,式(3)可简化为式(4)第1个公式。为分析方便,假定试验中σ2=σ3,ε2=ε3=-νε1,则式(3)可简化为式(4)第2个公式。
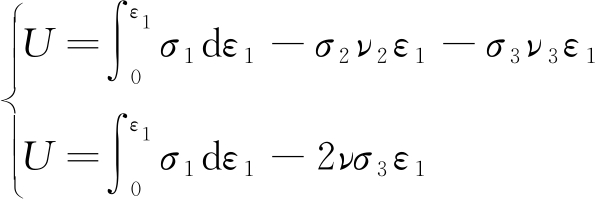
(4)
式中,ν为泊松比;ν2,ν3为各向异性材料不同方向的泊松比。
(2)弹性应变能计算公式为

(5)
(6)
(7)
式中, E为材料损伤后弹性模量,随着损伤增加,由无损伤时初始弹性模量E0逐渐减小至0[16];I2为应力张量第二不变量;![]() 分别为应力及广义应力偏量第二不变量。
分别为应力及广义应力偏量第二不变量。
由式(3)~(7)可看出:① 泊松比及应力张量第二不变量对弹性应变能计算有影响。ν=0.5时,Ue仅与J2及E有关,与I2无关;I2<0时,泊松比越小Ue越大;反之,I2>0时,泊松比越大Ue越大。② 偏量弹性应变能与张量弹性应变能均对材料物理过程有影响。因此,仅考虑UeJ2或UeI2对岩石扩容、屈服或破坏及岩爆的影响,必然存在一定问题。③ 弹性应变能随弹性模量减小而增加。因此,在其他条件不变情况下,随着损伤增加材料弹性应变能将逐渐增加。④ 泊松比对总能量具有显著影响。
可见,泊松比对总能量U、弹性应变能Ue(或张量弹性应变能UeI2,或可释放应变能Ur)具有显著影响。因此,泊松比在物质物理过程中具有十分重要作用。
基于能量转化是物质物理过程的本质属性,在判别高应变能环境下深部岩体是否扩容、屈服或破坏及岩爆可能性时,相应的扩容准则、强度准则及岩爆判据均应能够体现能量转化的属性,否则其计算精度与适用性必然会受到限制。
外力输入总能量一部分转化为耗散能![]() 使材料损伤程度加剧,从而导致单元体破坏时所需的表面能
使材料损伤程度加剧,从而导致单元体破坏时所需的表面能![]() 逐渐降低;另一部分转化为单元体可释放应变能
逐渐降低;另一部分转化为单元体可释放应变能![]() 且
且![]() 时,单元体将发生破坏[16]。基于此,对岩体扩容、破坏及岩爆进行简单分析。由于岩体是包含各种地质缺陷的非均质体,当破坏的单元体
时,单元体将发生破坏[16]。基于此,对岩体扩容、破坏及岩爆进行简单分析。由于岩体是包含各种地质缺陷的非均质体,当破坏的单元体![]() 引起的体积增加大于未破坏单元体体积的压缩量时,岩石发生扩容;随着荷载的进一步增加,当破坏的单元体
引起的体积增加大于未破坏单元体体积的压缩量时,岩石发生扩容;随着荷载的进一步增加,当破坏的单元体![]() 形成贯通的破裂面时,岩石发生破坏;当岩石可释放应变能大于破坏所需的表面能,
形成贯通的破裂面时,岩石发生破坏;当岩石可释放应变能大于破坏所需的表面能,![]() 构成了碎裂岩块的动能。可见,可释放应变能是精确描述岩体扩容、破坏及岩爆关键。
构成了碎裂岩块的动能。可见,可释放应变能是精确描述岩体扩容、破坏及岩爆关键。
基于已有研究成果[7-19],扩容准则与强度准则均能用统一表达式(8)表示。为了解式(8)与能量守恒定律及可释放应变能关系,在其左右两边同时乘以3/(2E),得到以能量形式表示的扩容准则与强度准则,如式(9)所示;反之,式(9)左右两边同时除以3/(2E),得以应力不变量表示的扩容准则与强度准则,如式(8)所示。
J2=f(I1,J3,K1,K2,K3)
(8)
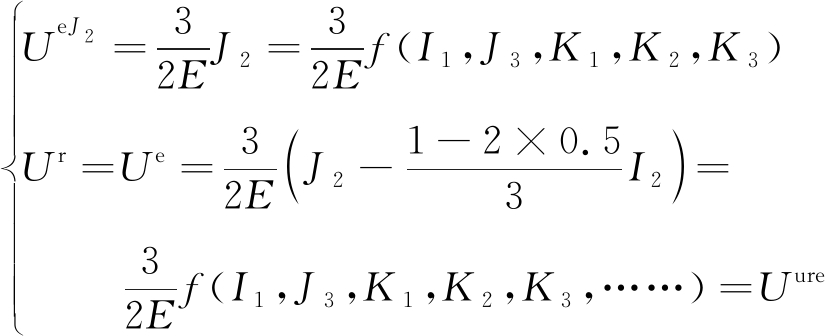
(9)
式中,J3为应力偏量第三不变量;I1为应力张量第一不变量;Ki(i=1,2,3,……)为材料参数;Uure为材料破坏时极限抵抗能。
式(9)左边为弹性应变能,根据量纲和谐原理,显然式(9)右边Uure也应为能量。因此,称之为材料破坏时极限抵抗能。
张量弹性应变能UeI2及其他因素引起的可释放应变能Urx均属于可释放应变能范畴,而不属于耗散能Ud,因此,弹性应变能的释放应是张量弹性应变能与偏量弹性应变能同时释放。由式(1),(2)与式(8),(9)可以看出,已有扩容准则与强度准则具有以下特点:
(1)已有扩容准则与强度准则仅反映了偏量弹性应变能UeJ2的影响,但未完整体现可释放应变能是材料扩容与屈服或破坏的基本原理[7-19]。可见,已有扩容准则与强度准则本质上也是弹性应变能形式强度准则。
(2)当前扩容准则与强度准则不能计算震源释放的应变能Urx及支护结构抗力对深部岩体的稳定性影响。
(3)已有扩容准则与强度准则将材料在任意应力水平下扩容及破坏时泊松比恒看作0.5。由此可见,当且仅当不考虑Urx,且材料在扩容与破坏时泊松比等于0.5或泊松比与0.5较为接近条件下,扩容准则与强度准则计算精度与适用性才可能较好。
综上所述,一方面若扩容准则与强度准则未能体现可释放应变能是材料扩容及屈服或破坏发生的内在机理,则其计算精度与适用性必然会较低;另一方面这也表明从可释放应变能角度建立扩容准则及强度理论,将能够有效地提高其计算精度。
岩爆强弱通常会被划分为无岩爆活动、弱岩爆活动、中等岩爆活动及高岩爆活动4个等级。一方面,大部分岩爆判据未能体现可释放应变能释放是岩爆发生的内在机理[23-26];另一方面,当前岩爆判据只能解决深地空间是否发生岩爆,但不能对能量释放后深地空间是否还会发生岩爆或其他失稳现象进行预测。
鉴于可释放应变能是材料扩容、屈服或破坏及岩爆发生的内在机理[12,15-19],这为建立扩容准则、强度准则及岩爆判据的统一表达式提供了理论基础。为建立能反映深地环境中变形能高度积聚的扩容准则、强度准则及岩爆判据,以式(9)第1个公式为基础,并考虑深部岩体的完整性及支护结构产生的抗力等影响因素,提出当可释放应变能Ur达到相应的临界抵抗能后,岩石就会发生扩容、屈服或破坏及岩爆,并参考平衡失稳、发生动力失稳过程还必须满足动力过程的准则[28-29],建立能描述扩容、屈服或破坏及岩爆的广义统一强度理论。其中,式(10)为能量形式表示的广义统一强度理论,该式左右两边同时除以3/(2E),可得以应力不变量表示的广义统一强度理论(式(11))。为便于建立扩容准则、强度准则及岩爆判据的统一表达式,引入广义统一强度理论判据指数RG(式(12))。
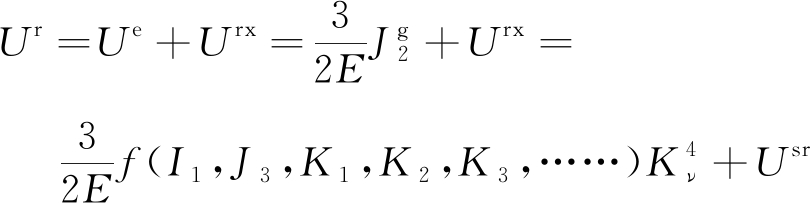
(10)
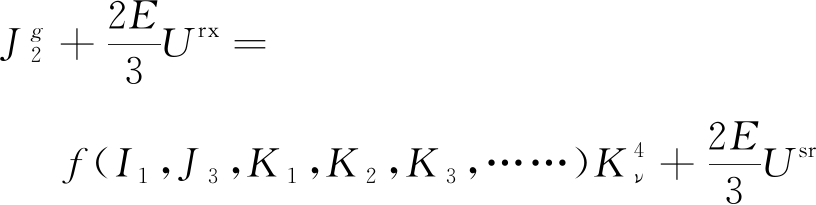
(11)

(12)
(13)
式中,Kν为深部岩体完整性系数,反映了岩体完整性,取值范围0~1.0,对于岩石Kν=1.0;Usr为支护结构在单位体积的围岩上产生的抵抗能,与支护结构抗力相对应;RG称为广义统一强度理论判据指数;Ksf为工程结构的安全系数,与RG互为倒数,可用于计算工程结构在原岩应力、支护结构及震源释放应变能等因素共同作用下安全裕度。
需要说明:一方面,非理想弹塑性材料岩石的泊松比确定较为困难[17-19,27,30-33];另一方面,借鉴已广泛地应用于边坡、深埋隧洞及矿产资源开采等工程领域的经验型强度准则,如H-B强度准则[34-37]与地球物理研究中常用的经验性强度准则Byerlee强度准则[38]等,将广义统一强度理论中泊松比看作是一个可通过对试验数据拟合而得变形参数(为了表述方便仍称为泊松比),且对其大小不作限制,从而避免理想弹塑性材料泊松比取值范围-1.0~0.5的限制。
由式(10)~(13)可以看出,广义统一强度理论具有如下特点:
(1)广义统一强度理论体现了可释放应变能Ur是材料扩容、屈服或破坏及岩爆的内在机理,既能计算高应变能环境下深部岩体扩容、屈服或破坏,又能计算是否发生岩爆。
(2)广义统一强度理论体现了原岩应力、岩体完整性、泊松比、弹性模量、震源释放应变能Urx及支护结构的抵抗能等对深部岩体稳定性影响。
(3)广义统一强度理论能够直接计算出不同支护条件与不同震级条件下,深地工程的安全系数。由广义统一强度理论(式(12))可以看出,支护结构抵抗能能够明显地减轻震害,即地下工程的震害小于上部结构震害根本原因是地下工程的支护结构产生抵抗能。
(4)广义统一强度理论的统一主要体现在以下3个方面:① 广义统一强度理论的数学表达式表征的物理涵义与可释放应变能是岩体扩容、破坏及岩爆发生的内在机理相统一。② 实现了扩容准则、强度准则及岩爆判据的数学表达式的统一,便于判断深部岩体是扩容、破坏抑或是岩爆。③ 将地震释放的应变能与支护结构影响统一于同一个表达式,实现了地震前后及支护前后数值计算模型的统一。
综上所述,广义统一强度理论解决了现有扩容准则、强度准则及岩爆判据不能直接计算震源释放应变能及支护结构对岩体稳定性影响。
为了利用已有研究成果,以M-C强度准则(式(14))为基础,并结合式(12),初步建立的广义M-C统一强度理论(GUM-C)如式(15)所示,显然,ν=0.5,Urx=Usr=0时蜕化为M-C强度准则。
(14)
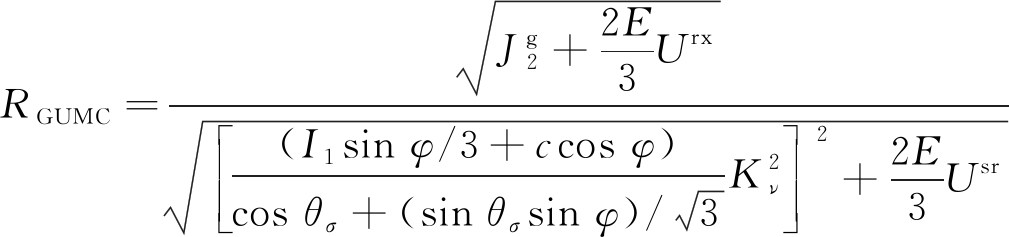

(15)
式中,RGUMC为广义M-C统一强度理论(GUM-C)判据指数;c,φ分别为材料黏聚力与摩擦角;θσ为罗德角。
由于岩爆判据常涉及岩石单轴抗压强度(σc)及抗拉强度(σt)。因此,在试验资料缺少情况下,式(15)中c,φ与σc及σt关系可按式(16)[14]确定。
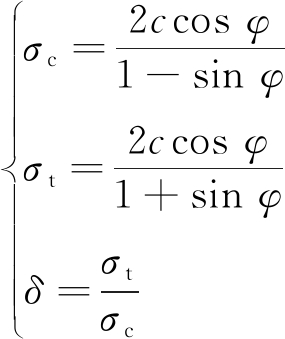
(16)
式中,δ为单轴抗拉强度与单轴抗压强度之比。
由于强度为材料的固有属性,其不会因震源释放应变能Urx或支护结构抵抗能Usr的存在而增加或减小。因此,依据试验资料对式(15)进行率定时,Urx=Usr=0。为确定广义M-C统一强度理论界限值,以侯文诗等[7]给出的扩容应力(表1)为模拟样本(期望模拟结果见表1),提出扩容界限值为0.9,并参考文献[18]岩爆分级界限值,得出广义M-C统一强度理论扩容、屈服或破坏及岩爆判据分级标准如式(17)所示。表1中,νd为由扩容应力拟合而得泊松比。
表1 岩石峰值应力扩容应力参数[7]
Table 1 Parameters of dilatation and peak[7]
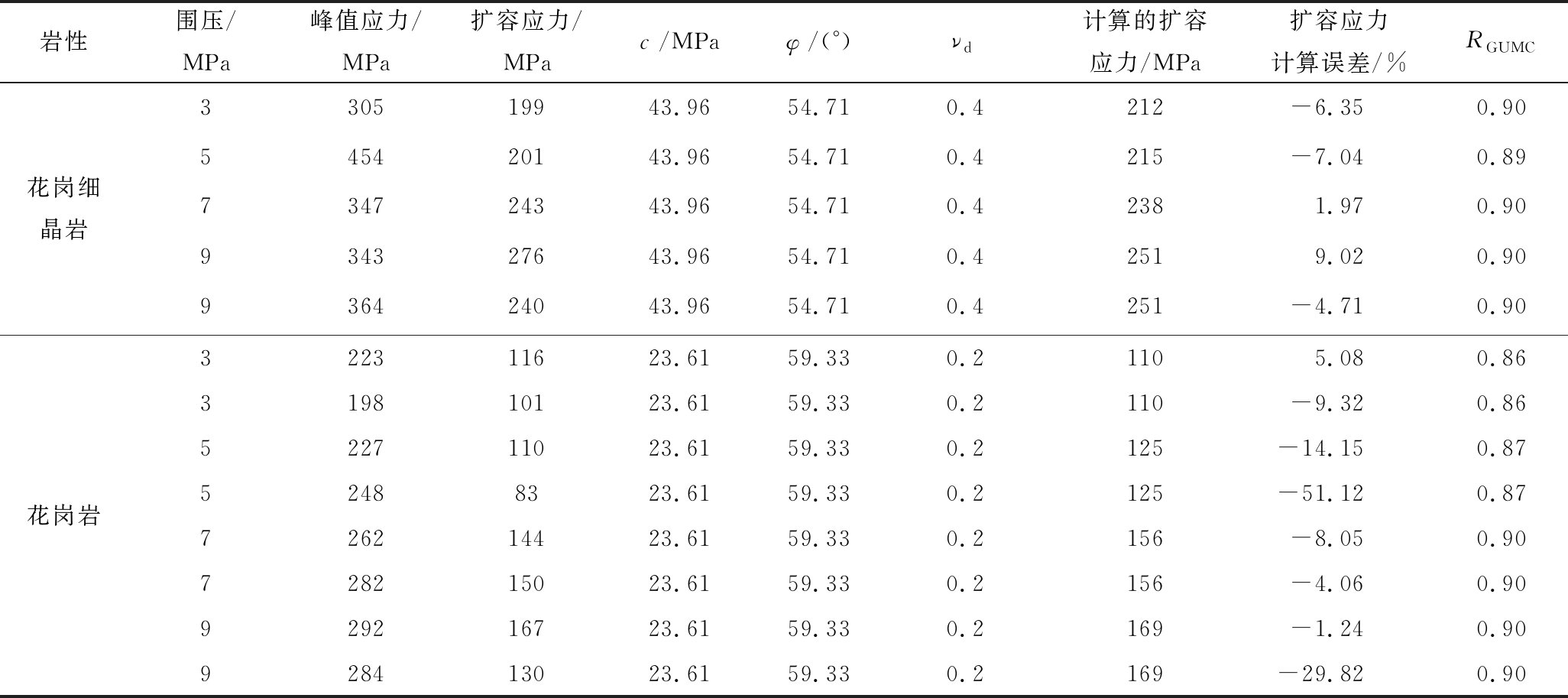
注:黏聚力c与摩擦角φ由峰值强度拟合而得。
岩性围压/MPa峰值应力/MPa扩容应力/MPac/MPaφ/(°)νd计算的扩容应力/MPa扩容应力计算误差/%RGUMC花岗细晶岩330519943.9654.710.4212-6.35 0.90545420143.9654.710.4215-7.040.89734724343.9654.710.42381.970.90934327643.9654.710.42519.020.90936424043.9654.710.4251-4.710.90花岗岩322311623.6159.330.21105.080.86319810123.6159.330.2110-9.320.86522711023.6159.330.2125-14.150.8752488323.6159.330.2125-51.120.87726214423.6159.330.2156-8.050.90728215023.6159.330.2156-4.060.90929216723.6159.330.2169-1.240.90928413023.6159.330.2169-29.820.90

(17)
由表1可以看出:花岗细晶岩扩容应力随围压增加表现为逐渐增大趋势,计算的理论扩容应力误差较小,RGUMC=0.89~0.90;由于花岗岩扩容应力离散性较大,这导致了计算的理论扩容应力误差也较大,RGUMC=0.86~0.90。因此,考虑岩石离散性,扩容应力界限值取0.90。
为验证广义统一强度理论在扩容应力计算中的有效性,利用式(17)对三轴压缩条件下花岗岩与砂岩的扩容应力进行了计算。由表2可看出:广义M-C统一强度理论计算结果与试验结果基本一致,但围压小于25 MPa时,砂岩扩容应力的计算结果相对较差,且νd偏小。
由于原岩应力、岩体完整性及施工扰动等多种因素均对深部岩体扩容有影响。因此,根据表2计算结果,可将深地空间扩容分为3种情况:① 不考虑震源释放的应变能影响,对ν=0时深部岩体的扩容进行计算。显然,若ν=0时无扩容,则在无其他能量输入情况下,施工后期岩体将不会出现扩容现象。② 不考虑震源释放的应变能影响,若ν=0时存在扩容现象,则可利用式(17)反演得出岩体扩容的极限泊松比,据此利用不同时段测定的泊松比判断岩体是否扩容,或依据泊松比随时间演化规律判断深部岩体将何时停止扩容。③ 若理论计算表明深部岩体不存在扩容现象,但监测资料表明深地存在扩容现象,则可利用式(17)反演地震释放的应变能Urx,这从理论上解决了扩容是地震发生的先兆问题[5]。④ 由式(17)可看出,增加支护结构抵抗能或减小侧向变形与轴向变形比值(泊松比),均能控制深部岩体扩容。
表2 岩石峰值应力扩容应力参数
Table 2 Parameters of dilatation and peak

岩性围压/MPa峰值应力/MPa扩容应力/MPac/MPaφ/(°)νd计算的扩容应力/MPa扩容应力计算误差/%RGUMC花岗岩[39]0175.00135.0031.9351.520.40133.001.340.905206.00170.0031.9351.520.40162.004.650.9010265.00215.0031.9351.520.40190.0011.630.9020367.00277.0031.9351.520.49257.007.250.9030450.00355.0031.9351.520.49318.0010.350.9040504.00402.0031.9351.520.49380.005.570.9050567.00461.0031.9351.520.49442.004.140.90砂岩[40]20113.0345.0217.9628.120.0767.05-48.930.9025130.4054.5917.9628.120.0768.99-26.380.9030146.0069.7917.9628.120.1073.99-6.020.9035159.7274.9917.9628.120.1075.28-0.390.9040167.9483.7817.9628.120.1075.809.520.90
可见,广义M-C统一强度理论既可用于高应变能环境下深部岩体扩容及地震预测,又为深地空间监测提供新思路,即应加强深地空间侧向变形与轴向变形比值(泊松比)变化趋势监测。因此,基于深地空间侧向变形与轴向变形比值的监测数据,可利用广义M-C统一强度理论对能量释放后深地空间是否还会发生岩爆或其他失稳现象进行初步预测。
为验证广义M-C统一强度理论,对白云岩真三轴强度进行了计算(Urx=Usr=0),结果如表3,4及图1,2所示。

图1 白云岩屈服强度计算
Fig.1 σ1 by test and yield strength criterion of dolomite
表3 广义统一强度理论材料参数
Table 3 Parameters in the full energy twin-shear unified strength theory
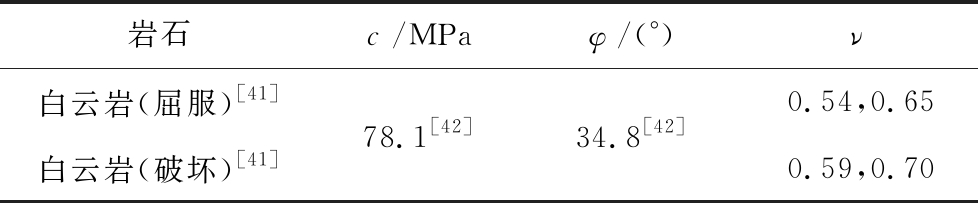
岩石c/MPaφ/(°)ν白云岩(屈服)[41]白云岩(破坏)[41]78.1[42]34.8[42]0.54,0.650.59,0.70
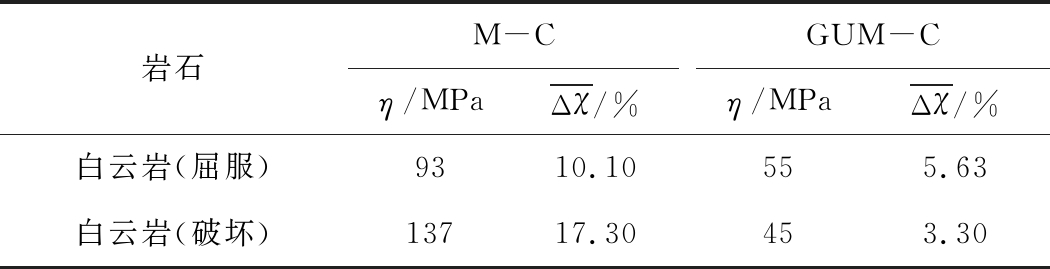
由于真三轴试验时最小主应力与中间主应力范围较广(白云岩试验时最小主应力为25~145 MPa、中间主应力25~516 MPa)。因此,在广义M-C统一强度理论对试验数据进行拟合时采用了2个拟合泊松比,并用均方根误差[44]、平均误差处理的各强度准则第1主应力计算误差(表4)。
表4 最大主应力均方根误差与平均误差
Table 4 Root-mean-square error of σ1
岩石M-Cη/MPaΔχ/%GUM-Cη/MPaΔχ/%白云岩(屈服)9310.10555.63白云岩(破坏)13717.30453.30

图2 白云岩破坏强度计算
Fig.2 σ1 by test and failure strength criterion of dolomite
(18)
(19)
(20)
式中,Δ χi为第i样品计算误差;σTi为第i样品最大主应力;σCTi为第i样品理论计算的最大主应力;![]() 为平均误差;n为试验数量;η为均方根误差。
为平均误差;n为试验数量;η为均方根误差。
由表3,4及图1,2可以看出,广义M-C统一强度理论能较好地描述岩石屈服强度与破坏强度。比如,广义M-C统一强度理论计算屈服强度与破坏强度平均误差分别为5.63%,3.30%,远小于M-C强度理论误差10.10%,17.30%。
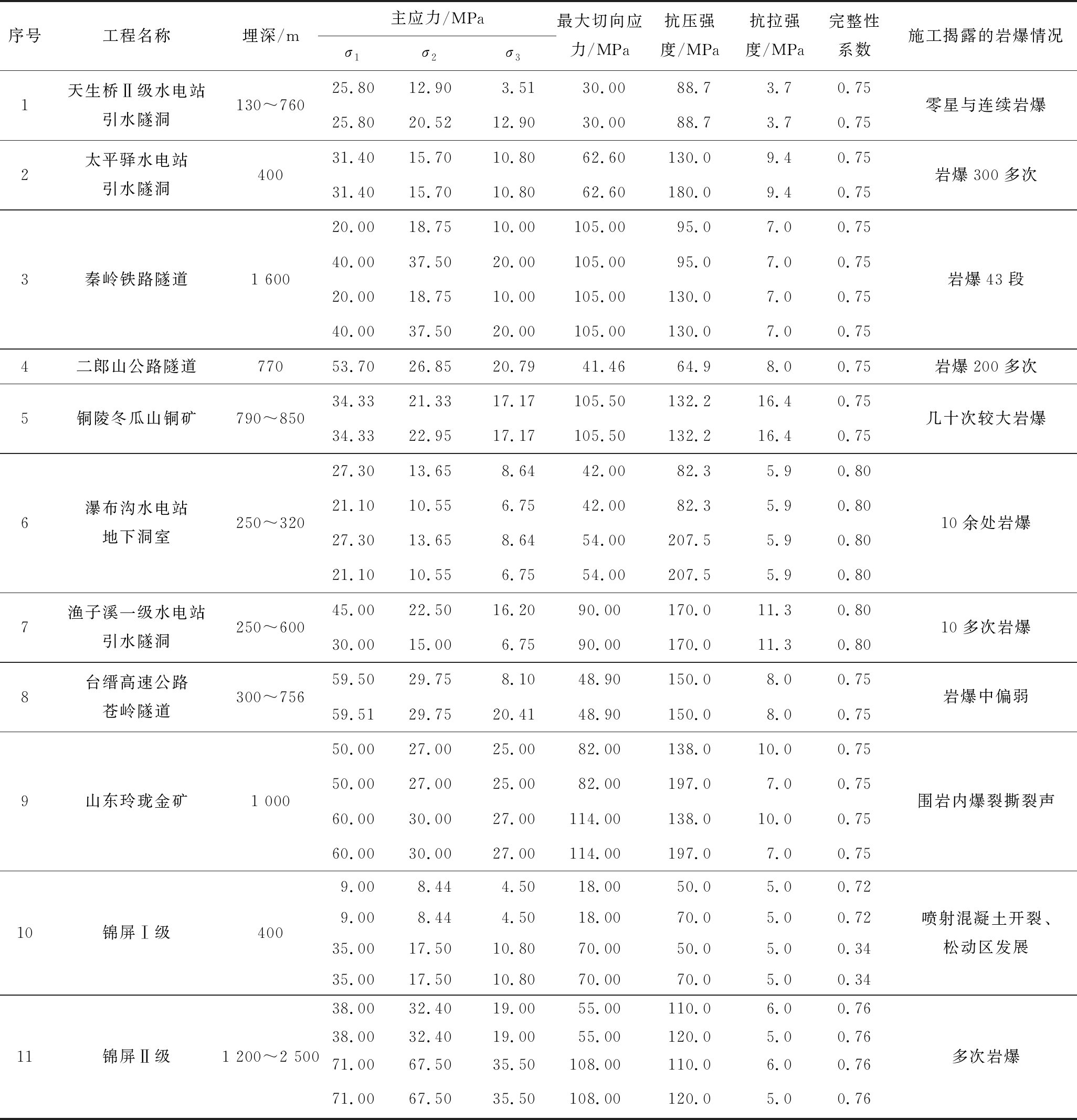
表5中典型工程的实测资料(比如,锦屏I级工程中喷射混凝土开裂、松动区发展)表明:① 岩爆既可在临空面形成后较短时间内发生,也可经过一段时间的应力调整后发生;② 支护结构的抵抗能小于岩体释放的应变能时,支护结构将产生破坏。可见,深地空间岩爆与时间有关。
表5 典型工程岩爆实例[24,27]
Table 5 Results of rockburst in rock engineering projects[24,27]
序号工程名称埋深/m主应力/MPaσ1σ2σ3最大切向应力/MPa抗压强度/MPa抗拉强度/MPa完整性系数施工揭露的岩爆情况1天生桥Ⅱ级水电站引水隧洞130~76025.8012.903.5130.0088.73.70.7525.8020.5212.9030.0088.73.70.75零星与连续岩爆2太平驿水电站引水隧洞40031.4015.7010.8062.60130.09.40.7531.4015.7010.8062.60180.09.40.75岩爆300多次3秦岭铁路隧道1 60020.0018.7510.00105.0095.07.00.7540.0037.5020.00105.0095.07.00.7520.0018.7510.00105.00130.07.00.7540.0037.5020.00105.00130.07.00.75岩爆43段4二郎山公路隧道77053.7026.8520.7941.4664.98.00.75岩爆200多次5铜陵冬瓜山铜矿790~85034.3321.3317.17105.50132.216.40.7534.3322.9517.17105.50132.216.40.75几十次较大岩爆6瀑布沟水电站地下洞室250~32027.3013.658.6442.0082.35.90.8021.1010.55 6.7542.0082.35.90.8027.3013.65 8.6454.00207.55.90.8021.1010.55 6.7554.00207.55.90.8010余处岩爆7渔子溪一级水电站引水隧洞250~60045.0022.5016.2090.00170.011.30.8030.0015.00 6.7590.00170.011.30.8010多次岩爆8台缙高速公路苍岭隧道300~75659.5029.758.1048.90150.08.00.7559.5129.7520.4148.90150.08.00.75岩爆中偏弱9山东玲珑金矿1 00050.0027.0025.0082.00138.010.00.7550.0027.0025.0082.00197.07.00.7560.0030.0027.00114.00138.010.00.7560.0030.0027.00114.00197.07.00.75围岩内爆裂撕裂声10锦屏Ⅰ级4009.008.444.5018.0050.05.00.729.008.444.5018.0070.05.00.7235.0017.5010.8070.0050.05.00.3435.0017.5010.8070.0070.05.00.34喷射混凝土开裂、松动区发展11锦屏Ⅱ级1 200~2 50038.0032.4019.0055.00110.06.00.7638.0032.4019.0055.00120.05.00.7671.0067.5035.50108.00110.06.00.7671.0067.5035.50108.00120.05.00.76多次岩爆
岩爆受多种因素(包括时间)的影响,为验证广义M-C统一强度理论有效性,岩爆预测时可按如下步骤进行:① Urx=0,对ν=0 时岩爆进行计算。显然,若ν=0时无岩爆,则在无其他能量输入情况下,后期将不会发生岩爆。② Urx=0,若ν=0时存在岩爆,则可利用式(17)反演出岩爆的极限泊松比,据此利用不同时段测定泊松比预测深地岩爆强弱,或依据泊松比随时间的演化规律判断岩爆何时停止。③ 由式(17)可得出,地震释放的应变能Urx超过某一临界值,深地空间将发生岩爆;或由式(17)反演现有支护结构下深部岩体能够承受的震源释放的应变能临界值。④ 由式(17)可得,增加支护结构抵抗能或减小侧向变形与轴向变形比值(泊松比),可控制深地岩爆发生。
岩爆势Prb判据[24]为

(21)
式中,σθ为洞室切向的最大应力。
由表6典型岩爆工程的实例计算结果可以看出:① 泊松比对扩容、静力破坏及岩爆有显著影响。t=0,ν=0时,广义M-C统一强度理论计算表明这些典型工程均会发生岩爆现象,且与岩爆势计算结果及岩爆的实际情况基本一致;t=t1,ν=0.1时,仅有瀑布沟水电站的地下洞室可能会发生扩容与破坏,但其他工程仍会发生岩爆,且与岩爆的实际情况基本一致,这表明ν≤0.1时大部分工程存在发生岩爆可能;t=t2,ν=0.35时,大部分工程扩容基本停止,即在无外部能量输入,且ν>0.35条件下,深地空间将保持稳定。② 从时序角度看,广义M-C统一强度理论能体现深地空间不同时段的破坏模式,比如未扩容、扩容、屈服或破坏抑或岩爆。③ 从物理涵义来看,与其他岩爆判据(包括岩爆势判据)相比,广义M-C统一强度理论体现了可释放应变能是岩爆发生的内在机理,既能预测高应变能环境下深部岩体岩爆倾向性,又能判断深地岩体破坏或扩容与否。④ 岩体完整性、弹性模量、黏聚力与摩擦角均对广义M-C统一强度理论预测结果有影响。
表6 典型岩质工程在不同时段的计算结果
Table 6 Calculated results of in rock engineering projects in different time
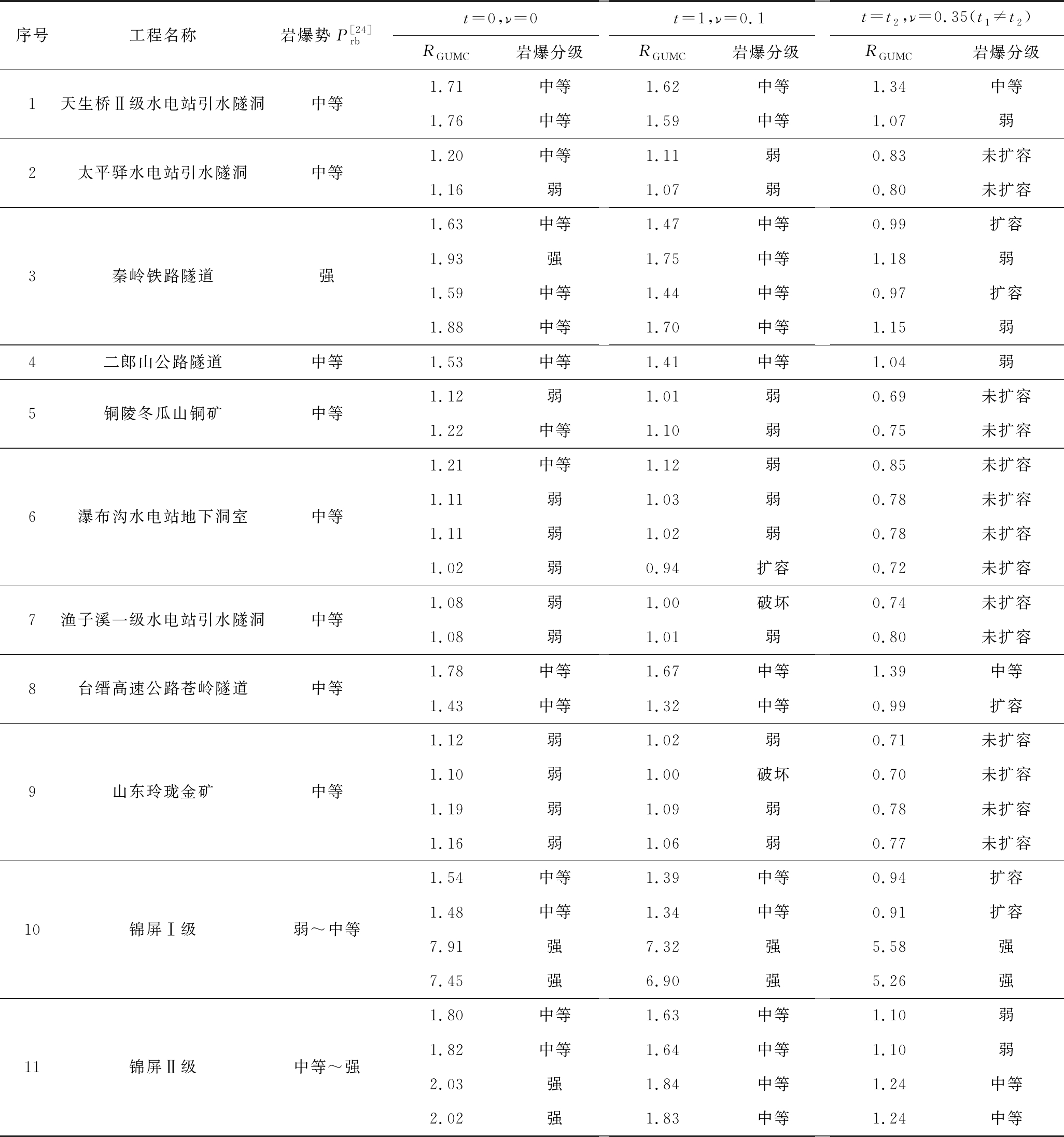
注:t为不同的开挖时段。
序号工程名称岩爆势P[24]rbt=0,ν=0t=1,ν=0.1t=t2,ν=0.35(t1≠t2)RGUMC岩爆分级RGUMC岩爆分级RGUMC岩爆分级1天生桥Ⅱ级水电站引水隧洞中等1.71中等1.62中等1.34中等1.76中等1.59中等1.07弱2太平驿水电站引水隧洞中等1.20中等1.11弱0.83未扩容1.16弱1.07弱0.80未扩容3秦岭铁路隧道强1.63中等1.47中等0.99扩容1.93强1.75中等1.18弱1.59中等1.44中等0.97扩容1.88中等1.70中等1.15弱4二郎山公路隧道中等1.53中等1.41中等1.04弱5铜陵冬瓜山铜矿中等1.12弱1.01弱0.69未扩容1.22中等1.10弱0.75未扩容6瀑布沟水电站地下洞室中等1.21中等1.12弱0.85未扩容1.11弱1.03弱0.78未扩容1.11弱1.02弱0.78未扩容1.02弱0.94扩容0.72未扩容7渔子溪一级水电站引水隧洞中等1.08弱1.00破坏0.74未扩容1.08弱1.01弱0.80未扩容8台缙高速公路苍岭隧道中等1.78中等1.67中等1.39中等1.43中等1.32中等0.99扩容9山东玲珑金矿中等1.12弱1.02弱0.71未扩容1.10弱1.00破坏0.70未扩容1.19弱1.09弱0.78未扩容1.16弱1.06弱0.77未扩容10锦屏Ⅰ级弱~中等1.54中等1.39中等0.94扩容1.48中等1.34中等0.91扩容7.91强7.32强5.58强7.45强6.90强5.26强11锦屏Ⅱ级中等~强1.80中等1.63中等1.10弱1.82中等1.64中等1.10弱2.03强1.84中等1.24中等2.02强1.83中等1.24中等
综上所述,广义M-C统一强度理论将扩容准则、强度准则及岩爆判据统一于同一个数学表达式,便于判断深部岩体扩容、破坏或岩爆。
Byerlee通过岩石的摩擦滑动试验,提出了一个适用于地球物理研究的经验性强度准则,并特别指出最小主应力大于104 MPa时,试验点多集中于强度曲线上方或下方,即岩石强度与岩性及滑动面的粗糙程度无关,如式(21)[38,44]所示。
σ1=3.1σ3+180,σ3>104 MPa
(21)
由于具有与M-C强度准则相似的数学表达式,因此,一方面Byerlee强度准则也不能反映中间主应力影响;另一方面Byerlee强度准则可看作是M-C强度准则或广义M-C统一强度理论特例。基于此,提出广义Byerlee强度理论(该理论也属于广义统一强度理论的范畴),如式(22)所示。显然,泊松比等于0.5时,广义Byerlee强度理论蜕化为Byerlee强度准则。
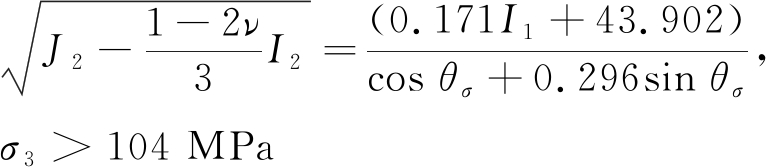
(22)
由图3可看出:泊松比ν等于0.45时,广义Byerlee强度理论位于Byerlee强度准则下方,相差-4.96%~-9.16%;泊松比等于0.55时,广义Byerlee强度理论位于Byerlee强度准则上方,相差4.97%~8.87%。可见,广义Byerlee强度理论计算精度更高且有可能更接近于实际强度。因此,广义统一强度理论应用于地球物理研究将具有更高的计算精度。

图3 拜尔利强度准则
Fig.3 Byerlee strength criterion
从能量角度来看,Byerlee强度准则计算精度较高原因可能是高压(最小主应力大于104 MPa)条件下,岩体破坏时泊松比较为接近0.5所致;另外,为了进一步提高Byerlee强度准则计算精度,参照广义M-C强度理论,建议在地球物理研究过程中采用广义Byerlee强度理论进行计算。
综上所述,广义统一强度理论(广义Byerlee强度理论也属于广义统一强度理论范畴)适用于深部岩体计算。
陈宗基等[5]提出可利用岩体的扩容对地震进行预报;郭建强等[12]建立了能对地震的发生进行初步预警的扩容准则,但未涉及地震条件下支护结构对深部岩体的影响,即没有反映支护结构抵抗能对震害影响。
在抗震设防烈度较高地区,可利用式(17)计算与扩容、屈服或破坏、弱岩爆活动及中等岩爆活动相对应的支护结构的临界抵抗能;反之,在支护结构抵抗能确定条件下,根据岩体吸收的应变能监测数据,通过式(17)计算深地空间是否发生扩容、破坏及岩爆。
假定深部岩体物理力学参数为:φ=30°,c=10 MPa,E=50 GPa,Kν=0.75;原岩应力σ1=30 MPa,θσ=-30°。利用式(17)探讨泊松比、支护结构抵抗能及震源释放应变能等对深地空间的稳定性影响。
由图4~6可以看出:① 随泊松比增加,判据指数RGUMC非线性减小,且泊松比越大深地空间发生扩容、破坏或岩爆事件概率越小。比如,泊松比分别为0,0.40及0.55时,相对应的判据指数为1.46,1.19及0.42,这表明深地空间相应会发生中等岩爆活动、弱岩爆活动及未扩容。② RGUMC随支护结构抵抗能增加而越小,即支护结构抵抗能是地下工程震害较小的主要原因。③ 随支护结构抵抗能Usr增加,泊松比越小RGUMC减小的趋势越明显,但当Usr超过某一临界值时(泊松比越小临界值越大),RGUMC逐渐趋于平缓。由此可得,超过一定阈值后,支护结构对深地空间稳定性影响将不明显。④ 随震源释放应变能Urx的增加,RGUMC逐步增加,但增加速率表现为逐渐减小趋势。可见,广义M-C统一强度理论能对受震源释放应变能影响的深地空间的稳定性进行计算。

图4 RGUMC随ν变化趋势
Fig.4 Relation between RGUMC and ν

图5 RGUMC随抵抗能变化趋势
Fig.5 Relation between RGUMC and Usr

图6 RGUMC随地震释放应变能变化趋势
Fig.6 Relation between RGUMC and Urx
综上所述,广义M-C统一强度理论将高应变能环境下深部岩体与支护结构看作一个整体结构,实现了地震与非地震条件下深地空间扩容、静力破坏及岩爆计算模型的统一。基于此,建议采用支护结构抵抗能而非支护结构抗力的方法进行深地空间计算与设计。
尽管广义统一强度理论对高应变能环境下岩体的扩容、屈服或破坏及岩爆倾向性预测有较高精度,但仍需在以下几个方面作深入研究:
(1)广义统一强度理论与章梦涛教授失稳理论主要区别体现在2个方面:① 章梦涛等[28-29]通过物质质量守恒、动量守恒及能量守恒,提出平衡失稳及动力失稳发生的必要条件与充分条件。笔者以章梦涛教授提出的平衡失稳与动力失稳发生的充分条件为基础,参考其他强度准则的研究成果未考虑2种现象发生的必要条件,建立了广义统一强度理论。② 所释放能量大于所消耗的能量是上述2种现象发生的充分条件[28-29],由于岩体本身复杂性及上覆岩层移动与流(气)体移动也比较复杂,本文广义统一强度理论未考虑上覆岩层下沉所做的外力功与流(气)体的流动势能,但考虑了地震或其他因素释放应变能(比如爆炸冲击波)与支护结构提供的抵抗破坏的能量。
(2)特别是在岩层移动或液(气)体流动比较明显的矿区,为了进一步提高广义统一强度理论的计算精度,应开展考虑上覆岩层移动与液(气)体流动的广义统一强度理论的研究。
(3)笔者以经典强度准则为基础,建立了广义统一强度理论,另外应开展以岩爆判据为基础的广义统一强度理论研究,并对比分析2种方法建立的广义统一强度理论计算精度与适宜性。
(4)针对深部资源开采中岩石多为砂岩、泥岩及煤岩等,并考虑到软硬岩之间变形特性与破坏模式差别,对广义统一强度理论在软岩中精度与适用性作进一步研究。
(5)为了尽快实现广义统一强度理论数值计算,探讨该理论在π平面轨迹,并针对存在的尖点问题提出修正方法。
(6)极限抵抗能对广义强度理论精度有明显影响,应从理论与试验2个方面,开展极限抵抗能计算方法探讨。
(1)与单元体上的剪应力和正应力组合达到某一极限值就会相应地发生扩容、屈服或破坏及岩爆的传统强度理论有所不同,从可释放应变能与支护结构抵抗能出发,借鉴由强度数据最佳拟合得到的经验性强度准则,通过引入变形参数建立了能精确地描述高应变能环境下深部岩体扩容、破坏及岩爆的广义统一强度理论,并针对扩容、屈服或破坏与岩爆提出4个分级界限值(0.9,1.0,1.2和1.9)。
(2)广义统一强度理论实现了3个层面统一:① 实现了广义统一强度理论的数学表达式表征的物理涵义与可释放应变能是岩体扩容、屈服或破坏及岩爆发生的内在机理的统一,这为从根本上提高扩容应力、屈服或破坏强度及岩爆预测精度提供了理论基础。② 实现了扩容准则、强度准则与岩爆判据表达式的统一,便于判断深部岩体是发生了扩容、屈服或破坏,抑或是岩爆。③ 将震源释放的应变能与支护结构抵抗能统一于同一个表达式,利于深部岩体稳定性分析。
(3)广义统一强度理论综合考虑了地应力、岩体完整性、弹性模量、黏聚力与摩擦角、泊松比、震源释放应变能及支护结构抵抗能等因素对深部岩体稳定性影响,并指出当抵抗能超过阈值后,支护结构对深部岩体扩容、屈服或破坏及岩爆影响将不再明显。
(4)从能量角度来看,高压条件下Byerlee强度准则计算精度较高根本原因是深部岩体破坏时泊松比与0.5较为接近所致。在深部地球物理研究过程中,为了进一步提高计算精度可采用广义Byerlee强度理论进行计算。
(5)广义统一强度理论将深部岩体与支护结构看作一个整体结构,实现了地震与非地震条件下深部岩体稳定性计算,并从理论上得出了地下工程震害较小内在原因。据此建议采用支护结构抵抗能的方法进行深部岩体稳定性计算与设计。
(6)广义统一强度理论对扩容应力、真三轴强度、典型岩爆工程实例计算表明,该理论对扩容、静力破坏及岩爆预测是合理可行的。
[1] 钱七虎,李树忱. 深部岩体工程围岩分区破裂化现象研究综述[J]. 岩石力学与工程学报,2008,27(6):1278-1284.
QIAN Qihu,LI Shuchen. A review of research on zonal disintegration phenomenon in deep rock mass engineering[J]. Chinese Journal of Rock Mechanics and Engineering,2008,27(6):1278-1284.
[2] 李术才,王汉鹏,钱七虎,等. 深部巷道围岩分区破裂化现象现场监测研究[J]. 岩石力学与工程学报,2008,27(8):1545-1553.
LI Shucai,WANG Hanpeng,QIAN Qihu,et al. In-situ monitoring research on zonal disintegration of surrounding rock mass in deep mine roadways[J]. Chinese Journal of Rock Mechanics and Engineering,2008,27(8):1545-1553.
[3] 姜耀东,赵毅鑫,刘文岗,等. 深部开采中巷道底鼓问题的研究[J]. 岩石力学与工程学报,2004,23(14):2396-2401.
JIANG Yaodong,ZHAO Yixin,LIU Wengang,et al. Research on floor heave of roadway in deep mining[J]. Chinese Journal of Rock Mechanics and Engineering,2004,23(14):2396-2401.
[4] 黄万朋,高延法,王军. 扰动作用下深部岩巷长期大变形机制及控制技术[J]. 煤炭学报,2014,39(5):822-828.
HUANG Wanpeng,GAO Yanfa,WANG Jun. Deep rock tunnel’s long large deformation mechanism and control technology under disturbance effects[J]. Journal of China Coal Society,2014,39(5):822-828.
[5] 陈宗基,康文法. 在岩石破坏和地震之前与时间有关的扩容[J]. 岩石力学与工程学报,1983,2(1):11-21.
CHEN Zongji,KANG Wenfa. Time dependent dilatancy prior to rock failure and eathqakes[J]. Chinese Journal of Rock Mechanics and Engineering,1983,2(1):11-21.
[6] BRIDGMAN P W. Volume changes in the plastic stages of simple compression[J]. Journal of Applied Physics,1949,20(12):1241-1251.
[7] 侯文诗,李守定,李晓,等. 岩石扩容起始特性与峰值特性的比较[J]. 岩土工程学报,2013,35(8):1478-1485.
HOU Wenshi,LI Shouding,LI Xiao,et al. Comparison between dilatancy onset and peak of different rocks[J]. Chinese Journal of Geotechnical Engineering,2013,35(8):1478-1485.
[8] 尹光志,鲁俊,李星,等. 中间主应力对砂岩扩容及强度特性影响[J]. 煤炭学报,2017,42(4):879-885.
YIN Guangzhi,LU Jun,LI Xing,et al. Influence of intermediate principal stress on dilation and strength characteristics of sandstone[J]. Journal of China Coal Society,2017,42(4):879-885.
[9] RATIGAN J L,VAN Sambeek L L,DEVRIES K L,et al. The influence of seal design on the Development of the disturbed rock zone in the WIPP alcove seal tests[R]. Topical Report RSI-0400,prepared by Parsons Brinkerhoff San Francisco,Abbuquerque,NM,1991.
[10] HUNSCHE U E. Failure behavior of rock salt around underground cavities[A]. 7th International Symposium on Salt[C]. Kyoto,1992.
[11] 郝铁生,梁卫国,张传达. 基于三剪能量屈服准则的地下水平盐岩储库腔壁稳定性分析[J]. 岩石力学与工程学报,2014,33(10),1997-2006.
HAO Tiesheng,LIANG Weiguo,ZHANG Chuanda. Analysis of wall stability for underground horizontal gas storage in bedded salt rock based on yield criterion of triple shear energy[J]. Chinese Journal of Rock Mechanics and Engineering,2014,33(10):1997-2006.
[12] 郭建强,黄武峰,刘新荣,等. 基于可释放应变能的岩石扩容准则[J]. 煤炭学报,2019,44(7):2094-2102.
GUO Jiangqiang,HUANG Wufeng,LIU Xinrong,et al. Rock dilation criteria development based on releasable strain energy[J]. Journal of China Coal Society,2019,44(7):2094-2102.
[13] YU Maohong. Advances in strength theories for materials under co-mplex stress state in the 20th Century[J]. Advances in Mechanics,2004,34(4):529-560
[14] 俞茂宏. 双剪理论及其应用[M]. 北京:科学出版社,1998.
[15] 谢和平,鞠杨,黎立云,等. 岩体变形破坏过程的能量机制[J]. 岩石力学与工程学报,2008,27(9):1729-1740.
XIE Heping,JU Yang,LI Liyun,et al. Energy mechanism of deformation and failure of rock masses[J]. Chinese Journal of Rock Mechanics and Engineering,2008,27(9):1729-1740.
[16] 谢和平,鞠杨,黎立云. 基于能量耗散与释放原理的岩石强度与整体破坏准则[J]. 岩石力学与工程学报,2005,24(17):3003-3010.
XIE Heping,JU Yang,LI Liyun. Criteria for strength and structural failure of rocks baded on energy dissipation release principles[J]. Chinese Journal of Rock Mechanics and Engineering,2005,24(17):3003-3010.
[17] 郭建强,刘新荣,黄武锋,等. 基于弹性应变能的Mohr-Coulomb强度准则讨论[J]. 同济大学学报(自然科学版),2018,46(9):1168-1174.
GUO Jianqiang,LIU Xinrong,HUANG Wufeng,et al. Discussion on M-C strength criterion based on elastic strain energy[J]. Journal of Tongji University(Natural Science),2018,46(9):1168-1174.
[18] 郭建强,刘新荣. 强度准则与岩爆判据统一的研究[J]. 岩石力学与工程学报,2018,37(S1):3340-3352.
GUO Jianqiang,LIU Xinrong. Study on the uniformity between strength criterion and rockburst criterion[J]. Chinese Journal of Rock Mechanics and Engineering,2018,37(S1):3340-3352.
[19] 郭建强,刘新荣,王军保,等. 基于弹性应变能的岩石强度准则[J]. 岩土力学,2016,37(S2):129-136.
GUO Jianqiang,LIU Xinrong,WANG Junbao,et al. Investigation on strength criterion of rock based on elastic strain energy[J]. Rock and Soil Mechanics,2016,37(S2):129-136.
[20] YOU MQ. True-triaxial strength criteria for rock[J]. International Journal of Rock Mechanics and Mining Sciences,2009,46(1):115-127
[21] LIU M D,CARTER J P. General strength criterion for geomaterials. International Journal of Geomechanics,2003,3:253-259
[22] LEE Y,PIETRUSZCZAK S,CHOI B. Failure criteria for rocks based on smooth approximations to Mohr-Coulomb and Hoek-Brown failure functions[J]. International Journal of Rock Mechanics and Mining Sciences,2012,56:146-160.
[23] 宫凤强,闫景一,李夕兵. 基于线性储能规律和剩余弹性能指数的岩爆倾向性判据[J]. 岩石力学与工程学报,2018,37(9):1993-2014.
GONG Fengqiang,YAN Jingyi,LI Xibing. A new criterion of rock burst proneness based on the linear energy storage law and the residual elastic energy index[J]. Chinese Journal of Rock Mechanics and Engineering,2018,37(9):1993-2014.
[24] 尚彦军,张镜剑,傅冰骏. 应变型岩爆三要素分析及岩爆势表达[J]. 岩石力学与工程学报,2013,32(8):1520-1527.
SHANG Yanjun,ZHANG Jingjian,FU Bingjun. Analyses of three parameters for strain mode rockburst and expression of rockburst potential[J]. Chinese Journal of Rock Mechanics and Engineering,2013,32(8):1520-1527.
[25] 张镜剑,傅冰骏. 岩爆及其判据和防治[J]. 岩石力学与工程学报,2008,27(10):2034-2042.
ZHANG Jingjian,FU Bingjun. Rockburst and its criteria and control[J]. Chinese Journal of Rock Mechanics and Engineering,2008,27(10):2034-2042.
[26] ZHANG J J,FU B J,LI Z K,et al. Criterion and classification for strain mode rockbursts based on five-factor comprehensive method[A]. Proceedings of the 12th ISRM International Congress on Rock Mechanics[C]. 2012:1435-1440.
[27] 郭建强,赵青,王军保,等. 基于弹性应变能岩爆倾向性评价方法研究[J]. 岩石力学与工程学报,2015,30(9):1886-1893.
GUO Jianqiang,ZHAO Qing,WANG Junbao,el al. Rockburst prediction based on elastic strain energy[J]. Chinese Journal of Rock Mechanics and Engineering,2015,30(9):1886-1893.
[28] 章梦涛,徐曾和,潘一山,等. 冲击地压和突出的统一失稳理论[J]. 岩石力学与工程学报,1991,16(4):48-53.
ZHANG Mengtao,XU Cenghe,PAN Yishan,etl al. A united instability theory on coal(rock) burst and outburst[J]. Chinese Journal of Rock Mechanics and Engineering,1991,16(4):48-53.
[29] 章梦涛. 冲击地压失稳理论与数值模拟计算[J]. 岩石力学与工程学报,1987,6(3):197-204.
ZHANG Mengtao. Instability theory and mathematical model for coal/rock bursts[J]. Chinese Journal of Rock Mechanics and Engineering,1987,6(3):197-204.
[30] 尤明庆. 岩石的力学性质[M]. 北京:地质出版社,2007.
[31] 马洪岭. 超深地层盐岩地下储气库可行性研究[D]. 武汉:中国科学院武汉岩土力学研究所,2010.
MA Hongling. Study of feasibility of rock salt underground gas storage in ultra-deep formation[D]. Wuhan:Institute of Rock and Soil Mechanics,Chinese Academy of Sciences,2010.
[32] 黄润秋,黄达. 卸荷条件下花岗岩力学特性试验研究[J]. 岩石力学与工程学报,2008,27(11):2205-2213.
HUANG Runqiu,HUANG Da. Experimental research on mechanical properties of granites under unloading condition[J]. Chinese Journal of Rock Mechanics and Engineering,2008,27(11):2205-2213.
[33] LAKES R. Foam structures with a negative Poisson′s ratio[J]. Science,1987,235:1038-1041.
[34] HOEK E,BROWN E T. Empirical strength criterion for rock masses[J]. Journal of Geotechnical and Geoenvironmental Engineering,ASCE,1980,106(9):1013-1035.
[35] HOEK E,BROWN E T. Underground excavations in rocks[M]. London:Institution of Mining and Metallurgy,1980:527.
[36] HOEK E,WOOD D,SHAH S. A modified Hoek-Brown criterion for jointed rock masses[A]. HUDSON J A ed. Proceedings of the Rock Characterization,Symposium of ISRM[C]. London:British Geotechnical Society,1992:209-214.
[37] 朱合华,张琦,章连洋. Hoer-Brown强度准则研究进展与应用综述[J]. 岩石力学与工程学报,2013,32(10):1945-1963.
ZHU Hehua,ZHANG Qi,ZHANG Lianyang. Review of research progresses and applications of Hoek-Brown strength criterion[J]. Chinese Journal of Rock Mechanics and Engineering,2013,32(10):1945-1963.
[38] BYERLEE J D. Friction of rocks[J]. Pure and Applied Geophysics,1978,116:615-626
[39] 胡云华. 高应力下花岗岩力学特性试验及本构模型研究[D]. 武汉:中国科学院武汉岩土力学研究所,2008.
HU Yunhua. Study on mechanical properties of granites under high pressure condition and its constitutive models[D]. Wuhan:Institute of Rock and Soil Mechanics,Chinese Academy of Sciences,2008.
[40] 刘文博. 高应力作用下砂岩加卸载损伤本构模型及流变特性研究[D]. 阜新:辽宁工程技术大学,2020.
LIU Wenbo. Study on the constitutive model and rheological properties of sandstone damage under high stress[D]. Fuxin:Liaoning Technical University,2020.
[41] MOGI K. Experimental rock mechanica[M]. London:Taylor and Francis,2007.
[42] AL-AJMI A M,ZIMMERMAN R W. Relation between the Mogi and the Coulomb failure criteria[J]. International Journal of Rock Mechanics and Mining Sciences,2005,42(3):431.
[43] 周辉,李震,杨艳霜,等. 岩石统一能量屈服准则[J]. 岩石力学与工程学报,2013,32(11):2170.
ZHOU Hui,LI Zhen,YANGYanshuang,et al. Unified energy yield criterion of rock[J]. Chinese Journal of Rock Mechanics and Engineering,2013,32(11):2170.
[44] 陈颙,黄庭芳,刘恩儒. 岩石物理学[M]. 合肥:中国科学技术大学出版社,2009:158-188.