
移动阅读

移动阅读
HUANG De,LIU Jian,LIU Yong,et al. Experimental research on combination selection of observation feature of resistance variation fault in mine ventilation[J]. Journal of China Coal Society,2021,46(12):3922-3933.
矿井通风系统不仅为井下提供新鲜风流,排出污染空气和稀释有毒有害气体,也在矿井生产安全保障、灾害防治、隐患排除及应急救灾中有着不可或缺的作用[1-4]。但当矿井通风系统中的巷道发生冒落、片帮等现象时,会导致其断面积发生持久性变化,从而引起对应风阻发生持久性变化,文献[5]将这种风阻发生持久性变化的现象称为矿井通风阻变型故障,并将矿井通风阻变型故障诊断转换为分类问题,利用支持向量机(SVM)进行求解,获得了较好的诊断性能。为了避免风量单一特征所产生的不适定性,文献[6]提出风量与风压相结合的复合特征阻变型故障位置诊断方法,以多维互补的特征信息提高阻变型故障诊断的准确率。文献[7-8]针对监控系统无法直接确定阻变故障位置和大小的问题,利用监控系统风速、风压等监测值进行网络分析,提出了逐步线性回归分析法,并根据建立的阻变故障专家系统获取阻变故障位置及可能发生阻变的原因。文献[9]根据层次分析法中权重的大小制定了矿井通风网络异常的判别准则,并利用BP神经网络和监控系统监测的风速、风压等数据实现了大平煤矿通风网络异常的原因判别。文献[10]针对阻变型故障诊断分类需要故障样本参与训练的问题,提出了一种混合编码方式的自适应进化策略算法,在阻变型故障诊断时不仅可同时进行阻变故障位置和故障量的诊断,也避免了故障样本的参与,以风量作为特征进行试验,结果表明基于多目标优化的观测特征选择模型的可行性和准确性。文献[11]分别以风量、风压单一特征和风量-风压复合特征作为进化算法的适应函数参数,利用协方差矩阵进化策略方法进行求解,试验得出风量-风压复合特征比风量或风压单一特征获得更高的阻变故障位置诊断准确率和更低误差的阻变故障量诊断性能,并指出少量观测特征也可获得较高准确率的故障诊断性能。
目前针对矿井通风阻变型故障诊断观测特征选择的研究主要集中于风速传感器布设位置方面。文献[12]以逐步线性回归分析方法,确定了引起矿井通风网络风速传感器报警的分支集合,确定了角联结构矿井通风网络风速传感器布设方案。文献[13]为扩大煤矿瓦斯监测子系统的监测范围,实现对局部瓦斯超限事故的及时预警,提出了一种结合遗传算法和离散二元粒子群优化算法的传感器覆盖模型混合算法,以实现用最少数量的气体传感器来预测整个矿井瓦斯体积分数的目标。文献[14]针对风速观测点位置进行了优化布设研究,基于邻域粗糙集属性约简算法提出了阻变型故障诊断的风速观测点位置优化方法,并建立了风速观测点扫帚布设模型。在矿井通风阻变型故障诊断观测点选择方面,单一观测特征数量和复合特征组合优化选择方面的研究尚少,导致阻变型故障诊断难免出现以下情况:① 不必要的位置布设观测点,在一定程度上增加了阻变型故障诊断的成本;② 所有分支或节点作为观测点易导致观测点之间出现冗余或不相关特征,限制甚至降低了阻变型故障诊断学习器的性能;③ 当监督学习模型的样本数量受到限制时,未经优化选择的观测特征在训练和预测过程中容易出现过拟合或欠拟合的现象,从而降低了故障诊断模型的泛化能力,无监督学习模型的种群参数大小随特征维度的增加而增大,从而导致求解模型的复杂度递增。
监督学习下的训练样本集往往具有高维特征的特点,但并不是所有训练样本集的特征都是必须的,甚至存在很多与阻变故障诊断任务无关的特征,特征维度的降低对提高诊断性能具有极其重要的意义[15-17]。为了消除属性中多余和无关的特征,可使用多种方法对高维特征数据进行适当的分类得以解决,而理论和实践表明特征选择是剔除冗余无关特征最为行之有效的方法之一[18-20]。基于此,笔者以最小的观测点数量和训练交叉验证误差为目标,建立基于多目标优化的观测特征选择模型。以基于统计的数据挖掘算法k-近邻算法(kNN)[21]作为阻变故障诊断方法,非支配排序遗传算法II(NSGA-II)[22]作为多目标优化求解方法,对矿井通风网络实例分别对风量单一特征、风压单一特征、节点压能单一特征、风量-风压复合特征、风量-节点压能复合特征、风压-节点压能复合特征和风量-风压-节点压能复合特征等7种特征方案进行观测特征选择试验,以未进行观测点优化选择和相同观测点数量下的随机观测点位置方案作为对照组,在相同试验条件下,分别进行监督学习的阻变故障诊断试验,分析矿井通风阻变故障观测特征类型、位置及其数量的优劣性。最后通过文献[10]所提供的无监督学习阻变故障诊断模型对优化选择的观测特征方案进行验证分析。
基于多目标优化的观测特征选择模型可有效避免不必要地点安装传感器,降低传感器安装数量,从而节省矿井通风阻变故障诊断所需成本;在有效剔除冗余或不相关观测特征后,可提高阻变故障诊断学习器的性能和泛化能力。为矿井通风系统故障诊断观测特征选择提供新的理论和方法,可及时发现矿井通风系统中阻变的位置和程度,对保障通风系统可靠性有重要的应用价值,同时为矿井通风实时网络解算监控系统搭建方案提供决策性依据,在矿井智能通风的实践中可广泛应用。
对于一个矿井通风网络图G=(V,E),V为网络中节点的集合,其中|V|=m,即V={v1,v2,v3,…,vm},m为节点数量;E为网络分支的集合,其中|E|=n,即E={e1,e2,e3,…,en},n为分支数量。矿井通风阻变故障位置仅考虑分支对应位置,以eλ表示阻变发生的位置,称为阻变故障位置或故障位置,其中λ为阻变故障位置对应分支编号索引,λ∈[1,n];以Δrλ表示阻变分支eλ发生故障的阻变故障量,rλ为未发生阻变故障时分支eλ的风阻,其中Δrλ∈(-rλ,+∞),单位为N·s2/m8。对于整个矿井通风网络,阻变故障量ΔR=(Δr1,Δr2,…,Δri,…,Δrn),当Δri=0时,表示分支ei未发生故障,不属于故障位置,其中i=1,2,…,n。笔者所研究的是单故障源[5],因此每次仅考虑矿井通风网络中的一个故障位置进行研究,即Δrλ≠0,Δri=0,且i≠λ,λ及其对应的Δrλ为故障诊断模型的求解变量。以巷道风速转换的风量q、巷道两端静压差h和节点压能p作为阻变故障诊断的观测点,每一个故障位置发生一次阻变故障对应一组观测值,因此,阻变故障位置诊断训练样本T可描述为

(1)
其中,q,h,p下标前部分表示故障位置对应的编号,后部分表示故障位置对应的样本序号,上标后部分表示网络分支或节点编号,故障训练样本总数![]() 为故障位置ei对应的样本数量。对于风量、风压和节点压能都作为候选观测点的情况,特征维度M=2n+m。以连续变量故障量Δri替换式(1)中的离散变量故障位置ei,则获取阻变故障量诊断训练样本。
为故障位置ei对应的样本数量。对于风量、风压和节点压能都作为候选观测点的情况,特征维度M=2n+m。以连续变量故障量Δri替换式(1)中的离散变量故障位置ei,则获取阻变故障量诊断训练样本。
k-近邻算法用于确定与特定参数最接近的训练实例数量k[23],在分类问题中,它是一种通过检查新对象到特征空间中最接近的相邻训练样本的距离来对新对象进行分类的方法,已在数据挖掘、统计模式识别、图像处理等领域的许多应用中被广泛使用[24]。对于阻变故障位置诊断,输入样本实例![]() 其中c为样本序号,故障位置eλ为输出变量,则k-近邻阻变故障位置诊断的数学模型如下:
其中c为样本序号,故障位置eλ为输出变量,则k-近邻阻变故障位置诊断的数学模型如下:
(1)在指定距离度量的情况下,分别计算输入诊断实例xλ与训练样本T中所有样本的距离;
(2)对所有距离进行排序,找出k个距离最小的点,将所获得的k个点所组成的邻域记作Nk(xλ);
(3)获取Nk(xλ)中的k个邻近训练样本对应的故障位置ez,其中z∈[1,n];
(4)从k个故障位置中寻找类别出现次数最多的故障位置,并定义为预测的阻变故障位置eλ,即
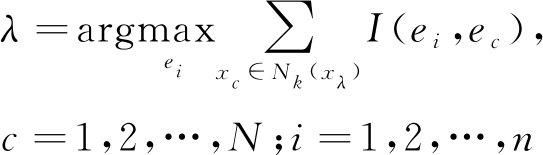
(2)
其中,I为指示函数,当ei=ec时,I=1,否则I=0。
笔者以欧式距离作为距离度量,即在求样本实例之间的距离时,以式(3)进行计算。
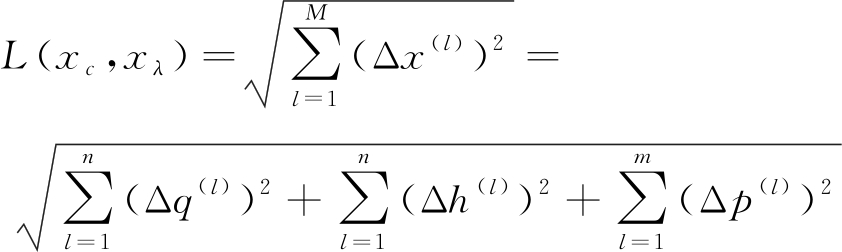
(3)
式中,![]() 为特征序号。
为特征序号。
对于阻变故障量回归诊断,则根据最小均方根误差(RSME)确定步骤(4)中的最优值Δrλ,即
(4)
其中,Δri为第i个故障位置回归预测的阻变故障量;Δrc为第c个样本实例对应的阻变故障量。
由此,根据式(1)的训练样本和式(2)可获得矿井通风阻变故障位置eλ,由式(1)变换所得的阻变故障量训练样本和式(4)可获得对应的矿井通风阻变量,即阻变故障量Δrλ。
设风量观测点数量为nq,风压观测点数量为nh,节点压能观测点数量为np,被选择的观测点数量分别为nfq,nfh和nfp。在进行观测特征选择时,以所有分支的风量、风压或所有节点的压能作为候选特征,即nq=nh=n,np=m。以阻变故障位置诊断观测点选择为例,最小的观测点数量和训练交叉验证误差为目标的观测特征选择模型可表示为
(5)
(6)
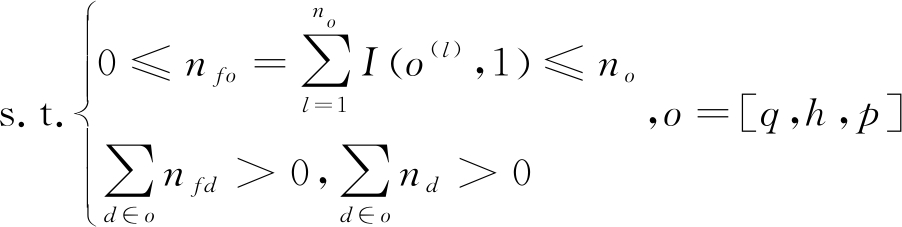
(7)
式中,ncv为不重复的交叉验证次数;s为交叉验证集序号;Ns为第s组交叉验证集样本数;c′为交叉验证集样本序号;y为样本对应的阻变故障位置;![]() 为以选择的观测点作为特征,利用k-近邻阻变故障诊断模型预测的阻变故障位置;o为观测点类型,d为观测点类型序号。
为以选择的观测点作为特征,利用k-近邻阻变故障诊断模型预测的阻变故障位置;o为观测点类型,d为观测点类型序号。
观测特征优化选择模型的编码为布尔类型,“0”表示未被选择的观测点,“1”表示被选择的观测点。函数f1为编码为“1”对应的所有观测特征进行ncv次交叉验证的平均误差,函数f2为求解编码中非零的数量,可由L0范数表示,但考虑L0范数不易于优化求解,因此使用L2范数进行求解,不仅防止过拟合现象,也可提升观测特征选择模型的泛化能力。称被选择的观测点占候选观测点数量的比例为观测点覆盖率,则目标函数f2表示相对观测点覆盖率。
试验过程使用NSGA-Ⅱ多目标优化求解方法求解观测特征选择模型,其求解过程如下。
步骤1:模型参数设定和初始化。由矿井通风网络拓扑信息获取分支数量n和节点数量m,根据观测点类型初始化观测点对应的候选特征数。初始化NSGA-Ⅱ算法的参数,包括最大迭代代数NI,种群大小NG,交叉概率cr,变异概率mr。
步骤2:染色体编码。由设定的各观测点类型对应的候选特征数确定编码长度为M=nq+nh+np,则使用二进制编码方式得到实数对应的编码B∈[0,2M-1]。
步骤3:染色体解码。对二进制编码B=[b1,b2,…,bnq,bnq+1,…,bnq+nh,bnq+nh+1,…,bnq+nh+np]进行解码,编码长度为候选特征长度M=nq+nh+np。解码原则为:若bl=1,则第l个编码对应的特征x(l)被选择,否则不被选择。染色体解码过程如图1所示,其中(a)表示编码对应的二进制数值,(b)表示假定的一个种群编码,(c)为以解码原则获取特征对应的样本,样本总数为N,特征数为(b)中编码对应实数之和。

图1 染色体解码示例
Fig. 1 Example of chromosome decoding
步骤4:适应值计算。将步骤3中所获取的样本按训练集80%,测试集20%的原则进行ncv次交叉分割,利用k-近邻阻变故障诊断模型进行对所有交叉验证集进行训练和预测,通过式(5)计算获得f1对应的适应值,利用编码原则及图1(b)中“1”的数量统计可获得nfq,nfh和nfp,通过式(6)和式(7)计算得到f2对应的适应值。
步骤5:快速非支配排序。将步骤4中计算所得的适应值采用快速非支配排序方法得到多样的非优劣解[22],将种群中的个体调配到不同的非优劣支配前沿集合中,根据适应值之间的差异性计算出个体之间的拥挤度,并通过二进制锦标赛操作求出种群密度最小的个体,从而获取得到新种群。
步骤6:交叉变异操作。对步骤5所获取的新种群进行交叉和变异操作,将交叉变异产生的新个体与父代的种群进行合并,进一步得到新种群。
步骤7:终止条件。利用交叉变异后的新种群编码,根据步骤3解码原则和步骤4适应值计算方法重新进行适应值计算、快速非支配排序和交叉变异操作,直至达到最大迭代次数,获取相对最小的f1和f2,以及此时染色体编码对应的观测特征。
为了验证基于多目标优化的观测特征选择模型的可行性和适应性,分别以风量、风压、节点压能3种单一特征和风量-风压、风量-节点压能、风压-节点压能和风量-风量-节点压能4种复合特征作为特征选择方案,进行观测特征选择组合试验。
使用文献[5]中的多源多汇矿井通风网络作为试验实例,如图2所示,其中|V|=71,|E|=100,e1和e2为进风井分支,e9,e39和e78为回风井分支。1,2,3号主要通风机分别安装在e39,e9和e78分支对应的回风井末端,特性方程分别为

图2 试验矿井通风网络实例
Fig.2 Ventilation network of test mine
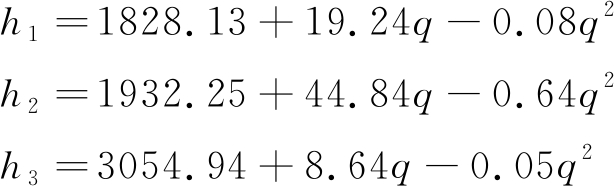
式中,h1,h2,h3分别为1,2,3号风机的静压。
以文献[5]中表4对应的风阻作为矿井通风网络实例的初始风阻,在未发生阻变故障的情况下,1号风机的工况风量为205.95 m3/s,风压为2 350.97 Pa;2号风机的工况风量为65.11 m3/s,风压为2 131.98 Pa;3号风机的工况风量为203.61 m3/s,风压为2 644.41 Pa。
假设故障位置不包括源汇对应的分支,根据式(1)描述的样本,针对试验矿井通风实例的每条潜在故障位置进行不同程度的500次阻变故障模拟,获得对应的故障训练样本。
考虑有风门或风窗等构筑物的巷道风阻降低的概率较大,其对应的潜在故障位置样本中90%阻变范围为[0.01r,0],10%的阻变范围为[0,2.1r]。而对于无构筑物巷道发生风阻增大的概率较大,其对应的潜在阻变分支样本90%阻变范围为[0,201r],10%的阻变范围为[0.9r,0]。共设计7组试验方案,具体描述见表1,每组试验方案均对应一个对照试验组,分别以全部候选、优化选择和相同维度的随机特征作为观测点进行比对试验。
表1 观测特征组合试验方案
Table 1 Observation feature combination test scheme

方案特征类型候选特征类型及数量特征维度Ⅰ风量nq=100,nh=0,np=0100Ⅱ风压nq=0,nh=100,np=0100Ⅲ节点压能nq=0,nh=0,np=7171Ⅳ风量-风压nq=100,nh=100,np=0200Ⅴ风量-节点压能nq=100,nh=0,np=71171Ⅵ风压-节点压能nq=0,nh=100,np=71171Ⅶ风量-风压-节点压能nq=100,nh=100,np=71271
由矿井通风网络试验实例可知,候选观测特征维度最小为71,最大为271,样本数量为47 500,故障位置类别数为95。试验包括试验准备、阻变模拟、观测特征选择和验证4个阶段,观测特征组合试验的流程如图3所示。

图3 试验流程
Fig.3 Test procedure
试验准备阶段包括矿井通风网络拓扑检查和模型参数设定,根据对不同试验方案获取候选观测点类型和数量的多次试验测试,设定模型参数的最大迭代次数为1 000,种群大小为观测候选特征维度的2倍,交叉概率为0.95,变异概率为0.01,风量精度为0.001 m3/s,风压精度为0.1 Pa,k为3,交叉验证次数ncv为3。阻变模拟即样本构造阶段,通过随机不重复地改变指定故障位置的风阻大小进行仿真模拟,根据候选观测点类型获取阻变故障样本。为了确保样本的多样性和均衡性,训练样本按潜在故障位置编号升序方式进行重排后,每间隔400个样本随机选取一个样本进行样本重组,并选择其中的80%作为交叉验证集,剩余的20%作为测试集。对交叉验证集进行3折交叉分割得到S1,S2和S3三个训练子集,分别以S1,S2和S3作为交叉验证测试集,其他2项作为训练集进行训练和预测即可计算平均交叉验证误差。利用k-近邻阻变故障诊断模型和基于多目标优化的观测特征选择模型对样本进行训练和最优求解可得到被选择的观测点。利用选择的观测点,对相同的样本进行训练,并以剩余的20%样本作为测试集进行阻变故障位置诊断和阻变故障量预测验证试验,同时以相同的特征作为适应值参数,利用混合编码的自适应进化策略算法进行无样本模型验证试验,分析验证试验结果的精度和误差以验证阻变故障诊断模型的准确性和观测特征选择模型的可行性。
通过比较不同样本比例与训练和交叉验证准确率之间的关系,确定试验样本数量是否达到训练的需求,每组方案均以样本数的10%~100%进行随机均衡选择和三折交叉分割,得到如图4所示的试验结果,其中横坐标为训练样本比例,左侧纵坐标为表示训练或交叉验证准确率,右侧纵坐标为训练时间。

图4 不同样本比例模型复杂度与预测能力的关系
Fig.4 Relationship between complexity and predictive ability of different sample ratios
不同样本比例模型复杂度与预测能力关系的试验结果显示,方案Ⅰ中所有分支的风量作为候选特征时,0.3的样本比例即可达到90%以上平稳的交叉验证准确率和95%的训练准确率,直到100%样本的验证准确率未超过91%,训练准确率稳定保持在95%,诊断准确率高于文献[5]支持向量机阻变故障诊断模型的78.11%。方案Ⅱ中所有分支的风压作为候选特征时,即使0.1的样本比例也可达到96%以上的交叉验证准确率和100%的训练准确率。方案Ⅲ中所有节点的压能作为候选特征时,0.3的样本比例可达到92%以上的交叉验证准确率和100%的训练准确率,当样本比例超过0.6时,验证准确率稳定保持在96%~98%。方案Ⅳ中所有分支的风量和风压作为候选特征时,0.1的样本比例样本数为4 750,可达到97.5%以上的交叉验证准确率和100%的训练准确率,略低于文献[6]样本数量23 550时,使用支持向量机的98.23%准确率。方案Ⅴ中所有节点的压能和分支的风量作为候选特征时,0.4的样本比例可达到96%以上的交叉验证准确率和100%的训练准确率,当样本比例超过0.4时,验证准确率稳定保持在96%~98%。方案Ⅵ中所有节点的压能和分支的风压作为候选特征时,训练和交叉验证准确率与方案Ⅲ的结果保持相同趋势。方案Ⅶ中所有节点的压能和分支的风压和风量作为候选特征时,训练和交叉验证准确率与方案Ⅴ的结果保持相同趋势。
综上所述,当样本比例增加时,模型的训练准确率均保持较高且稳定的状态,交叉验证准确率先快速增大而后保持稳定状态,样本数量达到模型预测的需求。由图4中平均训练时间与样本比例的关系可知,训练时间与样本比例(模型复杂度)呈线性递增的关系,在故障诊断过程中应综合考虑预测能力与模型复杂度确定样本数量。笔者为了便于组合方案测试分析,组合特征选择所涉及试验的样本数均为47 500,即总数的100%样本作为训练和交叉验证样本进行试验。
统计所有试验方案的不同样本比例平均训练时间,结果如图5所示。试验结果显示,无论样本比例如何变化,方案Ⅳ所需要的训练时间最大,即模型复杂度最大,预测能力结果(图4)显示,此方案对应的预测能力最强。方案Ⅲ所需要的训练时间最少,单其预测能力强于方案Ⅰ的预测能力。方案Ⅰ、方案Ⅱ和方案Ⅶ的训练时间保持一致,方案Ⅴ和方案Ⅵ的训练时间保持一致,均高于方案Ⅲ和低于方案Ⅳ的训练时间。

图5 不同样本比例的平均训练时间方案对比
Fig.5 Comparison of average training time with sample ratios
因此,在未进行特征优化选择时,平均训练时间与观测点类型数无明显关系,但2种观测点类型方案中有节点压能观测点类型参与诊断的训练时间均较少,而模型复杂度与预测能力并非呈递增关系。因此,矿井通风阻变故障观测点类型及组合方案有优化选择的空间。
使用式(5)~(7)基于多目标优化的观测特征选择模型对所有试验方案分别进行观测点多目标优化选择试验,其求解的Pareto解集如图6所示,其中横坐标表示10倍的相对观测点覆盖率,纵坐标表示10倍的平均交叉验证误差。结果显示,Pareto解集分布较平滑而均匀,要得到更低的交叉验证误差,需要有更多的观测点布设,但当观测点覆盖率达到一定量级时,交叉验证误差趋于平稳,即交叉验证误差不受观测点覆盖率的支配。所有方案试验结果的相对观测点覆盖率均小于0.5,即理论观测点数应为候选观测点的一半以下,其对应的交叉验证误差均小于0.2,在相同观测点覆盖率的情况下方案Ⅳ可获得更低的交叉验证误差,方案Ⅰ对应的交叉验证误差最高,交叉验证误差排序为方案Ⅳ<方案Ⅶ<方案Ⅴ<方案Ⅱ<方案Ⅲ<方案Ⅵ<方案Ⅰ,与未进行观测点选择的故障诊断结果保持一致,如图4所示,由此可说明阻变故障诊断准确率与观测特征类型存在着密切的关系。

图6 不同方案Pareto解集
Fig.6 Pareto solution set of different schemes
以0.05为步长,选择Pareto解集中相对观测点覆盖率0.05~0.40对应的被选观测特征,利用各试验方案中剩余的20%测试集进行k-近邻阻变故障诊断试验,得到结果如图7所示。结果表明无论观测特征类型及其组合方式如何变化,相对观测点覆盖率低于0.2时,与测试准确率呈递增关系,高于0.2时其对应的准确率保持稳定不变。对于确定的特征类型或组合特征类型,其观测点覆盖率高于0.2后,随观测点覆盖率的增加,其准确率未见明显提高趋势,即故障诊断准确率收敛于稳定的状态,风量特征类型对应的测试准确率收敛于90%,其他观测点类型和组合方式收敛于98%,与相同样本不进行观测特征选择方案的交叉验证准确率接近。因此,无论观测点类型如何变化,仅需候选观测点数量的20%左右即可获得与观测点覆盖率为100%对应的故障诊断准确率。

图7 观测点覆盖率对测试准确率的影响
Fig.7 Impact of observation point coverage on test accuracy
以所有观测点作为特征,即观测点覆盖率为100%的方案作为试验对照组,以k-近邻阻变故障位置诊断训练集的交叉验证误差最接近且不大于对照组误差的方案作为验证组,以与验证组具有相同观测点覆盖率为0.2的随机观测特征方案作为试验组,分别进行监督学习模型阻变故障位置和阻变故障量诊断试验分析,试验结果分别如图8,9所示。阻变故障位置诊断模型试验结果显示,各试验方案中验证组与对照组具有相同且大于90%的阻变故障位置诊断准确率,试验组故障诊断准确率均低于90%,且不同观测点类型其准确率不稳定;而验证组与试验组的训练时间保持一致,对照组的训练时间为验证组的3~10倍不等。以用于评价回归模型优劣程度的R2作为阻变故障量回归预测评价指标。阻变故障量回归预测试验中验证组和对照组的R2保持在0.99,试验组最高R2也可达到0.99,最低低于0.8;验证组与试验组具有相同的观测点覆盖率,试验过程中训练时间相同,且受到观测点类型变化的影响较小,对照组的训练时间为验证组的6~10倍。综上,观测点优化选择后20%的观测点覆盖率可达到观测点覆盖率100%的阻变故障位置诊断准确率和阻变故障量回归预测R2,训练时间可缩短60%,甚至可缩短至90%,说明观测特征优化选择在确保故障诊断性能的情况下,很大程度上降低了阻变故障诊断模型的复杂度。随机选择的观测点位置也有一定概率会获得较高的故障诊断性能,但故障诊断性能难以保持稳定的状态,试验结果与文献[14]使用粗糙集进行特征选择的结果保持一致。

图8 监督模型k-近邻阻变故障位置对比分析
Fig.8 Comparison analysis of windage alteration position of supervised model k-nearest neighbor algorithm

图9 监督模型k-近阻变故障量对比分析
Fig.9 Comparison analysis of the resistance variable of the supervised model k-nearest neighbor algorithm
为了验证观测特征优化选择的有效性,以监督学习模型的观测特征作为无样本模型的适应值参数,在相同试验参数设置的条件下,利用混合编码自适应进化策略算法对验证组、对照组和试验组分别进行阻变故障位置诊断和阻变故障量回归预测一体化试验,试验结果如图10所示。结果显示对照组的故障诊断准确率集中于95%,验证组结果在80%~90%,试验组低于50%~70%。对于阻变故障量回归预测的R2,验证组除风量单一特征为0.86外,其他方案所选择的特征均高于0.95,对照组除风量、风压和节点压能综合特征为0.82外,其他方案结果均高于0.95,试验组保持在0.90~0.95。因此,基于多目标优化的观测特征选择模型得到的优化特征同样适用于无样本模型,说明利用观测特征选择模型进行阻变故障特征选择所得的结果具有一定的有效性和可靠性,但未完全剔除无样本故障诊断模型中的冗余和不相关特征,仍有优化提升的空间。

图10 无样本模型验证对比分析
Fig.10 Comparison analysis of sample free model validation
通过保持无样本模型的种群大小和迭代次数等参数不变,对所有试验方案的不同观测点覆盖率分别进行试验,得到如图11(a)~(g)所示阻变故障位置诊断时间消耗与观测点覆盖率的结果,通过控制其他参数不变,改变种群大小进行试验,得到如图11(h)所示阻变故障位置诊断时间消耗与种群大小关系结果。由观测点覆盖率、种群大小与无样本模型阻变故障位置诊断所消耗时间的试验结果可知,在相同种群大小的条件下,观测点类型的变化和观测点覆盖率的增加并不会导致模型复杂度的改变,但是种群大小与模型复杂度呈线性递增的关系,试验结果与文献[10]和[11]一致,且文献研究表明模型复杂度的增加很大程度上会提升模型的故障诊断准确率和降低诊断误差。因此,在实际应用时需综合考虑模型复杂度与故障诊断的性能,同时对于无样本模型可适量增加观测点覆盖率。


图11 无样本模型特征类型与预测时间消耗关系
Fig.11 Relationship between feature types of sample-free model and prediction time consumption
(1)建立了矿井通风阻变故障观测特征组合优化选择方案,提出了一种基于多目标优化的观测特征选择模型,在降低观测点数量的同时,确保故障诊断监督模型和无监督模型的诊断性能。
(2)组合观测点类型的布设方案更利于进行阻变故障诊断,在条件允许的情况下,监督阻变模型不宜单独将风速传感器作为观测特征。
(3)观测点优化选择后20%的观测点覆盖率可达到未进行优化选择的阻变故障位置诊断准确率和阻变故障量回归预测性能,训练时间可缩短60%~90%,观测特征优化选择在确保故障诊断性能的情况下,很大程度上降低了阻变故障诊断模型复杂度。随机选择的观测点位置也有一定概率会获得较高的故障诊断性能,但故障诊断性能难以保持稳定状态。
(4)多目标观测特征选择方法所确定的观测点布设方案对无样本模型仍有效,但在实际应用时需综合考虑模型复杂度与故障诊断的性能,同时对于无样本模型可适量增加观测点覆盖率。
[1] 刘剑,宋莹,李雪冰,等. 基于LDA的均直巷道断面突扩风速分布规律实验研究[J]. 煤炭学报,2016,41(4):892-898.
LIU Jian,SONG Ying,LI Xuebing,et al. Experimental study on wind speed distribution of the straight roadway and sudden enlarged sections based on LDA[J]. Journal of China Coal Society,2016,41(4):892-898.
[2] JIA J,JIA P,LI Z. Theoretical study on stability of mine ventilation network based on sensitivity analysis[J]. Energy Science & Engineering,2020,8(8):2823-2830.
[3] NI W,LIU B,GAI W. The research on integrated visual information management system of the mine ventilation and safety[J]. Procedia Engineering,2011,26:2070-2074.
[4] 张庆华,姚亚虎,赵吉玉. 我国矿井通风技术现状及智能化发展展望[J]. 煤炭科学技术,2020,48(2):97-103.
ZHANG Qinghua,YAO Yahu,ZHAO Jiyu. Status of mine ventilation technology in China and prospects for intelligent development[J]. Coal Science and Technology,2020,48(2):97-103.
[5] 刘剑,郭欣,邓立军,等. 基于风量特征的矿井通风系统阻变型单故障源诊断[J]. 煤炭学报,2018,43(1):143-149.
LIU Jian,GUO Xin,DENG Lijun,et al. Resistance variant single fault source diagnosis of mine ventilation system based on air volume characteristic[J]. Journal of China Coal Society,2018,43(1):143-149.
[6] 刘剑,刘丽,黄德,等. 基于风量-风压复合特征的通风系统阻变型故障诊断[J]. 中国安全生产科学技术,2020,16(1):85-91.
LIU Jian,LIU Li,HUANG De,et al. Resistance variant fault diagnosis of ventilation system based on composite features of air volume and air pressure[J]. Journal of Safety Science and Technology,2020,16(1):85-91.
[7] 赵丹,刘剑,潘竞涛. 基于网络分析的矿井通风智能诊断专家系统[J]. 安全与环境学报,2011,11(4):206-210.
ZHAO Dan,LIU Jian,PAN Jingtao. A renovated network-based intelligent diagnosis mining-ventilation expertise system[J] Journal of Safety and Environment,2011,11(4):206-210.
[8] 赵丹. 基于网络分析的矿井通风系统故障源诊断技术研究[D]. 阜新:辽宁工程技术大学,2011.
ZHAO Dan. Study on fault source diagnosis technology for mine ventilation system based on network analysis[D]. Fuxin:Liaoning Technical University,2011.
[9] 胡青伟. 大平煤矿通风系统异常诊断研究[D]. 徐州:中国矿业大学,2019.
HU Weiqing. Research on abnormal diagnosis of ventilation system in Daping Coal Mine[D]. Xuzhou:China University of Mining & Technology,2019.
[10] HUANG D,LIU J,DENG L. A hybrid-encoding adaptive evolutionary strategy algorithm for windage alteration fault diagnosis[J]. Process Safety and Environmental Protection,2020,136:242-252.
[11] 刘剑,尹昌胜,黄德. 矿井通风阻变型故障复合特征无监督机器学习模型[J]. 煤炭学报,2020,45(9):3157-3165.
LIU Jian,YIN Changsheng,HUANG De. Unsupervised machine learning model for resistance variant fault diagnosis of mine ventilation system with composite features [J]. Journal of China Coal Society,2020,45(9):3157-3165.
[12] 赵丹,刘剑,陈占君,等. 矿井风速故障源诊断及角联结构传感器布设[J]. 中国安全科学学报,2012,22(11):88-92.
ZHAO Dan,LIU Jian,CHEN Zhanjun,et al. Mine wind velocity fault source diagnosis and transducer placement for corner-linked structure[J]. China Safety Science Journal,2012,22(11):88-92.
[13] ZHAO D,ZHANG H,PAN J. Solving optimization of a mine gas sensor layout based on a hybrid GA-DBPSO algorithm[J]. IEEE Sensors Journal,2019,19(15):6400-6409.
[14] 刘剑,蒋清华,刘丽,等. 矿井通风系统阻变型故障诊断及风速传感器位置优化[J].煤炭学报,2021,46(6):1907-1914.
LIU Jian,JIANG Qinghua,LIU Li,et al. Resistance variant fault diagnosis of mine ventilation system and position optimization of wind speed sensor[J]. Journal of China Coal Society 2021,46(6):1907-1914.
[15] XUE B,ZHANG M,BROWNE W N,et al. A survey on evolutionary computation approaches to feature selection[J]. IEEE Transactions on Evolutionary Computation,2016,20(4):606-626.
[16] 吴克伟,谢昭,高隽,等. 一种协同演化下的二元邻域判定误分纠错方法[J]. 计算机学报,2014,37(11):2276-2286.
WU Kewei,XIE Zhao,GAO Jun,et al. A binary neighbors discriminative method in collaborative evolution for error correction [J]. Chinese Journal of Computers,2014,37(11):2276-2286.
[17] CHEN C,TSAI Y,CHANG F,et al. Ensemble feature selection in medical datasets:Combining filter,wrapper,and embedded feature selection results[J]. Expert Systems,2020,37(5):e12553.
[18] 马波,蔡伟东,赵大力. 基于GAN样本生成技术的智能诊断方法[J]. 振动与冲击,2020,39(18):153-160.
MA Bo,CAI Weidong,ZHAO Dali. Intelligent diagnosis method based on GAN sample generation technology[J]. Journal of Vibration and Shock,2020,39(18):153-160.
[19] CAI J,LUO J,WANG S,et al. Feature selection in machine learning:A new perspective[J]. Neurocomputing,2018,300:70-79.
[20] KIZILOZ H E. Classifier ensemble methods in feature selection[J]. Neurocomputing,2021,419:97-107.
[21] HASTIE T,TIBSHIRANI R. Discriminant adaptive nearest neighbor classification[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,1996,18(6):607-616.
[22] DEB K,PRATAP A,AGARWAL S,et al. A fast and elitist multiobjective genetic algorithm:NSGA-II[J]. IEEE Transactions on Evolutionary Computation,2002,6(2):182-197.
[23] MADRAY I,SUIRE J,DESFORGES J,et al. Relative angle correction for distance estimation using k-nearest neighbors[J]. IEEE Sensors Journal,2020,20(14):8155-8163.
[24] HE Q P,WANG J. Fault detection using the k-nearest neighbor rule for semiconductor manufacturing processes[J]. IEEE Transactions on Semiconductor Manufacturing,2007,20(4):345-354.