
移动阅读

移动阅读
LI Xijian,XUE Haiteng,CHEN Liuyu,et al. Energy dissipation laws and hole safety dimensions of coal and gas outburst shock wave passing through door wall [J]. Journal of China Coal Society,2021,46(12):3934-3947.
煤与瓦斯突出(简称“突出”)是一种破坏力极强且机理复杂的矿井动力现象,突出瞬时喷出的高压瓦斯流往往会严重破坏防突风门及通风设施,造成瓦斯逆流[1]。尽管防突风门能够在一定程度上阻挡冲击波[2],但冲击波仍会穿越防突风门孔洞(如风窗、防突风门底坎、水沟)破坏正常通风系统,致使瓦斯波及到其他区域,增大了人员窒息和瓦斯爆炸等次生灾害事故发生的可能性。因此,掌握突出冲击波穿越防突风门孔洞能量演化规律,并制定科学的防突风门技术标准是减少突出次生灾害事故发生的关键。
自19世纪发生第1次煤与瓦斯突出以来,世界各国研究者基于物理试验[3-5]、数学模型[6-9]和数值模拟[10-11]等手段不断探索突出发生机理,取得了丰富成果。不同维度的试验和物理模型进一步完善了突出机理,但由于诱发突出事故发生的影响因素复杂,目前的研究成果并不能完全抑制突出灾害事故发生。ZHOU等[12-13]分析了不同类型巷道煤粉与气流的相互作用机理和冲击波与瓦斯流的形成、传播过程,认为冲击波在丁字型巷道衰减效果最好,相邻巷道压力突变范围和瓦斯流量影响范围随掘进巷道和相邻巷道的夹角增大而增大。WANG等[14]结合数值模拟和试验研究了突出冲击波和瓦斯流动特性,发现冲击波和气流传播到交叉口时,出现湍流、反射和衍射现象,且大部分冲击波和气流向交叉口对面路段巷道传播。孙东玲等[15]、许江等[16]利用自主研发的突出试验装置,探讨了突出煤-瓦斯两相流在巷道内的运移规律。王凯等[17-19]综合分析了直角、截面积变化和直角拐弯巷道对突出冲击波传播过程的影响规律。这些理论成果为更好地认识煤与瓦斯突出机理、突出冲击波在巷道内的传播特征和预防突出灾害奠定了坚实的基础,但对突出冲击波与通风设施的相互作用研究较少。
实现通风设施在灾变条件下的有效性,能够最大限度地减少突出冲击波的破坏[20]。代树红等[21]基于静动力学分析,优化了钢构防突风门结构。李峰等[20]研究了瓦斯爆炸冲击载荷作用下的矩形风窗破坏机理,提升了矩形风窗在灾变条件下的有效性。程卫民等[22]模拟了突出后防突风门的破坏,研究指出门垛最薄弱的地方是风筒所在位置。以上研究重点集中在冲击波作用于通风设施的结构破坏特征,忽略了突出冲击波穿越门墙孔洞时的能量演化规律研究,例如防突风门底坎,根据《煤与瓦斯突出反向防突风门设置技术条件》[23],反向的防突风门的通车风门必须设置底坎,且门扇底端距离轨道面高度不得大于20 mm,那么,在该尺寸条件下,一旦发生煤与瓦斯突出,穿越防突风门底坎的冲击波能否造成瓦斯逆流还尚无定论。因此,在这方面的研究中还存在以下几方面不足:① 突出冲击波穿越防突风门孔洞的能量传播与衰减规律研究较少;② 确定突出冲击波穿越防突风门孔洞安全尺寸大小试验研究尚未完善。
据此,笔者在理论分析的基础上,利用自主研发的“煤与瓦斯突出能量传播模拟与参数测定试验装置”,结合数值模拟手段研究了突出冲击波穿越防突风门底坎时的能量耗散规律,并根据瓦斯逆流判据,确定了安全防突风门底坎尺寸,以期为制定科学的防突风门技术标准及矿井瓦斯防治提供理论支撑。
对于一维正冲击波,如图1所示。把相对于波阵面而言质点朝向波阵面流动的区域称为波前,相反的一边称为波后。用带下标“0”表示波前的量。根据质量、动量和能量守恒关系,可得一维平面情况下,间断面上冲击波穿越防突风门底坎基本关系式[24]为

图1 冲击波传播示意
Fig.1 Schematic diagram of shock wave propagation
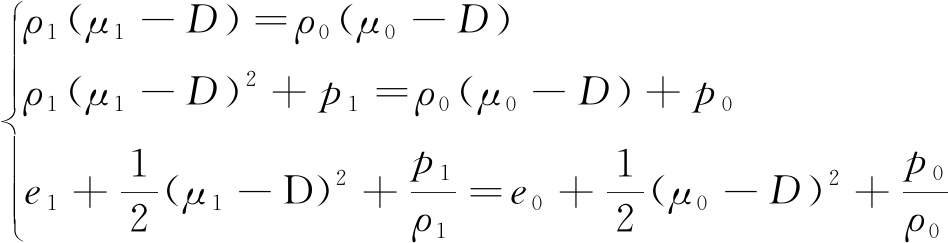
(1)
式中,D为冲击波速度,m/s;μ0,ρ0,p0分别为波前介质的速度(m/s)、密度(kg/m3)、压力(kPa);μ1,ρ1,p1分别为波后介质的速度(m/s)、密度(kg/m3)、压力(kPa);e0,e1为波前/后冲击波内能,kJ。
状态方程可写为
(2)
式中,e为冲击波内能,kJ;γ为气体压缩系数,取1.4;p为压力,kPa;ρ为密度,kg/m3。
冲击波穿越防突风门底坎如图2所示,图2(b)中H为风门底坎。假设冲击波波阵面在单位时间内从Ⅰ—Ⅰ面穿越防突风门底坎传播到Ⅱ—Ⅱ面,突出冲击波在传播过程中经历了巷道横截面积变化,波阵面强度发生突变。流体质点经过波阵面Ⅰ—Ⅰ后突跃参数变为μ1,ρ1,p1,经过防突风门底坎后突跃参数变为μ2,ρ2,p2。

图2 冲击波穿越防突风门底坎示意
Fig.2 Schematic diagram of shock wave passing through the bottom sill of outburst prevention wind door
假设冲击波在传播过程中没有能量损失,且冲击波波阵面在截面积变化前后的传播速度相等,忽略冲击波波阵面反射和绕射的变化过程。将式(1),(2)应用到图2中Ⅰ—Ⅰ,Ⅱ—Ⅱ组成的矩形区域内冲击波波阵面[25],可得
ρ1(μ1-D)S1=ρ0(μ0-D)S0
(3)
式中,S1为巷道截面积,m2;S0为防突风门底坎截面积,m2。
(4)
(5)
Ⅰ—Ⅰ,Ⅱ—Ⅱ组成的矩形区域中间的部分为控制体,根据假设和动量定理。控制体所受合外力F为
F=p0S0-p2S0
(6)
控制体单位时间内质点动量变化[18]为
ρ1(μ1-D)2S1=ρ0(μ0-D)2S0
(7)
单位时间内作用在控制体上的合外力等于控制流体的动量变化,因此:
p0S0-p2S0=ρ1(μ1-D)2S1=ρ0(μ0-D)2S0
(8)
将式(5)~(7)代入式(8)可得突出冲击波穿越防突风门底坎后的出射波超压:

(9)
式(9)中,参数p0,S1,γ为定值,p1可通过试验测得,而矿井中的风门底坎尺寸不同,因此,穿越防突风门底坎的出射波超压p2只与防突风门底坎截面积S0有关。对于突出冲击波穿越2道防突风门底坎时在巷道中的传播过程,可视为冲击波2次由小截面进入到大截面,研究表明[18],冲击波由小截面进入到大截面时,由于巷道扩大导致冲击波膨胀而衰减,冲击波超压变小,而且,S0越小,截面积变化率S1/S0越大,冲击波膨胀越大,超压越小。所以,矿井风门底坎尺寸越小,越能够有效阻挡冲击波,避免灾害事故发生。取极限条件S0=0时,p2=p1,冲击波无法穿越风门底坎继续向前传播。
试验研究的主要目的是为了模拟煤与瓦斯突出冲击波穿越防突风门底坎时的能量传播与衰减规律,因此,试验装置设计主要考虑以“流动相似”为主导相似准则。基于“流动相似”准则可知,两流体的流动相似需满足几何相似、运动相似和动力相似[26]。
(1)几何相似。几何相似是流体相似基础,即模型的几何相似准则要求模型和原型中2个流场的几何形状相似,模型试验与实物对应长度、面积等成比例,可表示为
λl=lp/lm
(10)
其中,λl为几何相似常数;lp为原型线性长度;lm为模型线性长度。当λl确定后,则面积相似常数λA、体积相似常数λV、质量相似常数λm、时间相似常数λt等参数也随之确定,表达式为
(11)
(2)运动相似。运动相似是指在流体质点的运动轨迹几何相似的基础上,相对应运动时间成比例,即速度场相似,其包括了速度相似和加速度相似,其表达式为
λv=vp1/vm1
(12)
式中,λv为速度相似常数;vp1为原型速度;vm1为模型速度。
λa=ap1/am1
(13)
式中,λa为加速度相似常数;ap1为原型加速度;am1为模型加速度。
(3)动力相似。动力相似是指模拟试验的模型与实际原型流场内对应点上的流体微元(质点)上的各种力(重力、黏滞力、弹性力等)中同种力的大小成比例,方向相同。表达式为
λF=Fp/Fm
(14)
式中,λF为力的相似常数;Fp为原型特征力;Fm为模型特征力。
取井下巷道截面的平均尺寸为4 m×4 m,本次试验选取模拟巷道的尺寸为20 cm×20 cm,则模型的几何相似常数为
λl=lp/lm=20
(15)
试验选取的巷道风速范围与实际的风速范围相同,即
λv=vp1/vm1=1
(16)
本次试验气体流动过程主要存在2个主体部分:第1部分为突出腔体高压气体泄放过程,此过程影响气体流动的主要因素为弹性力,应满足马赫数相似;第2部分为气体在巷道中的传播运移过程,此过程气体流动主要受黏滞力的影响,应满足雷诺数相似。
根据马赫数的定义
(17)
其中,Ma为马赫数;μ为流体速度,m/s;c为声速,m/s;下标p,m代表试验原型和模型对应参数。理想气体声速只是温度T的函数[24],而通常假设原型温度和模型温度相等[27],即Tp=Tm,则cp=cm,并且原型和模型的流体速度相等。因而可近似认为马赫数相同,能够反映煤与瓦斯突出冲击波产生的气流速度。
非圆形巷道断面井巷雷诺数可表示[28]为
Re=4μmS/(νV)
(18)
其中,Re为雷诺数;ν为巷道中瓦斯和空气混合物的运动黏性系数,笔者取14.4×10-6 m2/s[29];S为巷道截面积,m2;V为巷道断面周长,m。当矿井巷道风流速度为1 m/s时,Re>200 000,此时已进入流体的“自模化状态”,雷诺数和流动阻力已基本无关[28-31],因此不需要考虑原型和模型雷诺数。
试验所用自行搭建的“煤与瓦斯突出能量传播模拟与参数测定试验装置”如图3(b)所示。试验共设计5个测点,依次为1,2,3,4,5号测点,测点1布置在分支巷道,距直巷道0.16 m,测点2距突出腔体2 m,测点3距突出腔体2.5 m,测点4距突出腔体2.72 m,测点5距突出腔体3.22 m,试验系统压力传感器布置如图3(a)所示,试验系统如图3(d)所示。第1道防突风门距突出腔体2.5 m,第2道防突风门距突出腔体2.9 m,2道防突风门间隔0.26 m。为保证试验的安全性,试验所充气体为惰性气体氮气(N2)。将突出腔体抽真空1 h后,打开连接气瓶高压管上的阀门向突出腔体内充装氮气。充气压力分别为0.50,0.74,1.00 MPa,以0.1 MPa为1阶梯进行阶梯式充气,直至压力达到设定值并稳定,关闭连接气瓶的高压管阀门,静止30 s,用手动的方式搬动快速卸压装置,模拟启动突出。突出前,打开供风系统,通风动力设备为大型吸尘器,其功率为5 400 W,电压为220 V,频率为50 Hz。试验采用TP-1MP型冲击波传感器(图3(c)),压力传感器在试验巷道上的安装方式为管内安装,即压力传感器的感应面与突出冲击波的传播方向平行,如图3(e)所示。数据采集终端如图3(f)所示。

图3 数据测试器材及试验系统示意
Fig.3 Schematic diagram of data test equipment and test system
根据《煤与瓦斯突出反向风门设置技术条件》[23],反向的防突风门的通车风门必须设置底坎,门扇底端距离轨道面高度不得大于20 mm。因此,以20 mm为最大防突风门底坎尺寸,取间隔为5 mm,研究压力为0.50,0.74,1.00 MPa,防突风门底坎尺寸20,15,10,5,1 mm条件下的冲击波超压随时间变化规律。各尺寸条件下,1,2号测点所测数据一致,如图4所示,其他测点试验结果如图5所示。为便于分析,将第1道压力峰值简称“峰1”、第2道压力峰值简称“峰2”、第3道压力峰值简称“峰3”。图6为冲击波在直巷道、分支巷道及封堵分支巷道Ⅲ—Ⅲ截面传播示意。图4中,1号测点图中红色箭头所指为该区域局部放大图,黑色箭头所指为峰2位置。由图4~7可知:

图4 1,2号测点冲击波超压试验结果随时间变化曲线
Fig.4 Change curves of shock wave overpressure experiment results with time at measuring points 1,2

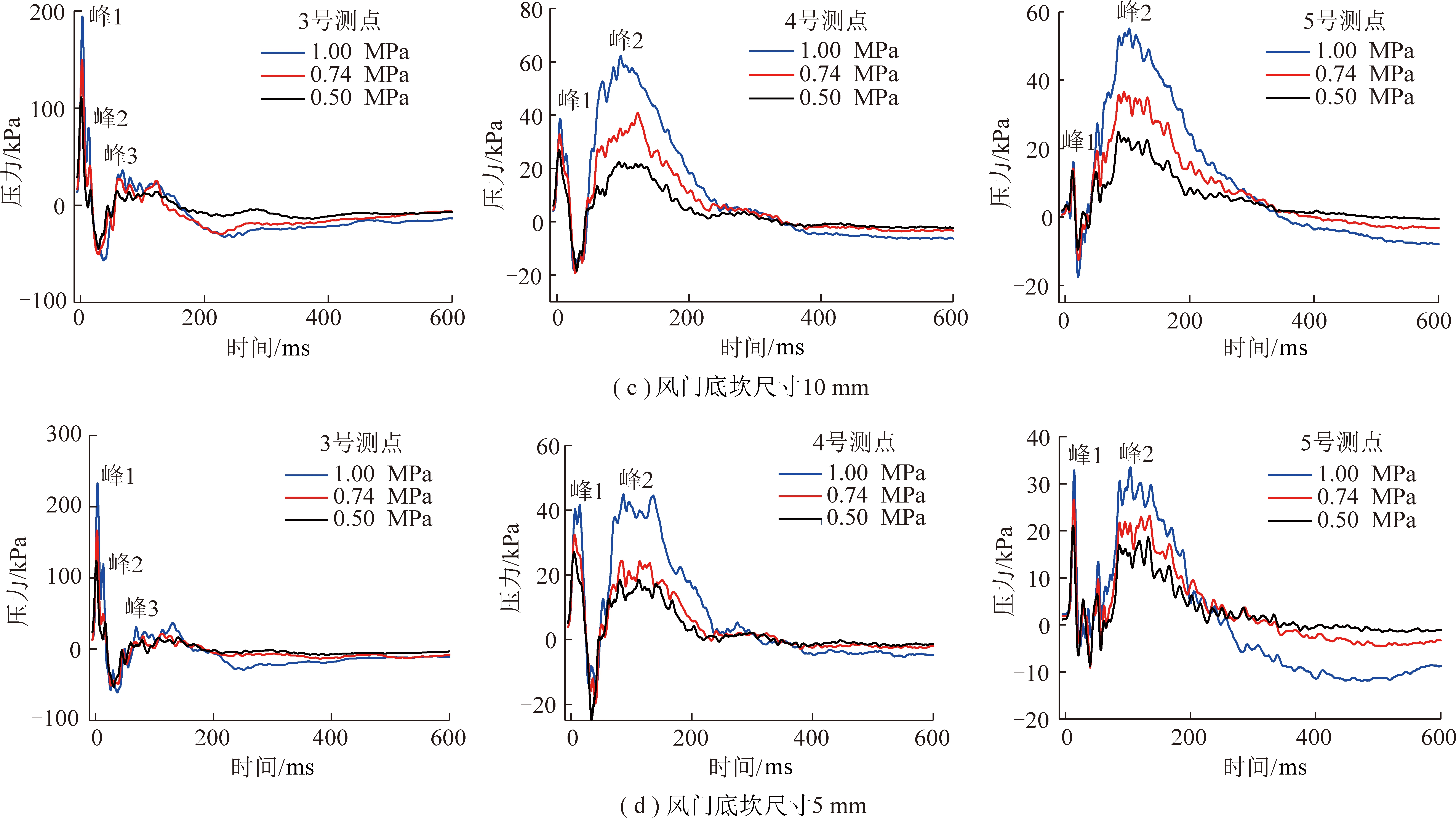

图5 3,4,5号测点冲击波超压试验结果随时间变化曲线
Fig.5 Change curves of shock wave overpressure experiment results with time at measurement points 3,4,and 5

图6 冲击波在巷道中传播示意
Fig.6 Schematic diagram of shock wave propagation in the tunnel
(1)突出冲击波涌入巷道后,首先产生的入射冲击波被1,2,3号测点监测到,形成1,2,3号测点的峰1。入射冲击波与分支巷拐角壁面碰撞反射,产生的冲击波很快被1号测点再次监测到,形成1号测点的峰2。入射冲击波与第1道防突风门撞击,产生的反射冲击波经过1,2,3号测点被监测到,形成1号测点的峰3及2,3号测点的峰2。反射冲击波传播到突出腔体与突出挡板撞击再次反射,形成的冲击波再次经过2,3号测点被监测到,形成2,3号测点的峰3。入射冲击波与防突风门撞击除发生反射现象外,还有部分冲击波绕过防突风门,沿防突风门底坎继续向前传播被4号测点监测到,形成4号测点的峰1。4号测点峰2由分支巷A点传播到C点再传播到D1点的冲击波引起。
(2)各压力条件下,对比各防突风门底坎尺寸条件下5号测点峰1出现时间可以发现:防突风门底坎尺寸为20,15 mm,5号测点峰1的出现时间为3 ms左右,与1,2,3,4号测点峰1的出现时间相近,说明防突风门底坎尺寸为该尺寸时,5号测点峰1超压由直巷道中传播的入射冲击波引起,同时也说明,防突风门底坎尺寸在上述尺寸条件下,2道防突风门不能完全阻挡直巷道冲击波入侵,极可能会引起风流逆转,造成瓦斯逆流。防突风门底坎尺寸为10,5,1 mm时,5号测点峰1超压逐渐增大,且峰1出现的时间为13.4 ms左右,比防突风门底坎尺寸为20,15 mm时,5号测点峰1的出现时间较晚,由此推断防突风门底坎尺寸为10,5,1 mm时,5号测点峰1超压由分支巷A点传播到C点再传播到D1点的冲击波产生,说明当最大瓦斯压力为1 MPa,防突风门底坎尺寸为10 mm以下时,2道防突风门几乎能够有效隔绝直巷道冲击波的入侵,防止瓦斯逆流,保障门外作业人员的人身安全。但随着矿井开采深度增加,煤与瓦斯突出强度不断增大,因此,在不影响矿井正常作业的情况下,为了保证风门外作业人员的安全,防突风门底坎尺寸越小越好。而5号测点的峰2由分支巷的冲击波引起。图7为分支巷道Ⅲ—Ⅲ截面封堵条件下(图6(c)),5号测点冲击波超压随时间变化曲线,可以看出5号测点的最大超压峰值出现在35 ms以后,比未封堵分支巷道Ⅲ—Ⅲ截面时,5号测点峰1值的出现时间更晚,说明峰1由A点传播到B点再传播到D1点的冲击波引起。同时对比未封堵和封堵分支巷道Ⅲ—Ⅲ截面条件下5号测点的峰值压力,可以看出封堵分支巷道Ⅲ—Ⅲ截面时5号测点峰值压力明显降低,究其原因冲击波在传播到5号测点前的路径增长,在传播过程中受巷道壁面阻力及冲击波与各巷道拐角壁面发射,致使冲击波压力衰减,从而使得5号测点所监测到的冲击波超压降低。由封堵分支巷道Ⅲ—Ⅲ截面5号测点峰值出现时间及峰值压力,一方面可验证未封堵分支巷道Ⅲ—Ⅲ截面,防突风门底坎尺寸为10,5,1 mm,5号测点峰1产生的原因,另一方面也可说明4,5号测点峰2由分支巷的冲击波引起。同时也说明,当分支巷道与防突风门较近时,应在分支巷道安装相应的防逆流装置。

图7 封堵分支巷道5号测点冲击波超压变化曲线
Fig.7 Variation curves of shock wave overpressure at No. 5 measuring point of blocked branch roadway
(3)在各尺寸、压力条件下,对比1、2号测点超压峰值,发现2号测点超压峰值大于1号测点,说明当冲击波通过交叉口时,冲击波主要在直巷道传播,同时也说明,在直巷道设置防突风门可有效阻挡大部分冲击波的破坏。对比2,3号测点超压峰值,可以发现3号测点超压峰值大于2号测点超压峰值,这主要是因为3号测点位置距离防突风门较近,入射冲击波和反射冲击波叠加后使得3号测点冲击波峰值抬升,这与前人研究一致[32]。对比3,4号测点的超压峰值,可以发现冲击波由于受到防突风门的阻滞作用,4号测点的超压峰值大幅度衰减。
(4)各压力条件下,对比4,5号测点的超压峰值,可以发现当防突风门底坎为20,15 mm时,5号测点大于4号测点超压峰值,而当防突风门底坎为10、5 mm时,4号测点大于5号测点的超压峰值,究其原因防突风门底坎尺寸越小,入射波与防突风门的接触面积变大,冲击波受2道防突风门的阻滞作用增强,大部分冲击波与第1道防突风门撞击产生反射冲击波,致使3号测点的超压峰值增大,而能够穿越第1道防突风门底坎的部分冲击波遇第2道防突风门再次反射,冲击波在反射过程中能量损耗致使5号测点所监测到的冲击波超压峰值降低。当防突风门底坎为1 mm时,4号测点监测到的超压峰值为6 kPa,冲击波几乎不能穿越防突风门底坎向前传播。充气压力越大,冲击波超压越大,这与前人研究成果一致[17]。
由于物理试验巷道网络的复杂性,数值模拟软件无法实现收敛,因此,根据研究内容重点,将试验巷道进行简化,建立突出冲击波三维模型。模型主要包括突出腔体和巷道通风网络2个部分。突出腔体的尺寸为50 cm×30 cm×30 cm,模拟巷道尺寸为20 cm×20 cm。模拟巷道中共布置5个测点,坐标分别为:测点1(2.25,0,-0.4)、测点2(2.5,0,-0.15)、测点3(2.85,0,-0.15)、测点4(3.05,0,-0.15)及测点5(3.45,0,-0.15),模拟测点布置位置与试验一致,如图8所示。初始条件见表1。

图8 巷道模拟几何模型
Fig.8 Roadway simulation geometry model
表1 模型初始化参数设置
Table 1 Model initialization parameter settings

位置参数初始化值巷道内气体类型空气气体流速/(m·s-1)0瓦斯体积占比/(m3·m-3)0气体温度/K300试验压力/MPa0腔体内气体类型CH4瓦斯体积占比/(m3·m-3)1气体温度/K300试验压力/MPa0.50,0.74,1.00
图9,10为时间t=4,6,7,8 ms,试验压力0.50,0.74,1.00 MPa,防突风门底坎尺寸20 mm和15 mm冲击波传播过程模拟结果。为了更清楚地看清冲击波穿越2道风门压力变化,数值模拟显示最大压力为40 kPa。
(1)由图9可知,防突风门底坎尺寸为20 mm,试验压力为1 MPa,t=4 ms时,冲击波尚未撞击到风门,但在防突风门前已有压力扰动,压力为0.13 Pa;t=5 ms时,一部分冲击波与风门撞击、反射,另一部分冲击波绕过第1道防风门继续向前传播,2道风门间最大压力为11.64 kPa;t=6 ms时,冲击波穿越第2道防突风门,最大压力为26.01 kPa。当试验压力为0.74,0.50 MPa,t=4 ms时,冲击波未撞击到防突风门,在风门前无压力扰动;t=5 ms时,冲击波与第1道防突风门相撞,风门后的气体受冲击波扰动,最大压力在风门后上隅角位置,压力为1.59 kPa,冲击波发生绕射现象;t=6 ms时,冲击波穿越第1道风门,最大压力在第2道风门前,由入射波和反射波叠加所致使,此时第2道风门后的气流受冲击波扰动,压力为1.73 kPa;t=7 ms时,冲击波穿越第2道风门继续向前传播,最大压力为14 kPa。从图9还可以看出,突出压力越低,同一时间内冲击波传播位置距风门越远,说明突出压力越底,冲击波传播速度越慢。

图9 风门底坎尺寸20 mm冲击波传播过程模拟结果
Fig.9 Simulation results of the shock wave propagation process with a size of 20 mm at the bottom of the flap
(2)由图10可得,当防突风门底坎为15 mm,试验压力为1.00 MPa,t=5 ms时,冲击波与防突风门撞击、反射,没有绕过防突风门底坎继续向前传播;t=6 ms时,冲击波穿越第1道防突风门,t=7 ms穿越第2道防突风门底坎,这与防突风门底坎为20 mm时,冲击波穿越2道防突风门底坎的时间较晚,说明防突风门底坎尺寸越小,受防突风门的阻滞作用越强,冲击波穿越难以穿越防突风门底坎继续向前传播,这与试验所得结论一致。试验压力为0.50,0.74 MPa时,由于突出压力降低,冲击波穿越2道风门后的压力大幅度减小,冲击波的传播规律与防突风门底坎为20 mm时的一致。
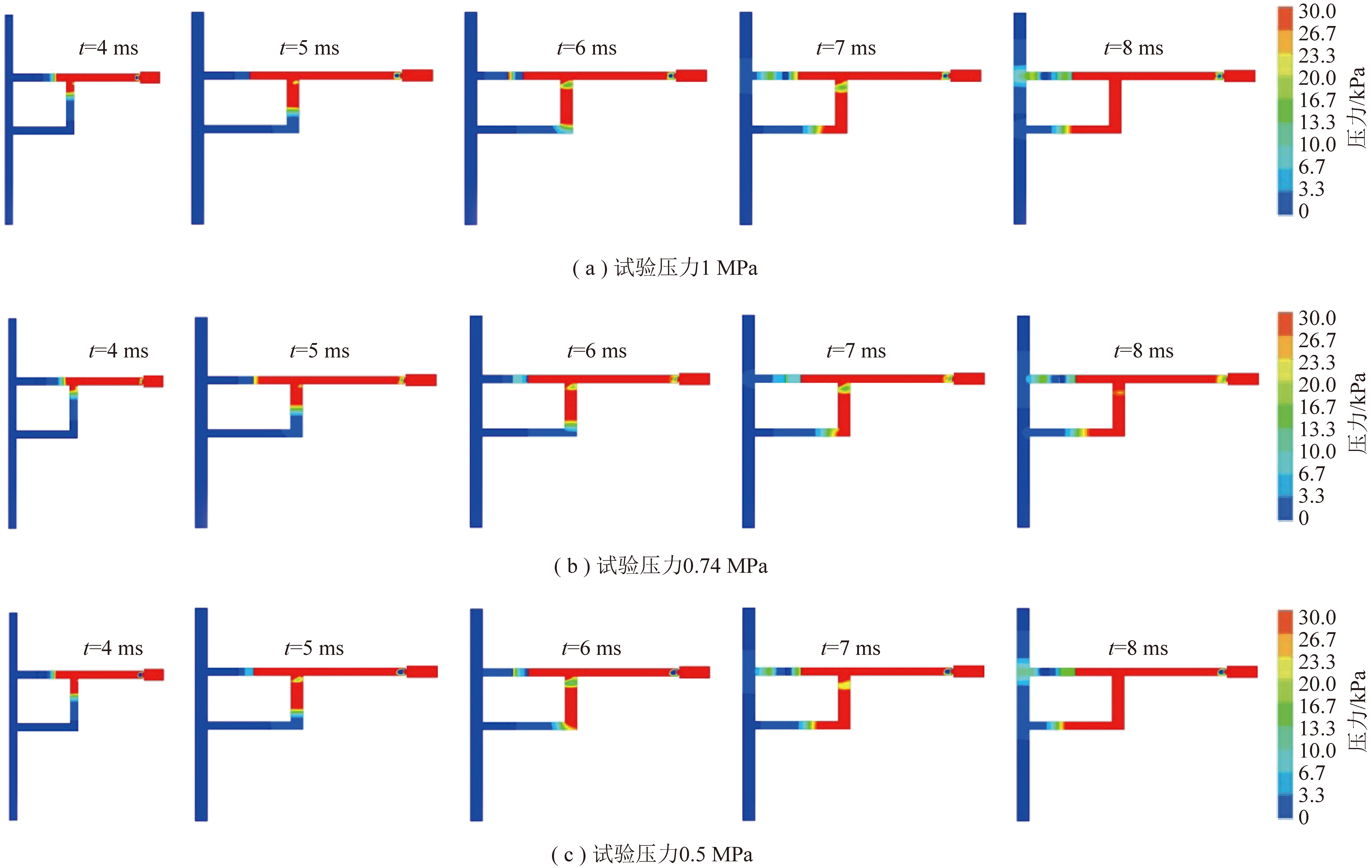
图10 风门底坎尺寸15 mm冲击波传播过程模拟结果
Fig.10 Simulation results of the shock wave propagation process with a size of 15 mm at the bottom of the flap
图11,12为试验压力0.50,0.74,1.00 MPa,防突风门底坎尺寸20,15,10,5,1 mm冲击波超压随时间变化曲线。
由图11,12可得:
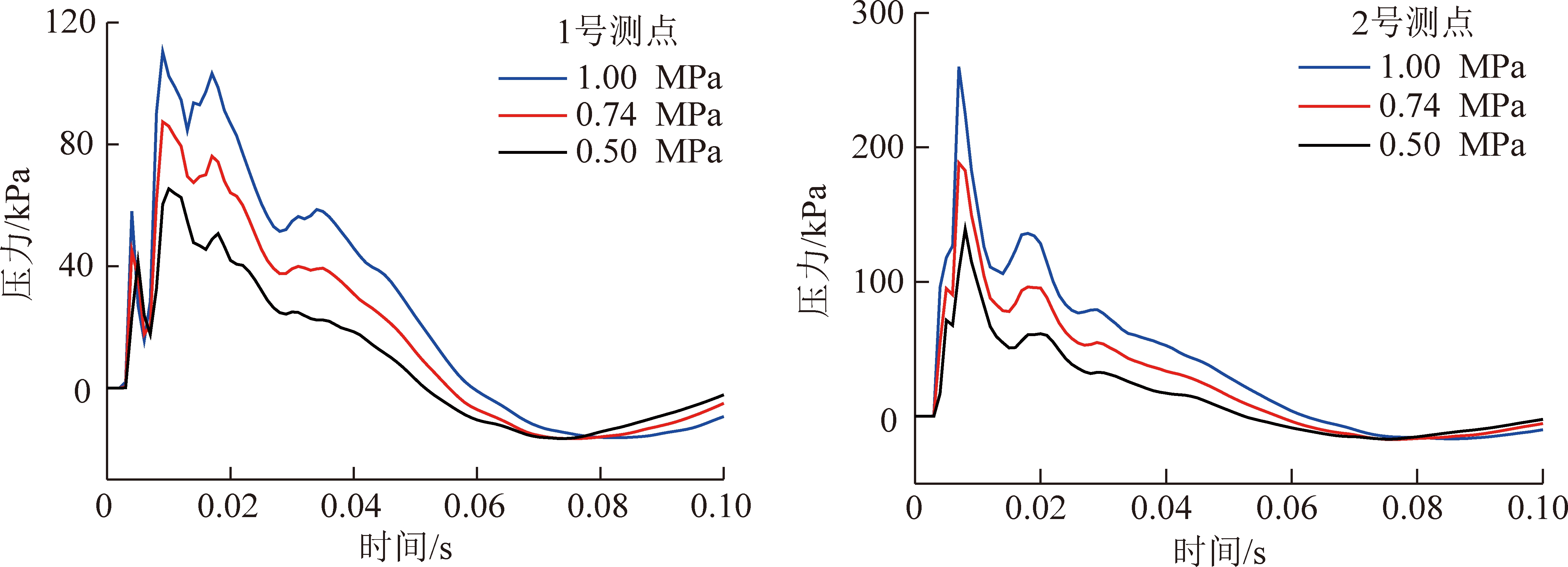
图11 1,2号测点冲击波超压模拟结果随时间变化曲线
Fig.11 Change curves of shock wave overpressure simulation results with time at measuring points 1,2
(1)2号测点超压峰值大于1号测点,冲击波通过交叉口时,大部分冲击波会流入直巷道,少部分冲击波会流入相邻分支巷道;3号测点超压峰值大于2号测点,主要是由于入射冲击波和反射冲击波叠加所致;由于受防突风门阻滞作用,4号测点超压峰值大幅度降低;随着防突风门底坎尺寸的变小,4号测点第1道超压峰值逐渐减小,且当防突风门底坎尺寸为1 mm时,4号测点第1道超压峰值为5 kPa,冲击波几乎无法穿越防突风门底坎向前传播;充气压力越大,冲击波超压越大。上述所得结论与试验结果一致。
(2)由于数值模拟巷道模型简化,且尚未考虑高压气体对煤体做功,因此,模拟得出的各测点最大超压均大于试验,但总体趋势一致,证明合理的简化数值模拟模型是可行的。从图中5号测点第1道压力峰值不难发现,由于数值模拟得出的冲击波压力较大,导致防突风门底坎为10,5 mm时,仍有冲击波能够穿越2道防突风门底坎继续向前传播,当防突风门底坎为1 mm时,2道防突风门能够有效隔绝直巷道冲击波的入侵。
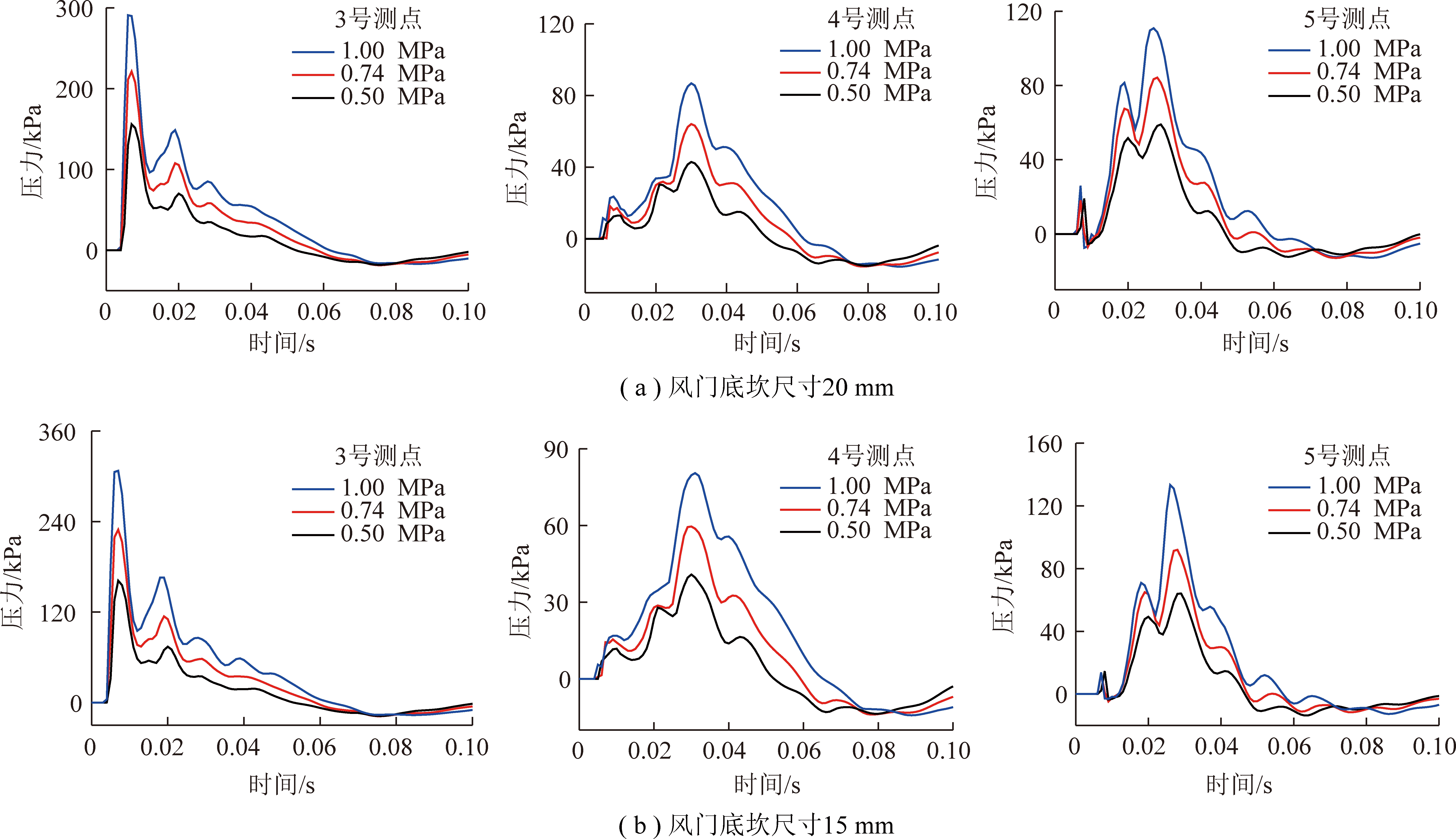

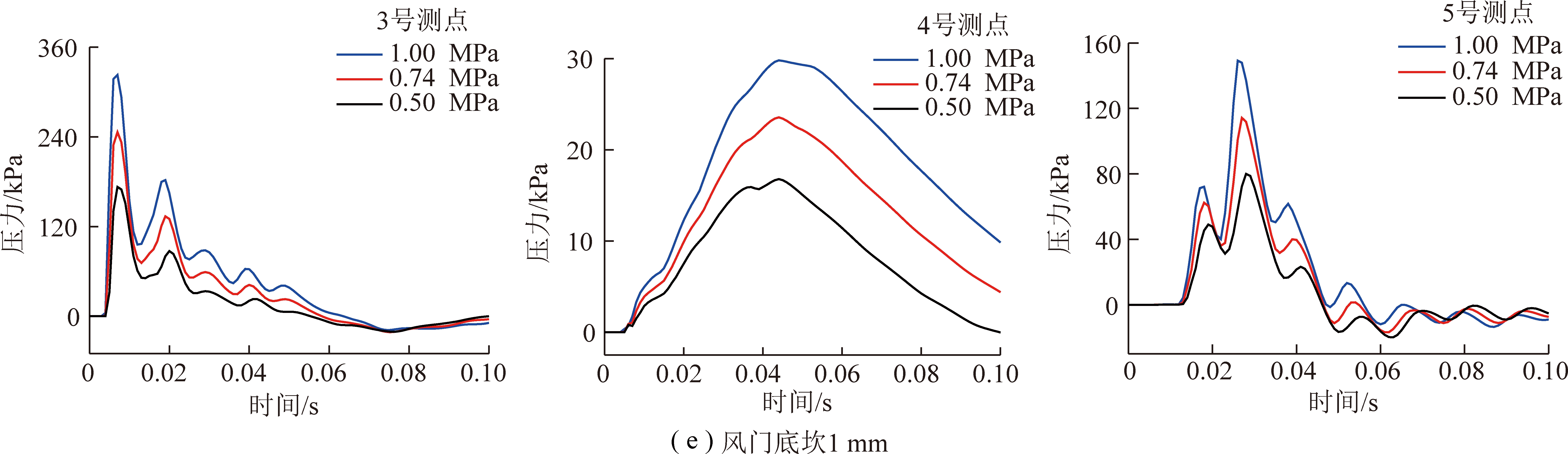
图12 3,4,5号测点冲击波超压模拟结果随时间变化曲线
Fig.12 Change curves of shock wave overpressure simulation results at measurement points 3,4,and 5
突出后瓦斯能够发生逆流的条件是突出冲击波穿越2道防突风门底坎后的总能量大于巷道通风阻力[33],其理论条件为
(19)
式中,ρ为空气密度,kg/m3;g为重力加速度,m/s2;Z0,Z2分别为波前/后巷道的高度,m;hR为通风阻力,Pa;μ2为穿越第2道风门后冲击波波阵面速度,m/s;μ3为通风条件下风流的速度,m/s;P0为大气压力,取101.325 kPa;P2为穿越第2道风门后冲击波压力,kPa。
穿越第2道风门后冲击波波阵面速度μ2[31]可表示为
(20)
式中,c1为声速,取340 m/s。
通风阻力为摩擦阻力和局部阻力之和[33],即
(21)
式中,hf为摩擦阻力,Pa;hp为局部阻力,Pa;α为摩擦阻力系数,N·s2/m4;L为巷道的长度,m;Q为局部断面风量,m3/s;ξ为局部阻力系数,无因次。
而穿越2道防突风门底坎后的冲击波不能够继续在巷道中传播是不发生瓦斯逆流的理想条件,即突出冲击波不与巷道壁面摩擦产生摩擦阻力。因此,只考虑巷道中的局部阻力,式(21)可描述为
(22)
局部阻力系数[26]可表示为
ξ=(1-S0/S1)2
(23)
将式(22)代入式(19)可得
(24)
假设巷道为水平直巷,不存在高度差,则式(24)可表示为
(25)
基于式(25)可得瓦斯逆流判据为
(26)
将式(20),(23)代入式(26),可得
(27)
令![]() 则式(27)可描述为
则式(27)可描述为
P2>ΔP
(28)
由3.2节第2条结论可知,5号测点所监测的2道超压峰值主要由2个部分冲击波引起:① 由直巷道中传播的冲击波穿越2道防突风门底坎后的冲击压力引起;② 由传播至分支巷道的冲击波产生。由于试验装置是基于相似理论建立,致使4,5号测点受分支巷冲击波影响较大,出现第2波压力峰值,这种现象在实际矿井中不会发生。因此,仅以5号测点的峰1压力值(P2)作为判断瓦斯逆流依据。
将表2参数数值代入式(27)可得ΔP,再将ΔP与P2作比较,当P2>ΔP时,发生瓦斯逆流。以试验数据为例,计算结果见表3。
表2 模型计算参数
Table 2 Model calculation parameters

参数数值c1/(m·s-1)340Q/(m3·min-1)3.60S1/m20.04ρ/(kg·m-3)1.29μ3/(m·s-1)1.50
表3 试验及模型参数对比
Table 3 Test and model parameter comparison
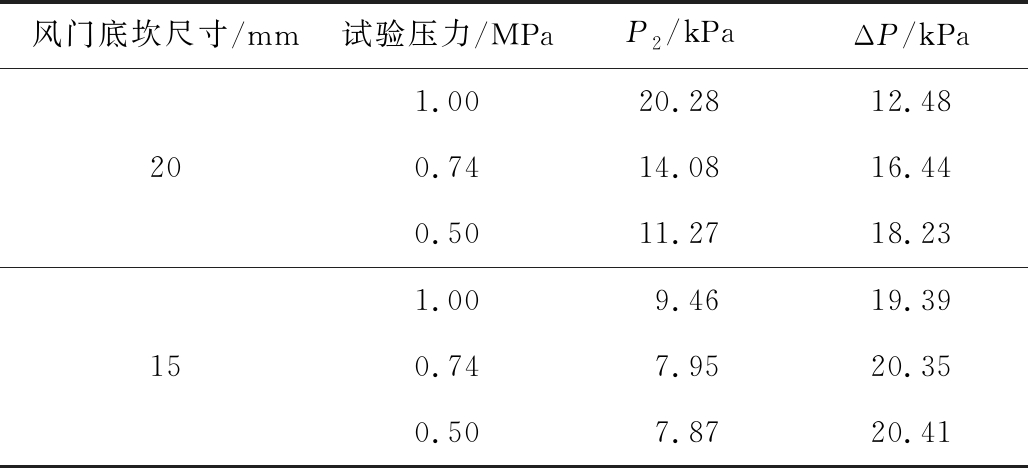
风门底坎尺寸/mm试验压力/MPaP2/kPaΔP/kPa201.0020.2812.480.7414.0816.440.5011.2718.23151.009.4619.390.747.9520.350.507.8720.41
由表3可知,防突风门底坎尺寸为20 mm时,突出压力为1.00 MPa,P2>ΔP,突出压力为0.74,0.50 MPa,P2<ΔP;防突风门底坎尺寸为15 mm以下时,各压力条件下,P2均小于ΔP。由此说明,当防突风门底坎尺寸为20 mm,突出压力为1.00 MPa时,穿越2道防突风门底坎后的压力大于巷道的通风阻力,会产生瓦斯逆流现象,突出压力为0.50,0.74 MPa时,不会造成瓦斯逆流现象。而当防突风门底坎尺寸为15 mm以下时,穿越2道风门底坎后的冲击波超压不会致使气流逆转,造成瓦斯逆流。
同理,将数值模拟结果代入式(27),可得到当防突风门底坎尺寸为20 mm时,各压力条件下,P2均大于ΔP,会造成瓦斯逆流。防突风门底坎尺寸为15 mm以下时,不会产生瓦斯逆流现象,与试验计算结果一致。综上表明,在一定压力条件下,防突风门底坎尺寸为20 mm时,突出冲击波穿越2道防突风门后产生的超压能够使风流逆转,造成瓦斯逆流。而防突风门底坎尺寸为15 mm以下时,各压力条件下,突出冲击波产生的超压不会造成瓦斯逆流,说明矿井防突风门的安全尺寸为15 mm。而且,根据冲击波对人体的伤害程度(表4),在该尺寸条件以下,穿越2道防突风门底坎后的压力不会对人体产生伤害,进一步证明了防突风门底坎设计值为15 mm是可行的。
表4 冲击波超压对人体的伤害程度[25]
Table 4 Damage of shock wave overpressure to human body

超压/kPa伤害作用<20受到惊吓20~30轻微伤害30~50听觉器官损伤或骨折50~100内脏严重损伤或死亡>100大部分人员死亡
(1) 利用自主研发的煤与瓦斯突出能量传播模拟与参数测定试验装置,进行了突出冲击波穿越防突风门底坎物理模拟试验,得到:撞击防突风门后的入射冲击波和反射冲击波叠加效应显著,且叠加后的冲击波对周围设备和人员的毁伤作用增强;由于受防突风门的阻滞作用,穿越风门底坎后的冲击波超压大幅度降低,且防突风门底坎尺寸越小,阻滞效果越明显,反射冲击波超压越大;防突风门底坎尺寸为20,15 mm时,仍有部分冲击波能够穿越风门底坎继续向前传播。
(2)进行了突出冲击波穿越防突风门底坎三维数值模拟,模拟结果表明:突出压力越低,冲击波传播速度越慢;防突风门底坎尺寸为1 mm时,2道防突风门能够有效隔绝直巷道中冲击波的入侵。试验结果与数值模拟结果得出结论是一致的。
(3)基于试验、数值模拟结果,结合突出冲击波超压与巷道阻力能量关系和冲击波超压对人体的伤害程度,可确定矿井防突风门的底坎尺寸为15 mm以下是合理的。
[1] FAN Chaojun,LI Sheng,LUO Mingkun,et al. Coal and gas outburst dynamic system[J]. International Journal of Mining Science and Technology,2017,27(1):49-55.
[2] 李国军,邓良泽,王德全,等. FM反向防突风门在古宋煤矿的应用[J].矿业安全与环保,1998(3):43-44.
LI Guojun,DENG Liangze,WANG Dequan,et al. Application of FM reverse anti-outburst door in Gusong Coal Mine [J]. Mining Safety and Environmental Protection,1998(3):43-44.
[3] 李术才,李清川,王汉鹏,等.大型真三维煤与瓦斯突出定量物理模拟试验系统研发[J].煤炭学报,2018,43(S1):121-129.
LI Shucai,LI Qingchuan,WANG Hanpeng,et al. Research and development of large-scale true three-dimensional coal and gas outburst quantitative physical simulation test system[J]. Journal of China Coal Society,2018,43(S1):121-129.
[4] YIN Guangzhi,JIANG Changbao,WANG J G,et al.A new experimental apparatus for Coal and gas outburst simulation[J]. Rock Mechanics and Rock Engineering,2016,49(5):2005-2013.
[5] LI Hui,FENG Zengchao,ZHAO Dong,et al. simulation experiment and acoustic emission study on coal and gas outburst[J]. Rock Mechanics and Rock Engineering,2017,50(8):2193-2205.
[6] ZHANG R L,LOWNDES I S. The application of a coupled artificial neural network and fault tree analysis model to predict coal and gas outbursts[J]. International Journal of Coal Geology,2010,84(2):141-152.
[7] XUE S,WANG Y C,XIE J,et al. A coupled approach to simulate initiation of outbursts of coal and gas-model development[J]. International Journal of Coal Geology,2011,86:222-230.
[8] KANG P C. A new mechanistic model for prediction of instantaneous coal outbursts - Dedicated to the memory of Prof. Daniel D. Joseph[J]. International Journal of Coal Geology,2011, 87(2):72-79.
[9] WU S Y,GUO Y Y,LI Y X,et al. Research on the mechanism of coal and gas outburst and the screening of prediction indices[J]. Procedia Earth and Planetary Science,2009,1(1):173-179.
[10] JING X,GAO M, YU B,et al. Coal permeability model on the effect of gas extraction within effective influence zone[J]. Geomechanics and Geophysics for Geo-Energy and Geo-Resources, 2015, 1(1-2):15-27.
[11] ZHOU Aitao,WANG Kai,WANG Li,et al. Numerical simulation for propagation characteristics of shock wave and gas flow induced by outburst intensity[J].International Journal of Mining Science and Technology,2015,25(1):107-112.
[12] ZHOU Aitao,WANG Kai,FAN Lingpeng,et al. Propagation characteristics of pulverized coal and gas two-phase flow during an outburst[J]. PloS One,2017,12(7):0180672.
[13] ZHOU Aitao,WANG Kai,WU Zeqi. Propagation law of shock waves and gas flow in cross roadway caused by coal and gas outburst[J]. International Journal of Mining Science and Technology,2014,24(1):23-29.
[14] WANG Kai,ZHOU Aitao,ZHANG Jianfang,et al. Real-time numerical simulations and experimental research for the propagation characteristics of shock waves and gas flow during coal and gas outburst[J]. Safety Science,2012,50(4):835-841.
[15] 孙东玲,曹偈,苗法田,等. 突出煤-瓦斯在巷道内的运移规律[J]. 煤炭学报,2018,43(10):2773-2779.
SUN Dongling,CAO Jie,MIAO Fatian,et al. Outburst coal-gas migration law in the roadway[J]. Journal of China Coal Society,2018,43(10):2773-2779.
[16] 许江,程亮,周斌,等. 突出过程中煤-瓦斯两相流运移的物理模拟研究[J]. 岩石力学与工程学报,2019,38(10):1945-1953.
XU Jiang,CHENG Liang,ZHOU Bin,et al. Physical simulation of coal-gas two-phase flow migration during outburst[J]. Chinese Journal of Rock Mechanics and Engineering,2019,38(10):1945-1953.
[17] 王凯,周爱桃,魏高举,等. 直巷道中突出冲击气流的形成及传播特征研究[J]. 采矿与安全工程学报,2012,29(4):559-563.
WANG Kai,ZHOU Aitao,WEI Gaoju,et al. Research on the formation and propagation characteristics of protruding impinging airflow in straight roadways [J]. Journal of Mining and Safety Engineering,2012,29(4):559-563.
[18] 王凯,周爱桃,魏高举,等.巷道截面变化对突出冲击波传播的影响[J]. 煤炭学报,2012,37(6):989-993.
WANG Kai,ZHOU Aitao,WEI Gaoju,et al. The influence of roadway cross-section changes on the propagation of outburst shock waves[J]. Journal of China Coal Society,2012,37(6):989-993.
[19] 王凯,周爱桃,张建方,等. 直角拐弯巷道中瓦斯突出冲击气流传播特征研究[J]. 中国矿业大学学报,2011,40(6):858-862.
WANG Kai,ZHOU Aitao,ZHANG Jianfang,et al. Study on the characteristics of gas outburst impingement airflow propagation in right-angle turning roadways[J]. Journal of China University of Mining and Technology,2011,40(6):858-862.
[20] 李峰,何子建,张悦,等. 冲击载荷作用下矩形风窗动态分布特征与破坏机理[J]. 煤炭学报,2020,45(9):3166-3175.
LI Feng,HE Zijian,ZHANG Yue,et al. Dynamic distribution characteristics and failure mechanism of rectangular windshield under impact load[J]. Journal of China Coal Society,2020,45(9):3166-3175.
[21] 代树红,王正延,徐延,等. 钢构防突风门结构安全性的静动力学分析[J]. 中国安全科学学报,2017,27(12):74-79.
DAI Shuhong,WNG Zhengyan,XU Yan,et al. Static and dynamic analysis of the safety of the steel anti-blast door structure[J]. Chinese Safety Science Journal,2017,27(12):74-79.
[22] 程卫民,王刚,周刚,等. 煤与瓦斯突出后对防突风门破坏的数值模拟[J]. 重庆大学学报,2009,32(3):314-318.
CHENG Weimin,WANG Gang,ZHOU Gang,et al. Numerical simulation of damage to the anti-air outburst door after coal and gas outburst[J]. Journal of Chongqing University,2009,32(3):314-318.
[23] MT 1066—2008,煤与瓦斯突出矿井反向风门设置技术条件 [S]. 北京:煤炭工业出版社,2009.
[24] 李维新. 一维不定常流与冲击波[M]. 北京:国防工业出版社,2003:202-302.
[25] 顾毅成. 工程爆破安全[M]. 合肥:中国科学技术大学出版社,2009.
[26] 韦善阳. 瓦斯异常涌出气体运移规律及影响范围研究[D]. 北京:中国矿业大学(北京),2013.
WEI Shanyang. Study on the migration law and influence range of abnormal gas emission[D]. Beijing:China University of Mining and Technology(Beijing),2013.
[27] 曹偈,孙海涛,戴林超,等. 煤与瓦斯突出动力效应的模拟研究[J]. 中国矿业大学学报,2018,47(1):113-154.
CAO Jie,SUN Haitao,DAI Linchao,et al. Simulation study on the dynamic effects of coal and gas outburst[J]. Journal of China University of Mining & Technology,2018,47(1):113-154.
[28] 张国枢. 通风安全学[M]. 徐州:中国矿业大学出版社,2011:13-51.
[29] 董利辉. 突出高浓瓦斯气体运移扩散及逆流扩展规律研究[D]. 北京:中国矿业大学(北京),2018.
DONG Lihui. Research on the migration,diffusion and countercurrent expansion of high-concentration gas [D]. Beijing:China University of Mining and Technology(Beijing),2018.
[30] 张莉莉,王峰. 水力学[M]. 北京:清华大学出版社,2015.
[31] 苗法田,孙东玲,胡千庭. 煤与瓦斯突出冲击波的形成机理[J].煤炭学报,2013,38(3):367-372.
MIAO Fatian,SUN Dongling,HU Qianting. The formation mechanism of coal and gas outburst shock wave[J]. Journal of China Coal Society,2013,38(3):367-372.
[32] 杨亚东,李向东,王晓鸣,等. 长方体密闭结构内爆炸冲击波传播与叠加分析模型[J]. 兵工学报,2016,37(8):1449-1455.
YANG Yadong,LI Xiangdong,WANG Xiaoming,et al. Explosion shock wave propagation and superposition analysis model in a rectangular closed structure[J]. Acta Armamentarii,2016,37(8):1449-1455.
[33] 周爱桃. 瓦斯突出冲击气流传播及诱导矿井风流灾变规律研究[D].北京:中国矿业大学(北京),2012.
ZHOU Aitao. Research on the propagation of gas outburst impact airflow and the catastrophic law of induced mine airflow [D]. Beijing:China University of Mining and Technology(Beijing),2012.