巷道围岩稳定性一直是采矿工程研究的热点问题之一。巷道问题不仅仅是平面问题，井下巷道实际上会受到三向应力作用，在不同的应力作用条件下，特别是非静水压力条件下，巷道围岩的破坏、稳定性具有较为明显的差异性[1]。其中，偏应力与应变能密度可以反映巷道围岩破坏趋势与塑性区形态[2-6]，因此，笔者基于两者对非静水压力条件下巷道围岩偏应力场与破坏规律进行深入研究，对巷道围岩稳定性分析及巷道支护具有重要的理论价值与指导作用。
对于巷道围岩偏应力场分布与破坏规律，已有不少专家进行了较为深入的研究。余伟健等基于平面问题，推导得出在不同应力条件下巷道围岩偏应力分布情况，建立了偏应力场与塑性区分布的本构方程，提出不同侧压系数下巷道围岩可形成典型正对称失稳模式和典型角对称失稳模式[2]。潘岳等通过理论分析推导得到围岩弹性、硬化和软化区应力分布表达式，用重积分计算了各区的偏应力应变能[7]。许磊等以山西某煤矿轨道巷超高段为研究对象，采用UDEC模拟不同巷高时巷道围岩偏应力分布情况，对巷道顶底板、两帮的偏应力变化程度进行了比较，最终提出了针对性的支护技术[8]。骆开静等深入研究了中间主应力和围岩流变特性对巷道围岩位移和围岩塑性区的影响，最终发现忽视岩石流变特性会高估围岩岩性，中间主应力在一定范围内能控制巷道变形与塑性区扩展[9]。张小波等以D-P屈服准则推算出了双向等压条件下，巷道围岩弹塑性、塑性区半径和位移的解析解，发现了中间主应力对围岩应力分布的重要性[10]。陈梁等根据D-P屈服准则与非关联流动法则，推导了静水压力下深部圆形巷道围岩应力、变形及塑性区半径的封闭解析解[11]。王宏伟等基于M-C准则，将巷道当成平面问题，推导出了非静水压力条件下圆形巷道围岩破碎区及塑性区的应力与围岩解析解[12]。袁超等以软弱破碎巷道为对象，研究了侧压系数、黏聚力与内摩擦角对巷道塑性区的影响程度[13]。
目前针对巷道围岩偏应力场与破坏规律的研究，往往是将巷道简化为平面问题，不考虑巷道在三向应力非静水压力条件下巷道围岩偏应力分布特点与破坏形态，此时，相当于忽略巷道轴向方向的应力作用，对于巷道任意围岩单元而言，其力学强度会被高估，造成围岩破坏范围理论分析结果小于真实值，从而造成一定的工程隐患[1,9-11]。因此，针对三向应力状态下巷道围岩稳定性的理论分析有待进一步探究。笔者基于前人研究成果，对三向应力非静水压力条件下巷道围岩偏应力与应变能密度分布规律进行了深入研究，从而反映巷道围岩破坏形态，最终通过数值模拟与工程现场对理论进行了验证。
1 巷道围岩偏应力场理论
1.1 巷道围岩单元主应力
井下巷道位于三向应力场之中，以圆形巷道为例，建立合理的坐标系，巷道受力与围岩应力状态如图1所示。
图1 巷道受力与围岩应力状态示意
Fig.1 Stress state of roadway and surrounding rock
图1中，σx为垂直于巷道轴向的水平应力;σz为垂直于巷道轴向的垂直应力;σy为平行于巷道轴向的应力。σr，σθ，τrθ，σv分别为巷道围岩单元所受到的径向应力、切向应力、剪应力以及平行巷道轴向的应力。
弹性状态下，以图1为例，各应力大小[14-15]为
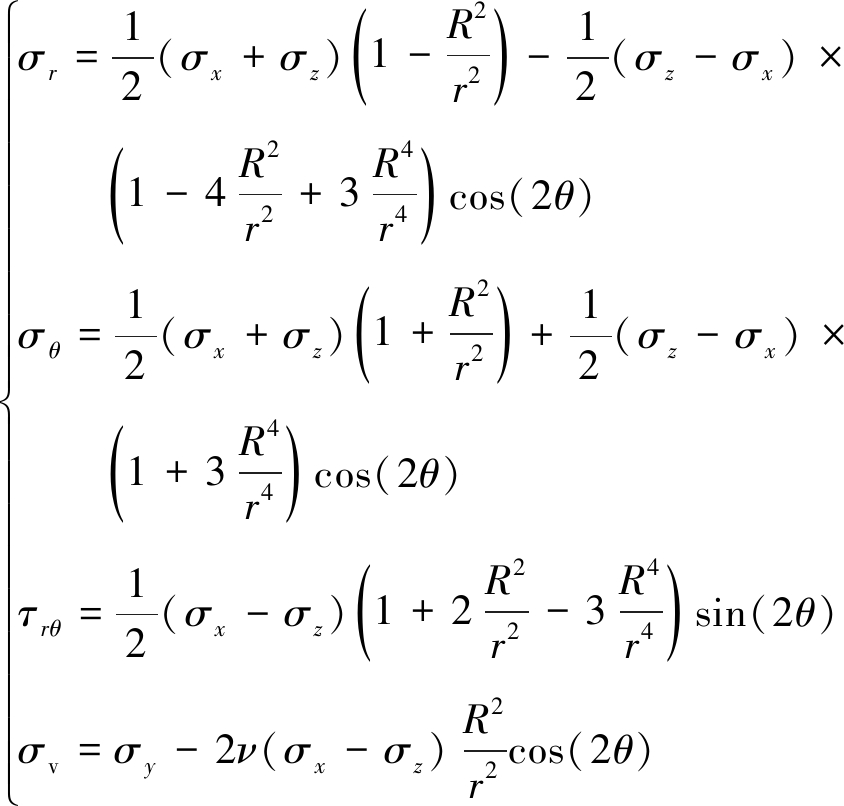
(1)
式中，R为巷道半径;r为围岩单元距离巷道中心的距离;θ为围岩单元位置与水平方向夹角;ν为围岩泊松比。
在图1垂直Y轴的平面上，巷道围岩单元的主应力转化公式为
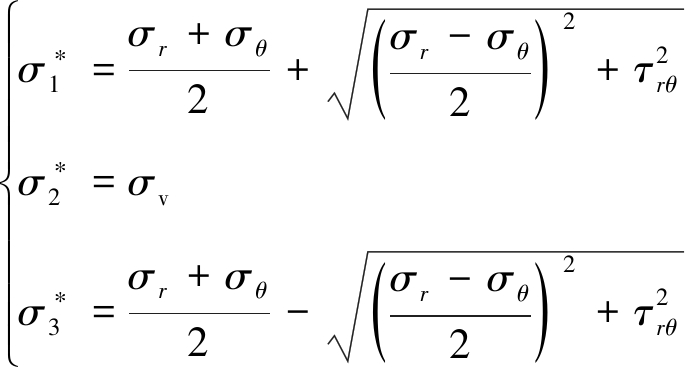
(2)
式中，
为巷道围岩单元所受主应力。
将式(1)代入式(2)，可得到巷道围岩主应力大小:
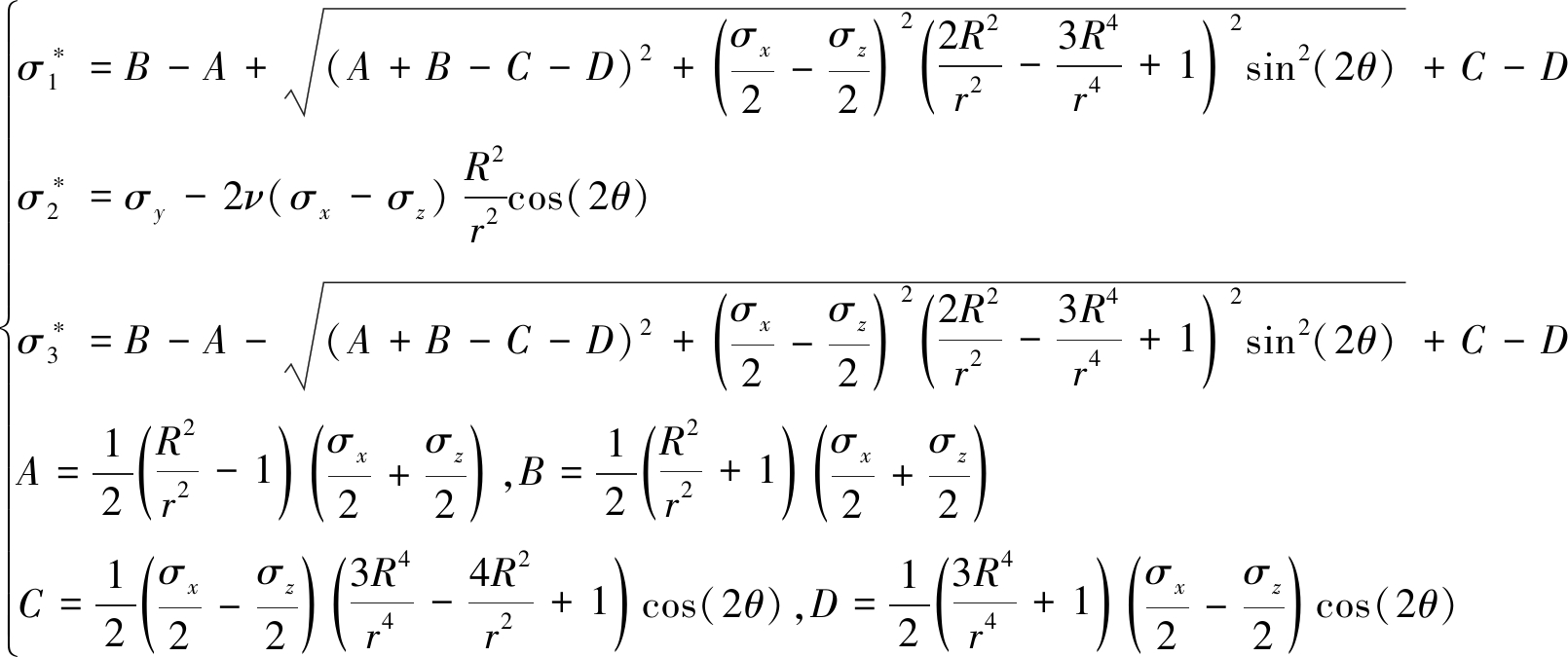
(3)
式中，主应力
并不是按照
的大小顺序进行标注的，此处仅为符号代表，原因在于巷道处于三向应力状态之中，σx，σy，σz三个方向应力大小未知，无法判断主应力的大小，因此需要分类讨论，从式(2)中可以明显看出，无论巷道处在何种应力状态下，都有
而
与
的大小顺序则存在3种情况，分别为:①
②
③
后续理论推导要根据3种情况进行分类讨论。
1.2 巷道围岩偏应力场
经典岩土塑性力学认为，岩体单元所受应力可以分解为球应力与偏应力，其中，球应力控制单元的体积变形，而偏应力控制着单元的形状变形，因此，偏应力控制着岩体单元的塑性破坏，对岩体塑性破坏的影响有着重要意义，探究巷道在三向受力状态下的偏应力分布规律，可以为巷道围岩塑性区分布规律提供一定的理论基础[2-3]。
已知最大、最小主偏应力S1，S3的计算公式为
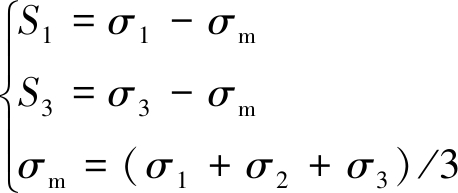
(4)
式中，σ1，σ2，σ3分别为岩体单元所受的最大、中间、最小主应力;σm为平均应力。
上述已知巷道围岩单元主应力的大小分为3种情况，因此，巷道围岩偏应力场的理论推导也需分类讨论，以
的情况为例，此时
最大、最小主偏应力表达式为
(5)
将式(3)代入式(5)便可得到最大、最小主偏应力的计算表达式。同理，推导可得另外2种情况的偏应力表达式。总计3种情况下的最大、最小主偏应力的计算表达式如式(6),(7)所示。根据式(6),(7)可知，在计算巷道围岩主偏应力时，需要将巷道所处环境应力值代入式(3)计算得到巷道主应力值，再根据主应力值比较结果计算主偏应力值。
(6)
(7)
图(1)中，巷道所处应力环境σx，σy，σz可用式(8)[16]表示：
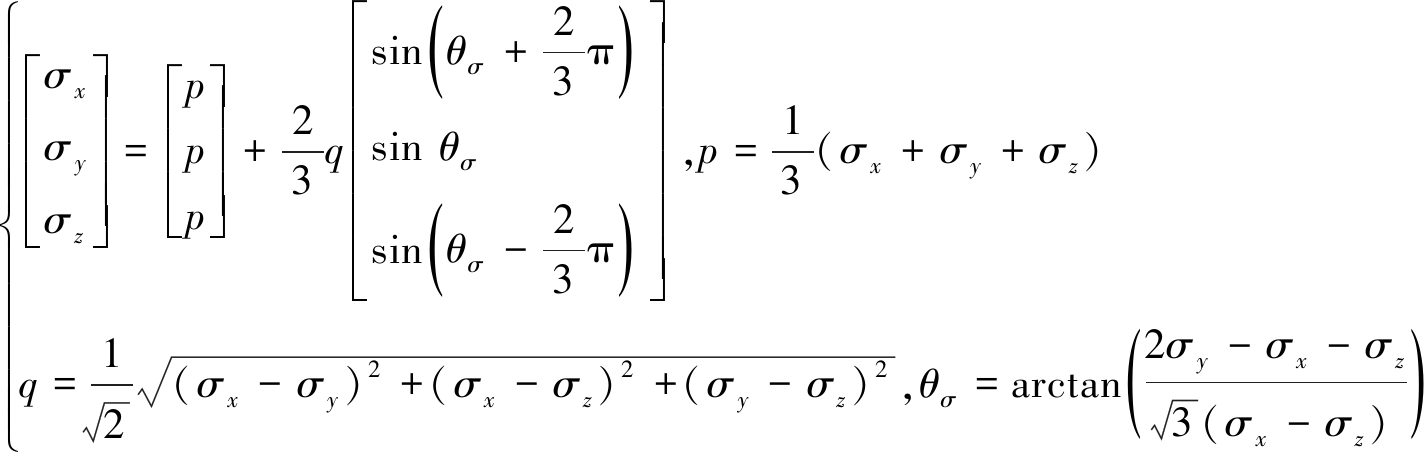
(8)
其中，p为球应力;q为偏应力;θσ为Lode角，该值可以表示σx,σy,σz三个应力之间的相对比值关系。基于式(8)，笔者认为，巷道在处于等p、等q的应力状态中，随着θσ值的变化，巷道围岩单元所受应力状态会发生变化，巷道围岩单元主偏应力大小也会发生变化，从而产生不同程度的围岩破坏，因此，该处取巷道处于等p、等q应力环境下探究巷道围岩偏应力分布规律，取p=20 MPa;q=15 MPa，θσ范围为[-30°，330°]，根据式(8)，获得σx，σy，σz的应力加载方案，如图2所示。
图2中，在σx，σy，σz三个应力之中，根据最大的方向应力定义巷道处于该应力主导的应力场之中，即巷道可能处于3种应力场之中，分别为σx主导型应力场，θσ范围为[-30°，30°]∪[270°，330°];σy主导型应力场，θσ范围为[30°，150°];σz主导型应力场，θσ范围为[150°，270°]。根据图2，选取3种主导应力场的6种情况计算巷道围岩主偏应力分布，分别为θσ为 0°，60°，120°，180°，240°，300°共6种情况。在2.1节中已知大小顺序需要进行比较，从而在式(6)，(7)中选取合适的计算公式。以θσ为60°，180°，300°为例，联立式(3)，(8)，计算得到3种主导应力场中巷道r=5 m处围岩主应力分布结果，如图3所示。
图2 等p、等q条件下应力与θσ关系
Fig.2 Relationship between stress and θσ under equal p and q conditions
图3 巷道围岩主应力分布
Fig.3 Distribution of principal stress in surrounding rock of roadway
由图3可以看出，巷道围岩应力在不同的主导型应力场中，大小顺序不同，但均为1.1节中描述的3种情况，验证了上述理论的正确性。在σy主导型应力场中，即θσ=60°时，
在σz主导型应力场中，即θσ=180°时，
在σx主导型应力场中，即θσ=300°时，
根据大小顺序，选择合适的公式即可计算巷道围岩偏应力分布。
基于图2，可以看出在上述计算偏应力分布的6种方案中，巷道所受的三向应力大小是固定的，分别为28.7，20.0，11.3 MPa，但加载方案不一样。为探究主导应力对巷道偏应力场分布的影响，在上述6种方案中，增大1.5倍的主导应力大小，即增加6组对比计算方案，应力大小为43.0，20.0，11.3 MPa。12组计算方案应力大小以及主应力大小顺序计算结果见表1。
表1 巷道围岩偏应力计算方案
Table 1 Calculation scheme of deviator stress of surrounding rock of roadway
应力场类型σxσyσzσ∗1,σ∗2,σ∗3大小σx主导型28.7λ11.320.0σ∗1≥σ∗3≥σ∗228.7λ20.011.3σ∗1≥σ∗2≥σ∗3σy主导型11.328.7λ20.0σ∗2≥σ∗1≥σ∗320.028.7λ11.3σ∗2≥σ∗1≥σ∗3σz主导型11.320.028.7λσ∗1≥σ∗2≥σ∗320.011.328.7λσ∗1≥σ∗3≥σ∗2
表1中，λ取值1.0或1.5，计算2种情况下巷道围岩最大主偏应力分布规律;巷道半径R=2 m，根据
顺序代入式(6)，求解得到r=5 m处巷道最大主偏应力S1分布规律。计算结果如图4所示。
图4 巷道围岩最大主偏应力场分布
Fig.4 Distribution of maximum principal deviator stress field of surrounding rock of roadway
通过图4的求解结果，可发现巷道围岩最大主偏应力分布存在以下规律:
(1)即使巷道处于等p、等q的应力环境中，但处于不同的主导型应力场中，巷道围岩偏应力分布存在较大差别。处于σx主导型应力场的巷道围岩偏应力S1呈“8”字形分布;处于σy主导型应力场的巷道围岩偏应力S1呈圆形分布;处于σx主导型应力场的巷道围岩偏应力S1呈横“8”字形分布。
(2)巷道在同种主导型应力场之中，保持主导应力不变时，无论λ取值1或1.5，等p、等q条件下其余两方向应力大小的改变对巷道围岩偏应力分布影响较小。例如θσ=0°与θσ=300°时，仅改变除主导应力外的其余两个方向的应力对巷道围岩偏应力分布形态改变程度较小。
(3)在同种主导型应力场之中，若增加主导应力，保持其余两方向主应力大小不变的情况下，巷道围岩单元偏应力大小会发生变化，该种变化主要为数值变化，围岩偏应力分布形态不发生明显改变，当λ增大时，同一深度处的围岩单元偏应力增大。例如在σy主导型应力场中，σy增大1.5倍，即巷道轴向应力增大1.5倍，巷道围岩偏应力增大，该现象说明轴向应力大小对巷道围岩破坏有影响，仅考虑两向应力作用会高估巷道围岩力学强度。
(4)处于σx主导型应力场的巷道顶板偏应力大于两帮，该种情况下，巷道应注重顶底板支护;处于σy主导型应力场的巷道围岩顶底板与两帮偏应力大小差别不大，若巷道围岩岩性较差时，应注意全断面支护;处于σz主导型应力场的巷道两帮处的偏应力大于顶底板，因此巷道两帮此时的支护不可忽视。
综上可知，在不同的应力环境下，巷道围岩偏应力场的分布形式有较大区别，巷道支护因此也要具有一定的针对性，对于已知应力环境的巷道，通过计算其围岩偏应力场分布情况，可对巷道支护维稳起到一定的指导作用。
2 非静水压力条件下巷道围岩应变能密度分布规律
对于处于三向应力非静水压力条件下的巷道，为研究巷道围岩破坏形态，可采用应变能密度(SED)理论进行分析计算，应变能密度作为一个相对值，可以演示应变能的积累和耗散[17]。基于图1，巷道围岩单元应变能密度公式为
(9)
式中，E为围岩弹性模量。
巷道围岩在开挖后或受到采动应力影响时，单元内部将储存应变能，每个单元体能够储存的应变能是有限的，当巷道围岩单元应变能密度达到破坏阈值时，会产生塑性区[4-5]，因此，研究巷道围岩应变能密度分布规律，在一定程度可反映巷道围岩破坏形态。
基于1.2节中巷道围岩偏应力分布规律可知，巷道顶底板与两帮的应变能密度分布是研究重点，联立式(3)，(8)，(9)，计算得到巷道围岩在不同偏应力比M(M=q/p)时顶底板与两帮的应变能密度分布规律，如图5所示。
图5 不同偏应力比情况下3种主导型应力场中巷道顶底板与两帮应变能密度分布
Fig.5 Strain energy density distribution of roof,floor and two sides of roadway with three dominant stress fields under different deviator stress ratios
通过图5可以看出，巷道处在不同的主导型应力场中，应变能密度分布规律如下：
(1)等p、等q条件下，围岩顶底板与两帮的应变能密度大小明显不同，在σx与σy主导型应力场中，巷道顶底板应变能密度大于两帮，而在σz主导型应力场中，巷道两帮应变能密度大于顶底板。
(2)σx主导型应力场与σy主导型应力场应变能密度分布进行对比，σx主导型应力场中巷道顶板应变能密度较大，σy主导型应力场中巷道两帮应变能密度较大。在p,q值较大时，σx主导型应力场中顶底板与两帮的应变能密度差值大于σy主导型应力场，说明在σx主导型应力场中顶底板与两帮破坏程度差异性较大，而σy主导型应力场中顶底板与两帮破坏程度差异性较小。在σz主导型应力场中，巷道顶底板与两帮应变能密度在p，q值较大时两者之间差值较大，说明此时两帮较顶底板破坏更严重。
(3)等p、不等q情况下，3种主导型应力场中巷道顶底板与两帮应变能密度均随偏应力比M的增大而增大，说明在保持球应力p不变的情况下，增大偏应力q会加剧巷道围岩的破坏。等q、不等p情况下，巷道顶底板与两帮应变能密度均随偏应力比M的减小而增大，且应变能密度增大幅度较大，说明在保持偏应力q不变的情况下，增大球应力p同样会加剧巷道围岩的破坏。
对于在不同主导型应力场中的巷道围岩应变能密度分布形态，结合图5，取等p、不等q与等q、不等p两种方案计算巷道围岩应变能密度分布规律。在等p、不等q方案中，p=10 MPa，q分别取10，20，30，40，50 MPa。等q、不等p方案中，q=10 MPa，取p=20,30,40，50 MPa。2种方案中分别计算θσ=60°，180°，300°时巷道围岩r=5 m处应变能密度分布规律。计算结果如图6，7所示。
图6 等p、不等q情况下巷道围岩应变能密度分布
Fig.6 Strain energy density distribution of roadway surrounding rock under the condition of equal p and unequal q
图7 等q、不等p情况下巷道围岩应变能密度分布
Fig.7 Strain energy density distribution of roadway surrounding rock under the condition of equal q and unequal p
通过图6，7可知，M>1与M<1时，巷道围岩应变能密度分布规律具有较为明显的差异。M<1时，无论巷道处于何种主导型应力场之中，巷道围岩应变能密度均呈现为椭圆形，且应变能密度大小随着偏应力比M的减小而增大。θσ=60°，300°时，巷道顶底板应变能密度大于两帮密度，而θσ=180°时，巷道两帮应变能密度大于顶底板密度。M>1时，在不同主导型应力场中，巷道围岩应变能密度分布规律具有明显差异，但应变能密度均随M值的增大而增大。θσ=300°时，巷道应变能密度分布呈现出“8”字形，巷道两帮应变能密度小于顶底板;θσ=60°时，巷道应变能密度分布呈现近似的正方形分布，但巷道应变能密度最大值约在θ为45°，135°，225°，315°处，呈现出一定的对角式发育;θσ=180°时，巷道应变能密度呈现出“X”形分布，巷道两帮处应变能密度大于顶底板，巷道应变能密度最大值同样约在θ为45°，135°，225°，315°处，呈现出一定的对角式发育。
巷道围岩应变能密度形态能一定程度上反映巷道破坏形态，基于此，针对图6，7中M为1/5，5时θσ=60°，180°，300°共6种情况进行巷道塑性区数值模拟，模拟采用摩尔库伦模型，通过FLAC3D提取巷道塑性区，结果如图8所示。通过对比巷道围岩应变能密度分布，塑性区模拟结果与理论分析结果较为吻合。
图8 巷道围岩塑性区模拟结果
Fig.8 Simulation results of plastic zone of surrounding rock of roadway
综上可知，三向应力状态下，计算巷道围岩应变能密度分布规律一定程度上可以反映塑性区形态，对巷道支护设计具有一定的指导作用。对于σx主导型应力场，巷道顶板的破坏往往较为严重，因此需注重巷道顶底板支护方案。对于σy主导型应力场，巷道在围岩条件较差时，应注重全断面支护;对于σz主导型应力场，巷道两帮可能会出现严重破坏，因此巷道两帮的支护不可忽视，且σz主导型应力场中，巷道塑性区可能会出现“X”形恶性扩展，此时应注意巷道肩角处的破坏，其支护应根据实际问题进行针对性设计。
3 工程实例
山西回坡底煤矿主采10号与11号煤层，10号煤层平均厚度为2.65 m，11号煤层平均厚度3.2 m，两煤层之间平均间距为6.62 m，属于近距离煤层开采。本处研究巷道为东一采区11-102工作面的运输巷——1021巷。1021巷上方主采10号煤层的10-102工作面与10-103工作面已成为采空区，10-102工作面与10-103工作面之间形成的孤岛煤柱平均宽度约为25 m，1021巷距离孤岛煤柱边缘距离为10 m。1021巷断面为矩形，宽4.6 m，高3.3 m。巷道位置与工作面分布如图9所示。
图9 1021巷位置与工作面分布
Fig.9 Location of 1021 roadway and working face distribution
由于孤岛煤柱应力集中影响，1021巷所受应力发生偏转，通过理论分析与回坡底煤矿提供的地应力测试报告得出巷道所受最大主应力σ1来自孤岛煤柱方向，最小主应力σ3来自采空区方向，中间主应力σ2垂直巷道轴向，σ1=31.56 MPa，σ2=28 MPa，σ3=13.72 MPa，应力偏转角为20°。将数据代入式(6)计算得到1021巷道最大主偏应力分布，如图10所示，图中，R为1021巷道半径。
图10 1021巷围岩偏应力S1分布
Fig.10 Distribution of deviatoric stress S1 in surrounding rock of 1021 roadway
通过图10可以看出，由于巷道所受应力发生偏转，因此巷道围岩偏应力呈现倾斜的“8”字形分布。对于巷道顶部，S1在靠近孤岛煤柱一侧较大，远离煤柱一侧较小;对于巷道底板，巷道在远离孤岛煤柱一侧S1较大，靠近煤柱一侧较小;对于靠近孤岛煤柱一侧的巷帮，巷帮下部S1较大，上部较小;远离煤柱一侧巷帮上部S1较大，下部较小。
从1021巷偏应力分布来看，1021巷无论是顶底板还是两帮均会出现非对称性破坏。1021巷现场破坏情况与支护方式如图11所示。
图11 巷道破坏情况与断面支护
Fig.11 Roadway failure and cross section support
理论计算结果已知，1021巷围岩会出现明显的非对称性破坏，但从图11可知，1021巷采用了对称性支护，该种支护方式不能保证1021巷围岩的稳定性，巷道顶板与两帮均出现了较为严重的破坏，底板由于是裸露支护状态，从而产生了非对称性底臌现象，底臌量在远离煤柱一侧较大。1021巷现场实际破坏情况与偏应力分布理论计算结果较为吻合，验证了理论的正确性。
对于巷道围岩塑性区的破坏形态，根据实际现场数据，代入式(9)计算得到巷道围岩应变能密度分布，如图12所示。
图12 1021巷围岩应变能密度分布
Fig.12 Strain energy density distribution of surrounding rock of 1021 roadway
由图12可知，巷道围岩应变能密度呈倾斜的“8”字形分布，与巷道围岩S1的分布规律保持一致性。根据巷道围岩应变能密度分布规律可以推测，巷道顶板在靠近孤岛煤柱一侧塑性区范围较大，围岩破坏程度较高;底板在远离煤柱一侧塑性区范围较大;离孤岛煤柱较近一侧巷帮，下部塑性区范围较大;离煤柱较远一侧巷帮，上部塑性区范围较大。
对于1021巷围岩塑性区情况，基于文献[18]计算得出1021巷围岩塑性区边界，所得结果如图13所示，巷道围岩塑性区理论计算结果与上述S1及应变能密度计算结果保持一致。同时，针对回坡底煤矿1021巷的塑性区范围，现场对巷道顶底板进行钻孔窥视，根据钻孔裂隙发育情况确定了巷道顶底板裂隙分布轨迹，发现顶底板裂隙分布轨迹与围岩应变能密度理论计算结果较为吻合，同时也验证了上述S1、围岩应变能密度分布规律理论的正确性，同时说明探究非静水压力条件下巷道围岩偏应力场与应变能密度分布规律，可对巷道支护设计起到一定的指导作用。
图13 巷道围岩塑性区
Fig.13 Plastic zone of surrounding rock of roadway
针对1021巷的非对称性破坏，在1021巷原有的支护基础上，针对性的提出了如图14的巷道支护方案。
图14 1021巷支护改进方案
Fig.14 Improvement scheme of 1021 roadway support
巷道顶板采用W钢带简式桁架锚索与单体锚索平行布置的非对称支护技术，主要支护顶板破坏变形较大一侧，排距1 800 mm。桁架锚索中心点与巷道中线之间的偏心距为900 mm。底板由原来的裸露支护改为单体锚索平行布置的非对称支护技术，间排距1 200 mm×1 800 mm。巷道两帮由原来的纯锚杆支护改进为锚杆索支护，靠近孤岛煤柱一侧巷帮，锚索主要支护巷帮破坏变形较大的下部位置;远离孤岛煤柱一侧巷帮，锚索主要支护巷帮破坏变形较大的上部位置，排距均为1 600 mm。该支护方案最终在回坡底煤矿局部区域进行了工业性试验，调整了支护参数，巷道表面位移监测结果显示巷道在15 d内围岩变形剧烈，之后逐渐平稳，巷道两帮最终移近量约为105 mm，底臌量为90 mm，顶板下沉量为52 mm，巷道围岩稳定性较好，巷道断面未出现较为明显的变形。
4 结 论
(1)在不同的主导型应力场中，巷道围岩偏应力分布具有显著差异，主导应力对巷道围岩偏应力大小具有重要影响，主导应力增大，围岩偏应力增大。σx主导型应力场中的巷道应注重顶底板支护;处于σy主导型应力场的巷道围岩岩性较差时，应注意全断面支护;处于σz主导型应力场的巷道两帮处的支护不可忽视。
(2)等p、等q条件下，在σx与σy主导型应力场中，巷道顶底板应变能密度大于两帮，而在σz主导型应力场中，巷道两帮密度大于顶底板。等p、不等q情况下，巷道顶底板与两帮应变能密度均随偏应力比M的增大而增大;等q、不等p情况下，巷道顶底板与两帮应变能密度均随偏应力比M的减小而增大。
(3)巷道围岩应变能密度分布形态可以反映巷道围岩塑性区形态。等p、不等q与等q、不等p两种方案，在不同的主导型应力场中，巷道围岩应变能密度分布形态具有显著差异。偏应力比M<1时，无论何种主导型应力场，巷道围岩应变能密度均为椭圆形，M>1时，巷道围岩应变能密度会出现“8”字形与“X”形分布。应变能密度理论分析结果与巷道塑性区数值模拟结果较为吻合，验证了理论的正确性。
(4)回坡底1021巷围岩偏应力S1与应变能密度规律均呈倾斜的“8”字形分布，理论分析结果显示巷道会出现非对称性破坏，该结果与巷道破坏情况、钻孔窥视结果较为吻合。对1021巷提出围岩非对称支护技术，现场应用效果良好。探究非静水压力下巷道围岩偏应力与应变能密度分布规律对巷道支护设计有一定指导作用。
[1] ZUO Jianping，WANG Jintao，JIANG Yunqian.Macro/meso failure behavior of surrounding rock in deep roadway and its control technology[J].Journal of Coal Science & Engineering，2019，6(3):301-319.
[2] 余伟健，吴根水，袁超，等.基于偏应力场的巷道围岩破坏特征及工程稳定性控制[J].煤炭学报，2017，42(6):1408-1419.
YU Weijian,WU Genshui,YUAN Chao,et al.Failure characteristics and engineering stability control of roadway surrounding rock based on deviatoric stress field[J].Journal of China Coal Society,2017，42(6):1408-1419.
[3] 陈昊祥，王明洋，戚承志，等.深部圆形巷道围岩能量的调整机制及平衡关系[J].岩土工程学报，2020，42(10):1849-1857.
CHEN Haoxiang，WANG Mingyang，QI Chengzhi，et al.Mechanism of energy adjustment and balance of rock masses near a deep circular tunnel[J].Chinese Journal of Geotechnical Engineering，2020，42(10):1849-1857.
[4] 朱斯陶，姜福兴，王绪友，等.特厚煤层掘进面围岩能量积聚特征及诱冲机制研究[J].岩土工程学报，2019，41(11):2071-2078.
ZHU Sitao，JIANG Fuxing，WANG Xuyou，et al.Energy accumulation characteristics and rockburst mechanism of surrounding rock at heading face of extra-thick coal seam[J].Chinese Journal of Geotechnical Engineering，2019，41(11):2071-2078.
[5] 文志杰，田雷，蒋宇静，等.基于应变能密度的非均质岩石损伤本构模型研究[J].岩石力学与工程学报，2019，38(7):1332-1343.
WEN Zhijie,TIAN Lei,JIANG Yujing,et al.Research on damage constitutive model of inhomogeneous rocks based on strain energy density[J].Chinese Journal of Rock Mechanics and Engineering，2019，38(7):1332-1343.
[6] LI Xibing，WENG Lei.Numerical investigation on fracturing behaviors of deep-buried opening under dynamic disturbance[J].Tunnelling and Underground Space Technology，2016，54:61-72.
[7] 潘岳，李爱武，戚云松.圆巷开挖围岩偏应力应变能生成的分析解与图解[J].岩土工程学报，2007，29(12):1780-1786.
PAN Yue,LI Aiwu,QI Yunsong.Analysis and illustration on deviatoric stress strain energy generation of surrounding rock in circuar tunnel excavation[J].Chinese Journal of Geotechnical Engineering，2007，29(12):1780-1786.
[8] 许磊，吴焕凯，李博，等.巨高巷道围岩稳定及控制[J].岩石力学与工程学报，2014，33(S2):3891-3902.
XU Lei,WU Huankai,LI Bo,et al.Stability and control of surrounding rock in ultra-high roadway[J].Chinese Journal of Rock Mechanics and Engineering，2014，33(S2):3891-3902.
[9] 骆开静，董海龙，高全臣.考虑流变和中间主应力的巷道围岩变形分区[J].煤炭学报，2017，42(S2):331-337.
LUO Kaijing,DONG Hailong,GAO Quanchen.Deformation division for surrounding rock of circular roadway by considering rheology and the intermediate principal stress[J].Journal of China Coal Society,2017，42(S2):331-337.
[10] 张小波，赵光明，孟祥瑞.基于Drucker-Prager屈服准则的圆形巷道围岩弹塑性分析[J].煤炭学报，2013，38(S1):30-37.
ZHANG Xiaobo,ZHAO Guangming,MENG Xiangrui.Elastoplastic analysis of surrounding rock on circular roadway based on drucker-prager yield criterion[J].Journal of China Coal Society，2013，38(S1):30-37.
[11] 陈梁，茅献彪，李明，等.基于Drucker-Prager准则的深部巷道破裂围岩弹塑性分析[J].煤炭学报，2017，42(2):484-491.
CHEN Liang,MAO Xianbiao,LI Ming,et al.Elastoplastic analysis of cracked surrounding rock in deep roadway based on drucker-prager criterion[J].Journal of China Coal Society，2017，42(2):484-491.
[12] 王宏伟，张登强，邓代新，等.非静水压力条件下巷道围岩破碎区应力分布特征[J].煤炭学报，2020，45(11):3717-3725.
WANG Hongwei,ZHANG Dengqiang,DENG Daixin,et al.Study on stress distribution characteristics of roadway surrounding rock damaged zone under non-hydrostatic pressure[J].Journal of China Coal Society，2020，45(11):3717-3725.
[13] 袁超，张建国，王卫军，等.基于塑性区分布形态的软弱破碎巷道围岩控制原理研究[J].采矿与安全工程学报，2020，37(3):451-460.
YUAN Chao，ZHANG Jianguo，WANG Weijun，et al.Controlling principles of surrounding rock in soft and broken roadway based on the distribution pattern of plastic zone[J].Journal of Mining & Safety Engineering，2020，37(3):451-460.
[14] 尹光志，鲁俊，张东明，等.真三轴应力条件下钻孔围岩塑性区及增透半径研究[J].岩土力学，2019，40(S1):1-10.
YIN Guangzhi,LU Jun,ZHANG Dongming,et al.Study on plastic zone and permeability-increasing radius of borehole surrounding rock under true triaxial stress conditions[J].Rock and Soil Mechanics,2019，40(S1):1-10.
[15] 章光，吴金刚，杨龙杰.非等压应力场上向长距离穿层瓦斯抽采钻孔密封长度研究[J].岩石力学与工程学报，2018，37(S1):3422-3431.
ZHANG Guang，WU Jingang，YANG Longjie.Determination of the sealing length of upward long crossing boreholes for gas drainage under unequal stress fields[J].Chinese Journal of Rock Mechanics and Engineering，2018，37(S1):3422-3431.
[16] 尹光志，鲁俊，李星，等.应力Lode角对砂岩变形特性影响[J].岩石力学与工程学报，2017，36(9):2081-2091.
YIN Guangzhi,LU Jun,LI Xing,et al.Influence of stress Lode angle on deformation characteristics of sandstone[J].Chinese Journal of Rock Mechanics and Engineering,2017,36(9):2081-2091.
[17] TAO Ming，ZHAO Huatao，LI Xibing,et al.Failure characteristics and stress distribution of pre-stressed rock specimen with circular cavity subjected to dynamic loading[J].Tunnelling and Underground Space Technology，2018，81:1-15.
[18] 王卫军，董恩远，袁超.非等压圆形巷道围岩塑性区边界方程及应用[J].煤炭学报，2019，44(1):105-114.
WANG Weijun,DONG Enyuan,YUAN Chao.Boundary equation of plastic zone of circular roadway in non-axisymmetric stress and its application[J].Journal of China Coal Society,2019，44(1):105-114.
