冲击地压是世界范围内煤矿最严重的动力灾害之一,中国、加拿大、波兰、俄罗斯、美国和澳大利亚等国家煤矿安全生产均受到冲击地压灾害的严重威胁[1-5]。2019年国家煤矿安全监察局组织调研查明,我国生产矿井中鉴定确认冲击地压矿井132个,至少涉及195个主采煤层,冲击地压矿井的煤炭产量约占我国煤炭总产量的12%[6-7]。2018-10-20,山东能源集团龙郓煤业发生21人事故,2019-06-09,吉林煤业集团公司龙家堡煤矿发生9人事故,2020-02-22,山东新巨龙煤业有限公司龙堌矿发生4人事故[8]。
冲击地压的机理和理论是实现冲击地压监测预警和有效防治的前提和基础。国际上最早研究冲击地压发生机理始于1915年,提出了一系列冲击地压发生理论。从“强度理论”、“刚度理论”、“能量理论”、“冲击倾向性理论”到后来的“三准则”理论[9]、“变形系统失稳理论”[10]、“三因素”理论[11]、“冲击启动”理论[12]、冲击地压扰动响应失稳理论[13]、冲击地压扩容理论[14]和强度弱化减冲理论[15]等。此外,随着数学、力学、数值计算与试验研究等方法以及多学科的交叉应用,冲击地压发生的微细观机理研究也取得了大量的研究成果[16-18]。这些理论都从不同角度在一定程度上揭示了冲击地压发生的基本原理与条件,对于认识煤矿冲击地压发生机理起到了重要的推动作用。但是,作为世界级难题,冲击地压具有复杂性,目前还没有给出一个描述冲击地压基础性、根本性问题的理论公式。
具体表现在:① 没有给出煤岩力学参数、巷道或采场几何参数、原岩应力或采动应力满足什么样的公式就将发生冲击地压;② 没有给出冲击地压危险性和冲击倾向性之间的理论关系。目前所有具有冲击地压危险的矿井都要进行冲击倾向性鉴定,包括单轴抗压强度、弹性能指数、冲击能指数和动态破坏时间。针对获得的冲击倾向性参数、地应力或采动应力指标,还没有给出一个计算冲击地压危险性的理论公式,对冲击危险性进行评价和预警或对冲击地压防治后的危险性进行效果评价;③ 不能对冲击地压矿井存在一个冲击地压发生临界开采深度给出理论解释;④ 还没有给出冲击地压发生的临界载荷,无法对冲击地压防治工程进行安全设计,给出安全系数;⑤ 没有给出支护在冲击地压发生过程中的作用。目前由于采煤工作面综采液压支架支护强度较大,采煤工作面冲击地压几乎消除,冲击地压事故90%发生在巷道中,近5 a来有记录的冲击地压事故均发生于工作面超前回采巷道,巷道冲击地压事故累计发生10余起,伤亡人数近百人。巷道支护强度在冲击地压防治中起到什么作用,还需理论公式加以揭示。
笔者在简化提出冲击地压发生的力学模型基础上,给出了冲击地压发生的理论公式,并采用该理论公式,对冲击地压的一些基础性、根本性问题进行分析。
1 冲击地压发生的力学模型
1.1 冲击地压发生的几何模型
井下存在各种各样的煤体结构,冲击地压发生的典型几何模型是巷道。将近90%以上冲击地压灾害发生于巷道,巷道冲击地压一直是冲击地压机理、监测预警与防治工作的重中之重[13,19-20],包括回采工作面超前巷道、工作面开切眼等类巷道结构等,如图1(a)所示。
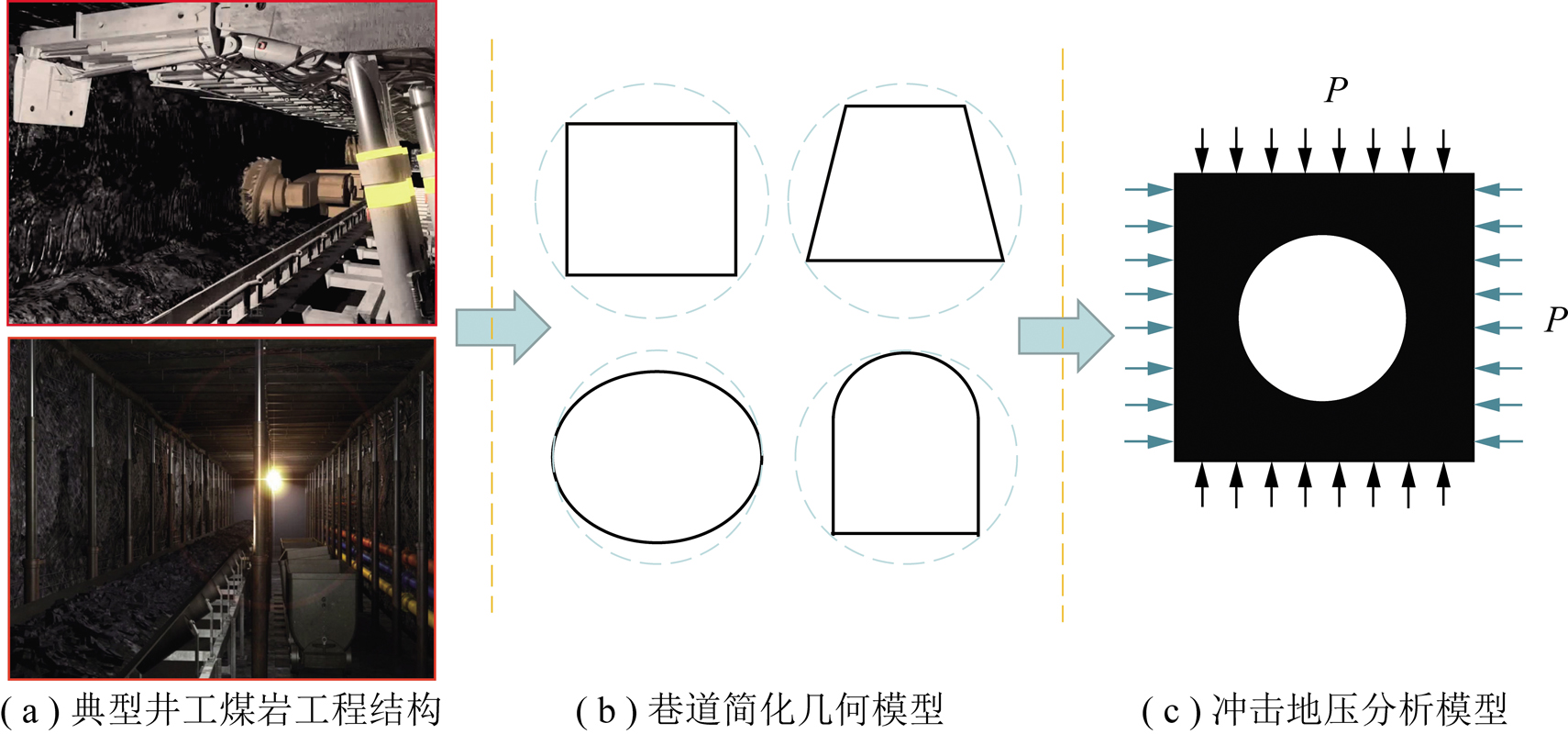
图1 多种断面形状煤岩结构简化几何模型
Fig.1 Simplified geometric model with various section shape of coal and rock structure
井工巷道断面形状虽然可能各有差别,典型如矩形巷道、圆形巷道、梯形巷道、直墙拱形巷道等,但对于冲击地压发生来说,巷道围岩中具有承压、蓄能特性的弹性区是释放能量、导致冲击启动的主体区,如图1(b)所示。任何断面形状的巷道,其承压蓄能结构的轮廓边界线均可近似为巷道断面实际轮廓线的外接圆,出现明显的“巷道承载外接圆效应”。现场巷道围岩破坏也表明,非圆形巷道轮廓线与其外接圆轮廓线所包围的面积正是易变形、垮落的软化破碎区的一部分,是冲击显现的主体区域。煤矿冲击地压的分析对象将抽象为最典型的圆形巷道,如图1(c)所示。
1.2 冲击地压发生力学模型边界载荷条件
笔者将圆形巷道边界载荷简化为等压的静水压力,即远场地应力P。依据如下:① 我国地应力相关研究成果表明,随着煤炭向深部开采,采深越大,水平地应力与垂直地应力数值越接近相等。对于深部开采条件,模型的静水压力边界条件假设符合我国深井地应力的一般规律;② 等压巷道冲击地压理论分析模型具有解析简明直观的优势,临界条件的理论公式简洁且能有效指导工程现场的防冲设计;③ 可采用修正系数法,将等压边界条件下揭示的巷道冲击地压发生临界条件进行修正,以实现进一步满足指导非等压防冲工程结构的需要。此外,将巷道内的支护应力简化为圆形巷道内壁面上的均匀内压强。
需指出的是,工程巷道边界载荷条件一般会形成静动加荷效应。针对巷道冲击地压传统划分的基本类型(煤体压缩应变型、顶板断裂诱发型和断层错动诱发型)[5],笔者将顶板断裂和断层错动视为诱发巷道冲击的远场扰动因素,并将远场扰动应力等效视为地应力增量。因此,本文研究成果将适用于静载自发型巷道冲击地压和扰动诱发型巷道冲击地压,对纯动载强震型冲击地压将另做探究。
1.3 煤岩体变形破坏的本构关系
从单轴压缩条件下煤岩标准试件的应力应变全程曲线上看,煤岩受载变形分为“压实致密(OA)”、“弹性变形(AB)”、“塑性强化(BC)”、“损伤软化(CD)”和“残余变形(DE)”5个阶段,如图2所示。从冲击地压孕育、发生与显现物理过程来看,煤岩样单轴压缩性质应分为峰前阶段和峰后阶段。峰前阶段煤岩以压实致密、弹性形变与弹性能积蓄为主要特征,峰后阶段煤岩以损伤累积、残余形变与能量耗散为主要特征。
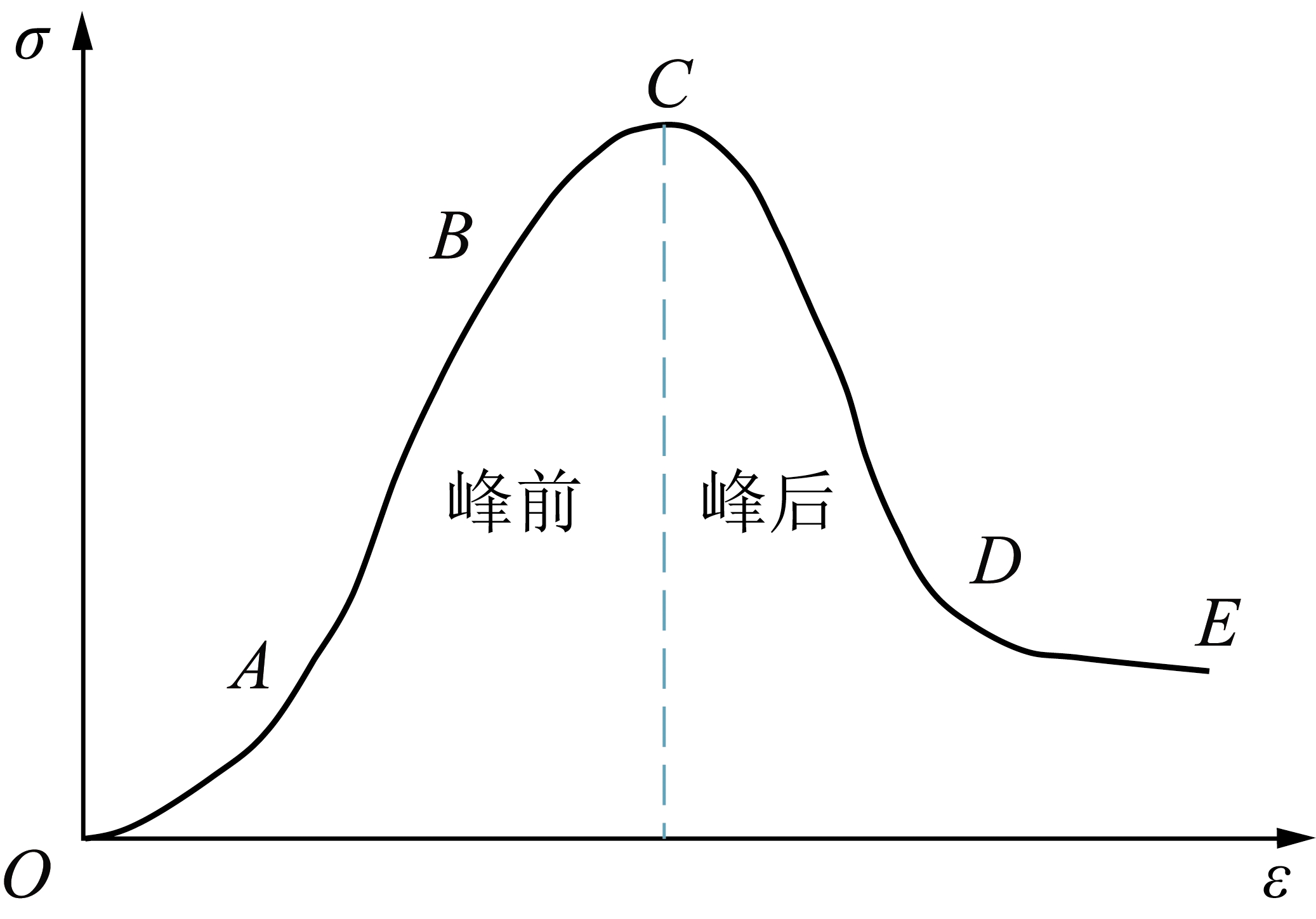
图2 煤岩试件单轴抗压应力-应变曲线
Fig.2 Uniaxial compressive stress-strain curve of coal rock specimen
1.3.1 煤岩体的“双线性”本构关系
由煤矿现场巷道观察可知,大部分煤岩巷道围岩处于深部煤岩弹性承载、浅部煤岩塑性软化屈服承载状态。据此,冲击地压力学分析模型应为“弹性区-塑性软化区”两分区结构[13,21],如图3所示,相应的煤岩本构应选取双线性本构模型。

图3 冲击地压巷道 “两分区”结构模型[13]
Fig.3 “Two zone” structure model of rockburst roadway[13]
对于脆性极强的岩体,单轴压缩条件下岩样应力应变曲线中的残余阶段不明显,甚至出现缺失的现象,应力整体表现为峰前线性攀升、峰后急速下降的特征;对于此类本构属性的岩石,通常简化为“双线性”本构关系,主要包括弹性阶段和峰后软化阶段,如图4所示;此类岩石巷道冲击地压灾害与硬岩岩爆灾害极为相似,巷道冲击启动时,巷道围岩塑性软化深度一般较小,崩落岩块冲击速度较大。
在“双线性”本构关系假设中,将峰值强度前简化为线弹性,弹性模量为E,煤岩的单轴抗压强度为σc,对应的应变为εc,完全损伤状态下煤岩应变为εf。峰值强度后,假设峰后煤岩呈现线性应变软化,煤岩塑性软化模量为λ。超过峰值强度后,煤岩损伤变量D为线性各向同性损伤演化,即于煤岩峰值强度处,D=0;达到完全破坏,D=1。
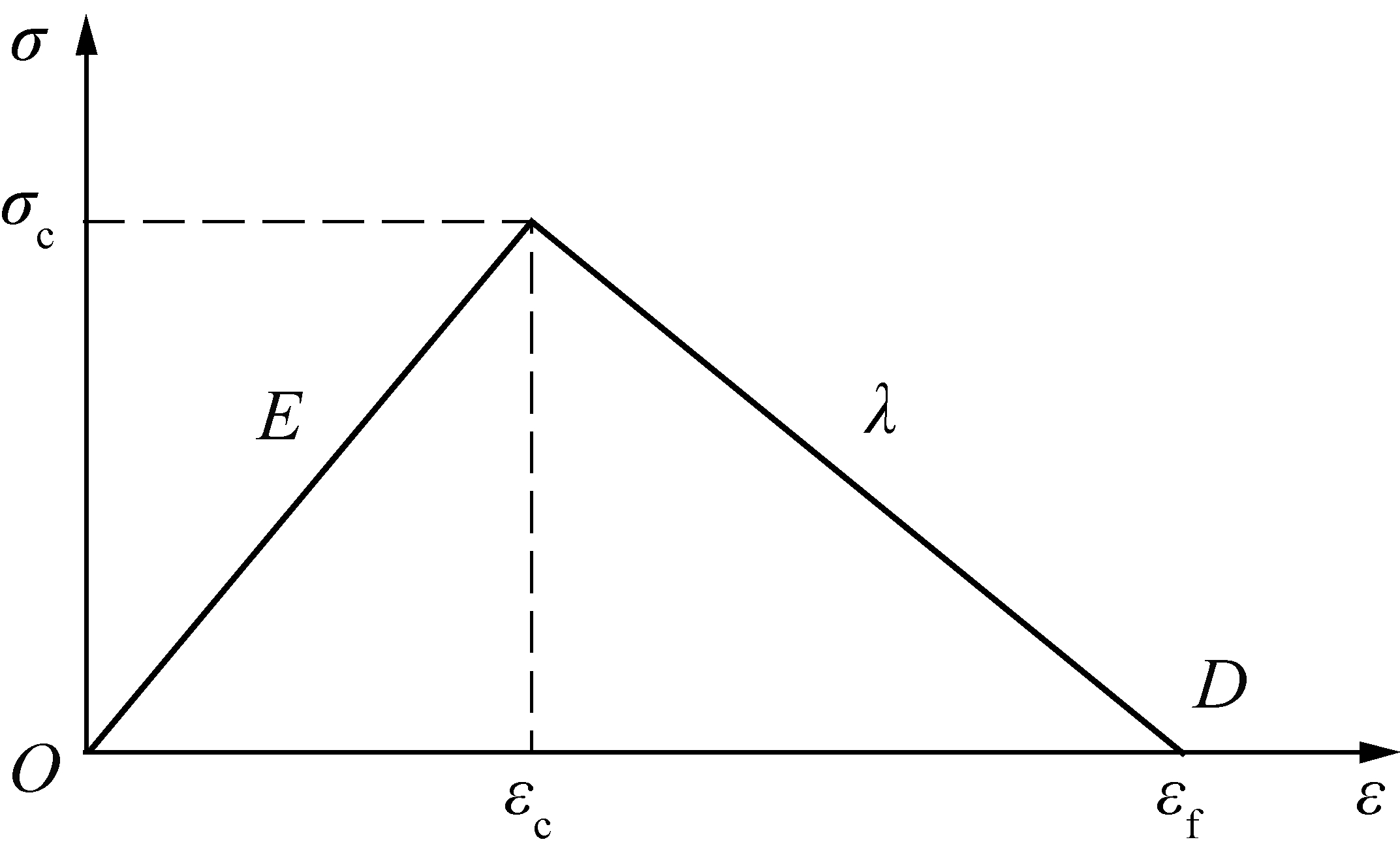
图4 煤岩体两线性本构模型
Fig.4 Bilinear constitutive relation of coal and rock
根据煤岩体的“双线性”本构关系模型和峰后线性损伤演化可知,煤岩体的应力应变关系方程、一维线性损伤演化方程,分别如式(1),(2)所示:
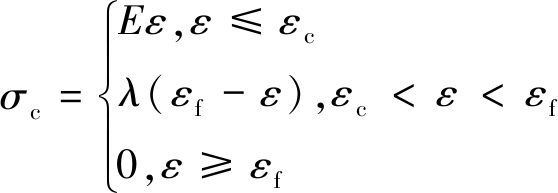
(1)
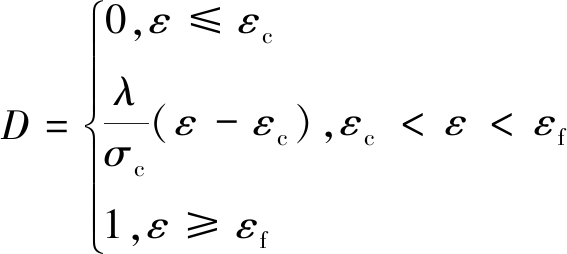
(2)
进一步地,三维情况下煤岩损伤演化方程为
![]()
(3)
![]()
(4)
式中,![]() 为等效应变;ε1,ε2和ε3分别为第一主应变、第二主应变和第三主应变。
为等效应变;ε1,ε2和ε3分别为第一主应变、第二主应变和第三主应变。
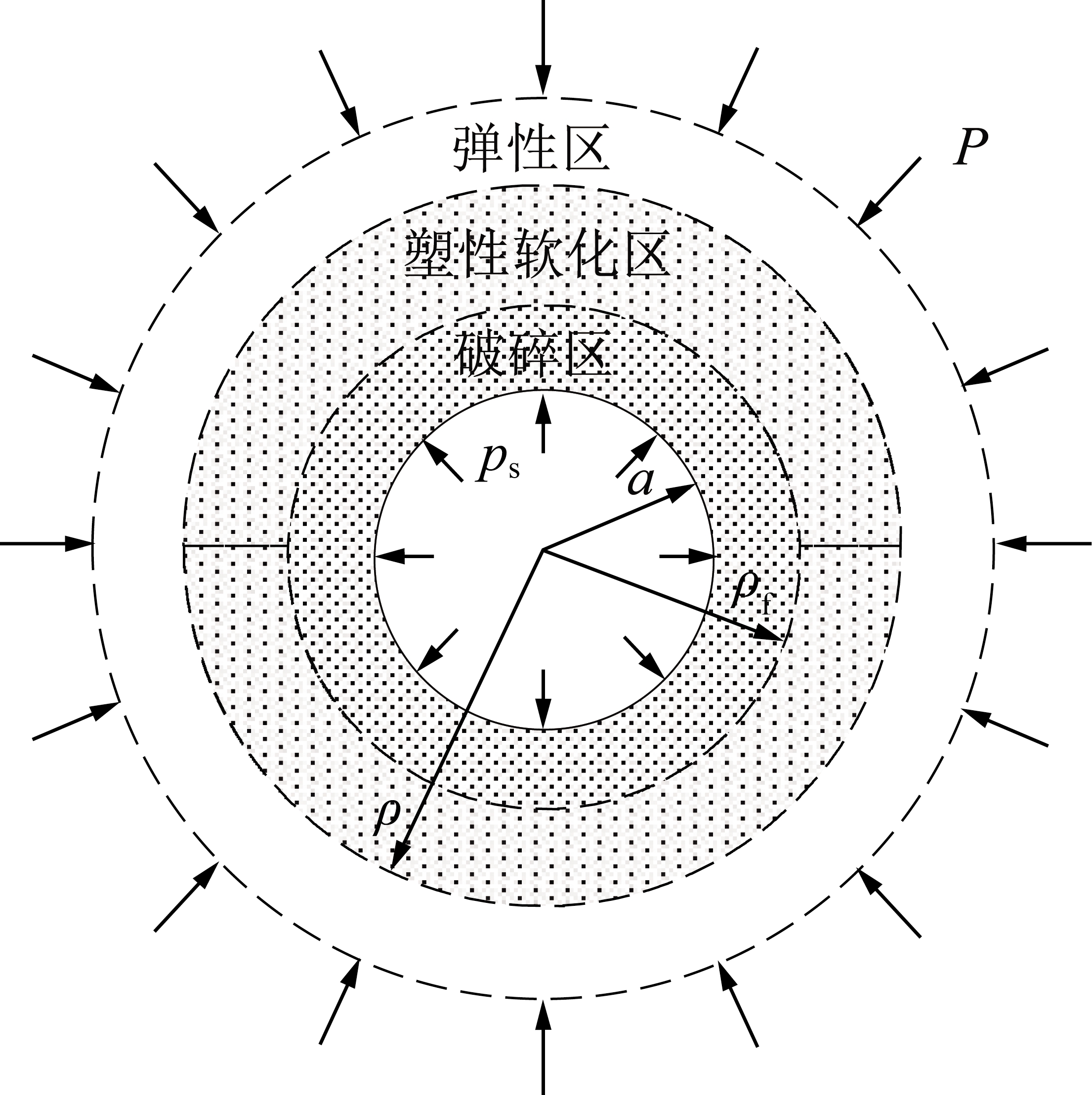
图5 冲击地压巷道 “三分区”结构模型[23]
Fig.5 “Three zones” structure model of rock burst roadway[23]
1.3.2 煤岩体的“三线性”本构关系
进入深部开采后,大部分煤岩巷道围岩处于深部煤岩弹性承载、浅部煤岩塑性软化屈服承载,甚至残余破碎承载状态。据此,冲击地压力学分析模型应为“弹性区-塑性软化区-破碎区”3分区结构[22-23],如图5所示,相应的煤岩本构应选取三线性本构模型。
对于脆性较弱的煤岩体,单轴压缩条件下煤岩样应力应变曲线中的残余阶段较为明显,应力整体表现为峰前线性攀升、峰后急速下降与残余阶段缓慢衰减的特征;对于此类本构属性的岩石,通常简化为“三线性”本构关系,主要包括弹性阶段、软化阶段和残余阶段,如图6所示;此类煤岩巷道冲击地压灾害,巷道冲击启动时,巷道围岩塑性软化深度一般较大,破坏抛出煤体速度相对较小、煤体量大,多发于深部煤层巷道。
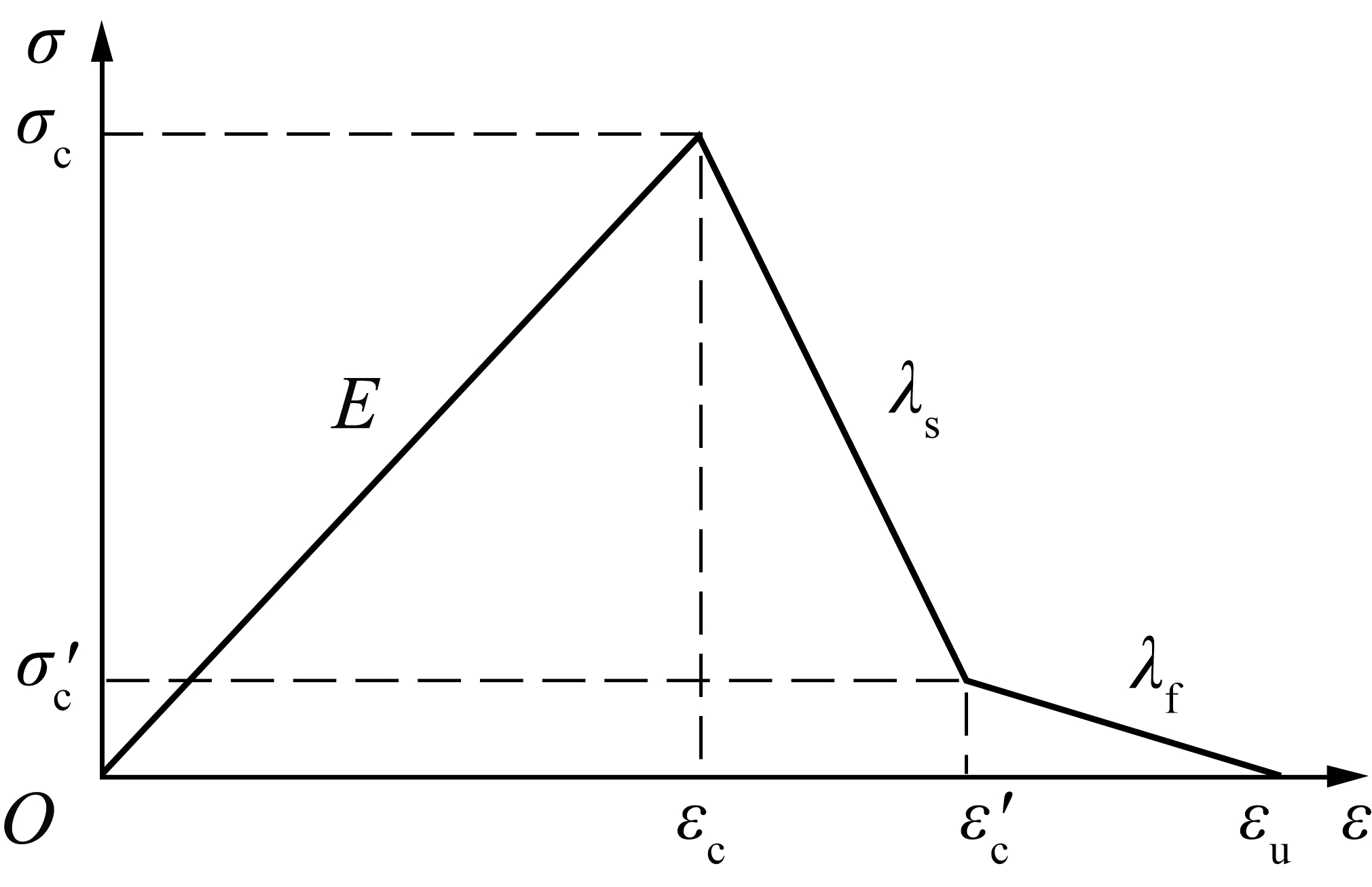
图6 考虑残余强度的煤岩三线性本构关系
Fig.6 Linear constitutive relationship of coal and rock considering residual strength
在“三线性”本构关系假设中,峰值强度前简化为线弹性。ε′c为残余强度对应的应变,εu为完全损伤状态下煤岩应变。峰值强度后,假设峰后煤岩呈现双线性应变软化,煤岩塑性软化模量、残余模量分别为λs和λf,煤岩残余强度σ′c=ξσc,其中,ξ为煤岩残余强度系数。超过峰值强度后,煤岩损伤变量D为线性各向同性损伤演化,即于煤岩峰值强度处,D=0;于残余强度处,D=1-ξ;达到完全破坏,D=1。
根据煤岩体的“三线性”本构关系模型和峰后线性损伤演化,可知,煤岩体的应力-应变关系方程、线性损伤演化方程,分别如式(5),(6)所示:
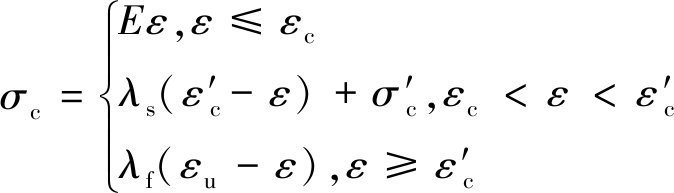
(5)
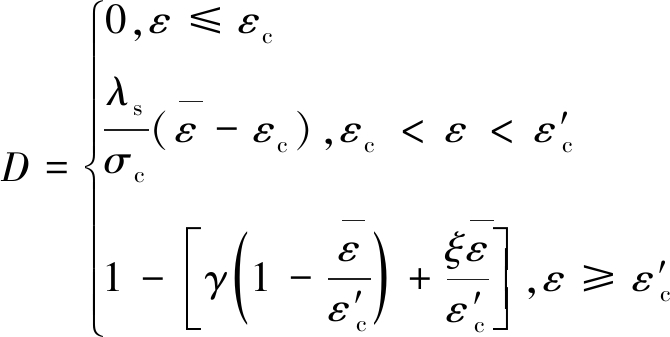
(6)
式中,γ为中间变量,γ=λf/E+(1-ξ)λf/λs+ξ。
1.4 冲击地压发生的力学判据
基于冲击地压发生的扰动响应失稳理论,对于给定的煤岩体变形系统(巷道),在远场地应力P作用下,产生的塑性软化区半径为ρ。假设某时刻系统处于平衡状态,对于地应力P的一个微小扰动ΔP,这时煤岩体塑性软化区半径由ρ增加到ρ+Δρ。若响应Δρ是有界的或有限的,则此时平衡状态是稳定的。即对于任意给定小数![]() 总有数
总有数![]() 存在,使得当微小扰动ΔP满足条件:
存在,使得当微小扰动ΔP满足条件:
![]()
(7)
则响应Δρ总可以满足下面不等式:
![]()
(8)
若系统处于非稳定平衡状态,则无论扰动ΔP,都会导致塑性软化区半径的无限增长,即
![]()

(9)
式(9)即为冲击地压发生的扰动响应判别准则,其物理意义在于[24]:在应力增量dP的作用下(诸如,顶板断裂、断层错动或爆破振动等形式的采动应力增量),塑性软化区半径增量dρ发生极大扩展,表征了巷道冲击地压本质是围岩塑性区边界非线性增速失稳扩展及其带来的一系列的宏观响应。
2 冲击地压发生的理论解
2.1 基于双线性本构关系的模型解算
针对如图3所示的两分区冲击地压巷道力学模型,设巷道半径a,塑性软化区半径ρ,巷道内壁支护应力为ps,远处受地应力P作用。定义冲击倾向性指数K=λ/E。取单位长度进行计算,巷道围岩破坏采用摩尔-库仑屈服破坏准则,视其为静水压力状态的轴对称平面应变问题。
由弹性理论,结合在弹性与软化区交界处满足莫尔-库伦准则σθ(ρ)=mσr(ρ)+σc。因此,弹性区径向应力σr、环向应力σθ为
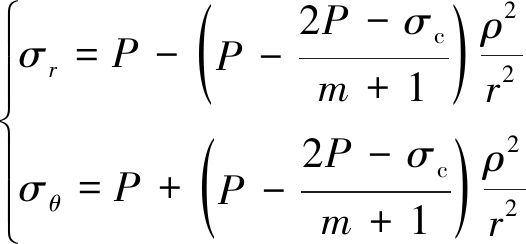
(10)
式中,![]() 为煤岩内摩擦角;r为半径。
为煤岩内摩擦角;r为半径。
塑性软化区内(a<r<ρ)材料损伤的情况下,有效应力分量为![]() 将莫尔-库仑屈服准则中的应力用有效应力代替,得
将莫尔-库仑屈服准则中的应力用有效应力代替,得
![]()
(11)
在软化区内,由几何方程和体积不可压缩假设,得软化区内等效应变![]()
![]()
(12)
据式(2),可进一步得软化区内损伤演化方程为
![]()
(13)
不考虑体积力,将σθ=mσr+(1-D)σc 代入平衡方程:
![]()
(14)
由边界条件σr(a)=ps,得软化区内径向应力分量为
![]()
(15)
由r=ρ处径向应力连续条件,得到两分区巷道系统方程:
![]()
(16)
根据扰动响应失稳判据,![]()
 ,得到冲击地压发生时的临界软化区半径ρcr:
,得到冲击地压发生时的临界软化区半径ρcr:
![]()
(17)
将式(17)代回式(16),得到发生冲击地压时的临界载荷Pcr:
![]()
(18)
一般取内摩擦角φ=30°,代入式(18),得
![]()
(19)
当支护力ps=0时,得
![]()
(20)
当冲击倾向性指数K取值区间为[2.5, ]时,得到
]时,得到
Pcr=(0.5~0.7)σc
(21)
这与实际工程中给出的硐室岩爆经验判据(0.3~0.7)σc相一致[25-26]。
2.2 基于三线性本构关系的模型解算
针对如图5所示的三分区冲击地压巷道力学模型。破碎区半径为ρf,在此模型中,冲击倾向性指数K将等于λs/E。
由弹性理论,结合在弹性区与塑性软化区交界处满足莫尔库伦准则σθ(ρ)=mσr(ρ)+σc条件,得弹性区径向应力σr、环向应力σθ为
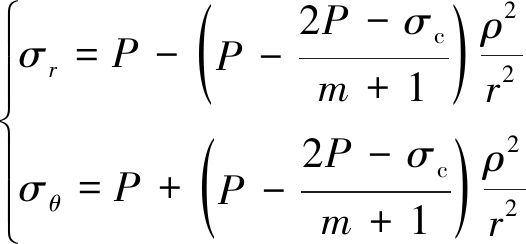
(22)
与式(13)同理,在塑性软化区内(ρf<r<ρ)内,煤岩损伤演化方程为
![]()
(23)
不考虑体积力,将σθ=mσr+(1-D)σc 代入平衡方程式(14)。
设破碎区与塑性软化区交界处应力为pf,结合此边界条件,得塑性软化区径向应力分量:
![]()
(24)
与式(12)同理,在破碎区内,由体积不可压缩条件,得破碎区内等效应变![]()
![]()
(25)
据式(6),可进一步得破碎区煤岩损伤演化方程为
![]()
(26)
由式(10),将σθ=qσr+(1-D)σc代入平衡微分方程得
![]()
(27)
式中,![]() 为损伤煤岩内摩擦角。
为损伤煤岩内摩擦角。
结合边界条件σr=a=ps,得破碎区对塑性软化区的边界作用应力pf:
![]()
(28)
其中,![]()
由r=ρ径向应力连续条件,联立式(22),(24)与(28),得巷道系统方程:
![]()
(29)
根据扰动响应失稳判据,![]()
 ,得到冲击地压发生的临界破碎区半径ρfcr、临界软化区半径ρcr、临界载荷Pcr分别为
,得到冲击地压发生的临界破碎区半径ρfcr、临界软化区半径ρcr、临界载荷Pcr分别为
![]()
(30)
![]()
(31)
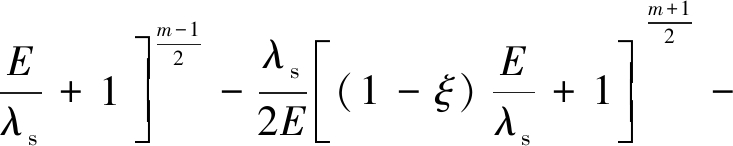
![]()
(32)
![]()
(33)
当λs=λf,ξ=0或ρf=a,“3分区”巷道模型将退化为“两分区”巷道模型。相应地,临界塑性软化区半径计算公式(31)将退化为式(17),临界载荷计算公式(32)将退化为式(18)。
为充分考虑巷道断面形状对冲击地压发生的影响并强化理论公式工程应用的普适性,基于圆形巷道冲击地压发生临界载荷计算公式,进一步提出考虑断面形状的工程巷道临界载荷修正计算式![]()
![]()
(34)
其中,η为巷道断面形状系数,建议取值0.9~1.0。需要指出的是,该系数取值受到实际工程条件的综合影响,应为经验性系数,具体取值可通过物理模型试验方法、数值计算方法和现场冲击地压历史事件工程对比法等总结归纳得出。为加强各矿区临界条件计算值的对比分析,下文η值暂取1.0。
3 冲击地压发生的临界载荷理论公式
根据以上对冲击地压发生的力学分析模型的解析分析结果,现给出冲击地压发生的临界载荷Pcr计算的基本理论公式,如式(35)所示。可知,冲击地压发生的临界载荷Pcr与煤岩单轴抗压强度σc、冲击倾向性指数K密切相关。
![]()
(35)
K表征了煤岩冲击倾向性,与冲击能指数KE的本质相同。具体地,煤岩冲击倾向性指数K越大,冲击地压发生临界载荷Pcr越低。
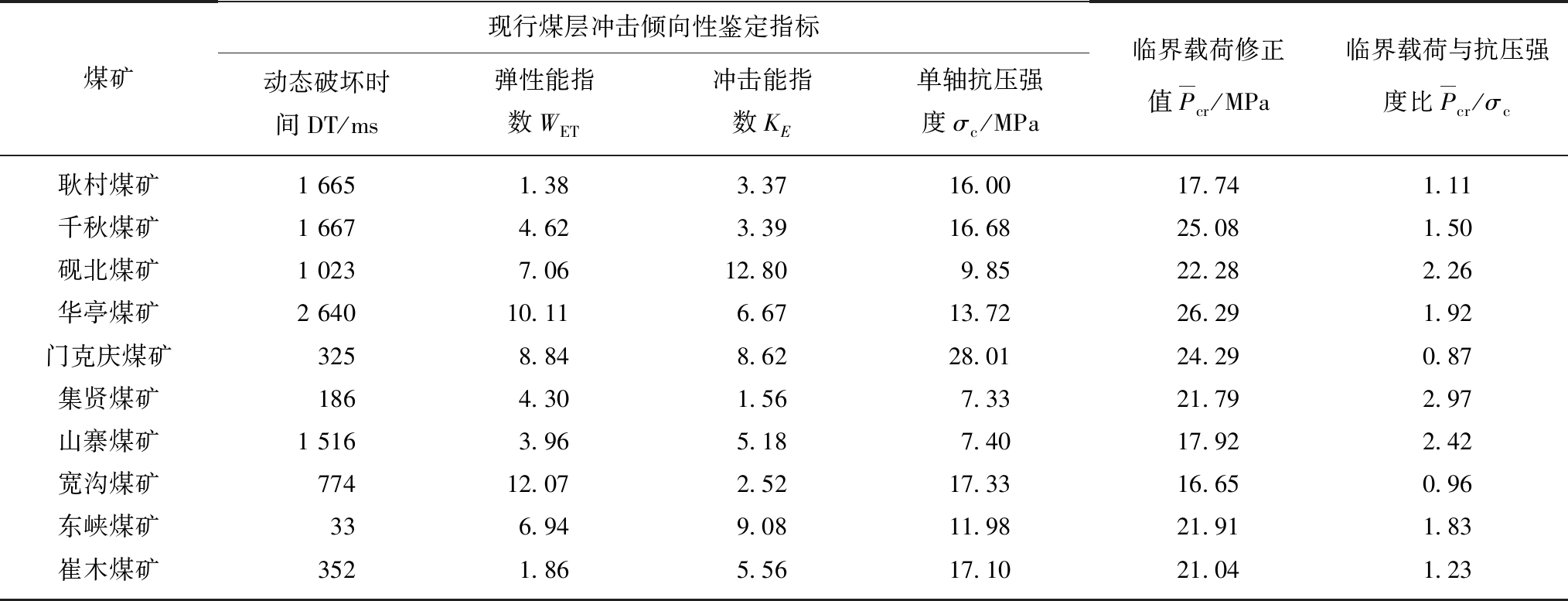
特别地,虽然从理论公式中可以看到,煤岩单轴抗压强度σc越大,临界载荷Pcr越高,但统计研究发现[27],对于脆性显著的岩石材料而言,煤岩单轴抗压强度σc增大往往意味着其冲击倾向性也大幅增加,这就导致了强度大的岩石巷道冲击危险性低的结论并不绝对成立,这一规律也是单轴抗压强度为什么可以作为冲击倾向性鉴定指标的原因所在。我国部分煤矿冲击地压发生的临界载荷计算理论值见表1。
表1 我国部分煤矿冲击地压发生的临界载荷理论值(ps =0)
Table 1 Calculation of critical load of rock burst of coal mines in China(ps=0)
煤矿现行煤层冲击倾向性鉴定指标动态破坏时间DT/ms弹性能指数WET冲击能指数KE单轴抗压强度σc/MPa临界载荷修正值Pcr/MPa临界载荷与抗压强度比Pcr/σc耿村煤矿1 6651.383.3716.0017.741.11千秋煤矿1 6674.623.3916.6825.081.50砚北煤矿1 0237.0612.809.8522.282.26华亭煤矿2 64010.116.6713.7226.291.92门克庆煤矿3258.848.6228.0124.290.87集贤煤矿1864.301.567.3321.792.97山寨煤矿1 5163.965.187.4017.922.42宽沟煤矿77412.072.5217.3316.650.96东峡煤矿336.949.0811.9821.911.83崔木煤矿3521.865.5617.1021.041.23
4 冲击倾向性与冲击危险性的理论关系
冲击倾向性定义为煤岩试件发生冲击破坏能力的介质固有属性,可通过实验室测试鉴定获得。冲击倾向性的表征对象为煤岩介质,因而全称为“煤岩冲击倾向性”,相应地,其评价工作称为“煤岩冲击倾向性鉴定”。在我国现行国家标准(GB/T 25217.2—2010)中,煤层冲击倾向性鉴定指标有4个[28],包括:动态破坏时间DT、弹性能指数WET、冲击能指数KE与单轴抗压强度。由冲击地压发生临界载荷理论公式(35)可知,冲击倾向性表征的理论指标为单轴抗压强度和冲击能指数。
冲击危险性定义为特定地质赋存条件下工程巷道发生冲击地压显现的可能性及危险程度,需要采用理论分析、数值计算、室内与现场试验等方法分析获得。冲击危险性的表征对象为工程巷道。针对采区冲击危险性开展的评价工作应称为“采区冲击危险性评价”,针对回采工作面称为“回采工作面冲击危险性评价”,针对掘进巷道称为“掘进巷道冲击危险性评价”等。目前国内外较为普遍采用综合指数法评价冲击危险性,还没有公认的冲击危险性理论表征指标和判据,因而现有研究也就未能从理论层面辩明冲击倾向性与冲击危险性之间的关系。
基于冲击地压发生的临界载荷理论公式,定义冲击危险性为工程巷道实际地应力P和临界载荷修正值![]() 的比值,其实质为实际应力接近临界应力的程度。
的比值,其实质为实际应力接近临界应力的程度。
![]()
(36)
其中,Kcr为表征冲击危险性的临界应力指数;地应力P越高,巷道冲击危险性的临界应力指数Kcr越大,冲击危险性越高,即发生冲击地压的可能性越高。由式(36)结合冲击地压发生临界载荷理论公式(35),可知:煤岩冲击倾向性是冲击危险性的主控因素之一。
煤岩冲击倾向性鉴定是巷道冲击危险性评价的前提,通过冲击危险性评价得到的冲击危险区域及其危险等级是冲击地压防治的依据。因此,冲击地压理论公式的提出为冲击倾向性鉴定、冲击危险性评价、监测预警与工程治理的一体化研究搭建了桥梁,并提供了量化依据。
5 冲击地压发生临界采深理论公式
每个矿井都存在一个发生冲击地压的临界开采深度[19],即煤层开采水平处于地表以下的深度小于此值时,冲击地压几乎不发生,大于此深度时,冲击地压频繁发生,且强度也越来越大,冲击地压发生的临界采深示意如图7所示。据统计[20],苏联基泽洛夫和库茨涅茨等矿区冲击地压开始发生的深度为180~400 m,波兰煤矿的冲击地压临界深度为200 m。德国煤矿冲击地压的临界深度为300~400 m。英国煤矿冲击地压的临界深度为120~300 m。关于我国煤矿,门头沟矿的临界深度约200 m,大台矿约为460 m,陶庄矿约为480 m,唐山矿约为540 m。
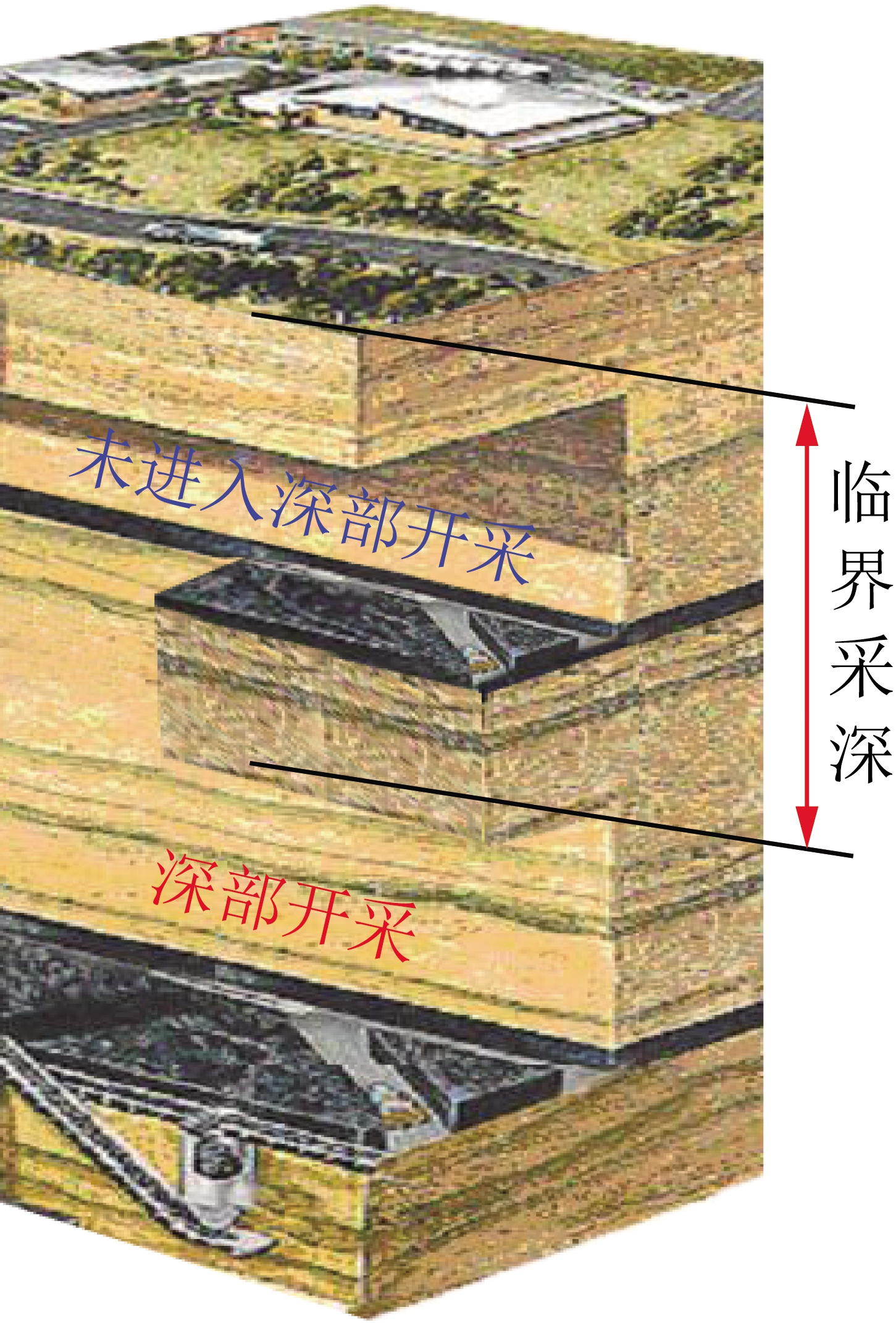
图7 煤矿冲击地压发生的临界采深示意
Fig.7 Diagram of critical mining depth of rockburst
然而,由于现有冲击地压的理论研究未能系统量化揭示出冲击地压发生的临界条件、主控因素及其规律,因此,未能对冲击地压发生存在一个矿井临界开采深度给出理论解释。冲击地压发生理论公式将成为定量验算某一矿区临界开采深度或定量预测新建矿井临界开采深度的重要理论依据。
一般来说,开采深度越大,煤体应力越高,煤体变形和积蓄的弹性能越多,发生冲击地压的可能性越大。若不考虑构造应力,设煤层上覆岩层的容重为γg,巷道埋深为H,则上覆岩层压力导致远场地应力P=γgH。在冲击地压启动的临界状态下,![]() 则发生冲击地压的临界开采深度Hcr:
则发生冲击地压的临界开采深度Hcr:
![]()
(37)
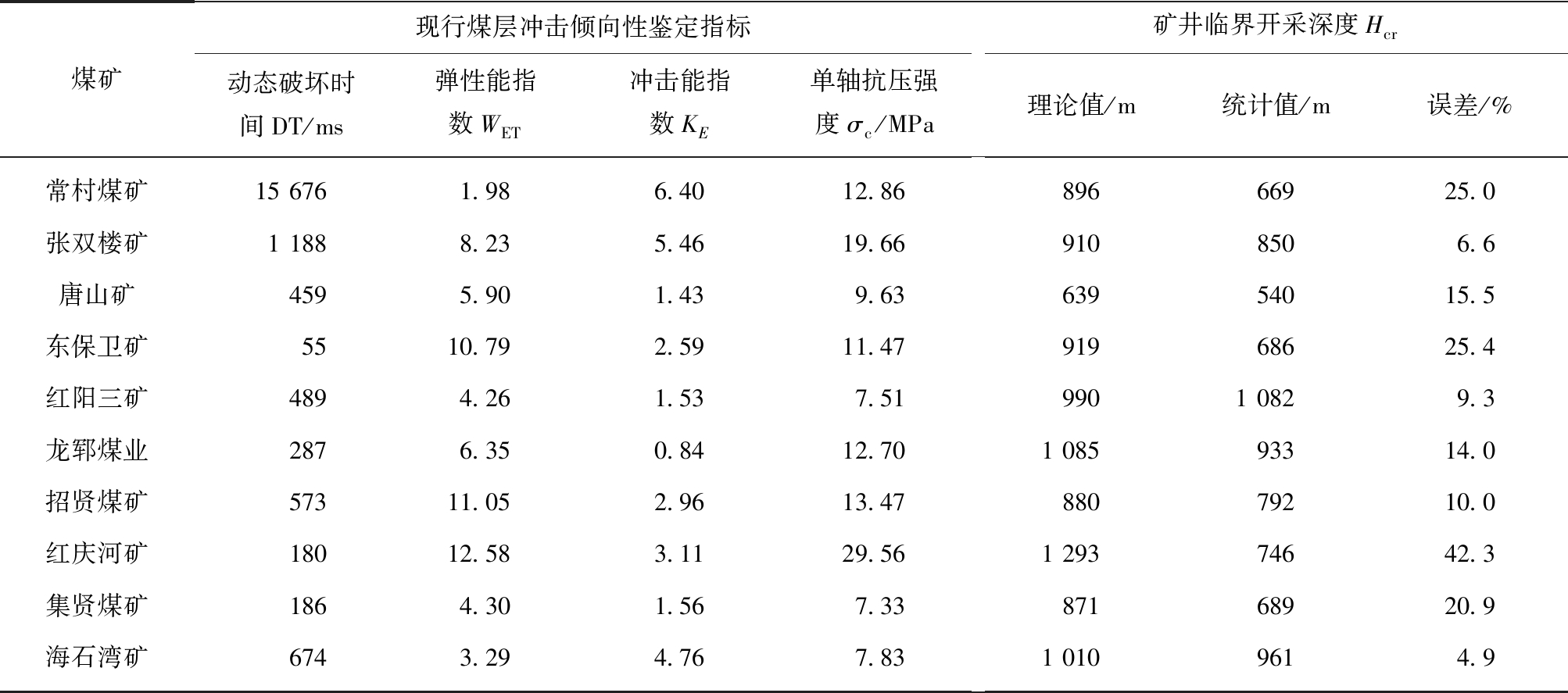
基于式(37)定义的关于冲击地压发生的矿井临界开采深度计算方法,计算得到了我国部分煤矿典型冲击地压发生的临界开采深度理论值,见表2,并与实际工程的统计值进行对比。通过对比可知,冲击地压发生的矿井临界开采深度理论值一般比实际工程统计值要高,这主要是由煤层赋存环境中不同程度的地质构造应力造成的。
表2 我国部分煤矿冲击地压发生的临界采深值(ps=0)
Table 2 Calculation of critical load of rock burst of coal mines in China(ps=0)
煤矿现行煤层冲击倾向性鉴定指标动态破坏时间DT/ms弹性能指数WET冲击能指数KE单轴抗压强度σc/MPa矿井临界开采深度Hcr理论值/m统计值/m误差/%常村煤矿15 6761.986.4012.8689666925.0张双楼矿1 1888.235.4619.669108506.6唐山矿4595.901.439.6363954015.5东保卫矿5510.792.5911.4791968625.4红阳三矿4894.261.537.519901 0829.3龙郓煤业2876.350.8412.701 08593314.0招贤煤矿57311.05 2.9613.4788079210.0红庆河矿18012.583.1129.561 29374642.3集贤煤矿1864.301.567.3387168920.9海石湾矿6743.294.767.831 0109614.9
6 支护作用影响冲击地压发生的理论公式
从理论层面清楚掌握支护对巷道冲击地压启动的影响机制及其规律对于巷道防冲支护设计至关重要。由冲击地压发生临界指标的理论公式,绘制“围岩-支护”系统中随着环境应力增加巷道围岩塑性软化及破碎深度的发育规律曲线,如图8所示。从理论曲线来看,巷道围岩塑性软化区或破碎区边界演化呈现非线性增速扩展规律,特别地,当巷道达到冲击启动临界载荷Pcr时,围岩塑性区和破碎区边界将发生扩展增量为无穷大的演化趋势。因此,也进一步印证了巷道冲击地压本质是围岩塑性区边界非线性增速失稳扩展及其带来的一系列的宏观响应。
分析可知,支护对冲击地压巷道围岩稳定性的影响主要体现在2个方面:① 支护强度增加将有效抑制围岩破碎发育速度;② 支护强度增加将大幅度提升冲击地压启动的门槛值-临界载荷Pcr。科学合理支护将对巷道围岩具有防冲防冒的双重稳控功能。
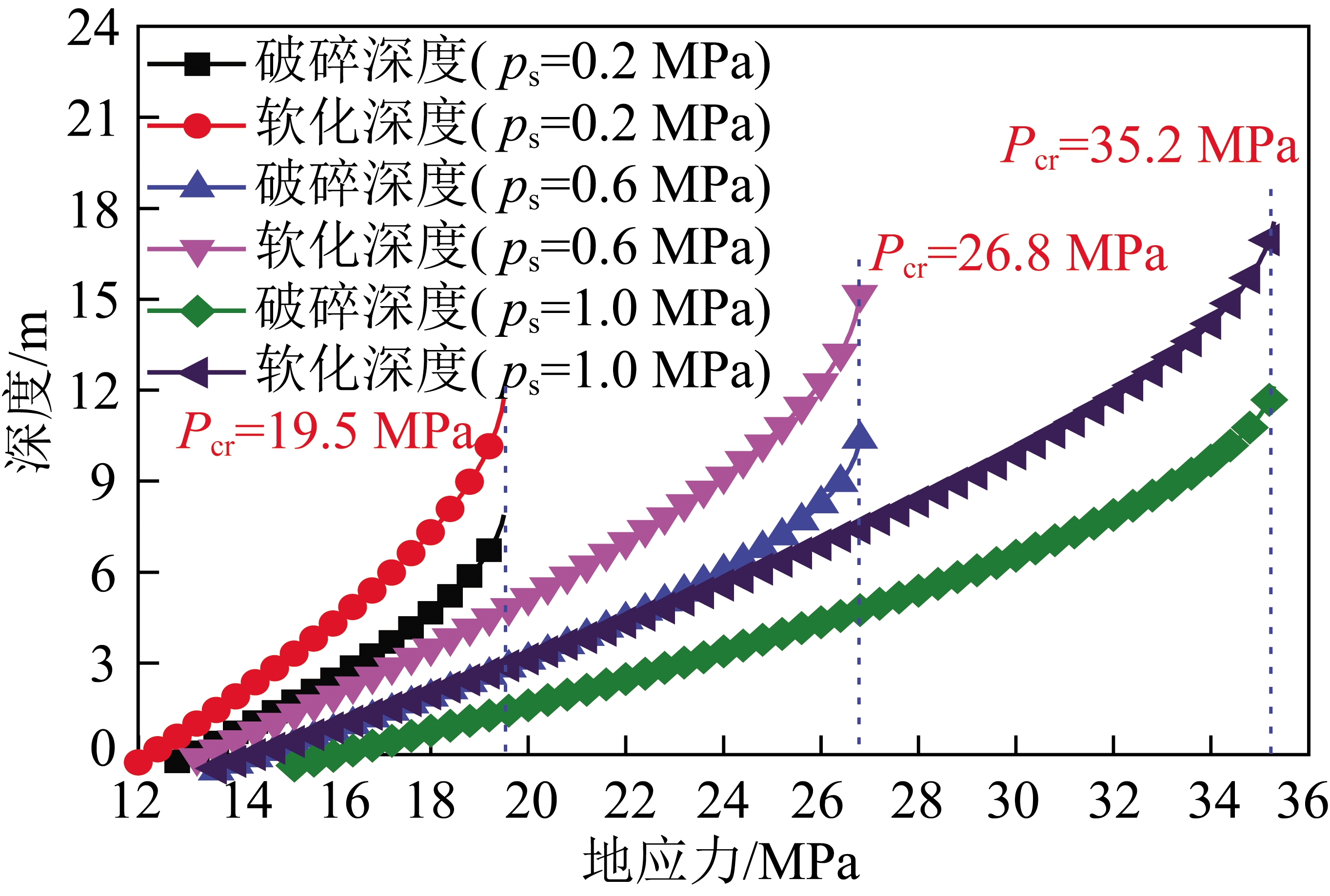
图8 支护对巷道围岩软化区与破碎区扩展的影响[23]
Fig.8 Influence of support on softening or fracture zone expansion of roadway surrounding rock[23]
为进一步直观阐明支护对巷道冲击地压临界载荷的影响规律,由式(19),对临界载荷Pcr和支护应力ps做增量形式计算,得
![]()
(38)
式中,ΔPcr为冲击地压启动的临界载荷增量,MPa;Δps为支护应力增量,MPa。
由式(38)可知,巷道支护强度增加能够提升冲击地压启动的临界载荷,而提升程度将取决于围岩的冲击倾向特征。例如,当K=1时,当支护应力ps增加25%时,冲击地压启动的临界载荷将提升1倍。
7 冲击地压防治的安全系数
安全系数是工业设计中广泛应用的重要指标。然而,由于冲击地压领域中长期缺少冲击地压发生的临界条件理论计算公式,防冲安全系数一直未能被科学定义。
基于冲击地压发生的临界载荷理论公式(35),定义特定地应力P条件下巷道的防冲安全系数Ns:
![]()
(39)
重要的是,通过限定防冲安全系数Ns,可以有效实现巷道防冲支护强度的量化设计,从而达到防冲装备选型的目的,此方法称为防冲支护的安全系数设计法。采用此方法,核算我国部分煤矿巷道支护的防冲能力见表3。
表3 我国部分煤矿巷道支护的防冲能力定量核算
Table 3 Quantitative calculation of anti-impact ability of roadway support
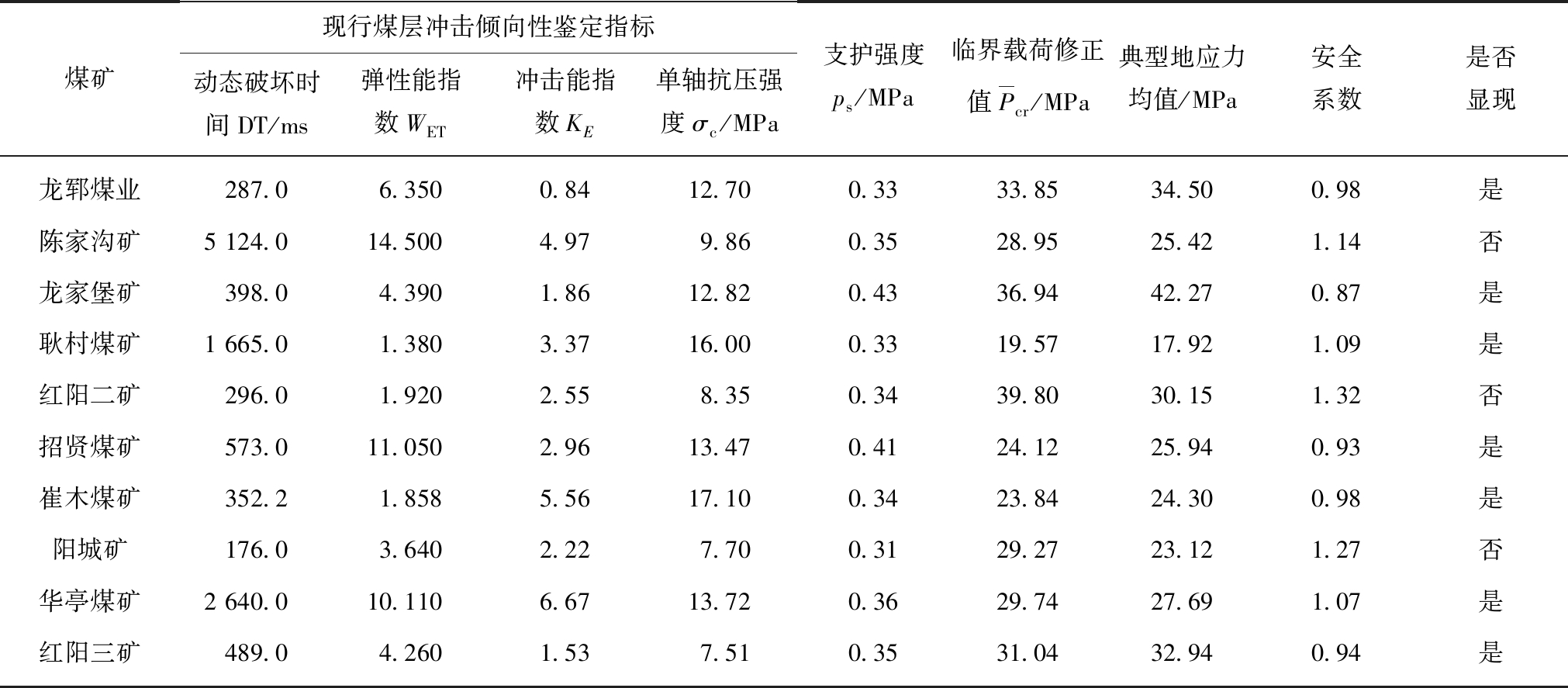
煤矿现行煤层冲击倾向性鉴定指标动态破坏时间DT/ms弹性能指数WET冲击能指数KE单轴抗压强度σc/MPa支护强度ps/MPa临界载荷修正值Pcr/MPa典型地应力均值/MPa安全系数是否显现龙郓煤业287.06.3500.8412.700.3333.8534.500.98是陈家沟矿5 124.014.5004.979.860.3528.9525.421.14否龙家堡矿398.04.3901.8612.820.4336.9442.270.87是耿村煤矿1 665.01.3803.3716.000.3319.5717.921.09是红阳二矿296.01.9202.558.350.3439.8030.151.32否招贤煤矿573.011.050 2.9613.470.4124.1225.940.93是崔木煤矿352.21.8585.5617.100.3423.8424.300.98是阳城矿176.03.6402.227.700.3129.2723.121.27否华亭煤矿2 640.010.1106.6713.720.3629.7427.691.07是红阳三矿489.04.2601.537.510.3531.0432.940.94是
8 结 论
(1)基于煤矿冲击地压发生的扰动响应失稳理论,构建了冲击地压发生的力学分析模型,给出了冲击地压发生临界指标及其理论公式,实现了冲击地压启动临界条件的定量计算,旨在深化推进煤矿冲击地压机理、评价、监测预警与防治工作向系统化、参数化与定量化方向发展。
(2)建立了与几何结构参数、环境载荷和煤岩物性参数直接相联系的冲击地压发生的力学分析模型。探究了解析分析涉及的几何模型、边界条件与煤岩本构方程,明确冲击地压力学判据及其物理意义,即表征冲击地压本质是围岩塑性区边界非线性增速失稳扩展及其带来的一系列的宏观响应。
(3)辩明了冲击倾向性与冲击危险性的理论关系。冲击倾向性表征对象为煤岩介质,而冲击危险性的表征对象为工程巷道(包括其他工程结构或区域);煤岩冲击倾向性是工程结构冲击危险性的主要影响因素之一,并明确巷道冲击危险性表征指标包括围岩临界软化区半径、临界破碎区半径和临界载荷。
(4)临界载荷是表征巷道在特定地应力环境中受扰发生冲击地压难易程度的最重要指标之一,也是冲击地压防治理论中应力控制论的理论基础。基于临界载荷的理论公式,提出了冲击地压发生的矿井临界开采深度的理论界定方法。
(5)基于冲击地压发生的理论公式,明确了支护强度增加不仅具有有效抑制围岩破碎发育速度的作用,还具有大幅提升冲击启动临界载荷的功能。由此,提出防冲支护的安全系数设计方法。
[1] COOK N G W,HOEK E,PRETORIUS J P G,et al.Rock mechanics applied to the study of rockbursts[J].Journal of the Southern African Institute of Mining and Metallurgy,1965,66(10):435-528.
[2] 佩图霍夫.煤矿冲击地压[M].北京:煤炭工业出版社,1980.
[3] LINKOV A M.Rockbursts and the instability of rock masses[J].International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts,1996,33(7):727-732.
[4] 姜耀东,潘一山,姜福兴,等.我国煤炭开采中的冲击地压机理和防治[J].煤炭学报,2014,39(2):205-213.
JIANG Yaodong,PAN Yishan,JIANG Fuxing,et al.State of the art review on mechanism and prevention of coal bumps in China[J].Journal of China Coal Society,2014,39(2):205-213.
[5] 潘一山,李忠华,章梦涛.我国冲击地压分布、类型、机理及防治研究[J].岩石力学与工程学报,2003,22(11):1844-1851.
PAN Yishan,LI Zhonghua,ZHANG Mengtao.Distribution,type,mechanism and prevention of rockburst in China[J].Chinese Journal of Rock Mechanics and Engineering,2003,22(11):1844-1851.
[6] 潘一山,肖永惠,李忠华,等.冲击地压矿井巷道支护理论研究及应用[J].煤炭学报,2014,39(2):222-228.
PAN Yishan,XIAO Yonghui,LI Zhonghua,et al.Study of tunnel support theory of rockburst in coal mine and its application[J].Journal of China Coal Society,2014,39(2):222-228.
[7] 齐庆新,欧阳振华,赵善坤,等.我国冲击地压矿井类型及防治方法研究[J].煤炭科学技术,2014,42(10):1-5.
QI Qingxin,OUYANG Zhenhua,ZHAO Shankun,et al.Study on types of rock burst mine and prevention methods in China[J].Coal Science and Technology,2014,42(10):1-5.
[8] 齐庆新,李一哲,赵善坤,等.我国煤矿冲击地压发展 70 年:理论与技术体系的建立与思考[J].煤炭科学技术,2019,47(9):1-40.
QI Qingxin,LI Yizhe,ZHAO Shankun,et al.Seventy years development of coal mine rockburst in China:Establishment and consideration of theory and technology system[J].Coal Science and Technology,2019,47(9):1-40.
[9] 章梦涛.冲击地压失稳理论与数值模拟计算[J].岩石力学与工程学报,1987,6(3):197-204.
ZHANG Mengtao.Instability theory and mathematical model for coal/rock bursts[J].Chinese Journal of Rock Mechanics and Engineering,1987,6(3):197-204.
[10] 章梦涛.冲击地压机理的探讨[J].阜新矿业学院学报,1985(S1):65-72.
ZHANG Mengtao.Study of rockburst mechanism[J].Fuxin Ming Institute,1985(S1):65-72.
[11] 齐庆新,史元伟,刘天泉.冲击地压粘滑失稳机理的实验研究[J].煤炭学报,1997,22(2):144-147.
QI Qingxin,SHI Yuanwei,LIU Tianquan.Mechanism of instability caused by viscous sliding in rock burst[J].Journal of China Coal Society,1997,22(2):144-147.
[12] 潘俊锋,宁宇,毛德兵,等.煤矿开采冲击地压启动理论[J].岩石力学与工程学报,2012,31(3):586-596.
PAN Junfeng,NING Yu,MAO Debing,et al.Theory of rockburst start-up during coal mining[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(3):586-596.
[13] 潘一山.煤矿冲击地压扰动响应失稳理论及应用[J].煤炭学报,2018,43(8):2091-2098.
PAN Yishan.Disturbance response instability theory of rock burst in coal mine[J].Journal of China Coal Society,2018,43(8):2091-2098.
[14] 潘立友,蒋宇静,李兴伟,等.煤层冲击地压的扩容理论[J].岩石力学与工程学报,2002,21(S1):2301-2303.
PAN Liyou,JIANG Yujing,LI Xingwei,et al.Dilatation theory of rock burst[J].Chinese Journal of Rock Mechanics and Engineering,2002,21(S1):2301-2303.
[15] 窦林名,陆菜平,牟宗龙,等.冲击矿压的强度弱化减冲理论及其应用[J].煤炭学报,2005,30(6):690-694.
DOU Linming,LU Caiping,MOU Zonglong,et al.Intensity weakening theory for rockburst and its application[J].Journal of China Coal Society,2005,30(6):690-694.
[16] 谢和平,PARISEAU W G.岩爆的分形特征及机理[J].岩石力学与工程学报,1993,12(1):28-37.
XIE Heping,PARISEAU W G.Fractal character and mechanism of rock bursts[J].Chinese Journal of Rock Mechanics and Engineering,1993,12(1):28-37.
[17] 唐春安.岩石破裂过程中的灾变[M].北京:煤炭工业出版社,1993.
[18] 冯夏庭,陈炳瑞,张传庆,等.岩爆孕育过程的机制、预警与动态调控[M].北京:科学出版社,2013.
[19] 潘一山.煤矿冲击地压[M].北京:科学出版社,2018.
[20] DAI Lianpeng,PAN Yishan,WANG Aiwen,et al.Experimental study on the self-protection performance of anchor bolts with energy-absorbing tails[J].Rock Mechanics and Rock Engineering,2020,53:2249-2263.
[21] 于学馥,郑颖人,刘怀恒,等.地下工程围岩稳定分析[M].北京:煤炭工业出版社,1983.
[22] 蒋斌松,张强,贺永年,等.深部圆形巷道破裂围岩的弹塑性分析[J].岩石力学与工程学报,2007,26(5):982-986.
JIANG Binsong,ZHANG Qiang,HE Yongnian,et al.Elastoplastic analysis of cracked surrounding rocks in deep circular openings[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(5):982-986.
[23] 潘一山,代连朋,李国臻,等.煤矿冲击地压与冒顶复合灾害研究[J].煤炭学报,2021,46(1):112-122.
PAN Yishan,DAI Lianpeng,LI Guozhen,et al.Study on compound disaster of rock burst and roof falling in coal mines[J].Journal of China Coal Society,2021,46(1):112-122.
[24] DAI Lianpeng,PAN Yishan,LI Zhonghua,et al.Quantitative mechanism of roadway rockbursts in deep extra-thick coal seams:Theory and case histories[J/OL].Tunnelling and Underground Space Technology,2021,1-14,https://doi.org/10.1016/j.tust.2021.103861.
[25] HOEK E,BROWN E T.Underground excavations in Rock[M].Abingdon:Taylor & Francis,1990.
[26] HOEK E,MARINOS P G.Tunnelling in overstressed rock[A].Proceedings of Rock Engineering in Difficult Ground Conditions-Soft Rocks and Karst-Vrkljan[C].London:Taylor and Francis Group,2010:49-60.
[27] 齐庆新,彭永伟,李宏艳,等.煤岩冲击倾向性研究[J].岩石力学与工程学报,2011,30(S1):2736-2742.
QI Qingxin,PENG Yongwei,LI Hongyan,et al.Study of bursting liability of coal and rock[J].Chinese Journal of Rock Mechanics and Engineering,2011,30(S1):2736-2742.
[28] GB/T 25217.2—2010.冲击地压测定、监测与防治方法.第2部分:煤的冲击倾向性分类及指数的测定方法[S].
