页岩储层低孔低渗,开采过程中需要大规模水力压裂,而地应力是指导储层压裂施工的必要参数,对提高压裂施工效果具有重要作用[1]。因此地应力的研究受到国内外学者广泛关注。最初认为地层沉积过程中只产生垂向变形,水平方向的变形受到限制,地应力为水平、垂直方向,且为上覆岩层的分量,两者满足线性关系,TALOBRE等认为2个应力分量相等,TERZAGHI和RICHART认为地应力分量大小的比值为地层泊松比的数学式[2],此外基于这种单轴应变还提出了尼克经验公式、Mattews&Kelly经验公式、Anderson经验公式,New-berry经验公式等[3-5],也有学者在单轴应变的基础上添加较正项来提高水平应力的精度[6-8],但该方法认为一个断块内是个常数,而实测数据表明不同深度的是不同的。随着认识深入,研究发现板块运动会造成地层在x方向发生水平变形,存在水平应力场,学者以弹性力学理论为基础,经过一定的假设条件和边界条件推演出各种地应力模型,如摩尔库伦应力模型法,压实模型等[9-11],这些模型采用实验方法获取力学特征,实验数据工作量大,不能获取连续地应力剖面。为了获取连续的地应力剖面,开始采用测井资料计算地层应力[12-14],该方法应用密度测井积分估算垂直应力,然后根据地层特点选择适当的模型计算水平地层压力,如多孔弹性水平应变模型法,双轴应变模型法,黄氏模型,组合弹簧经验公式等[15-18]。这些模型将岩石假设为各向同性的线弹性体,沉积和构造过程中不发生相对位移。在各向异性地层应力研究中,LEKHNITSKII[19]首先提出了考虑各向异性影响的孔洞周边应力集中的解析方法,AMADEI等[20]在该解析方法的基础上推导出横向各向同性和正交各向异性地层的计算地应力方法,邓金银,王越之等[21-22]也推导了基于横向各向同性模型的地应力计算公式,邹贤军[23]、田鹤[24]等利用测井资料获取了连续地应力剖面,但过程简单,未给出相关参数的计算方法。
针对上述问题,笔者理论推导页岩横向各向同性本构关系,给出各弹性系数的计算公式,并结合现场水力压裂资料反演构造应变系数,最终建立页岩储层地应力测井评价方法。该方法不仅可以获取连续的地应力剖面,而且采用实验求解和现场反演方式明确和简化参数的求解过程,避免了参数计算方法模糊,求解难的问题。
1 区域地质概况
渝东南地区位于重庆地区东南部和四川盆地的东部,南与黔北交接,东与湘西为邻。该地区属于上杨子板块前陆盆地,位于川中隆起与黔中隆起之间,是上杨子板块的重要组成部分。该地区构造活动强烈,地层剥蚀严重。从北西到南东方向表现为隔挡式褶皱向隔槽式褶皱的渐变,是由盖层滑脱带向冲褶带的渐变过渡区。渝东南地区古生代主要沉积海相地层,其中下古生界地层出露最完整,上古生界地层发育不完整,部分地层缺失,中生界和第四系覆盖于老地层之上。由于受加里东晚期构造运动影响,在早志留世,渝东南地区受到东南方向的挤压应力作用,地层不断抬升,因此形成了中、下志留系统和泥盆系或石炭系之间的假整合接触。其后,经历多次构造运动改造,形成现今构造格局。研究区位于渝东南部黔江地区,构造上地处武陵—湘鄂西“槽~挡”过渡区,构造形态以NE 向复向斜和复背斜相间分布为主。3组相对紧闭的背斜带间夹3组核部宽缓而翼部相对陡立的向斜带,呈NNE 向展布,同时在背斜构造发育一系列NNE 向或近NW 向断裂构造。区内断层发育,主要断裂走向与褶皱轴线基本一致,走向北东、断面倾向北西;以与褶皱伴生的、大致呈北北东向的断层为主,其次为一些规模较大的与褶皱无关的北北东—北东向的正断层。大断层有王家湾冲断层和鹰家坝冲断层。
如图1所示,区内发育的主要构造单元有桐麻园背斜、咸丰背斜、铜西向斜、宜居背斜、濯河坝向斜、天馆背斜、龚滩向斜等。区内向斜构造相对宽缓,有利于页岩气保存成藏。研究区较完整地发育震旦系—三叠系海相地层,但区块范围内地表出露最老地层为中上寒武统,震旦系—下寒武统地层仅在邻区西北彭水老厂坪背斜及南部秀山鸡公岭背斜一带局部出露。上奥陶统五峰组—下志留统龙马溪组地层沿濯河坝等向斜翼部出露。根据区域地质调查及QD1,QD2,QQ1 井钻探揭示,本区自上而下主要发育第四系,三叠系嘉陵江组、大冶组,二叠系长兴组—梁山组,泥盆系水车坪组,下志留统小河坝组、新滩组、龙马溪组及上奥陶统五峰组、临湘组,中奥陶统宝塔组等地层。

图1 区域构造纲要
Fig.1 Outline of regional structure
2 页岩地层地应力计算
地层的各向异性常分为三斜各向异性,单斜各向异性,正交各向异性和横向各向同性等4类,其中大多数的各向异性利用TI模型进行模拟,该模型认为存在一条对称轴,即在垂直介质对称轴的面上,各个方向的物理性质相同,与沿着对称轴方向上的物理性质不同。页岩在地层构造和埋深条件下,呈低孔低渗特征,且具有良好的分层结构,呈横向各向同性特征,可利用TI地层模拟。通过电镜扫描和声力学试验,页岩内部裂纹平行排列,水平裂缝和层理面导致其水平和垂直方向的物理性质不同,因此,页岩具有垂直对称轴的横向各向同性,为典型的VTI地层。
笔者从广义Hooke定律出发,描述页岩的应力应变关系:
tij=Cijklekl (i,j,k,l=1,2,3)
(1)
式中,tij为应力张量分量形式;Cijkl为表征物质特性的4阶刚度张量分量;ekl为应变张量的分量形式。
Cijkl有34=81个分量,可根据广义的4阶张量的多个对称关系来减少刚度矩阵中独立元素的个数。根据应力应变张量的对称关系和从热力学角度考虑:
Cijkl=Cjikl,Cijkl=Cijlk,Cijkl=Cklij
(2)
接下来,利用Voigt法,将每对下角标用单个下角标代替。具体为:11转换为1,22转换为2,33转换为3,23转换为4,13转换为5,12转换为6。将Cijkl转换为6×6的矩阵来表示,这样可将介质简化为21个刚度元素,但是,这表征的是极度各向异性的弹性矩阵所需的独立常数个数。页岩为各向同性岩石的周期性薄层所构成的地下岩石,由于波长远大于地层的厚度,可等价于具有垂向对称轴的横向各向同性介质,对应的独立变量个数为5个,具体的弹性系数矩阵为
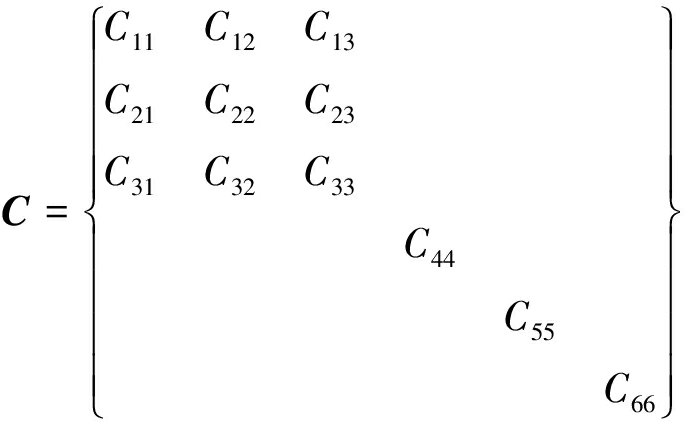
(3)
对于直井:
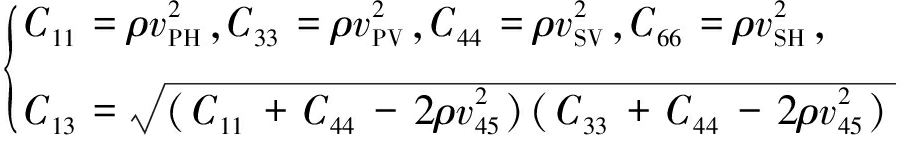
(4)
式中,ρ为密度,g/cm3; vPH和vPV分别为水平方向和垂直方向的纵波波速,m/s;vSH和vSV分别为水平方向和垂直方向的横波波速,m/s;v45为与地层对称轴成45°的纵波波速,m/s。
利用横向各向同性模型计算地应力需要确定5个弹性参数,C33和C44通过测井的纵横波速度直接求取,C66通过斯通利波资料反演得到。若想表征横向各向同性地层的弹性性质还需要一定的假设条件确定C11和C13两个参数。SUAREZ-RIVERA针对页岩的横向各向同性特征提出了改进的MANNE模型,关系式为
![]()
(5)
式中,K1,K2为经验参数,通过岩芯的超声波测试获取。
模型中,K1,K2两个参数值是岩芯实验所测量得到的定值,采用渝东南龙马溪组岩芯实验数据测量如图2所示,得到最佳拟合公式为

图2 龙马溪组页岩样品刚度系数统计关系
Fig.2 Statistical relationship of the stiffness coefficient of
Longmaxi shale samples
![]()
(6)
求取横向各向同性地层的弹性系数后,即可获得垂直和水平方向的弹性模量(Ev,Eh)与泊松比(νv,νh)。

(7)
地层的水平应力主要由上部岩层重力和地质构造运动共同作用产生,对于水平层理面地层提出了基于页岩横向各向同性关系的地应力计算模型:
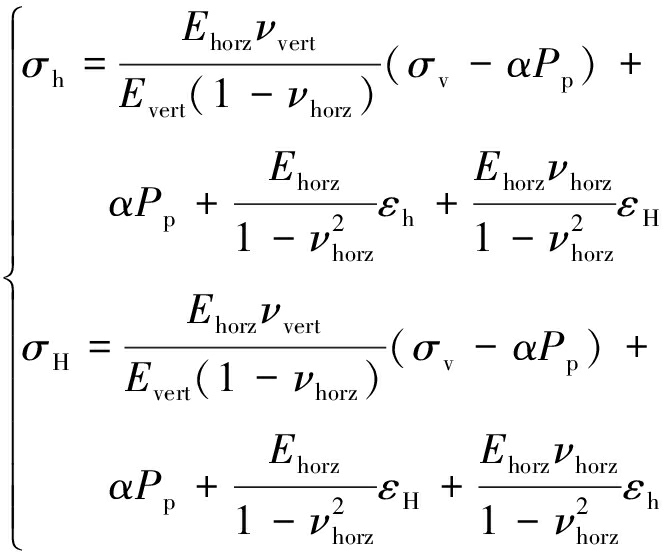
(8)
式中,σh,σH为最小和最大水平主应力,MPa;Evert,Ehorz为横向各向同性模型的竖直和水平方向的静态弹性模量,MPa;νvert,νhorz为横向各向同性模型的竖直和水平方向的静态泊松比;σv为上覆压力,MPa;α为孔隙弹性系数;Pp为地层孔隙压力,MPa;εH,εh分别为水平最大、最小构造应变系数。
天然页岩地层一般斜层理面发育,地层倾角会引起垂向应力的水平分量发生改变,因此,考虑地层倾角的影响十分必要。多孔介质有效应力理论认为,页岩各向异性只影响到骨架应力,不会对孔隙压力造成影响,但直接引入地层倾角计算,不仅会使垂向应力对水平地应力的分量计算复杂,而且还需要将斜率坐标中的柔度矩阵转换到水平坐标系中,再根据逆矩阵关系计算弹性系数,给实际应用带来不便。笔者为考虑模型的实际适用性,引入侧压系数描述地层倾角对地应力的影响,得到适用于任意地层倾角地层水平地应力的计算模型。

(9)
式中,k为地层侧压系数。
3 页岩岩石力学实验
3.1 页岩巴西破裂实验
实验室内采用巴西劈裂法测定岩石抗拉强度,将压裂深度对应的井下岩芯切成直径50 mm,厚度为25 mm的圆盘形试样,并置于岩石力学试验机,沿着圆柱体直径方向施加集中载荷,试件受力后会沿着受力的直径方向裂开,岩石抗拉强度σt的计算公式为
![]()
(10)
式中,pmax为岩石破坏时的最大压力,kN;D为岩石试件的直径,mm;L为岩石试件的长度,mm。
页岩抗张强度分布在2.84~10.49 MPa,平均为5.38 MPa,抗张强度整体较强。在不同层理方向上具有明显的离散性,充分说明了页岩力学性质的各向异性。同时,从试验结果(图3)来看,除了个别岩样,其他劈裂试验的断口方向与层理方向基本吻合,进一步表明该地区页岩的抗张特性具有层理方向性效应。尽管本地区页岩的抗拉强度具有一定的各向异性,但在层理倾角变化的各个方向中,页岩抗拉强度远小于抗压强度,这表明渝东南下志留统龙马溪组页岩在负载不大时极易出现拉伸破坏。

图3 页岩抗张实验结果
Fig.3 Shale tensile experiment results
3.2 页岩三轴抗压试验
利用邻井压裂施工曲线求取构造应变系数需要相应的弹性模量、泊松比等参数,计算邻井压裂层位在原地条件下的净围压约为35 MPa,该井3 400 m深度处的围压为50 MPa,为此,笔者利用MTS-815型三轴岩石力学测试系统,完成垂直层理和水平层理方向试样0,35,50 MPa的三轴实验,得到对应围压下的弹性模量、泊松比、内摩擦角和黏聚力等。试验时每个围压至少成功3个试样,具体步骤如下,试样用密封套密封后,在两端机上压头,然后向试样施加围压达到预设定值,在保持围压不变的条件下向试样施加轴向压力直至破坏,实验过程中计算机软件自动采集数据。50 MPa条件下试样的三轴应力-应变曲线如图4所示,由图4可以看到,页岩总体呈脆性破坏特征,所测试岩样的弹性模量在16~32 GPa,垂直方向上的弹性模量大于水平方向的弹性模量,泊松比分布在0.1~0.3。

图4 垂直和水平层理方向页岩在50 MPa围压下3个重复样的三轴试验
Fig.4 Triaxial test of vertical and horizontal bedding shale under 50 MPa confining pressure (three replicate samples)
3.3 页岩声发射试验
岩石声发射实验是准确获得地应力的常规手段,为了测定岩样在地下所受3个主地应力,在井下岩芯垂直和3个各相隔45°角的水平方向取芯,加工成标准试样,然后利用MTS-815岩石力学试验和美国生产的声发射测试仪完成岩芯的岩石力学测试和声发射实验,将该4个岩芯在地下所受的正压力(图5)代入式(11)求得试样在地下所受的地应力:

图5 页岩声发射测试结果
Fig.5 Shale acoustic emission test results
![]()
(11)
式中,σx为0°岩芯Kaiser点应力;σy为90°岩芯Kaiser点应力;σxy为45°岩芯Kaiser点应力;θ为最大水平主应力方位角。
根据各岩芯的凯塞尔效应测试结果,估算得到岩芯对应取芯深度处的水平最大、最小主应力见表1。
表1 页岩声发射实验结果
Table 1 Shale acoustic emission experiment results

编号深度/m水平最大主应力取值/MPa梯度/(MPa·hm-1)水平最小主应力取值/MPa梯度/(MPa·hm-1)第1组2 72063.232.3752.881.84第2组3 15078.712.2860.231.91第3组3 40380.942.4064.891.90
4 参数计算
4.1 动静力学参数
岩石的动态弹性模量是指岩石在各种动载荷或周期变化载荷(如声波、冲击、震动等)作用下所表现出的力学性质参数,可以由声速测量、测井或地震资料给出,静态弹性模量则是在静载荷作用下岩石表现出的力学参数,需要在实验室进行测量。而井眼的变形和破坏属于相对较慢的静态过程,因此在利用测井资料进行岩石力学评价研究时必须进行力学参数的动、静态转换。该工区动静弹性模量的关系如图6所示,由图6可以看出,垂直和水平方向的动态弹性模量均大于静态弹性模量,垂直方向的弹性模量总体略大于水平方向的弹性模量,而本地区泊松比变化不大,且无共性规律,采用平均值计算。

图6 动、静力学参数转换关系
Fig.6 Conversion relationship between dynamic and
static mechanics parameters
4.2 构造应变系数
水力压裂是目前进行深部应力原位测试最为有效的方法,也是深部最小水平主应力测试最直接的方法,在国内外得到了较为广泛的应用。从压裂施工压力曲线可获得压裂层段的破裂压力和闭合压力如图7所示。

图7 水力压裂压力典型曲线
Fig.7 Typical curve of hydraulic fracturing pressure
一般认为闭合压力等于水平最小主应力,根据水力压裂原理,水力裂缝产生时压力系统存在如下关系:
Pf=3σH2-σH1-αPp+St
(12)
式中,Pf为地层破裂压力,MPa;σH1和σH2分别为水平最小、最大主应力,MPa;St为地层抗张强度,MPa。
利用工区邻井水力压裂施工曲线(图8),得到压裂层段的破裂压力为60.1 MPa,水力压裂缝的闭合压力为44.8 MPa,利用上述方法得到最大主应力方向与最小主应力方向构造应变系数分别为4.618×10-4,3.978×10-5。

图8 水力压裂施工曲线
Fig.8 Construction curves of hydraulic fracturing
4.3 Biot系数
Biot系数是地层可压缩性、孔隙度与体积模量的函数,是一个非常重要的流体力学参数,决定地层有效应力的大小。笔者通过声波测井资料确定Biot系数:
![]()
(13)
其中,α1为Biot系数;ρb,ρm分别为地层和岩石骨架密度,g/cm3;vP,vS分别为地层的纵横波波速,m/s;vmP,vmS分别为岩石骨架的纵横波波速,m/s。测得的页岩参数为:ρm=2.65 g/cm3,vmP=5 950 m/s,vmS=3 000 m/s。
5 结果与验证
利用该模型计算渝东南某页岩气井的地应力,孔隙压力通过当前深度的静水压力乘以地区的经验系数1.2算得,得到地应力平面图和地应力剖面图(图9,10)所示。由图9,10可以看出,分析深度范围内弹性系数C44<C66,表明该页岩地层为VTI地层,呈现明显的各向异性特征,该井地应力整体较高,水平最大地应力梯度为2.14~2.79 MPa/hm,平均为2.45 MPa/hm,水平最小地应力梯度为1.68~2.17 MPa/hm,平均为1.95 MPa/hm。

图9 地应力
Fig.9 Ground stress

图10 地应力剖面
Fig.10 In-situ stress profile
选取本文模型、黄氏模型、组合弹簧模型计算3个深度点的地应力值并利用声发射实验值进行验证,计算对应模型的平均误差,结果见表2。由表2可知,利用黄氏模型计算的水平最小和最大主应力的平均误差分别为23.27%,38.54%,这是由于该模型未考虑水平变形引起的构造应力,组合弹簧模型考虑了水平变形产生的附加应力,其最大水平主应力的误差在22.88%,最小水平主应力的误差在16.23%左右,精确度较黄氏模型有了较为显著的提升,但是忽略了页岩的分层结构,将页岩地层当作各向同性介质处理,而实际页岩储层水平和垂直方向的弹性模量差异明显,因此该模型计算出的地应力误差也较大,且各向异性特征越明显层段的误差会越大,本文模型对地层最大、小地应力的预测最大误差都控制在7%以内,较之其他方法更接近于实测地应力数据,这是由于本模型没有简单的把页岩储层当作各向同性,而是从页岩的构造特征出发,理论推导了页岩的横观各向同性,更符合地层的实际情况。因此,本文建立的模型可用来进行页岩储层水平地应力的计算。
表2 模型对比及误差分析结果
Table 2 Model comparison and error analysis results

井深/m黄氏模型σh/MPaσH/MPa组合弹簧模型σh/MPaσH/MPa本文模型σh/MPaσH/MPa2 72039.5739.5942.0246.5752.0067.113 15046.7846.8152.2862.9563.7285.883 40350.3850.4054.8462.8966.5885.09平均误差/%23.2738.5416.2322.886.793.35
6 结 论
(1)岩样的抗拉强度分布在2.87~10.49 MPa内,随着层理倾角的变化,抗张和单轴抗压特性都表现出较强的离散性,页岩层理发育对岩石力学性质影响较大,建议在该地区页岩气钻井、压裂改造的设计中应充分考虑页岩力学特征的各向异性。
(2)渝东南页岩地层的动态弹性模量大于静态弹性模量,垂直方向的弹性模量大于水平层理方向的弹性模量,对泊松比而言,垂向泊松比与水平泊松比整体差异不大,无明显规律。
(3)建立了符合页岩特性的地应力评价模型,计算结果与岩石声发射的测量结果的相对误差均小于7%,平均为5.07%,与传统的地应力模型相比,横向各向同性的地应力模型能够更准确的反应页岩储层的实际情况。
[1] 张广智,陈娇娇,陈怀震,等.基于页岩岩石物理等效模型的地应力预测方法研究[J].地球物理学报,2015,58(6):2112-2122.
ZHANG Guangzhi,CHEN Jiaojiao,CHEN Huaizhen,et al.Prediction for in-situ formation stress of shale based on rock physics equivalent model[J].China Journal of Geophysics,2015,58(6):2112-2122.
[2] 王志刚.基于优化方法的地应力与套管承载规律研究[D].青岛:中国石油大学,2009.
WANG Zhigang.Research on in-situ stress based on optimum technique and bearing law of casing pipe[D].Qingdao:China University of Petroleum,2009.
[3] FAN Xiangyu,GONG Ming,ZHANG Qiangui,et al.Prediction of the horizontal stress of the tight sandstone formation in eastern Sulige of China[J].Journal of Petroleum Science and Engineering,2014 (113):72-80.
[4] TUTUNCU A N,PODIO A L SHARMA M M.Effects of stress,frequency and clay content on compressional and shear velocities and attenuations in tight gas sandstones[J].Geophysics,1992,46:49-56.
[5] STEPHEN Prensky.Borehole Breakouts and In-situ Rock Stress-A Review[J].The Log Analyst,1992.
[6] COX J W.The High Resolution DIPeeter reveals diP-related borehole and formation characteristics[A].PaPerD,In 1lth Annual Logging Symposium Transactions:Soeiety of Professional Well Log Analysts[C].1970.
[7] KAVANAGH K T,CLOUGH R W.Finite element application in the characterization of elastic solids[J].Int J Solids Structures,1972(7):11-23.
[8] JIZBA D,NUR A.Static and dynamic moduli of tight gas sandstones and their relationship to formation properties[A].SPWLA 31st Annual Logging Symposium[C].Lafayette LA,1990:1-21.
[9] DURHUUS J,AADNOY B S.In situ stress from inversion of fracturing data from oil wells and bore hole image logs[J].Journal of Petroleum Science and Engineering,2003,38(3):121-130.
[10] 赵军龙,孙鹏,蔡振东,等.鄂尔多斯盆地Z区长8超低渗透率储层地应力特征研究[J].测井技术,2015,39(1):72-77.
ZHAO Junlong,SUN Peng,CAI Zhendong,et al.Characteristics of geostress in ultra-low permeability reservoirs in Chang 8 of Z Area in Ordos Basin[J].WLT,2015,39(1):72-77.
[11] 马建海,孙建孟.用测井资料计算地层应力[J].测井技术,2002,26(4):347-352.
MA Jianhai,SUN Jianmeng.Calculation of formation stress using logging data[J].WLT,2002,26(4):347-352.
[12] 刘之的,夏宏泉,汤小燕,等.成像测井资料在地应力计算中的应用[J].西南石油大学学报(自然科学版),2005,27(4):9-12.
LIU Zhidi,XIA Hongquan,TANG Xiaoyan,et al.Journal of southwest petroleum institute[J].Journal of Southwest Petroleum University:Science & Technology Edition,2005,27(4):9-12.
[13] 范翔宇,康海涛,龚明,等.川东北山前高陡构造地应力精细计算方法[J].西南石油大学学报,2012,34(3):41-46.
FAN Xiangyu,KANG Haitao,GONG Ming,et al.Fine calculation method study of crustal stress of high-steep conformation in Northeast Sichuan[J].Journal of Southwest Petroleum University:Science & Technology Edition,2012,34(3):41-46.
[14] 郑莲慧,单钰铭,蒋晓红,等.ADS法在深层致密砂岩储层地应力计算中的应用[J].天然气技术与经济,2014(4):21-24.
ZHENG Lianhui,SHAN Yuming,JIANG Xiaohong,et al.ADS method to calculate geo stress in deep and tight sandstone reservoirs[J].Coiled-tubing Drilling Technology,2014(4):21-24.
[15] 侯明勋,葛修润.三维地应力计算模型研究[J].岩土力学,2007,28(10):2017-2021.
HOU Mingxun,GE Xiurun.Study on fitting analysis od initial stress field in rock masses[J].Rock and Soil Mechanics,2007,28(10):2017-2021.
[16] 杨宇,汪三谷,郭春华,等.川西低渗气藏单井地应力计算方法综合研究[J].天然气工业,2006,26(4):32-34.
YANG Yu,WANG Sangu,GUO Chunhua,et al.Comprehensive study on the stress calculation method of single well in low permeability gas reservoir in West Sichuan[J].Natural Gas Industry,2006,26(4):32-34.
[17] 黄荣樽.地层破裂压力预测模式的探讨[J].华东石油学院学报,1984(4):335-347.
HUANG Rongzun.A modelfor predicting formation fracture pressure[J].Journal of the University of Petroleum,China,1984(4):335-347.
[18] 马天寿.页岩气水平井井眼坍塌失稳机理研究[D].成都:西南石油大学,2015.
MA Tianshou.Research on the mechanisms of borehole collapse instability for horizontal wells in shale gas reservoirs[D].Chengdu:Southwest Petroleum University,2015.
[19] LEKHNITSKII S G.Theory of elasticity of an anisotropic body[M].Moscow:MIR Publishers,1963.
[20] AMADEL B.Rock anisotropy and the theory of stress measurements[M].Springer Verlag,1983.
[21] 邓金根,陈峥嵘,耿亚楠,等.页岩储层地应力预测模型的建立和求解[J].中国石油大学学报:自然科学版,2013,37(6):59-64.
DENG Jingen,CHEN Zhengrong,GENG Yanan,et al.Prediction model for in-situ formation stress in shale reservoirs[J].Journal of China University of Petroleum (Edition of Natural Sciences),2013,37(6):59-64.
[22] 王越之.各向异性地层应力的推算及深孔地层破裂压力的预测[J].岩石力学与工程学报,1998,17(3):322-329.
WANG Yuezhi.Determination of in-situ stresses in anisotropic strata and prediction of breakdown pressure acting on deep well-wall[J].Chinese Journal of Rock Mechanics and Engineering,1998,17(3):322-329.
[23] 邹贤军,陈亚琳.四川盆地涪陵地区龙马溪组页岩横向各向同性地应力测井评价方法[J].天然气地球科学,2018,29(12):1775-1780,1808.
ZOU Xianjun,CHEN Yalin.Geostress logging evaluation method of Longmaxi Formation shale in Fuling area based on transversely isotropic model,Sichuan Basin[J].Natural Gas Geoscience,2018,29(12):1775-1780,1808.
[24] 田鹤,曾联波,舒志国,等.页岩横向各向同性地应力预测模型中弹性参数的确定方法[J].地质力学学报,2019,25(2):166-176.
TIAN He,ZENG Lianbo,SHU Zhiguo,et al.Method for determining elastic parameters for the prediction model of shale transversely isotropic geostress[J].Journal of Geomechanics,2019,25(2):166-176.
