将矿井发生巷道冒落变形、风门开关或者破损、风机性能下降、巷道掘进延伸或者报废等引起通风系统风量发生异常变化的现象称为矿井通风系统阻变型故障[1]。故障发生后通风系统风量和通风阻力分布将发生变化，文献[1]从数值模拟实验和现场试验方面证明，根据通风系统风量的监测值可以利用SVM[2]、GA[3]等人工智能的方法诊断发生矿井通风系统阻变型故障的位置及故障量。研究表明风量监测点的数量越多，监测点的位置越合理故障诊断准确度就越高。巷道的风量是根据风速传感器监测值间接获得的。根据速度场结构近似恒定原理，可以将单点时均风速线性转换为断面平均风速，进而根据巷道的断面积求解出巷道的风量[4]。由于监测系统本身的技术原因以及经济原因，在所有巷道安设传感器是不适宜的。由此引出的问题是:如何合理地布置最少数量的风速传感器，达到满足实际需求的故障位置及故障量诊断的准确度。笔者提出了不需先验知识的基于邻域粗糙集属性约简算法(NRS)[5]的风速传感器安设位置优化方法，并通过实际煤矿的仿真实验及金属矿山的现场工业试验对此方法进行了验证。

在传感器位置优化方面，由于矿井温度、瓦斯含量对改善生产环境，降低事故率有重要意义[6-7]，因此针对瓦斯传感器、火源位置探测器安设位置的研究较多，针对风速传感器位置优化的研究较少。文献[8]利用分区法确定矿井火灾传感器的全局位置，初步实现了监测矿井火灾传感器的优化布置。文献[9-10]提出了瓦斯传感器的宏观布点方法。文献[11]根据灵敏度确定风速传感器的安设位置。文献[12]提出了一种基于列约简、禁忌搜索和Pareto蚁群算法的三阶段混合Pareto蚁群算法的甲烷传感器优化布置模型。文献[13]提出根据监测数据对传感器的位置实时调节的方法。在水管网、输油管道、燃气管道等复杂管网领域，对泄漏点诊断、监测点优化布置等有较多研究[14-25]。

在粗糙集约简方法中，将大量的条件属性约简成部分条件属性，利用最少的数据特征达到和原始数据相同甚至更高的分类能力，风速传感器安设位置优化的核心是从所有分支中确定出对矿井通风系统阻变型故障监测最重要的分支，因此将粗糙集应用于风速传感器的安设位置优化。但是经典粗糙集理论只能解决离散型数据，为了改进这一缺陷提出的邻域粗糙集算法可以直接解决数值型数据，避免了离散化造成的数据损失[26]。

矿井通风系统阻变型故障诊断包括2个方面:一是故障位置诊断;二是故障量诊断。利用矿井通风仿真系统MVSS[27]模拟故障仿真样本构建邻域粗糙集决策表进行属性约简，得到重要度大的条件属性的约简集合，亦即安设传感器的分支位置，最后利用SVM进行故障诊断，验证该方法的有效性。

1 通风系统阻变型故障诊断与传感器位置优化模型

1.1 通风系统阻变型故障诊断模型

矿井通风网络G=(V,E)中，其中V为节点集合，V={V1,V2,…,Vm}，节点数m=|V|;E为分支集合，E={e1,e2,…,en}，分支数n=|E|，分支对应的风量、风阻、阻力向量记为

(1)

已知风阻求风量的网络解算为

Q=f(R)

(2)

理论上，矿井同一时刻发生多个故障的可能性是有的，但发生的几率非常低，所以本文仅考虑单故障源问题[1]，将实际故障分支记为ef，风阻变化量(故障量)记为Δrf，故障发生后故障分支的风阻记为rf，且rf=r0+Δrf，r0为故障分支的原始风阻。将故障后通风网络的风阻向量R′=(r1,r2,…,rf,…,rn)代入式(2)计算得到故障后通风网络的风量向量为Q′=(q′1,q′2，…,q′f,…,q′n)。所谓基于风量特征的故障诊断，就是根据故障后的风量Q′,判断阻变型故障位置ei以及故障量Δri的过程，可以看作是网络解算的逆过程，写成公式如下:

(3)

式中，Δr′f为诊断故障量;e′f为诊断故障位置。

1.2 风速传感器位置优化模型

矿井安设风速传感器的分支集合记为Es，Es∈E，传感器数量为ns=|Es|，风速传感器监测的风量集合记为Q′s，Q′s∈Q′。所谓传感器安设位置优化，即用最少数量的传感器监测风量，使得诊断故障位置e′f与实际故障位置ef、诊断故障量Δr′f与实际故障量Δrf误差最小，传感器位置优化模型可以写成:

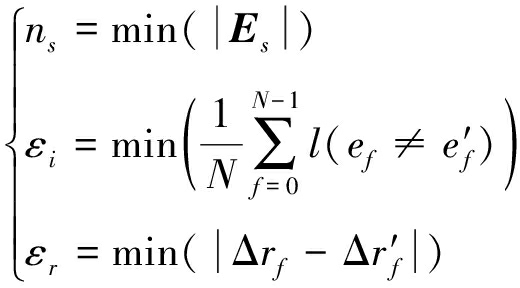
(4)

式中,εi为故障位置诊断误差;εr为故障量诊断误差;l(x)为指示函数，即

(5)

2 基于邻域粗糙集的风速传感器位置优化方法

假设矿井通风系统共发生p次阻变型故障，第k次故障的故障位置为故障量为此时通风网络的风量向量为这3者的集合构成一个故障样本xk。故障分支ef累计p次故障组成的风量列向量为为一个条件属性;通风网络全部n条分支累计p次故障的风量列向量集合构成总的条件属性Qp×n。P次故障位置构成的列向量记为故障量构成的列向量记为故障位置和故障量的集合构成决策属性，记为Ef∪ΔRf。

将故障位置、故障量、故障风量统称为故障参数，所有故障参数构成矿井通风系统阻变型故障决策表[28]，见表1。

其中，U={x1,x2,…,xp-1,xp}为论域，即故障样本的集合。矿井通风系统阻变型故障决策表可以表示为

NDT=〈U,Qp×n∪(Ef∪ΔRf),Γ,φ〉

(6)

式中，为各属性值的集合;φ=U×(Qp×n∪Ef∪ΔRf)→Γ，为样本xp属性值的映射函数。

设Qw为任意w组条件属性的集合，Qw⊆Qp×n，定义Qw相对于决策属性的重要度为

sig(Qw,Qp×n,Ef∪ΔRf)=γQp×n(Ef∪ΔRf)-

γQp×n-Qw(Ef∪ΔRf)

(7)

式中，γQw(Ef∪ΔRf)为Qw相对于决策属性的依赖度:

(8)

式中，POSQw(Ef∪ΔRf)为决策属性的下近似，也称为决策正域。

决策属性将论域U划分为N个等价类:X1,X2,…,XN，定义决策属性对Qw的下近似和上近似为

(9)

(10)

式中，

(11)

(12)

δ(x)为邻域信息粒子[26-27]，定义为

δ(xi)={xj|xj∈U,Δ(xi,xj)≤δ}

(13)

其中，δ为邻域半径，δ≥0，定义任一条件属性Qi的邻域半径[29]为

δ(Qi)=stdQi/λ

(14)

式中,stdQi为条件属性Qi的标准差;λ为需设定的参数，用于根据数据分类精度调整邻域大小。

任意条件属性集合Qw相对于决策属性的重要度是关于邻域半径中参数λ的一个复杂函数，定义为

sig(Qw,Qp×n,Ef∪ΔRf)=F(λ)

(15)

安设传感器分支的风量集合Q′s应满足:

(1)γQ′s(Ef∪ΔRf)=γQp×n(Ef∪ΔRf)，即安设传感器分支的风量和全部分支风量具有相同的分类能力。

(2)安设传感器分支的风量集合中无冗余，即∀Qi∈Q′s,γQ′s(Ef∪ΔRf)>γQ′s-Qi(Ef∪ΔRf)。

3 应用实例

图1为晋城某矿通风网络图G=(V,E)，分支数|E|=100，节点数|V|=71，各分支原始风阻、风量见表2。安设在e9,e39和e78等3个分支上的通风机特性曲线分别为

H(q)=1 932.25+44.84q-0.64q2，

H(q)=1 828.13+19.20q-0.08q2，

H(q)=3 054.94+8.64q-0.05q2

利用矿井通风仿真系统MVSS，对一般巷道的增阻故障、风门等构筑物的降阻故障进行模拟，故障风阻值采用线性等步长方法以及正态随机方法生成。共进行9 503次仿真生成9 503个故障样本。其中的4 752个样本用于构造矿井通风系统阻变型故障决策表，决策表数据结构形式见表3。

由式(15)可知，某一分支对故障诊断是否重要取决于λ的取值大小。根据式(6)～(14)编写Matlab程序用不同的λ值对表3分别以故障位置和故障量为决策属性进行约简，λ取值区间分别定义为[1～40],[5～105]，约简结果分别见表4，5。

表4,5的分支就是故障诊断所需安设传感器的位置。表4对应的传感器位置如图1中的彩色分支所示。从表4,5看出，λ取值不同，对决策具有重要影响的分支及其数量是不同的，总体趋势是λ越大，邻域半径越小，具有重要影响的分支数越少，亦即所需安设的传感器数量越少。在λ取值相同的情况下，故障位置诊断与故障量诊断所对应的重要分支数也是不同的，故障量诊断对应的重要分支数大于并且覆盖故障位置诊断所对应的重要分支。

将λ取值、约简分支亦即传感器位置，传感器位置所在分支风阻值大小关系进行分析，形成一个扫帚型模型，如图2所示。巷道风阻值较大的传感器位置构成了扫帚把，对故障诊断准确度影响最大的是扫帚把，应将传感器优先安设在扫帚把上。较小风阻值的传感器位置构成了扫帚头。λ越大，邻域半径越小，扫帚头越小，亦即传感器数量越少。λ越小，邻域半径越大，扫帚头越大，亦即传感器数量越多。

4 模型校验

参照文献[1]的方法，将表4,5中传感器位置的分支风量作为风量特征值，将表3中未使用的4 751个样本用于故障诊断，不同的传感器诊断精度如图3,4所示。

由图3,4可知，λ取值和传感器安设数量、故障诊断准确度呈现负相关关系。λ取值越大，邻域半径越小，安设传感器的数量越少，故障诊断的准确度越低。而传感器安设数量和故障诊断准确度呈现正相关关系，传感器数量越多故障诊断准确度越高，效果越好。

如图5,6所示，在检测实验中，以表4,5中20个监测故障位置传感器、39个监测故障量传感器的最优位置分别对检测样本进行测试，故障位置诊断准确度达到84.255 9%。故障量诊断相对误差小于5%的样本数为73.22%。

金川二矿通风网络有1 006条分支和870个节点，利用本文方法优选出18个传感器位置，利用人工測风的方法，进行4道风门打开、1台井下机站停机试验，5个故障位置诊断全部正确。

5 结 论

(1)邻域粗糙集简约算法不仅能够对用于通风系统阻变型故障的位置诊断，而且可以进行故障量诊断。

(2)传感器的数量与邻域粗糙集的λ参数有关，λ越大，邻域半径越小，传感器数量越少。

(3)阻变型故障诊断准确率与传感器数量呈正相关关系。

(4)λ取值、传感器位置，传感器所在分支风阻值的关系形如一把扫帚，称传感器位置优化扫帚模型。较大风阻值的传感器构成了扫帚把，较小风阻值的传感器构成了扫帚头。λ越大，邻域半径越小，扫帚头越小，亦即传感器数量越少。λ越小，邻域半径越大，扫帚头越大，亦即传感器数量越多。

(5)根据扫帚模型，传感器应优选在风阻值较大的巷道上，而且呈分散状。

参考文献（References）:

[1] 刘剑,郭欣,邓立军,等.基于风量特征的矿井通风系统阻变型单故障源诊断[J].煤炭学报,2018,43(1):143-149.

LIU Jian,GUO Xin,DENG Lijun,et al.Resistance variant single fault source diagnosis of mine ventilation system based on air volume characteristic[J].Journal of China Coal Society,2018,43(1):143-149.

[2] CORTES C,VAPNIK V.Support-vector networks[J].Machine Learning,1995,20(3):273-297.

[3] HOLLAND J H.Adaptation in natural and artificial systems[M].Ann Arbor:University of Michigan Press,1975.

[4] 刘剑,李雪冰,宋莹,等.基于速度场系数的主通风机风量单点统计测量方法[J].有色金属工程,2018,8(2):114-117.

LIU Jian,LI Xuebing,SONG Ying,et al.On the conversion between the mean airflow velocity and that of the individual pointin the underground mine tunnels[J].Nonferrous Metals,2018,8(2):114-117.

[5] HU Qinghua,YU Daren,LIU Jinfu,et al.Neighborhood rough set based heterogeneous feature subset selection[J].Information Sciences,2008,178(18):3577-3594.

[6] YI Xin,REN Lifeng,MA Li,et al.Effects of seasonal air temperature variation on airflow and surrounding rock temperature of mines[J].International Journal of Coal Science & Technology,2019,6(3):388-398.

[7] YUAN Ruifu,CHEN Chunlin,WEI Xiao,et al.Heat-fluid-solid coupling model for gas-bearing coal seam and numerical modeling on gas drainage promotion by heat injection[J].International Journal of Coal Science & Technology,2019,6(4):564-576.

[8] 刘伟,周心权,谭文辉,等.用分区法优化布置火源探测传感器的研究用分区法优化布置火源探测传感器的研究[J].煤炭工程师,1998(4):3-5.

LIU Wei,ZHOU Xinquan,TAN Wenhui,et al.Study on the optimum arrangement of fire source detection sensors by zoning method[J].Coal Engineer,1998(4):3-5.

[9] 孙继平,唐亮,陈伟,等.基于监测覆盖范围的瓦斯传感器无盲区布置[J].煤炭学报,2008,33(8):946-950.

SUN Jiping,TANG Liang,CHEN Wei,et al.No-blind-zone placement of gas sensor based on monitoring coverage[J].Journal of China Coal Society,2008,33(8):946-950.

[10] 孙继平,唐亮,李春生,等.风量比例法在甲烷传感器优化布置中的应用[J].煤炭学报,2008,33(10):1126-1130.

SUN Jiping,TANG Liang,LI Chunsheng,et al.Application of air volume Proportion rule in optimal placement of gas sensor in mine[J].Journal of China Coal Society,2008,33(10):1126-1130.

[11] 潘竟涛,赵丹,李宗翔,等.大明矿通风系统故障源诊断及风速传感器的布置[J].煤炭学报,2013,38(S1):153-158.

PAN Jingtao,ZHAO Dan,LI Zongxiang,et al.Diagnosis of ventilation system fault source and arrangement of wind speed sensor in Daming Mine[J].Journal of Coal Mine,2013,38(S1):153-158.

[12] LIANG Shuanghua,HE Jing,ZHENG Hui.Research on the HPACA algorithm to solve alternative covering location model for methane sensors[J].Procedia Computer Science,2018,139:464-472.

[13] COHEN A F,FISHER T J,WATSON R A,et al.Location strategy for methane,air velocity,and carbon monoxide fixed-point mine-monitoring transducers[J].IEEE Transactions on Industry Applications,2008,IA-23(2):375-381.

[14] KABIR G,TESFAMARIAM S,FRANCISQUE A,et al.Evaluating risk of water mains failure using a Bayesian belief network model[J].European Journal of Operational Research,2015,240(1):220-234.

[15] AYADI A,GHORBEL O,BENSALAH M S,et al.Kernelized technique for outliers detection to monitoring water pipeline based on WSNs[J].Computer Networks,2019,150:179-189.

[16] ZHANG Kui,YAN Hexiang,ZENG Han.A practical multi-objective optimization sectorization method for water distribution network[J].Science of the Total Environment,2019,656:1401-1412.

[17] 王伟哲,郄志红,刘美侠,等.基于改进遗传算法的供水管网故障监测点布置优化[J].水力发电学报,2012,31(1):15-19,37.

WANG Weizhe,PI Zhihong,LIU Meixia,et al.Layout optimization of water supply network fault monitoring points based on improved genetic algorithm[J].Journal of Hydropower,2012,31(1):15-19,37.

[18] LIU Cuiwei,LI Yuxing,XU Minghai.An integrated detection and location model for leakages in liquid pipelines[J].Journal Of Petroleum Science And Engineering,2019,175:852-867.

[19] AIDA-ZADE K R,ASHRAFOVA E R.Localization of the points of leakage in an oil main pipeline under non-stationary conditions[J].Journal of Engineering Physics and Thermophysics,2012,85(5):1148-1156.

[20] OYEDEKO K F,BALOGUN H A.Modeling and simulation of a leak detection for oil and gas pipelines via transient model:A case study of the Niger Delta[J].Journal of Energy Technologies and Policy,2015,5(1):16-27.

[21] SHAMLOO H,HAGHIGHI A.Optimum leak detection and calibration of pipe networks by inverse transient analysis[J].Journal of Hydraulic Research,2010,48(3):371-376.

[22] ZHOU Jun,PENG Jinghong,LIANG Guangchuan,et al.Layout optimization of tree-tree gas pipeline network[J].Journal of Petroleum Science and Engineering,2019,173:666-680.

[23] HOU Longfei,QIAN Xinming,DU Bingxuan.Optimization of the gas leak monitoring points distributed underground[J].Journal of Loss Prevention in the Process Industries,2017,47:95-103.

[24] CHENG Shujuan.Studies of the small leakage in buried gas pipeline under the condition of soil properties[J].Applied Mechanics and Materials,2014,2974:2266-2270.

[25] SANTOS R B,DE SOUSA E O,DA SILVA F V,et al.Detection and on-line prediction of leak magnitude in a gas pipeline using an acoustic method and neural network data processing[J].Brazilian Journal of Chemical Engineering,2014,31(1):145-153.

[26] PAWLAK Z.Rough sets[J].International Journal of Computer & Information Sciences,1982,11(5):341-356.

[27] 贾进章,刘剑,耿晓伟.矿井通风仿真系统数学模型[J].辽宁工程技术大学学报,2003,22(S1):88-90.

JIA Jinzhang,LIU Jian,GENG Xiaowei.Mathematical model of mine ventilation simulation system[J].Journal of Liaoning University of engineering and technology,2003,22(S1):88-90.

[28] LIN T Y.Granular computing on binary relations I:Data mining and neighborhood systems[J].Rough Sets in Knowledge Discovery,1998,18(1):107-121.

[29] ZADEH L A.Towards a theory of fuzzy information granulation and its centrality in human reasoning and fuzzy logic[J].Fuzzy Sets and Systems,1997,90(2):111-127.

Resistance variant fault diagnosis of mine ventilation system and position optimization of wind speed sensor

LIU Jian1,2,JIANG Qinghua1,2,LIU Li1,2,WANG Dong1,2,HUANG De1,2,DENG Lijun1,2,ZHOU Qichao 1,2

(1.College of Safety Science and Engineering,Liaoning Technical University,Huludao 125105,China; 2.Key Laboratory of Mine Thermal Dynamics and Prevention,Ministry of Education,Liaoning Technical University,Huludao 125105,China)

Abstract:The abnormal change of the air volume in the ventilation system caused by the change of the roadway caving or deformation,the door opening or damage,the transportation vehicle blocking and so on is called the mine ventilation system resistance variant fault.According to the monitoring value of roadway air volume after the fault,the fault location and fault amount can be diagnosed by artificial intelligence methods such as support vector machine (SVM) and genetic algorithm (GA).The core problem is how to determine the minimum number and locations of sensors installed underground.Through the fault diagnosis simulation experiment of the actual mine and the field experiment of the metal mine,a method of optimizing the installation position of the wind speed sensor based on the attribute reduction algorithm of the neighborhood rough set without prior knowledge is proposed.According to the importance of the roadway air volume to the fault position and the fault amount,the reduction branch obtained is the optimal position of the sensor to be installed.The research shows that the number of sensors is related to the size of artificial neighborhood radius.The larger the neighborhood radius is,the more sensors are installed,and the higher the accuracy of fault diagnosis is.A broom model is proposed to describe the optimal relationship among the value of λ,neighborhood radius,sensor location,wind resistance value of the branch where the sensor is located and the accuracy of fault diagnosis.The branch with larger wind resistance forms the broom handle,and the branch with smaller wind resistance forms the broom head.The broom model requires that the sensor should be preferentially arranged on the broom handle with larger wind resistance value.The shape of the broom model is related to the value of λ.The larger the value of λ is,the smaller the neighborhood radius is,the smaller the broom head is,that is to say,the fewer the number of sensors.The smaller the neighborhood radius is,the larger the broom head is,that is to say,the more sensors there are.The research results provide a new method to determine the installation position of wind speed sensor,and realize the identification of mine ventilation system resistance variant fault by using less wind speed sensor monitoring data.

Key words:resistance variant fault;neighborhood rough set;fault diagnosis;wind speed sensor;broom model

中图分类号:TD722

文献标志码:A

文章编号:0253-9993(2021)06-1907-08

收稿日期:2019-12-19

修回日期:2020-03-19

责任编辑:钱小静

DOI:10.13225/j.cnki.jccs.2019.1768

基金项目:国家重点研发计划资助项目(2017YFC0804401);国家自然科学基金资助项目(51574142)

作者简介:刘 剑(1962—)，男，内蒙古赤峰人，教授，博士生导师。E-mail:lj1961@vip.sina.com

引用格式:刘剑，蒋清华，刘丽,等.矿井通风系统阻变型故障诊断及风速传感器位置优化[J].煤炭学报,2021,46(6):1907-1914.

LIU Jian,JIANG Qinghua,LIU Li,et al.Resistance variant fault diagnosis of mine ventilation system and position optimization of wind speed sensor[J].Journal of China Coal Society,2021,46(6):1907-1914.