采动地表建、构物的损害主要归因于地表点的移动和变形,经典的开采沉陷理论与方法主要集中在静态预计研究领域[1-3],但由于地表移动、变形是一个复杂的动态过程,与开采速度,煤层采深和倾角、顶板管理方法,上覆岩层力学性质等因素密切相关[4-7],掌握地表点随时间的动态变化规律同样具有重要意义,能够更准确的分析采动地表移动变形与采矿地质因素的关系,可为采后损害鉴定、采前建筑物保护、采空区土地再利用等供技术支撑。在实践中,国内外最主要的动态预计方法多是通过用静态预计公式乘以相应的时间函数来实现的[8-10],我国开采沉陷动态预计始于20世纪80年代,许多学者做了大量工作。崔希民、彭小沾等[11-12]在动态预计研究中,对Knothe时间函数进行了深入的研究,给出了5种时间系数的确定方法,同时指出了该时间函数的不足,并给出了理想的时间函数分布形态。LUO Yi和CHENG Jianwei[13]通过研究美国长壁开采地表变形规律,对Knothe时间函数进行改进,使其适应倾斜煤层开采时的动态预计。胡青峰等[14]进一步阐述了Knothe时间系数的影响因素,探讨了时间系数的直接求取方法。张凯等[15]采用生长函数模型对正态分布时间函数进行了优化,解决了其密度函数的有效积分域亏损随时间参数c而减小的问题。郭旭炜等[16]给出了分段Konthe时间函数的动态求参方法,解决了其参数不随时间变化的不足。陈磊等[17]采用水准与 InSAR技术相结合估算幂指数 Knothe 时间函数模型的参数,并用实例说明使用该方法可提高动态预计精度。王军保等[18]采用岩石力学的非定常流变模型,将Knothe时间系数看作非常量,构建了一种新的动态沉陷预计公式。李怀展等[19]提出了一种基于加权法和地质力学参数敏感性的地表沉降动态预测方法,并用实例证明了该方法可以提高地表动态沉降的预测精度。杨泽发等[20]建立了Logistic模型与InSAR观测值之间的函数关系,然后利用InSAR观测值估计Logistic模型参数,进而再采用Logistic模型进行动态预计。很多研究者还给出了不同的动态预计方法[21-23],如地表动态沉降预测的Richards模型、基于双因素时间函数的地表点动态沉降预计模型等。
通过对已有文献分析可知,现有动态沉陷预计模型多是纯理论的,没有结合足够的工程应用,且大多数预计模型的参数求取非常不易,推广应用较为困难。通过分析还可知,Knothe时间函数在动态预计研究中占有重要地位,同时,不少学者也指出了该函数的应用局限性。为此,很多学者对其进行过改进[24-26],笔者也曾在Knothe时间函数的基础上构建了“优化分段Knothe时间函数模型”[27](以下简称:“优化分段时间函数”),提高了动态预计精度、扩展了该函数的适应性;另外,在走向主断面动态预计研究方面,很多学者做过研究,给出了相应的方法,但在倾向主断面动态沉陷预计方面,现有的研究涉及不多,但笔者认为对其进行研究很有必要,相较于对整个下沉盆地的计算而言,研究主断面上的动态预计模型及算法,可以大大节省计算时间,快速得到预计结果。
笔者以“优化分段时间函数”为基础,以概率积分模型为影响函数,重点探讨缓倾斜矩形或近矩形工作面开采地表倾向主断面动态预计方法问题,并设计相应算法,为动态预计的多方面工程应用提供解决方案。
1 倾向主断面动态预计模型构建
1.1 倾向主断面沉陷预计基本原理
设煤层在走向上达到了充分采动,倾向上为有限开采,倾向主断面上的地表沉降变形可采用等影响原理来计算[1],具体可采用图1进行辅助说明。图1中,AB为实采边界;s1为下山拐点偏距;s2为上山拐点偏距;CD为AB煤层开采时的计算边界。
在计算公式建立的过程中,选择图1中过A点的直线和地表交点(P)作为坐标原点,垂直指向下方表示地表下沉(W),而地表点的坐标可用y轴表示,y轴为沿地表水平指向右方,Wy为y轴方向的下沉。考虑到煤炭开采拐点偏移距的影响,如果开采AB煤层,根据等影响原理,AB开采所引起的地表倾向主断面上点的下沉可用W0(y)表示,采用式(1)进行计算[1]:

图1 有限开采地表倾向主断面预计等影响计算原理
Fig.1 Equal effect principle in inclined principal section prediction when finite mining
W0(y)=W(y-LAC′;t1)-W(y-LAC′-L;t2)
(1)
LAC′=(H1-s1sin α)cot θ0-s1cos α
(2)
![]()
(3)
![]()
(4)
其中,LAC′为AC′的距离;t1,t2为计算时所对应的上下山边界参数;α为煤层倾角;θ0为开采影响传播角;H1和H2为下山和上山采深;D1为AB煤层长度;W0为最大下沉值;y为地表点坐标。式(1)即为AB煤层采动引起的地表下沉静态(终态)计算式。
1.2 动态预计时间函数
时间函数是动态预计的重要组成部分,可用于动态预计的时间函数有很多,选择什么样的时间函数,在一定程度上决定着动态预计精度的高低,本文采用 “优化分段时间函数”[27],该时间函数是笔者曾改进过的,并用实践证明了它的可靠性,改进后的时间函数提高了原函数的预测精度及对不同地质采矿条件的适应性。另外,笔者还曾对其参数的确定方法进行了详细讨论[28],推导了其时间参数的直接法计算公式,方便了计算编程,“优化分段时间函数”模型如式(5)所示,其函数图像如图2所示:
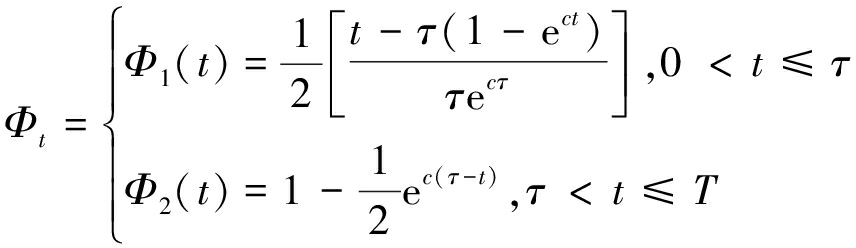
(5)
式中,t为任意给定的预计时刻;τ为最大下沉速度出现的时刻;c为时间系数,与覆岩力学性质相关;T为下沉总时间。

图2 优化分段时间函数图像形态
Fig.2 Segmented optimization time function
1.3 倾向主断面动态预计模型建立
在动态预计中,通常要按照一定的原则将煤层划分为不同的动态开采单元[29]。倾向主断面动态开采单元的划分和地表沉陷的动态发展规律可用图3进行说明,各单元的长度用开采速度v乘以相应的开采时间t表示。由于各单元开采顺序不同,在预计时刻其对地表点的影响时间也不同,先开采的单元影响大,后开采的单元影响小。第n个单元开采后,第1个单元采后所经历的时间是t1,t2,…,tn之和,其对地表的影响最大,第2个单元采后所经历的时间是t2,t3,…,tn之和,其影响次之,最后1个单元由于刚采完毕,其影响未波及地表。假设第1个动态单元对地表的下沉影响用W1(y)表示,第2个单元影响用W2(y)表示,第n个单元影响用Wn(y)表示。

图3 倾向动态单元开采对地表点下沉的动态影响
Fig.3 Dynamic influence when mining strike section dynamic unit on surface subsidence
各动态单元开采对地表沉陷的影响,也符合有限开采原理,可按有限开采相关公式计算,但需要改变相应的概率积分参数。根据有限开采倾向主断面下沉预计公式,下面给出从第1个单元到第n个单元开采的地表下沉计算公式
![]()
(6)
其中,LAC′由式(2)求取;W(y)由式(4)计算;![]() 为第1个动态单元下山方向计算边界到坐标原点的距离;
为第1个动态单元下山方向计算边界到坐标原点的距离;![]() 为第1个动态单元上山方向的边界相对于坐标原点的距离;
为第1个动态单元上山方向的边界相对于坐标原点的距离;![]() 为对应的第1个动态单元下山边界参数;
为对应的第1个动态单元下山边界参数;![]() 为对应的第1个动态单元上山边界参数。通过分析各动态单元和整个开采单元的关系,可推导出
为对应的第1个动态单元上山边界参数。通过分析各动态单元和整个开采单元的关系,可推导出![]() 的计算公式为
的计算公式为

(7)
如果将第1个动态单元下山主要影响半径用![]() 表示;上山主要影响半径用
表示;上山主要影响半径用![]() 表示,那么式(7)中涉及的对应概率积分参数可按式(8)进行计算:
表示,那么式(7)中涉及的对应概率积分参数可按式(8)进行计算:
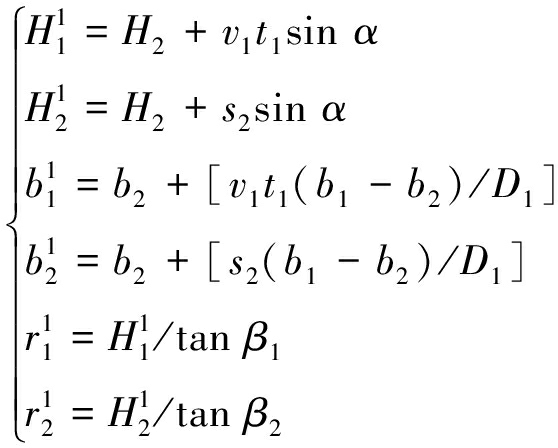
(8)
其中,b1为下山方向水平移动系数;b2为上山方向水平移动系数;tan β1为下山方向主要影响角正切;tan β2为上山方向主要影响角正切。以上均指第1个动态开采单元的相关参数。
第2个动态单元开采时,参照式(6)~(8),可给出W2(y)为
![]()
(9)
式(9)中涉及到的各参数计算方法为

(10)
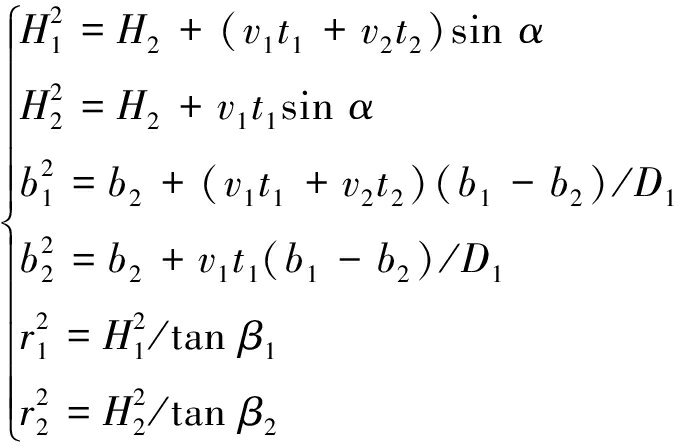
(11)
式中,![]() 为第2个动态单元下山采深;
为第2个动态单元下山采深;![]() 为第2个动态单元上山采深;
为第2个动态单元上山采深;![]() 为第2个动态单元下山方向影响半径;
为第2个动态单元下山方向影响半径;![]() 为第2个动态单元上山方向影响半径。
为第2个动态单元上山方向影响半径。
同理Wn(y)可由上述推导类比得到,具体如下:
![]()
(12)
第n个动态单元相关参数可由式(13)和(14)求取:

(13)

W1(y),W2(y),…,Wn(y)是计算1~n个动态单元开采后单独对地表的终态(静态)影响,如果计算某个时刻T的地表动态下沉,需要将每个单元的静态影响值乘以各单元在T时刻对应的时间函数值,再进行叠加求和,即可得到T时刻的地表下沉值,计算方法如式(15)所示。需要强调的是:在计算W1(y),W2(y),…,Wn(y)过程中均考虑了拐点偏距的影响,坐标原点设在了图1中的P点处。
W(y,t)=Φ(t)W1(y)+Φ(t-t1)W2(y)+…+
Φ(t-t1-t2-…-tn-1)Wn(y)=
![]()
(15)
预计T时刻的地表变形如:曲率、倾斜、水平变形和水平移动,可根据相应的概率积分法计算公式,参照上述下沉公式的推导过程得出,限于篇幅,这里不再重复。
2 倾向主断面动态预计算法
地表移动变形计算公式建立之后,为了能够用计算机语言来实现计算过程,编制预计程序,则需要研究相应的算法,在倾向主断面动态预计中要考虑每个动态单元的相应参数,如:各单元水平移动系数,上下山采深及主要影响半径等。当预计精度不高时,可带入各参数的平均值进行计算,如果直接将原有的概率积分参数代入计算,预计精度则会大大降低。另外,分别计算各动态单元参数不但能提高预计精度,还可提高本文模型的应用范围,扩展其对于较大倾角煤层开采的适用性。
2.1 算法基本思想
计算各个单元的y坐标是算法中较为复杂的部分,开采传播角的影响使得下沉和变形拐点向下山方向移动。如图1所示,可以将各动态单元的计算长度以L为基础按比例内插求取,动态移动变形计算步骤如下:
Step 1:计算走向方向充分采动程度系数(Cxm),在动态计算结果中乘以该系数,可以使得计算结果更为精确,也与实际情况相符合。
Step 2:计算预计T时刻各单元所对应的时间函数值(PHT)。这是计算各单元对地表影响值大小的关键参数,表明了各单元的终态影响在T时刻对应的时间调整系数。
Step 3:确定动态预计的计算坐标系,即确定坐标原点、下沉轴和y轴(用以表示地表点的位置);计算上山和下山方向各单元对应的y值大小,这是概率积分法的主要参数之一。
Step 4:计算预计T时刻各单元的上下山采深、主要影响半径、主要影响角正切,以便代入各动态单元对应的公式进行计算。
Step 5:对每个动态单元按照公式W1(y),W2(y),…,Wn(y)进行计算,得到各单元影响静态下沉值,计算完成后分别乘以对应的时间函数值PHIT),再求和,即可得到预计T时刻的动态下沉。
2.2 算法的实现
计算模型和算法的难点在于:考虑拐点偏移距时,1~n个动态单元对应的计算长度Li如何确定?它是概率积分模型主要参数之一,要计算Li,需先确定各单元所对应的上、下山方向的y值;另外,在工作面概率积分参数已知时,各动态单元相应参数如何计算,也是需要重点注意的问题。倾向主断面动态预计算法伪代码见表1。
3 倾向主断面动态预计实例
3.1 动态预计实例1
以文献[1]中介绍的某工作面为例,对其进行倾向主断面动态预计,该工作面具体情况如下:走向长1 000 m,倾向长250 m,上山采深H2=279 m,下山采深H1=322 m,煤层倾角=12°,下沉系数q=0.78,采厚m=1.45 m,主要影响角正切tan β1=2.2,tan β2=2.0,开采影响传播角θ0=81.6°,水平移动系数b1=0.36,b2=0.30,拐点偏距s1=30 m,s2=28 m;覆岩岩性为中硬,用垮落法管理顶板。动态预计参数为:动态单元长度采用有效尺寸分割法[29]确定,确定为0.1H0(H0为工作面平均采深),开采速度v为5.0 m/d,时间函数参数τ和c按照笔者在文献[28]中所介绍的方法自动计算,动态预计程序按本文模型及算法编制。
表1 倾向主断面动态预计算法伪代码
Table 1 Pseudocode of dynamic subsidence prediction algorithm for inclined main section

倾向主断面沉降变形动态预计:计算下沉量W、倾斜I、曲率K、水平移动U、水平变形 εInput:输入静态预计概率积分参数Output:输出预计T时刻地表的W、I、K、U、ε 的动态预计结果Begin初始化数组L1n和L2n,保存动态单元上下山边界距坐标原点的长度值初始化数组H1n和H2n,两数组用于保存第1个单元到第n个单元对应的上下山开采深度初始化数组Tanbita1n和Tanbita2n及数组r1n和r2n初始化数组b1n、b2n、Wyn、Iyn、Kyn、Uyn、Eyn、初始化数组Wyd、Iyd、Kyd、Uyd、Eyd,保存动态下沉,倾斜,曲率水平移动和水平变形计算Cxm %走向充分采动程度系数。计算PHIT % 各动态单元时间函数值的计算for i=1:NN % NN 为动态单元总数 for y=BJx:WGKD:BJs % BJx计算下边界,BJs计算上边界,WGKD为网格间隔 Wyn(j,m)=Cxm∗(((erf(n1n(j)∗(y-L1n(j)))+1)∗(w0/2))-((erf(n2n(j)∗(y-L2n(j)))+1)∗(w0/2))); % 将各动态单元地表影响的终态下沉值保存在数组Wyn中,倾斜,曲率,水平移动和变形略。endforendforfor i=1:NNWyd1(j,:)=PHT(j).∗Wyn(j,:); % 计算各动态单元在预计T时刻的动态移动变形值,即将各单元的终态影响乘以对应的时间函数值,倾斜,曲率,水平移动和变形略。endforWyd=sum(Wyd1); % 将各动态单元的动态影响进行求和即可得到地表预测点或范围的动态移动变形值。End
如果工作面是“从上山向下山方向开采”,在不同的预计时刻对工作面倾向主断面进行动态预计,根据预计结果,可绘制如图4所示的动态下沉和倾斜曲线。
由图4可知,由于开采速度较小,采深又较大,当T=200 d时,工作面实际开采了100 m,由于顶板的悬臂支撑,此时的下沉和倾斜都很小。随着T值的增大,已开采的动态单元数越来越多,地表的沉陷范围越来越大,受开采影响的地表点的下沉和倾斜也逐渐增加。如果给定时间足够大,如在T=800 d时进行动态预计,地表的下沉和倾斜与T=1 200 d预计的下沉曲线非常接近,因此可认为T=1 200 d时的预计结果为静态结果,即地表趋于稳定时的终态下沉曲线,也说明T=800 d时地表移动变形基本就已经趋于了稳定。
图4的“动态预计-下沉”中,黑色曲线是地表下沉的终态曲线,其拐点不在计算边界垂直上方,也不在开切眼的垂直上方,而是距离开切眼有一定的距离,向着下山方向偏移,位于图中O点处,这是因为受到了开采影响传播角的影响。
为了验证程序的理论正确性,需要进行对比研究,假设“工作面再从下山向上山方向开采”,在对应的时刻再次进行动态预计,根据预计结果,则可得到如图5所示的地表下沉和倾斜图。
将不同开采方式的2图进行对比可知,图4中地表点的下沉和倾斜是从左向右进行传播的,而图5则正好相反,这说明,开采顺序不同,地表各点出现最大下沉和倾斜值的时刻是不同的,在对地表建筑物进行保护的过程中,判断地表点移动和变形最大值出现的时刻和位置至关重要。通过对比还可知,无论开采方式是选择上山开采还是选择下山开采,倾向主断面上各点的终态下沉是完全相同的,即,图4,5中,T=1 200 d时的曲线是完全重合的,此时无论给定的预计时刻T如何增加,受影响地表点的范围和移动变形值都不会再发生任何改变,在理论上说明了模型和算法的科学性。

图4 上山开采倾向主断面下沉和倾斜动态预计
Fig.4 Dymamic subsidence and inclination when mining along downhill direction

图5 下山开采倾向主断面下沉和倾斜动态预计
Fig.5 Dymamic surface subsidence and inclination when mining along uphill direction
3.2 动态预计实例2
为验证本文模型和算法精度的可靠性,以官地矿 29401采煤工作面倾向主断面为研究对象,对其开采进行动态预计,对比预计结果和实测数据,统计预计精度。
3.2.1 动态预计
官地29401工作面基本情况见文献[28],在此不再列举。为简化编程算法,在预计前先将实际工作面和地表监测点转换为以工作面走向为横轴的坐标系,如图6所示。

图6 工作面与测点分布
Fig.6 Distribution of monitoring points and working face
根据29401工作面倾向主断面9次观测结果绘制的下沉曲线如图7所示。

图7 倾向观测线实测下沉量
Fig.7 Measured subsidence of tend towards line
利用本文算法编制的动态预计程序,在与实际观测对应的时刻,进行了9次动态预计,得到的下沉预计结果如图8所示。
3.2.2 预计精度分析
在开始阶段,地表的移动变形值都很小,本文抽样选择了第4,5,7,9次观测成果,将其与动态预计结果进行对比来统计预测精度。实测与预测结果对比如图9所示。

图8 倾向观测线预计下沉量
Fig.8 Prediction subsidence of tend towards line
采用文献[14]和[27]所介绍的方法,对抽样的4次预测与实测结果进行统计分析,得到的统计数据见表2。由表2可知,预测绝对中误差最小为±54 mm,最大为±452 mm,预测相对中误差除了第7次较大外,其他相对误差分布在8.5%左右,在动态预计中精度相对较高,能够满足绝大多数工程需要。

图9 第4,5,7,9次预测下沉与实测下沉对比
Fig.9 Comparison between predicted subsidence and measured subsidence at the 4th,5th,7th and 9th
表2 动态预计精度统计
Table 2 Statistical table of dynamic prediction accuracy

观测日期中误差/mm最大值/mm相对误差/%观测日期中误差/mm最大值/mm相对误差/%2009-11-02(第4次)±543 4398.42009-12-07(第5次)±2105 1738.82010-02-22 (第7次)±4525 23110.22010-06-08(第9次)±3795 3158.5
4 结 论
(1)以“优化分段Knothe时间函数”为基础,结合概率积分法,建立了适应于缓倾斜、矩形或近似矩形工作面开采时的倾向主断面地表沉陷动态预计模型。
(2)根据动态预计原理和所建模型,给出了倾向主断面动态预计详细流程,设计了对应的计算机编程算法,计算流程清晰明了,算法简洁。
(3)预计实践1表明:采用本文模型及算法,预计的地表动态移动变形规律与理论所揭示的移动过程相符合,证明了模型及算法的科学性;预计实践2表明:29401工作面倾向观测线动态预计最大相对误差在整体上可以控制在8.5%左右,证明了模型在预计精度上的可靠性。
[1] 何国清,杨伦,凌赓娣,等.矿山开采沉陷学[M].徐州:中国矿业大学出版社,1995.
[2] 郭增长,柴华彬.煤矿开采沉陷学[M].北京:煤炭工业出版社,2013.
[3] 黄乐亭,王金庄.地表动态沉陷变形规律与计算方法研究[J].中国矿业大学学报,2008,37(2):211-215.
HUANG Leting,WANG Jinzhuang.Research on laws and computational methods of dynamic surface subsidence deformation[J].Journal of China University of Mining & Technology,2008,37(2):211-215.
[4] 崔希民,陈立武.沉陷大变形动态监测与力学分析[M].北京:煤炭工业出版社,2004.
[5] CUI Ximin,WANG Jiachen,LIU Yisheng.Prediction of progressive surface subsidence above longwall coal mining using a time function[J].International Journal of Rock Mechanics and Mining Sciences,2001,38(7):1057-1063.
[6] CUI Ximin,MIAO Xiexing,WANG Jinan,et al.Improved prediction of differential subsidence caused by underground mining[J].International Journal of Rock Mechanics and Mining Sciences,2000,37(4):615-627.
[7] NIE Lei,WANG Hongfei,XU Yan,et al.A new prediction model for mining subsidence deformation:The arc tangent function model[J].Natural Hazards,2015,75(3):2185-2198.
[8] GONZALEZ Nicieza C,ALVAREZ Fernandez I M,MENENDEZ Diaz A,et al.The influence of time on subsidence in the Central Asturian Coalfield[J].Bulletin of Engineering Geology and the Environment,2007,66(3):319-329.
[9] 胡青峰,崔希民,康新亮,等.Knothe时间函数参数影响分析及其求参模型研究[J].采矿与安全工程学报,2014,31(1):122-126.
HU Qingfeng,CUI Ximin,KANG Xinliang,et al.Impact of parameter on Knothe time function and its calculation model[J].Journal of Mining & Safety Engineering,2014,31(1):122-126.
[10] HAN Haoliang,CUI Bo.Modeling of surface subsidence based on time function[J].Advanced Materials Research,2012,422:318-321.
[11] 崔希民,缪协兴,赵英利,等.论地表移动过程的时间函数[J].煤炭学报,1999,24(5):453-456.
CUI Ximin,MIAO Xiexing,ZHAO Yingli,et al.Discussion on the time function of time dependent surface movement[J].Journal of China Coal Society,1999,24(5):453-456.
[12] 彭小沾,崔希民,臧永强,等.时间函数与地表动态移动变形规律[J].北京科技大学学报,2004,26(4):341-344.
PENG Xiaozhan,CUI Ximin,ZANG Yongqiang,et al.Time function and prediction of progressive surface movements and deformations[J].Journal of University of Science and Technology Beijing,2004,26(4):341-344.
[13] LUO Yi,CHENG Jianwei.An influence function method based subsidence prediction program for longwall mining operations in inclined coal seams[J].Mining Science and Technology,2009,19(5):592-598.
[14] HU Qingfeng,DENG Xubiao,FENG Ruimin,et al.Model for calculating the parameter of the Knothe time function based on angle of full subsidence[J].International Journal of Rock Mechanics and Mining Sciences,2015,78:19-26.
[15] 张凯,胡海峰,廉旭刚,等.地表动态沉陷预测正态时间函数模型优化研究[J].煤炭科学技术,2019,47(9):235-240.
ZHANG Kai,HU Haifeng,LIAN Xugang,et al.Optimization of surface dynamic subsidence prediction normal time function model[J].Coal Science and Technology,2019,47(9):235-240.
[16] 郭旭炜,杨晓琴,柴双武,等.分段Knothe 函数优化及其动态求参[J].岩土力学,2020,41(6):1-8.
GUO Xuwei,YANG Xiaoqin,CHAI Shuangwu,et al.Optimization of segmented Knothe function and its dynamic parameter calculation[J].Rock and Soil Mechanics,2020,41(6):1-8.
[17] CHEN Lei,ZHANG Liguo,TANG Yixian,et al.Analysis of mining-induced subsidence prediction by exponent Knothe model combined with InSAR and leveling[J].ISPRS Annals of the Photogrammetry,Remote Sensing and Spatial Information Sciences,2018(IV-3):53-59.
[18] 王军保,刘新荣,李鹏,等.MMF模型在采空区地表沉降预测中的应用[J].煤炭学报,2012,37(3):411-415.
WANG Junbao,LIU Xinrong,LI Peng,et al.Study on prediction of surface subsidence in mined-out region with the MMF Mode[J].Journal of China Coal Society,2012,37(3):411-415.
[19] LI Huaizhan,ZHA Jianfeng,GUO Guangli.A new dynamic prediction method for surface subsidence based on numerical model parameter sensitivity[J].Journal of Cleaner Production,2019,233:1418-1424.
[20] YANG Zefa,LI Zhiwei,ZHU Jianjun.Deriving dynamic subsidence of coal mining areas using insar and logistic model[J].Remote Sensing,2017,9(2):125-144.
[21] 王正帅,邓喀中.采动区地表动态沉降预测的Richardson模型[J].岩土力学,2011,32(6):1664-1668.
WANG Zhengshuai,DENG Kazhong.Richards model of surface dynamic subsidence prediction in mining area[J].Rock and Soil Mechanics,2011,32(6):1664-1668.
[22] 孙闯,徐乃忠,刘义新,等.基于双因素时间函数的松散地层条件下地表点动态沉降预计[J].岩土力学,2017,38(3):821-826.
SUN Chuang,XU Naizhong,LIU Yixin,et al.Prediction of dynamic subsidence of ground point under loose stratum based on two-factor time function[J].Rock and Soil Mechanics,2017,38(3):821-826.
[23] 王军保,刘新荣,刘小军.开采沉陷动态预测模型[J].煤炭学报,2015,40(3):516-521.
WANG Junbao,LIU Xinrong,LIU Xiaojun.Dynamic prediction model for mining subsidence[J].Journal of China Coal Society,2015,40(3):516-521.
[24] 刘玉成,曹树刚,刘延保.改进的Konthe 地表沉陷时间函数模型[J].测绘科学,2009,34(5):16-17,31.
LIU Yucheng,CAO Shugang,LIU Yanbao.The improved Knothe time function for surface subsidence[J].Science of Surveying and Mapping,2009,34(5):16-17,31.
[25] 常占强,王金庄.关于地表点下沉时间函数的研究—改进的克诺特时间函数[J].岩石力学与工程学报,2003,22(9):1496-1499.
CHANG Zhanqiang,WANG Jinzhuang.Study on time function of subsidence:The improved Knothe time function[J].Chinese Journal of Rock Mechanics and Engineering,2003,22(9):1496-1499.
[26] 沈震,徐良骥,郭辉,等.一种改进的开采沉陷动态下沉模型[J].测绘科学,2016,41(12):238-242.
SHEN Zhen,XU LiangJi,GUO Hui,et al.An improved dynamic deformation model of mining subsidence[J].Science of Surveying and Mapping,2016,41(12):238-242.
[27] 张兵,崔希民.开采沉陷动态预计的分段Knothe时间函数模型优化[J].岩土力学,2017,38(2):541-547,556.
ZHANG Bing,CUI Ximin.Optimization of segmented Knothe time function model for dynamic prediction of mining subsidence[J].Rock and Soil Mechanics,2017,38(2):541-547,556.
[28] 张兵,崔希民,赵玉玲,等.优化分段 Knothe 时间函数求参方法[J].煤炭学报,2018,43(12):3379-3386.
ZHANG Bing,CUI Ximin,ZHAO Yuling,et al.Parameter calculation method for optimized segmented Knothe time function[J].Journal of China Coal Society,2018,43(12):3379-3386.
[29] 吴侃,靳建明.时序分析在开采沉陷动态参数预计中的应用[J].中国矿业大学学报(自然科学版),2000,29(4):413-415.
WU Kan,JIN Jianming.Prediction of dynamic mining subsidence parameters by time series analysis method[J].Journal of China University of Mining & Technology,2000,29(4):413-415.
[30] 余学义,张恩强.开采损害学[M].北京:煤炭工业出版社,2010.
