注浆加固是大水矿区防治水的重要手段,像肥城[1]、焦作[2]、邯邢矿区[3]、峰峰[4]和淮北[5]等,都使用注浆加固技术解决底板水防治问题。注浆过程中,套管作为注浆工具,用来辅助注浆和及时封堵钻孔施工中的出水。注浆完成后,高压封孔,套管被浆液充满,凝固浆液和套管成为底板岩体的组成部分,增强了岩体的性能。当加固深度较大、含水层水压高时,需要施加多级套管,套管长度加大,如赵固矿区施加3级套管,长度40~80 m,沿工作面推进方向上每500 m开采单元消耗套管长度累计8 000余米。现场实践中,注浆套管破断形态表明浆液充填套管发挥抵抗岩层变形的作用,实验也表明浆液充填套管具有很好的抗弯刚度。为研究浆液充填套管对岩层变形影响机制,以套管为研究对象,建立分布支承压力作用下注浆加固套管在底板岩层空间中的力学作用模型,对浆液充填套管作用机制进行理论分析并验证。
底板注浆加固方面的研究成果很多,注浆加固技术也很成熟。注浆设计时以浆液扩散半径和底板破坏深度为依据,相关理论成果围绕这些重要问题开展,相对而言,关于浆液充填套管对岩层变形影响的研究较少[6-8]。一些关于注浆套管的研究,大多是针对套管的布置方法等[1,9]。在功能上,浆液充填套管类似混凝土钢管和微型桩等结构,而这方面的研究较多,如钢管高强混凝土构件的抗弯性能实验[10-13],可提供很好的研究基础。考虑到抗弯刚度、轴向和法向强度,忽略套管作用不太合适。当浆液凝固与套管、围岩耦合时能够提高底板岩体抵抗变形的性能,浆液充填套管组合对煤层底板岩层变形影响不可忽视。
为研究浆液充填套管对岩层变形的影响,分析浆液充填套管在底板岩体中的作用过程和对底板岩层变形的影响机制,以套管为研究对象,建立分布支承压力作用下注浆加固套管在底板岩层空间中的力学作用模型,对浆液充填套管作用机制进行理论分析并验证,有利于更好地发挥注浆套管的作用。
1 浆液充填套管抗弯性能与破断形态
1.1 抗弯性能分析
注浆套管抗弯性能通过抗弯加载试验得到,基本原理如图1(a)所示。虽然钢管的抗弯力学性能研究很多,但设计标准不易统一[10]。文献[11-12]以直径为108 mm的Q235无缝钢管试件为例,采用纯水泥浆充填套管并进行抗弯加载试验,得到荷载p与跨中挠度f曲线如图1(b)所示。

图1 注浆套管抗弯试验
Fig.1 Bending test of grouting casing pipes
工程上为使用方便,一般忽略套管开裂点,将弯矩-曲率全过程曲线简化为3段折线:弹性段、弹塑性段和强化段,弯矩-曲率(M-φ)全曲线[12]的表达式为
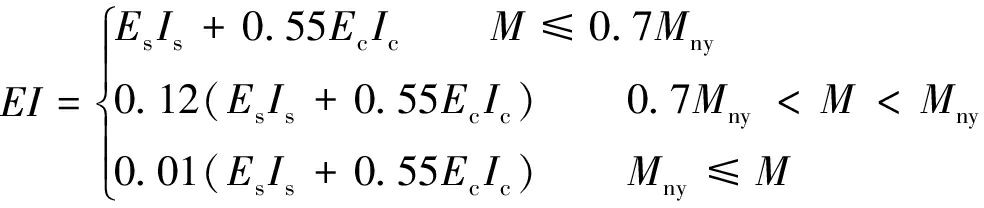
(1)
式中,EI为钢混构件截面的弯曲刚度;Es为钢管弹性模量;Is为钢管截面惯性矩;Ec为混凝土弹性模量;Ic为混凝土截面惯性矩;Mny为名义钢混构件截面受弯承载力,可按0.24N0rc,其中,N0为钢管混短柱轴压承载力;rc为核心混凝土横截面半径。
1.2 套管布置与破断形态
赵固矿区水文地质条件非常复杂,曾发生过突水淹井事故17次,淹采区14次。采用全覆盖注浆加固底板。开采山西组煤层平均厚度6.0 m,工作面埋深约700 m。区域内水压最高6.0 MPa以上,防治水问题严峻,采用全覆盖注浆加固底板岩层。从工作面开切眼沿走向长度500 m范围为第1阶段,底板注浆改造工程设计钻孔142个,进尺24 113 m。每个注浆孔下二级套管,一级套管直径为φ127 mm,套管长度10~18 m;二级套管直径为φ108 mm,套管长度40~80 m。消耗套管长度8 000余米。高水压区域,注浆工程施加长套管,水害严重的区域施加三级套管。注浆封堵裂隙过程中有多层灰岩时,要随时准备注浆,受高水压威胁需要施加多级套管,加固深部灰岩时套管长度会增加。工作面运输巷中一个钻场典型注浆钻孔布置如图2所示。

图2 工作面底板预注浆典型钻孔布置示意
Fig.2 Borehole layout of the grouting reconstruction drilling
in the floor
返修期间搜集到一些注浆套管,受到高地应力的作用发生弯曲或者破断,如图3所示。破断面表明浆液充填效果很好,多级套管之间、套管与浆液能够紧密耦合。当工作面开采后,在支承压力作用下,围岩应力分布变化,岩层扰动作用导致套管发生弯曲或破断。注浆套管的破断形态表明注浆套管破断前曾对岩体变形起到一定的抵抗作用。

图3 加固套管弯曲破断
Fig.3 Broken reingorcement casing pipes
2 分布支承压力作用下套管的空间应力求解
2.1 分布支承压力与套管受力模型
工作面开采形成采空区,在采空区四周分布着支承压力,可分为8个矩形区域(I~Ⅷ),如图4(a)所示。其中I~IV区支承压力为主体,V~Ⅷ区相对较小,暂忽略。支承压力q(x)在y方向线性分布[14],x方向属于三角形分布载荷。在局部坐标系中:
![]()
(2)
式中,k为应力集中系数;γ为上覆岩层的平均容重,kN/m3;H为埋藏深度,m;β为煤壁至集中应力峰值处距离,m;λ为集中应力峰值处至超前支承压力边界距离,m。
开采前在底板岩层中布置套管,如图4(b)所示,注浆封孔后,浆液、套管和围岩紧紧耦合,套管与岩层是作用与反作用的关系,分析套管变形需要求解套管上点的空间应力。

图4 分布支承压力与套管受力模型
Fig.4 Distributed abutment pressure and casing stress model
2.2 空间应力求解
以分布支承压力I区为例。将I区支承压力分块,分为一个矩形均布荷载δ1和两个三角形荷载Δ1和Δ2,如图5(a)所示。分别求解3块支承压力作用下的应力,然后叠加得到I区支承压力作用下的总应力(σij)I,再将4个区域的支承压力(I,II,III和IV)叠加得到套管上一点的空间应力。

图5 支承压力分块
Fig.5 Bearing pressure blocks
2.2.1 矩形均布支承压力外侧一点N的应力求解
先求均布荷载δ1角点下M的应力,然后按照图6,经过辅助线法和应力叠加法,转换公共角点,可以求得任一点N的应力σij。

图6 辅助线和叠加法计算采空区底板内任意点应力分布
Fig.6 Calculation of the stress distribution through auxiliary line
and superposition
矩形均布支承压力角点下M的应力求解。根据BOUSSINESQ和MINDLIN已解答的集中荷载作用下应力解[15-17],在局部坐标系中,经积分得到矩形(abcd)基底分块支承压力作用下角点下M点的应力(σij):
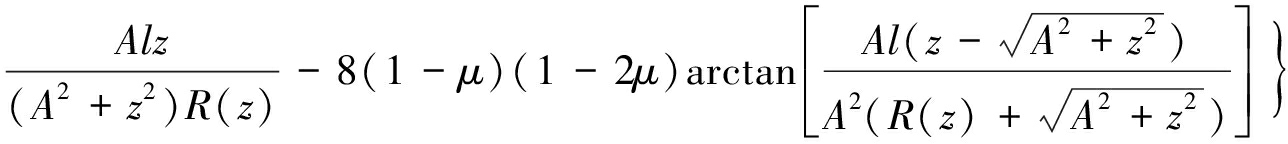
(3)
![]()
(4)
![]()
(5)
![]()
(6)
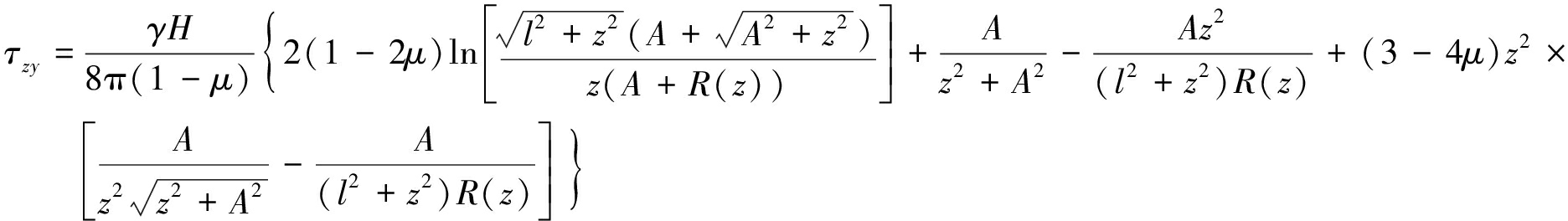
(7)

(8)
其中,![]() 为分区(Ⅰ区)支承压力区长度;l为分块(δ1)矩形分布荷载区宽度。
为分区(Ⅰ区)支承压力区长度;l为分块(δ1)矩形分布荷载区宽度。
矩形均布支承压作用下N点(图6)处的应力分布求解。分别求出矩形面积Nfag,Nfbh,Nedg和Nech在角点下N点的空间应力状态,然后按下式叠加:
(σij)δ1=σij(Nfag)+σij(Nfbh)-σij(Nedg)-σij(Nech)
(9)
2.2.2 三角形分布支承压力作用下点N的应力(σij)Δ1
三角形分布支承压力q(x)为线性荷载,与矩形均布荷载求解差距大,积分较复杂。以Δ1为例,通过积分计算得到矩形基底三角形分布支承压力(Δ1)作用下角点下M点的应力(σij)Δ1,在局部坐标系中,积分结果为
![]()
(10)
![]()
(11)
![]()
(12)
![]()
(13)
![]()
(14)
![]()
(15)
其中,![]() 为分块(Δ1)三角形分布荷载区宽度。
为分块(Δ1)三角形分布荷载区宽度。
然后,可按照式(9)的方法求解三角形分布支承压力作用下点N的应力(σij)Δ1。同理,可得(σij)Δ2。这样得到支承压力I区作用下底板岩体中N点的应力(σij)I:
(σij)I=σij(δ1)+σij(Δ1)+σij(Δ2)
(16)
2.2.3 四周总分布支承压力作用下套管上一点N的空间应力
将4个区的计算得到的空间应力叠加,得到采空区四周支承压力作用下底板岩层中一点N的应力(σij)N:
(σij)N=(σij)I+(σij)II+(σij)III+(σij)IV
(17)
2.3 空间中套管上点N正应力和切应力
围岩与套管接触点处存在一对作用力与反作用力。若给定围岩中一点的受力情况,则可得到套管上对应点的作用力。将图4中的套管取出,单独进行受力分析。套管上任一点N的空间应力状态如图7(a)所示。取一斜截面,其法线方向与套管弯曲平面的法线垂直,倾角为α;Sx,Sy,Sz为斜截面上全应力S在坐标轴上的投影分量。套管在斜截面上的投影及套管上一点的受力如图7(b)所示。

图7 空间中套管上点的应力状态
Fig.7 Stress state of point on casing pipes in space
2.3.1 套管上一点正应力σα
若已知N点的空间应力 则倾角为α的斜截面上的正应力σα可求得
则倾角为α的斜截面上的正应力σα可求得
σα=σxμ2+σyv2+σzw2+2(σxyμv+σyzvw+
σzxwμ)=σijninj
(18)
式中,μ,v,w为斜截面法线的方向余弦;ni,nj为指标符号,表示方向余弦。
2.3.2 套管上一点切应力τα
因为应力分量Sj=σijni(i,j=1,2,3),斜截面上的全应力![]() 所以倾角为α的斜截面上的切应力τα可求得
所以倾角为α的斜截面上的切应力τα可求得
![]()
(19)
2.4 浆液充填套管力学作用机制
基于浆液充填套管的抗弯刚度,分析其力学作用机制。工作面开采后形成底板破坏带是不可抗的大变形,其破坏深度与煤层采高(工艺)、底板岩性组合、埋深、岩石完整性及承受水压等因素密切相关。随着工作面推进,煤炭采出形成支承压力区,一部分底板岩体由弹性状态转变为塑性状态,形成底板破坏区。为说明套管抗弯性能对岩层变形作用情况,选择某一特定开采区域(开采条件一致)进行研究。选择底板岩体达到弹塑性极限平衡临界瞬态进行分析,此时底板岩体塑性变形即将发生,同时也能够满足弹性力学条件。根据矿压和土力学相关理论[18-20],底板破坏形态如图8所示,在弹塑性极限平衡瞬态,形成一准破坏滑动面。

图8 基于抗弯刚度的套管作用机制示意
Fig.8 Schematic diagram of casing pipes action mechanism
based on bending stiffness
以准滑动面为界,套管可分为两段,下段套管变形较小视为固定端,上段套管变形较大视为自由端。假定处于准滑动区内的套管为自由端,自由端长度rZ取大值,按照未施加套管时最大准破坏深度Dmax计算,rZ=Dmax/cos α。围岩稳定区内套管受固定端约束,自由端受岩体分布力作用。考虑套管抗弯性能,套管抗弯变形主要由套管上正应力引起,式(17)已经求得自由段套管上任一点的正应力σN。
因此,空间中倾角β套管阻抗底板注浆加固体变形在界点处产生套管弯矩为
Mβ(x,y,z)=![]() σN[(Dmax-z)/cos α]d/cos αdz
σN[(Dmax-z)/cos α]d/cos αdz
(20)
其中,Dmax为未注浆加固时准最大破坏深度;d为套管的直径;α=90°-β。σ=Ml/Iz,l为纵向面与中性层的距离;Iz为横截面对中性轴的惯性矩。
套管的弯曲强度条件为σmax=Mmax/W≤[σ]。其中,[σ]为注浆套管弯曲许用应力;W为注浆套管抗弯截面系数。
按照在分布力作用下的悬臂梁,计算套管顶端点O最大挠度为
cos α](Dmax-z)2/cos2αdz
(21)
所以,套管承受的底板垂向的最大变形量为:ωmax=ωOcos β。弯曲许用应力强度条件下套管可以控制底板变形,而且底板变形量为ωmax=ωOcos β。
3 套管对煤层底板岩体变形影响的数值分析
3.1 数值模型
参考现场条件建立模型长540 m,宽440 m,高214 m,模型中设6个钻场,沿着巷道方向钻场间距100 m,每个钻场按照设计布置7个钻孔,采空区外侧加固套管暂未考虑,如图9所示。选用直径φ108 mm的无缝套管,设定弹性模量为200 GPa,抗拉强度为245 MPa,抗内压强度98 MPa,抗挤强度95 MPa。参考该研究区的相关资料[21],本次数值计算中使用的岩体主要力学参数见表1。计算了无套管和施加套管2种情形。套管根据垂高分为25 m和40 m两种方案,比较分析套管长度对岩层变形的影响。
表1 顶底板岩体力学参数
Table 1 Mechanical parameters of rock and floor mass

岩层抗拉强度/MPa泊松比内摩擦角/(°)弹性模量/GPa黏聚力/MPa顶板岩层1.40.243226.08.50煤层1.30.25204.01.25灰岩5.30.304050.03.60泥岩1.40.243226.08.50中粒砂岩1.70.263528.58.50砂质泥岩2.10.283631.08.20粗粒砂岩1.50.233523.06.50细粒砂岩1.60.223322.07.00底板岩层5.30.304050.03.60

图9 数值模型
Fig.9 Numerical model
3.2 模拟结果分析
3.2.1 套管位移形态与围岩变形分析
选取套管所在剖面,得到工作面开采60,80和100 m时,套管与围岩变形破坏如图10所示。由图10可以看出,随着工作面推采,采空区下方底板岩体变形破坏,套管也发生变形,而且随着底板破坏区变大,发生弯曲变形的套管长度亦增大,垂向位移变化与围岩变形破坏紧密联系。套管位移变化以破坏区底部为界,上方变形明显大于下方,呈现弯曲变形。工作面开采60,80和100 m时套管最大变形分别为1.4,2.0和2.2 cm。

图10 工作面开采不同距离时套管位移形态与围岩变形破坏
Fig.10 Casing pipes displacement shape and surrounding rock
deformation and failure at different mining distance of working face
3.2.2 监测点位移量变化
测点布置。沿着工作面推进方向布置2条测线,每条测线在垂直方向布置10个测点。其中,1号测线距离开切眼10 m,监测点序号和在岩层中与煤层底板的距离如图11所示。

图11 监测点布置和不同条件下监测点位移曲线
Fig.11 Layout of monitoring points and their
displacement curves under different conditions
测线中的1号监测点位移显示,随着工作面开采,位移逐渐增大。以开采60 m为例,无套管时监测点位移6.92 cm,施加垂高25 m套管时,位移降低为6.73 cm;施加垂高40 m套管时,位移降低为6.49 cm。施加套管时监测点位移变形量小于未施加套管时的变形量,且套管长度越大变形量越小,计算结果表明套管能够起到阻抗变形的作用。开采100 m时1号测线10个监测点位移曲线存在拐点,底板岩层变形存在差异性,在变形较大区域,套管对岩层变形的影响比较明显。
4 注浆工程应用
实际生产中,很多矿区面临煤层带压开采问题,常采用井下预注浆加固煤层底板岩层,能够保证矿井的正常生产,如峰峰、肥城、焦作等矿区。为了确保安全,矿井生产时先注浆再开采。因此,当工作面开采时,监测到底板数据一般为岩体加固后的底板破坏效果,是浆液充填套管和围岩耦合作用的结果。相比较而言,一般在矿井生产初期或者巷道掘进时更容易比较和分析注浆前后的岩层变形情况。也可以根据作用力与反作用力的关系,通过套管的变形表征和监测围岩的变形,根据套管的破坏形态分析注浆效果。
赵固矿区水压和地应力都非常高,尤其是矿井生产初期,底板岩体变形严重,发生底臌,严重处高达2 m以上,后期采用注浆加固,底臌变形得到有效控制,取得良好效果,几处典型的底板岩层变形及加固后效果情况见表2,巷道底板变形得到大大改善。与巷道相比,工作面开采空间大,底板更易变形破坏。但是,矿井正常生产过程中,采用井下长套管全覆盖注浆加固底板岩层,然后推采工作面(图2)。目前矿井工作面回采多年,基本保障矿井的安全生产,井下注浆效果理想,但注浆工程量很大,注浆成本很高。
表2 底板岩体变形及加固后效果
Table 2 Deformation and reinforcement effect of floor
rock mass

井下位置底臌变形量/m措施效果工作面回风巷道>2.5长套管加固 良好沿胶带上山与东横贯V交叉处>2.0长套管加固 良好I盘区中辅助运输上山0.5长套管加固 良好I盘区辅助运输上山与东横贯VI交叉处0.5长套管加固 良好
5 结 论
(1)以套管为研究对象,建立了分布支承压力作用下底板岩层中注浆加固套管的空间受力模型,将采空区四周分布支承压力分区,积分得到矩形基底三角形和矩形支承压力角点下的任一点M的应力状态,并运用叠加法得到了采空区下方底板岩层中套管上任一点的空间应力。
(2)建立以浆液充填套管为中心的力学模型,分析弹塑性极限平衡条件下岩层变形特征和套管受力特点,阐明了套管对准破坏区岩层变形的影响机制,得到了浆液充填套管在界点处的弯矩理论公式和基于套管抗弯刚度和许用应力的容许变形公式。
(3)数值计算结果表明随着底板破坏区变大,发生弯曲变形的套管长度亦增大,垂向位移变化与围岩变形破坏紧密联系,套管位移变化以破坏区底部为界,上方变形明显大于下方,呈现弯曲变形。施加套管时监测点位移变形量小于未施加套管时的变形量,且套管长度越大变形量越小。
[1] 施龙青,邱梅,牛超,等.肥城煤田奥灰顶部注浆加固可行性分析[J].采矿与安全工程学报,2015,32(3):356-361.
SHI Longqing,QIU Mei,NIU Chao,et al.Feasibility analysis of grouting reinforcement of Ordovician top in Feicheng coalfield[J].Journal of Mining & Safety Engineering,2015,32(3):356-361.
[2] 陈新明.大埋深复杂水文地质条件工作面防治水技术研究[D].北京:中国矿业大学(北京),2013:53-59.
CHEN Xinming.Study of the water prevention technology on the working face under great death and complicated hydrogeological conditions[D].Beijing:China University of Mining & Technology(Beijing),2013:53-59.
[3] 赵庆彪.奥灰岩溶水害区域超前治理技术研究及应用[J].煤炭学报,2014,39(6):1112-1117.
ZHAO Qingbiao.Ordovician limestone karst water disaster regional advanced governance technology study and application[J].Journal of China Coal Society,2014,39(6):1112-1117.
[4] 赵兵文,关永强.大采深矿井高承压奥灰岩溶水综合治理技术[J].煤炭科学技术,2013,41(9):75-78.
ZHAO Bingwen,GUAN Yongqiang.Comprehensive treatment technology of high pressure-bearing Ordovician Limestone Karst Water in large mining depth mine[J].Coal Science and Technology,2013,41(9):75-78.
[5] 张伟,庞迎春,王永龙.工作面底板浅部灰岩注浆改造技术与实践[J].煤炭技术,2008,27(10):102-104.
ZHANG Wei,PANG Yingchun,WANG Yonglong.Reformation technology and practice of lime rock grouting at Shallow section of working face floor[J].Coal Technology,2008,27(10):102-104.
[6] 许延春,李见波.注浆加固防治底板突水机理与应用[M].北京:煤炭工业出版社,2017:76-78.
[7] LI Jianbo.Water inrush from pregrouting fractures induced by mining activities and its engineering control method optimization[J].Advances in Civil Engineering,2019(5):1-10.
[8] 李见波,许延春,王新梅.注浆加固套管抗弯性能对煤层底板变形的影响[J].采矿与安全工程学报,2017,34(2):336-341.
LI Jianbo,XU Yanchun,WANG Xinmei.The effect of flexural behavior of the grouting reinforcement casing on coal seam floor deformation[J].Journal of Mining & Safety Engineering,2017,34(2):336-341.
[9] 张智峰,毛冬冬,苏本泉.新安煤矿三级套管深孔注浆治水技术研究[J].煤,2015,24(7):17-19.
ZHANG Zhifeng,MAO Dongdong,SU Benquan.Technology of governing the water by grouting cement deeply in three-stage casing deeply on Xin’an coal mine[J].Coal,2015,24(7):17-19.
[10] 白晨光,贾立宏,马金普,等.抗弯功能微型桩在基坑支护中的应用[J].岩土工程学报,2006,28(S):1656-1658.
BAI Chenguang,JIA Lihong,MA Jinpu,et al.Application of micropiles with anti-bending function to retaining and protection of foundation excavation[J].Chinese Journal of Geotechnical Engineering,2006,28(S):1656-1658.
[11] 唐咸远,杨和平,肖杰,等.注浆微型钢管桩抗弯承载力及抗弯刚度研究[J].工业建筑,2016,46(10):89-94.
TANG Xianyuan,YANG Heping,XIAO Jie,et al.Experimental study of flexural behavior of ground microsteel pipe piles[J].Industrial Construction,2016,46(10):89-94.
[12] 钱稼茹,王刚,赵作周,等.钢管高强混凝土构件截面弯矩-曲率全曲线研究[J].工业建筑,2004,34(8):70-72,89.
QIAN Jiaru,WANG Gang,ZHAO Zuozhou,et al.Research on section moment-curvature relation curves of steel tube confined high-strength concrete members[J].Industrial Construction,2004,34(8):70-72,89.
[13] 王力尚,钱稼茹.钢管高强混凝土应力-应变全曲线试验研究[J].建筑结构,2014,34(1):11-12.
WANG Lishang,QIAN Jiaru.Experimental research on complete axial compressive stress-strain curve of high-strength concrete filled steel tubular columns[J].Building Structure,2014,34(1):11-12.
[14] 孟祥瑞,徐诚辉,高召宁,等.采场底板应力分布及破坏机理[J].煤炭学报,2010,35(11):1832-1836.
MENG Xiangrui,XU Chenghui,GAO Zhaoning,et al.Stress distribution and damage mechanism of mining floor[J].Journal of China Coal Society,2010,35(11):1832-1836.
[15] MINDLIN R.Force at a point in the interior of a semi-infinite solid[J].Physics,1936,7(5):195-202.
[16] 徐芝纶.弹性力学简明教程(第三版)[M].北京:高等教育出版社,2002:160-163.
[17] 袁聚云,赵锡宏.竖向均布荷载作用在地基内部时的土中应力公式[J].上海力学,1995,16(3):213-221.
YUAN Juyun,ZHAO Xihong.Formulas for the calculation of stress in soil subjecting to distributed loading beneath the surface of ground[J].Shanghai Mechanics,1995,16(3):213-221.
[18] 钱鸣高,石平五,许家林.矿山压力与岩层控制[M].徐州:中国矿业大学出版社,2010:188-190.
[19] 郑大同.地基极限承载力计算[M].北京:中国建筑工业出版社,1979.
[20] PRANDTL L.Uber die Eindringungs festigkeit Harte plastischer Baustoffeund die Festigkeit von Schneiden[J].Journal of Applied Mathematics and Mechanics,1921,1(1):15-20.
[21] 贾明魁,许延春,魏世义,等.高突水危险大采高工作面底板注浆加固改造防治水技术[R].焦作煤业(集团)新乡能源有限公司,中国矿业大学(北京),2011:27-28.
