准确描述岩石强度与变形是评价工程岩体安全和稳定性的基础,现有应力强度理论与破坏准则很难有效描述岩石复杂的强度变化与整体破坏行为[1]。岩石破坏是能量驱动下的一种状态失稳现象[2],受载岩石变形过程伴随能量演化,峰前以能量积聚为主,峰后主要表现为能量耗散与释放,岩石变形破坏可看成是不同形式能量相互转换的结果。因此,从能量角度研究岩石变形和失稳,更接近其破坏本质[3-5]。
基于能量守恒理论,国内外学者对岩石加卸载过程能量演化规律开展了大量研究,取得了丰富的研究成果。具有代表性的有:谢和平等[6-8]阐述了岩石变形破坏过程能量耗散与损伤、能量释放与整体破坏的关系,定义了基于能量耗散与释放原理的岩石强度失效准则和岩体整体破坏准则。张志镇等[9-11]研究了不同岩石类型能量演化的异同点,建立了岩石能量演化随加载条件的自我抑制模型,揭示了岩石能量耗散的围压效应。宫凤强、李淼等[12-13]分别研究了动静态劈裂过程岩石能量构成与耗散特征,揭示了动静荷载作用下岩石能量耗散机制及各向异性特征。与此同时,许江等[14]、杨磊等[15]、尹光志和苏国韶[16-17]、李杨杨等[18]分别研究了含孔隙水砂岩、煤岩组合体、不同加载速率以及循环加卸载等条件下岩石能量积聚与耗散特征,丰富了岩石能量理论的研究成果。
现有研究常聚焦于室内试验,多是针对特定加卸载条件、岩样类型以及其他条件下(含水率、温度[19]等)岩石能量演化特征的描述,研究对象着重关注岩石屈服、峰值等特征点,对于贯穿岩石变形破坏全过程的能量实时演化及分配规律认识不足[9]。岩石能量积聚、耗散及其状态间的转化决定了其内部裂隙扩展和变形破坏,虽然从能量角度反演岩石破坏路径对实验结果意义不大,但对于评估工程岩体区域稳定、精准定位加固位置至关重要。目前,实验室常用岩石破坏监测手段有声发射定位[20],CT扫描[21],SEM电镜扫描[22],CCD相机[23]等,其中,仅有声发射可以实时定位受载岩样变形破坏路径,但该方法多用于单轴压缩试验,且存在操作复杂、误差大等缺点,很难推广应用于工程岩体的监测。分析工程岩体稳定性时多是基于围岩应力场、位移场及支护场的耦合作用关系进行综合评判。
为增加能量理论模型分析工程问题时的适用性,笔者基于能量守恒和有限差分理论,推导岩石能量耗散有限差分方程式,采用FISH语言将其应用于FLAC3D应变软化本构模型。以室内试验结果验证采用耗散能演化描述受载岩石变形破坏的合理性,进一步讨论能量耗散模型在深部高应力巷道中的应用,揭示工程岩体峰后变形破坏全过程耗散能演化特征与分配规律,为从能量耗散角度评估工程岩体安全和稳定性提供理论依据,弥补FLAC3D软件采用塑性区定性判断地下工程围岩破坏时的不足。
1 岩石能量耗散的室内实验
1.1 岩石单、三轴压缩试验
试验岩样取自徐矿集团三河尖煤矿吴庄区运输大巷,选取岩性均匀、结构完整的取芯岩柱加工岩样,采用GCTS-RTX3000岩石力学试验系统进行单轴和常规三轴压缩试验,测试岩石基本力学参数,围压等级设置为0,5,15和25 MPa,测试结果分别如图1和表1所示。
表1 常规单、三轴试验结果
Table 1 Results of uniaxial and triaxial tests

围压/MPa峰值强度/MPa残余强度/MPa弹性模量/GPa泊松比黏聚力/MPa内摩擦角/(°)074.501.748.340.21597.5125.818.050.2017.0739.6615137.0160.529.480.1725184.8590.4911.030.14

图1 岩石应力-应变曲线
Fig.1 Stress-strain curves of the rock samples
1.2 岩石能量耗散特征
岩样在试验机外力作用下产生变形,假设该物理过程与外界没有热交换,即封闭系统,外力功所产生的总输入能量为Wz,根据热力学第一定律[6]得到
Wz=We+Wd
(1)
式中,We为岩石可释放弹性应变能;Wd为耗散能。
由式(1)可知,岩石总输入能量Wz一部分作为可释放的弹性能储存在其内部,另一部分则伴随岩石变形破坏耗散和释放,此过程不可逆[8-9]。岩石损伤程度越高,耗散能越大,残余弹性能越少。
对于单轴压缩试验,试样总输入能量Wz等于轴向输入能量Wa;而常规三轴压缩试验,轴向输入能量Wa应包含试样总输入能量Wz以及环向膨胀对液压油做功所释放能量Wh两部分,为此,常三轴压缩条件下岩石总输入能量[6]可表示为
Wz=Wa-Wh=![]() σ1dε1-2
σ1dε1-2![]() σ3dε3
σ3dε3
(2)
式中,ε1,ε3分别为轴向应变和环向应变;σ1,σ3分别为轴向应力和围压。
根据弹性力学相关理论,岩石可释放弹性能We[6]可由下式计算:
![]()
(3)
式中,![]() 分别为轴向和环向的弹性应变。
分别为轴向和环向的弹性应变。
则岩石耗散能Wd可由下式求得
Wd=Wz-We
(4)
采用式(2)~(4)分别计算岩样总输入能量Wz、弹性能We和耗散能Wd,如图2所示。由图2可知,岩样总输入能量随轴向应变增加逐渐增大,应力达到峰值前主要以弹性能形式储存在岩样内部,耗散能变化不大。当岩样加载至峰后阶段,岩样总输入能量依然持续增加,但主要伴随峰后破坏而耗散,此外,岩样内部储存的大部分弹性能也将转化成耗散能释放,能量转化程度与岩样变形破坏程度正相关。

图2 室内试验岩样能量演化规律
Fig.2 Evolution law of energy of rock samples in laboratory test
2 FLAC3D能量耗散模型的开发
FLAC3D采用显示差分算法,在给定t时刻应力值![]() 和Δt时间步总应变增量Δεi,进而求解t+Δt时刻应力状态
和Δt时间步总应变增量Δεi,进而求解t+Δt时刻应力状态![]() 该求解过程用到了主应力σ1,σ2和σ3,主应力和主应力方向由应力张量确定,并按顺序排列(压应力为负)[25]:
该求解过程用到了主应力σ1,σ2和σ3,主应力和主应力方向由应力张量确定,并按顺序排列(压应力为负)[25]:
σ1<σ2<σ3
(5)
相应的主应变增量Δεi[25]可分解为
![]()
(6)
其中,![]() 分别为弹、塑性应变增量。屈服前只有
分别为弹、塑性应变增量。屈服前只有![]() 屈服后Δεi可按式(6)求得。
屈服后Δεi可按式(6)求得。
单元体弹性应变增量和应力增量之间的关系[25]可表示为
![]()
(7)
其中,Si为弹性应变增量![]() 的线性函数,下脚标“j”表示从i=1至i=j范围的组件,j等于模型维数,取j=3,根据广义胡克定律,单元体各方向应力增量和应变增量可展开[25]如下:
的线性函数,下脚标“j”表示从i=1至i=j范围的组件,j等于模型维数,取j=3,根据广义胡克定律,单元体各方向应力增量和应变增量可展开[25]如下:
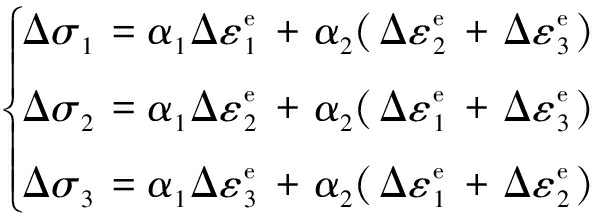
(8)
式中,α1,α2为切变模量G和体积模量K控制的岩石材料常数,其中,α1=K+4G/3,α2=K-2G/3。
基于Mohr-Coulomb的应变软化模型在峰后软化过程控制强度参数描述材料的峰后软化行为,对于剪切破坏,非关联流动法则[25]改写为
![]()
(9)
式中,λs为塑乘因子;gs为剪切势函数,其表达式为
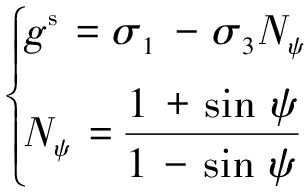
(10)
式中,ψ为剪胀角。
因此,联立式(6),(7)和(9),由总应变表示的应力增量Δσi表达式[25]为
进而求解得到t+Δt时刻应力![]() 为
为
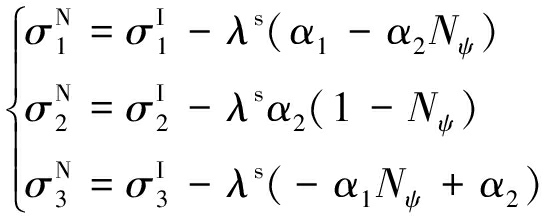
(12)
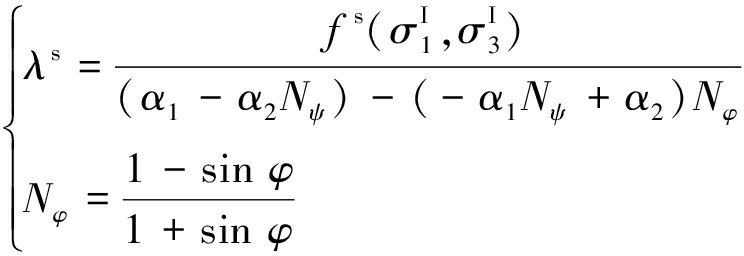
(13)
式中,φ为内摩擦角。
根据FLAC3D应变软化模型屈服准则,岩体材料剪切破坏面上应力[25]满足:
![]()
(14)
式中,c为黏聚力。
拉伸破坏面上应力[25]满足:
ft=σ3-σt=0
(15)
式中,σt为抗拉强度。
式(14)和(15)分别为FLAC3D应变软化模型判定材料压剪破坏和张拉破坏的失稳准则。
然而,计算单元能量时,需要采用指针函数捕捉单元t时刻应力![]() 时间步应变增量Δεi以及t+Δt时刻单元应力分量
时间步应变增量Δεi以及t+Δt时刻单元应力分量![]() 计算Δt时间步单元平均应力分量
计算Δt时间步单元平均应力分量![]() 进而求解单元总能量,及其对应的可释放弹性能和耗散能。
进而求解单元总能量,及其对应的可释放弹性能和耗散能。
如图3所示,采用单元t时刻应力![]() 和t+Δt时刻应力
和t+Δt时刻应力![]() 的平均值表征Δt时间步单元应力
的平均值表征Δt时间步单元应力![]() 即
即

图3 单元能量计算简图
Fig.3 Schematic diagram for the energy calculation
![]()
(16)
假设t时刻对应第n循环,t+Δt时刻对应第n+1循环,则第n+1循环内总能量增量可表示为
![]()
(17)
第n循环至第n+1循环运算的物理意义表示岩体受外力作用时,某一运算时步内单元网格应力-应变行为的差分运算。t+Δt时刻单元总能量等于n+1循环总能量增量累加,即
![]()
(18)
不考虑峰后弹性模量衰减,单元可释放弹性应变能可由下式计算:
![]()
(19)
则单元耗散能计算式如下:
![]()
(20)
采用FISH语言将岩石能量耗散模型写入FLAC3D应变软化模型中,具体开发过程如图4所示。模型建立后,首先遍历单元网格,并对单元编号,设置运算终点Q,定义单循环运算时步m;运算之前首先捕捉各单元初始应力![]() 启动第1循环运算,捕捉m时步后单元应力
启动第1循环运算,捕捉m时步后单元应力![]() 和应变增量Δεi,计算单元能量;之后判定运算是否到达设置终点,若是,则将计算能量赋值给相应单元,打印能量演化云图,导出数据并结束;若否,则启动下一循环,直至到达设置运算终点。需要注意,采用能量模型模拟室内加卸载试验时,一般采用位移加载,设置运算终点为Step时间步。
和应变增量Δεi,计算单元能量;之后判定运算是否到达设置终点,若是,则将计算能量赋值给相应单元,打印能量演化云图,导出数据并结束;若否,则启动下一循环,直至到达设置运算终点。需要注意,采用能量模型模拟室内加卸载试验时,一般采用位移加载,设置运算终点为Step时间步。

图4 单元能量计算流程
Fig.4 Energy calculation flow for the model cells
3 模型校验与运算
3.1 岩样模型建立
建立标准岩样数值模型,尺寸φ×H=50 mm×100 mm,共划分17 280单元,如图5所示。模型底部固定位移边界,四周施加环向边界应力模拟围压,上边界通过施加轴向位移对岩样加压,加载速率2.5×10-5 mm/step,计算时忽略岩石自重影响。
模型采用基于Mohr-Coulomb的应变软化本构模型,以表1给出的岩样力学参数对模型进行初始赋值。岩石峰后软化阶段黏聚力和内摩擦角随应变的变化数据由试验结果计算得到,见表2。
表2 岩石峰后软化参数
Table 2 Post-peak parameters of rock samples

塑性应变εpsc/MPaφ/(°)塑性应变εpsc/MPaφ/(°)017.0739.660.015 09.0336.110.002 516.9139.640.175 07.5632.180.005 015.5340.360.020 05.8031.660.007 513.7240.830.050 01.5133.300.010 012.3540.120.500 01.5133.300.012 510.3539.331.000 01.5133.30
依据图5建立的数值模型,表1和2所列岩石力学参数进行数值分析,图6给出了模拟岩样应力应变曲线与试验结果的对比,由图6可知,不同围压下岩样应力应变曲线模拟结果较为匹配试验结果,单轴压缩和低围压条件下岩样脆性特征得到较好描述,表明所选取的岩石参数和数值本构模型合理,可用于后续能量模块的模拟分析。

图5 岩样数值模型
Fig.5 Numerical model of rock samples

图6 应力-应变曲线校验
Fig.6 Verifications of the stress-strain curves
3.2 岩样能量模型校验
考虑到耗散能是由岩石总能量减去弹性应变能计算得到,限于篇幅,校验能量模型时只校验总能量和耗散能两个指标。如图7(a)所示,不同围压下岩样总能量数值模拟结果与试验结果基本吻合,表明FISH语言编写的能量算法可靠性较强。
但需要指出的是,模拟岩样峰后耗散能演化曲线与试验结果吻合度较好,但峰前存在差异性,如图7(b)所示。峰前阶段,岩样试验耗散能主要呈缓慢线性增加;加载至峰值80%时,耗散能近似指数增加;一旦到达峰后某破坏点,耗散能演化为斜率较大的直线增长,最终进入残余阶段。数值模拟可近似反演耗散能演化趋势,耗散能在峰后增长曲线与试验结果匹配较好,且总量大致相等;但峰前阶段存在显著差异,模拟峰前耗散能近似等于0,主要原因是能量模型峰前假设不发生塑性变形,无法准确描述孔隙、松软岩体初始压密阶段和峰前塑性阶段,导致围压越大,峰前耗散能相差越大。但是,对于地下工程岩体的分析更关注于峰后变形破坏,由于该模型可较好模拟岩石峰后能量耗散特征,可用于岩石峰后变形破坏的模拟。

图7 能量模型校验
Fig.7 Verifications of the energy model
3.3 岩样峰后破坏路径反演
图8给出了不同围压下岩石破坏模式对比,其中,数值模拟给出的是岩石残余阶段耗散能密度演化云图,对应试验岩样残余阶段破坏照片。由图8可知,岩样单轴压缩试验呈纵向劈裂破坏,模拟岩样耗散能集中区域位于岩样中线偏上位置,并向周边演化出一“八”字分支集中线,岩样耗散能演化沿中线呈轴对称分布,反映了岩样单轴压缩时的纵向劈裂特征,与试验结果吻合度较高。随着围压增加,试验岩样逐渐向剪切破坏演化,破断角逐渐减小;模拟岩样在5 MPa时耗散能密度集中成“y”型分布,长边集中程度显著大于短边,为岩样主破断面;随围压进一步增加,其破坏模式演化成斜切面,且围压越大,耗散能越大,破断角越小,与试验结果基本吻合,表明采用耗散能密度演化揭示岩石峰后破坏行为是可行的。

图8 岩石破坏模式校验
Fig.8 Verifications of the failure modes of rock samples
工程现场,准确掌握围岩变形破坏路径,精准定位加固位置是控制其稳定的前提。为此,反演岩石峰后耗散能演化过程可为揭示其主破坏区演化、评判岩石稳定性提供新途径。图9给出了围压25 MPa时不同峰后目标点岩样耗散能密度演化云图。岩样初始进入峰后阶段(B点),经历裂隙孕育形成初始主裂隙面,并随着轴向应变增加,主裂隙面耗散能逐渐增加,一旦岩样进入残余阶段(F点),主裂隙面耗散能密度增幅减小并趋于稳定,表明岩样此时已发生宏观破断,继续加载将导致其结构失稳。

图9 围压25 MPa岩样峰后破坏路径
Fig.9 Post-peak destruction path of rock sample with a confining pressure of 25 MPa
4 能量耗散模型的应用
将能量耗散模型应用于分析吴庄区运输大巷,尝试从能量耗散角度揭示巷道变形破坏路径,为巷道加固提供依据。建立试验巷道三维数值模型,尺寸X×Y×Z=60 m×40 m×60 m,水平、底边界限制位移,上边界施加20 MPa载荷模拟巷道800 m埋深,依据地应力测试结果,取侧压系数0.8。巷道断面宽×高=5 m×4 m,模拟巷道锚杆支护参数与现场一致。
模拟采用应变软化模型,由于岩石实验参数无法直接应用于工程岩体,模拟前需校验岩体参数。基于实验获取的岩石强度参数衰减规律,采用RocLab软件进行岩体参数转换,以获取的初始岩体参数进行赋参,以实测巷道变形作为已知值,校验获取的岩体参数见表3,4。同时,为防止单元畸变中断运算,模拟时未设置set large命令。由于巷道周边围岩受力多处于三向不等压状态,计算单元能量时考虑中间主应力,各应力分量增量计算方法见式(12),再由式(17)~(20)分别计算单元总能量、弹性能和耗散能。
表3 校验岩体参数(峰前)
Table 3 Calibrated parameters of the rock masses

弹性模量/GPa泊松比黏聚力/MPa内摩擦角/(°)抗拉强度/MPa2.090.263.6130.360.4
图10给出了试验巷道模拟结果与现场对比图。试验巷道开挖后,采用锚网索支护,巷道顶帮变形得到控制,顶帮变形均在200 mm以内;但底臌严重,最大底臌量接近1 000 mm,模拟巷道变形与现场实测数据基本吻合。
表4 校验岩体参数(峰后)
Table 4 Calibrated parameters of the rock masses
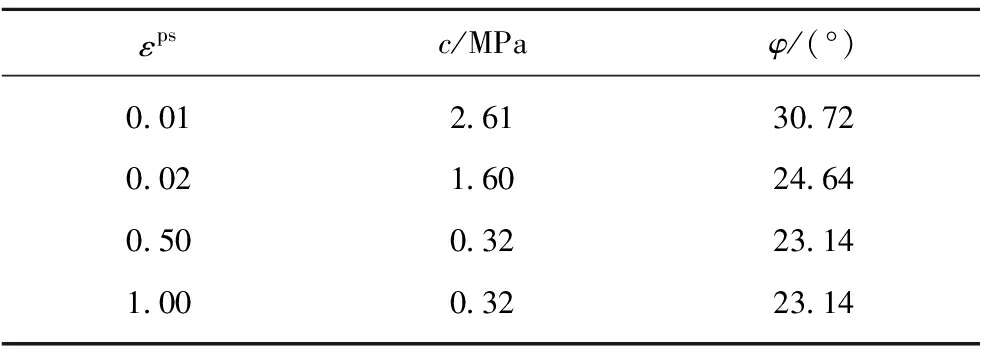
εpsc/MPaφ/(°)0.012.6130.720.021.6024.640.500.3223.141.000.3223.14

图10 试验巷道变形破坏对比
Fig.10 Comparisons on the roadway deformations
模拟巷道塑性区主要集中于两帮和底板,基于软件拉剪屈服破坏准则,仅可以区分底帮围岩变形破坏方式,但很难量化底帮围岩的破坏程度,也就无法准确定位巷道后期加固区域。而利用开发的能量耗散模型,从巷道耗散能集中区分布可实现对巷道围岩主失稳区域的实时定位,同时,依据围岩耗散能集中程度可以量化岩体变形破坏程度。如图10所示,巷道底板破坏后,底角位置分别存在两个耗散能集中区,均呈条状分布,一条贯通与底角,诱发底角剪切破坏;另一条则向底板中部演化,加剧底臌。
基于3.3节,研究开发的能量耗散模型除可定位围岩主破坏位置,还可以通过控制运算时步反演巷道变形破坏路径。图11给出了不同时步对应的巷道围岩耗散能密度演化云图,运算平衡时对应的耗散能云图如图10所示。由图11可知,巷道开挖后耗散能集中区位于巷道两底角处,表明直角相比于拱形更易产生剪切破坏,这与前人研究结论相吻合。随着时间增加,巷道底角破坏后,耗散能集中区域将向深部围岩转移,并逐渐演化成带状分布,一端向巷道两帮转移,一端朝向巷道底板方向,诱发巷道底臌和两帮收敛。对于破坏后的巷道,如对底帮尤其是底角围岩不加以控制,剧烈底臌将进一步引发巷帮松动破坏,甚至危及顶板稳定,最终诱发巷道整体灾变失稳。

图11 巷道破坏路径演化模拟
Fig.11 Simulated results of the failure paths of roadway
对于试验巷道,后期采用了巷帮短锚索和底板锚杆(索)加固,巷道大变形得到有效控制。限于篇幅,具体参数不再赘述。综上,研究开发的能量耗散模型对于反演巷道变形破坏路径和定位巷道主破坏位置提供了一条新途径,可为巷道失稳预测预报和加固设计提供了参考,具有较强的实用价值。
5 结 论
(1)基于能量平衡和有限差分理论,推导了岩石耗散能有限差分方程式,采用FISH语言将其写入FLAC3D应变软化模型,补充了软件能量计算模块。通过与室内试验对比,该模型可有效描述岩石峰后变形特征及破坏路径。
(2)利用开发的能量耗散模型分析了深部巷道能量演化规律,采用耗散能演化不仅可定位巷道主破坏位置,同时可有效反演围岩全过程变形破坏路径,为巷道变形预测及加固设计提供了一条新途径。
(3)岩石能量耗散模型在FLAC3D中的实现,扩展了FLAC3D软件的适用范围,一定程度上弥补了常规采用塑性区定性判断地下工程围岩破坏及其稳定的不足,具有重要的理论意义和现场实用价值。
[1] 文志杰,田雷,蒋宇静,等.基于应变能密度的非均质岩石损伤本构模型研究[J].岩石力学与工程学报,2019,38(7):1332-1343.
WEN Zhijie,TIAN Lei,JIANG Yujing,et al.Research on damage constitutive model of inhomogeneous rocks based on strain energy density[J].Chinese Journal of Rock Mechanics and Engineering,2019,38(7):1332-1343.
[2] 侯连浪,刘向君,梁利喜,等.割理对煤岩加载过程能量演化特征影响数值模拟[J].煤炭学报,2020,45(3):1061-1069.
HOU Lianlang,LIU Xiangjun,LIANG Lixi,et al.Numerical simulation of effect of cleats on energy evolution of coal and rock in loading process[J].Journal of China Coal Society,2020,45(3):1061-1069.
[3] 马振乾,姜耀东,李彦伟,等.加载速率和围压对煤能量演化影响试验研究[J].岩土工程学报,2016,38(11):2114-2121.
MA Zhenqian,JIANG Yaodong,LI Yanwei,et al.Experimental research on influence of loading rate and confining pressure on energy evolution of coal[J].Chinese Journal of Geotechnical Engineering,2016,38(11):2114-2121.
[4] 武仁杰,李海波,李晓锋,等.冲击载荷作用下层状岩石破碎能耗及块度特征[J].煤炭学报,2020,45(3):1053-1060.
WU Renjie,LI Haibo,LI Xiaofeng,et al.Broken energy dissipation and fragmentation characteristics of layered rock under impact loading[J].Journal of China Coal Society,2020,45(3):1053-1060.
[5] 张东明,白鑫,尹光志,等.含层理岩石单轴损伤破坏声发射参数及能量耗散规律[J].煤炭学报,2018,43(3):646-656.
ZHANG Dongming,BAI Xin,YIN Guangzhi,et al.Analysis of acoustic emission parameters and energy dissipation characteristics and damage evolution of bedding rock failure process under uniaxial compression[J].Journal of China Coal Society,2018,43(3):646-656.
[6] 谢和平,鞠杨,黎立云.基于能量耗散与释放原理的岩石强度与整体破坏准则[J].岩石力学与工程学报,2005,24(17):3003-3010.
XIE Heping,JU Yang,LI Liyun.Criteria for strength and structural failure of rocks based on energy dissipation and energy releaseprinciples[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(17):3003-3010.
[7] 谢和平,鞠杨,黎立云,等.岩体变形破坏过程的能量机制[J].岩石力学与工程学报,2008,27(9):1729-1740.
XIE Heping,JU Yang,LI Liyun,et al.Energy mechanism of deformation and failure of rock masses[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(9):1729-1740.
[8] 谢和平,彭瑞东,鞠杨,等.岩石变形破坏过程中的能量耗散分析[J].岩石力学与工程学报,2004,23(21):3565-3570.
XIE Heping,PENG Ruidong,JU Yang,et al.Energy dissipation of rock deformation and fracture[J].Chinese Journal of Rock Mechanics and Engineering,2004,23(21):3565-3570.
[9] 张志镇,高峰.受载岩石能量演化的围压效应研究[J].岩石力学与工程学报,2015,34(1):1-11.
ZHANG Zhizhen,GAO Feng.Confining pressure effect on rock energy[J].Chinese Journal of Rock Mechanics and Engineering,2015,34(1):1-11.
[10] 张志镇,高峰.3种岩石能量演化特征的试验研究[J].中国矿业大学学报,2015,44(3):416-422.
ZHANG Zhizhen,GAO Feng.Experimental investigations on energy evolution characteristic of coal,sandstone and granite during loading process[J].Journal of China University of Mining & Technology,2015,44(3):416-422.
[11] 张志镇,高峰.单轴压缩下岩石能量演化的非线性特性研究[J].岩石力学与工程学报,2012,31(6):1198-1207.
ZHANG Zhizhen,GAO Feng.Research on nonlinear characteristics of rock energy evolution under uniaxial compression[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(6):1198-1207.
[12] 宫凤强,罗松,李夕兵,等.红砂岩张拉破坏过程中的线性储能和耗能规律[J].岩石力学与工程学报,2018,37(2):352-363.
GONG Fengqiang,LUO Song,LI Xibing,et al.Linear energy storage and dissipation rule of red sandstone materials during the tensile failure process[J].Chinese Journal of Rock Mechanics and Engineering,2018,37(2):352-363.
[13] 李淼,乔兰,李庆文.高应变率下预制单节理岩石 SHPB 劈裂试验能量耗散分析[J].岩土工程学报,2017,39(7):1336-1343.
LI Miao,QIAO Lan,LI Qingwen.Energy dissipation of rock specimens under high strain rate with single joint in SHPB tensile tests[J].Chinese Journal of Geotechnical Engineering,2017,39(7):1336-1343.
[14] 许江,张媛,杨红伟,等.循环孔隙水压力作用下砂岩变形损伤的能量演化规律[J].岩石力学与工程学报,2011,30(1):141-148.
XU Jiang,ZHANG Yuan,YANG Hongwei,et al.Energy evolution law of deformation and damage of sandstone under cyclic pore water pressures[J].Chinese Journal of Rock Mechanics and Engineering,2011,30(1):141-148.
[15] 杨磊,高富强,王晓卿,等.煤岩组合体的能量演化规律与破坏机制[J].煤炭学报,2019,44(12):3894-3902.
YANG Lei,GAO Fuqiang,WANG Xiaoqing,et al.Energy evolution law and failure mechanism of coal-rock combined specimen[J].Journal of China Coal Society,2019,44(12):3894-3902.
[16] 尹光志,马波,刘超,等.真三轴应力条件下加卸荷速率对砂岩力学特性与能量特征的影响[J].煤炭学报,2019,44(2):454-462.
YIN Guangzhi,MA Bo,LIU Chao,et al.Effect of loading and unloading rates on mechanical properties and energy characteristics of sandstone under true triaxial stress[J].Journal of China Coal Society,2019,44(2):454-462.
[17] 苏国韶,陈智勇,蒋剑青,等.不同加载速率下岩爆碎块耗能特征试验研究[J].岩土工程学报,2016,38(8):1481-1489.
SU Guoshao,CHEN Zhiyong,JIANG Jianqing,et al.Experimental study on energy dissipating characteristics of rockburst fragments under different loading rates[J].Chinese Journal of Geotechnical Engineering,2016,38(8):1481-1489.
[18] 李杨杨,张士川,文志杰,等.循环载荷下煤样能量转化与碎块分布特征[J].煤炭学报,2019,44(5):1411-1420.
LI Yangyang,ZHANG Shichuan,WEN Zhijie,et al.Energy conversion and fragment distribution characteristics of coal sample under uniaxial cyclic loading[J].Journal of China Coal Society,2019,44(5):1411-1420.
[19] 张蓉蓉,经来旺.SHPB试验中高低温作用后深部砂岩破碎程度与能量耗散关系分析[J].煤炭学报,2018,43(7):1884-1892.
ZHANG Rongrong,JING Laiwang.Analysis on the fragment and energy dissipation of deep sandstone after high/low temperature treatment in SHPB tests[J].Journal of China Coal Society,2018,43(7):1884-1892.
[20] 蒋景东,陈生水,徐婕,等.不同含水状态下泥岩的力学性质及能量特征[J].煤炭学报,2018,43(8):2217-2224.
JIANG Jingdong,CHEN Shengshui,XU Jie,et al.Mechanical properties and energy characteristics of mudstone under different containing moisture states[J].Journal of China Coal Society,2018,43(8):2217-2224.
[21] 赵毅鑫,龚爽,滕腾,等.单轴多级循环加载下原煤加卸载响应比演化特征[J].岩石力学与工程学报,2018,37(5):1096-1105.
ZHAO Yixin,GONG Shuang,TENG Teng,et al.Characteristics of the load/unload response ratio of raw coal under uniaxial multi-level cyclic loading[J].Chinese Journal of Rock Mechanics and Engineering,2018,37(5):1096-1105.
[22] 沙鹏,伍法权,常金源.大理岩真三轴卸载强度特征与破坏力学模式[J].岩石力学与工程学报,2018,37(9):2084-2092.
SHA Peng,WU Faquan,CHANG Jinyuan.Unloading strength and failure pattern of marble under true triaxial test[J].Chinese Journal of Rock Mechanics and Engineering,2018,37(9):2084-2092.
[23] 杨小彬,韩心星,刘恩来,等.循环加卸载下花岗岩非均匀变形演化的声发射特征试验研究[J].岩土力学,2018,39(8):2732-2739.
YANG Xiaobin,HAN Xinxing,LIU Enlai,et al.Experimental study on the acoustic emission characteristics of non-uniform deformation evolution of granite under cyclic loading and unloading test[J].Rock and Soil Mechanics,2018,39(8):2732-2739.
[24] 王春波,丁文其,乔亚飞.硬化土本构模型在FLAC3D中的开发及应用[J].岩石力学与工程学报,2014,33(1):199-208.
WANG Chunbo,DING Wenqi,QIAO Yafei.Development and application of hardening soil constitutive model in FLAC3D[J].Chinese Journal of Rock Mechanics and Engineering,2014,33(1):199-208.
[25] Itasca Consulting GROUP Inc.FLAC3D 5.0 manual[M].Minneapolis:ICG,2010.
