喷雾是主要的矿井粉尘防治技术之一，其在落尘抑制、浮尘治理等方面均有重要应用。液滴防治粉尘机理及其关键影响因素一直是本领域研究热点与难点。前人常将喷雾除尘机理总结为惯性碰撞、接触阻留、扩散效应、凝并等，并主要开展雾化参数对除尘效果影响研究、液滴对粉尘润湿研究等[1]。
在雾化参数与除尘效率研究方面，程卫民、孙其飞、李亚俊等[2-4]通过实验发现，在较高喷雾压力下，液滴可以更加有效地捕捉空气中呼吸性粉尘，喷雾压力与液滴大小间接相关，与液滴速度直接相关。聂文等[5]通过测定受0.4 m/s气流影响的压力喷嘴雾化特性得出压力增大、距喷嘴轴向距离减小、液滴粒径减小等结论。王鹏飞等[6]通过测试多种螺旋喷嘴除尘效率发现，相同耗水量下，除尘效率随喷嘴压力增大而增大，随喷嘴直径增大而减小。AZAROV等[7]通过水气溶胶系统实验发现液滴与悬浮尘粒的凝聚取决于浮尘的分散成分。WANG等[8]运用一种基于双流体框架模型的湿法除尘数学模型发现除尘效率不会随喷雾量的增大而提高。
在液滴对粉尘的润湿研究方面，常使用座滴法和静态接触角来评估液滴的润湿性能[9-13]。如李庆钊等[14]系统地分析了煤尘物理性质及其润湿行为，研究了不同表面活性剂对润湿煤尘的影响。刘谦等[15]通过实验观察液滴在煤表面接触角随时间的变化情况，并发现随着烷基糖苷溶液浓度的增大，溶液在煤表面形成的接触角减小。周刚等[16]通过一系列不同表面活性剂接触角的实验发现，随孔隙率增大和超微孔体积百分比的减小，接触角逐渐减小，煤尘更容易被润湿。桂哲等[17]采用对比分析法，通过表面张力、接触角以及沉降实验研究煤尘润湿性的影响因素，发现表面张力、接触角、沉降时间不是评价表面活性剂的决定因素。事实上，在座滴法中，静态接触角仅是接触角的瞬态值，液滴滴落在固体表面后，接触角会发生缓慢变化。杨静等[18]考虑了座滴法中液滴接触煤表面后的缓慢变化过程，提出了扩散—渗透常数这一指标，用以描述静态接触角的动态变化。
可见，前人通过理论分析、实验和数值模拟研究，分析了影响除尘效率的参数、液滴在粉尘表面的静态润湿和静态润湿角的缓慢变化。液滴撞尘并对其进行动力润湿过程受液滴动能、粉尘表面特性、环境因素等多方面影响，液滴会出现展铺、断裂、破碎等不同运动形态。液滴对粉尘的动力润湿特性及关键因素影响机制仍需深入研究。为更好的理解液滴对粉尘动力润湿过程，笔者运用数值模拟法开展研究，分析了影响液滴动力润湿粉尘的重要参数。研究成果对提高液滴利用率和粉尘防治效率具有重要的指导意义。
1 数值模拟方法
1.1 VOF模型
本模拟采用流体体积法VOF(Volume of Fluid)来进行液滴表面追踪，该模型通过计算每个单元内体积分布情况捕捉相的界面[19-21]。该方法追踪界面精确，可考虑到界面融合与分离，在高精度离散格式下能够很好的保证物理量守恒[22]。在VOF模型中，不同流体组分共用一套动量方程，计算时在全流场的每个计算单元内都记录下各流体组分所占有的体积率。从微观角度看，液滴与尘粒撞击属于非稳态过程[23]。
在计算网格中，对于第q相，根据质量守恒，连续性方程为
∇aq=0
(1)
动量方程为
∇p+∇[μ(∇V+
∇VT)]+ρg+F
(2)
式中，t为时间;V为速度矢量;p为压力;ρ为密度;μ为动力黏度;g为重力加速度;F为容重。
单元内物性参数取值为各相体积分数的加权平均值，在两相流中，如果相的下标用1和2表示，第2相体积分数会被追踪，每一单元中密度ρ、动力黏度μ公式为
ρ=a2ρ2+(1-a2)ρ1
(3)
μ=a2μ2+(1-a2)μ2
(4)
1.2 模型设置
液滴撞击球形尘粒模型如图1所示。尘粒粒径设为D，液滴初始位于尘粒正上方，下落初速度V0，液滴中心与尘粒中心间距为3D。计算域是边长为10D的正方形。为保证液滴如预期撞击尘粒表面，模拟环境气压为理想状态标准大气压，且不考虑外部扰动气流对撞尘过程影响。通过改变尘粒表面粗糙厚度和粗糙度常数值来拟合其粗糙度[24]。尘粒表面初始为干燥无液状态。尘粒粒径D在模拟中选择了2,20,200,2 000 μm四种情况，相关物性参数设置液滴密度为998.2 kg/m3，液滴黏度为1.003×10-3 Pa·s，液滴表面张力为0.072 N/m，空气密度为1.225 kg/m3,空气黏度为1.789 4×10-5 Pa·s，尘粒粒径D，尘表面粗糙厚度为0.015D，尘表面粗糙度常数为0.6。
图1 液滴撞击尘粒模型
Fig.1 Model of droplet impinging on dust particle
模拟中选择占用计算资源较少且收敛速度较快的PISO算法。对气液交界面采用几何重建法，梯度插值选用格林-高斯基于单元体默认法，压力插值方法选用PRESTO，动量方程采用二阶迎风离散法，湍动能和湍流耗散率均采用一阶迎风离散法。压力方程松弛因子设为0.4，动量方程松弛因子设为0.6。
1.3 参数说明
液滴接触尘粒瞬态如图2所示。定义液滴在尘粒顶端向两侧展铺的距离d为展铺长度;定义液滴中心顶端与尘粒顶端的高度差h为液滴中心高度。展铺系数D*为由液滴在尘粒上的展铺长度d和液滴初始粒径d0决定的，其计算式为
图2 液滴撞击尘粒瞬态
Fig.2 Transient state of water droplet hitting dust pellet
D*=d/d0
(5)
本文用到的其他无量纲变量如下：
无量纲液滴中心高度:
H*=h/d0
(6)
液尘粒径比:
θ=d0/D
(7)
液滴在运动过程中发生形变，故需计算形变度e，用以评估液滴形变程度。形变度是用来表征液滴截面接近圆的程度。若液滴区域边界光滑且呈圆形，其形变度为1;若液滴区域边界形变，则相应的形变度随之减小。形变越大，e越小，其计算式为
(8)
式中，dL为液滴水平直径;dV为液滴竖直直径。
2 结果与讨论
2.1 液滴近尘时的形变
在液尘粒径比分别为0.5,1，1.5时进行模拟，观测了液滴近尘时的形变。图3(a)展示了尘粒粒径为2 000 μm、初速度为15 m/s的不同粒径液滴接近尘粒表面的形貌图。可以发现随着粒径比逐渐增大，液滴形变程度依次递减。粒径比为0.5的液滴形变效果明显，形变度e为0.86;而粒径比为1.5时，形变度e为0.98。
图3 不同粒径比和初速度液滴的近尘形貌
Fig.3 Morphology of droplets with different particle size ratio and velocities near dust
液滴在近尘过程中，当液滴速度、液尘间距相同时，液滴形变程度随粒径比的增大而减小。这是由于液滴即将撞击尘粒时，液滴与尘粒表面间的空气被压缩，导致液滴下部压力增大被挤压，从而发生形态变化。当尘粒粒径一定时，随着液滴粒径的增大，液滴下部受粉尘影响的范围比例逐渐缩小，因此液滴形变越发不再明显。
当尘粒粒径为200 μm、液尘粒径比为0.5～1.5时，液滴粒径在100～300 μm。模拟发现，液滴以初速度为15 m/s接近尘粒表面时形变度在0.96～0.99。当尘粒粒径为20 μm、液尘粒径比为0.5～1.5时，液滴粒径在10～30 μm。液滴以初速度为15 m/s接近尘粒表面时形变度在0.98～1。当尘粒粒径为2 μm、液尘粒径比为0.5～1.5时，液滴粒径在1～3 μm。液滴以初速度为15 m/s接近尘粒表面时，液滴无明显形变。结果显示，当液尘粒径变小后，粒径比对液滴形变的影响减小，这是由于液滴和粉尘粒径较小时，2者间的空气夹层变小，进而对液滴的作用变小。此外，液滴粒径越小，液滴所受重力、阻力越小，受表面张力的影响愈大，液滴表现出较强的抵抗形变能力，这是尘粒粒径为2 μm、液尘粒径比在0.5～1.5时，液滴无明显形变的重要原因。
图3(b)展示了尘粒粒径为2 000 μm、粒径比为1时液滴近尘表面的形貌图。可以发现当液尘粒径比相同时，形变程度随速度的增大逐步增大。初速度为20 m/s的液滴在近尘时，形变度e为0.92，液滴竖直直径减小，水平直径增大。而当液滴初速度达到30 m/s时，形变度e为0.76。液滴的形状发生了明显变化，液滴两侧向外凸起形成尖刺状，竖直直径明显减小。显然，随着速度的增加，液滴形变受到了周围气体的影响。粒径比为1，尘粒粒径为20和200 μm时，模拟结果也发现了液滴形变随速度增大而增大。但粒径比为1，尘粒粒径为2 μm时，未发现液滴发生明显形变，微米级液滴依然表现出较好的抵抗形变能力。
2.2 液尘界面的气泡
模拟结果发现，液滴撞击尘粒表面时，交界面处有气泡产生。图4为尘粒粒径为2 000 μm、粒径比为1时，液滴撞击尘粒表面的气泡产生、断裂现象。如图4(a)所示，液滴以10 m/s接近尘粒，2者之间的部分空气未能及时溢出而形成一层气薄膜。随着液滴在尘粒表面展铺流动，气膜受到液滴向两侧流动的剪切作用，发生断裂形成多个气泡。部分气泡随着液滴展铺发生移动，从两侧边缘处溢出，未来得及流出的气体在液滴凹陷的底部形成气泡。随后气泡受到液体挤压再次发生断裂现象，再一次随着液滴的流动从两侧溢出。可见，由于压力、剪切应力的作用以及尘粒表面特性，当液滴撞击尘粒时，并不能将尘粒表面完全润湿包裹，而会在接触面上形成气泡，这势必影响液滴对尘粒的润湿。
图4 不同初速度液滴撞击尘粒后气泡断裂过程
Fig.4 Bubble fracture after the droplet with different initial velocity impinges on the particle
液滴速度是影响液滴与尘粒之间气泡断裂的重要因素之一。对比图4(a)～(c)，可以清晰地观察到液滴速度不同时，液滴撞击后气泡的断裂时间和移动速度不同。从液滴撞击尘粒表面到液滴展铺开始后的0.4 ms时间段内，气泡发生了2次断裂。随着液滴速度的增大，气泡发生第1次断裂的速度加快，断裂时间趋短且气泡向两侧的移动加快。当初速度为20 m/s时，气泡第1次断裂瞬间完成。因此当液滴速度越大，气泡断裂与移动速度越快。这是由于液滴速度增大，气泡所受剪切应力、压力等亦增，加速了气泡的断裂和移动。
尘粒粒径为2,20和200 μm时，模拟结果也发现了液尘之间的气泡生成，但由于空间尺度、时间尺度的急剧减小，气泡断裂这一过程并不明显。图5展示了尘粒粒径为2 μm、液滴速度为15 m/s、粒径比为1时，液尘间发现的气泡。
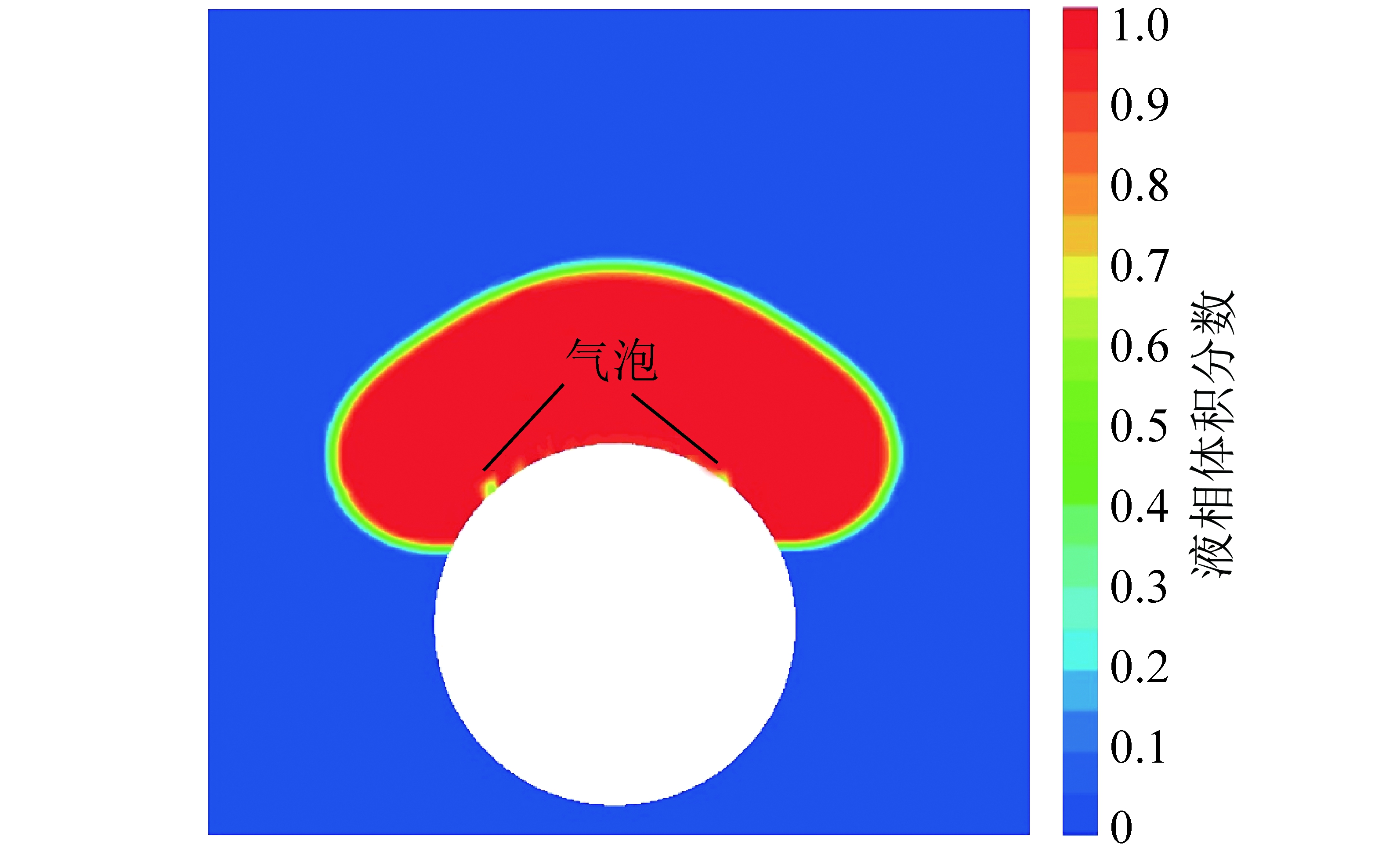
图5 2 μm尘粒与液滴之间的气泡
Fig.5 Trapped air bubbles between dust particle and droplet with a diameter of 2 μm
2.3 液滴展铺行为
液滴撞击尘粒表面，引起液滴受力发生变化，导致液滴发生形变，形成倒凹状液膜，其展铺行为可反映液滴对尘粒的润湿性能。为此，分析了液滴速度与液尘粒径比对展铺行为的影响。
2.3.1 速度对液滴展铺行为的影响
图6为粒径比为1情况下，不同速度液滴从接触尘粒至达到最大展铺长度期间的无量纲展铺系数变化。
如图6(b)所示，粒径200 μm的液尘撞击过程中，V0=15 m/s时，初始接触时间为42 μs;V0=35 m/s时，初始接触时间为18 μs。当尘液接触开始，无量纲展铺系数随时间逐渐增大，达到最大值3.14后将不再增大。这是由于无量纲展铺系数为展铺长度与液滴粒径之比，粒径比为1时液滴与尘粒粒径相同。而液滴在尘粒表面可能的最大展铺长度为尘粒圆周周长，故可得粒径比为1情况下，无量纲展铺系数的最大值为π。可见，数值模拟结果与理论值一致。此外，还发现液滴初速度越大，前期的展铺系数增长越快。这是因为液滴初速度大，具有较大的初始动能，从而加快了展铺速度。随着液滴的初始动能不断被表面张力和黏性力等消耗，其动能大部分转化为形变势能，展铺速度逐渐减小，展铺系数增长渐缓直至达到最大展铺系数。V0=15 m/s时，达到最大展铺系数用时55 μs;V0=35 m/s时，达到最大展铺系数用时26 μs。因此当液滴初速度越大，达到最大展铺系数所需时间越短。图6(a)～(d)中部分情况下的最大展铺系数未达到3.14，其原因是液膜在完全包裹尘粒之前就发生了断裂或回缩。
图6 不同速度下无量纲展铺系数
Fig.6 Dimensionless spreading coefficient at different speeds
展铺长度的增加，伴随着无量纲液滴中心高度H*的下降。H*下降的速度取决于液滴展铺的速度。模拟结果发现，液滴展铺速度越大，H*下降越快。H*随时间变化，下降速率由快变慢。液滴初速度越小，液滴在尘粒表面的展铺时间越长，H*下降越慢。液滴速度增加，其在尘粒表面展铺润湿时间缩短。
2.3.2 液尘粒径比对液滴展铺行为的影响
为定量研究粒径比对液滴展铺行为的影响，对比分析了粒径比不同而速度均为15 m/s情况下，液滴从接触尘粒至达到最大展铺长度期间的无量纲展铺系数变化，结果如图7所示。
如图7(b)所示，D=200 μm时，若液尘粒径比为0.5，撞击到表面用时47 μs，在3种粒径比情况中耗时最长。粒径比为1.5时，液滴在42 μs撞击到表面。液尘稳定接触并间隔一定相同时间情况下，粒径比为1.5的液滴展铺系数相对最小，粒径比为0.5的液滴展铺系数相对最大。这是因为当粒径比小于1时，液滴体积小于尘粒体积，初始的形变势能转换速率大;而粒径比大于1时，液滴体积大于尘粒体积，初始的形变势能转换速率低。此外，无量纲展铺系数在仅有粒径比不同情况下主要取决于液滴直径。随着液尘粒径比增大，无量纲展铺系数相应减小。此结论在图8(a),(c)亦可见。图8(d)中显示了D=2 μm时，不同粒径比情况下无量纲展铺系数变化，可见，粒径比为1.5时无量纲展铺系数最大值稍高于粒径比为1时。这是由于当液滴粒径在微米级时，表面张力极大的抑制了液滴的展铺，而增大液尘粒径比，即增大液滴总量，可提高无量纲展铺系数，但提高幅度有限。
图7 不同粒径比无量纲展铺系数
Fig.7 Dimensionless spreading coefficients at different particle size ratios
图8 残留在尘粒表面的微液滴
Fig.8 Micro droplets remaining on the surface of dust particles
液滴撞击尘粒表面后，无量纲液滴中心高度逐渐降低，其下降速率由快变慢。D=20，200,2 000 μm时，模拟结果均显示随着粒径比增大，初始无量纲液滴中心高度增大。尘液接触后，液滴逐渐流失，液膜最终断裂。D=2 μm时，随着粒径比增大，初始无量纲液滴中心高度亦增大，但由于微米级液滴粒径过小，表面张力克服了液滴断裂趋势，液滴展铺出现回缩振荡。
从模拟结果可见，尘粒粒径限制了液滴的最大展铺长度，当尘粒粒径分别为20,200,2 000 μm时，若增大液滴粒径，使粒径比大于1，只是增大了流失的液量，而大部分液滴没有参与润湿尘粒表面的过程。当尘粒粒径为2 μm时，相应的微米级液滴由于较强的表面张力，在展铺过程中未发生断裂。
2.4 液滴在尘粒表面的滞留
图8展示了粒径比为1时，初速度为15 m/s液滴分别撞击20，200,2 000 μm尘粒过程末期，在尘粒表面的滞留情况。可见，液滴最终断裂，有少量微液滴滞留在尘粒表面。这是由于随着液滴在尘粒表面展铺，逐渐流失，初始动能不断地被耗散。最终，液滴发生断裂，动能消耗殆尽，尘液间的固液粘附滞留了剩余的微量液滴。
而粒径比在0.5～1.5，初速度为15 m/s液滴撞击2 μm尘粒过程中，均未见液滴发生断裂，最终液滴整体附着在尘粒表面。这是由于微米级液滴有较大的抵抗形变能力，其展铺过程受到明显抑制，发生了回缩振荡，当其初始动能耗散后，整体滞留在尘粒表面。
3 结 论
(1)液滴近尘时，随着液尘粒径比的增大，液滴形变程度降低，2者呈负相关。液滴速度越大，其形变程度越大，2者呈正相关。随着粒径降低，液滴抵抗形变能力逐渐增强。
(2)液滴撞击到尘粒表面时，2者之间有气泡生成，阻碍润湿过程。液滴速度决定了气泡断裂时间和移动速度，液滴速度越大，气泡受压力和剪切应力作用，断裂越快。
(3)液滴展铺过程中，液滴速度越大，越易达到最大展铺系数和最小液滴中心高度。随着液尘粒径比增大，初始无量纲液滴中心高度增大。液滴撞击尘粒表面后，无量纲液滴中心高度逐渐降低，其变化幅度逐渐降低。当尘粒粒径分别为20,200,2 000 μm时，随着液尘粒径比增大，无量纲展铺系数相应减小;液尘粒径比大于1时，增大液滴粒径不会提高对尘粒的包裹程度;展铺结束后，有少量微液滴滞留在尘粒表面。
(4)当尘粒粒径为2 μm、粒径比在0.5 ～ 1.5时，液滴展铺过程受到明显抑制，尽管粒径比大于1时无量纲展铺系数最大值稍有增加，但增加量十分微小。展铺结束后，液滴整体滞留在尘粒表面。
[1] 周刚.综放工作面喷雾降尘理论及工艺技术研究[D].青岛:山东科技大学,2009.
ZHOU Gang.Study on the theory and technology of spray dust removal in fully mechanized caving face[D].Qingdao:Shandong University of Science and Technology,2009.
[2] 程卫民,聂文,周刚,等.煤矿高压喷雾雾化粒度的降尘性能研究[J].中国矿业大学学报,2011,40(2):185-189,206.
CHENG Weimin,NIE Wen,ZHOU Gang,et al.Study on dust removal performance of atomized particle size of high-pressure atomization in coal mine[J].Journal of China University of Mining and Technology,2011,40(2):185-189,206.
[3] 孙其飞,邹常富,栾旭东,等.高压喷嘴雾化参数的实验研究[J].金属矿山,2018(8):164-168.
SUN Qifei,ZOU Changfu,LUAN Xudong,et al.Experimental study on atomization parameters of high-pressure nozzle[J].Metal Mine,2018(8):164-168.
[4] 李亚俊.高压雾化特性及降尘技术试验研究[J].有色金属(矿山部分),2019,71(6):66-68，88.
LI Yajun.Experimental study on high pressure atomization characteristics and dust removal technology[J].Nonferrous Metals(Mining Section),2019,71(6):66-68,88.
[5] 聂文,程卫民,周刚,等.掘进面喷雾雾化粒度受风流扰动影响实验研究[J].中国矿业大学学报,2012,41(3):378-383.
NIE Wen,CHENG Weimin,ZHOU Gang,et al.Experimental study on atomized particle size as affected by airflow disturbance at the heading face[J].Journal of China University of Mining and Technology,2012,41(3):378-383.
[6] 王鹏飞,刘荣华,汤梦,等.煤矿井下高压喷雾雾化特性及其降尘效果实验研究[J].煤炭学报,2015,40(9):2124-2130.
WANG Pengfei,LIU Ronghua,TANG Meng,et al.Experimental study on atomization characteristics and dust removal effect of high-pressure atomization in underground coal mine[J].Journal of China Coal Society,2015,40(9):2124-2130.
[7] AZAROV A V,ZHUKOVA N S,ANTONOV F G.Water-spray systems reducing negative effects of fine-dispersion dust at operator’s workplaces of machine-building industries[J].Procedia Engineering,2017,206:1407-1414.
[8] WANG Pei,SHEN Shuai,ZHOU Ling,et al.Turbulent aggregation and deposition mechanism of respirable dust pollutants under wet dedusting using a two-fluid model with the population balance method[J].International Journal of Environmental Research and Public Health,2019,16(18):3359.
[9] 王军.悬滴法测量高温熔体表面张力实验系统的研制[D].青岛:青岛理工大学,2018.
WANG Jun.Development of an experimental system for measuring surface tension of high temperature melt by suspension drop method[D].Qingdao:Qingdao University of Technology,2018.
[10] 钱健行.润湿角测定装置设计及其应用研究[D].沈阳:东北大学,2014.
QIAN Jianhang.Design and application of wetting angle measuring device[D].Shenyang:Northeastern University,2014.
[11] ERBIL H Y.The debate on the dependence of apparent contact angles on drop contact area or three-phase contact line:A review[J].Surface Science Reports,2014,69(4):325-365.
[12] BORMASHENKO E.Physics of solid-liquid interfaces:From the Young equation to the superhydrophobicity(Review Article)[J].Low Temperature Physics,2016,42(8):622-635.
[13] 徐英峰,冯海明.对润湿剂润湿煤尘影响因素的研究[J].中国煤炭,2005(3):42-43.
XU Yingfeng,FENG Haiming.Study on the influence factors of wetting agent wetting coal dust[J].China Coal,2005(3):42-43.
[14] LI Qingzhao,LIN Baiquan,ZHAO Shuai,et al.Surface physical properties and its effects on the wetting behaviors of respirable coal mine dust[J].Powder Technology,2013,233:137-145.
[15] 刘谦,郭玉森,赖永明,等.不同变质程度煤表面动态行为与临界表面张力的研究[J].矿业安全与环保,2015,42(6):35-39.
LIU Qian,GUO Yusen,LAI Yongming,et al.Study on surface dynamic behavior and critical surface tension of coal with different metamorphic grades[J].Mining Safety & Environmental Protection,2015,42(6):35-39.
[16] ZHOU Gang,QIU Han,ZHANG Qi,et al.Experimental investigation of coal dust wettability based on surface contact angle[J].Journal of Chemistry,2016:9452303.1-8.
[17] 桂哲,刘荣华,王鹏飞,等.表面活性剂对煤尘润湿性能的影响[J].黑龙江科技大学学报,2016,26(5):513-517.
GUI Zhe,LIU Ronghua,WANG Pengfei,et al.Experimental study on surfactant effect on coal dust wettability[J].Journal of Heilongjiang University of Science and Technology,2016,26(5):513-517.
[18] 杨静,谭允祯,顾景梅,等.动态接触角测定法研究润湿剂对煤尘的润湿性能[J].煤矿安全,2008,39(12):7-10.
YANG Jing,TAN Yunzhen,GU Jingmei,et all.Study on wetting of coal dust by measuring dynamic contact angle[J].Safety in Coal Mines,2008,39(12):7-10.
[19] HIRT C W,NICHOLS B D.Volume of fluid(VOF) method for the dynamic of free boundaries[J].Journal of Computational Physics,1981,39(1):201-225.
[20] 宋云超.气液两相流动相界面追踪方法及液滴撞击壁面运动机制的研究[D].北京:北京交通大学,2013.
SONG Yunchao.Foundamental study on the interface tracking method of gas-liquid two phase flows and drop-let impacting onto the surface[D].Beijing:Beijing Jiaotong University,2013.
[21] CHIRCO L,DA VI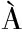
R,MANSERVISI S.VOF evaluation of the surface tension by using variational representation and Galerkin interpolation projection[J].Journal of Computational Physics,2019,395:537-562.
[22] GOPALA V R,WACHEM B G M.Volume of fluid methods for immiscible-fluid and free-surface flows[J].Chemical Engineering Journal,2008,141(1-3):204-221.
[23] YARIN A L.Drop impact dynamics:Splashing,spreading,receding,bouncing[J].Annual Review of Fluid Mechanics,2006,38(1):159-192.
[24] FERAY Guleryuz L,OZAN S,KASMAN S,et al.The influence of process parameters of edm on the surface roughness of aluminum matrix composites reinforced with SiC Particulates[J].Acta Physica Polonica A,2013,123(2):421-423.
