煤矿掘进巷道前方的断层、陷落柱及老窑采空区等地质异常体严重影响了正常生产作业，而且此类异常体经常伴随有水害及瓦斯突出等影响矿工人身安全的地质灾害，因此对掘进巷道开展地球物理超前探测有十分重要的意义[1]。在众多地球物理探测手段中，弹性波勘探是一种比较成熟且有效的方法[2]，但以炸药作为震源的传统弹性波勘探存在很多局限性:第1，掘进巷道空间狭窄排风条件有限，容易导致瓦斯聚集，炸药引爆过程存在较大的安全隐患;第2，利用炸药开展勘探时，必须停止采掘、运输及支护等其他施工，并且要为风筒、采掘机及掘进巷道其他设备的脆弱部分加装额外保护装置，影响正常生产作业;第3，炸药激发结束后，产生大量粉尘，严重影响矿工作业环境。基于上述约束，将掘进机截割煤岩的振动能量作为震源的随掘地震勘探技术逐渐受到行业的关注，其在避免炸药震源带来的各种安全隐患的同时，可以在掘进过程中实时对前方地质异常体开展同步探测[3-4]。但由于掘进机截割煤岩的能量小于炸药激发的振动能量，并且掘进巷道环境复杂，存在各种电缆、锚护设备、风筒、水泵等设备，在很大程度上降低了采集数据的信噪比[5]。为了提升矿井地震勘探数据的信噪比，很多学者采用了小波阈值去噪方法开展噪声衰减或信号识别，取得了一定效果[6-8]，但由于小波变换在频率尺度方向存在扩散的特点，造成了频率方向的分辨率降低[9-12]。因此，当信号的频率成分复杂或者信噪比较低时，传统小波阈值去噪方法将受到限制，影响噪声衰减效果。基于此，笔者引入了基于L1范数约束反演的煤矿随掘噪声压制方法，分别用模拟数据和实际数据证实了其具有比传统小波阈值去噪方法更高保真度的优势。
1 方法原理
1.1 传统阈值类小波去噪方法
源自截割煤岩的随掘信号经过互相关计算后，具有了波形相关的特点，而噪声一般呈随机分布，因此将时间域数据转换至时频域后，有效信号和噪声具有不同的系数分布特征。基于此，在时频域通过选取合适的阈值保留有效信号，反变换至时间域可以达到衰减噪声的目的。
据上所述，传统阈值类小波变换通常采用如下步骤开展数据去噪处理:
(1)将含噪数据通过式(1)所示的小波变换转入小波域[13]:
(1)
式中，Xs(a,b)称为小波系数;a为母小波的尺度变换度量;d(t)为时间域信号;ψ*为母小波ψ(t)的复共轭，此处的母小波选用的是与地震信号相似的Ricker子波;b为母小波的时移度量。
(2)根据信号和噪声在小波域的系数特征差异，设计不同的阈值方法对小波系数开展阈值运算，其中应用最广泛的阈值方法为硬阈值[14](式(2))和软阈值法[15](式(3)):
(2)
(3)
式中，gop为阈值结果;g为待阈值处理的数据;λ为设置的阈值;sgn(g)为g的符号函数。
(3)通过小波逆变换将小波域数据转回时间域，即可完成噪声衰减。
鉴于不同的数学运算特征，上述2种常用阈值方法在应用过程中存在不同的缺陷，首先对于硬阈值方法，虽然阈值后的信号符合原始信号的形态特征，但阈值结果在±λ处是间断的，在信号反变换回时间域时,易产生Pseudo-Gibbs现象[16];其次对于软阈值方法，虽然一定程度上解决了硬阈值方法处理后时频域系数的整体连续性问题，但当|g|≥λ时，阈值结果与g之间总存在恒定的偏差，将直接影响反变换至时间域的图像与真实图像的逼近程度，影响去噪效果。当|g|<λ时，将系数置为0，很可能将微弱信号同噪音一并衰减。为改善上述阈值方法的缺陷，学者们提出了不同的改进方法[16-19]，虽然去噪效果都获得了不同程度的提高，但由于小波变换存在尺度方向扩散的缺点[20-21]，造成时频分辨率降低，反变换至时间域后降低了有效信号的保真度，基于此，笔者提出了基于L1范数约束反演的小波域去噪方法。
1.2 基于L1范数约束反演的小波去噪方法
建立在互相关计算后的随掘信号在时频域相对于环境噪声呈现稀疏性特点的基础上，基于L1范数约束的小波域去噪方法以稀疏反演的思想求解去噪问题。其将随掘互相关之后的数据由小波域重构为时间域的过程写为
d=Wx+c
(4)
其中，d为时间域的随掘互相关数据;W为小波逆变换;x为小波域中随掘互相关数据的有效信号;c为噪声。由于噪声的加入，直接求解有效信号是一个典型的不适定反问题[22]，为了优化上述反演问题，基于有效信号在小波域呈现稀疏性的特征，在求解过程中加入L1范数约束将式(4)写为
(5)
其中，
为保真部分;‖x‖1被称为1范数约束部分;λ则是调节2部分的权重因子，当λ取值较大时，即代表1范数约束部分占较大权重，模型稀疏性增加，求解稳定，取值较小时，即放大了原反演问题的不适定缺陷，无法求取最优解。λ的具体取值视噪声水平而定，当噪声水平较高时，取值较大，反之则取小值。
求解式(5)的1范数优化问题，已经发展了很多方法。诸如:AMP[23](近似信息传递方法)、ISTA[24](迭代收缩阈值算法)、SPGL1[25](谱投影梯度法)等。其中本文采用的是在ISTA方法上改进的快速迭代收缩阈值算法:FISTA[26]。FISTA不仅将复数纳入计算范畴，也在很大程度上提高了ISTA的计算效率，其基本迭代策略步骤如下:
第1步:赋初值q1=x0,β=1;其中x0可赋0值;q为创建的与xi和xi-1相关的中间变量，下角标i表示迭代次数，β为伴随迭代更新的过渡参数。
第2步:计算式(6)
(6)
其中，WH代表W的逆变换;α为控制迭代步长的参数。
第3步:计算式(7)
(7)
第4步:计算式(8)
(8)
第5步:若满足迭代终止条件，则结束迭代，输出结果x;若不满足迭代终止条件，重复第2～4步。
2 算 例
2.1 模型数据
采用3种主频的Ricker子波模型构建原始数据，其中主频分别包括了40与60 Hz以及20与60 Hz复合频率的3种类型的信号，如图1所示，同时，图1也展示了连续小波变换和基于L1范数约束反演小波变换的差异。
图1中，图1(a)为构建的原始数据，图1(b)为连续小波变换结果，图1(c)为基于L1范数约束反演的小波变换。对比2种变换方法，可以发现，基于L1范数约束反演的方法在时间和频率方向都提高了分辨率。当信号频率成分复杂时(图1(a)，1～120 ms的复合频率信号)，传统小波变换(图1(b))的时频分辨率明显低于基于L1范数约束反演的小波变换(图1(c))，这种高分辨率的优势将为后续对应去噪方法的改进提供原理优势。
图1 连续小波变换和基于L1范数约束反演小波变换的时频域系数对比
Fig.1 Comparison of time-frequency-domain coefficients between CWT(continuous wavelet transform) and CWT based on L1-norm constrained inversion
在模型数据的基础上，分别加入信噪比为10.8,6.8和1.2的随机噪声，并分别利用传统的小波阈值去噪方法和L1范数约束反演的小波去噪方法开展噪声衰减处理，如图2所示，其中信噪比的值[27]由式(9)计算得出
图2 不同信噪比的模拟数据去噪结果对比
Fig.2 Comparison of denoising results of analog data with different signal-to-noise ratios
(9)
式中，d′为去噪结果，下标rms代表均方根值。
图2中，图2(b)蓝色实线表示原始未加噪数据，黑色实线代表传统阈值的小波去噪结果，红色实线是L1范数约束反演的小波去噪结果，对比可以看出，虽然2种方法都在很大程度上衰减了随机噪声，但在信号细节保护方面，后者优势更明显。
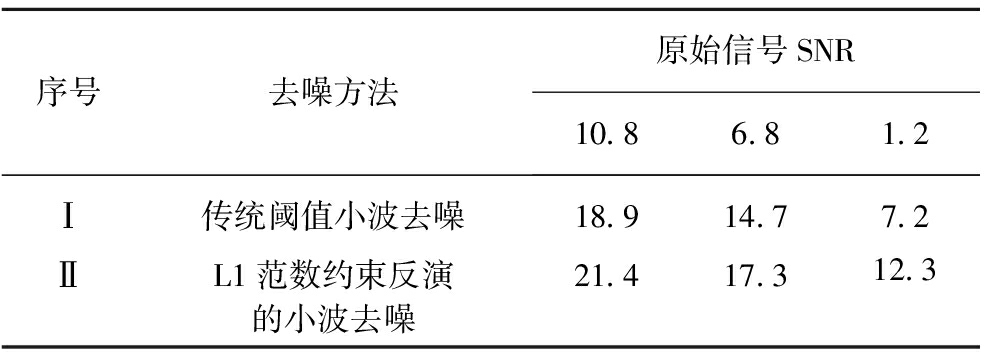
为了量化2种方法的对比结果，用式(9)计算信噪比，计算结果见表1。
表1 2种方法的去噪结果对比
Table 1 Comparison of denoising results by two different methods
序号去噪方法原始信号SNR10.86.81.2Ⅰ传统阈值小波去噪18.914.77.2ⅡL1范数约束反演的小波去噪21.417.312.3
为了更清晰对比2种去噪方法的区别，将分离结果中30～111 ms的复合频率数据作了局部细节对比及信噪比计算，如图3所示。
图3 不同信噪比的模拟数据去噪结果局部细节对比
Fig.3 Local details comparison of denoising results of analog data with different signal-to-noise ratios
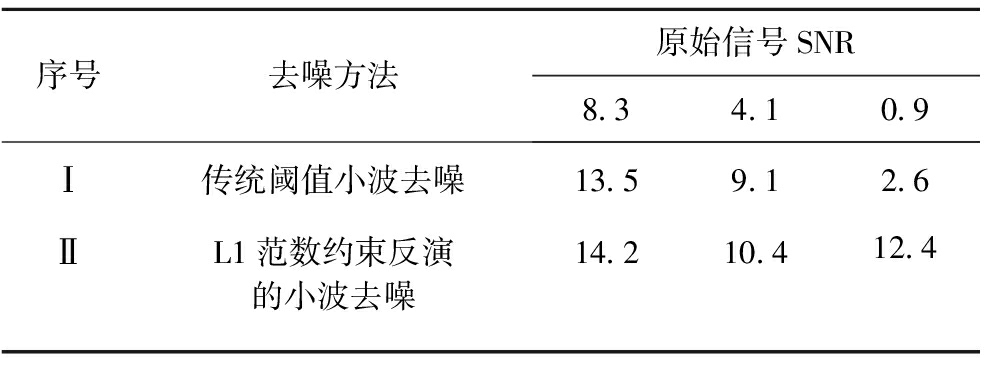
图3分别对应图2中30～111 ms的局部细节，图3的细节对比进一步反映了L1范数约束反演方法的高保真度优势。同样地，根据式(9)计算信噪比。计算结果见表2。
表2 不同方法的去噪结果对比(局部)
Table 2 Comparison of denoising results by two different methods(Partial)
序号去噪方法原始信号SNR8.34.10.9Ⅰ传统阈值小波去噪13.59.12.6ⅡL1范数约束反演的小波去噪14.210.412.4
由表2中同样可以看出，当原始信号的信噪比较高时，2种方法去噪结果相当，但当信噪比降低时，基于L1范数约束反演的小波去噪方法表现更佳。
2.2 实际数据
在山西某煤矿开展的随掘试验中抽取了某一时段的数据，进行了2种方法的去噪效果对比。其中实际数据的道间距为5 m，采样率为0.25 ms，共计22个检波器，原始数据如图4所示。
图4 掘进机截割煤岩的振动信号
Fig.4 Vibration signals of coal-rock excavated by the roadheader
从图4可以看出，检波器既接收到了掘进机的振动信号，同时也记录到了上文提到的其他噪声，严重降低了信号的信噪比。原始数据通过互相关后得到类似脉冲震源的记录，如图5(a)所示。
由图5可以看出,基于L1范数约束反演的去噪结果具有更高的保真度。与上文模型数据的对比类似，为了从细节上对比2种方法的差异，分别由图5中抽取了2道包含有效信号的数据段并放大细节，如图6所示。
图5 实际数据去噪结果对比
Fig.5 Comparison of denoising results of field data
图6 实际数据去噪结果局部细节对比
Fig.6 Local details comparison of denoising results of field data
图6分别是从第1，10道抽取的时间片段，其中，蓝色实线表示原始数据，黑色实线代表传统小波阈值去噪结果，红色实线是基于L1范数约束反演的去噪结果。对比可以看出，L1范数约束反演方法不仅完成了随机噪声的衰减，而且在保护原始信号细节方面较常规阈值方法更具优势，去噪结果的保真度更高。
3 结 论
(1)基于L1范数约束反演的小波域去噪方法建立在有效信号相对于噪声在时频域呈现稀疏性特征的基础上，可以在很大程度上完成噪声的衰减。
(2)相比于传统的小波阈值去噪方法，基于L1范数约束反演的小波去噪方法很大程度上降低了时频系数扩散的影响，当信号频率复杂并且信噪比较低时，其在保护原始信号细节上更具优势，去噪结果的保真度更高。
(3)通过基于L1范数约束反演的时频域去噪方法，将提高随掘数据的信噪比，有利于改善后期初至拾取、偏移成像等随掘数据的处理质量。
[1] 程久龙,李飞,彭苏萍,等.矿井巷道地球物理方法超前探测研究进展与展望[J].煤炭学报,2014,39(8):1742-1750.
CHENG Jiulong,LI Fei,PENG Suping,et al.Research progress and development direction on advanced detection in mine roadway working face using geophysical methods[J].Journal of China Coal Society,2014,39(8):1742-1750.
[2] 程建远,朱梦博,王云宏,等.煤炭智能精准开采工作面地质模型梯级构建及其关键技术[J].煤炭学报,2019,44(8):2285-2295.
CHENG Jianyuan,ZHU Mengbo,WANG Yunhong,et al.Cascade construction of geological model of longwall panel for intelligent precision coal mining and its key technology[J].Journal of China Coal Society,2019,44(8):2285-2295.
[3] 李亚豪,程久龙,姜旭,等.基于互相关的随掘地震超前探测有效信号提取方法研究[J].中国矿业,2020,29(5):82-85,114.
LI Yahao,CHENG Jiulong,JIANG Xu,et al.Research on effective signals extraction method of seismic while drilling ahead detection based on cross-correlation[J].China Mining Magazine,2020,29(5):82-85,114.
[4] 霍晶晶,查华胜,苗园园,等.突出煤层巷道随掘超前探测技术研究[J].煤矿开采,2018,23(6):19-23.
HUO Jingjing,ZHA Huasheng,MIAO Yuanyuan,et al.Advanced exploring technology during driving of roadway with outburst coal seam[J].Coal Mining Technology,2018,23(6):19-23.
[5] 程久龙,高峰,孙晓云,等.随掘地震去噪方法研究[A].2014年中国地球科学联合学术年会[C].2014.
[6] 唐守锋,童敏明,潘玉祥,等.煤岩破裂微震信号的小波特征能谱系数分析法[J].仪器仪表学报,2011,32(7):1521-1527.
TANG Shoufeng,TONG Minming,PAN Yuxiang,et al.Energy spectrum coefficient analysis of wavelet features for coal rupture micro-seismic signal[J].Chinese Journal of Scientific Instrument,2011,32(7):1521-1527.
[7] 刘敏,王恩元,刘贞堂,等.小波降噪在煤岩微震信号处理中的应用[J].矿业研究与开发,2011,31(2):67-70.
LIU Min,WANG Enyuan,LIU Zhentang,et al.Application of wavelet denoising in processing the micro-seismic signal of coal-rock[J].Mining Research and Development,2011,31(2):67-70.
[8] 蔡剑华,李晋.基于频率域小波去噪的大地电磁信号工频干扰处理[J].地质与勘探,2015,51(2):353-359.
CAI Jianhua,LI Jin.Suppression of power line interference on MT signals based on the frequency domain wavelet method[J].Geology and Exploration,2015,51(2):353-359.
[9] AHRABIAN A,MANDIC D P.A class of multivariate denoising algorithms based on synchrosqueezing[J].IEEE Transactions on Signal Processing,2015,63(9):2196-2208.
[10] 韩利,刘春成,张益明,等.地震复谱分解技术及其在烃类检测中的应用[J].地球物理学报,2016,59(3):1095-1101.
HAN Li,LIU Chuncheng,ZHANG Yiming,et al.Seismic complex spectral decomposition and its application on hydrocarbon detection[J].Chinese J Geophys,2016,59(3):1095-1101.
[11] MOUSAVI S M,LANGSTON C A,HORTON S P,et al.Automatic microseismic denoising and onset detection using the synchrosqueezed continuous wavelet transform[J].Journal of Geophysics,2016,81(4).
[12] MOUSAVI S M,LANGSTON C A.Automatic noise-removal/signal-removal based on general cross-validation thresholding in synchrosqueezed domain and its application on earthquake data[J].Geophysics,2017,82(4):1-58.
[13] DAUBECHIES I.Ten lectures on wavelets[M].Philadelphia:Society for Industrial and Applied Mathematics,1992.
[14] 赵瑞珍,宋国乡,王红.小波系数阈值估计的改进模型[J].西北大学学报,2001,19(4):625-628.
ZHAO Ruizhen,SONG Guoxiang,WANG Hong.Better threshold estimation of wavelet coefficients for improving denoising[J].Journal of Northwestern Polytechnical University,2001,19(4):625-628.
[15] DONOHO D L.Denoising by soft-thresholding[J].IEEE Transactions on Information Theory,1995,41(3):613-627.
[16] 陶红艳,秦华峰,余成波.基于改进阈值函数的小波域去噪算法的研究[J].压电与声光,2008,30(1):93-95.
TAO Hongyan,QIN Huafeng,YU Chengbo.De-noising algorithm based on improved threshold function in wavelet domain[J].Piezoelectric and Acoustooptic,2008,30(1):93-95.
[17] 姚建红,张海鸥,张守宇,等.改进小波阈值算法在电能质量去噪中的应用[J].自动化与仪器仪表,2016(2):57-58.
YAO Jianhong,ZHANG Haiou,ZHANG Shouyu,et al.Application of improved wavelet thresholding algorithm in power quality denoising[J].Automation & Instrumentation,2016(2):57-58.
[18] 邓玉娟.基于小波变换的语音阈值去噪算法研究[D].重庆:重庆大学,2009.
DENG Yujuan.Study of threshold de-noising algorithm of speech signal based on wavelet transformation[D].Chongqing:Chongqing University,2009.
[19] AKRAM J,CHEN Z,EATON D,et al.Time-frequency denoising of microseismic data[A].Seg Technical Program Expanded[C].2016:2750-2754.
[20] DAUBECHIES I,LU J,WU H T.Synchrosqueezed wavelet transforms:An empirical mode decomposition-like tool[J].Applied and Computational Harmonic Analysis,2011,30(2):243-261.
[21] QIANG L,HAN L G,CHEN J Y,et al.Separation of inhomogeneous blended seismic data[J].Applied Geophysics,2015,12(3):327-333.
[22] 曹静杰.反问题的最优化方法研究及其在图像恢复中的应用[D].北京:北京交通大学,2008.
CAO Jingjie.The study of optimization methods for inverse problems and its applications in image restoration[D].Beijing:Beijing Jiaotong University,2008.
[23] MALEKI A,MONTANARI A.Analysis of approximate message passing algorithm[A].Information Sciences and Systems(CISS),2010,44th Annual Conference[C].IEEE,2010:1-7.
[24] DAUBECHIES I,DEFRISE M,DE Mol C.An iterative thresholding algorithm for linear inverse problems with a sparsity constraint[J].Communications on Pure and Applied Mathematics,2004,57(11):1413-1457.
[25] VAN Den Berg E,FRIEDLANDER M P.Probing the pareto frontier for basis pursuit solutions[J].SIAM Journal on Scientific Computing,2008,31(2):890-912.
[26] BECK A,TEBOULLE M.A fast iterative shrinkage-thresholding algorithm for linear inverse problems[J].SIAM Journal on Imaging Sciences,2009,2(1):183-202.
[27] MAHDAD A,DOULGERIS P,BLACQUI
RE G.Separation of ble-nded data by iterative estimation and subtraction of blending interference noise[J].Geophysics,2011,76(3):Q9-Q17.
