重介质选煤是常用的煤炭洗选工艺之一，其是将密度介于精煤和矸石之间的重介质悬浮液和原煤混合后送入重介质旋流器，在离心力和重力的作用下实现精煤和矸石的分离。重介质旋流器因分选精度高、分选密度调节范围宽、适应能力强等特点，在选煤工艺中广泛使用[1-2]。
先进控制是提升重介质选煤效率和稳定性的重要手段之一，其实现往往需要依托过程动态数学模型，因此重介质选煤过程模型的研究一直是矿物分选领域的重要研究内容之一。现有的研究成果主要研究集中在静态模型、流体力学模型、数据驱动模型、质量守恒模型等。如文献[3]通过多项方程式拟合实验数据法的方法，建立了一种将配分因子作为相对密度和矿石粒度函数的重介质选煤静态模型。文献[4]采用同样的建模与策略构建了一种能够表示分选效率的静态模型。然而静态模型仅能用于工艺设计与优化，难以基于此设计闭环控制控制系统。文献[5]通过使用Fluent等软件求解Navier-Stokes方程建立了重介质旋流器的计算机流体动力学(Computational Fluid Dynamics,CFD)模型。文献[6-8]将CFD法与离散元法相结合，建立了煤粒在重介质旋流器中的动态模型，但CFD模型过于复杂而难以用于控制器设计[9]。当前，数据驱动建模方法由于较少依赖先验知识，难以机理建模或缺乏机理知识的复杂工业过程中被广泛使用。文献[10]采用机器学习模型，建立了基于变块宽增量随机配置网络的精煤灰分模型。文献[11]针对重介质选煤过程动态时变与精煤灰分数据稀缺感知的问题，提出了基于在线自适应半监督学习的精煤灰分模型。但上述基于机器学习方法的数据驱动模型是在模型输入特征空间映射到复杂高维非线性特征空间基础上，再进行回归计算，模型结构相对复杂，无法直接用于控制器设计。
质量平衡模型是一种描述原料投入、产量与损耗之间关系的机理模型，文献[12]基于矿浆中各物料的质量平衡关系，建立了重介质选煤动态模型，被用于设计了重介质选煤过程模型预测控制器与自适应控制器[13-14]。但所建立的质量平衡模型对不确定的模型参数，主要是依靠经验或实验试凑来获得，难以精确描述实际动态过程，给实际控制系统的设计带来难题。因此，重介质选煤过程控制系统性能的提高迫切需要进一步开展模型参数的优化方法研究，以提高模型质量。
受这一问题驱动，笔者致力于采用捕食-食饵优化(Prey-Predator Optimization,PPO)算法[15]对重介质选煤过程动态模型参数进行优化。PPO是一种新型元启发式优化算法，相较于传统算法，具有收敛速度快、对最优值敏感等优点。在PPO算法框架中，搜索步长是决定对最优值搜索程度的重要因素，传统方法将Best Prey以恒定的搜索步长对最优值进行搜索。此时，如果搜索步长过小将导致收敛过慢，过大则可能导致在临近最优解时被跳过，从而陷入局部最优。文献[16]根据判断Prey与最优值之间的距离来选择步长，可快速调整2者之间距离，达到快速收敛的目的，但依然需要依托在人为设定步长的基础上;文献[17]利用递减函数来实现搜索步长随迭代的自适应变小，但搜索步长只能机械性变小，无法自适应调整算法的搜索能力。
为此，笔者应用增强学习思想，提出增强PPO(Reinforcement PPO,RPPO)算法，主要思想是，搜索个体利用神经网络将自身的状态信息映射到动作集合，通过动作来控制搜索步长的增减以及网络权重的更新，从而使优化模型中搜索个体通过不断学习自身历史信息来选择模型参数，建立数据驱动的优化模型参数自适应调整策略，最终提高优化性能。此外，充分考虑机理模型参数众多，难以对模型参数直接进行优化的难题，采用了低差异的Sobol’序列与基于方差的Sobol’参数灵敏分析相结合的方法[18]，分析了在建模过程中产生的不确定性参数对精煤中灰分含量的影响，确定各参数对模型输出的重要性，进而对这些“重要的”模型采用RPPO算法进行寻优。通过与其他传统启发式优化算法进行对比，分析了所提算法的性能;且采用实际数据验证了所提模型的准确性。
1 重介质选煤过程与动态模型
1.1 重介质选煤过程描述
典型的重介质选煤过程如图1所示[19]，经过筛选加工的原煤和由合格介质桶传输出的密度适中的重介质悬浮液共同加入混料桶中。经充分混合后，矿浆由矿浆泵打入到重介质旋流器，在离心力和重力的作用下，密度小于重介质悬浮液的煤矿在重介质旋流器上方聚集，相反，密度大于重介质悬浮液的矿物杂质由重介质旋流器底流口流出。重介质旋流器的溢流和底流经脱水脱介处理后，分别形成精煤和尾矿，送下一道工序;脱水脱介筛将残余的介质溶液送入磁选机中进行回收;从磁选机回收的介质与从高浓介质桶中的高浓度介质、稀释水以一定比例共同加入合格介质桶中，经过混合后进行再次工艺循环。
图1 重介质选煤过程工艺流程
Fig.1 Flow diagram of classical dense medium coal separation process
1.2 重介质选煤动态模型
重介质选煤过程主要分为矿浆混合、重介质分选以及重介质回收3个动态过程。
1.2.1 混合过程模型
原煤经过破碎等工艺后，与来自合格介质桶传输的重介质悬浮液在混料桶中进行充分混合。由质量平衡定理可得混合过程模型为
(1)
(2)
(3)
Wi=Qmbρmb
(4)
其中，ρmb和ρm分别为重介质旋流器入矿混合矿浆密度及重介质悬浮液密度;
为ρmb关于时间的导数；Qmb和Qm分别为重介质旋流器入矿混合矿浆体积流量及重介质悬浮液体积流量;Wore和Vmb分别为给煤量及混料桶中混合矿浆体积;xi,c和xore,c分别为灰分、硫、水、挥发物在重介质旋流器入矿混合矿浆及原煤中的质量分数;Wi为重介质旋流器的给矿量;xi,m为混合矿浆中重介质悬浮液的质量分数。
1.2.2 重介质分选过程模型
从混料桶中流出的混合矿浆送入重介质旋流器，在离心力和重力的作用下，煤与矿物杂质分别在底流和溢流矿浆中被排出，根据质量平衡定理可建立如下的重介质分选过程模型:
ρm)xi.ash]-xu,c[Wi-Qoρo-KoVo(ρo-ρm)xi,C]-
Ku,cVuρu(ρc-ρm)(xi,c-xu,c)}
(5)
ρm)xi.ash]-xu,m[Wi-Qoρo-KoVo(ρo-ρm)xi,C]-
Ku,mVuρu(ρo,m-ρm)(xi,m-xu,m)}
(6)
ρm)xi.ash]-xu,c[Wi-Qoρo-KoVo(ρo-ρm)xi,C]-
Ko,cVoρo(ρm-ρc)(xi,c-xo,c)}
(7)
ρm)xi.ash]-xu,m[Wi-Qoρo-KoVo(ρo-ρm)xi,C]-
Ko,mVuρu(ρm-ρu,m)(xi,m-xo,m)}
(8)
(9)
(10)
其中，xi,ash为灰分在重介质旋流器入矿混合矿浆中的质量分数；xo,c和xo,m分别为溢流中各组分及重介质的质量分数;xu,c和xu,m分别为底流中各组分及重介质的质量分数;xi,C为重介质旋流器入矿混合矿浆中的碳质量分数,xi,C=1-xi,m-∑cxi,c;Qo，ρo和Vo分别为溢流中的矿浆流速、密度和体积;Qu，ρu和Vu分别为底流中的矿浆流速、密度和体积;ρc为各组分的密度;ρo,m，ρu,m分别为溢、底流中重介质的密度;Ku,c=[Ku,ash，Ku,S，Ku，H2O，Ku,vol]，Ku，Ko，Ku,m，Ko,m以及Ko,c=[Ko,ash，Ko,S，Ko,H2O，Ko,vol]为重介质旋流器的相关参数;
分别为xo,c，xo,m，xu,c，xu,m，ρo，ρu关于时间的导数；假设重介质旋流器中混合煤浆按照α比例分成溢流和底流2个部分，可得溢流和底流的体积及流速，即
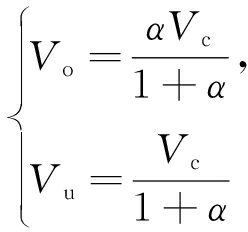
(11)
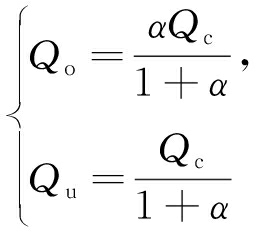
(12)
式中，Vc为重介质旋流器中矿浆体积，假设其不变。
1.2.3 重介质回收过程模型
重介质选煤过程需要通过对旋流器产物进行脱介、脱水来回收磁性介质，回收的介质与高浓介质在合格介质桶中经稀释水按照期望的介质浓度进行调节。为保证模型的精确性，需考虑介质回收中的损耗。因此假设介质从重介质旋流器到磁选机的回收率为β，介质从磁选机到合格介质桶的回收率为γ，磁选机出口的重介质密度维持在ρrm，从而可建立的重介质回收过程模型为
磁选机可回收到的介质质量mm:
(13)
其中，
和
分别为重介质悬浮液的体积流量及密度;ρw为水的密度。
磁选机可回收到的介质体积流量Qrm:
(14)
合格介质桶内部动态模型:
(15)
(16)
(17)
其中，Qmm，ρmm分别为高浓介质的体积流量及密度;Vcor为重介质溶液在合格介质桶中的体积;Qw为稀释水的体积流量;ΔP，Cw和lw分别为阀门系数、阀门开度和阀门压差。
在上述动态模型中，待确定的模型参数有α，Ku，Ko，Ku,ash，Ko,ash等13个，实际过程中难以直接测量。由模型可以看出，对上述参数进行优化，是一个复杂的非线性优化问题，启发式优化算法是解决这一问题的有效方法。然而，过多的模型参数会大大增加优化算法的复杂性和难度。实际上，模型输出可能仅对一部分参数敏感，其它参数对模型品质不起决定性作用。因此，可通过参数灵敏度分析来确定模型参数的“重要性”，然后只对“重要的”模型参数进行寻优，大大简化计算负荷，并有利于最优值的求解[20]。
2 基于参数灵敏度与增强捕食-食饵的模型参数优化
2.1 参数灵敏度分析
参数灵敏度分析研究了机理模型输出的变化如何归因于其输入参数的变化。从参数变化范围的角度可将灵敏度分析方法分成局部灵敏度分析和全局灵敏度分析方法。局部灵敏度只能在参数范围内进行小范围灵敏度分析，难以应用在非线性模型中;而全局灵敏度分析则考虑了参数在整个取值范围内的变化。同时，考虑到重介质选煤过程动态模型具有强非线性、不确定性参数多等特点，一般的局部灵敏度分析方法难以用于对此模型的分析，而Sobol’灵敏分析方法作为一种单次可处理多输入变量的全局灵敏度分析方法，与重介质选煤过程动态模型特点十分契合。因此，文本采用基于方差的Sobol’参数灵敏度方法对上述重介质选煤过程动态模型参数进行灵敏度分析。
首先在各个模型参数允许的取值范围内进行采样，并求得模型输出，将模型输出的方差归因于某些参数或某些参数的集合，对模型输出的影响大小定义为模型灵敏度。
Sobol’方法定义只含各参数或各阶参数集合的模型输出偏方差与模型输出总方差的比值为各参数以及参数之间的灵敏度:
(18)
其中，1≤i1<…<is≤d， 1≤ s ≤d， d为参数的个数，文中d =13;下标i1…is为变量可能所含的参数，变量所含项的最高次数为s;Si1…is为各阶参数的灵敏度;Vi1…is为各阶参数的偏方差;V为总方差。同时，有
(19)
其中，S下标的个数为灵敏度的阶数，如Si为一阶灵敏度，用于估计单独参数i对模型输出的影响;Sij为二阶灵敏度，表示参数i，j之间的组合对模型输出的影响;S12…d为d阶灵敏度，用于计算不同参数组合对模型输出影响。另定义参数i在f(x)中的全阶灵敏度为STi=1-V-i/V，用于计算含有参数i的灵敏度总和，其中，V-i为不包含参数i的其余参数偏方差。
一般情况下,上述方差通过积分求得[21]，但由于重介质选煤动态模型复杂难以直接解析求得积分，因此本文基于蒙特卡罗法估计总方差和偏方差，具体步骤为:
(1)采样序列。为保证所生成样本的独立性，每次采样时利用Sobol’序列[22]生成一个N×2d的矩阵，并将前d列称为AN×d，其余d列称为BN×d，其中N为样本大小;为探究各参数对结果的影响，需进一步构建矩阵
矩阵的第u列分别等于BN×d的第u列，其余列源自AN×d，同理可构造矩阵
(2)灵敏度计算。在生成
后，需要将各矩阵代入本文中描述的选煤过程模型f(x)中，并将所得f(A),代入式(20)～(22)计算得到灵敏度:
(20)
(21)
(22)
式中，f(A)j下标j为采样矩阵的第j行。
式(22)用于计算某参数的全阶灵敏度，以此作为模型参数的灵敏度的最终判断依据，可确定各参数对模型的“重要性”。基于此，将相对“不重要”的模型参数固定在经验值，继而采用元启发式优化算法对“重要的”模型参数进行寻优。
2.2 增强捕食-食饵优化算法
本文提出的增强捕食-食饵优化(Reinforcement Prey-Predator Optimization,RPPO)算法是一种基于捕食者(Predator)与食饵(Prey)之间相互作用的元启发式算法。其首先需要定义m个可行解，{ϑ1,ϑ2,…,ϑi,…,ϑm}，并将每个可行解赋予生存值(Sv)，Sv可通过计算目标函数得到，且与目标函数性能成正比例关系。通过Sv大小做出以下分类:最小可行解称作Predator，最大可行解称作Best Prey，其余称作Prey。在完成各角色分配后，Predator会追捕Prey，而Prey自然会远离Predator，而且会倾向于跟随生存值更高且位置较近的Prey运动，如果不满足跟随概率，则只会在保证远离Predator的情况下做随机方向运动。不同于Prey，Best Prey则不需要担忧Predator的追捕，只考虑寻找更好的躲避处，即专注于对最优解的搜索(Exploitation)即可。采用增强学习方法不断寻找最优的搜索步长，从而保证了算法的收敛速度和准确性。
2.2.1 更新可行解位置
(1)Best Prey
(23)
其中，ξ1∈[0,1]分布;dl为一个随机向量;‖·‖为欧氏距离;Best Prey沿着dl方向在自身周围采用较小的搜索步长(λmin)对最优值进行搜索，防止跳过最优值。
(2)Prey
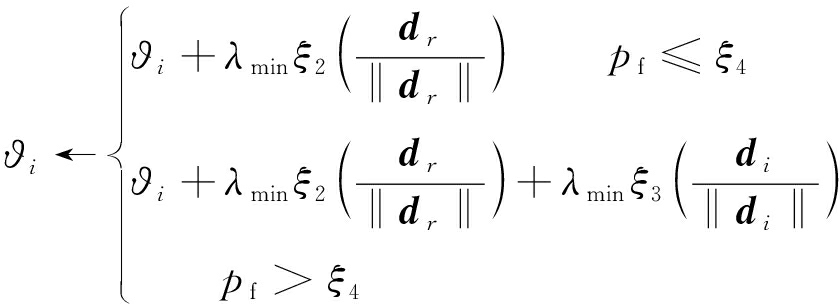
(24)
其中，ξ2,ξ3,ξ4∈[0,1]且服从均匀分布;Pf为Prey向其他Prey靠拢的概率，如果Pf≤ ξ4，Prey只会沿随机方向dr运动来躲避Predator;反之，Prey还会以di方向跟随其他Prey;λmax为Prey的探索步长;根据文献[15]得
ϑj-ϑi)
(25)
在式(25)中，di由其他Prey的方向及其生存值共同决定。其中，u为比例参数，对Sv(ϑj)在di中的贡献进行缩放。
在式(24)中，dr为Prey躲避Predator的方向，Prey应沿着离Predator较远的方向移动，因此，需先做以下判断:
(26)
dr1=‖ϑp.d-(ϑi+dr)‖
(27)
dr2=‖ϑp.d-(ϑi-dr)‖
(28)
其中，dr1，dr2为Prey分别沿着±dr方向移动后与Predator的欧式距离。
(3)Predator
(29)
其中，ξ5,ξ6∈[0,1]且服从均匀分布;
为离Predator最近的Prey。
算法在运行过程中会涉及到探索、搜索2种步长，探索步长主要是在迭代前期对可行解空间的探索，扩大种群个体的可搜索空间;而搜索步长是在迭代后期针对可行解现有空间的搜索，搜索步长过大不利于对现有空间充分搜索，过小则需要冗余的迭代次数才能寻得最优解，因此适当的搜索步长对算法最终寻得的最优解起着至关重要的作用。为避免因搜索步长固定不变而导致算法寻优能力不足的问题，本文采用增强学习的思想，用种群中的个体代表智能体，通过让其对自身历史经验的学习来选择动作，依据个体采取的动作来判断搜索步长的变化，整个算法流程如图2所示。
图2 增强捕食-食饵优化算法流程
Fig.2 Flow diagram of RPPO
2.2.2 基于增强学习的自适应搜索步长
选择Prey作为增强学习个体，通过设定个体的动作、状态及奖惩机制，建立增强学习模型，实现搜索步长的自适应调整。增强学习的思想是个体接收当前状态，并通过神经网络将状态映射到相应的动作，环境根据所选动作更新状态，与此同时，通过奖惩机制计算所采取的动作相应的奖惩，并据此更新神经网络，逐渐获取与环境相一致的状态-动作映射。本文所定义的动作、状态及奖惩机制如下:
(1)动作。个体设定3种动作:步长加速、步长减速、步长不变，即
(30)
其中，
为个体在第t次迭代中的搜索步长;σ为步长变化因子。在神经网络输出层中，被选中动作相对应的输出节点为1，未选中的为0。
(2)状态。个体的T个历史状态组成状态集合Statet， Statet会随着选择动作而产生相应的变化，并由式(31)来更新。
(31)
其中，
为个体第t次迭代的生存值。sign(x)为符号函数，定义为
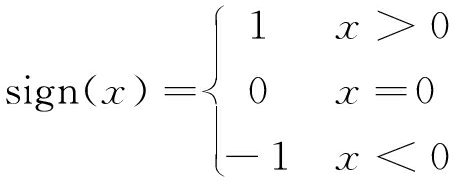
(32)
(3)奖惩机制。每次迭代中，当个体与最优解的距离变小时，应当给予奖励;反之，应当收到惩罚:
(33)
(4)状态-动作映射。选用单隐含层神经网络来映射状态与动作之间的关系。以式(31)得到的状态集合作为神经网络的输入，即输入节点有T个;将动作集合中的3种动作作为3个输出节点，并通过式(34)选择将要执行的动作:
y=min|1-yi| 1≤i≤3
(34)
其中，y为与1距离最小的输出节点;yi为神经网络第i个输出节点，当i取1,2,3时，分别对应步长加速、减速与不变3个动作，即
动作
(35)
本文将隐含层和输出层的激活函数设为Sigmoid函数，隐含层到输出层的权重更新公式:
(36)
其中，η为神经网络的学习率;g为隐含层的输出;di为输出节点i的期望输出，设定当个体受到奖赏，即Feedbackt=+1时，di=1，否则为0;yi为输出节点i的实际输出。同样，可得到输入层到隐含层权重公式:
(37)
式中，
为网络输入连接到隐含层节点j的权重;x为输入层的输入;gj为隐含层节点j的值;wij为隐含层节点j与输出节点i之间的连接权。
RPPO算法每次迭代都会先确定搜索步长，然后通过所描述方程进行更新Best Prey，普通Prey及Predator的位置。具体描述如下:
输入:可行解(x1,x2,…,xm)，最大迭代次数Niter，状态向量T，步长变化因子σ，神经网络学习率η，目标函数Fit，PPO算法参数(λmax，λmin，Pf)
(1)将可行解作为Fit的输入，得到x的生存值Sv;
(2)初始化神经网络;
(3)for t =1:Niter
按Sv从小到大对可行解排序;
利用式(29)更新Predator位置;
for i=2:m-1
根据式(24)更新Prey位置;
i=i+1;
End
根据式(23)更新Best Prey位置;
当前所受奖惩Feedbackt由式(33)计算;
利用式(36),(37)更新神经网络权重;
根据式(31)更新状态集合;
下一代步长可由式(30)得到;
t=t+1;
End
(4)选择Sv的可行解作为最终结果;
输出:Best Prey的位置及生存值
3 实 验
精煤中灰分是决定煤炭的质量主要因素，因此，本文主要研究对象为分选动态过程模型中精煤灰分模型，并以其为目标函数。在给煤量不断变化情况下，本文将探究通过所提方法对模型参数进行优化后，精煤灰分模型是否能够较好跟随实测精煤灰分。
3.1 灵敏度分析
原煤给煤量Wore的变化情况如图3所示;同时，根据各参数的实际物理含义[12]，并通过工艺知识或实验确定其取值范围，见表1;而选煤模型运行过程中所需设备参数值见表2。
表1 模型参数取值范围
Table 1 Range of each model parameters
模型参数取值下限取值上限α1.0002.600Ku0.153 70.285 5Ko0.153 70.285 5Ku,ash0.50×10-410.00×10-4Ko,ash0.50×10-410.00×10-4Ku,S2.73×10-45.07×10-4分选过程模型Ko,S2.73×10-45.07×10-4Ku,H2O0.21×10-40.39×10-4Ko,H2O1.05×10-41.95×10-4Ku,vol6.23×10-611.57×10-6Ko,vol6.23×10-411.57×10-4Ku,m2.73×10-45.07×10-4Ko,m3.36×10-46.24×10-4
表2 设备参数取值
Table 2 Values of equipment parameters
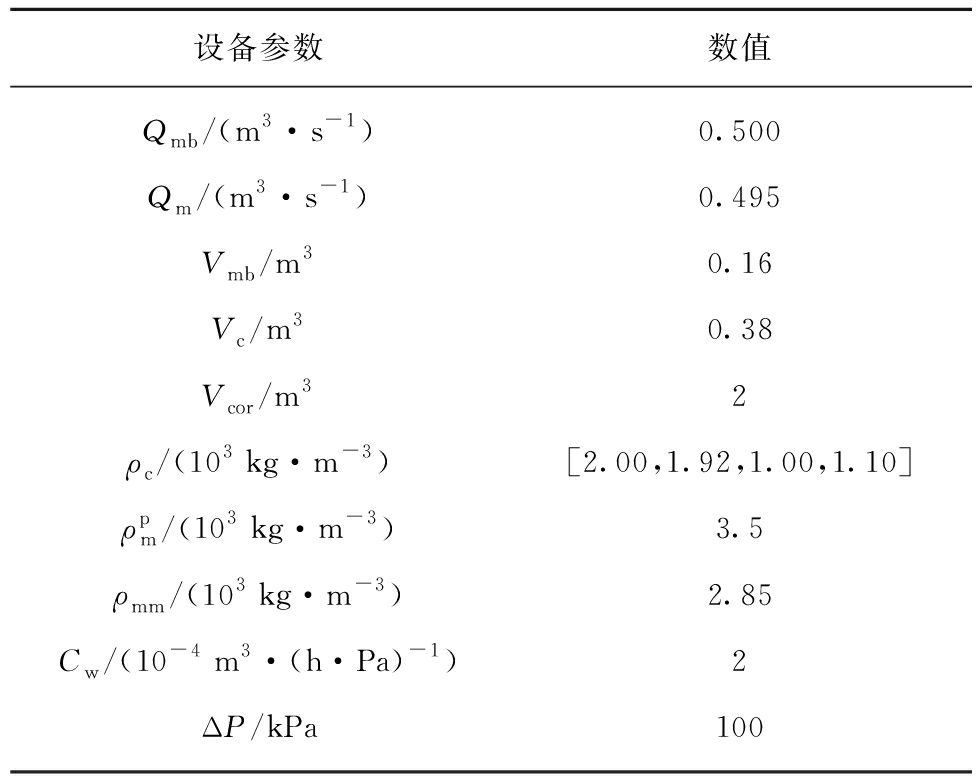
设备参数数值Qmb/(m3·s-1)0.500Qm/(m3·s-1)0.495Vmb/m30.16Vc/m30.38Vcor/m32 ρc/(103 kg·m-3)[2.00,1.92,1.00,1.10]ρpm/(103 kg·m-3)3.5ρmm/(103 kg·m-3)2.85Cw/(10-4 m3·(h·Pa)-1)2ΔP/kPa100
图3 原煤的给煤量变化曲线
Fig.3 Curve of raw coal feed rate
在此范围内，利用Sobol’序列进行采样，以采样所得参数集为输入，运行重介质分选过程模型。通过Sobol’方法对多参数变化下的各模型进行分析，得到各模型参数的一阶灵敏度及全阶灵敏度，如图4，5所示。
图4，5利用箱型图表示各参数在完整工艺过程中的灵敏度变化范围，其中，菱形为所有时刻灵敏度的均值。从图4，5可知，虽各参数的一阶灵敏度和全阶灵敏度有所差别，但不影响参数“重要性”的判断，因此文中将不考虑各参数之间的高阶灵敏度。同时，本文认定灵敏度均值大于0.05且变化范围较大的参数为“重要”参数，需要将其进行进一步的参数优化。由图5可知重介质分选过程模型中只有α，Ku,ash，Ko,ash符合上述要求，说明在设计重介质回收过程模型参数时，应考虑对这些参数进行优化。而对于输出结果影响较小的参数，将通过工程经验确定其近似值。
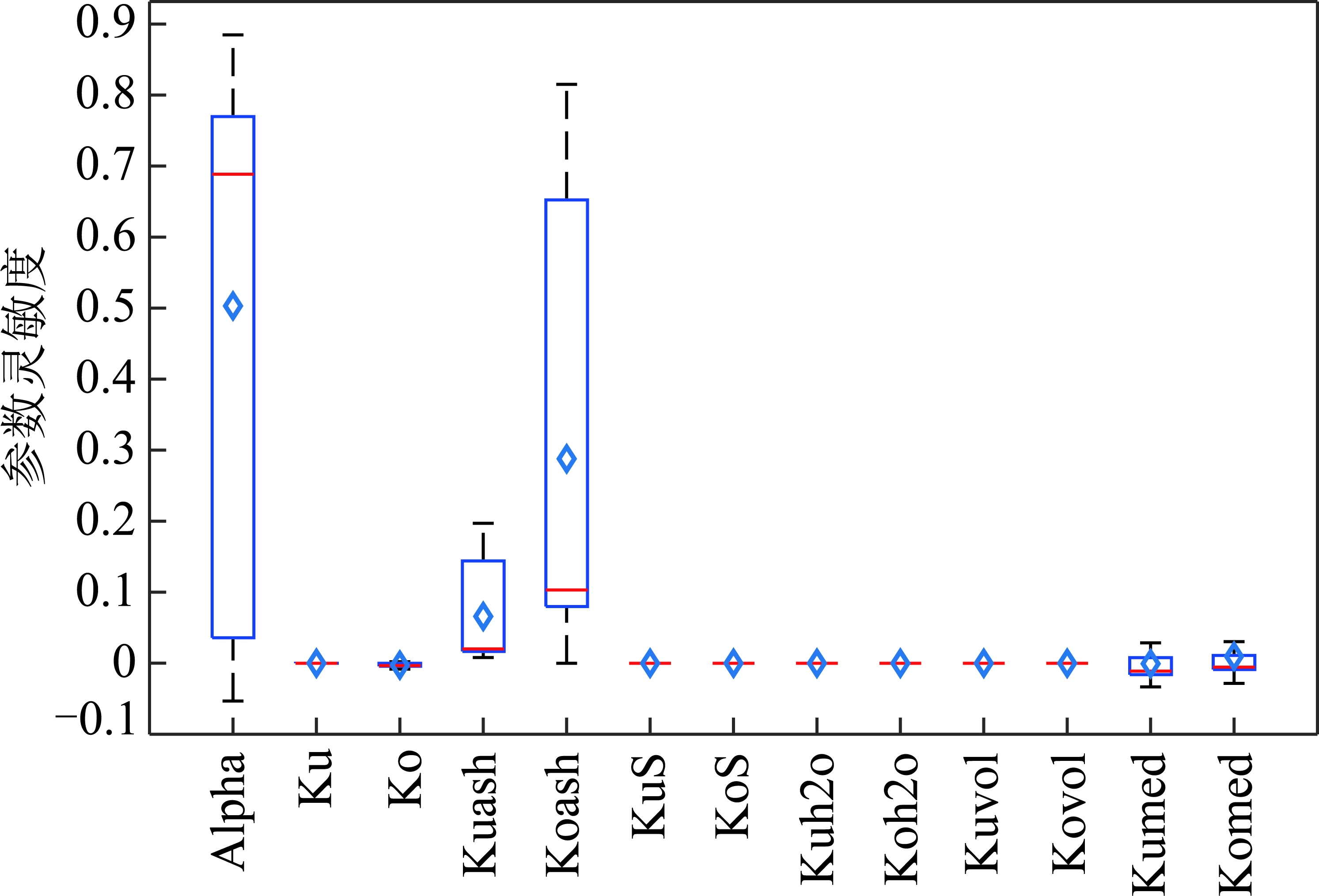
图4 模型参数的一阶灵敏度
Fig.4 First-order indices of each model parameters
图5 模型参数的全阶灵敏度
Fig.5 Total-effect indices of each model parameters
3.2 参数优化
为使所建立模型能更好的描述选煤过程，本文以每一时刻模型仿真输出与实际过程24 h测量数据之间的差距为目标函数，整个工业过程中每一时刻的差距之和越小说明优化所得的参数越合适，即所有差距和的倒数越大越好:
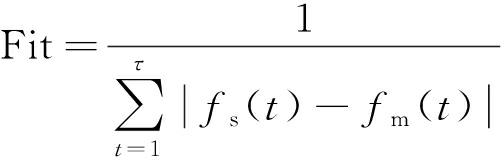
(38)
其中，Fit为目标函数;t为模型运行过程中的某时刻;fs为所建立的模型输出;fm(t)为实际测量数据;τ为模型运行时间。
为验证RPPO在重介质选煤模型参数优化过程中的有效性，本文将其与PPO、遗传算法(Genetic Algorithm,GA)[23]以及粒子群算法(Particle Swarm Optimization,PSO)[24]在相同初始条件下运行，各算法对目标函数的寻优过程如图6所示。本文根据实验经验得出各参数取值，见表3。
表3 各算法参数设置
Table 3 Parameters of each algorithm
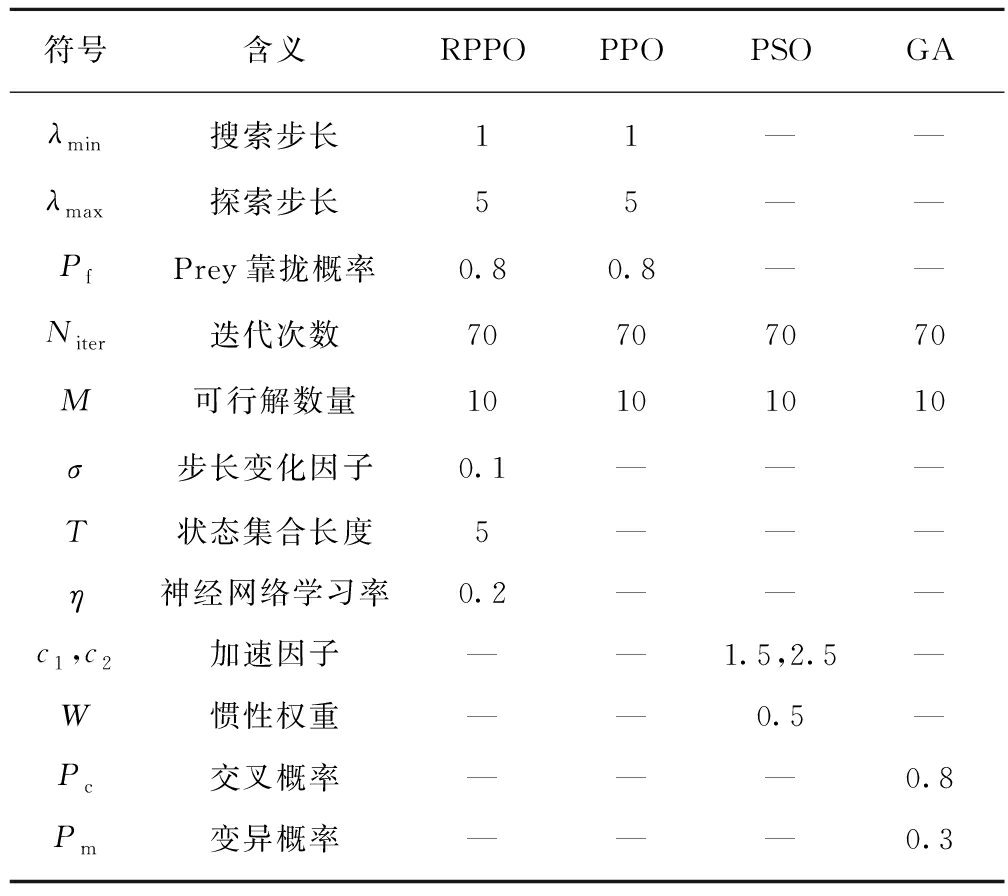
符号含义RPPOPPOPSOGAλmin搜索步长11——λmax探索步长55——PfPrey靠拢概率0.80.8——Niter迭代次数70707070M可行解数量10101010σ步长变化因子0.1———T状态集合长度5———η神经网络学习率0.2———c1,c2加速因子——1.5,2.5—W惯性权重——0.5—Pc交叉概率———0.8Pm变异概率———0.3
图6 目标函数随迭代次数的变化情况
Fig.6 Variation of the objective function with iterations
为了避免初始条件的随机性对实验结果的影响，本文采取了种群同一初始位置的方法，使得4种算法初始条件相同，并基于此初始位置进行30次重复试验。图6为某一次对比实验结果，其他结果类似。由图6可看出，在开始迭代的初期，RPPO和PSO可快速将目标函数收敛在理想最优值附近，这说明RPPO和PSO在迭代初期可以实现很好的探索;结束迭代过程后，以RPPO算法的结果最为突出，说明了RPPO中Best Prey的后期搜索能力相较于其他算法有所提高。在整个寻优过程中，个体的搜索步长变化如图7所示，个体可根据自身的历史信息来判断所处搜索空间的形势，进而选择不同的动作，保证了对现处地形的充分搜索，可避免选择次优解。
图7 搜索步长变化
Fig.7 Variation diagram of exploitation step lengths
表4给出了整个24 h的实验统计结果。从表4可看出，RPPO和PSO寻找最优值能力相当;在平均值、最差值及标准差指标中，RPPO和PPO表现较好且接近，表明这2种算法的稳定性都较高。说明相较于其他3种算法，RPPO兼顾寻优能力及稳定性，因此，本文选用RPPO来进行重介质选煤的参数进行优化。
表4 4种算法统计结果
Table 4 Statistical results of the four algorithms
算法最优值平均值最差值标准差GA2.398 01.695 91.128 30.371 7PPO2.497 22.434 02.297 80.043 8PSO2.516 92.236 91.513 20.273 0RPPO2.524 62.471 92.338 10.041 1
为使所建立模型贴合实际工艺过程，本文基于已建立的重介质分选过程模型，进行了各优化算法对比寻优实验，将所得的模型参数代入重介质分选过程模型公式得到整个工艺过程的精煤灰分，如图8所示。其中，RPPO所优化的模型参数为(1.389 7，6.270 0×10-4，7.934 4×10-4)。
图8 模型仿真结果与实际测量数据对比
Fig.8 Comparison curves between the simulation results and actual measurement data
为了更清楚的表明所提算法的性能，图8给出了具有代表性的30 min内的对比实验结果。从工业过程来看，由RPPO所得灰分曲线图与实际采样数据最为接近，PPO次之;计算得各算法(按图例从上至下)与实测数据的均方误差分别为0.009 3，0.004 6，0.006 6，0.004 2。图9为不同算法优化所得模型的误差概率密度函数(Probability Density Function，PDF)对比图，图9中，各PDF曲线是以误差的均值为中心值所得，显然，RPPO与PPO算法的PDF曲线中心点更接近0，且RPPO的PDF曲线更高，与其他方法相比标准差更小;图10为以0为中心值的各算法PDF曲线，从图10可以看出，RPPO算法的PDF曲线最高且窄，效果明显优于其他算法。综上，可得RPPO相较于传统PPO及其他传统算法能够更精确的估计重介质选煤模型参数，便于基于模型的进一步工作展开。
图9 不同算法建模误差PDF对比(以均值为中心)
Fig.9 PDF comparison curves of modeling errors based on mean values by different algorithms
图10 不同算法建模误差PDF对比(以0为中心)
Fig.10 PDF Comparison curves of modeling errors based on 0 by different algorithms
4 结 论
(1)针对一个典型由矿浆混合、重介质分选和重介质回收3部分组成的重介质选煤过程，建立基于质量平衡重介质选煤过程动态数学模型。
(2)基于所建立模型，首先利用Sobol’参数灵敏度分析方法分析出“重要的”模型参数，进而采用自适应步长的RPPO算法进行模型参数优化，从而提高了重介质选煤动态模型精度，使其更接近真实的工业过程。
(3)从实验结果可以看出，本文所提的方法相较于传统PPO等算法可自适应控制步长，搜索能力有所增强，进而能够避免选择次优解且稳定性高;应用在重介质选煤模型参数优化中可充分发挥RPPO的优势，寻找到最佳的模型参数，使得模型输出更贴合实际工业采样数据。
(4)本文所提的灵敏度分析与增强捕食-食饵优化相结合的模型参数优化策略，不限于本文所研究的典型重介质选煤过程模型，可推广用于解决煤炭领域其他过程或装备的建模问题。
[1] 张凌智,代伟,马小平.重介质选煤过程先进控制:研究进展及展望[J].工矿自动化,2020,46(8):21-27，69.
ZHANG Lingzhi,DAI Wei,MA Xiaoping.Advanced control of dense medium coal separation process:Research progresses and prospects[J].Industry and Mine Automation,2020,46(8):21-27，69.
[2] NAPIER-MUNN T.The dense medium cyclone-past,present and future[J].Minerals Engineering,2018,116:107-113.
[3] NAPIER-MUNN T J.Modelling and simulating dense medium separation processes-A progress report[J].Minerals Engineering,1991,4(3-4):329-346.
[4] SCOTT I A,NAPIER-MUNN T J.A dense-medium cyclone model based on the pivot phenomenon[J].Transactions of the Institution of Mining and Metallurgy (Section C:Mineral Processing Extractive Metallurgy),1992,101:61-76.
[5] NARASIMHA M,BRENNAN M S,HOLTHAM P N,et al.A comprehensive CFD model of dense medium cyclone performance[J].Minerals Engineering,2007,20(4):414-426.
[6] CHU K W,WANG B,YU A B,et al.CFD-DEM study of the effect of particle density distribution on the multiphase flow and performance of dense medium cyclone[J].Minerals Engineering,2009,22(11):893-909.
[7] CHU K W,WANG B,YU A B,et al.CFD-DEM modelling of multiphase flow in dense medium cyclones[J].Powder Technology,2009,193(3):235-247.
[8] SHEN L J,HU Y F,CHEN J Z,et al.Numerical simulation of the flow field in a dense-media cyclone[J].Mining Science and Technology (China),2009,19(2):225-229.
[9] CORTES C,GIL A.Modeling the gas and particle flow inside cyclone separators[J].Progress in energy and combustion Science,2007,33(5):409-452.
[10] DAI W,LI D,ZHOU P,et al.Stochastic configuration networks with block increments for data modeling in process industries[J].Information Sciences,2019,484:367-386.
[11] DAI W,HU J,CHENG Y,et al.RVFLN-based online adaptive semi-supervised learning algorithm with application to product quality estimation of industrial processes[J].Journal of Central South University of Technology,2019,26(12):3338-3350.
[12] MEYER E J,CRAIG I K.The development of dynamic models for a dense medium separation circuit in coal beneficiation[J].Minerals Engineering,2010,23(10):791-805.
[13] 代伟,张凌智,褚菲，等.重介质选煤过程模型与数据混合驱动的自适应运行反馈控制[J].控制理论与应用,2020,37(2):283-294.
DAI Wei,ZHANG Lingzhi,CHU Fei,et al.Model-data hybrid driven adaptive operational feedback control of dense medium coal preparation process[J].Control Theory & Applications,2020,37(2):283-294.
[14] ZHANG L J,XIA X H.A model predictive control for coal beneficiation dense medium cyclones[J].IFAC Proceedings Volumes,2014,47(3):9810-9815.
[15] TILAHUN S L,ONG H C.Prey-Predator algorithm:A mew metaheuristic algorithm for optimization problems[J].International Journal of Information Technology & Decision Making,2015:1331-1352.
[16] GRILLANDA N,CHIOZZI A,MILANI G,et al.Efficient meta-heuristic mesh adaptation strategies for NURBS upper-bound limit analysis of curved three-dimensional masonry structures[J].Computers & Structures,2020,236:106271.
[17] TILAHUN S L,NGNOTCHOUYE J M T.Prey predator algorithm with adaptive step length[J].International Journal of Bio-Inspired Computation,2016,8(4):195-204.
[18] SOBOL’ I M.Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates[J].Mathematics & Computers in Simulation,2001,55(1-3):271-280.
[19] DAI W,ZHANG L,FU J,et al.Model-data-based switching adaptive control for dense medium separation in coal beneficiation[J].Control Engineering Practice,2020,98:104241.
[20] 温亮,周平.基于多参数灵敏度分析与遗传优化的铁水质量无模型自适应控制[J/OL].自动化学报:1-15[2021-09-27].https://doi.org/10.16383/j.aas.c180741.
WEN Liang,ZHOU Ping.Model free adaptive control of molten iron quality based on multi-parameter sensitivity analysis and GA Optimization[J/OL].Acta Automatica Sinica:1-15[2021-09-27].https://doi.org/10.1 6383/j.aas.c180741.
[21] SALTELLI A,ANNONI P,AZZINI I,et al.Variance based sensitivity analysis of model output.Design and estimator for the total sensitivity index[J].Computer Physics Communications,2010,181(2):259-270.
[22] SOBOL’ I M.On the distribution of points in a cube and the approximate evaluation of integrals[J].Ussr Computational Mathematics & Mathematical Physics,1967,7(4):86-112.
[23] 温廷新,陈晓宇,邵良杉，等.参数优化GA-ELM模型在露天煤矿抛掷爆破的预测[J].煤炭学报,2017,42(3):630-638.
WEN Tingxin,CHEN Xiaoyu,SHAO Liangshan,et al.Prediction on parameters optimized GA-ELM model for cast blasting in open-pit mine[J].Journal of China Coal Society,2017,42(3):630-638.
[24] 钱建生,厉丹.基于PSO优化改进的Snake模型煤矿环境目标检测[J].煤炭学报,2011,36(11):1949-1954.
QIAN Jiansheng,LI Dan.Snake model based on PSO optimization for coal mine environment object detection[J].Journal of China Coal Society,2011,36(11):1949-1954.
