砂岩是沉积岩中常见的一种,节理在砂岩内部分布极为广泛[1]。节理表面通常是粗糙的,当边坡发生滑动后,节理表面不断磨损,粗糙度不断降低,摩擦力不断发生变化,许多工程问题的发生与节理表面的性质密切相关[2-4]。
矿山开采过程中,砂岩受到外界载荷的扰动作用,内部节理逐渐扩展、贯通形成滑移面。砂岩滑动过程中,节理表面凸体不断磨损,摩擦力也随着变化,进而影响砂岩滑动的稳定性,当节理表面凸体提供的摩擦力不能够克服坡体的下滑力时,则可能发生滑坡灾害,威胁人身生命财产安全。因此,研究砂岩滑动过程中摩擦因数变化规律,对砂岩滑动稳定性的控制具有重要的意义。
多年来,学者们提出了许多模型预测节理摩擦因数。BARTON等[5-6]提出了一个预测摩擦因数的经验模型,在模型中引入了节理粗糙度系数JRC(Joint Roughness Coefficient,JRC)。赵坚[7]认为BARTON模型过高地估测了岩石节理的摩擦因数,为了克服这一缺陷,提出了考虑JRC和节理吻合系数JMC(Joint Matching Coefficient,JMC)的摩擦因数预测模型。LIU等[8]对10条标准粗糙度轮廓进行了数字化处理,计算了每条轮廓的粗糙度指数,提出了基于粗糙度指标的摩擦因数预测模型。班力壬等[9]为了克服采样间距取值对粗糙度指标大小的影响,将岩石节理面划分为一系列连续的长方体微凸体,提出了描述形貌面粗糙度的指标,并分析了粗糙度指标与JRC之间的关系。BABANOURI等[10]进行了大量直剪试验,探讨了弹性模量,JRC和基础摩擦角对摩擦因数的影响。唐志成等[11]对具有不同形貌特征的节理进行了直剪试验,采用坡度均方根表征节理的三维形貌特征,并提出相应的摩擦因数预测模型。陈曦等[12]充分考虑节理形貌参数的影响,将峰值剪胀角表示为初始剪胀角的关系函数,讨论了初始剪胀角与正压力的关系,提出了一个与正压力相关的摩擦因数模型。金磊磊等[13]借助三维激光扫描和3D打印技术,浇筑具有自然节理形貌的人工节理试样,并进行正常压力下的剪切试验,建立了含有三维形貌参数摩擦因数预测模型。节理粗糙度是影响摩擦因数的重要因素,滑动过程中节理表面的凸体被磨损、剪断,节理粗糙度会随着剪切不断变化,学者们对节理粗糙度的变化进行了大量研究。SCHNEIDER[14]研究了粗糙度对节理剪胀角的影响,并提出了负指数模型来描述节理剪胀角的演化规律。PLESHA[15]基于人工节理的循环剪切试验结果,采用以损耗功为变量的负指数函数来表征节理剪胀角的衰减。HOMAND等[16]研究了循环剪切过程中节理表面的变化情况,用剪切前、后节理表面面积的变化定义粗糙度退化指标,并对退化指标随循环次数的变化关系进行了研究。刘博等[17]利用节理微凸体形态变化过程的概化模型,分别确定剪胀角与剪胀率、微凸体剪断率以及表面基础摩擦角之间的关系。金俊超等[18]根据大量试验资料,考虑硬岩弹塑性变形破坏过程中强度参数及剪胀角变化,提出一种峰后强度参数及剪胀角演化模型。滑动过程中接触面积不断变化,接触面积对摩擦因数的预测有很大影响。LI等[19]提出了实际接触面积和名义平坦的粗糙表面的静摩擦因数的表达式。NGUYEN等[20]研究了接触面积和摩擦因数在滑动过程中的变化规律。FATHI等[21]将节理面建模为1组三角形平面,利用剪切之前试件表面三维坐标,确定岩石节理接触面积。PIRZADA等[22]对页岩、石灰石和砂岩节理进行了大量的直接剪切实验,发现摩擦因数主要受接触面积影响。
以上学者对节理粗糙度与摩擦因数的关系,节理粗糙度的表征、变化以及接触面积对摩擦因数的影响进行了试验及理论分析。但是目前对于滑动过程中节理粗糙度变化对摩擦因数的影响研究尚无大量展开,而滑动过程中摩擦因数的变化影响砂岩滑动的稳定性。为此,笔者以砂岩为研究对象,采用金刚石磨片与砂岩节理表面滑动模拟砂岩节理表面凸体磨损的过程,在自制滑动摩擦试验装置上进行砂岩节理滑动摩擦试验,分析滑动过程中摩擦因数的变化规律,利用激光共聚焦扫描显微镜对节理粗糙度进行估算,建立砂岩节理摩擦因数预测模型。
1 砂岩滑动摩擦试验
1.1 试件准备
制备试件时先将砂岩加工成为20 mm×20 mm×40 mm的长方体岩块,然后使用试验机对岩块进行劈裂试验,得到尺寸为20 mm×20 mm×20 mm的试件。砂岩试件密度为2.36 g/cm3。试验前,在试样节理表面涂上黑色涂层,剪切后磨损区域变成白色,而未磨损区域保持不变。通过对比试验前后的节理表面,可以得到表面损伤区域变化。
1.2 表面粗糙度及质量的测定
在试验之前,先测量试样节理的初始形态以评估三维粗糙度。在试件表面选取4个区域,采用激光共聚焦扫描显微镜OLS4000进行表面形貌测试,选取算术平均高度Sa作为评估表面三维粗糙度参数,测试结果取平均值,记为试件的初始粗糙度Sa0,扫描尺寸:2 560 μm × 2 560 μm,取样截止波长λc=800 μm,激光共聚焦扫描显微镜如图1所示。三维形貌测定的只是局部形貌,如果测定试件表面全部形貌非常耗时。节理表面由许多的平行轮廓组成,利用激光共聚焦扫描显微镜OLS4000在平行于滑动方向上选取J1,J2,J3,J4,J5五条剖面进行剖面轮廓测试估算节理的粗糙度系数。

图1 激光共聚焦扫描显微镜
Fig.1 Laser confocal scanning microscope
1.3 试验过程
在自制滑动摩擦试验装置上采用金刚石磨片与砂岩节理表面进行滑动摩擦试验,滑动摩擦装置及示意图分别如图2,3所示。金刚石磨片粒度为120目,置于上盒中。将试件置于下盒中,下盒两侧分别有压力传感器,当滑块滑动时压力传感器记录滑动过程中剪应力的信号,经动态应变仪(采样频率为20 Hz)在计算机终端输出。

图2 滑动摩擦试验装置
Fig.2 Reciprocating sliding friction test device

图3 滑动摩擦试验示意
Fig.3 Schematic diagram of sliding friction test
砂岩节理摩擦因数μi的试验值由式(1)确定:
![]()
(1)
式中,σn为正应力,试验中取0.11 MPa;τi为第i次滑动过程中的最大剪应力,MPa。
试验时,试件在初始位置和最大位移(50 mm)之间往复匀速运动,导轨滑动速度为10 mm/s。试件每往复滑动1次,将试件拆卸,采用高分辨率相机对节理表面进行拍摄,然后将试件图像导入到AutoCAD中描出损毁区域,并计算损毁区域面积Ai,将受损区域中面积大于0.02 mm2的定义为损毁区域;采用电子分析天平称量试件的质量,试件称量3次取平均值,磨损质量记为mi;采用激光共聚焦扫描显微镜OLS4000在第1次滑动形成的磨损范围内选取A,B,C,D四个区域进行表面形貌测试,测试结果取平均值;然后每滑动1次,对以上4个区域进行表面形貌测试,表面粗糙度记为Sai(下角标i表示滑动次数)。为了减少结果偏差,试验时砂岩试件共计往复滑动10次。
2 试验结果与分析
2.1 试验结果
图4为第1次滑动后在试件表面选取的表面形貌测试区域位置图,图5,6分别为第1次和第6次滑动后C,D两个区域表面粗糙度测试结果图。

图4 第1次滑动后表面形貌测试结果
Fig.4 Surface topography test results after the 1st cycle

图5 第6次滑动后表面形貌测试结果
Fig.5 Surface topography test results after the 6th cycle
由于A,B,C,D四个位置的初始表面形貌在滑动之前不确定,取试验前Sa0作为初始三维粗糙度测试结果。磨损质量、磨损面积和表面粗糙度测试结果见表1。
2.2 滑动过程中表面粗糙度变化规律
从表1中可以看出随着滑动次数的增加磨损区域表面粗糙度逐渐减小。第1次滑动后,表面粗糙度下降了34.56%,由于砂岩节理表面的初始粗糙度值较大,微凸体之间发生啮合摩擦,仅有少数微凸体发生接触,实际接触面积较小,接触区域的微凸体所受法向应力水平较高,微凸体被剪断,粗糙度迅速降低。随着滑动次数的增加,表面粗糙度降低趋势逐渐变慢,第3次滑动后,表面粗糙度下降了3.51%,此时节理表面较高的微凸体已被剪断、磨平,较低的微凸体与金刚石磨片发生接触,接触面积增加,接触区域微凸体所受法向应力下降,表面粗糙度降低趋势变缓。滑动次数继续增加,表面粗糙度逐渐减小,当滑动7次后,表面粗糙度的变化已不到1%,此时试件表面接触区域与金刚石磨片表面达到相互匹配的稳定状态。

图6 表面形貌测试区域位置
Fig.6 Location of surface topography test
表1 磨损质量、总磨损面积率、表面粗糙度随滑动次数变化
Table 1 Wear mass,total wear area rate and surface roughness of wear zone with cycles
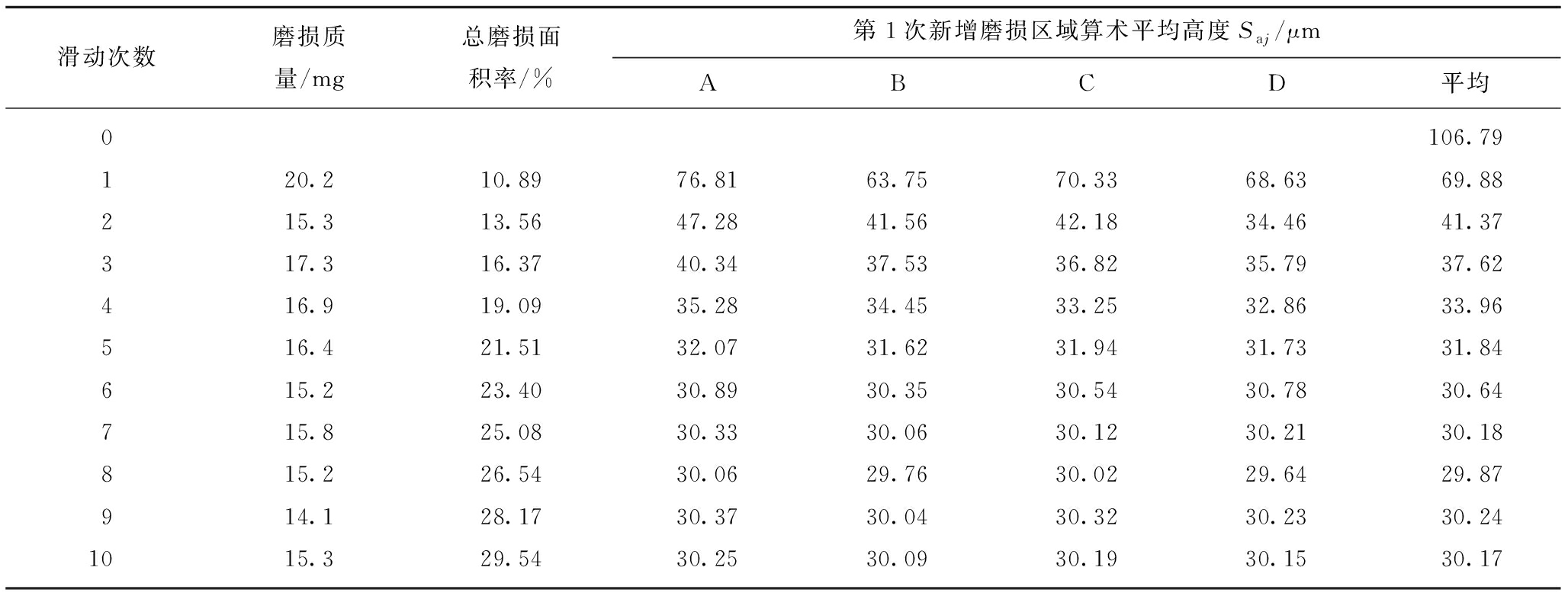
滑动次数磨损质量/mg总磨损面积率/%第1次新增磨损区域算术平均高度Saj/μmABCD平均0106.79120.210.8976.8163.7570.3368.6369.88215.313.5647.2841.5642.1834.4641.37317.316.3740.3437.5336.8235.7937.62416.919.0935.2834.4533.2532.8633.96516.421.5132.0731.6231.9431.7331.84615.223.4030.8930.3530.5430.7830.64715.825.0830.3330.0630.1230.2130.18815.226.5430.0629.7630.0229.6429.87914.128.1730.3730.0430.3230.2330.241015.329.5430.2530.0930.1930.1530.17
2.3 磨损质量、磨损面积和摩擦因数变化规律
分析表1和图7可知,第2次滑动后,新增磨损面积在总磨损面积的占比为19.69%,第6次滑动后,新增磨损面积在总磨损面积的占比已降到10%,随着滑动次数的增加磨损面积的增加趋势逐渐变慢;第1次滑动时,由于试件表面比较粗糙,磨损质量较大为20.2 mg,随着滑动次数的增加,磨损质量逐渐减小,当6次滑动后,磨损质量减小为15.2 mg,此时磨损质量基本稳定,在15.0 mg附近波动;第1次滑动时,摩擦因数最大为0.732,随着滑动的进行摩擦因数不断减小,当第6次滑动后,摩擦因数已下降至0.533,此时摩擦因数已下降了近30%,摩擦因数已基本稳定。对磨损面积、磨损质量和摩擦因数变化趋势进一步分析,将其分为以下3个阶段。

图7 摩擦因数、磨损质量和磨损面积率随滑动次数变化
Fig.7 Variation of friction coefficient,wear mass and wear area with cycles
(1)初始滑动阶段(Ⅰ)。此阶段由于磨损面积较小,接触区域法向应力水平较高,金刚石磨片与试件表面发生啮合摩擦,磨损质量较大,摩擦因数也较大。
(2)磨合阶段(Ⅱ)。此阶段磨损面积分为2部分,一部分为原有磨损面积,一部分为新增磨损面积,总磨损面积增加趋势逐渐变慢,新增磨损面积占总面积的比例不断降低,而原有磨损区域节理表面的微凸体不断被剪断、磨平,表面粗糙度逐渐降低,磨损质量逐渐减小,但是新增磨损面积在总磨损面积的占比仍大于10%,所以第3次滑动后总磨损质量出现增大。此阶段摩擦因数也分为原有磨损区域的残余摩擦和新增磨损区域的啮合摩擦两部分,在滑动过程中,啮合摩擦与残余摩擦交替占优,在第4次滑动后摩擦因数出现增大的跳跃现象。
(3)稳定滑动阶段(Ⅲ)。第6次滑动后,进入稳定滑动磨损阶段,原有磨损区域的粗糙度已趋于稳定,新增磨损面积在总面积的比重越已不足10%,新增磨损区域对总磨损质量的贡献也越来越小,磨损质量波动的幅度逐渐减小;新增磨损区域的啮合摩擦对总摩擦因数的贡献也越来越小,摩擦因数最终趋于一个稳定值。
2.4 节理粗糙度系数的估算
由于节理粗糙度对摩擦因数的影响很大,因此对节理粗糙度进行定量评估对于准确预测摩擦因数至关重要。算术平均高度Sa测定的只是局部三维形貌,反映了磨损区域表面粗糙度随着滑动变化的过程。为了更好反应试件整体粗糙度对摩擦因数的影响,利用剖面轮廓来估算节理的粗糙度系数。统计参数轮廓的一阶导数的均方根(Z2)已被广泛用于描述2D节理粗糙度。TSE和CRUDEN[24]提出表征岩石节理粗糙度,均方根(Z2)常用于定量评估粗糙度,计算公式为
![]()
(2)
式中,L为节理轮廓的长度;dx为沿采样线的相邻点之间的水平距离;dy为垂直于采样线的相邻点之间的距离;xi,yi为等距采样点i的坐标;N为离散点的个数。
沿剪切方向选取平行于剪切方向的等间距的5个剖面轮廓,J1距离边界2 mm,剖面之间间距为4 mm。图8给出了初始节理剖面轮廓的测试结果。

图8 节理剖面粗糙度测试结果
Fig.8 Test results of joint profile roughness
将每条剖面线的图像以jpg格式保存并导入到AutoCAD中。在AutoCAD中,将图像按比例尺缩放为实际尺寸20 mm。然后在轮廓的整个长度上构造一系列间隔为0.2 mm的垂直线,将交点的坐标导出。利用交点的坐标分别计算5条剖面线的均方根(Z2)值。每滑动1次采用激光共聚焦扫描显微镜对剖面形貌进行一次测试。为了降低重新测试剖面形貌的误差,用滑动后发生磨损位置轮廓替换滑动前剖面相应位置的轮廓,图9为磨损区域随滑动次数变化图。

图9 磨损区域随滑动次数变化
Fig.9 Variation of the wear area with the number of sliding
图9中蓝色线条范围内为磨损区域,红色线条为剖面位置,蓝色线条范围内的红色剖面线是替换轮廓的范围。
TSE和CRUDEN[23]认为剖面轮廓均方根(Z2)与节理粗糙度系数(JRC)的函数表示为
JRC=32.2+32.47lg Z2
(3)
根据式(3)计算剖面线的JRC值,试样的JRC值取5条剖面线的平均值。剖面线均方根及节理粗糙度系数的计算结果见表2。
结合图9和表2可知,J1剖面发生磨损区域占总轮廓的35%,节理粗糙度系数降低了9.66%;J2剖面发生磨损区域占总轮廓的29%,节理粗糙度系数降低了19.35%;J3剖面发生磨损区域占总轮廓的58%,节理粗糙度系数降低了31.35%;J4剖面发生磨损区域占总轮廓的30%,节理粗糙度系数降低了21.20%;J5剖面发生磨损区域占总轮廓的5%,节理粗糙度系数降低了3.00%,节理粗糙度系数都是随着滑动次数的增加不断降低,发生摩擦区域越大,节理粗糙度系数降低的越多。根据图9,第1次滑动时,J2和J3发生磨损区域分别占总轮廓14%和28%,新增磨损区域较大,所以粗糙度系数降低较快,而J1,J4和J5这3条剖面发生磨损区域在总剖面轮廓中占比较小,粗糙度系数降低较少。第2次滑动时,新增磨损区域较少,粗糙度降低主要是由已磨损区域的粗糙度降低引起的,第2次滑动的节理粗糙度系数降低较少。随着滑动次数的增加,J2,J3和J4剖面的新增磨损区域逐渐增大,磨损区域在总剖面轮廓中占比较大,节理粗糙度系数降低较大;J1和J5两条剖面发生磨损的区域较少,节理粗糙度系数降低较少。所以,节理粗糙度系数主要受磨损区域面积影响,局部粗糙度对节理粗糙度系数影响较小。
表2 剖面轮廓均方根及节理粗糙度系数随滑动次数变化结果
Table 2 Root mean square of the profile and the joint roughness coefficient with cycles

滑动次数J1Z2JRCJ2Z2JRCJ3Z2JRCJ4Z2JRCJ5Z2JRCJRC平均值00.306 515.530.196 49.250.213 610.430.219 210.800.211 910.3211.2610.305 515.480.187 38.580.197 19.300.217 910.720.207 810.0510.8220.305 415.480.187 08.550.196 69.260.216 210.590.207 710.0310.7830.304 615.430.186 08.470.189 58.740.213 410.420.207 610.0310.6240.300 715.260.185 88.470.182 98.250.213 310.410.207 610.0310.4850.297 415.100.175 27.640.174 37.560.213 310.410.207 510.0210.1560.297 315.090.174 87.600.173 57.500.213 310.410.207 610.0310.1270.279 614.230.174 37.570.171 57.340.188 18.640.207 510.029.5680.278 914.190.174 07.540.170 37.240.187 28.570.207 410.029.5190.276 114.050.173 37.480.169 87.190.186 88.540.207 510.029.46100.275 714.030.173 07.460.169 47.160.186 48.510.207 510.029.43
3 滑动过程中砂岩节理摩擦因数预测模型
3.1 滑动过程中砂岩节理摩擦因数预测模型
根据 BARTON和CHOUBEY[6]对摩擦因数的定义,摩擦因数μ可以表示为
![]()
(4)
式中,φb为基础摩擦角;JCS为节理面壁强度,对新鲜节理取单轴压缩强度σc,文中试件σc=28.76 MPa。
赵坚[7]认为式(4)预测岩石节理的摩擦因数比真实摩擦因数大,为了克服这一缺陷,提出了利用节理吻合系数(JMC)修正摩擦因数模型。则砂岩第1次滑动过程中摩擦因数μ1表示为
![]()
(5)
式中,JMC为节理吻合系数;JRC0为砂岩试件节理的初始节理粗糙度系数,取滑动前5条剖面线节理粗糙度系数的平均值11.26。
3.2 节理摩擦因数预测模型的修正
同一个试件节理基础摩擦角不变,按照文献[24]选取φb=21.5°。赵坚[7]认为天然节理的吻合JMC值通常介于0.5~0.8。根据试验结果,第1次滑动摩擦因数的试验值为0.731,初始节理粗糙度系数JRC0=11.26,将第1次试验结果代入式(5),可得JMC=0.54。将表2中初始粗糙度系数JRC0及前9次JRC的平均值代入式(5)得到摩擦因数的预测值,摩擦因数预测值与试验值对比如图10所示。

图10 摩擦因数预测值与试验值对比
Fig.10 Comparison of predicted and tested values of friction coefficient
由图10可知,摩擦因数的预测值高于摩擦因数的试验值。节理粗糙度系数是表征试件整体形貌的一个参数,而摩擦因数的降低是由磨损区域面积增加和粗糙度降低所引起的。SCHNEIDER[14]对天然岩石节理试样进行了摩擦试验,研究了节理粗糙度对粗糙节理剪切行为的影响,认为节理剪胀角的衰减符合负指数变化。磨损面积对节理粗糙度系数影响较大,用磨损面积的负指数变化来表示节理粗糙度系数的衰减,则第i次滑动过程中摩擦因数表示为
(i=1,2,3,…, n)
(6)
式中,a为修正系数;Ati为总磨损面积率。
对上述摩擦因数模型的预测精度进行分析,以平均估算误差作为精度指标,其表达式为
![]()
(7)
式中,δ为平均估算误差;![]() 为第i次摩擦因数的试验值;
为第i次摩擦因数的试验值;![]() 为模型估算第i次摩擦因数的预测值。
为模型估算第i次摩擦因数的预测值。
根据式(6)有
aAti<1
(8)
由表1可知,0.1<Ati≤1.0,所以a的取值范围在1~10。当a取不同值时,摩擦因数预测值随滑动次数变化曲线如图11所示。

图11 不同修正系数时摩擦因数预测值随滑动次数变化
Fig.11 Predicted value of friction coefficient varies with the number of sliding for different values of a
由图11可知,a的取值越大,摩擦因数的预测值越小,摩擦因数的变化范围也越大,摩擦因数的衰减越快;a的取值越小,摩擦因数的预测值越大,摩擦因数的变化范围也越小。根据式(7)计算第2~10次滑动摩擦因数试验值与不同a的取值得到的误差,发现当a=2.5时,摩擦因数预测值与试验值误差最小为2.89%。
4 结 论
(1)通过对磨损区域表面粗糙度变化分析,得出随着滑动次数的增加磨损区域表面粗糙度逐渐减小并最终趋于一个稳定值。在初始滑动阶段,砂岩节理表面的初始粗糙度值较大,金刚石磨片与试件表面发生啮合摩擦发生剧烈磨损,砂岩节理表面的微凸体被剪断,表面粗糙度迅速下降;随着滑动的进行,节理表面的微凸体不断被剪断、磨平,表面粗糙度降低趋势变缓,7次滑动后,磨损区域与金刚石磨片表面已基本匹配,算术平均高度值趋近于30 μm。
(2)通过对滑动过程中磨损面积、磨损质量和摩擦因数变化进行分析,将滑动过程分为初始滑动、磨合和稳定滑动3个阶段。在初始滑动阶段,磨损面积较小,磨损质量和摩擦因数都较大;在磨合阶段,新增磨损面积不断减小,但新增磨损面积在总磨损面积的占比仍大于10%,磨损质量和摩擦因数出现局部跳动的现象;在稳定滑动阶段,新增磨损面积在总磨损面积的占比小于10%,磨损质量和摩擦因数都逐渐趋于稳定,最终在某一稳定值附近波动。
(3)利用激光共聚焦扫描显微镜对砂岩节理表面轮廓进行了测量,采用磨损面积修正了含轮廓的均方根的摩擦因数预测模型,模型能够反映滑动过程中砂岩节理摩擦因数的变化,当修正系数a=2.5时,摩擦因数预测值与试验值吻合良好,最小误差为2.89%。
[1] MARC-ANDRÉ Brideau,YAN Ming,STEAD Doug.The role of tectonic damage and brittle rock fracture in the development of large rock slope failures[J].Geomorphology,2009,103(1):30-49.
[2] 安文博,王来贵.表面活性剂作用下煤体力学特性及改性规律[J].煤炭学报,2020,45(12):4074-4086.
AN Wenbo,WANG Laigui.Mechanical properties and modification of coal under the action of surfactant[J].Journal of China Coal Society,2020,45(12):4074-4086.
[3] 宋义敏,邓琳琳,吕祥锋,等.岩石摩擦滑动变形演化及声发射特征研究[J].岩土力学,2019,40(8):2899-2906,2913.
SONG Yimin,DENG Linlin,LÜ Xiangfeng,et al.Study of acoustic emission characteristics and deformation evolution during rock frictional sliding[J].Rock and Soil Mechanics,2019,40(8):2899-2906,2913.
[4] AN Wenbo,WANG Laigui,CHEN He.Mechanical properties of weathered feldspar sandstone after experiencing dry-wet cycles[J].Advances in Material Science and Engineering,2020:1-15.
[5] BARTON N.Review of a new shear-strength criterion for rock joints[J].Engineering Geology,1973,7(4):287-332.
[6] BARTON N,CHOUBEY V.The shear strength of rock joints in theory and practice[J].Rock Mechanics,1977,10(1):1-54.
[7] 赵坚.岩石节理剪切强度的JRC-JMC新模型[J].岩石力学与工程学报,1998,17(4):349-357.
ZHAO Jian.A new JRC-JMC shear strength criterion for rock joint[J].Chinese Journal of Rock Mechanics and Engineering,1998,17(4):349-357.
[8] LIU Q,TIAN Y,LIU D,et al.Updates to JRC-JCS model for estimating the peak shear strength of rock joints based on quantified surface description[J].Engineering Geology,2017,228:282-300.
[9] 班力壬,戚承志,燕发源,等.岩石节理粗糙度新指标及新的JRC确定方法[J].煤炭学报,2019,44(4):1059-1065.
BAN Liren,QI Chengzhi,YAN Fayuan,et al.A new method for determine the JRC with the new roughness parameters[J].Journal of China Coal Society,2019,44(4):1059-1065.
[10] BABANOURI N,ASADIZADEH M,HASAN-ALIZADE Z.Modeling shear behavior of rock joints:A focus on interaction of influencing parameters[J].International Journal of Rock Mechanics and Mining Sciences,2020,134:104449.
[11] 唐志成,黄润秋,张建明,等.含坡度均方根的节理峰值剪切强度经验公式[J].岩土力学,2015,36(12):3433-3438.
TANG Zhicheng,HUANG Runqiu,ZHANG Jianming,et al.Empirical peak shear strength criterion for rock joints based on slope root-mean-square[J].Rock and Soil Mechanics,2015,36(12):3433-3438.
[12] 陈曦,曾亚武,孙翰卿,等.基于Grasselli形貌参数的岩石节理初始剪胀角新模型[J].岩石力学与工程学报,2019,38(1):133-152.
CHEN Xi,ZENG Yawu,SUN Hanqing,et al.A new model of the initial dilatancy angle of rock joints based on Grasselli’s morphological parameters[J].Chinese Journal of Rock Mechanics and Engineering,2019,38(1):133-152.
[13] 金磊磊,魏玉峰.基于三维形貌和剪胀效应的软-硬节理抗剪强度模型[J].工程力学,2020,37(12):180-190.
JIN Leilei,WEI Yufeng.Calculation model for the shear strength of soft-hard joints based on three-dimensional morphology and dilatancy effect[J].Engineering Mechanics,2020,37(12):180-190.
[14] SCHNEIDER H J.The friction and deformation behaviour of rock joints[J].Rock Mechanics,1976,8(3):169-184.
[15] PLESHA M E.Constitutive models for rock discontinuities with dilatancy and surface degradation[J].International Journal for Numerical and Analytical Methods in Geomechanics,2010,11(4):345-362.
[16] HOMAND F,BELEM T,SOULEY M.Friction and degradation of rock joint surfaces under shear loads[J].International Journal for Numerical and Analytical Methods in Geomechanics,2001,25(10):973-999.
[17] 刘博,李海波,刘亚群.循环剪切荷载作用下岩石节理变形特性试验研究[J].岩土力学,2013,34(9):2475-2481,2488.
LIU Bo,LI Haibo,LIU Yaqun.Experimental study of deformation behavior of rock joints under cyclic shear loading[J].Rock and Soil Mechanics,2013,34(9):2475-2481,2488.
[18] 金俊超,佘成学,尚朋阳.硬岩弹塑性变形破坏过程中强度参数及剪胀角演化模型研究[J].岩土力学,2019,40(11):4401-4411.
JIN Junchao,SHE Chengxue,SHANG Pengyang.Study on strength parameters and dilation angle evolution models in hard rock elasto-plastic deformation and failure process[J].Rock and Soil Mechanics,2019,40(11):4401-4411.
[19] LI L,ETSION I,TALKE F E.Contact area and static friction of rough surfaces with high plasticity index[J].Journal of Tribology,2010,132(3):31401-31401.
[20] VAN-MANH Nguyen,HEINZ Konietzky,THOMAS Früehwirt.New methodology to characterize shear behavior of joints by combination of direct shear box testing and numerical simulations[J].Geotechnical & Geological Engineering,2014,32(4):829-846.
[21] FATHI A,MORADIAN Z,RIVARD P,et al.Geometric effect of asperities on shear mechanism of rock joints[J].Rock Mechanic and Rock Engineering,2016,49(3):801-820.
[22] PIRZADA M A,ROSHAN H,SUN H,et al.Effect of contact surface area on frictional behaviour of dry and saturated rock joints[J].Journal of Structural Geology,2020,135.
[23] TSE R,CRUDEN D M.Estimating joint roughness coefficients[J].International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts,1979,16(5):303-307.
[24] ZHAO Guochao,WANG Laigui,ZHAO Na,et al.Analysis of the variation of friction coefficient of sandstone joint in sliding[J].Advances in Civil Engineering,2020:1-12.
