由于露天开采工艺所限,我国露天矿端帮边坡压煤数量巨大。近年来,随着国内矿产资源的日益减少和国家对煤炭资源“安全、高效、绿色、智能”开发理念的不断落实,煤炭开采逐渐由易采资源开采向深部资源和复杂难采资源开采过渡,露天矿端帮压煤及残煤回收逐步得到人们重视。端帮采煤机开采技术是将传统的露天开采技术和井工开采技术相结合,发展起来的一种快速灵活、安全高效、经济环保的露天矿端帮压煤开采工艺,现今已经在国外各主要采煤大国广泛成功应用,这也为我国露天矿端帮压煤开采提供了新的途径。端帮采煤机开采的实质是在边坡下部煤层出露位置沿煤层施工一系列垂直于边坡走向的巷硐,开采全程无支护,通过巷硐之间保留的支撑煤柱来支承上覆岩土体质量。“露采”与“巷采”2种采矿方法的采动效应相互叠加、相互影响,最终在边坡一定深度范围内形成了一个动态的空间形态多元化的复合系统,巷间支撑煤柱一旦发生破坏,很可能导致煤柱群的连锁失稳,从而诱发端帮采场的大面积滑坡,最终破坏露天矿的正常采、运、排系统并造成巨大的经济损失和人员伤亡。
要在实现最大限度提高端帮压煤采出率的同时保证边坡的稳定,关键在于确保开采全过程巷道群支撑煤柱的稳定,支撑煤柱的稳定性可以理解为在一定时间和一定工程地质条件下,煤柱因受力而发生弹塑性变形或产生裂隙,但不产生突变性垮落或坍塌的性能。国内外许多专家学者围绕采动边坡变形失稳规律、地下开采条带煤柱强度和载荷计算、煤柱尺寸设计和稳定性分析判别等问题已经开展了比较深入的研究。20世纪90年代,SALAMON MDG[1]和GALVIN J M[2]通过对澳大利亚和南非大量的支撑煤柱数据进行了调查和分析,基于室内测试结果和煤柱尺寸效应给出了可以用来估算煤柱强度的经验公式。熊仁钦[3]研究了采煤工作面煤壁内的塑性区范围,推导出了三维应力状态下估算煤壁内塑性区宽度的理论公式,认为煤壁内塑性区宽度不仅与煤体各处的应力状态有关,而且还与采深及其它力学参数有关。孙世国、朱建明、丁鑫品等[4-7]研究和探讨了在地下与露天共同开采条件下边坡岩体变形破坏的空间属性及其分布规律,为该类矿山的后续开采设计及边坡岩体动态分析提供了科学依据。王旭春等[8]指出了目前普遍应用的威尔逊计算理论存在因简化带来的问题,通过对三向应力状态下的煤柱极限强度影响因素分析,给出了不受地质采矿条件约束的煤柱强度计算公式。刘文岗、张德军等[9-10]分析了SHM端帮开采技术应用的评估内容、煤柱设计计算、安全设计、采出率、灾害类型等关键问题,采用理论分析和数值模拟等方法研究了边坡角、多煤层开采顺序、煤柱宽高和间距等重要影响参数对边坡稳定的影响。陈彦龙、王东、王瑞等[11-13]基于突变理论推导出端帮采场支撑煤柱发生突变失稳的必要条件和屈服区宽度计算公式,采用数值模拟的方法以煤柱拉伸剪切塑性区宽度为判据确定了合理煤柱宽度。虽然已经在端帮采场覆岩破坏和支撑煤柱变形失稳等方面取得了一定的成果,但巷道群与边坡时空耦合特征决定了端帮采煤机开采条件下的端帮采场边坡安全问题是一个比较特殊的三维问题,受研究维度和方法限制,目前关于端帮采场覆岩的移动破坏规律尚不明确,关于采动边坡稳定控制理论与方法仍有待完善,现有研究成果尚不能完全满足实际生产需要。笔者结合3DEC分析软件的功能特点,通过模拟再现煤层采出、巷道群形成、巷间煤柱破坏、边坡变形失稳的全过程,力求揭示端帮采场巷道群及边坡岩体移动破坏特征与应力分布规律,对端帮采场覆岩变形破坏过程进行阶段划分,探明采动边坡变形失稳的关键阶段、触发条件和关键部位,以巷间煤柱合理留设为突破口提出端帮采场边坡稳定的控制方法。
1 端帮采场覆岩移动破坏的数值模拟分析
1.1 模型构建与分析方案
1.1.1 工程地质条件
内蒙古鄂尔多斯地区某露天矿采用单斗-卡车开采工艺,核定生产能力为3.0 Mt/a,工程地质与水文地质条件简单,煤系地层近水平,主采6号煤和9号煤,煤层赋存稳定,平均厚度分别为14.65 m和4.3 m,平均赋存深度分别为110 m和140 m,端帮最终边坡角约为38°,最大高度为160 m,边坡岩体主要为砂质泥岩、泥岩和不同粒径的砂岩,属于软弱—半坚硬岩层,节理裂隙较发育,边帮压覆可回收资源储量约为1 300万t。结合实际条件,为了最大限度地开发和利用煤炭资源,减少浪费,决定采用端帮采煤机进行边帮压煤回收,首先回收9号煤层,待回收结束且内排覆盖至6号煤层底板标高,再对6号煤层进行回收,边帮压煤回收顺序为上行开采。因此,边坡最下部9号煤层的安全回收是端帮采煤技术在该矿区推广应用的关键。
1.1.2 模型构建与力学参数
根据研究区域工程地质条件对边坡地层结构、岩性构成进行概化,结合3DEC数值模拟软件的特点,构建端帮采场覆岩移动破坏数值分析模型如图1所示。模拟开采9号煤层,模型尺寸X×Y×Z=200 m×400 m×180 m,巷硐尺寸X×Y×Z=3 m×193 m×4.3 m,巷硐数为28个,巷硐深度根据露天矿地表界在9号煤层的正射投影回缩20 m确定,巷间支撑煤柱宽度设定为2m,采场左右两侧各留设30 m边界煤柱。采用理想弹塑性本构模型和 Mohr-Coulomb 破坏准则来描述岩块的变形破坏特征,采用Coulomb slip破坏准则来描述节理的变形破坏特征[14-15]。

图1 端帮采场覆岩变形破坏数值分析模型
Fig.1 Numerical analysis model of overburden deformation and failure of the mining slope
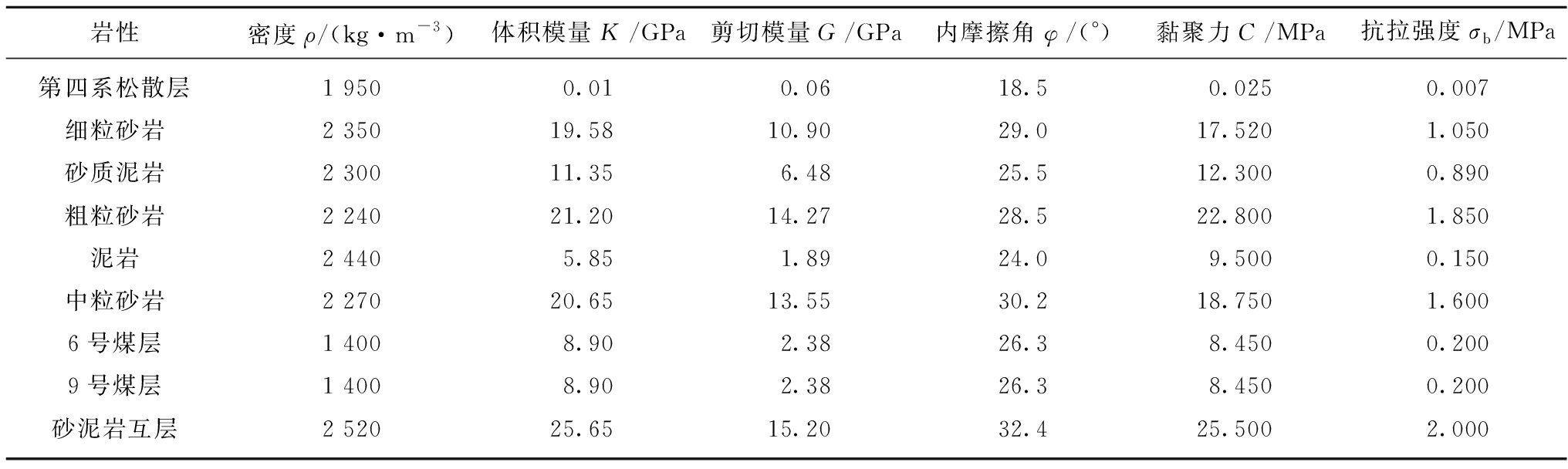
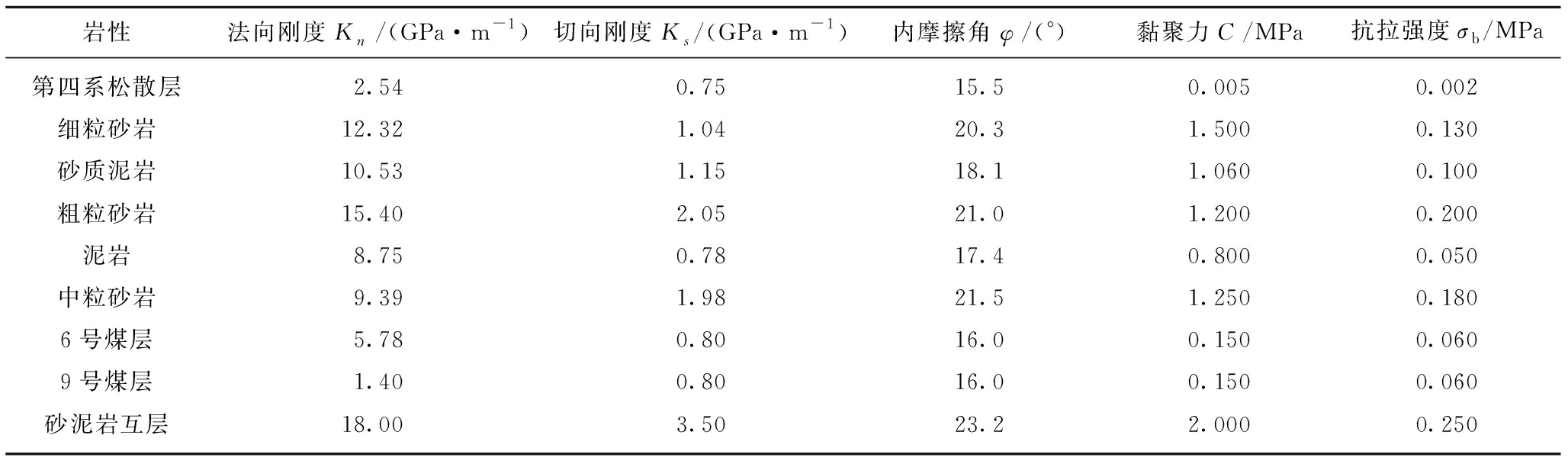
以岩石物理力学性质试验成果为基础,本次模拟分析用到的岩土体变形参数基于材料损伤理论和RMR分类法得到,强度参数基于Hook-Brown强度准则弱化处理得到,结构面刚度参数采用修正后的Bandis剪切刚度经验公式计算获得[16]。岩土体与结构面物理力学参数取值分别见表1,2。
表1 岩土体物理力学参数
Table 1 Value of physical and mechanical parameters of rock and soil mass
岩性密度ρ/(kg·m-3)体积模量K/GPa剪切模量G/GPa内摩擦角φ/(°)黏聚力C/MPa抗拉强度σb/MPa第四系松散层1 9500.010.0618.50.0250.007细粒砂岩2 35019.5810.9029.017.5201.050砂质泥岩2 30011.356.4825.512.3000.890粗粒砂岩2 24021.2014.2728.522.8001.850泥岩2 4405.851.8924.09.5000.150中粒砂岩2 27020.6513.5530.218.7501.6006号煤层1 4008.902.3826.38.4500.2009号煤层1 4008.902.3826.38.4500.200砂泥岩互层2 52025.6515.2032.425.5002.000
表2 结构面物理力学参数
Table 2 Physical and mechanical parameters of the structural plane
岩性法向刚度Kn/(GPa·m-1)切向刚度Ks/(GPa·m-1)内摩擦角φ/(°)黏聚力C/MPa抗拉强度σb/MPa第四系松散层2.540.7515.50.0050.002细粒砂岩12.321.0420.31.5000.130砂质泥岩10.531.1518.11.0600.100粗粒砂岩15.402.0521.01.2000.200泥岩8.750.7817.40.8000.050中粒砂岩9.391.9821.51.2500.1806号煤层5.780.8016.00.1500.0609号煤层1.400.8016.00.1500.060砂泥岩互层18.003.5023.22.0000.250
1.1.3 模拟分析与监测方案
初始地应力场达到平衡并对速度位移场清零后,沿9号煤层底板垂直于边坡走向自右向左按顺序依次进行巷硐施工,为了能够实时获取端帮采场岩体的应力分布和变形移动特征参数,在巷道群两侧边界和各巷间煤柱中心位置垂直于边坡走向布置29条监测线,沿X轴方向由1~29编号。端帮采场应力和变形监测线布置如图2所示。在每条监测线上设置13个应力监测点,其中1~7号监测点位于煤柱与顶板接触位置,用于监测巷道群施工过程中支撑煤柱竖向应力演化情况,8~13号监测点位于煤层顶板上部较坚硬的岩体内,用于监测采场上部边坡岩体水平应力演化情况。此外,分别在7,15和23号监测线对应的边坡各台阶坡顶及地表相应位置另设16个位移监测点,用于监测边帮压煤开采全过程各平盘水平和竖向变形情况。比如,自右向左第7条监测线,其应力监测点编号为7-1~7-13,位移监测点编号为7-19~7-34。端帮采场7号监测线应力和位移监测点位置如图3所示。

图2 端帮采场应力和变形监测线布置示意
Fig.2 Schematic diagram of stress and deformation monitoring line arrangement of the mining slope

图3 7号监测线应力和变形监测点位置示意
Fig.3 Schematic diagram of stress and deformation monitoring points of line 7
1.2 采动边坡岩体变形移动特征
端帮开采诱发边坡及地表变形移动特征如图4所示。由边坡Y向位移云图(图4(a))可知,受巷道群施工影响,采场覆岩可根据水平变形特征划分为上、中、下3个区域,上部区域和下部区域均朝向边坡临空面产生了不同程度的水平移动,尤其以下部区域巷道群上方附近岩体最为显著,最大水平变形值约为21.1 cm,中部区域各台阶朝向边坡临空面的水平变形值有限,甚至为负值。由边坡Z向位移云图(图4(b))可知,采场上覆岩体竖向变形已经发展至边坡表面,竖向变形值以边坡中部区域最为显著,最大竖向变形值约为51.8 cm,边坡下部区域巷道群上方附近岩体竖向变形值有限,甚至为正值,以上特征表明,端帮采场发生最大竖向变形的位置处于巷道群沿边坡走向几何中心深部。通过对7,15和23号监测线各监测点变形数据对比分析可知,端帮采场岩体水平变形和竖向变形最大值均出现在巷道群沿边坡走向对称中心(15号监测线)位置,分析结果与现场监测数据基本吻合。

图4 端帮采场边坡及地表变形移动特征
Fig.4 Deformation and movement characteristics of the side slope and surface under the coal extract condition
边坡中部断面(15号监测线)岩土体变形移动特征如图5所示。由15号监测断面Y向位移云图和各监测点水平变形曲线(图5(a))可知,巷道群顶部附近垂直于边坡走向一定深度范围内的岩体和边坡最上部多级台阶均产生了明显的水平变形,中部区域各监测点累积变形值较小。边坡上部15-30监测点和边坡下部15-20监测点水平变形值均较大,边坡中部15-24监测点水平变形值最小,约为4.5 cm。由15号监测断面Z向位移云图和各监测点竖向变形曲线(图5(b))可知,边坡发生最大竖向变形的区域位于坡体内巷道群深部,变形影响已经向上扩展至边坡表面,受边坡应力场与巷道群应力场的耦合作用影响,上覆岩体竖向变形呈现出明显的“偏态”特征。竖向变形等值线发生朝向边坡临空面的明显偏移,导致边坡中部15-26监测点竖向变形值较大。15-20监测点水平和竖向变形受巷道群施工影响最为剧烈,巷道群施工至17 000时步(距离15号监测线5个巷硐,约26 m)时,该监测点Y向位移变化趋势突然增强,直到27 000时步(经过15号监测线5个巷硐,约26 m)时,变化趋势才逐渐减弱。

图5 边坡中部断面岩土体变形移动特征
Fig.5 Deformation and failure characteristics of rock and soil mass in the middle section of the mining slope
1.3 采动边坡岩体应力分布特征
边坡中部断面(15号监测线)位置岩土体应力分布特征如图6所示。由15号监测断面Y向应力云图和各监测点水平应力曲线(图6(a))可知,巷道群施工结束后,边坡底部岩体前缘受压、后缘受拉。受巷道群施工影响,应力曲线呈上下有规律波动,各监测点水平应力均为压应力,且由巷硐浅部至深部逐渐增大,15-12监测点水平应力值达到最大,但最深处的15-13监测点反而有所减小。由15号监测断面Z向应力云图和各监测点竖向应力曲线(图6(b))可知,深部区域支撑煤柱所受压应力集中程度明显,各监测点竖向应力均为压应力,同样由巷硐浅部至深部逐渐增大,15-6监测点竖向应力值达到最大,但最深处的15-7监测点反而有所减小。巷道群施工至17 000时步(距离15号监测线5个巷硐,约26 m)时,各监测点水平和竖向应力开始逐渐增大,到22 000时步(15号监测线位置)突然减小,减小幅度较大,在27 000时步(经过15号监测线5个巷硐,约26 m)以后开始保持稳定。由边坡中部断面位置煤柱竖向应力随巷硐深度变化曲线如图7所示,受已形成坡面的影响,随着巷硐深度位置向边坡内部转移,煤柱承受的竖向应力逐渐增大,当深度增大到170 m时,竖向应力达到峰值,随后又突然减小,当深度增大到193 m(巷硐末端位置)时,竖向应力减小至最低,随后呈现出缓慢增大的趋势,到达坡顶线在9号煤层正射投影位置时逐渐恢复至原岩应力大小,该现象正是距离巷硐末端一定范围内的巷间煤柱未发生明显不连续破坏的根本原因。

图6 边坡中部断面岩土体应力分布特征
Fig.6 Stress distribution characteristics of rock and soil mass in the middle section of the mining slope

图7 边坡中部断面位置煤柱竖向应力随巷硐深度变化曲线
Fig.7 Vertical stress of coal pillar varies with the depth of the tunnel in the middle section of the mining slope
2 端帮采场覆岩移动破坏过程的阶段划分
研究与实践表明,端帮采场覆岩移动破坏过程是一个动态的地质力学行为过程,可以将该过程划分为表生改造、结构改造、时效变形、最终失稳(稳定)4个阶段,各阶段都有其不同的特点。
2.1 表生改造阶段
表生改造为露天开采形成端帮边坡及边坡应力重分布的过程,是与露天矿剥采过程相伴生的地质力学行为,应力重分布过程中的边坡变形属于卸荷回弹性质的变形。表生改造一方面起到释放坡体原岩应力,促进边坡应力场再次形成的作用;另一方面,这个过程的发生形成了边坡浅表部的“卸荷松弛带”,卸荷松弛带破坏了边坡的岩体结构,导致岩体宏观强度和结构面强度的降低,形成边坡继续变形的几何和力学边界条件,从而劣化了岩体的物理力学性质,该阶段的最终结果为边坡表层岩土体最大主应力方向顺着边坡表面且量值较小,而边坡内部岩土体的最大主应力方向转为竖直向下且量值逐渐增大。表生改造阶段边坡岩土体竖向主应力如图8所示。

图8 表生改造阶段竖向主应力
Fig.8 Vector diagram of vertical principal stress in the supergene transformation stage
2.2 结构改造阶段
在已形成的端帮边坡下部沿煤层施工一系列垂直于边坡走向的巷硐,这些巷硐并排布置且具有一定的空间尺寸,此时端帮采场上覆岩体部分重量转由巷间煤柱承担,露采与巷采效应相互叠加,在动静组合载荷作用下,巷道群沿边坡走向几何中心深部区域巷间煤柱所受实际应力σs远大于极限应力σp,导致多个相邻煤柱围绕中心煤柱集体发生压剪破坏而失去承载能力,其上部岩体随即发生垮落,因此结构改造的实质是采场上覆岩体变形破坏及应力再分布的过程。该阶段最大的特点是巷道群施工导致边坡的完整结构遭到破坏,深部巷间煤柱坍塌促使端帮采场覆岩变形破坏分区开始形成,在巷间煤柱破坏区域周边较硬岩体内形成“砌体梁”结构,破坏区域上部关键岩块之间的铰接作用孕育着边坡内部强大的水平挤压力,该阶段是端帮采场覆岩移动破坏的关键阶段。结构改造阶段边坡岩土体最大剪应力如图9所示。

图9 结构改造阶段最大剪应力
Fig.9 Vector diagram of maximum shear stress in the structure modification stage
2.3 时效变形阶段
时效变形是在表生改造或结构改造阶段结束后,紧接着发生的一种随时间逐渐发展的变形。表现在变形监测曲线上,就是边坡形成或巷道群施工结束后,位移还在继续发展,并可能保持一定的速率。研究与实践表明,当边坡内具有倾向坡外的缓倾结构面、且倾角与残余摩擦角接近的边坡、存在软弱基底的边坡、由近直立中—薄层状岩层构成的陡倾边坡、碎裂结构岩体边坡以及堆积体(散体)边坡等5类边坡极容易进入时效变形阶段[17]。实际上,端帮采场覆岩随时间发生的变形破坏或失稳也是一种典型的结构改造阶段后的时效变形,在岩层近水平的情况下,时效变形主要体现在以下几个方面:
(1)端帮采场下部区域岩体朝向临空面的水平变形。该区岩土体的变形主要为巷间煤柱破坏区域周边坚硬岩块铰接结构的变形(滑动)失稳所致。由于边坡深部区域巷间煤柱的破坏,其上部岩体发生破断下沉,坚硬岩块之间相互咬合形成铰接结构,在变形(滑动)失稳过程中将水平挤压力传递至边坡下部岩层,当某岩层接触面的抗剪强度不能抵抗该力的作用时,接触面上部岩层便发生朝向边坡临空面的相对移动。
(2)端帮采场中部区域岩体的竖向变形。实际上该区岩土体的变形是两类变形矢量之和,一者是由于边坡深部区域巷间煤柱破坏引起该区岩体发生朝向边坡下后方的移动,二者是在重力作用下边坡附近岩体发生了朝向临空面的移动,两类变形的水平分量相互抵消,因此总体上该区岩体以竖向变形为主。
(3)端帮采场上部区域岩土体沿坡面向下的变形移动。该区岩土体变形的主要诱因为失去了侧向支承作用,当下部采动强度较大时,上部岩层面甚至会由近水平发展为与边坡面顺倾,由于发生在边坡上部,一旦进入加速变形将很难控制,因此端帮采场上部区域是采动边坡发生变形失稳的关键区域。若上部区域边坡由松散堆积体构成,则最有可能的失稳模式为散体物料内部的圆弧滑动,若上部区域边坡由含软弱夹层的岩体构成,则最有可能的失稳模式为沿顺倾结构面的顺层滑动,基于以上分析,在稳定系数Fs<1的情况下,端帮采场上部区域岩土体将进入时效变形阶段。
(4)最终失稳(稳定)阶段。时效变形的过程,也是蠕滑卸荷的过程,随着蠕滑量的增加,“砌体梁结构”将出现变形失稳或滑落失稳,铰接岩块对周围岩体的水平挤压力逐渐变小,直至消失。在长期载荷作用下,当关键区域的稳定性系数Fs∞逐渐转变为大于1,潜在滑面提供的抗滑力足以平衡滑体的下滑力时,边坡时效变形速度将逐渐减小,直至变形稳定;否则,潜在滑面提供的抗滑力始终不能平衡滑体的下滑力,边坡关键区域的变形量将超过边坡稳定的许可变形量,最终将发生滑坡失稳。最终失稳(稳定)阶段边坡岩土体位移如图10所示。

图10 最终失稳(稳定)阶段位移
Fig.10 Vector diagram of displacement in the final instability (stability) stage
3 基于巷间煤柱合理留设的端帮采场覆岩稳定控制方法
3.1 巷道群上覆岩体“扩大压力拱”的形成演化规律
端帮采场巷道群深部区域支撑煤柱的压剪破坏是采场覆岩发生变形失稳的触发条件。在最大限度回收边帮压煤的同时保证巷间煤柱不发生破坏是问题的关键。根据矿山压力与岩层控制理论,单个巷硐围岩的应力分布影响范围一般以切向应力超过原岩应力的5%处为界,若相邻巷硐间距小于2倍单巷硐影响半径,则巷硐围岩应力会产生叠加效应,由于端帮采场巷硐间距相对较小,巷间煤柱应力叠加在所难免,在巷道群施工过程中,如果巷间煤柱尺寸过小导致压缩变形过大或发生破坏失稳,上部载荷将通过上覆岩体转移至周围相邻的煤柱承担,当这一现象连续发生时,将在巷道群上方形成一个“扩大压力拱”[6,18]。研究结果表明,在巷间煤柱尺寸较小且巷道群规模较大的情况下,扩大压力拱的高度和跨度与上覆岩体厚度和关键硬岩层位置等因素有关[19-20]。巷道群上覆岩体扩大压力拱形成过程如图11所示。

图11 巷道群上覆岩体“扩大压力拱”形成过程示意
Fig.11 Schematic diagram of “distensible pressure arch” formation process in the overlying strata of roadway groups
为了验证端帮采场巷间煤柱“扩大压力拱”的真实存在,进一步探明其形成演化规律,围绕上述模拟分析获得的巷间煤柱应力监测数据进行讨论。对比分析表明,在各监测线煤柱与顶板接触位置布设的7个竖向应力监测点中,6号监测点应力显现规律最为明显,端帮采场各监测线6号监测点竖向应力随巷硐施工全过程演化特征曲线如图12所示。通过分析可知:

图12 端帮采场各监测线6号监测点竖向应力分布特征曲线
Fig.12 Vertical stress distribution characteristic curve of No.6 monitoring point in each monitoring line of the mining slope
(1)在巷硐未施工之前,端帮边坡各监测线6号监测点竖向应力基本保持定值,巷硐的施工,破坏了地层原岩应力的平衡状态,导致巷硐周边岩体的应力重新分布和应力集中,在工作面前方形成应力增高
区,后方形成应力降低区,并逐渐向前方转移,因此各监测点竖向应力发生有规律的上下波动,如果将每一巷硐施工结束视为一个应力状态,对多个状态的应力分布曲线进行叠加处理,可以视为一列横波在各支撑煤柱之间沿巷道群施工方向传播。叠加处理还发现巷硐6施工结束时7号监测线位置出现的应力峰值在后续各状态的应力分布曲线中同样存在,且巷硐12施工结束时14号监测线位置、巷硐18施工结束时20号监测线位置均出现了同样的情况。分析认为7号、14号和20号监测线应力峰值位置即为扩大压力拱拱脚位置,以上现象一方面表明端帮采场巷道群“扩大压力拱”的存在,另一方面也表明在其他条件一定的情况下,随着巷道群的施工,扩大压力拱的跨度增大到一定程度后基本保持定值。
(2)在本文已知的工程地质条件与采矿条件下,某露天矿端帮各监测线6号监测点位置的竖向应力基本保持在2.5 MPa,巷道群施工方向前方煤壁承受的竖向应力首先增大至初始值的1.5~1.8倍,待该位置煤柱形成后,其所受竖向应力快速减小至初始值的0.5~0.7倍,在7,14和20号监测线位置先后共形成3个“扩大压力拱”,跨度为30~35 m,拱脚处的应力最大值为4.0~4.5 MPa,数值模拟与现场实测结果基本吻合。
3.2 巷间煤柱的合理留设方法
端帮采场巷间煤柱包括临时支撑煤柱和永久隔离煤柱两类,两类煤柱宽度设计应考虑的因素包括上覆岩体的厚度、岩性构成、煤岩体物理力学性质、煤层厚度、采高和巷硐宽度等。实际上,煤柱宽高比越大,煤柱稳定性越好,但同时边帮压煤的采出率越低,因此巷间煤柱宽度的合理留设是解决以上问题的关键。关于端帮采场临时支撑煤柱宽度的确定方法已在相关文献中进行了一定研究,这里专门针对永久隔离煤柱的合理留设进行讨论。为了防止端帮采场巷间煤柱破坏失稳的“多米诺骨牌效应”,实际生产中每隔一定数量的临时支撑煤柱留设一个永久隔离煤柱,通过上述关于端帮采场巷间煤柱“扩大压力拱”形成演化规律的讨论,可以将压力拱的拱脚位置作为永久隔离煤柱的留设位置,实际生产中压力拱的拱脚位置可以通过现场实测和数值分析等方法获得,也可通过经验公式进行估算。
ABEL等[21-22]通过对国外55处沉积矿床的测量数据的统计分析,给出了巷道群施工过程中与上覆岩体厚度相关的压力拱最大跨度估算公式为
lLTD=-10-4H2+0.270 1H
(1)
式中,H为上覆岩层平均厚度。
上述研究实例中各监测线6号监测点上覆岩体厚度为121 m,代入式(1)计算得到扩大压力拱最大跨度为34.14 m,与数值分析结果基本吻合,即在该露天矿地质条件和采矿条件下,应每隔5~6个临时支撑煤柱留设1个永久隔离煤柱。
基于极限平衡分析理论,永久隔离煤柱安全系数Fs计算公式[23-24]可表示为
![]()
(2)
![]()
(3)
![]()
(4)
![]()
(5)
式中,σp为煤柱的极限应力;σs为永久隔离煤柱所受实际应力;γ为上覆岩体加权容重;H′为扩大压力拱最大高度;Wz为煤柱宽度;Wd为巷硐宽度;Hd为煤柱原始高度;W为扩大压力拱最大跨度;k为压力拱修正系数;fk为岩石坚固系数。其中:
当k=4.0~5.0,fk≤0.8时,为不稳定岩石;
当k=3.0~4.0,0.8<fk≤4时,为中等坚硬岩石;
当k=1.5~2.0,5<fk≤8时,为坚硬岩石;
当k=1.0,fk≥10时,为极坚硬岩石。
实际生产中永久隔离煤柱所受实际应力可以通过现场实测和数值分析等方法获得,也可通过经验公式进行估算。如前所述,采用现场实测和数值分析相结合的方法得到本实例中永久隔离煤柱所受实际应力最大值为4.5 MPa,正常情况下永久隔离煤柱安全系数建议取1.3[6],将实际参数代入式(2),计算可得本文所述条件下露天矿端帮采场永久隔离煤柱宽度至少应大于5.6 m。
本实例中巷硐宽度为3 m,煤柱原始高度为4.3 m,上覆岩体加权容重为24 kN/m3,岩体为中等坚硬,将以上参数依次代入式(4)和(5),可反算出k/fk≈3.58,与式(6)中k值取3时fk取值取0.8计算结果相当,以上方法在一定程度上解决了采用式(5)和(6)计算扩大压力拱最大高度时较难取值的困扰。应用与实践进一步表明,在边坡地层近水平条件下,采用该方法对端帮采场永久支撑煤柱尺寸进行计算是可行的,研究成果为端帮采场永久隔离煤柱合理留设提供了理论依据,对于保证端帮采场边坡稳定安全具有实际意义。
4 结 论
(1)端帮采场覆岩移动破坏全过程模拟研究结果表明,在地层近水平条件下,受“露采”与“巷采”2种采动效应叠加影响,采场边坡岩土体变形破坏和应力分布表现出新的特征:沿边坡走向,岩体变形最大值出现在巷道群沿边坡走向几何中心区域;垂直于边坡走向,距离巷硐末端一定长度范围是支撑煤柱承受最大值竖向应力的位置。端帮采场覆岩发生变形破坏的触发条件是在动静组合载荷作用下,巷道群沿边坡走向几何中心深部区域巷间煤柱所受实际应力大于极限应力,诱发多个相邻煤柱围绕中心煤柱集体发生压剪破坏而产生较大的不连续变形所致。
(2)根据采场覆岩移动破坏特征,可以将端帮采场边坡变形破坏过程划分为表生改造、结构改造、时效变形和最终失稳(稳定)4个阶段,其中结构改造阶段是边坡发生变形破坏的关键阶段,端帮采场边坡发生变形失稳的关键区域为边坡上部区域,若上部区域边坡由松散堆积体构成,则最有可能的失稳模式为散体物料内部的圆弧滑动,若上部区域边坡由含软弱夹层的岩体构成,则最有可能的失稳模式为沿软弱岩层的顺层滑动。
(3)结合鄂尔多斯地区某露天矿端帮煤开采,揭示了巷道群上覆岩体“扩大压力拱”的形成过程及其演化规律,提出了基于巷间煤柱合理留设的端帮采场覆岩稳定控制方法,给出了端帮采场扩大压力拱最大跨度和永久隔离煤柱参数的确定方法,通过应用与实践,验证了理论公式的适用性。
[1] SALAMON M D G,OZBAY MU,MADDEN B J.Life and design of bord-and-pillar workings affected by pillar scaling[J].Journal-South African Institute of Mining and Metallurgy,1998,6:135-145.
[2] GALVIN J M,HEBBLEWHITE B K,SALAMON M D G.University of new south wales coal pillar strength determinations for Australian and South African Condition[A].Proceedings of The Second International Workshop on Coal Pillar Mechanics and Design[C].1999,63-71.
[3] 熊仁钦.关于煤壁内塑性区宽度的讨论[J].煤炭学报,1989,14(1):16-22.
XIONG Renqin.The discussion on the width of plastic zone in coal wall[J].Journal of China Coal Society,1989,14(1):16-22.
[4] 孙世国,王思敬.露天转地下开采边坡岩体滑移机制的探讨[J].岩石力学与工程学报,2000,19(1):126-129.
SUN Shiguo,WANG Sijing.Study of sliding mechanism for slope due to the excavation from open pit into underground mining[J].Chinese Journal of Rock Mechanics and Engineering,2000,19(1):126-129.
[5] 朱建明,冯锦艳,彭新坡,等.露井联采下采动边坡移动规律及开采参数优化[J].煤炭学报,2010,35(7):1089-1094.
ZHU Jianming,FENG Jinyan,PENG Xinpo,e tal.The failure law of mine slope and the optimization of boundary parameter between open-pit and underground combined mining[J].Journal of China Coal Society,2010,35(7):1089-1094.
[6] 丁鑫品,李绍臣,王俊,等.露天矿端帮煤柱回收井工开采工作面推进方向的优化[J].煤炭学报,2013,38(11):1923-1928.
DING Xinpin,LI Shaochen,WANG Jun,et al.Optimization of underground mining development direction about end slope coal pillar recovery of open-pit coal mine[J].Journal of China Coal Society,2013,38(11):1923-1928.
[7] 丁鑫品,王振伟,李伟.采动边坡失稳的动力过程及典型变形破坏机理[J].煤炭学报,2016,41(10):2606-2611.
DING Xinpin,WANG Zhenwei,LI Wei.Dynamic process and typical deformation-failure mechanism of mining slope[J].Journal of China Coal Society,2016,41(10):2606-2611.
[8] 王旭春,黄福昌,张怀新,等.AH威尔逊煤柱设计公式探讨及改进[J].煤炭学报,2002,27(6):604-608.
WANG Xuchun,HUANG Fuchang,ZHANG Huaixin,et al.Discussion and improvement for A.H.Wilson’s coal pillar design[J].Journal of China Coal Society,2002,27(6):604-608.
[9] 刘文岗,王雷石,富强.SHM端帮开采技术及其应用的关键问题[J].煤炭工程,2012(6):1-4.
LIU Wengang,WANG Leishi,FU Qiang.SHM highwall mining technology and key issues of application[J].Coal Engineering,2012(6):1-4.
[10] 张德军.边帮采煤技术在乌兰煤矿的应用[J].煤炭工程,2017,49(12):38-40,45.
ZHANG Dejun.Application of side coal wall mining technology in Wulan Coal Mine[J].Coal Engineering,2017,49(12):38-40,45.
[11] 陈彦龙,吴豪帅.露天矿端帮开采下的支撑煤柱突变失稳机理研究[J].中国矿业大学学报,2016,45(5):859-865.
CHEN Yanlong,WU Haoshuai.Catastrophe instability mechanism of rib pillar in open-pit highwall mining[J].Journal of China University of Mining & Technology,2016,45(5):859-865.
[12] 王东,姜聚宇,韩新平,等.褐煤露天矿端帮开采边坡支撑煤柱稳定性研究[J].中国安全科学学报,2017,27(12):62-67.
WANG Dong,JIANG Juyu,HAN Xinping,et al.Stability of supporting coal pillar for slope highwall mined in lignite surface mine[J].China Safety Science Journal,2017,27(12):62-67.
[13] 王瑞,闫帅,柏建彪,等.端帮开采下煤柱破坏宽度计算及失稳机制研究[J].岩土力学,2019,40(8):3167-3180.
WANG Rui,YAN Shuai,BAI Jianbiao,et al.Theoretical analysis of the destabilization mechanism and the damaged width of rib pillar in open-pit highwall mining[J].Rock and Soil Mechanics,2019,40(8):3167-3180.
[14] 吴琼,唐辉明,王亮清,等.基于三维离散元仿真试验的复杂节理岩体力学参数尺寸效应及空间各向异性研究[J].岩石力学与工程学报,2014,33(12):2419-2432.
WU Qiong,TANG Huiming,WANG Liangqing,et al.Three-dimensional distinct element simulation of size effect and spatial anisotropy of mechanical parameters of jointed rock mass[J].Chinese Journal of Rock Mechanics and Engineering,2014,33(12):2419-2432.
[15] 李同录,罗世毅,何剑,等.节理岩体力学参数的选取与应用[J].岩石力学与工程学报,2004,23(13):2182-2186.
LI Tonglu,LUO Shiyi,HE Jian,et al.Determination and application of mechanical parameters for jointed rock masses[J].Chinese Journal of Rock Mechanics and Engineering,2004,23(13):2182-2186.
[16] 王贺,高永涛,金爱兵,等.节理岩体刚度参数选取与三维离散元模拟[J].岩石力学与工程学报,2014,33(S1):2894-2900.
WANG He,GAO Yongtao,JIN Aibing,et al.Determination of stiffness parameters of jointed rock masses with 3DEC simulation[J].Chinese Journal of Rock Mechanics and Engineering,2014,33(S1):2894-2900.
[17] 郑颖人,陈祖煜,王恭先.边坡与滑坡工程治理[M].北京:人民交通出版社,2007.
[18] 钱鸣高,石平五,许家林.矿山压力与岩层控制[M].徐州:中国矿业大学出版社,2010.
[19] 秦乐尧,刘长武,方延强.近距离巷道群覆岩活动的扩大压力拱理论与岩柱荷载研究[J].金属矿山,2009(12):20-24.
QIN Leyao,LIU Changwu,FANG Yanqiang.Research on expansive pressure arch theory and rock pillar load about the activity of the covered rock mass in close laneways[J].Metal Mine,2009(12):20-24.
[20] 宋振骐,郝建,石永奎,等.“实用矿山压力控制理论”的内涵及发展综述[J].山东科技大学学报(自然科学版),2019,38(1):1-15.
SONG Zhenqi,HAO Jian,SHI Yongkui,et al.An overview of connotation and development of practical ground pressure contorl theory[J].Journal of Shandong University of Science and Technology(Natural Science),2019,38(1):1-15.
[21] ABEL J F.Soft rock pillars[J].International Journal of Mining & Geological Engineering,1988(6):215-248.
[22] POULSEN B A.Coal pillar load calculation by pressure arch theory and near field extraction ratio[J].International Journal of Rock Mechanics and Mining Sciences,2010,47(7):1158-1165.
[23] SALAMON M D G,MUNRO A H.A study of the strength of coal pillars[J].J Sth Afr Inst Min Metal,1967,68(2):55-67.
[24] MERWE Nielen van der.New pillar strength formula for South African coal[J].New pillar strength formula for South African coal,2003,103(5):281-292.
