一般地,自然界岩体含有诸如层理、节理、裂隙及软弱层等结构面,其对岩体结构稳定性起重要作用(主要表现为剪切破坏)[1-2]。岩体结构面剪切力学特性影响因素极为复杂,其中岩性组合形式为关键影响因素之一[3-6],深入探究软硬互层岩体结构面在特定条件下的剪切力学特性对分析与评价边坡、隧道及水(核)电等岩体工程长期稳定性具有重要理论和现实意义。
目前,国内外有关软硬互层岩体结构面剪切力学特性的研究已取得了一定成果[2-17]。HOEK[7]和BANDIS[8]等指出了含水率、法向压力及硬性岩层起伏度(粗糙度)对软硬互层岩体结构面抗剪强度和变形性能具支配作用;董遵德等[9]通过现场慢剪试验获取了软弱夹层的有效应力抗剪强度参数。许江等[10]通过浇筑素混凝土复制硬性岩层,探究了含黄泥充填物软弱结构面的剪切强度(变形)及形貌演化特征;李鹏等[11]以膨润土和砂岩碎屑模拟充填物,探究了软弱结构面受含水率影响的剪切蠕变特性。已有文献大多以相似材料复制而成的物理模型为研究对象,进而探究“硬+软+硬”组合形式的结构面剪切力学特性(组合形式单一),且较少考虑硬性岩层起伏度和粗糙度的影响。实质上,如“软+硬”组合形式的结构面普遍存在于多数边坡之中,且结构面形态通常对边坡岩体失稳破坏构成重大影响[12]。然而,仅有少数文献对此展开了论述,如王伟等[13]基于不同含水率下的静力直剪试验,提出了土-岩石(“软+硬”)接触面的应力-位移力学模型;唐雯钰等[14]探讨了不同法向压力和硬性岩层凸台高度对软弱结构面剪切性能的影响。另外,PFC2D细观模拟可较直观精确地获得剪切全过程中的实时信息,即硬性或软弱结构面裂纹萌生、扩展、错动、磨损、局部破坏、完全断裂、贯通及滑移等渐进性损伤破坏演化特征及数量(能量)变化规律。LIU等[1]、YOON[15]、何春梅[12]及黄达等[16]均通过PFC2D离散元法获得了岩体结构面细观损伤演化全过程、颗粒损伤分布特征及典型破坏模式。总体而言,大多学者均以室内直剪试验和PFC2D细观模拟作为研究岩体结构面剪切力学特性的通用手段,且有关以现场原样加工制备而成的物理模型为研究对象,并考虑硬性岩层起伏度和粗糙度等多影响因素的软硬互层岩体结构面宏细观剪切力学特性的研究文献鲜有报道。
鉴于此,笔者基于已有研究基础[1-23],开展恒定法向压力下的室内直剪试验,充分考虑含水率、法向压力及一阶起伏角的影响,系统地探究了“软+硬”和“硬+软+硬”组合形式下的结构面剪切变形及强度特性,并揭示了结构面宏观损伤特征及典型破坏模式;同时,应用PFC2D程序模拟了直剪试验全过程,分析了结构面细观损伤裂纹数量(能量)变化规律,揭示了结构面细观损伤演化过程及颗粒分布特征,并经对比分析结构面宏细观损伤力学行为后统一概化描述了其损伤劣化机理;据此,提出了结构面剪切强度估算公式,并根据典型边坡算例,采用极限平衡法和强度折减法验证了其合理性。
1 室内直剪试验
1.1 试验材料
自2003年蓄水以来,普遍分布于三峡库区的软硬互层边坡(图1)时常发生类型多且危害重的地质灾害[5,12,18-19],该种软硬互层边坡岩体结构面的力学特性受环境变化影响十分显著,绝大多数滑体均密集发育于此类坡体中。
试验以取自于三峡库区巫山段某滑坡场地的灰岩和强软化(崩解)黏性土(图1)作为试验原材料。使用岩石取芯(打磨)机和高压水射流切割机等设备加工灰岩原样,软弱层则通过黏性土原样重塑制备而成(图1)。测定灰岩和软弱层的物理力学参数(表1),为后续室内直剪试验及其PFC2D细观模拟提供理论依据和参考。

图1 现场取样、试样加工制备及其物理力学参数测定
Fig.1 In-situ sampling,specimens’ preparation and its determination of physical-mechanical parameters
表1 试验材料物理力学参数
Table 1 Physical-mechanical parameters of test materials

岩性含水率/%密度/(g·cm-3)抗压强度/MPa弹性模量/MPa泊松比黏聚力/kPa内摩擦角/(°)灰岩—2.6557.266 600.000.245 260.0044.5351.551.33106.430.30118.3330.13软弱层101.691.1397.490.28107.2829.34151.740.9288.740.2799.8627.19
1.2 试验模型
试验特别考虑了硬性岩层起伏度和粗糙度,即一阶(周期性三角形凸台)和二阶(三角形微凸体)起伏体(U1~U3),以较为真实地描述软弱层与硬性岩层接触面形态特征,并基于此将软硬互层岩体结构面概化设计为如图2所示的试验模型。根据文献[20],充分考虑试样加工制备和试验设备等条件,最终确定试验模型具体几何尺寸(图2)为:单个一阶起伏体长度L=30 mm,硬性岩层左右侧水平段长度 l=15 mm,“软+硬”组合形式下软弱层最大厚度H0=50 mm,“硬+软+硬”组合形式下软弱层最大厚度 h0=60 mm,“硬+软+硬”组合形式下硬性岩层左右侧竖直段高度h=20 mm,“硬+软+硬”组合形式下上下部分硬性岩层一阶起伏体尖端之间的竖直向距离 H1≈43 mm、H2=30 mm及H3≈8 mm,试验模型宽度d=50 mm,一阶起伏角α1=30°,α2=45°及α3=60°,二阶起伏角β=45°。同时,将加工制备好的灰岩和软弱层试样于剪切盒中进行夯压组合并对各类试验模型进行编号(M1~M4)。

图2 试验模型概化设计示意
Fig.2 Generalized design diagrams of test models
1.3 试验工况
该试验针对“软+硬”和“硬+软+硬”的组合形式下的结构面(分别为第1类和第2类结构面),在充分考虑含水率、法向压力及一阶起伏角(二阶起伏角不变的条件下)的变化对2类结构面的宏观剪切力学特性产生的影响下,其具体试验工况见表2。
表2 试验工况
Table 2 Test conditions
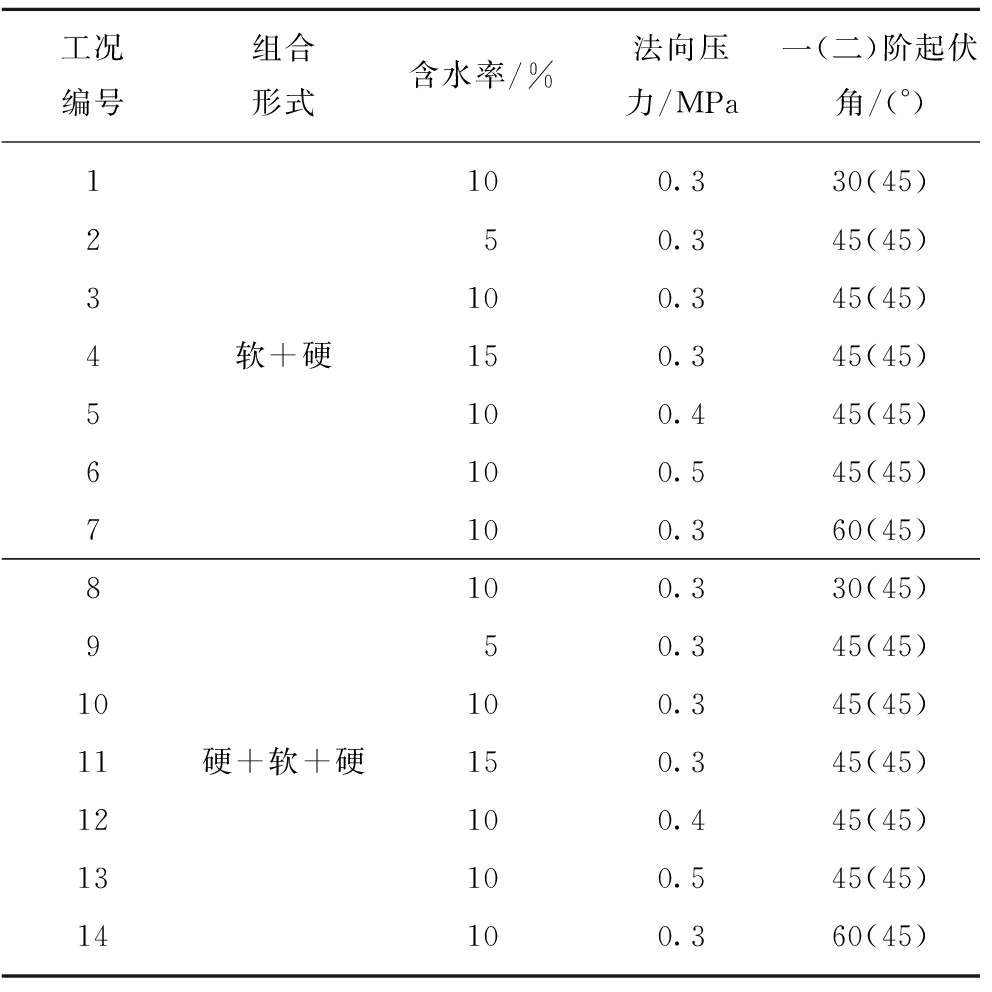
工况编号组合形式含水率/%法向压力/MPa一(二)阶起伏角/(°)1100.330(45)250.345(45)3100.345(45)4软+硬150.345(45)5100.445(45)6100.545(45)7100.360(45)8100.330(45)950.345(45)10100.345(45)11硬+软+硬150.345(45)12100.445(45)13100.545(45)14100.360(45)
1.4 试验设备
试验所采用的试验设备主要由加载系统、数据采集系统、监测系统及剪切装置组成(图3)。其中,加载系统为“山地城镇建设与新技术教育部重点实验室(重庆大学)”的WDAJ-600型微机控制电液伺服岩石剪切流变试验机,其轴(切)向最大试验力和位移行程均分别为600 kN 和100 mm,且试验力和位移加载速率均分别为0.1~100 kN/min 和0.001~10 mm/min,而测力和位移传感元件则分别为负荷式和磁致式传感器。数据采集系统包括多通道智能采集仪和电脑,而监测系统包括高速摄像机和电脑。剪切装置为自主研发设计的可视化、活动型及便携式剪切盒,可透过钢化玻璃窗口实时地观察和拍摄结构面宏观损伤破坏演化过程。

图3 试验设备及加载示意
Fig.3 Test equipments and loading diagrams
1.5 试验加载
以工况3号和10号的直剪试验过程为例(图3):加载前,将润滑剂(凡士林)均匀涂抹于剪切盒上、下盘接触面以降低其摩擦阻力,并确保试验机轴(切)向刚性加载头、端头及底座均与剪切盒相应位置对中;加载时,首先以试验力加载方式施加法向压力(速率为0.5 kN/min)直至目标值,然后维持恒定法向压力加载条件,最后以位移加载方式施加剪切荷载(速率为0.5 mm/min)直至结构面损伤破坏;加载终止,取下试验模型,观察、拍摄并记录结构面内外部损伤破坏形态。
2 试验结果及分析
2.1 结构面剪切变形及强度特性
图4为2类结构面的剪切应力(法向位移)与剪切位移之间的关系曲线,可将该关系曲线划分为AB,BC及CD三个变化阶段。基于图4(a),阶段AB:结构面处于初始非线性压剪变形状态,其剪切应力-剪切位移曲线近似呈“下凹弧形”变化,且一阶起伏体尖端附近软弱土体开始萌生裂缝并伴有微小垂直移动分量(剪胀)。阶段BC:结构面处于应力稳定增长压剪变形状态,其剪切应力-剪切位移曲线前后期分别近似呈线性和“上凹弧形”变化(剪切应力增幅由缓变急),而施加剪切荷载一侧的边缘一阶起伏体与软弱土体逐渐脱离(曲线出现突变点),且垂直移动分量(剪缩)增势先急后缓。阶段CD:结构面处于应力陡升-脆落塑性压剪变形状态,临近峰值剪切强度前结构面剪切应力-剪切位移曲线近似呈线性快速增长变化(软弱土体沿一阶起伏体尖端所在层面逐渐贯通),随后发生瞬时应力脆性跌落(刚性端头一侧的边缘一阶起伏体沿根部斜向瞬间脆性断裂),且垂直移动分量(剪缩)变化已趋于稳定。
基于图4(b),阶段AB:结构面处于初始非线性压剪变形状态,其剪切应力-剪切位移曲线近似呈“波浪状”变化,且剪切面两端软弱土体开始滋生裂缝并伴有微小垂直移动分量(剪胀)。阶段BC:结构面处于应力陡-缓升压剪变形状态,其剪切应力-剪切位移曲线前后期分别近似呈线性和“下凹弧形”变化(剪切应力增幅由急变缓),而剪切应力增长过程中并未出现显著峰值点,且垂直移动分量(剪缩)增势加剧(剪切面附近“土脊”和“小山包”被啃断后产生疏松效应)。阶段CD:结构面处于应力恒定塑性压剪变形状态,其剪切应力-剪切位移曲线近似呈“水平状”变化(剪切应力达峰值后几乎保持恒定),此时软弱层内部贯通并逐渐沿贯通面滑移,且垂直移动分量(剪缩)呈持续稳步增加趋势(增幅较小)。

图4 结构面剪切应力(法向位移)-剪切位移曲线
Fig.4 Curves of shear stress (normal displacement) versus shear displacement of rock discontinuity
2.2 结构面剪切力学特性影响因素分析
2.2.1 含水率
图5为不同含水率下2类结构面峰值(残余)剪切强度和峰值剪切(最大法向)位移的变化曲线。

图5 含水率对结构面剪切特性影响规律曲线
Fig.5 Curves about impact law of the moisture content on the shear properties of rock discontinuity
由图5(a)可知,2类结构面的峰值(残余)剪切强度均随含水率不断增大而近似线性逐渐降低;当含水率由5.0%增至15.0%时,第1类结构面的峰值和残余剪切强度分别由1.491 MPa和1.154 MPa降至0.615 MPa和0.527 MPa,而第2类结构面的峰值和残余剪切强度则分别由0.324 MPa和0.316 MPa降至0.199 MPa和0.196 MPa。由图5(b)可知,2类结构面的峰值剪切位移均随含水率不断增大而近似线性逐渐减小,而其最大法向位移则与之相反;当含水率从5.0%增至15.0%时,第1类结构面的峰值剪切位移从10.948 mm减至9.891 mm、最大法向位移从0.190 mm增至0.360 mm,而第2类结构面的峰值剪切位移则从14.973 mm减至11.973 mm、最大法向位移则从0.650 mm增至0.885 mm。水对软弱层的软化作用随含水率不断增大而逐渐加剧,此时软弱层的泥质矿物黏聚力及其剪切(法向)刚度大幅度降低,由此致使结构面剪切强度和变形性能发生不可恢复的劣化效应。
2.2.2 法向压力
图6为不同法向压力下2类结构面的峰值(残余)剪切强度和峰值剪切(最大法向)位移的变化曲线。

图6 法向压力对结构面剪切特性影响规律曲线
Fig.6 Curves about impact law of the normal stress on the shear properties of rock discontinuity
由图6(a)可知,2类结构面的峰值(残余)剪切强度均随法向压力逐渐增加而近似线性不断增大;当法向压力由0.3 MPa增至0.5 MPa时,第1类结构面的峰值和残余剪切强度分别由1.031 MPa和0.797 MPa增至1.559 MPa和1.302 MPa,而第2类结构面的峰值和残余剪切强度则分别由0.268 MPa和0.263 MPa增至0.372 MPa和0.362 MPa。由图6(b)可知:2类结构面的峰值剪切(最大法向)位移均随法向压力逐渐增加而近似线性不断增大;当法向压力从0.3 MPa增至0.5 MPa时,第1类结构面的峰值剪切和最大法向位移分别从10.344 mm和0.280 mm增至12.539 mm和0.794 mm,而第2类结构面的峰值剪切和最大法向位移则分别从14.301 mm和0.773 mm增至14.870 mm和1.224 mm。一般地,结构面剪切强度(变形)与法向压力大小密切相关,法向压力较低时结构面剪切变形增大的同时会伴有较小垂直移动分量(剪胀),而法向压力较高时结构面剪切变形明显增大,且持续压剪复合作用下硬性岩层一阶起伏体沿根部啃断或软弱层贯通(垂直移动分量主要为剪缩且较显著),致使结构面峰值剪切强度最终衰减为残余剪切强度。
2.2.3 一阶起伏角
图7为不同一阶起伏角下2类结构面的峰值(残余)剪切强度和峰值剪切(最大法向)位移的变化曲线。

图7 一阶起伏角对结构面剪切特性影响规律曲线
Fig.7 Curves about impact law of the first-order asperity angle on the shear properties of rock discontinuity
由图7(a)可知,第1类结构面的峰值剪切强度随一阶起伏角不断增大而近似线性逐渐增加,而其残余剪切强度则先增加后减小,当一阶起伏角为60°时其应力降十分显著(从1.460 MPa跌至0.684 MPa);第2类结构面的峰值(残余)剪切强度均随一阶起伏角不断增大而近似线性逐渐增加(变幅先缓后陡)。由图7(b)可知:2类结构面的峰值剪切位移总体上均随一阶起伏角不断增大而逐渐减小,且当一阶起伏角由45°增至60°时第2类结构面的峰值剪切位移降幅较显著(从13.831 mm降至7.466 mm);此外,2类结构面的最大法向位移总体上均随一阶起伏角不断增大而逐渐增加(变幅先缓后陡),且当一阶起伏角由45°增至60°时2类结构面的最大法向位移增幅较明显(分别从0.388 mm和0.568 mm增至0.865 mm和2.059 mm)。对于第1类结构面而言,随一阶起伏角逐渐变大,软弱层与硬性岩层接触面面积增大进而使软弱土体固结硬化效应加剧,同时刚性端头一侧的边缘一阶起伏体斜面受集中挤压荷载后沿根部斜向断裂,且施加剪切荷载一侧的边缘一阶起伏体斜面与软弱土体完全脱离,如此加速迫使结构面峰值剪切强度发生瞬时脆性跌落(应力降随一阶起伏角增大而越显著)。对于第2类结构面而言,随一阶起伏角不断变大,软弱层相对厚度逐渐小于三角形凸台高度,此时凸台对结构面剪切强度和变形性能影响较显著,并表现出凸台尖端附近软弱土体明显硬化且剪切面附近软弱土体接触效应明显增强。
2.3 结构面宏观损伤特征及典型破坏模式
图8为2类结构面的宏观损伤特征及典型破坏模式,结合图4可将结构面宏观损伤破坏发展历程划分为P1,P2及P3三个变化阶段。图8中,如“10.0%+0.3 MPa+30°”指含水率、法向压力及一阶起伏角依次为10.0%,0.3 MPa及30°。

图8 结构面宏观损伤特征及典型破坏模式
Fig.8 Macro-damage characteristics and typical failure modes of rock discontinuity
(1)第1类结构面。阶段P1:初始压剪复合作用下,刚性端头一侧的边缘一阶起伏体斜面附近软弱土体逐渐固结硬化,而施加剪切荷载一侧的边缘一阶起伏体与软弱土体之间呈脱离趋势,且一阶起伏体尖端附近软弱土体伴有微小竖向位移分量(萌生微裂缝),该阶段结构面主要表现为压剪-起裂破坏模式。阶段P2:持续压剪复合作用下,刚性端头一侧的边缘一阶起伏体斜面附近软弱土体局部抗压剪强度增强,且软弱土体沿一阶起伏体尖端所在平面逐渐发生错移滑动(裂缝数量扩增明显),而施加剪切荷载一侧的边缘一阶起伏体与软弱土体之间完全脱空(竖向位移分量明显变大),该阶段结构面主要表现为错动-脱空破坏模式。阶段P3:软弱土体沿一阶起伏体尖端所在平面完全贯通且裂缝迅速延伸、扩展(竖向位移分量趋于稳定),而刚性端一侧的边缘一阶起伏体所受集中压剪荷载迅速增大直至沿根部斜向脆性断裂(裂缝数量骤增);一阶起伏体断裂后嵌固于软弱土体内且断裂面较光滑,而软弱层贯通后软弱土体嵌固于三角形凸台之间且贯通面起伏不平,该阶段结构面主要表现为贯通-啃断破坏模式。一阶起伏角为30°时硬性岩层损伤破坏主要表现为三角形微凸体磨损,而一阶起伏角为45°和60°时硬性岩层损伤破坏则主要表现为三角形凸台断裂;在相同法向压力和含水率下,硬性岩层损伤度随一阶起伏角增大而逐渐显著且一阶起伏角较大时凸台沿根部啃断越彻底;相同含水率和一阶起伏角下,硬性岩层损伤度随法向压力增大而逐渐显著且法向压力较大时凸台啃断裂缝数量越多;在相同一阶起伏角和法向压力下,硬性岩层面损伤度随含水率增大而逐渐显著且含水率较大时凸台与软弱土体之间的嵌固效应相对越明显。
(2)第2类结构面。阶段P1:初始压剪复合作用下,软弱层内部土体颗粒相互挤压并滋生微小竖向位移分量,且剪切面两端软弱土体开始萌生微裂缝,该阶段结构面主要表现为压剪-起裂破坏模式。阶段P2:持续压剪复合作用下,剪切面两端萌生的微裂缝逐渐向软弱层内部延伸、扩展,且软弱层内部土颗粒间不断发生摩擦损伤后于剪切面附近形成“土脊”和“小山包”(裂缝数量明显增多),随后由于压剪效应增强致使“土脊”和“小山包”被逐渐啃断,此时剪切面附近软弱土体较疏松且竖向位移分量显著,该阶段结构面主要表现为磨损-啃断破坏模式。阶段P3:软弱层沿剪切面附近完全贯通(裂缝数量骤增),随后其上下两侧沿贯通面逐渐发生塑性滑移(竖向位移分量稳步增大),该阶段结构面主要表现为贯通-滑移破坏模式。软弱层内部贯通面起伏不平且磨损、啃断痕迹显著,而硬性岩层完好无损且其附近软弱土体所受影响甚微;相同法向压力和含水率下软弱层损伤度随一阶起伏角增大而逐渐显著,相同含水率和一阶起伏角下软弱层损伤度随法向压力增大而逐渐显著,相同一阶起伏角和法向压力下软弱层损伤度随含水率增大而逐渐显著,当一阶起伏角、法向压力及含水率均较大时贯通面平整度越低。
3 PFC2D直剪试验细观模拟
3.1 数值模型及细观参数
为了从细观角度揭示软硬互层岩体结构面的累积损伤演化过程(颗粒分布特征)及裂纹数量(能量)变化规律,应用PFC2D程序建立典型工况(表3)下的细观数值模型(几何尺寸如图2所示),以工况4号和13号为例(图9):剪切盒由编号为Wall 1号~Wall 8号的8块刚性墙体组合而成,其中,Wall 1号,Wall 2号,Wall 3号及Wall 8号组成剪切盒下盘,而Wall 4号,Wall 5号,Wall 6号及Wall 7号组成剪切盒上盘,且Wall 3号和Wall 7号作为翼墙以防止颗粒在加载过程中发生逃逸[21];在剪切盒范围内随机生成孔隙率为0.15的圆形颗粒共计20 546个,且颗粒半径在0.38~0.54 mm服从均匀分布;采用平行黏结模型进行颗粒材料的接触计算,且采用离散裂隙网格创建硬性岩层锯齿状节理,并在裂隙两侧0.60 mm范围内赋予颗粒材料光滑节理接触模型[22]。同时,采用“试错法”反复试算标定模型细观参数[12,21],以此获得的数值计算宏观参数见表4,对比表1和4可知2者物理力学参数值吻合较好(误差均小于±5%),即表明可采用表5中的细观参数进行颗粒流数值模拟。
表3 数值计算工况
Table 3 Numerical calculation conditions
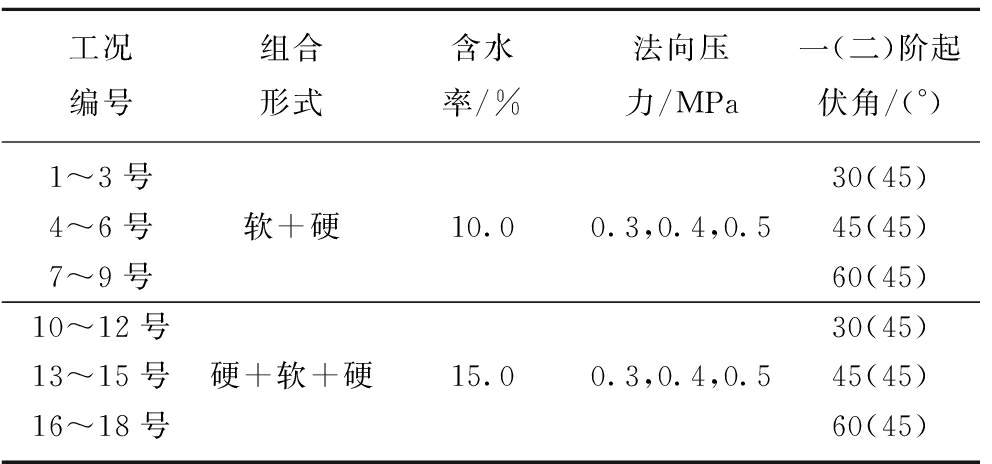
工况编号组合形式含水率/%法向压力/MPa一(二)阶起伏角/(°)1~3号30(45)4~6号软+硬10.00.3,0.4,0.545(45)7~9号60(45)10~12号30(45)13~15号硬+软+硬15.00.3,0.4,0.545(45)16~18号60(45)

图9 数值计算模型
Fig.9 Numerical calculation models
表4 数值计算宏观参数
Table 4 Macro-parameters of numerical calculations

岩性含水率/%密度/(g·cm-3)抗压强度/MPa弹性模量/MPa泊松比黏聚力/kPa内摩擦角/(°)灰岩—2.6556.496 7000.245 38044.31软弱层10.01.691.0998.820.28108.6129.03
图10为2类结构面的宏观试验结果与细观模拟结果之间的对比关系曲线。由图10可知,2类结构面的细观模拟所得曲线均具显著波动起伏形态,并呈现出与宏观试验所得曲线相吻合的阶段性发展变化规律;对于第1类结构面而言,其宏观试验与细观模拟所得峰值剪切强度(位移)分别为1.031 MPa(10.344 mm)和1.065 MPa(10.965 mm),而对于第2类结构面而言,其宏观试验与细观模拟所得峰值剪切强度(位移)分别为0.268 MPa(14.301 mm)和0.274 MPa(14.563 mm),即总体上宏观试验与细观模拟所得峰值剪切强度(位移)均较吻合;宏观试验与细观模拟所得结构面损伤破坏形态吻合较好,2者均揭露了结构面挤压、起裂、错动、磨损、脱空、贯通、啃断及滑移等现象。鉴于此,表明本文基于表5中的细观数值模拟参数,采用PFC2D离散元法研究2类结构面的细观剪切力学特性合理可行。

图10 宏观试验结果与细观模拟结果对比
Fig.10 Comparison between the macro test findings and meso simulation results
表5 数值计算细观参数
Table 5 Meso-parameters of numerical calculations

项目参数取值摩擦因数0.6最大半径/mm0.54弹性模量/GPa12圆形颗粒法向切向刚度比1.5最大最小半径比1.42体积密度/(g·cm-3)2.75键合方式1摩擦因数0.5剪胀角/(°)0光滑节理抗拉强度/MPa0剪切刚度/(GPa·m-1)80法向刚度/(GPa·m-1)80半径乘子1.0(1.0)剪切强度/MPa62.5(1.05)平行键(灰岩软弱层)法向强度/MPa48.5(0.85)弹性模量/GPa25(0.15)法向切向刚度比2.5(1.6)剪切法向强度标准差±5(±0.1)
3.2 结构面细观损伤裂纹数量及能量分析
图11为2类结构面的细观损伤裂纹数量(能量)与剪切位移之间的关系曲线(以工况4号和13号为例,其中,红色数字为裂隙数量)。由图11(a),(b)可知,2类结构面的细观损伤裂纹均包括剪切和拉伸裂纹,且细观损伤总裂纹、剪裂纹及拉裂纹数量均随剪切位移不断增大而呈逐渐增加的变化趋势(拉裂纹数量大于剪裂纹数量且第1类结构面中该种现象极为显著);同时,临近峰值剪切强度前细观损伤裂纹数量随剪切位移的变化曲线近似呈“下凹弧形”陡增,而后其增幅降低并近似呈线性增长的变化趋势;总体上,该变化曲线可划分为初期微增(区段Ⅰ)、中期近似“下凹弧形”陡增(区段Ⅱ)及后期近似线性缓增(区段Ⅲ)3个变化阶段,且第2类结构面的损伤裂纹数量较第1类结构面多。

图11 结构面细观损伤裂纹数量(能量)-剪切位移曲线
Fig.11 Curves of meso-damage crack quantity (energy) versus shear displacement of rock discontinuity
结构面细观损伤总能量即剪切过程中Wall 2号对试样所做外功,其包括剪拉耗散能(试样内部和接触面剪切、拉伸耗散能)和弹性应变能(储存于试样内部的可释放弹性应变能)。由图11(c),(d)可知:2类结构面的细观损伤总能量、剪拉耗散能及弹性应变能总体上均随剪切位移不断增大而呈逐渐增加的变化趋势(剪拉耗散能大于弹性应变能);此外,第1类结构面达峰值剪切强度后其细观损伤能量发生突变跌落,而第2类结构面达峰值剪切强度后其细观损伤能量随剪切位移几乎呈线性增长的变化趋势;总体上,该变化曲线可划分为初期微增(区段Ⅰ)、中期近似“上凹弧形”缓增(区段Ⅱ)及后期近似线性陡增(区段Ⅲ,具突变点、起伏状特征)3个变化阶段,且第1类结构面的损伤能量较第2类结构面大。
3.3 结构面细观损伤演化过程及颗粒分布特征
图12为2类结构面的细观损伤演化过程及颗粒分布特征(以工况4号和13号为例,其中红色数字为裂隙数量),可将其细观损伤演化过程划分为Q1,Q2及Q3三个变化阶段。

图12 结构面细观损伤演化过程及颗粒分布特征
Fig.12 Meso-damage evolution process and particle distribution characteristics of rock discontinuity
(1)第1类结构面。基于图12(a),阶段Q1:初始压剪复合作用下,一阶起伏体尖端附近软弱土体产生细观微裂纹(主要为拉伸破坏微裂纹),且临近Wall 4号一侧的边缘一阶起伏体与软弱土体之间开始萌生微裂隙,而细观损伤颗粒分布较稀疏,此时结构面表现出明显的剪胀效应。阶段Q2:持续压剪复合作用下,细观微裂纹自一阶起伏体尖端附近向两侧逐渐延伸、扩展(细观损伤颗粒分布逐渐加密),且临近Wall 6号一侧的边缘一阶起伏体斜面附近软弱土体开始产生剪切破坏微裂纹,而临近Wall 4号一侧的微裂隙显著增大(完全脱空),此时结构面表现出明显的剪胀-分离-剪缩效应。阶段Q3:软弱层沿一阶起伏体尖端所在平面完全穿透(贯通面逐渐拓宽),临近Wall 6号一侧的软弱土体局部细观微裂纹扩增贯通,而细观损伤颗粒分布较密集,且剪切破坏微裂纹自一阶起伏体斜面中部萌生并沿斜向延伸、扩展至根部而发生脆性断裂,此时结构面表现出明显的剪缩效应。
(2)第2类结构面。基于图12(b),阶段Q1:初始压剪复合作用下,剪切面两端开始萌生细观微裂纹,且微裂纹自起裂处向软弱层中部扩展、延伸时具有不同的路径走势(邻近Wall 6号一侧斜向下而邻近Wall 4号一侧斜向上),而细观损伤颗粒分布极为稀疏,此时结构面表现出明显的剪胀效应。阶段Q2:持续压剪复合作用下,剪切面附近土颗粒之间的相互磨损作用逐渐加剧(细观微裂纹继续扩展、延伸),且细观损伤颗粒间断性地分布于临近剪切面两侧(连通性较差),而软弱土体发生瞬时性啃断后细观颗粒损伤边界区范围呈扩增趋势,此时结构面主要表现出明显的剪胀-疏松-剪缩效应。阶段Q3:细观微裂纹自起裂端以不同走势向软弱层中部持续扩展、延伸后完全贯通,该贯通面边界区域范围明显变大并充填大量拉剪破坏损伤颗粒,随后贯通面上下两侧软弱土体沿其逐渐发生滑移,且硬性岩层对软弱层损伤程度存在一定的约束或促进作用,此时结构面主要表现为剪缩效应。
2类结构面的细观损伤颗粒于剪切面附近分别近似呈“倒U形”和“S形”分布,且细观颗粒损伤时颗粒间接触力倾角均在0°~360°,其中,损伤颗粒数量于0°~90°分布最多,于90°~180°分布次之,而于180°~270°和270°~0°基本一致且分布极少。
3.4 结构面宏细观损伤劣化机理统一概化描述
结合图4,8及12,可将2类结构面的宏细观损伤劣化机理统一概化描述过程划分为如图13所示的P1(Q1)、P2(Q2)及P3(Q3)三个变化阶段(以一阶和二阶起伏角均为45°的概化模型为例,其余不同起伏角条件与此类似)。

图13 结构面宏细观损伤劣化机理统一概化描述示意
Fig.13 Generalized describe diagrams for the macro-meso damage degradation mechanism of rock discontinuity
其中,阶段P1(Q1):2类结构面均产生剪胀效应,并均处于初始非线性压剪变形状态,且损伤裂纹数量均较少(分布稀疏),而第1类结构面下的空隙区较小,该阶段其结构面均表现为压剪-起裂破坏模式。阶段P2(Q2):2类结构面分别产生剪胀-分离-剪缩和剪胀-疏松-剪缩效应,并分别处于应力稳定增长和应力陡-缓升压剪变形状态,且损伤裂纹数量均增多(连通性增强),而第1类结构面下的空隙区变大(脱空),该阶段其结构面分别表现为错动-脱空和磨损-啃断破坏模式。阶段P3(Q3):2类结构面均产生剪缩效应,并分别处于应力陡升-脆落和应力恒定塑性压剪变形状态,且损伤裂纹数量均显著增加(分别近似呈“倒U形”和“S形”密集分布于剪切面附近,并形成相对规则的断裂面和破坏区),而第1类结构面下的空隙区显著扩增,该阶段其结构面分别表现为贯通-啃断和啃断-滑移破坏模式。特别地,尽管2类结构面在各因素(含水率、法向压力及一阶起伏角)影响下其最终损伤破坏形态有所差异,但其宏细观损伤演化过程及劣化机理仍基本保持一致。
4 结构面剪切强度估算公式及其算例验证
一般地,剪切强度是岩体结构面最重要的力学特性之一,且剪切过程中结构面损伤力学机理较复杂并受多因素影响。根据图6(a)和图7(b)不难看出2类结构面的峰值剪切强度均随法向压力和一阶起伏角增加而近似线性增大,故其剪切强度估算公式的表达形式服从摩尔-库伦准则[17]。为了明确结构面剪切强度估算公式的物理意义,特别是应能反映考虑硬性岩层一阶起伏角对结构面剪切强度的影响,将2类结构面的剪切强度估算公式的一般表达式定义为
τi=σnitan φi+ci=σnitan[fi(α)]+hi(α)
(1)
式中,i为第1类(i=1)和第2类(i=2)结构面的序号;τi为结构面剪切强度;σni为结构面法向压力;ci和φi分别为结构面黏聚力和内摩擦角;fi(α)和hi(α)均为与硬性岩层一阶起伏角α相关的函数(固定二阶起伏角β)。
同时,通过PFC2D直剪试验细观模拟获得的2类结构面的抗剪强度参数与一阶起伏角之间的关系曲线如图14所示。由图14可知:2类结构面的抗剪强度参数均随一阶起伏角增加而近似线性增大,进一步采用一元线性回归分析法拟合计算结果可得式(2)~(5)。联合式(1)~(5)可得2类结构面的剪切强度估算公式可分别用式(6)和(7)表示。

图14 结构面抗剪强度参数-一阶起伏角曲线
Fig.14 Curves of shear strength parameters versus first-order asperity angle of discontinuity
f1(α)=φ1=0.300 2α+21.523 0
(2)
h1(α)=c1=0.005 0α+0.000 9
(3)
f2(α)=φ2=0.409 7α+11.753 0
(4)
h2(α)=c2=0.000 1α+0.102 2
(5)
τ1=σn1tan(0.300 2α+21.523 0)+0.005 0α+
0.000 9
(6)
τ2=σn2tan(0.409 7α+11.753 0)+0.000 1α+
0.102 2
(7)
现假定图15为含2类典型结构面边坡的稳定性分析概化设计示意,其中,边坡坡角为60°,H=8.0 m,α=β=45°。根据图13所示的结构面损伤断裂面和破坏区特征,可将图15中MN两点之间的连线(虚线)假设为宏观滑动面(长度LMN和倾角θ分别为16.0 m和30°),而其附近一定区域(阴影部分)则为潜在滑动带。根据极限平衡法(平面滑移)和强度折减法[23],联合式(1)获得的边坡安全系数计算公式可分别用式(8),(9)和式(10),(11)表示。

图15 边坡稳定性分析概化设计示意及剪应变增量云图
Fig.15 Generalized design diagrams of slope stability analysis and nephograms of shear strain increment
Klemi=FRSi/Wisin θ=τiLMN/(Wisin θ)
(8)
τiLMN=Wicos θtan[fi(α)]+LMNhi(α)
(9)
cni=ci/Ksrmi=hi(α)/Ksrmi
(10)
![]()
(11)
式中,Klemi和Ksrmi分别为采用极限平衡法和强度折减法计算的边坡安全系数;FRSi为宏观滑动面抗滑力;Wi为滑体质量;cni和φni分别为结构面新的黏聚力和内摩擦角参数。
综上,根据式(6)~(9),采用极限平衡法计算的含2类典型结构面的边坡安全系数分别为Klem1=1.226和Klem2=1.012。特别地,根据式(2),(3),(10)及(11),通过FLAC3D强度折减程序求解边坡安全系数,其计算模型和参数分别如图15和表4所示,且软弱层与硬性岩层接触面采用“Interface”单元模拟,同时计算模型左、右及下侧均采用法向位移约束而其余侧则均采用自由边界条件,并对潜在滑动带的材料抗剪强度参数进行折减[13];由此采用强度折减法计算的含2类典型结构面的边坡安全系数分别为Ksrm1=1.272和Ksrm2=1.052,且其剪应变增量云图如图15所示。基于此,对比采用极限平衡法和强度折减法计算的边坡安全系数,尽管2种方法计算结果存在一定差异,但其偏差较小(3.75%和3.95%),表明所建立的2类结构面的剪切强度估算公式基本合理。
5 结 论
(1)第1类结构面剪切应力(法向位移)随剪切位移的变化可划分为初始非线性压剪变形、应力稳定增长压剪变形及应力陡升-脆落塑性压剪变形3个发展阶段;而第2类结构面下该变化则可划分为初始非线性压剪变形、应力陡-缓升压剪变形及应力恒定塑性压剪变形3个发展阶段。
(2)2类结构面峰值(残余)剪切强度、峰值剪切位移均随含水率增加而减小(最大法向位移则增大);2类结构面峰值(残余)剪切强度、峰值剪切(最大法向)位移均随法向压力增加而增大;第1类结构面峰值剪切强度随一阶起伏角增加而增大(残余剪切强度则先增大后减小),而第2类结构面峰值(残余)剪切强度随一阶起伏角增加而增大,且2类结构面峰值剪切位移总体上均随一阶起伏角增加而减小(最大法向位移则增大);各因素影响下2类结构面剪切过程中先后均产生剪胀、剪胀-分离(或疏松)-剪缩及剪缩效应。
(3)2类结构面细观损伤裂纹数量随剪切位移的变化总体上均可划分为初期微增、中期近似“下凹弧形”陡增及后期近似线性缓增3个发展阶段;2类结构面细观损伤能量随剪切位移的变化总体上可划分为初期微增、中期近似“上凹弧形”缓增及后期近似线性陡增(具有突变点、起伏状特征)3个发展阶段。
(4)对比分析2类结构面宏细观损伤演化过程(破坏特征)后对其劣化机理进行了统一概化描述,并将其典型破坏模式分别概括为压剪-起裂破坏、错动-脱空破坏、贯通-啃断破坏和压剪-起裂破坏、磨损-啃断破坏、贯通-滑移破坏各3种类型;2类结构面细观损伤颗粒分别近似呈“倒U形”和“S形”分布于剪切面附近,且颗粒间接触力倾角于0°~90°时损伤颗粒数量分布最多,总体上宏观试验结果与PFC2D细观模拟结果吻合较好。
(5)着重考虑硬性岩层起伏度对结构面剪切强度的影响,提出了2类结构面剪切强度估算公式,即τi=σnitan φi+ci=σnitan[fi(α)]+hi(α),并采用极限平衡法和强度折减法对典型边坡算例进行了稳定性分析,进一步验证了该公式的合理性。
[1] LIU X R,LIU Y Q,LU Y M,et al.Experimental and numerical study on pre-peak cyclic shear mechanism of artificial rock joints[J].Structural Engineering and Mechanics,2020,74(3):407-423.
[2] JU Y,SUN H F,XING M X,et al.Numerical analysis of the failure process of soil-rock mixtures through computed tomography and PFC3D models[J].International Journal of Coal Science & Technology,2018,5(2):126-141.
[3] 黄润秋.岩石高边坡稳定性工程地质分析[M].北京:科学出版社,2012.
[4] LIU H Y,HAN H Y,AN H M,et al.Hybrid finite-discrete element modelling of asperity degradation and gouge grinding during direct shearing of rough rock joints[J].International Journal of Coal Science & Technology,2016,3(3):295-310.
[5] 董金玉,杨继红,伍法权,等.三峡库区软硬互层近水平地层高切坡崩塌研究[J].岩土力学,2010,31(1):151-157.
DONG Jinyu,YANG Jihong,WU Faquan,et al.Research on collapse of high cutting slope with horizontal soft-hard alternant strata in Three Gorges reservoir area[J].Rock and Soil Mechanics,2010,31(1):151-157.
[6] JU Y W,LUXBACHER K,LI X S,et al.Micro-structural evolution and their effects on physical properties in different types of tectonically deformed coals[J].International Journal of Coal Science & Technology,2014,1(3):264-275.
[7] HOEK E,BRAY J.Rock slope engineering(3rd edition)[M].London:Institution of Mining and Metallurgy,1981.
[8] BANDIS S C,LUMSDEN A C,BARTON N R.Fundamentals of rock joint deformation[J].International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts,1983,20(6):249-268.
[9] 董遵德,袁澄文.岩体软弱夹层现场慢剪切试验研究[J].岩石力学与工程学报,1994,13(2):149-159.
DONG Zunde,YUAN Chengwen.Researches for controlled displacement-rate shear test in situ in rock mass soft intercalation[J].Chinese Journal of Rock Mechanics and Engineering,1994,13(2):149-159.
[10] 许江,瞿佳美,刘义鑫,等.循环剪切荷载作用下充填物对结构面剪切特性影响试验研究[J].岩土力学,2019,40(5):1627-1637.
XU Jiang,QU Jiamei,LIU Yixin,et al.Influence of filling material on the behavior of joints under cyclic shear loading[J].Rock and Soil Mechanics,2019,40(5):1627-1637.
[11] 李鹏,刘建,朱杰兵,等.软弱结构面剪切蠕变特性与含水率关系研究[J].岩土力学,2008,29(7):1865-1871.
LI Peng,LIU Jian,ZHU Jiebing,et al.Research on effects of water content on shear creep behavior of weak structural plane of sandstone[J].Rock and Soil Mechanics,2008,29(7):1865-1871.
[12] 何春梅.循环动载下泥质软岩力学行为及库区软硬互层边坡动力稳定性研究[D].重庆:重庆大学,2018.
HE Chunmei.Mechanical behavior of muddy soft rock and dynamic stability of soft-hard interbedded slopes in reservoir area under cyclic loading[D].Chongqing:Chongqing University,2018.
[13] 王伟,张芳,孙斌祥.土-结构接触面剪切试验与应力-位移模型[J].煤炭学报,2011,36(9):1469-1473.
WANG Wei,ZHANG Fang,SUN Binxiang.Tested and modeled shear stress-displacement behavior of soil-structure interfac[J].Journal of China Coal Society,2011,36(9):1469-1473.
[14] 唐雯钰,林杭.不同锯齿高度对软弱结构面剪切特性的影响[J].中南大学学报(自然科学版),2017,48(5):1300-1307.
TANG Wenyu,LIN Hang.Influence of dentate discontinuity height on shear properties of soft structure plane[J].Journal of Central South University(Science and Technology),2017,48(5):1300-1307.
[15] YOON J.Application of experimental design and optimization to PFC model calibration in uniaxial compression simulation[J].International Journal of Rock Mechanics and Mining Sciences,2007,44(6):871-889.
[16] 黄达,黄润秋,雷鹏.贯通型锯齿状岩体结构面剪切变形及强度特征[J].煤炭学报,2014,39(7):1229-1237.
HUANG Da,HUANG Runqiu,LEI Peng.Shear deformation and strength of through-going saw-tooth rock discontinuity[J].Journal of China Coal Society,2014,39(7):1229-1237.
[17] 蔡美峰.岩石力学与工程[M].北京:科学出版社,2013.
[18] 朱赛楠,殷跃平,李滨.二叠系炭质页岩软弱夹层剪切蠕变特性研究[J].岩土力学,2019,40(4):1377-1386.
ZHU Sainan,YIN Yueping,LI Bin.Shear creep behavior of soft interlayer in Permian carbonaceous shale[J].Rock and Soil Mechanics,2019,40(4):1377-1386.
[19] 刘新荣,许彬,刘永权,等.频发微小地震下顺层岩质边坡累积损伤及稳定性分析[J].岩土工程学报,2020,42(4):632-641.
LIU Xinrong,XU Bin,LIU Yongquan,et al.Cumulative damage and stability analysis of bedding rock slope under frequent microseisms[J].Chinese Journal of Geotechnicale Engineering,2020,42(4):632-641.
[20] MURALHA J,GRASSELLI G,TATONE B,et al.ISRM suggested method for laboratory determination of the shear strength of rock joints:Revised version[J].Rock Mechanics and Rock Engineering,2014,47(1):291-302.
[21] 刘新荣,邓志云,刘永权,等.岩石节理峰前循环直剪试验颗粒流宏细观分析[J].煤炭学报,2019,44(7):2103-2115.
LIU Xinrong,DENG Zhiyun,LIU Yongquan,et al.Macroscopic and microscopic analysis of particle flow in pre-peak cyclic direct shear test of rock joint[J].Journal of China Coal Society,2019,44(7):2103-2115.
[22] POTYONDY D O,CUNDALL P A.A bonded-particle model for rock[J].International Journal of Rock Mechanics and Mining Sciences,2004,41(8):1329-1364.
[23] CHENG Y M,LANSIVAARA T,WEI W B.Two-dimensional slope stability analysis by limit equilibrium and strength reduction methods[J].Computer and Geotechnics,2007,34(3):137-150.
