我国西部地区侏罗纪煤炭资源丰富[1],其侏罗系延安组煤层开采普遍受到顶板水害的威胁[2-3]。目前,采用钻孔进行大降深、大流量超前预疏放是煤矿顶板水害主要防治工程措施[4]。在一些特定的矿井地质、水文地质条件下,超前疏排煤层顶板直接或间接充水含水层水是惟一的防治手段[5]。顶板疏放水钻孔的设计(长度、仰角、数量等)直接关乎钻探工程量、疏放时间及疏放水效果[6],同时为工作面防排水系统设计以及制定可控疏放方案提供直接参考。
井下疏放水是利用钻孔孔口标高低于充水含水层水位标高的天然条件,使含水层地下水从钻孔中自然涌出,从而有效降低充水含水层水位(头)的方法。由于承压含水层水头较大,大降深、大流量的井下疏放水,与地面抽水有很大区别,常规井流理论不适用于井下疏放水过程。目前,有关煤层顶板疏放水量计算多采用点源线汇理论[6-8],根据多目标管理模型对钻孔参数进行优化[9]。该方法一方面适用性未得到充分验证[10],另一方面未考虑疏放水钻孔内复杂的流态特征[11],同时,不能解决钻孔穿透多个含水层的水量分配问题[12],导致计算精度不高,不能满足疏放水钻孔工程优化设计的要求,因此目前对疏放水钻孔参数的优化工作开展较少。
事实上,倾斜钻孔疏放水时钻孔内水流流态具有管道流特征[11],整个含水层-钻孔系统可分解为含水层和钻孔2个子系统。含水层子系统可以用渗流方程来刻画,而钻孔子系统可以近似看作为一个小型管道系统,通过渗流-管流耦合模型来描述。
“渗流-管流耦合模型”最早应用在供水水文地质水资源量评价领域[13-14],该模型充分考虑了钻孔内多流态并存的水流特征[11,13],已广泛用于水平井[15]、渗流井[16-17]、辐射井[18-19]等取水建(构)筑物水量计算中,效果良好。笔者借鉴“渗流-管流耦合模型”理论及能量守恒定律,以含水层-钻孔间水量交换量为耦合点,构建煤层顶板复合充水含水层倾斜疏放水钻孔定降深放水的含水层-钻孔系统耦合模型。以母杜柴登矿井井下疏放水工程为例,研究钻场内不同参数(角度、数量等)下钻孔涌水量的变化特征,确定钻场内钻孔最佳长度、仰角和数量等参数,为疏放水工程优化设计提供技术支撑。
1 基于含水层-钻孔水量交换的疏放钻孔水量计算模型
1.1 含水层子系统渗流模型
疏放水钻孔放水时,含水层中地下水流呈现明显的承压三维流,其渗流模型可表示为
![]()
(1)
式中,Kxx,Kyy和Kzz为沿x,y,z轴方向的主渗透系数,这里假设渗透系数的主方向和坐标轴的方向一致;h为水头高度;Ss为多孔介质的弹性释水率;t为时间。
1.2 钻孔子系统管流模型
疏放水钻孔近似看作一小型管道。当管道完全饱和时,其流动可以假定为沿管道轴线的一维流。19世纪50年代末,通过对直筒形管道中水流的实验表明,沿管道的水头损失与速度水头和管道长度直接相关,与管道直径成反比[20]。Darcy,Weisbach和其他水力学研究者提出以下适用于紊流和层流的一般方程:
![]()
(2)
在管道中v=nu,其中n=1,v=u。此时方程(2)可变为
![]()
(3)
式中,ΔH为沿程水头损失;f为摩擦因数;l为沿程长度;d为管道直径;u为流速;n为孔隙度;v为平均流速;g为重力加速度。
方程(3)中的摩擦因数是流量和管道相对粗糙度的函数。方程式(3)被称为Darcy-Weisbach方程。方程(3)变形为
![]()
(4)
管道中的流量为
![]()
(5)
其中,A为管道的过水断面积,即管道中的流量与含水层渗流中的流量计算公式形式上是一样;K′为管道中的“等效渗透系数”;J为管道中水力梯度。摩擦因数与雷诺数Re相关,不同的雷诺数Re分别对应不同的摩擦因数[19]。
(1)当Re≤3 000,水流呈层流时,摩擦因数可用以下公式计算[20],即
![]()
(6)
式中,υ为黏滞系数,那么
![]()
(7)
将式(7)代入式(5)得
![]()
(8)
(2)当Re>3 000,水流呈紊流时,摩擦因数可用以下公式计算[21],即
而![]() 则
则
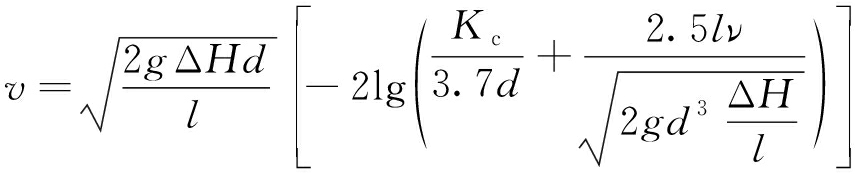
(9)
将式(9)代入式(4)[22]得
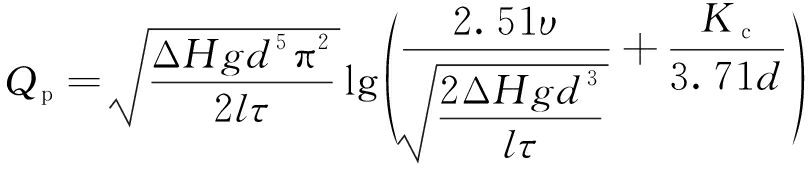
(10)
综上所述,钻孔中的流量计算公式为
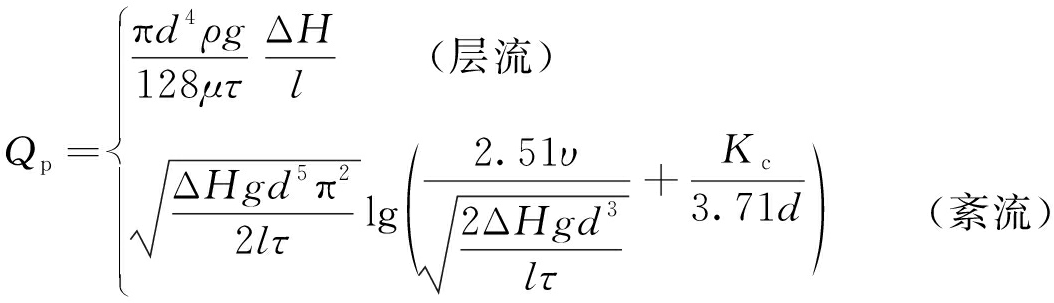
式中,Kc为钻孔内壁管壁的粗糙高度;μ为动力黏滞系数;τ为钻孔内壁粗糙度;ρ为水的密度。
1.3 含水层-钻孔系统耦合模型
根据能量守恒定律,含水层地下水流入钻孔的总流量等于钻孔内涌水量,即
∑Qex+Qp=0
(11)
其中,Qex为含水层与管道之间的交换水量,负号代表含水层流入管道,即含水层地下水进入钻孔的水量。
多孔介质地下水渗流区(含水层)与管道之间的水量交换,可根据两区域之间的水头差进行线性计算,即
Qex=α(hp-hi)
(12)
式中,α为含水层与管道交换区的水力传导系数;hp为交换区管道中的水头;hi为交换区含水层中的水头。
那么由式(11)可推出

(13)
这样,就将多孔介质地下水的渗流与钻孔中的管流耦合起来,方程(13)即为构建的含水层-钻孔系统复杂流态水流计算耦合模型。
方程(13)可通过改进管道流计算程序Conduit Flow Process(CFP)进行数值计算。CFP为在MODFLOW程序包上开发出来的,地下水渗流区根据MODFLOW进行离散化,利用CFP程序包将管道离散为一系列的节点和管子,两相邻节点用一根管子连接,地下水在相邻节点间通过管子传输,地下水渗流区和管道之间通过水量交换量进行耦合[22]。近年来,CFP程序已经开始用于层流和紊流的计算[23],能够很好地刻画岩溶等管道流[24]以及渗流井倾斜辐射管-含水层间复杂水流[25],模拟计算效果良好。
2 模型可靠性验证
为了验证该耦合模型,笔者采用母杜柴登矿井临时煤仓放水试验数据进行模型的可靠性验证。
2.1 研究区概况
母杜柴登矿井位于鄂尔多斯盆地呼吉尔特矿区,矿井地层自下而上由老至新发育有:三叠系上统延长组(T3y)、侏罗系中统延安组(J2y)、侏罗系中统直罗组(J2z)、侏罗系中统安定组(J2a)、白垩系下统志丹群(K1zh)和第四系全新统(Q4)(图1)。主要的含水层为第四系松散层(Q)潜水含水层、白垩系下统志丹群(K1zh)孔隙裂隙承压含水层、侏罗系直罗组(J2z)裂隙承压含水层以及侏罗系中延安组(J2y)碎屑岩类承压含水层,具体简述如下:

图1 地层综合柱状
Fig.1 Comprehensive stratigraphic column
(1)第四系松散层潜水含水层。含水层结构疏松,孔隙发育,透水性良好。含水层水位标高1 266.65~1 315.24 m,单位涌水量0.495~12.176 L/(s·m),含水层富水性中等~极强,渗透系数0.398 ~30.625 m/d。
(2)白垩系下统志丹群孔隙裂隙承压含水层。该含水层岩芯较为破碎,胶结程度相对较差,裂隙较发育,开启程度较好。含水层水位标高1 269.22~1 317.63 m,单位涌水量0.114~0.624 L/(s·m),含水层富水性中等,渗透系数0.034 ~1.424 m/d。
(3)侏罗系直罗组孔隙裂隙承压含水层。该含水层分布较为连续、稳定,同样是由一套砂岩与泥岩含、隔水层相互叠置的组合结构。含水层水位标高1 261.95~1 296.8 m,单位涌水量0.014~0.203 L/(s·m),含水层富水性弱至中等,渗透系数0.031 ~0.288 m/d。
(4)侏罗系延安组碎屑岩类承压含水层:延安组为含煤地层,煤层之间岩性以粉细砂岩、砂质泥岩和泥岩为主。砂岩分布不连续,砂质泥岩、泥岩厚度大,分布较稳定。由于埋藏深,砂岩含水层分布不连续,含水层富水性弱,渗透性差。
对矿井充水因素分析认为,煤层开采的直接充水含水层为侏罗系延安组三段、直罗组一段和二段的复合含水层,其中直罗组含水层富水性较强,水压较高,这3层含水层都是采前预疏放的对象。
2.2 模型验证
母杜柴登矿井临时煤仓放水试验是以TF1放水孔,以TG2,TG3作为井下观测孔。3个钻孔均从3-1煤层顶板开口,各钻孔参数及布设位置见表1。
表1 母杜柴登矿井临时煤仓放水试验钻孔参数
Table 1 Drilling parameters of drainage test in temporary coal bunker in Muduchaideng Coal Mine
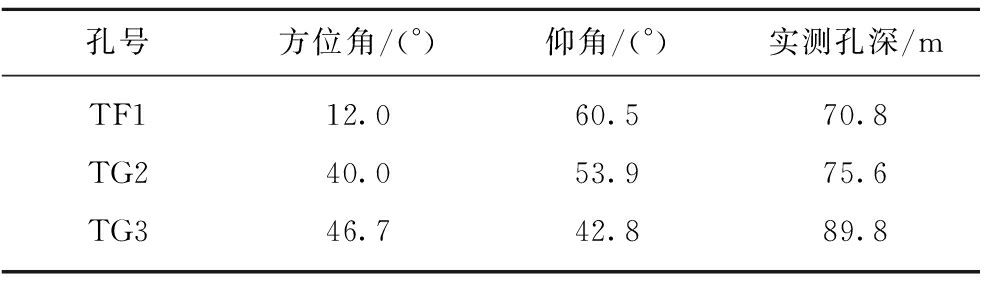
孔号方位角/(°)仰角/(°)实测孔深/mTF112.060.570.8TG240.053.975.6TG346.742.889.8
根据放水试验数据,其影响半径小于5 km,因此,本次建立10 km×10 km的理想模型;由于钻孔开口处为3-1煤层顶板,选择3-1煤层底板作为模型底板,模型垂向包括3-1煤层、3-1煤顶板延安组,2-2中煤层、2-2中煤顶板直罗组地层。由于本次目的主要为探讨倾斜钻孔的计算方法,因此建立的数值模型为均质各向异性含水层理想模型。模型边界概化为四周为变流量边界,模型中采用GHB边界处理,顶底板为隔水边界。
临时煤仓倾斜疏放水钻孔放水试验期间,地下水流服从三维达西流。采用下列数学模型[26-27]进行描述:

式中,n为第2类边界外法线方向;q(x,y,z,t)为四周侧向补给量;Hc为钻孔疏放水时定水头;Γ1为四周第2类流量边界;Γ2为底板边界;D为计算区范围。
本次模拟范围为10 km×10 km,模型坐标为x为0~10 km;y为0~10 km。首先采用100 m×100 m分别平行于x轴、y轴的正交网格对计算域进行平面剖分,对钻孔布设区域进一步精细剖分为2 m×2 m的网格,最终将模拟区剖分为492行×394列;为了精细刻画钻孔,垂向上采用水平切片方式将地层细分为22层:1~6层对应实际的直罗组底部中粗砂岩孔隙-裂隙承压含水层,7~21层对应实际的延安组砂岩孔隙-裂隙承压含水层,22层对应实际的3-1煤层。模拟时间为1 d,应力期划分与现场放水试验观测时间一致,共分为50个应力期,模拟的所有含水层初始水位为未扰动的含水层原始水位1 267.702 m。
以耦合数学模型为基础,利用MODFLOW软件进行数值计算,以放水试验过程中地下水水位和水量实测数据为依据,对数值模型进行识别验证,最终识别的水文地质参数见表2。主放水孔TF1,观测孔TG2和TG3在模型中计算结果与实测数据拟合结果如图2所示。由图2可以看出,地下水水位及水量数值计算值和实际观测值变化趋势基本一致,表明该数值模型合理可靠,所建立的地下水流数值模型可以用于倾斜钻孔的涌水量计算。
表2 模型各层水文地质参数
Table 2 Hydrogeological parameters of each layer
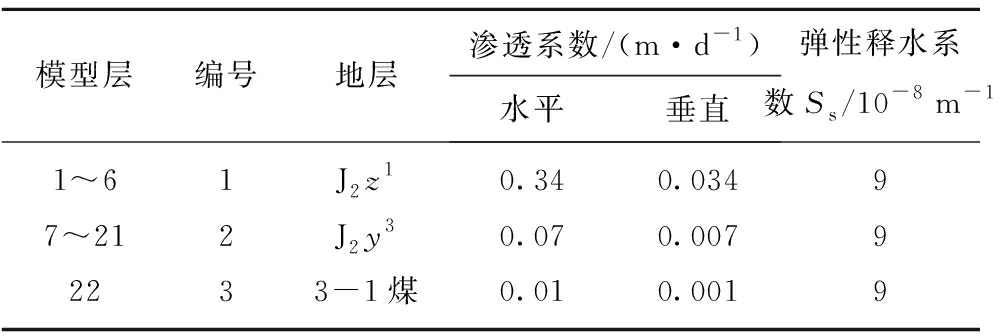
模型层编号地层渗透系数/(m·d-1)水平垂直弹性释水系数Ss/10-8 m-11~61J2z10.340.03497~212J2y30.070.00792233-1煤0.010.0019

图2 临时煤仓放水试验流量和降深模拟值与实测值拟 合曲线
Fig.2 Fitting curves of flow rate and drawdown of the simulated and measured value of temporary bunker dewatering test
3 钻孔参数优化
不同的疏放水钻孔参数(如单孔角度,单个钻场的钻孔数量)影响着总涌水量,进而决定疏放水持续时间和工程费用,为此需要开展母杜柴登矿井疏放水钻孔参数优化研究。
3.1 角 度
为了探讨仰角角度对钻孔涌水量的影响,设计一个垂向长度为120 m的钻孔,仰角分别为30°,45°,60°,75°,90°,分别计算不同仰角方案下的单孔涌水量以及单位长度涌水量(图3,4)。

图3 不同角度下钻孔单孔涌水量曲线
Fig.3 Water inflow curve of single borehole at different angles
由图3可知,钻孔仰角为30°时,单孔稳定涌水量约为222 m3/h;钻孔仰角为45°时,单孔稳定涌水量约为191 m3/h;钻孔仰角为60°时,单孔稳定涌水量约为165 m3/h;钻孔仰角为75°时,单孔稳定涌水量约为121 m3/h;钻孔仰角90°时涌水量与75°基本一致。根据母杜柴登矿井现场钻孔实际施工情况,45°钻场涌水量为160~180 m3/h,井底车场井下施工的一个仰角60°的生产用水钻孔,钻孔终孔涌水量为150~160 m3/h。由此可见,耦合模型计算的单孔涌水量和现场实际涌水量基本一致,计算精度有保证。
由图4可知,随着角度的不断增大,单孔涌水量不断减少。这是因为垂距一定时,随着角度的增大,钻孔斜长逐渐变小,有效长度减少,导致其涌水量变小。然而,随着角度增大,单位长度钻孔涌水量呈现先增加后减小的趋势。在仰角为60°时,钻孔单位涌水量达到最大。

图4 不同角度单位长度钻孔涌水量变化曲线
Fig.4 Variation curves of borehole water inflow per unit length at different angles
不同角度下的钻孔放水时的第1应力期的流场如图5所示。由图5可知,地下水流场为以钻孔为中心的降落漏斗,水流由含水层流向钻孔,钻孔内水流由钻孔最顶部向下流,符合现场实际情况。

图5 不同角度下钻孔放水时第1应力期流场
Fig.5 Flow field in the first stress period at different angles
综上所述,疏放水钻孔的最佳角度为60°,此时,钻孔单位长度涌水量最大,且主要涌水层位为直罗组一段含水层,约占总涌水量的81%(表3)。
表3 60°钻孔涌水量中各含水层水量占比
Table 3 Proportion of each aquifer in 60° borehole water inflow

角度/(°)不同含水层水量占比/%延安组三段直罗组一段直罗组二段总水量/(m3·h-1)603.8081.1015.10165
3.2 数 量
在钻孔单位长度涌水量达到最大的条件下,即垂向长度为120 m,仰角为60°时,设计6种不同钻孔数量组合方案,探讨钻孔数量对总涌水量及单位长度涌水量的影响(图6~8),6种不同钻孔组合方案如图6所示。设计钻场内施工6个钻孔,方位角以正北为起点,以60°递增均匀布置,其他方案则在此基础上抽稀即可。
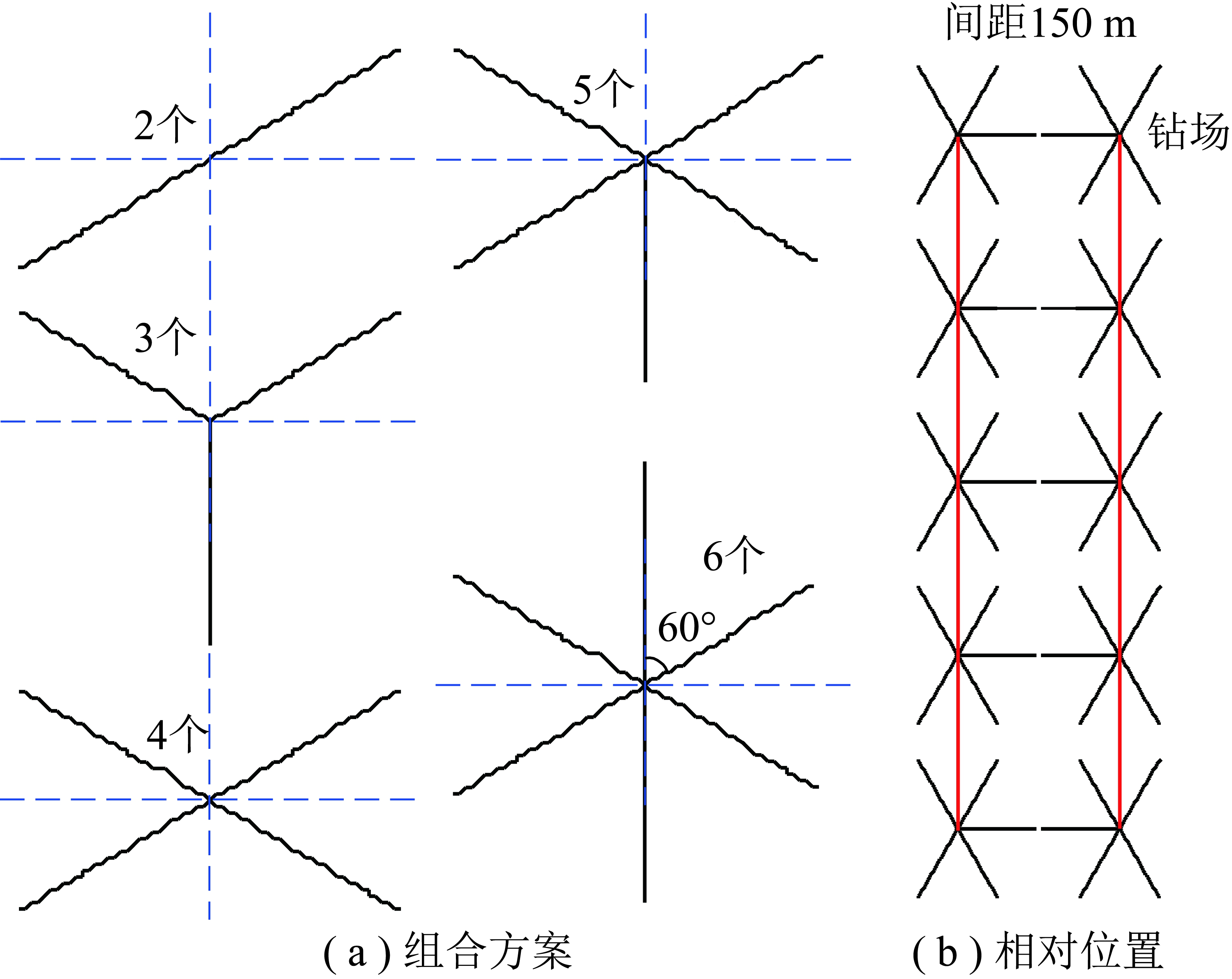
图6 组合方案示意及相对位置
Fig.6 Schematic diagram of combination scheme and relative position
由图7可知,钻孔数量为2个时,钻孔稳定总涌水量约为268 m3/h;钻孔数量为3个时,钻孔稳定总涌水量约为348 m3/h;钻孔数量为4个时,钻孔稳定总涌水量约为395 m3/h;钻孔数量为5个时,钻孔稳定总涌水量约为443 m3/h;钻孔数量为6个时,钻孔稳定总涌水量约为448 m3/h。钻孔数量增加到5个以后,钻孔总涌水量基本不再增加。
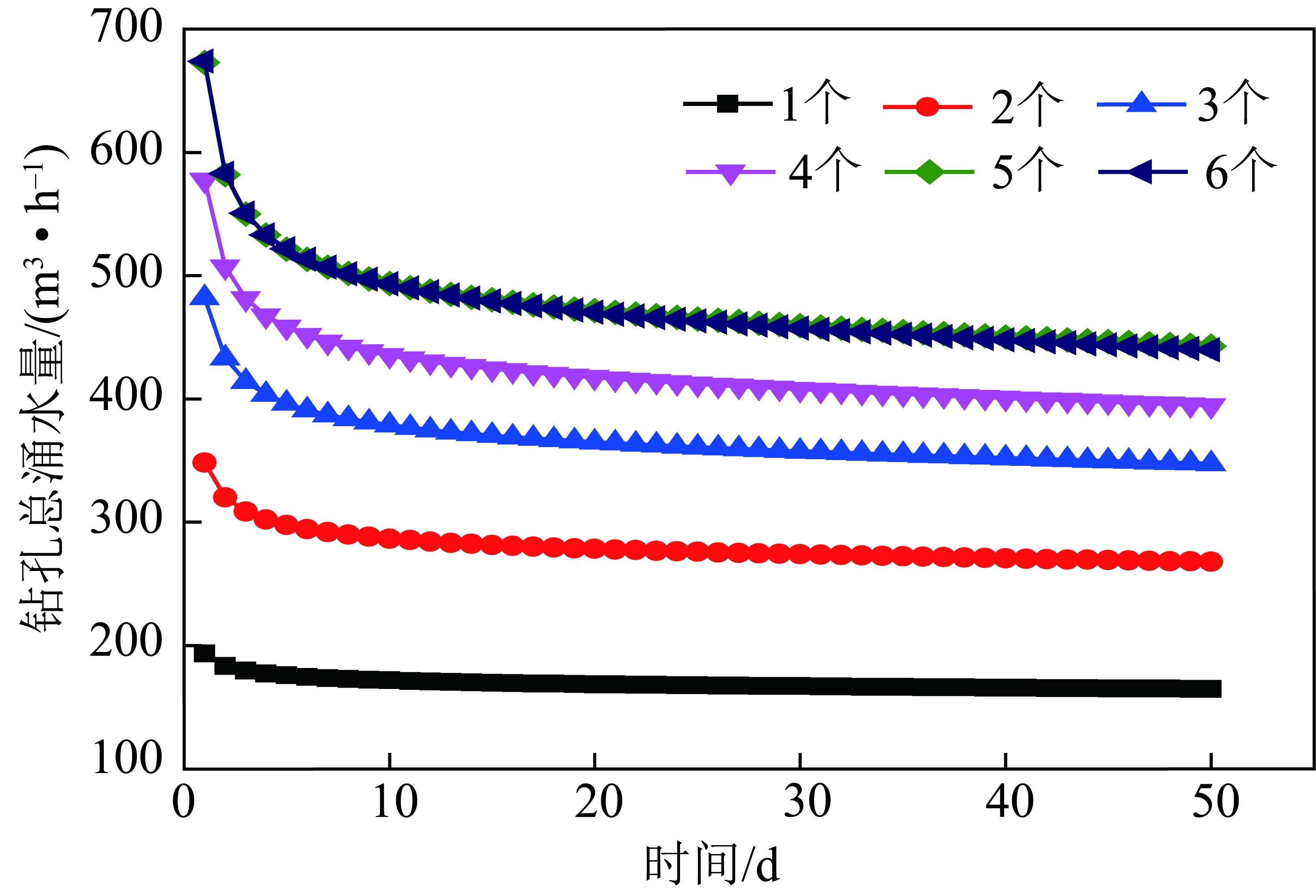
图7 不同方案下钻孔总涌水量历时曲线
Fig.7 Curves of total water inflow of boreholes under different schemes
由图8可知,随着钻孔数量增加,钻孔总涌水量不断增加,但是,单位长度的钻孔涌水量呈现逐步减小的趋势。由此可见,钻孔之间的干扰程度随着其数量的增加不断增大。

图8 不同方案下钻孔总涌水量对比
Fig.8 Comparison of total water inflow of boreholes under different schemes
综合以上考虑,单个钻场内部钻孔的数量宜为5个,超过5个后总涌水量增加不明显,增加的工程量为无效工程量。
4 600 m工作面疏放水效果
以钻孔仰角60°,垂向长度为120 m,单个钻场钻孔5个为组合,探讨150 m钻孔间距下600 m工作面范围内的疏放效果。此方案下钻场共布置10个钻场(5钻场×2巷),50个钻孔。假设3种定降深疏降模式,分别为780,830 m以及880 m。在工作面600 m范围内进行井下定水头疏放水,分别探讨其涌水量、降深以及流场分布情况。
4.1 钻场涌水量
根据模型计算结果,不同降深的钻孔总涌水量变化如图9所示。由图9可知,3种水头疏降方案下,钻孔总涌水量随时间逐步减小,最终趋于稳定。水头越小,钻孔的初始总涌水量越大,但随着时间的不断延续,最终3种水头下的钻孔总涌水量相差变小。
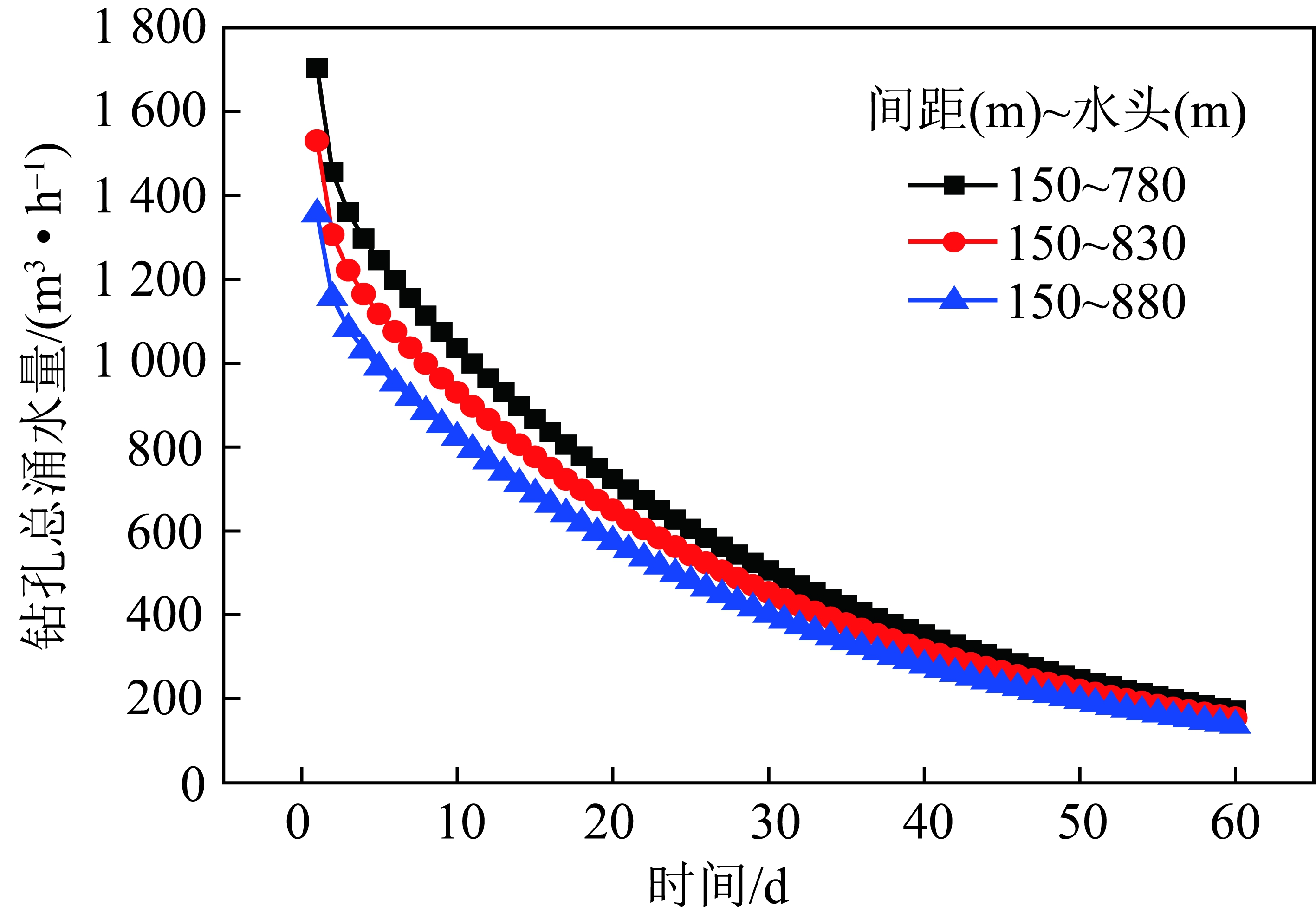
图9 不同降深的钻孔总涌水量历时曲线
Fig.9 Curves of total water inflow of boreholes with different drawdowns
60 d内,780 m定水头疏降时,钻孔总涌水量由第1天的1 700 m3/h降至170 m3/h,降幅达90%;830和880 m定水头疏降下,钻孔总涌水量由第1天的1 530,1 350 m3/h分别降至153,135 m3/h,降幅均为90%。
不同钻场内的钻孔总涌水量分布图如图10所示。由图10可知,600 m范围内工作面两端2个钻场(1,5和6,10)钻场总涌水量较大,内侧3个钻场总涌水量则相对较小,位于中间第3和第8钻场钻孔总涌水量最小。780 m定水头疏降时,两端钻孔总涌水量约为309 m3/h,中间钻场钻孔总涌水量约为142 m3/h。由此可见,钻场内钻孔总涌水量受周边钻场疏降的影响,由两端向内侧影响逐步增大。其他2个定降深疏降条件下,钻场总涌水量的变化趋势基本一致。
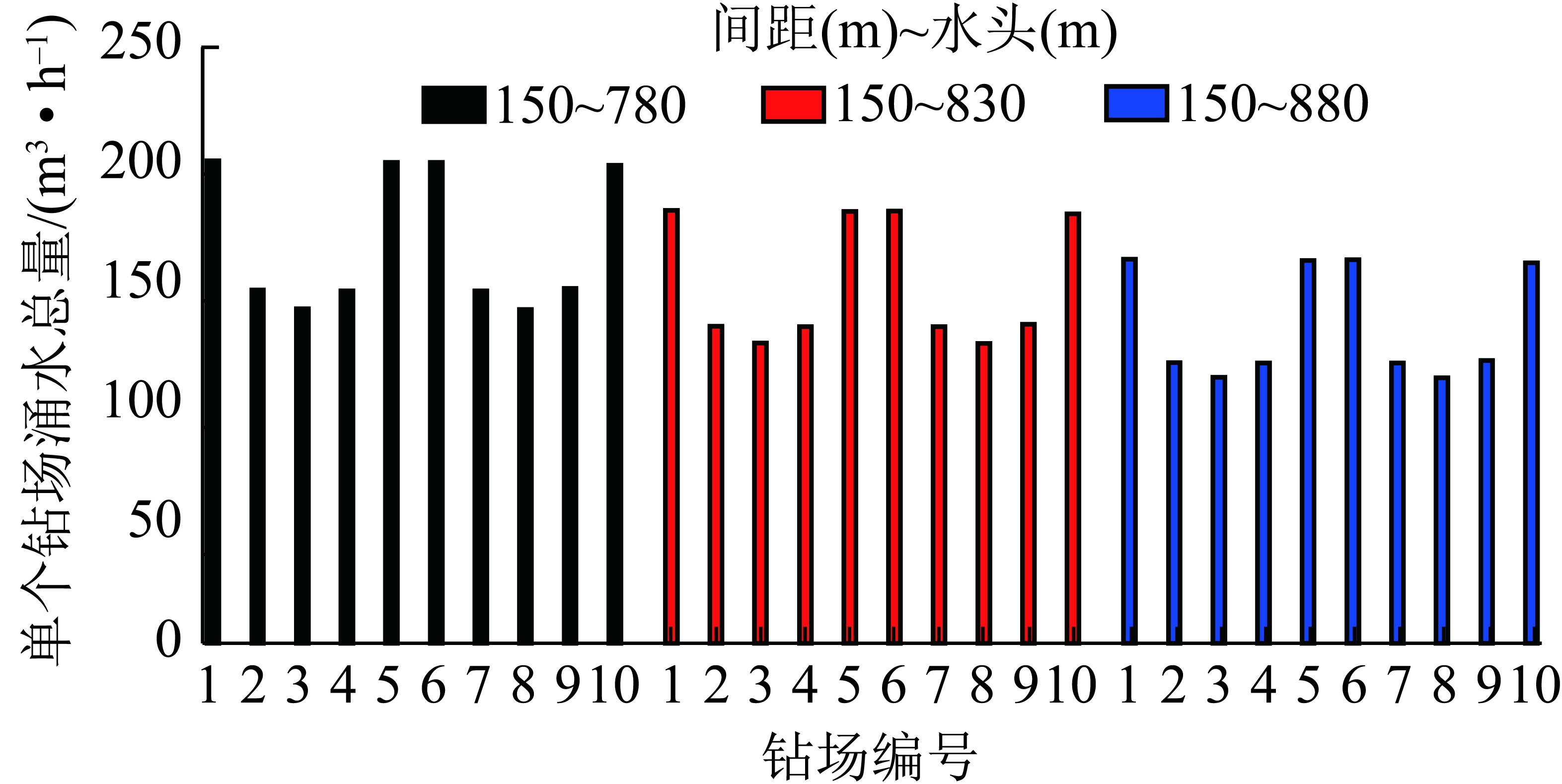
图10 第1天不同钻场内钻孔总涌水量
Fig.10 Total water inflow of different drilling field in the first day
4.2 降 深
不同定水头疏降方案下,工作面内部水头变化情况如图11所示。由图11可知,随着疏放时间的延续,不同方案下,工作面内部水头变化趋势均为由初始水头1 267.702 m降至不同的定水头(780,830和880 m),定水头越小,疏降的时间则相对越长。150 m钻场间距方案下,疏降至780,830和880 m的时间分别为155,125和100 d。

图11 不同降深下工作面内部水头变化历时曲线
Fig.11 Duration curves of water head change in working face under different drawdown
不同时间不同降深的范围有所不同如图12所示。由图12可知,随着时间延续,不同降深范围逐步增大(横向)。以200 m的降深为例,10 d之前,降深均小于200 m,10 d之后,随着时间延续,降深大于200 m的范围逐渐增大。同一时间内,小降深的范围大于大降深的范围(纵向)。
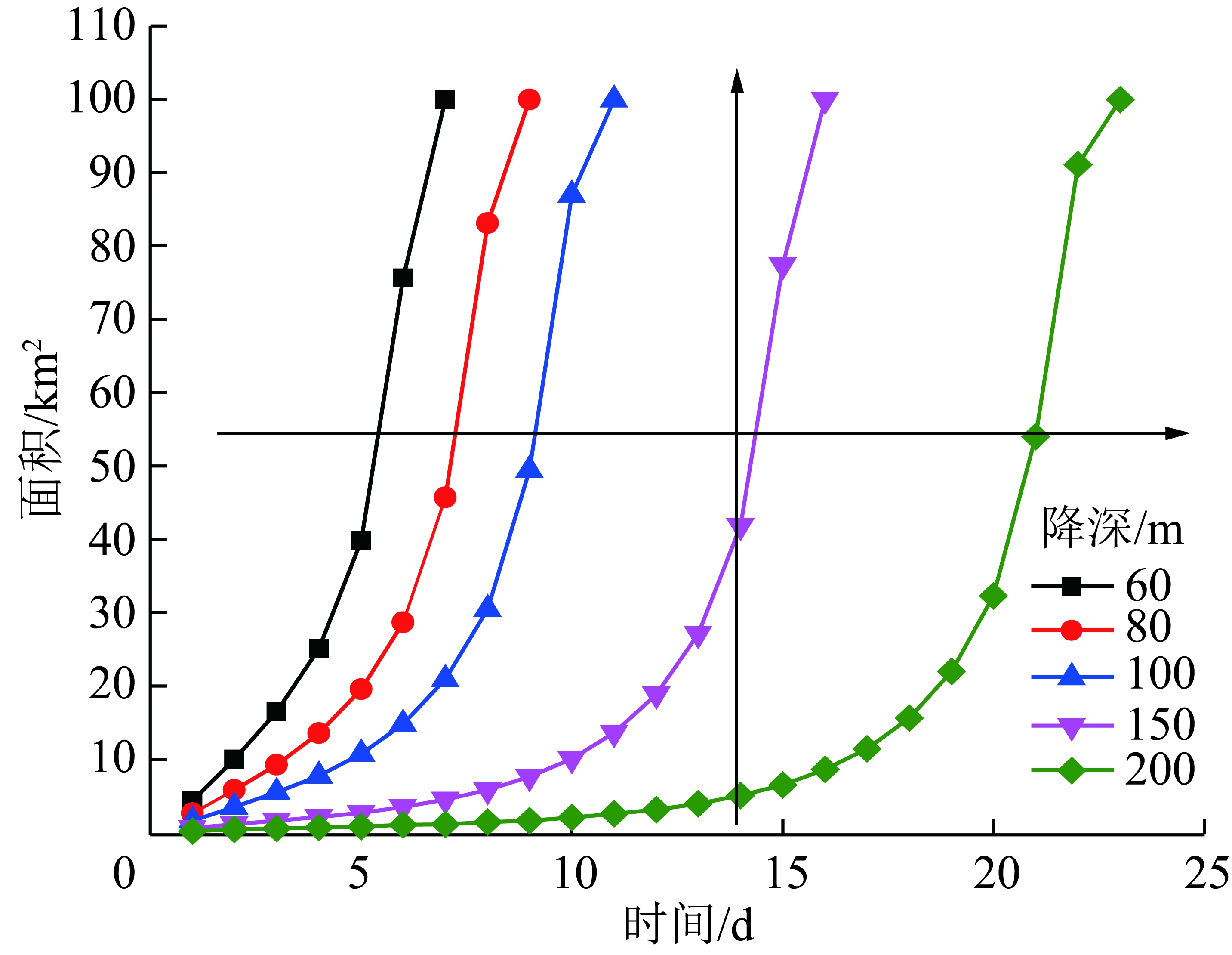
图12 定水头880 m方案下不同时间的降深范围曲线
Fig.12 Curves of drawdown range at different time under 880 m constant head scheme
4.3 流 场
随着疏放水工程推进,煤层顶板含水层的流场不断发生变化。剖面和平面流场图如图13,14所示。由图13,14可知,随着疏放时间延续,横剖面呈现以倾斜钻孔为中心的降落漏斗且范围逐步增大,平面上则呈现以全部钻场范围为中心的降落漏斗且范围逐渐增大。

图13 定水头880 m方案下横剖面流场(中心)
Fig.13 Flow field of cross section under 880 m constant head scheme (central location)

图14 定水头880 m方案下侏罗系含水层平面流场
Fig.14 Plane flow field of Jurassic aquifer under 880 m constant head scheme
5 结 论
(1)针对复合充水含水层倾斜疏放水钻孔涌水量计算方法不完善的问题,以能量守恒定律为基础,以“含水层-钻孔水量交换”为耦合点,建立了含水层-钻孔系统多流态水流计算的耦合模型。
(2)应用母杜柴登矿井临时煤仓井下放水试验的1个主放水孔水量和2个观测孔水位历时数据,验证了含水层-钻孔系统耦合模型的可靠性,可以很好解决倾斜钻孔在复合充水含水层中的水量分配问题。
(3)倾斜疏放水钻孔涌水量受到其角度和数量等参数的影响。随着角度增大,单位长度钻孔涌水量呈现先增加后减小的趋势,在仰角为60°时,钻孔单位涌水量最大。此外,随着单个钻场内钻孔数量的增多,钻孔总涌水量不断增加,钻孔数量超过5个后总涌水量增加并不明显。即钻孔的最优角度为60°,单个钻场内钻孔最佳数量为5个。
(4)150 m间距方案下600 m工作面范围内,不同疏降水头钻孔总涌水量、工作面内部降深、流场变化均不同。降深越大,钻孔的初始总涌水量越大,随着时间推移,最终钻孔总涌水量相差变小,直至稳定。钻场内钻孔总涌水量受到周边钻场疏降的影响,由两端向内侧影响逐步增大。同时,疏降定水头越小,疏降时间则相对延长。
[1] 董书宁,姬亚东,王皓,等.鄂尔多斯盆地侏罗纪煤田典型顶板水害防控技术与应用[J].煤炭学报,2020,45(7):2367-2375.
DONG Shuning,JI Yadong,WANG Hao,et al.Prevention and control technology and application of roof water disaster in Jurassic coal field of Ordos Basin[J].Journal of China Coal Society,2020,45(7):2367-2375.
[2] 靳德武,周振方,赵春虎,等.西部浅埋煤层开采顶板含水层水量损失动力学过程特征[J].煤炭学报,2019,44(3):690-700.
JIN Dewu,ZHOU Zhenfang,ZHAO Chunhu,et al.Dynamics process analysis of groundwater quantity loss of roof aquifer with shallow seam mining in Western China[J].Journal of China Coal Society,2019,44(3):690-700.
[3] 范立民.保水采煤面临的科学问题[J].煤炭学报,2019,44(3):667-674.
FAN Limin.Some scientific issues in water-preserved coal mining[J].Journal of China Coal Society,2019,44(3):667-674.
[4] 马莲净,赵宝峰.基于对数正态分布的井下疏放水钻孔水量分析[J].煤田地质与勘探,2019,47(3):140-146.
MA Lianjing,ZHAO Baofeng.Water yield analysis of underground drainage boreholes on the basis of logarithmic normal distribution[J].Coal Geology & Exploration,2019,47(3):140-146.
[5] 武强.我国矿井水防控与资源化利用的研究进展、问题和展望[J].煤炭学报,2014,39(5):795-805.
WU Qiang.Progress,problems and prospects of prevention and control technology of mine water and reutilization in China[J].Journal of China Coal Society,2014,39(5):795-805.
[6] 陈实,董书宁,李竞生,等.煤矿工作面顶板倾斜钻孔疏放水井流计算方法[J].煤炭学报,2016,41(6):1517-1523.
CHEN Shi,DONG Shuning,LI Jingsheng,et al.Analytical solution for slanted well in the roof of coal mine working face[J].Journal of China Coal Society,2016,41(6):1517-1523.
[7] ZHAN H,CAO J.Analytical and semi-analytical solutions of horizontal well capture times under no-flow and constant-head boundaries[J].Advances in Water Resources,2000,23(8):835-848.
[8] SAMANI N,KOMPANIZARE M,SEYYEDIAN H,et al.Flow to horizontal and slanted drains in anisotropic unconfined aquifers[J].Developments in Water Science,2004,55(1):427-440.
[9] 黄欢.锦界煤矿顶板水疏放技术优化研究[D].北京:煤炭科学研究总院,2017.
HUANG Huan.Optimization research on dewatering technology of roof water in Jinjie Mine[D].Beijing:China Coal Research Institute,2017.
[10] 陈崇希.岩溶管道-裂隙-空隙三重空隙介质地下水流模型及模拟方法研究[J].地球科学,1995,20(4):361-366.
CHEN Chongxi.Groundwater flow model and simulation method in triple media of karstic tube-fissure-pore[J].Earth Science-Journal of China University of Geosciences,1995,20(4):361-366.
[11] ZHAN H,WANG L V.On the horizontal-well pumping tests in anisotropic confined aquifer[J].Journal of Hydrology,2001,252(1):37-50.
[12] 焦赳赳,王旭升,成建梅,等.陈崇希教授的学术思想和成就综述[J].地球科学,2003(5):471-482.
JIAO Jiujiu,WANG Xusheng,CHENG Jianmei,et al.Academic thoughts and achievements of professor Chen Chongxi[J].Earth Science-Journal of China University of Geosciences,2003(5):471-482.
[13] 陈崇希,胡立堂.渗流-管流耦合模型及其应用综述[J].水文地质工程地质,2008(3):70-74.
CHEN Chongxi,HU Litang.A review of the seepage-pipe coupling model and its application[J].Hydrogeology & Engineering Geology,2008(3):70-74.
[14] 成建梅,陈崇希.广西北山岩溶管道-裂隙-孔隙地下水流数值模拟初探[J].水文地质工程地质,1994(4):50-54.
CHENG Jianmei,CHEN Chongxi,Preliminary study on numerical simulation of karst pipeline-fissure-pore groundwater flow in Beishan of Guangxi[J].Hydrogeology & Engineering Geology,1994(4):50-54.
[15] 陈崇希,万军伟.地下水水平井流的模型及数值模拟方法——考虑井管内不同流态[J].地球科学,2002,27(2):135-140.
CHEN Chongxi,WAN Junwei.A new model of groundwater flowing to horizontal well and the numerical simulation approach[J].Earth Science-Journal of China University of Geosciences,2002,27(2):135-140.
[16] WANG W,ZHANG G.Erratum:Numerical simulation of groundwater flowing to horizontal seepage wells under a river[J].Hydrogeology Journal,2008,16(1):199-199.
[17] 陈枭萌,杨海瑞,王玮,等.盘塘水源地渗流井取水方式下地下水允许开采量计算[J].水土保持通报,2014,34(3):190-194.
CHEN Xiaomeng,YANG Hairui,WANG Wei,et al.Calculation of allowable groundwater yield from seepage wells in Pantang Water Source Region[J].Bulletin of Soil and Water Conservation,2014,34(3):190-194.
[18] 陈鹏,王玮.辐射井取水方式数值模拟方法[J].人民黄河,2013,35(4):48-50.
CHEN Peng,WANG Wei.Numerical simulation approach of radial collector well[J].Yellow River,2013,35(4):48-50.
[19] WANG W,CHEN P,ZHENG Q,et al.A modified calculation model for groundwater flowing to horizontal seepage wells[J].Journal of Earth System Science,2013,122(2):407-418.
[20] VENNARD J K,STREET R L.Elementary fluid mechanics(5th ed.)[M].NEW York,John Wiley,1975:740.
[21] 吴持恭.水力学[M].北京:高等教育出版社,2007.
[22] SHOEMAKER W B,KUNIANSKY E L,BIRK S,et al.Documentation of a conduit flow process(CFP) for Modflow-2005:U.S.Geological Survey Techniques and Methods,Book 6[M].U.S.,2007.
[23] REIMANN T,HILL M E.Modflow-CFP:A new conduit flow process for Modflow-2005[J].Ground Water,2009,47(3):321-325.
[24] 赵良杰,夏日元,杨杨,等.基于CFP的岩溶管道流数值模拟研究——以桂林寨底地下河子系统为例[J].地球学报,2018,39(2):225-232.
ZHAO Liangjie,XIA Riyuan,YANG Yang,et al.Research on numerical simulation of karst conduit media based on CFP:A case study of Zhaidi Karst Underground River Subsystem of Guilin[J].Acta Geoscientica Sinica,2018,39(2):225-232.
[25] 畅俊斌,柯贤敏,王玮,等.渗流井辐射管-含水层间水量交换数值模拟研究[J].水文地质工程地质,2018,45(5):7-14.
CHANG Junbin,KE Xianmin,WANG Wei,et al.Numerical simulation of the water exchange between radiant tube and aquifer in a seepage well[J].Hydrogeology & Engineering Geology,2018,45(5):7-14.
[26] 赵春虎,靳德武,虎维岳.采煤对松散含水层地下水扰动影响规律及评价指标[J].煤田地质与勘探,2018,46(3):79-84.
ZHAO Chunhu,JIN Dewu,HU Weiyue.Study on influence rules and evaluation criteria of groundwater affected by mining in unconsolidated aquifers in Shendong Bulianta coal mine[J].Coal Geology & Exploration,2018,46(3):79-84.
[27] 刘基,靳德武,姬亚东,等.复杂水文地质条件下大型帷幕截流工程效果数值仿真分析[J].煤炭学报,2019,44(8):2427-2436.
LIU Ji,JIN Dewu,JI Yadong,et al.Numerical simulation analysis of closure effect of large curtain work with complex hydrogeological conditions[J].Journal of China Coal Society,2019,44(8):2427-2436.
