复杂地质条件巷道的掘进速度制约了煤矿的生产效率,尤其是硬岩掘进,因此,探寻一种高效掘进破碎煤岩方法是国内外学者不断探索的重要课题。国内外学者通过分析刀具破岩过程,相继提出了多种力学模型以揭示刀具破岩机理。NISHIMATSU[1]假定截割过程煤岩断裂面遵守莫尔-库伦准则,构建了煤岩切削力模型。EVANS等[2]根据最大拉应力破坏准则,建立了镐型截齿破碎煤岩的力学模型。牛东民[3]基于断裂力学给出了刀具切入煤岩直至煤岩崩落整个过程中平均切削力的计算方法。王鑫等[4]构建了煤岩在弹性变形、塑性变形和断裂失稳状态下截齿截割力以及煤岩应力表达式,实验验证了理论模型的准确性。刀具截割参数对其破岩性能有显著的影响,梁运培等[5-6]通过砂岩直线截割试验,研究了截割厚度和截线距对截齿破岩力、载荷波动性系数和截割比能耗的影响趋势,证实Evans的理论模型预测性相对较好。SU[7]模拟和理论研究了截齿前角和切削深度对切削力的影响规律。YASAR[8]给出了不同材料岩石的试验结果,探究了岩石强度、前倾角和切削深度对截齿切削力的影响趋势。刘春生等[9]针对煤岩层地质条件复杂致使采煤机无效调高等问题,提出了采煤机自主调高-调速二元协同控制模式及截割状态关联特征模型。虽然镐型和刀型截齿破岩机理及其性能被诸多学者研究且取得了一些有价值的结论,但是其仍然存在着某些技术难点与不足,尤其是截割破碎硬岩时截齿快速失效、振动剧烈等问题,导致现有刀具难以适应复杂地质条件下高效破岩的要求。
为了提高掘进复杂地质煤岩效率,降低能耗,国内外学者进行了盘型刀具研究。KOTWICA等[10-12]设计了具有复杂轨迹的微型圆盘刀具的新型截割头,适用于截割硬岩,通过现场实验分析了非对称圆盘刀具结构、材料参数和截割头运动参数对截割头载荷、振动和刀具磨损的影响。KHORESHOK等[13-14]针对采煤机和掘进机截割含固体岩石包裹体煤层的问题,提出了高效圆盘刀具截割破岩方法,其具有耐磨与产尘少等优点。DEHKHODA等[15-19]基于运动学和几何学,建立驱动圆盘截割(ADC)岩石的数学模型,实验验证了模型假设条件与预测结果的有效性。刘春生等[20-24]构建了碟盘刀具切削煤岩的力学机制及理论模型,控制单一变量(运动和结构参数)条件下,通过数值模拟与实验给出了碟盘刀具的载荷变化规律及评价了其截割性能。盘形刀具在美国、澳大利亚和波兰等国家和地区都是研究的热点,其有利于复杂地质条件巷道开采和硬岩机械截割技术发展,但是国内开展相关研究学者较少,尤其是在新型刀具研制和复合破岩方法方面,尚需进一步研究。
笔者在已有研究基础上,针对上述刀具破碎煤岩时存在磨损快、寿命短及截割含包裹体、硬岩等复杂地质效率低等问题,以及圆盘刀具适用于截割硬岩的特征,提出一种具有截-楔效应的碟盘刀具复合振动截割煤岩的方法。从刀具振动方向和姿态角度考虑,给出碟盘刀具轴向振动与径向进给截割的复合破岩方式,获得刀刃与煤岩破碎煤岩的载荷特性。所提出的破岩方法与以前的研究工作相比具有重要的创新意义:建立了刀刃轴向向下、向上振动和径向截割煤岩的作用载荷模型;构建了碟盘刀刃径向进给与轴向振动复合截割煤岩的载荷模型;揭示了截割厚度对刀具载荷的影响规律;笔者所建立模型均属于从基础理论研究方面构建的数学模型,可为工程实际应用问题提供理论参考。
1 碟盘截割状态与刀刃作用模式
1.1 碟盘刀具复合截割状态
悬臂式掘进机因其工作灵活,便于转弯、爬坡,复杂地质条件适应性强,断面形状任意等优势,广泛应用于煤矿巷道掘进。其工作结构多采用截齿(刀型、镐型)有序排列构成的截割头,但对于掘进复杂地质条件巷道,尤其针对硬岩截割时,截齿寿命显著降低,机器振动严重,大大降低了掘进机工作效能及可靠性。
碟盘刀具复合振动截割煤岩,可实现沿煤岩强度薄弱方向剪切或拉伸破岩,因此,与煤岩相互作用时,碟盘刀刃的载荷特性可反映:刀刃挤压损伤煤岩,致使裂纹形成和扩展;刀刃楔入煤岩,形成一定切削厚度,使楔面对煤岩产生剪切或拉伸作用;碟盘刀具不同振动复合截割,决定能量施加(作用)的作用点和方向,可形成不同的截割破碎效果。
碟盘刀具不同振动方向和不同姿态组合的复合截割状态,如图1所示。

图1 碟盘刀具振动复合截割姿态
Fig.1 Postures of vibration combined cutting of disc cutter
碟盘刀具径向x进给截割以及旋转ω和径向x进给截割为基础截割运动;不同振动方向包括轴向z振动、径向x振动、周向ω振动和摆动ω振动;不同姿态是指沿x方向和y方向成一定角度倾斜。碟盘刀具在基本截割基础上组合不同振动和姿态,以复合截割状态破碎煤岩,可实现低能高效破岩。碟盘刀刃的载荷特征是不同姿态和不同振动复合截割破碎性能的研究基础,在刀具水平于x和y方向的姿态下,本文以刀刃轴向振动复合径向截割煤岩为例,进行理论、数值模拟和实验研究,构建其载荷特征模型。
碟盘刀具径向进给与轴向振动复合截割煤岩,刀具与煤岩作用关系如图2所示。由图1轴向z振动部分所示,碟盘刀具轴向振动复合截割由x轴和z轴2个方向运动组成:沿x轴方向施加一个恒定不变的进给速度vj;沿z轴方向施加一个正弦函数的轴向位移,并且2个方向运动同时进行。当刀刃向z轴负方向振动时,作用煤岩载荷为T1,向z轴正方向振动时,作用煤岩载荷为T2,向x轴正方向径向进给时,作用煤岩载荷为T3。图2中,vz为轴向振动速度,mm/s;vj为径向进给速度,mm/s;α为楔面角度,(°);ψ为煤岩的崩落角,(°);T1、T2和T3分别为碟盘刀刃向下、向上和径向截割煤岩的作用载荷,N;hm为截割厚度,mm;h1为碟盘刀具接触煤岩高度,mm;R为碟盘刀具半径,R=125 mm;lm为煤岩崩裂长度,mm。

图2 刀具与煤岩作用关系
Fig.2 Relationship between cutter and coalrock petrogenesis
由图2可见,碟盘刀具由刀刃和楔面2部分组成,首先刀刃接触煤岩,进行挤压损伤,随着刀刃逐渐进入,楔面逐渐剪切或拉伸煤岩,直至形成大块崩落。文中以刀刃为研究对象,分析刀刃轴向振动截割煤岩的载荷模型及其特性。
碟盘刀具轴向振动复合截割煤岩的轨迹如图3所示。当轴向向下振动时,对煤岩的损伤范围呈月牙状变化,其碟盘刀刃压溃煤岩损伤区域为Ⅰ、Ⅱ和Ⅲ、Ⅱ区域的损伤范围大于Ⅰ区域,说明刀刃对煤岩向下振动作用显著,碟盘刀具经过的区域Ⅲ为重复截割损伤。碟盘刀具径向进给相同距离时,煤岩被压溃的区域由Ⅱ向两侧Ⅰ逐渐递减。

图3 轴向振动复合截割煤岩轨迹
Fig.3 Trajectory of axial vibration combined cutting coalrock
1.2 碟盘刀刃作用模式
煤岩在刀刃的挤压作用下会产生一个密实核,直至刀刃作用煤岩载荷增至临界值时,密实核爆破形成漏斗状破碎坑,其顶角θ的变化范围为60°~75°,煤岩硬度越高,θ越大。奥斯特洛乌什柯[25]认为球形压头破碎煤岩时,形成密实核阶段的主压力剪切体呈锥体状,θ与密实核锥体顶角γ呈2倍关系,即θ=2γ。按照剪切强度破碎煤岩,形成主压力体所需载荷T可依据Tcos γ=τtS+μ1Tsin γ求得,如图4所示,其中,τt为煤岩抗剪强度,MPa;S为主压力剪切体的表面积,mm2;γ为密实核锥体顶角,(°);μ1为煤岩内摩擦因数;dS1为刀刃轴向向下作用煤岩剪切体面积微元。

图4 主压力体与煤岩作用
Fig.4 Main pressure body and coal rock interaction
刀刃与煤岩作用载荷关系,如图5所示,数值模拟和理论模型中刀刃挤压煤岩损伤区域相吻合。煤岩破碎坑沿刀具周向呈锥形槽分布,根据密实核剪切体建立力学模型,由于刀具破碎煤岩时,其边缘圆周受力状态是变化的,故沿刀具圆周方向取微元分析刀刃破碎煤岩的力学特性[22]。图5中,ri为密实核等效锥体半径,mm,i=1、2和3,分别表示刀刃轴向向下、向上和径向截割;βi为刀刃作用煤岩载荷与水平方向的夹角,(°)。

图5 刀刃与煤岩作用关系
Fig.5 Relationship between blade and coalrock interaction
基于文献[20]碟盘刀具刀刃的受力分析,由图4可得,单位宽度刀刃作用载荷为
(1)
(2)
式中,dTi为破坏坑外载微元,i=1、2和3,分别表示刀刃轴向向下、向上和径向截割;dSi为剪切体面积微元。
2 碟盘刀刃运动分解作用载荷
根据刀具的结构特点,刀刃对煤岩的损伤作用有利于楔面形成大块崩落,因此,文中研究刀刃振动截割煤岩的力学特性,分别构建其轴向向下、向上振动,以及径向截割煤岩时的力学模型。
2.1 向下振动
碟盘刀刃向下振动时,对煤岩的作用载荷随着φ的变化呈逐渐递减趋势,刀刃集中载荷与作用位置,如图6所示。

图6 刀刃集中载荷与作用位置
Fig.6 Concentrated load and action position of blade
碟盘刀刃轴向向下振动时,刀刃挤压损伤下方煤岩,但不会造成煤岩大块破坏,刀刃轴向向下振动的同时伴随着径向运动,故对煤岩存在重复性损伤,并随振动频率增大,重复损伤频率增加,煤岩损伤能量累积。考虑刀刃振动频率对煤岩损伤的影响,以轴向速度与平均径向速度的比值近似反映轴向向下振动对煤岩的损伤情况。

(3)
式中,A为碟盘轴向振动幅值,mm;f为轴向振动频率,Hz。
由图5(a)可知,轴向向下振动时的等效锥体半径为
(4)
由图6所示,对刀刃作用载荷进行矢量分解:
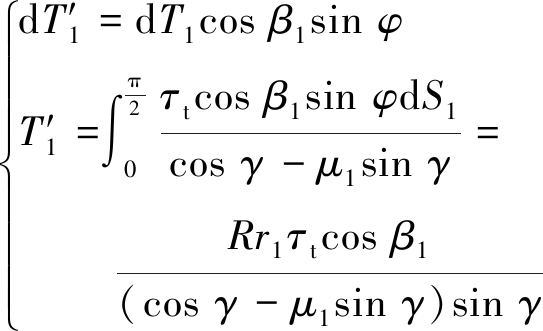
(5)
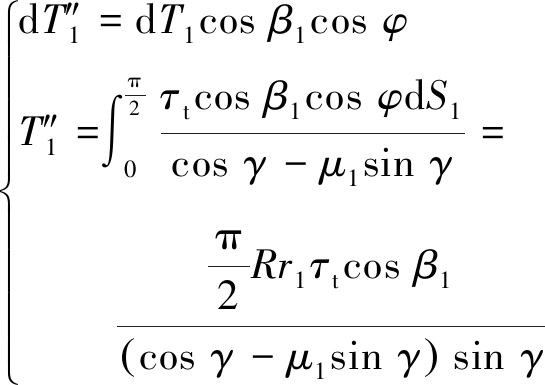
(6)
由式(5)、(6)可得,T1的集中力位置角度和等效集中载荷为
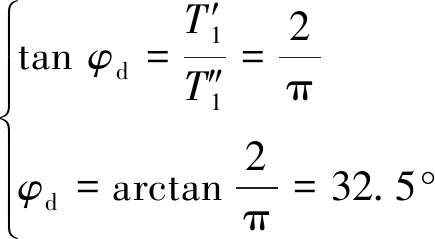
(7)
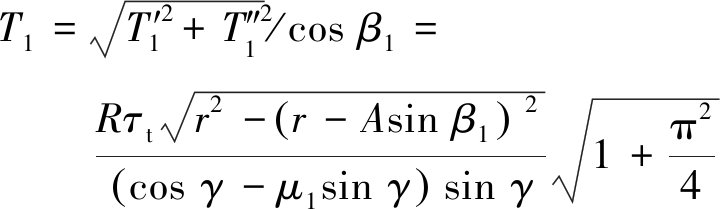
(8)
2.2 向上振动
刀刃轴向向上振动损伤楔面上方煤岩,其截割厚度较小,上方煤岩易形成大块崩落,损伤能量发散,煤岩重复性损伤较少。由式(2)可求得面积微元dS2,锥体等效半径r2为
r2=rsin β2
(9)
同理,对刀刃的作用载荷进行矢量分解,由式(1)、(2)和(9)可以得出
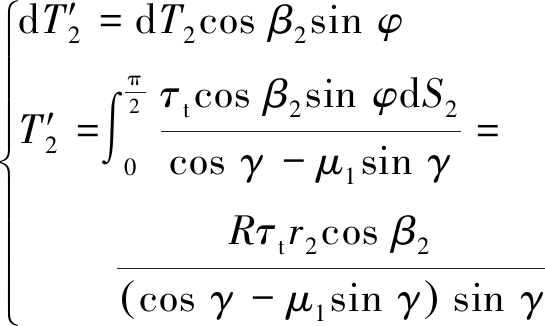
(10)

(11)
由式(10)、(11)可得,碟盘刀刃轴向向上振动时集中载荷作用位置角为
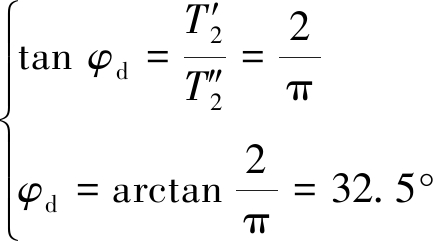
(12)
在φ=0°~90°内,其等效集中载荷为
![]()
![]()
(13)
2.3 径向截割
根据式(1)、(2)和图5(c)刀刃径向截割作用关系,基于上述的等效原理,获得刀刃作用载荷及其作用位置。碟盘刀刃径向截割煤岩时,刀刃向前推进致使煤岩崩落,不会作用于同一位置煤岩,便不存在重复性损伤,但轴向振动会造成煤岩损伤,故在径向截割剪切体面积计算中考虑了轴向振动对煤岩损伤的影响。由图5(c)可知,其面积微元dS3中锥体半径r3为
r3=rcos γsin βi
(14)
式中,i为1和2,分别表示轴向向下和向上。
同理,对刀刃的作用载荷进行矢量分解,由式(1)、(2)和(14)可得
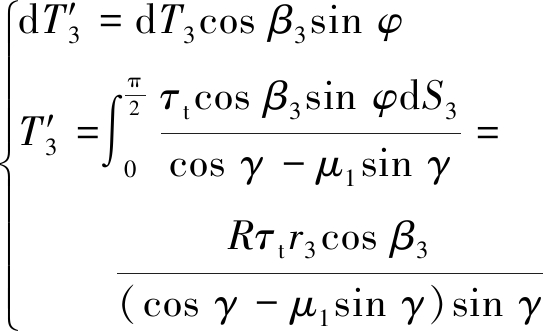
(15)

(16)
由式(15)、(16)可得径向截割时刀刃载荷作用点为
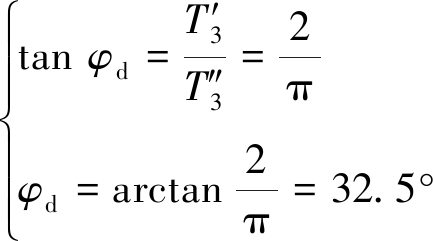
(17)
由此可知,T3与T2和T1的作用点相同。
在φ=0°~90°内,碟盘刀刃径向截割煤岩的等效集中载荷为
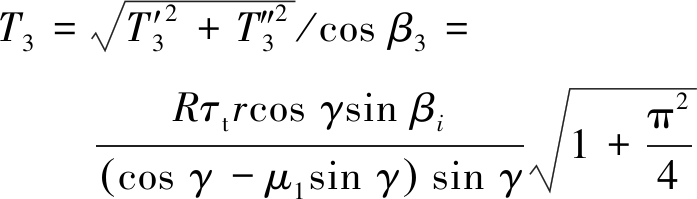
(18)
3 复合截割下刀刃作用载荷模型
基于位移应变等效力合成的方法,先将碟盘刀具径向进给复合轴向振动截割煤岩,分解成轴向向上、向下振动和单径向截割作用,分别建立碟盘刀刃作用载荷模型,再通过各个分解作用载荷的内部关系,构建刀刃特定工况点的载荷模型。
3.1 轴向向上振动
结合图6、7,将刀刃径向截割和轴向向上振动时作用载荷T3和T2进行正交分解,同时考虑摩擦作用,再进行矢量叠加可得整个碟盘刀刃径向截割复合轴向向上振动破碎煤岩的径向载荷Fjs和轴向载荷Fzs。图7中,Fjs和Fzs分别为碟盘刀刃轴向向上振动时的径向载荷和轴向载荷,N;Fjx和Fzx分别为碟盘刀刃轴向向下振动时的径向载荷和轴向载荷,N。

图7 刀刃作用载荷正交分解
Fig.7 Orthogonal decomposition of blade load
碟盘刀具轴向向上振动和径向截割破碎煤岩时,碟盘刀刃的径向载荷为
Fjs=2(T2cos β2cos φd+T3cos β3cos φd+f1Fzs)
(19)
其轴向载荷为
Fzs=2(T2sin β2-T3sin β3+f1Fjs)
(20)
式中,f1为刀刃与煤岩之间摩擦因数。
联立式(19)、(20)求得
T3(cos β3cos φd-2f1sin β3)]
(21)
T3(2f1cos β3cos φd-sin β3)]
(22)
3.2 轴向向下振动
同理,通过分析碟盘刀刃径向截割复合轴向向上振动破碎煤岩载荷,构建刀刃径向截割复合轴向向下振动破碎煤岩的径向载荷Fjs和轴向载荷Fzs模型。
刀刃轴向向下振动时的径向载荷为
Fjx=2(T1cos β1cos φd+T3cos β3cos φd+f1Fzx)
(23)
其轴向载荷为
Fzx=2(T1sin β1+T3sin β3+f1Fjx)
(24)
联立式(23)、(24)求得
T3(cos β3cos φd+2f1sin β3)]
(25)
T3(sin β3+2f1cos β3cos φd)]
(26)
由式(21)、(22)、(25)和(26)整理可得,碟盘刀刃径向截割复合轴向振动截割煤岩的载荷模型为

(27)
4 振动截割煤岩数值模拟与实验
从理论层面建立了碟盘刀刃轴向振动复合截割煤岩的力学模型,给出了其破坏准则及计算方法,再结合刀刃截割煤岩的模拟和实验,进一步研究刀刃的载荷特性。根据碟盘刀刃的几何尺寸、运动状态以及数值模拟应力分布情况,确定刀刃作用载荷角(β1、β2和β3)的范围。碟盘刀具与煤岩的参数见表1。其中,σy和σl分别为煤岩抗压强度和抗拉强度,MPa。
表1 碟盘刀具与煤岩参数
Table 1 Disc cutter and coal rock parameters

R/mmr/mmf/HzA/mmσy/MPaτt /MPaσl/MPa125335~55219.21.7~3.91.3~1.9α/(°)γ/(°)μ1f1β1/(°)β2/(°)β3/(°)50300.580.15~0.3060~8535~5520~45
4.1 数值模拟结果分析
利用ABAQUS软件建立碟盘刀具轴向振动复合截割煤岩数值模型,碟盘刀具为刚体材料,煤岩体尺寸为420 mm×280 mm×120 mm,选用Drucker-Prager塑性本构模型,网格划分均采用六面体C3D8R。碟盘径向进给速度vj=300 mm/s,轴向振动位移满足正弦函数[26],为保证刀具复合运动,沿x轴和y轴方向平移自由,z轴方向平移以及所有旋转均进行了约束,煤岩与刀具接触面与上表面没有约束,其余表面进行完全固定约束。
文中主要研究碟盘刀刃的载荷特性,设置截割厚度为7 mm,整个刀刃与煤岩作用,楔面不参与作用。碟盘刀刃无振动截割煤岩的应力云图,如图8所示,当振动频率为45 Hz时,其无振动和有振动的模拟径向载荷,如图9所示,以及刀刃振动截割煤岩的应力云图,如图10所示。根据已有刀具振动破岩的研究[27-28],可知振动频率在35~55 Hz有利于破岩,并且为与实验相互佐证,故在振动频率为35~55 Hz,间隔为5 Hz条件下,进行了数值模拟,部分振动频率下刀刃模拟载荷,如图11所示。

图8 无振动应力云图
Fig.8 Stress nephogram without vibration

图9 刀刃模拟径向载荷
Fig.9 Blade simulated radial load

图10 振动截割煤岩的应力云图
Fig.10 Stress nephogram of vibration cutting coalrock
由图8可以看出,煤岩体应力从刀刃中部向两侧递减,呈月牙状,其最大应力为56.53 MPa。由图9所见,碟盘刀刃无振动截割煤岩径向载荷呈锯齿状变化,达到稳定截割状态时,其载荷波动较小;有振动截割时径向载荷与轴向振动周期具有同步性。
由图10(b)、(d)可以看出,碟盘刀刃振动截割煤岩应力由中间向两侧逐渐递减,呈月牙状,其轴向向下、向上振动时煤岩最大应力分别为72.86和30.09 MPa,对比无振动时,向下振动应力较大,向上振动应力较小,与图9刀刃模拟径向载荷所反映情况一致,径向进给复合轴向振动有利于煤岩破碎。由图8、10对比可知,碟盘刀刃振动截割煤岩损伤范围大于无振动截割的。
由图11可知,刀刃径向和轴向载荷均与轴向振动位移呈周期性波动,并且载荷与轴向振动位移存在超前相位差,径向、轴向载荷与轴向位移相位差基本一致,载荷波动具有同时性。随着振动频率增大,刀刃径向载荷减小,正值轴向载荷基本保持不变,负值轴向载荷呈下降趋势,载荷与轴向位移之间的相位差逐渐减小,振动频率为45 Hz时,其相位角约为30°。

图11 不同振动频率下刀刃模拟载荷
Fig.11 Simulated load of blade under different vibration frequencies
4.2 实验验证与结果分析
碟盘刀具振动截割煤岩实验系统如图12所示,主要由液压泵站、振动机构、碟盘刀具和实验煤岩体等组成。液压泵站为振动机构的液压缸和液压马达提供动力,液压缸带动碟盘刀具径向进给截割,液压马达驱动碟盘刀具轴向振动。实验煤岩体的煤与水泥配比为1.2∶1,相同配比条件下,制作煤岩试样进行单轴抗压实验,得出实验煤岩的抗压强度为19.2 MPa,泊松比为0.24,弹性模量为4 029 MPa,数值模拟参数设置与实验保持一致。

图12 碟盘刀具振动截割实验系统
Fig.12 Experimental system of disc cutter vibration cutting
碟盘刀具振动截割实验系统还包括信息采集传感器和信息测试系统2部分,信息采集传感器有2位移传感器(① 拉线位移传感器(测进给速度)、② 磁致伸缩位移传感器(测振幅))、压力传感器测、加速度计和应变片等;信息测试系统包括INV3060采集仪、信息转换器和Coinv DASP V10软件等。传感器采集实验特征信息,再通过INV3060采集仪检测特征信息,经过去毛刺、降噪和频谱分析等信息处理手段,获取碟盘刀具振动截割煤岩多方面实验数据,其中径向载荷通过液压缸的压力传感器测得,轴向载荷通过振动机构上弹性轴的轴向应变片测得。
(1)刀刃载荷。当振动频率为45 Hz,振幅为2 mm,截割厚度为7 mm时,碟盘刀刃无振动和有振动截割煤岩的径向载荷及其细节,如图13所示,有振动轴向载荷及其细节,如图14所示。
由图13可以看出,刀刃有振动实验径向载荷明显小于无振动时,可知复合轴向振动可降低截割煤岩的径向载荷。由图14(a)可以看出,碟盘刀刃有振动负值轴向载荷明显大于正值轴向载荷,其正值轴向载荷即大于零的载荷,负值轴向载荷即小于0的载荷,刀刃向下振动煤岩挤压作用明显,轴向载荷较大。由图14(b)可知,碟盘刀刃载荷受轴向振动影响呈周期性波动,与轴向振动位移曲线存在超前相位差,其相位角约为25°。

图13 刀刃实验径向载荷
Fig.13 Radial load of blade experiment

图14 刀刃实验轴向载荷
Fig.14 Axial load of blade experiment
(2)碟盘刀具载荷。当振动频率为45 Hz,振幅为2 mm,截割厚度为14、18和27 mm时,碟盘刀具振动截割煤岩的径向载荷如图15所示,当截割厚度较大时,刀具振动截割煤岩主要靠刀刃和楔面2部分作用。

图15 不同截割厚度下刀具实验径向载荷
Fig.15 Experimental radial load of cutter with different cutting thickness
由图13、15可知,随截割厚度逐渐增大,刀具楔面逐渐参与振动截割煤岩。截割厚度为14和18 mm时,楔面参与振动截割煤岩作用较小,径向载荷变化小,但18 mm时楔面作用大于14 mm时楔面作用,径向载荷变化较明显。当截割厚度为27 mm时,楔面作用明显增大,径向载荷幅值变化剧烈,说明煤岩形成大块崩落更加明显。随着截割厚度增加,其径向载荷复杂程度更高,楔面作用下大块崩落现象更为明显。根据文献[21]不同截割厚度下碟盘刀具振动截割煤岩的数值模拟可知,截割厚度对其正值轴向载荷影响较大,其次是径向载荷,而对负值轴向载荷影响最小。
4.3 结果分析与讨论
由图9、13可得,碟盘刀刃无振动和有振动截割煤岩稳定段模拟的径向载荷均值分别为14.18和9.95 kN,实验的分别为17.20和9.36 kN。无振动模拟和实验的径向载荷均值均大于有振动的,表明增加轴向振动可减小截割煤岩的径向载荷,更利于破碎煤岩,且无振动和有振动时模拟与实验径向载荷均值的误差分别为17.56%和6.30%。
由图11、14模拟和实验可知,当刀刃还未运动到最大振幅处,其载荷就已达到了峰值,说明载荷与轴向振动位移存在相位差。综合模拟和实验结果载荷均超前于轴向位移,但径向载荷与轴向载荷波动具有同时性,随振动频率增大,其相位差逐渐减小,当振动频率为45 Hz时,相位角范围为25°~35°。刀刃轴向振动越接近最大振幅处,轴向位移的斜率越小,进入煤岩的相对量越少,所以运动到最大振幅处,轴向载荷并不会达到峰值。
根据表1参数以及式(27)分别求得碟盘刀刃轴向振动复合截割煤岩的理论载荷,并根据图11(c)、13、14所示数据统计出刀刃模拟和实验载荷。对比分析刀刃径向和轴向载荷的理论值、模拟值与实验值(最大振幅处对应载荷均值)。截割厚度为7 mm时,刀刃截割煤岩的载荷统计结果见表2,理论、模拟与实验载荷的误差见表3。
表2 刀刃振动截割煤岩载荷
Table 2 Load of blade vibration cutting coal rock
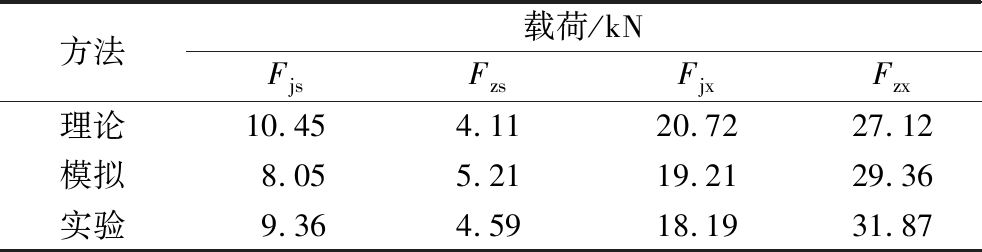
方法载荷/kNFjsFzsFjxFzx理论10.454.1120.7227.12模拟8.055.2119.2129.36实验9.364.5918.1931.87
表3 理论、模拟与实验载荷的误差
Table 3 Errors of theoretical,simulated and experimental loads

方法误差/%FjsFzsFjxFzx理论-实验11.6510.4613.9114.90模拟-实验13.9913.515.617.88
由表3可知,刀刃轴向向上振动时径向载荷的理论值、模拟值与实验值的误差分别为11.65%和13.99%,其轴向载荷误差分别为10.46%和13.51%;轴向向下振动时径向载荷的理论值、模拟值与实验值误差分别为13.91%和5.61%,其轴向载荷误差分别为14.90%和7.88%。碟盘刀刃振动截割煤岩载荷模型计算值、模拟值与实验值的误差满足工程载荷计算要求,由于理论上将刀刃近似为球形压头,且采用单一的破坏准则,数值模拟中忽略煤岩内部各向异性和碟盘运动参数的微小改变,因此,载荷模型计算值、模拟值与实验值存在上述的误差。
由式(21)碟盘刀刃轴向向上振动截割煤岩径向载荷的关系式,得出截割厚度为7 mm的理论径向载荷。根据文献[21]所给碟盘刀具楔面的径向载荷模型,结合刀刃径向载荷模型,得出截割厚度为14、18和27 mm的理论径向载荷,并与模拟和实验的径向载荷进行对比分析。不同截割厚度下,碟盘刀具振动截割煤岩的理论、模拟和实验的径向载荷对比,如图16所示。

图16 不同截割厚度下的径向载荷
Fig.16 Radial load under different cutting thickness
由图16可知,随着截割厚度增大,理论、模拟和实验的径向载荷均增大,其变化规律相吻合。不同截割厚度下,刀具理论、模拟与实验径向载荷的误差均值分别为12.01%和6.37%,间接验证了碟盘刀刃载荷模型的准确性。
5 结 论
(1)构建了碟盘刀刃作用煤岩的破坏准则及力学模型,建立了刀刃振动截割煤岩的载荷模型,给出了刀具结构参数与载荷之间的关系。
(2)碟盘刀刃有振动模拟和实验径向载荷均小于无振动的,并且无振动和有振动时模拟值与实验值的误差分别为17.56%和6.30%。刀刃载荷超前于轴向振动位移,载荷峰值不在振幅最大处,但径向载荷与轴向载荷波动具有同时性,并且随着振动频率增加,相位差减小。随着截割厚度增大,碟盘刀具理论、模拟和实验的径向载荷均增大,其变化趋势相吻合,且误差均值分别为12.01%和6.37%,其对刀具正值轴向载荷影响显著,其次是径向载荷,而对负值轴向载荷影响不明显。
(3)碟盘刀刃轴向向上和向下振动径向载荷理论值和数值模拟值与实验值的误差分别为11.65%、13.99%和13.91%、5.61%,以及轴向载荷误差分别为10.46%、13.51%和14.90%、7.88%。刀刃振动截割煤岩载荷的理论值、模拟值与实验值具有较好的吻合度,验证了所建立的刀刃载荷模型的正确性,为后续研究其他类型刀刃作用煤岩的载荷模型及特性奠定了基础。
[1] NISHIMATSU Y.The mechanics of rock cutting[J].International Journal of Rock Mechanics &Mining Sciences &Geomechanics Abstracts,1972,9(2):261-270.
[2] EVANS I.A theory of the picks cutting force for point-attack[J].International Journal of Mining Engineering,1984,9(2):63-71.
[3] 牛东民.煤炭切削力学模型的研究[J].煤炭学报,1994,19(5):526-530.
NIU Dongmin.Mechanical model of coal cutting[J].Journal of China Coal Society,1994,19(5):526-530.
[4] 王鑫,徐兰欣,陈洪月,等.基于弹-塑-断裂理论的镐型截齿截割机理研究与实验验证[J].振动与冲击,2021,40(3):165-171,194.
WANG Xin,XU Lanxin,CHEN Hongyue,et al.Cutting mechanism of conical pick based on elastic-plastic-fracture theory and test veri-fication[J].Journal of Vibration and Shock,2021,40(3):165-171,194.
[5] 梁运培,王想,王清峰.截割厚度与截线距对镐型截齿破岩力学参数的影响[J].振动与冲击,2018,37(3):27-33.
LIANG Yunpei,WANG Xiang,WANG Qingfeng.Effects of cut depth and cut spacing on tool forces acting on a conical pick in rock cutting[J].Journal of Vibration and Shock,2018,37(3):27-33.
[6] 王想,王清峰,梁运培.截割参数对镐型截齿截割比能耗的影响[J].煤炭学报,2018,43(2):563-570.
WANG Xiang,WANG Qingfeng,LIANG Yunpei.Effects of cutting parameters affecting on specific cutting energy of conical picks[J].Journal of China Coal Society,2018,43(2):563-570.
[7] SU O.Numerical modeling of cuttability and shear behavior of chisel picks[J].Rock Mechanics and Rock Engineering,2019,52(6):1803-1817.
[8] YASAR S.A general semi-theoretical model for conical picks[J].Rock Mechanics and Rock Engineering,2020,53(6):2557-2579.
[9] 刘春生,刘延婷,刘若涵,等.采煤机截割状态与煤岩识别的关联载荷特征模型[J].煤炭学报,2022,47(1):527-540.
LIU Chunsheng,LIU Yanting,LIU Ruohan,et al.Correlation load characteristic model between shearer cutting state and coal-rock recognition[J].Journal of China Coal Society,2022,47(1):527-540.
[10] KOTWICA K,SIENKIEWICZ P.Influence of constructional and kinematic parameters of the new solution of roadheader mining head on the effectiveness of its work[J].Multidisciplinary Aspects of Production Engineering,2018,1(1):101-107.
[11] KOTWICA K.Asymmetrical mini disk tools-possibilities of use and directions for further development[J].New Trends in Production Engineering,2019,2(1):223-232.
[12] KOTWICA K.Hard rock mining-cutting or disk tools[J].IOP Conference Series:Materials Science and Engineering,2019,545(1):1-11.
[13] KHORESHOK A,MAMETYEV L,NESTEROV V,et al.Justific-ation of the disk tool application for working bodies of mining machines[J].MATEC Web of Conferences,2019,297:03007.
[14] KHORESHOK A,MAMETYEV L,NESTEROV V,et al.Unitized attachment points of a disk tool for the working bodies of shearers and tunnelling machines[J].MATEC Web of Conferences,2019,297:03008.
[15] DEHKHODA S,DETOURNAY E.Mechanics of actuated disc cut-
ting[J].Rock Mechanics and Rock Engineering,2017,50(2):465-483.
[16] DEHKHODA S,DETOURNAY E.Rock cutting experiments with an actuated disc[J].Rock Mechanics and Rock Engineering,2019,52(2):3443-3458.
[17] DEHKHODA S,HILL B.Clearance angle and evolution of depth of cut in actuated disc cutting[J].Journal of Rock Mechanics and Geotechnical Engineering,2019,11(3):644-658.
[18] XU R,DEHKHODA S,HAGAN P C,et al.Evaluation of cutting fragments in relation to force dynamics in actuated disc cutting[J].International Journal of Rock Mechanics and Mining Sciences,2021,146:1-16.
[19] MOHAMMADNEJAD M,DEHKHODA S,FUKUDA D,et al.GPGPU-parallelised hybrid finite-discrete element modelling of rock chipping and fragmentation process in mechanical cutting[J].Journal of Rock Mechanics and Geotechnical Engineering,2020,12(2):310-325.
[20] 刘春生,徐玉芸,李德根,等.边缘牙齿形碟盘破碎煤岩的力学机理及其模型[J].煤炭学报,2018,43(1):272-279.
LIU Chunsheng,XU Yuyun,LI Degen,et al.Mechanical mechanism andmodel of fractured coal rock in edge-shaped disc-shaped disc[J].Journal of China Coal Society,2018,43(1):272-279.
[21] 刘春生,李德根,袁昊.碟盘刀具振动切削煤岩的理论力学模型与载荷特性[J].煤炭学报,2020,45(8):3015-3023.
LIU Chunsheng,LI Degen,YUAN Hao.Theoretical mechanicalmodel and load characteristics of coal rock vibration cutting with disc cutter[J].Journal of China Coal Society,2020,45(8):3015-3023.
[22] 袁昊.碟盘振动切削煤岩载荷的理论模型与模拟试验[D].哈尔滨:黑龙江科技大学,2019.
YUAN Hao.Theoretical model and simulation test of vibrating cutting of coal rock load by disc cutter[D].Harbin:Heilongjiang University of Science &Technology,2019.
[23] 刘春生,车长瑞.基于星点设计的碟盘刀具截割煤岩性能评价与预测[J].黑龙江科技大学学报,2021,31(2):169-176,183.
LIU Chunsheng,CHE Changrui.Performance evaluation and prediction of disc cutter cutting coal and rock based on star point design[J].Journal of Heilongjiang University of Science & Technology,2021,31(2):169-176,183.
[24] 刘春生,车长瑞,刘延婷,等.碟盘振动截割煤岩的参数优化与性能评价[J].黑龙江科技大学学报,2021,31(4):452-457.
LIU Chunsheng,CHE Changrui,LIU Yanting,et al.Parameter optimization and performance evaluation of disc vibration cutting coal and rock[J].Journal of Heilongjiang University of Science &Technology,2021,31(4):452-457.
[25] 张祖培,刘宝昌.碎岩工程学[M].北京:地质出版社,2004,40-41.
[26] 刘春生,袁昊,张艳军,等.不同楔面角度碟盘刀具切削煤岩的载荷与小波能量熵[J].黑龙江科技大学学报,2018,28(5):543-551.
LIU Chunsheng,YUAN Hao,ZHANG Yanjun,et al.Cutting load of coal-rock and wavelet energy entropy of disc cutters with different wedge angles[J].Journal of Heilongjiang University of Science &Technology,2018,28(5):543-551.
[27] 杨先伦,何世明,王涛.高频扭转冲击钻井PDC钻头切削齿瞬间碰撞破岩分析[J].断块油气田,2018,25(6):789-792.
YANG Xianlun,HE Shiming,WANG Tao.Analysis of instantaneous impactrock breaking of PDC cutting tooth for high frequency torsional percussion drilling[J].Fault-Block Oil &Gas Field,2018,25(6):789-792.
[28] 李兵,杨决算,韩福彬,等.PDC钻头谐振破岩模拟及室内试验研究[J].西部探矿工程,2020,32(10):35-37,40.
LI Bing,YANG Juesuan,HAN Fubin,et al.Simulation and laboratory test of PDC bit resonant rock breaking[J].West-China Exploration Engineering,2020,32(10):35-37,40.
