煤炭分选是煤炭洁净利用的基础，以密度差异为基础的重力选煤是最主要的选煤方法，重力或离心力是重选的主要驱动力，粒度和密度是这些力的组成部分，粒度严重影响了按密度分选的精确度，重选也不例外。深入研究粒度对重选效果的影响规律，对于提高分选效率、优化选煤工艺、开发新型分选设备具有重要指导意义。

分配曲线是不同密度级物料在某一产品中分配率的展示，是按密度分选效果好坏的直观表示。从分配曲线上可以得到多个分选指标，最具代表性的是分选密度和可能偏差。经长期研究和实践，积累了大量分选密度、可能偏差随粒度变化的数据和曲线。《Coal preparation》中列举了重介分选槽、重介旋流器、摇床、水介旋流器、跳汰等设备的分选指标随粒度变化的数据[1]。VENKOBA[2]搜集了29组不同分选方法分粒级分配曲线数据，得出分选密度、可能偏差随粒度增大单调下降的结论。ANUPAM等[3]分析26组可能偏差随粒度变化的数据后指出：对于所有湿法分选设备，可能偏差随粒度增大而减小的规律普遍存在，但其没有明确分选密度随粒度的变化。分选密度随粒度的变化有2种类型：① 与可能偏差相似，随粒度增大，分选密度减小，常在粗煤泥分选中出现[4]；② 呈鱼钩型，先减小后有所增大[5-6]，这种鱼钩型变化，多出现在宽粒级入料的重介旋流器分选中，我国的选煤实践[7]也证明了这一点。

重产物分配曲线与概率分布累积曲线非常相似，由分选密度、可能偏差构成的正态分布模型是最经典的分配曲线理论数学模型。实际分配曲线经常是不对称的，张荣曾[8]对于分配曲线的不对称性，提出了偏度系数概念。樊民强等[9]提出应用4类参数来表示分配曲线的形态：分选密度表示分选的位置、可能偏差表示分选的精度、偏度表示分配曲线的不对称性、峰度反映分配曲线两端的形态，并用这4类参数作模型参数，建立了分配曲线数学模型，实现了模型参数与分配曲线特性参数的统一。董连平等[10]以含偏斜系数的3参数广义正态分布函数为基础，新增一个峰度系数，构建了一个4参数分配曲线数学模型，提高了分配曲线数学模型的适应性和稳定性。ZHOU等[11]提出了一个正态分布-Laplace分布的组合模型来描述分配曲线的不对称性和长尾。目前统计学上更倾向于使用尾态而不是峰度来描述分布两端的形态[12]。樊民强等[13]以四分位数为基础，构建出由中位数(分选密度)、四分位偏差(可能偏差)、四分位偏度和尾态系数组成的4参数广义偏斜正态分布函数，实现了分配曲线在4阶形态参数基础上的量化分解，模型对各类分配曲线均有良好的拟合精度。

FERRARA[14]根据稳定介质条件下的重介分选原理绘制了包含密度δ、粒度d双变量的三维分配曲面。LYNCH[15]提出了基于Logistic分布的密度、粒度双变量分配曲面数学模型，开启了粒度对分选过程影响的量化描述。SCOTT等 [16]将旋转支点(pivot)对应的分配率Yp引入模型，增加了模型的适应性，KLIMA等 [17]也独立地提出了该模型。RAO等[18]采用高斯误差函数构建了分配曲面数学模型。DOU等[19]构建了基于Logistic分布的5参数密度、粒度双变量分配曲面数学模型，对重介分选和其他分选数据有良好的拟合精度。高建川等[20]基于沉降公式，采用有理式构建了包含密度、粒度的双变量6参数分配曲面数学模型，明确引入了四分位偏斜系数。

SCOTT、RAO、DOU建立了分选密度、可能偏差与粒度的关系式，但未考虑偏度、尾态与粒度的关系。高建川建立的模型虽然包含了偏度，但与粒度无关，表明其过于简化。要揭示分选效果和粒度的关系，既要深化粒度对分选密度、可能偏差的影响研究，还要开展粒度对偏度、尾态的影响研究。笔者以工业过程的分配曲线数据为基础，以基于四分位数的广义正态分布分配曲线数学模型为工具，从分选密度、可能偏差、偏度与尾态4个尺度就粒度对重介旋流器分配曲线形态的影响进行量化研究。

1 分配曲线和分配曲面数学模型

分配曲线和分配曲面数学模型，是量化解析粒度对重选效果影响的基础，下面是与本论文直接相关的数学模型。

(1)基于四分位数的广义偏斜正态分布分配曲线数学模型。

基于四分位数的广义偏斜正态分布分配曲线数学模型，能更精确地描述分配曲线的形态，本文采用的模型为

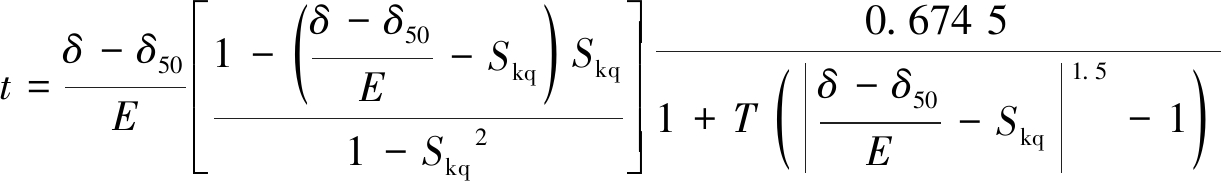
(1)

Y=100φ(t)

(2)

式中，t为标准正态分布的自变量；δ为颗粒密度；δ50为分选密度；E为可能偏差；Skq为分配曲线的四分位偏度；T为尾态系数，能较好地描述分配曲线两端的形态；φ(t)为正态分布函数；Y为分配率。

(2)Scott分配曲面数学模型。

Scott分配曲面数学模型以Logistic分布函数为基础，即

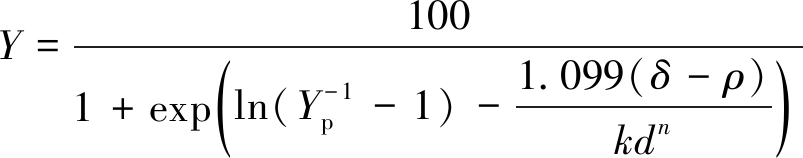
(3)

式中，d为粒度；ρ为某点的特殊密度，其与粒度无关，当密度为ρ时，所有粒级的分配率均为100×Yp，为分配曲面旋转支点对应的分配率；k、n为模型参数。

由式(3)可推导出δ50、E与粒度的关系：

(4)

(5)

(3)RAO分配曲面数学模型。

Rao模型是Scott模型的正态化表示，其表达式为

Y=50[1-erf(AdC(ρ-ρp)-B)]

(6)

式中，A、B、C、ρp为模型参数；erf( )为高斯函数。

由式(6)得到的分选密度、可能偏差与粒度的关系较为直观，即

(7)

(8)

(4)高建川分配曲面数学模型。

(9)

其中，a、b、c、d、n、ρ、σ为模型参数。将式(9)代入式(2)即可构建成正态分布型的分配曲面数学模型。由式(9)还可得到四分位偏度的表达式：

(10)

(11)

Skq=cσ

(12)

2 分配曲线数据及处理方法

表1中分配曲线数据来自本课题组对屯兰选煤厂无压给料三产品重介旋流器的单机检查试验，试验条件与详细数据等参见文献[21]。

选择分配曲线数学模型或密度-粒度双变量分配曲面数学模型，采用非线性拟合方法求出模型参数。以偏差平方和Q表示拟合精用，Q越小，说明模型精度越高。

(13)

式中，Ytest为分配率实验值；Ycal为分配率拟合值。

3 粒度对分配曲线形态参数的影响

采用式(1)、(2)作为分配曲线数学模型，对表1数据进行拟合，结果见表2。根据拟合结果，分别绘制分选密度、可能偏差、四分位偏度、尾态系数与粒度的关系曲线，如图1所示。

由图1可知，三产品重介旋流器一段分选密度随粒度的变化规律不单调，随粒度增大，分选密度先下降后上升，呈鱼钩形状。与相关文献[5-7]的结果一致。依据等速沉降原理，可推导出式(7)，得到分选密度随粒度减小的理论结果，但式(7)未必能准确反映超出等沉比的宽粒级物料的分选特性。过大的颗粒粒度，相对于旋流器直径不可忽略，其在旋流器中所占空间过大，会由于析离分层作用被细粒级挤到内旋流区进入溢流，进而产生大粒度分选密度有所提高的现象。二段分选密度随粒度的变化呈鱼钩形状，但鱼钩形态变缓。0.62 mm粒级分选密度有所下降，四分位偏度和尾态系数也如此，可能与该粒级在最大密度级分配率上存在试验误差有关。三产品重介旋流器一段、二段可能偏差随粒度增加单调下降。一段四分位偏度在细粒级为负值，随粒度增大，四分位偏度值逐步向坐标轴逼近。2.5 mm时为正值，是试验误差和追求最小拟合误差所致，实际上2.5 mm与4.5 mm粒级四分位偏度均取-0.007时，Q也只有2.5。二段四分位偏度随粒度增大先下降至最小值后又升高趋于0。一段和二段的尾态系数随粒度增大而逐步减少，至最小值后有所回升，一段趋于0.04，二段趋于0.07。

综上可以得出：① 分选密度随粒度增大先明显下降后上升，呈现鱼钩状。② 可能偏差随粒度增大而减小。③ 偏度、尾态随粒度非单调变化，但大粒度下均较低。若对极值点进行平滑，则可用单调关系进行处理。

4 分配曲面数学模型构建与优化

4.1 基于四分位数的密度-粒度双变量分配曲面数学模型构建

(1)分选密度与粒度的关系模型。

根据分选密度与粒度的关系曲线，提出一个由幂函数和指数函数构成的5参数数学模型，幂函数、指数函数均可单调下降或上升，两函数的乘积具有单调下降、单谷(鱼钩型)等多种变化，与一般重选和重介旋流器分选密度的变化相对应，并可简化成简单的幂函数形式：

(14)

其中，sgn(n)为符号函数，当n为正时，sgn(n)=1，公式的具体形式为

(15)

当n为负时，sgn(n)=-1，公式的具体形式为

(16)

式中，a1、a2、a3、n为模型参数。

(2)可能偏差与粒度的关系。

可能偏差与粒度的数学模型由幂函数构成，与可能偏差随粒度增大单调下降的基本趋势相对应。在幂函数的基础上增加常数项，进一步提高适应性。

(17)

式中，b0、b1、m为模型参数。

(3)四分位偏度与粒度的关系。

四分位偏度与粒度的关系研究较少，试验误差的影响也较大，根据曲线的形态，并考虑到对极值点的平滑，选择以幂函数为基础的3参数模型。

(18)

式中，c0、c1、p为模型参数。

(4)尾态系数与粒度的关系。

尾态系数与粒度的关系采用幂函数表示。

(19)

式中，t0、t1、q为模型参数。

4.2 密度-粒度双变量分配曲面数学模型优化

将分配曲线形态参数与粒度的关系式代入式(1)、(2)，构成了密度-粒度分配曲面数学模型，各参数组合下模型的拟合结果见表3(F5322为组合缩写，表示密度模型参数5个、可能偏差模型参数3个、偏度模型参数2个、尾态系数模型参数2个)。

4参数的Rao模型，拟合误差非常大。由3参数密度模型、3参数可能偏差模型构成的分配曲面模型F3300，拟合误差虽有所降低，但仍很大。在密度模型和可能偏差模型参数均取3时，引入偏度和尾态系数模型，总参数个数达到12个，F3333拟合误差进一步下降，二段下降幅度更大，但仍偏大。这些模型无法精确描述宽粒级重介旋流器的分配规律。

鉴于分选密度变化的非单调性，增加密度模型参数至4个，拟合误差均明显下降，当参数达到5个时，一段拟合偏差平方和仅为46.48，分选密度模型取5参数完全满足拟合精度要求。表3中列举了2个二段分配曲面拟合结果：一种是单纯以最小拟合误差为目标，此时0.62 mm分选密度下降；另一种是限定0.62 mm分选密度不下降，分选密度在0.62～6.00 mm粒级保持单调下降，而后又有所增加，分选密度随粒度变化呈鱼钩状。

F5333的拟合误差明显比F5300的拟合误差小，说明在分选密度模型和可能偏差模型精确的情况下，四分位偏度模型和尾态系数模型不可或缺，应引入。

F5322与F5333拟合误差已非常接近，说明四分位偏度、尾态系数模型中常数项可省略，说明当粒度增大时，偏度、尾态趋近于0，即重介旋流器分选时，大颗粒的分配曲线接近于正态分布。限定条件下二段F5333拟合误差较F5322降幅较大，但分配曲线在密度2.0 g/cm3后会有所下降，这与实际不符；由F5322得到的分配曲面形态更好。

F5320的拟合误差大于F5302，且F5302拟合误差与F5322相差不大，说明尾态系数对分配曲线的影响大于偏度系数。重介分选分配曲线本身对称性较好，且二段高密度分选时分配率在25%～75%的试验点很少，因此二段偏度对分配曲面拟合误差的影响较低。

将可能偏差模型中的常数项取消，F5222的拟合误差增加很少，说明在重介分选中，可能偏差与粒度之间的关系可用最简单的2参数幂函数来表示，即粒度越大，可能偏差越小，大颗粒的可能偏差趋近于0，分选精度达到理想值。

经上述分析，从拟合精度、分配曲线形态和模型参数数量3个方面考虑，推荐参数个数为11的F5222为重介旋流器分配曲面数学模型，即

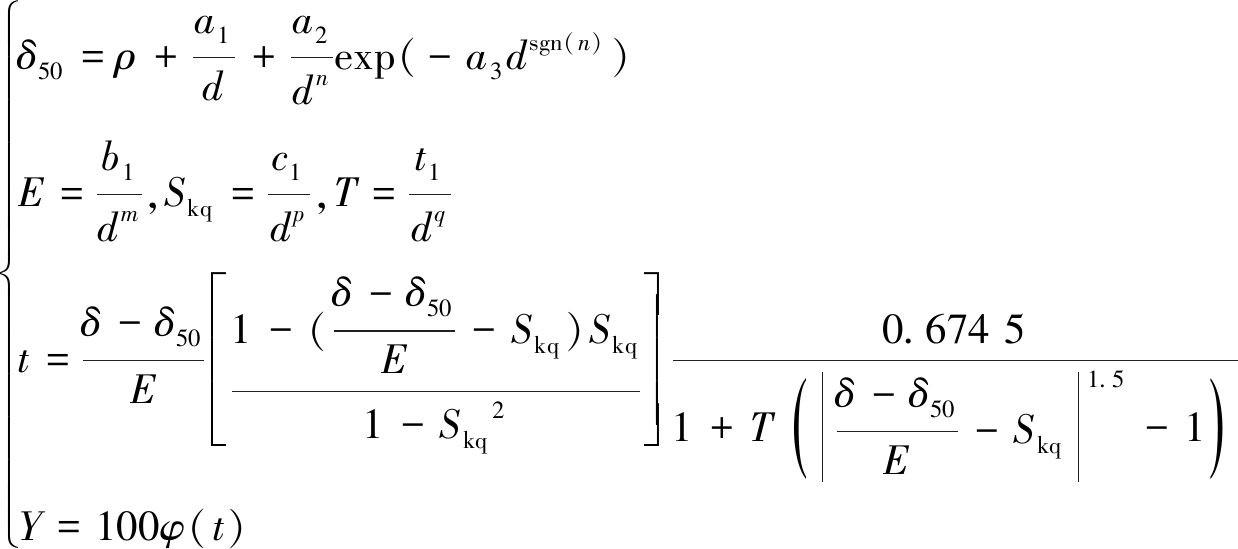
(20)

由表3可知，分配曲面模型组具有可扩展性，可根据具体分选过程，采用不同参数个数的数学模型来描述。经作者验算，14参数的F5333对粗煤泥水介分选、水力旋流器分级等过程的适应性更好。

4.3 曲面与曲线形态特性参数比较

11参数下各参数具体数据见表4。将11参数下分配曲面模型拟合得到的特性参数与各粒级分配曲线特性进行对比，散点为各粒级分配曲线拟合结果，曲线为分配曲面特性参数随粒度的变化曲线(图2)。二段分选图中有2条曲线，其中“拟合”是拟合误差最小时的结果，“拟合2”是限定a1>0、a2<0，使分选密度在低密度端不下降时的结果。

由图2可知,一段分选密度，分配曲面与分配曲线拟合数值吻合度高，很好地体现出分选密度随粒度变化的鱼钩形态。说明分选密度模型对一段分选密度变化适应性好，合理可靠。在最小拟合误差下二段分选密度面与线的数值在细粒级下吻合度很好，在限定条件下二段分选密度面与线整体吻合度更高，也呈现出一定的鱼钩形态。说明分选密度模型对二段分选密度的变化也有良好的适应性。无论一段和二段，可能偏差均随粒度增大而下降，分配曲面与分配曲线拟合数值吻合度良好，说明可能偏差模型合理可靠。分配曲面与分配曲线四分位偏度拟合数值吻合度一般。二段偏度分配曲面拟合2全域几乎为0，主要原因是分配曲线偏度拟合值小且波动较大，数值波动掩盖了真正的关系。但2段分选大粒级偏度值波动不大且近似为0，用幂函数来表示四分位偏度与粒度的关系在大粒度级具有一定的合理性。分配曲面与分配曲线尾态系数拟合值吻合度良好，整体上表现出一定的单调性，大粒度的尾态系数小，说明用幂函数来表示尾态系数与粒度的关系可行。

笔者尝试采用更多参数的模型来表达四分位偏度、尾态系数与粒度的关系，总体上拟合误差会继续下降，但降幅不明显，也反映出用幂函数作偏度、尾态系数模型的有效性。二段分选限定条件下的拟合，其面与线的数值整体吻合度更好，说明限定形态下的拟合结果可能更符合实际。对分配曲线或曲面的分析要综合考虑拟合误差和分配曲面形态，以消除个别数据误差对整体规律的影响。

4.4 宽粒级分配曲面形态

根据分配曲面模型，绘制密度-粒度双变量分配曲面如图3所示。由分配曲面可以看出，随密度增大，在重产物中的分配率增加，粗粒级陡峭程度好于细粒级，细粒级在低密度端上翘，在高密度端略降，细粒级分选效果略差。从粒度坐标上看，在低密度端，虽然分配率数据整体偏低，但随粒度增加，分配率下降，而高密度端的变化则相反，中间密度的变化呈先升高后下降的趋势。说明重介分选中粒度的影响也不能忽视，一定要合理选择重介旋流器分选的粒度上、下限。

5 结 论

(1)对于无压三产品重介旋流器，分选密度随粒度增大先减小后又有所增大，呈现鱼钩状。5参数的分选密度与粒度模型由幂函数和指数函数构成，能反映分选密度的多种变化规律，分选密度模型对分配曲面拟合精度影响最大。

(2)可能偏差随粒度增大而减小，其模型由2参数幂函数构成，大粒级的可能偏差在理论上趋近于0。

(3)研究了四分位偏度、尾态系数与粒度的关系，大粒级的偏度与尾态系数小，大粒级分选的分配曲线更趋近于正态分布。在本文数据样本下，尾态系数随粒度变化的幂函数关系较为显著，而偏度与粒度的幂函数关系的显著度不高。更为准确的关系，还需得到其他工业数据的校验。

(4)建立了一个全新的密度、粒度双变量分配曲面数学模型，在4阶形态参数尺度下揭示了粒度对重选的影响规律，为量化分析各类水力分级和重力分选过程粒度、密度的相互影响，提供了一个通用的高精度数学工具。

(5)分配曲面4阶形态参数与粒度的数学模型虽然借鉴了重选理论，但主要依据回归分析，其中隐含的机理仍需进一步研究。

参考文献（References）:

[1] JOSEPH W Leonard.Coal preparation [M].New York:SME Inc.,1991.

[2] VENKOBA Rao B.General gamma representation for product part-icle split in gravity concentrators[J].The European Journal of Mineral Processing and Environmental Protection,2005,5(1):84-93.

[3] ANUPAM A,BHATTACHARYA S,DE Korte G J.Effect of feed size and size distribution on the performance of dense medium cyclones:A critical review[J/OL].International Journal of Coal Preparation and Utilization,2017,37:618-639.

[4] GALVIN K P,DOOODCHI E,CALLEN A M,et al.Pilot plant trial of the reflux classifier [J].Minerals Engineering,2002,15:19-25.

[5] DAVIS J J,WOOD C J,LYMANG J.The use of density tracers for the determination of dense medium cyclone partition characteristics [J].Coal Preparation,1985,2:107-125.

[6] CELIK H.An analysis of mass balance and fractional particle size

distributions of coal and magnetite in a dense-medium cyclone circuit[J].International Journal of Coal Preparation and Utilization,2009,29:68-83.

[7] 赵树彦,张春林,徐学武,等.3GDMC1500/1100A型无压给料三产品重介质旋流器[J].洁净煤技术,2010,16(2):9-13.

ZHAO Shuyan,ZHANG Chunlin,XU Xuewu,et al.Study on 3GDMC1500/1110A three product dense medium cyclone with non-pressured feeding[J].Clean Coal Technology,2010,16(2):9-13.

[8] 张荣曾.重力分选中的分配曲线形态及特性参数的研究[J].煤炭学报,1980(1):37-46.

ZHANG Rongzeng．The shape and characteristic parameters of the partition curve of gravity separation[J].Journal of China Coal Society,1980(1):37-46.

[9] 樊民强,张荣曾.分配曲线特性参数及由其构成的数学模型[J].煤炭学报,1998,23(2):202-207.

FAN Minqiang,ZHANG Rongzeng.Characteristic parameters of distribution curve and a mathematic model built with these parameters[J].Journal of China Coal Society,1998,23(2):202-207.

[10] 董连平,樊民强,杨宏丽,等.基于广义偏斜正态分布的分配曲线数学模型[J].煤炭学报,2013,38(10):1856-1861.

DONG Lianping,FAN Minqiang,YANG Hongli,et al.Mathematical model for partition curve based on generalized normal skew distribution[J].Journal of China Coal Society,2013,38(10):1856-1861.

[11] ZHOU Q,WEI L,DONG Y,et al.A skew normal-Laplace model of partition curve based on probability characteristics[J].Minerals Engineering,2020,159:106630.

[12] WESTFALL P H.Kurtosis as peakedness,1905-2014.R.I.P.[J].American Statistician,2014,68(3):191-195.

[13] FAN Minqiang,LUO Canjin.Generalized skew-normal distributi-on model of partition curves based on quartile[J].International Journal of Coal Preparation and Utilization,2022,42(7):2219-2231.

[14] FERRARA G,SCHENA G D.Cycloning in dense media separation [C]//Proc.3rd Int.Conf.on Hydrocyclones.Oxford,1987:101-110.

[15] LYNCH A J,NAPIER-MUNN T J.Dense medium separation research at the Julius Kruttschnitt Mineral Research Centre [J].Transaction of the Institution of Mining and Metallurgy,1986,95:C221-C225.

[16] SCOTT I A,NAPIER-MUNN T J.Dense-medium cyclone model based on the pivot phenomenon [J].Transaction of the Institution of Mining and Metallurgy,1992,101:C61-C76.

[17] KLIMA M S,LUCKIE P T.Application of an unsteady-state pulp-partition model to dense-medium separations[J].Coal Preparation,1989,6:227-240.

[18] VENKOBA RAO B,KAPUR P C,RAHUL K.Modeling the size-

density partition surface of dense-medium separators[J].International Journal of Mineral Processing,2003,72:443-453.

[19] DOU Dongyang,LIU Gangyang,YANG Jianguo.Particle sizeincl-uded partition curve model of dense medium cyclones[J].International Journal of Coal Preparation and Utilization,2022,42:565-579.

[20] 高建川,董连平,杨宏丽,等.基于正态分布的旋流器密度-粒度分配曲面数学模型[J].煤炭学报,2016,41(11):2847-2852.

GAO Jianchuan,DONG Lianping,YANG Hongli,et al.Math model of density-size partition surface based on normal distribution for cyclone separation[J].Journal of China Coal Society,2016,41(11):2847-2852.

[21] 高建川.选煤过程中颗粒密度-粒度双变量分配规律研究[D].太原：太原理工大学,2016.

GAO Jianchuan.Study on particle density-size bivariate distribution regularities in coal preparation process [D].Taiyuan：Taiyuan University of Technology,2016.

Quantitative analysis of particle size impact on separation effect of heavy medium cyclone

FAN Minqiang1,TIAN Lei1,DONG Lianping1,YANG Runquan1,GAO Jianchuan2

(1.College of Mining Engineering,Taiyuan University of Technology,Taiyuan 030024,China;2.Shanxi Coking Coal Group,Taiyuan 030024,China)

Abstract:Distribution curve is the basis for evaluating the effect of gravity concentration.The shape of distribution curve can be expressed by the 4-order characteristic parameters including separation density,probable error,quartile skewness and tail state coefficient.The influence of particle size on the effect of gravity concentration can be decomposed into the influence of particle size on the shape parameters of distribution curve.Based on the distribution curve data of non-pressure three-product heavy medium cyclone at different particle sizes,the generalized skew-normal distribution model was adopted.It extracted the 4-order morphological parameters of distribution curve at different particle sizes of first coal stage and second stage respectively by using nonlinear regression method,revealing the basic law of the influence of particle size on the separation effect of non-pressure three-product heavy medium cyclone.The separation density first decreases and then increases with the increase of particle size.The probable error decreases with the increase of particle size.The skewness and tail coefficient approach 0 with the increase of particle size.That is,the larger the particle size is,the higher the separation accuracy is,the better the symmetry of the distribution curve is,the smaller the degree of the long tail is,and the closer the distribution curve is to the normal distribution.The mathematical model of separation density-particle size was established by combining power function and exponential function,the probable error-particle sizes mathematical model is constructed by using power function.The mathematical models of quartile deviation-particle size and tail coefficient-particle size are given for the first time in the form of power function.The interaction of density and particle size in gravity concentration process was unified into the generalized skew-normal distribution function based on quartile under the 4-order morphological parameters.And a high-precision density-particle size distribution surface mathematical model with the extensibility of model parameters was established to quantitatively analyze the interaction of particle size and density in various hydraulic classification and gravity concentration processes.It provides a general high-precision mathematical tool,which is of great significance to reveal the influence mechanism of particle size on separation.

Key words:heavy medium cyclone;distribution surface;particle size;separation density;probable error；quartile skewness；tail state coefficient

中图分类号:TD94

文献标志码:A

文章编号:0253-9993(2023)01-0460-10

移动阅读

收稿日期:2022-05-03

修回日期:2022-06-21

责任编辑:张晓宁

DOI:10.13225/j.cnki.jccs.2022.0650

基金项目:国家自然科学基金资助项目(51874208)

作者简介:樊民强(1964—),男,山西永济人,教授,博士。E-mail:fanminqiang@sohu.com

引用格式:樊民强，田蕾，董连平，等.粒度对重介旋流器分选效果影响的量化解析[J].煤炭学报,2023,48(1):460-469.

FAN Minqiang,TIAN Lei,DONG Lianping,et al.Quantitative analysis of particle size impact on separation effect of heavy medium cyclone[J].Journal of China Coal Society,2023,48(1):460-469.