磨料水射流以高压水流为载体,将磨料颗粒加速,相比于纯水射流,在切割花岗岩、金属、玻璃、陶瓷等硬性材料领域具有广阔的应用前景[1-4]。根据磨料供给方式,磨料水射流可分为前混合式、后混合式磨料水射流。自磨料水射流的概念提出之后,国内外学者对磨料水射流的流场、主要射流参数、加工性能、磨损等方面进行了大量研究[5-6]。近年来包括水力割缝、水力冲孔等水力化技术因其清洁高效特点,已成为煤矿卸压增透的主要方法[7-10],提高水射流破煤岩效率是提高卸压增透效果的重要研究内容。
随着研究技术的深入发展,煤矿卸压增透应用中磨料水射流技术也在不断改进[11]。张成光等[12]提出一种新型后混合式磨料水射流系统,对传统后混合式磨料水射流系统的重大改进和发明,采用ANSYS FLUENT与试验结合的方法,为新型后混合式磨料水射流系统的研制提供了理论基础。左伟芹等[13]针对现有前混合磨料射流系统不能实现磨料连续供给的问题,提出在系统中并联2个磨料罐,运用气动闸阀实现磨料罐在加砂、供料2个状态间切换,运用射流泵自行加砂,也为前混合磨料射流连续加砂提供新思路。卢义玉等[14]则针对这个问题,提出利用射流泵原理抽吸和混合磨料实现连续加料的新思路。另外针对前混合磨料水射流不能连续供砂及磨料混合不均匀等不足之处,学者提出一种新型射流——预混合磨料水射流。其技术思路为:预先将磨料和水按照一定的比例充分均匀混合,采用注浆泵吸入磨料/水混合物并通过柱塞加压,经高压管路泵送至喷嘴,形成预混合磨料水射流,切割破煤效果明显优于前混合磨料水射流,但目前相关技术理论研究比较薄弱。
随着计算流体力学的迅速发展,基于计算流体力学的数值模拟方法在研究复杂紊动流场方面具有很好的应用,获得了巨大的发展空间[15-19]。数值模拟可以获得更为全面和可视化良好的结果,便于分析多种工况条件下的流场变化规律。林晓东等[20]针对前混合式磨料射流磨料加速过程运动复杂、实验研究困难等问题,模拟前混合式磨料射流喷嘴不同阶段磨料粒子加速特征及磨料射流破碎靶体全过程,揭示了磨料粒子群在喷嘴中的运动轨迹及喷嘴结构对磨料粒子加速影响规律。DEEPAK等[21]数值模拟不同喷嘴对射流参数的影响,结果表明减小喷嘴的半径可以提高射流速度和射流压力,与其他轮廓喷嘴相比,射流压降较低。施红辉等[22]在数值模拟方法中应用SST κ-ω 湍流模型与VOF模型,研究了直喷嘴、锥形渐扩喷嘴和锥形渐缩喷嘴结构下的管内外气/液分布与水射流的流体力学特性。赵佳乐等[23]采用CFD-DEM耦合的方法模拟研究螺旋叶片数量、钻井液排量以及岩屑粒径对旋流井眼净化效果的影响规律。磨料质量分数是影响射流效果的重要因素,基于FLUENT软件,陈逢军等[24]研究表明适当提高磨料颗粒浓度能提高材料去除速率并降低表面粗糙度,米建宇等[25]采用SPH-FEM模拟后混合磨料水射流的过程并研究了磨料浓度等因素对后混合磨料水射流破岩效果的影响规律。其中,CFD-DEM耦合方法兼具软件FLUENT与EDEM的优点,使用方便后处理效果好,被越来越的研究人员接纳使用。但是预混合磨料水射流涉及气液固三相流动,基于VOF-DEM耦合模型研究磨料水射流时,模型中不能考虑离散相体积分数。
基于上述背景,为提高预混合磨料水射流破煤岩效率,笔者以预混合磨料水射流为研究对象,通过对经典VOF模型进行修正,基于CFD-DEM耦合计算方法,建立数值模型,研究不同磨料质量分数时磨料粒子速度及其速度分布、射流速度、能量转化效率,并与实验相结合,得出不同质量分数条件下磨料的运动规律,揭示磨料质量分数对其破岩效果的影响,进一步丰富水射流理论,为预混合磨料水射流应用提供技术支撑。
1 预混合磨料水射流冲击动能分析
CFD-DEM数值模拟是研究磨料水射流的重要方法。通过FLUENT-EDEM耦合模拟计算预混合磨料水射流中水与磨料颗粒的耦合加速过程,观察射流变化与磨粒颗粒的运动轨迹,分析预混合磨料水射流磨料加速规律和冲击动能。基于CFD-DEM模型研究磨料-水耦合运动时,模型包括连续相控制方程和颗粒相控制方程,颗粒相运动采用DEM模型描述;而为有效描述磨料颗粒对射流流场影响,在VOF模型的控制方程中需引进颗粒相体积分数及源相[26]。
1.1 控制方程
1.1.1 连续相控制方程
对于连续相,基于FLUENT中的VOF(Volume of Fluid)配合RNG κ-ε湍流模型对射流流场进行模拟。为描述磨料粒子对水射流流场的影响,在VOF多相流模型中添加颗粒相体积分数,在动量输运方程中增加动量源相。
连续相方程与动量方程的计算公式[26]为
![]() ∇·(εfuf)=0
∇·(εfuf)=0
(1)
∇·[εfμ(∇uf+∇ufT)]+ρg+Fst+Fpf
(2)
其中,εf为流体空隙率;t为时间;uf为流体运动速度;ρ为混合流体密度;p为压力;μ为混合流体动力黏度;Fst为自由界面附近的表面张力;Fpf为颗粒流体间相互作用项的反作用力;g为重力加速度。密度ρ和黏度μ由式(3)、(4)给出:
ρ=αwρw+αgρg
(3)
μ=αwμw+αgμg
(4)
式中,ρw为水的密度;ρg为空气的密度;μg为空气的黏度;μw为水的黏度;αw为计算区域中水的体积分数;αg为计算区域中空气的体积分数。
两相体积分数满足:
![]() ∇·(αwuf)=0
∇·(αwuf)=0
(5)
αw+αg=1
(6)
RNG κ-ε湍流模型形式上与标准κ-ε模型相似,但是ε方程中增加了一项,提高了高速流动的准确性。RNG κ-ε模型还考虑了涡流对湍流的影响,提高了旋涡流动的精度,并提供了湍流普朗特数的解析公式和一种从分析中获得有效的黏度,考虑低雷诺数的影响。这些特性使得在更广泛的流动中RNG κ-ε模型比standard κ-ε更准确和可靠。
对于不可压缩流体,RNG κ-ε湍流模型的控制方程[27]为
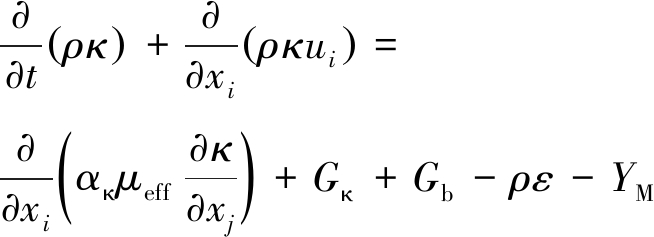
(7)

(8)
式中,μeff为液体的有效黏度,
为常数;κ为湍流动能;ε为耗散率;xi 、xj为笛卡尔坐标;ui和uj为沿i、j方向的速度;μt为涡流黏度;Gκ为速度梯度产生的湍流动能;Gb为由浮力产生的湍流动能;YM为可压缩湍流脉动扩张对总耗散率的影响;ακ为κ方程的湍流Prandtl数;αε为ε方程的湍流Prandtl数;Prt为湍流Prandtl数;T为温度;C1ε、C2ε、C3ε为经验常数;gi为重力加速度分量。
1.1.2 颗粒相运动方程
在FLUENT-EDEM中,采用离散元法(DEM)计算颗粒物相,根据牛顿第二定律,颗粒项的运动求解方程为
(9)
(10)
式中,mP为颗粒的质量;uP为颗粒速度;FD为颗粒曳力项;FG为重力项;FB为Magus浮力项;FL为升力项;FVM为虚拟质量力项;FP为压力梯度力项;IP为颗粒的惯性矩;ωP为颗粒旋转的角速度;Mfp为作用于颗粒上总的旋转矩。
其中,颗粒曳力FD采用Wenyu模型,表达式为
(11)
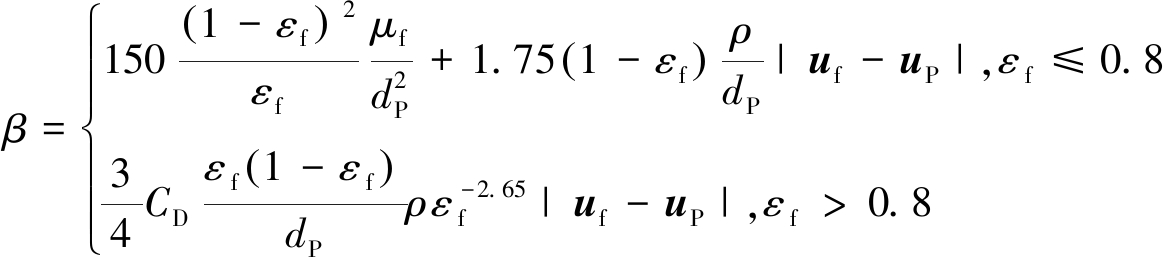
(12)
式中,β为计算系数;ρP为颗粒密度;dP为颗粒直径;CD为阻力系数;VP为颗粒体积。
颗粒其余各项受力表达式分别为
(13)
(14)
![]() ∇×u
∇×u
(15)
(16)
FP=-VP∇P
(17)
式中,μm为动态黏度;e为单位向量;CVM为虚拟质量系数;CL为升力系数;τ为时间变量。
磨料颗粒均为球形,磨料颗粒之间碰撞的接触力方程为
FC=∑Fn+Ft
(18)
式中,FC、Fn、Ft分别为颗粒的接触力、法向力和切向力。
将上述VOF以及DEM两个模型的控制方程写入接口程序,进行编译,最终实现实时、双向耦合。通过编好的用户自定义函数 (UDF)进行数据通信,可实现CFD-DEM方法在FLUENT-EDEM中的双向耦合。计算过程为:FLUENT软件将某一时间点的流场计算至收敛,将流场信息通过曳力模型转化为EDEM中作用在颗粒上的流体曳力,EDEM计算每个颗粒的外力,并由此更新颗粒位置、速度等信息,最后这些颗粒动力学参数以动量形式汇入FLUENT计算中,从而影响流场。
1.2 耦合模拟方法验证
文献[28]采用PIV方法进行前混合磨料水射流磨料颗粒在喷嘴外自由射流区域的速度测试实验,为验证上述耦合模拟方法的正确性,利用上述方法在软件FLUENT-EDEM开展了前混合磨料水射流的数值模拟计算。根据文献[28]模拟设置,喷嘴入口直径3 mm、出口直径1 mm、收敛段长6.8 mm、直管段60 mm,自由流域长60 mm、宽20 mm,射流压力15 MPa,磨料质量流量3 g/L,其余初始条件均与文献[28]保持一致,不再赘述。计算物理模型如图1所示,射流压力 15 MPa 时数值模拟及PIV实验中磨料颗粒速度随距离的变化情况如图2所示。

图1 计算物理模型
Fig.1 Computational physical model

图2 磨料颗粒运动速度随射流喷射距离的变化情况
Fig.2 Change of velocity of abrasive particles with the change of off distance
由图2可知,此研究方法下数值模拟结果速度波动较小,但实验结果与模拟结果两者总体趋势相同;对比二者速度可知,数值模拟磨料颗粒的最大运动速度略小于实际实验得出的运动速度,平均相差仅2.56%,速度最大误差约为 5.50%。因此,数值模型计算的粒子速度和PIV实验测定的粒子速度具有较好的一致性,此研究方法可靠性得以验证。
1.3 物理模型及网格划分
本文几何模型包含喷嘴前端部分管道、喷嘴及喷嘴外一定喷距的自由流场,计算物理模型如图3所示。X轴方向为重力方向。喷嘴采用圆锥形喷嘴模型,分为收缩段和直管段两部分,根据实验室内喷嘴实际尺寸,模拟喷嘴入口直径3 mm,出口直径1 mm,直管段与喷嘴出口直径之比为2∶1,收缩段的收缩夹角为28°,喷嘴总长6 mm,截面如图3所示。喷嘴前方设置直径12 mm、长20 mm管道以保证磨料混合均匀,减少计算误差。喷嘴后方自由流场区域长度60 mm,直径40 mm。管道入口中心处为原点,沿X轴走向20 mm处为喷嘴收敛段入口,26 mm处为喷嘴出口,86 mm处为外流域出口。
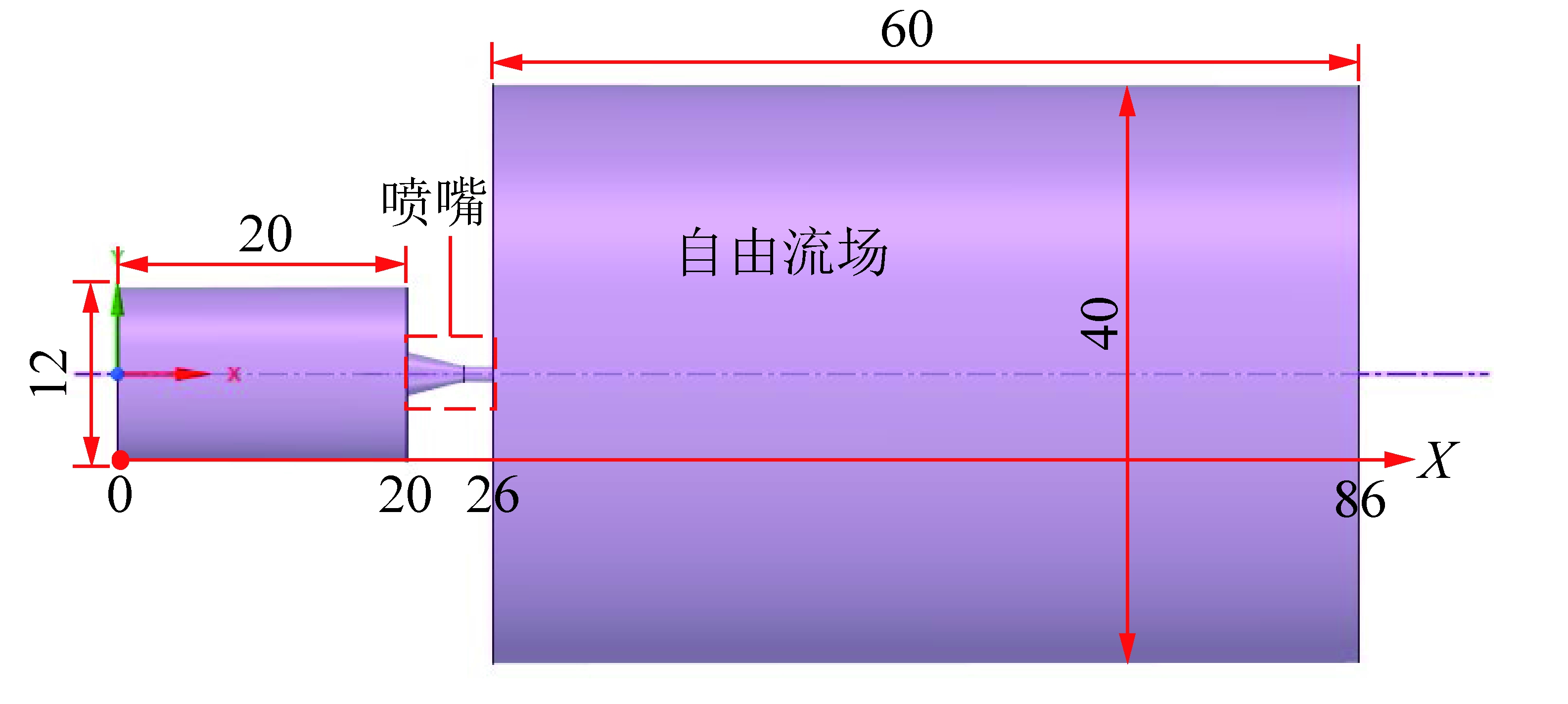
图3 数值模拟计算物理模型
Fig.3 Physical model of numerical simulation
为提高计算精度,使用ICEM结构性网格对射流喷嘴内部和自由流场进行网格划分,并对喷嘴内部及流场边界层进行局部加密。图4为计算模型网格划分情况,红色区域为加密区域,最小网格尺寸0.02 mm,计算域生成的网格总数约为22.8×105个,网格质量达到0.6以上,满足计算要求[29]。
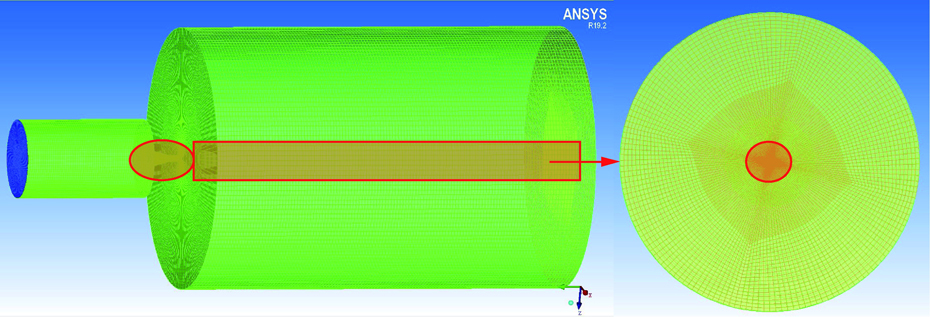
图4 网格划分与加密
Fig.4 Grid division and encryption
1.4 初始条件和边界条件
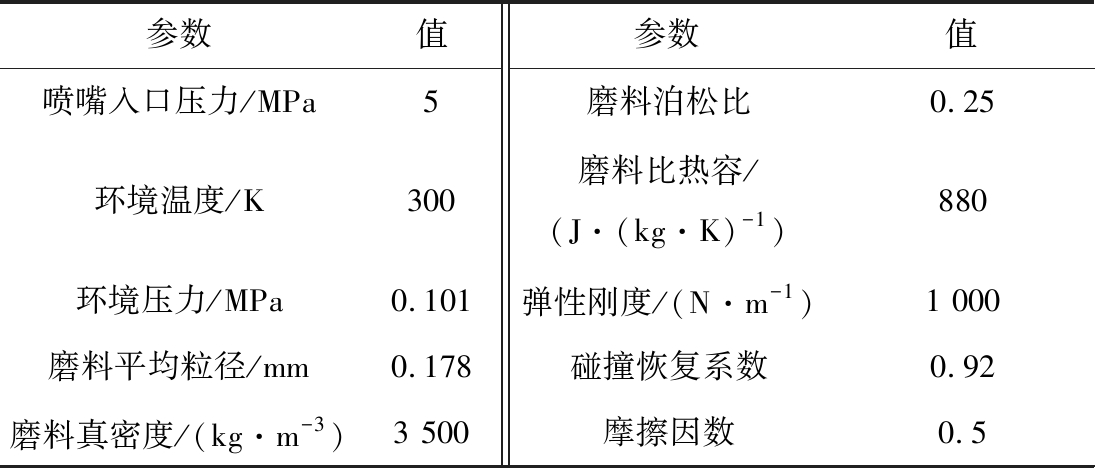
磨料水射流运动中颗粒受力较多,如曳力、重力、压力梯度力、虚拟质量力以及颗粒间的相互碰撞等,在模拟实验中均有考虑。射流压力为5 MPa,磨料种类为80目(0.178 mm)石榴石,围压为大气压,模拟计算所用初始条件和边界条件见表1。
表1 初始条件和边界条件
Table 1 Initial and boundary conditions
参数值参数值喷嘴入口压力/MPa5磨料泊松比0.25环境温度/K300磨料比热容/(J·(kg·K)-1)880环境压力/MPa0.101弹性刚度/(N·m-1)1 000磨料平均粒径/mm0.178碰撞恢复系数0.92磨料真密度/(kg·m-3)3 500摩擦因数0.5
1.5 模拟方案
为分析磨料质量分数对磨料加速规律和分布的影响,采用CFD-DEM并行计算磨料射流数值模型。数值模拟方案确定了磨料种类、射流压力和围压。质量分数分别是1%、3%、5%、7%、8%、9%、11%、12%、13%,计算5 MPa压力下纯水射流喷嘴出口流量的体积与不同质量分数时的流体密度、质量分数的乘积,得到对应的磨料质量流量分别为0.816 9、2.486 6、4.205 7、5.976 5、6.882 1、7.801 4、9.682 9、11.623 6 g/s。
1.6 数值模拟结果与分析
1.6.1 磨料粒子能量转化效率
按照上述设置条件进行数值模拟,得到了预混合磨料水射流运动过程。压力5 MPa、质量分数8%时不同时刻粒子的分布特征如图5所示。图5中,当时间0.001 s<t<0.018 s时,磨料粒子在管道内运动。当t>0.018 s,磨料粒子经喷嘴内部加速,运动至自由流场;在喷嘴附近,磨料集中在自由流场轴线附近,随着磨料颗粒向下游运动,磨料沿自由流场径向扩散。当t=0.035 s时,计算域内磨料粒子数量达到稳定,计算域内最终的粒子数量稳定在17 000个,计算域内磨料总动能趋于稳定。其余质量分数时磨料粒子稳定时间均在0.035 s左右,下面以t=0.04 s(计算域内粒子数量达到稳定后的时刻)为例,分析不同质量分数射流流场内磨料粒子的运动和分布规律。

图5 不同时间粒子分布特征
Fig.5 Particle distribution characteristics at different times
磨料粒子速度是磨料运动规律的重要表征,因此提取各质量分数条件下射流轴线位置处磨料粒子速度,研究质量分数变化对磨料颗粒速度的影响规律。图6为不同质量分数下射流轴线位置处磨料速度,可以看出,不同质量分数下的磨料颗粒具有相同的运动趋势。在管道中磨料速度较低,在喷嘴入口前开始加速,从喷嘴喷出后磨料加速一段距离后保持稳定运动。磨料的加速主要完成于喷嘴,经喷嘴加速后,不同质量分数下的磨料速度均超过70 m/s,相较于喷嘴入口处速度提高超过700%。研究表明,非淹没条件下纯水射流核心段长度在喷嘴出口直径的50倍以上,在射流核心段内水流维持喷嘴出口处速度,所以磨料粒子完成加速后仍保持原来速度运动,即在射流靶距50 mm范围内,粒子速度存在波动但未出现明显的衰减。但是不同质量分数时,其磨料最大速度存在差异。5 MPa压力下,质量分数为1%、5%、8%、11%、13%,其自由流域的磨料粒子最大速度分别为96.3、93.0、91.7、90.5、86.2 m/s。随着质量分数升高,磨料颗粒加速越不充分,磨料达到稳定时的最大速度降低。相较于质量分数13%,质量分数1%时磨料最大速度相差10.1 m/s。而磨料水射流冲击效果不仅受磨料速度影响,还与磨料质量密切相关,所以不能仅以磨料速度为标准判定5 MPa压力下的最优质量分数,还需考虑磨料质量分析磨料的冲击动能。

图6 不同质量分数下射流轴线磨料粒子速度
Fig.6 Abrasive particle velocity at jet axis at different mass fraction
根据上文的分析,考虑射流冲击时的磨料质量,分别提取EDEM数值模拟结果中不同磨料质量分数0.04 s时,0.007、0.014、0.020、0.026、0.036、0.046、0.056、0.066、0.076、0.086 m位置的动能。选取每个截面前0.5 mm的空间区域,计算该区域内所有磨料粒子的动能作为该断面处磨料冲击动能,以此观察不同位置的磨料动能变化。图7显示了质量分数1%、5%、8%、11%、13%时的磨料动能沿程变化。由图7可知,随X轴距离的增加磨料动能呈现先增大后稳定的趋势,其动能变化趋势与磨料速度变化趋势存在一致性。但是不同质量分数时磨料达到稳定后的动能存在差异,且与磨料速度规律稍有不同。随着磨料质量分数的增加,稳定后的断面磨料动能呈现先增大后减小的趋势,在质量分数为11%时达到峰值。5 MPa压力下,质量分数为1%、5%、8%、11%、13%时,其断面磨料最大冲击动能分别为0.50×10-4、1.16×10-4、1.53×10-4、1.88×10-4、1.67×10-4 J。随着磨料质量分数的增加,虽然单个磨料粒子速度逐渐减小,但颗粒数量的增加引起磨料总体动能呈现增加的趋势,如质量分数11%时,单个磨料加速不充分,速度较小,但整体磨料动能达到了最大。而质量分数大于11%时,断面磨料冲击动能不增反减。
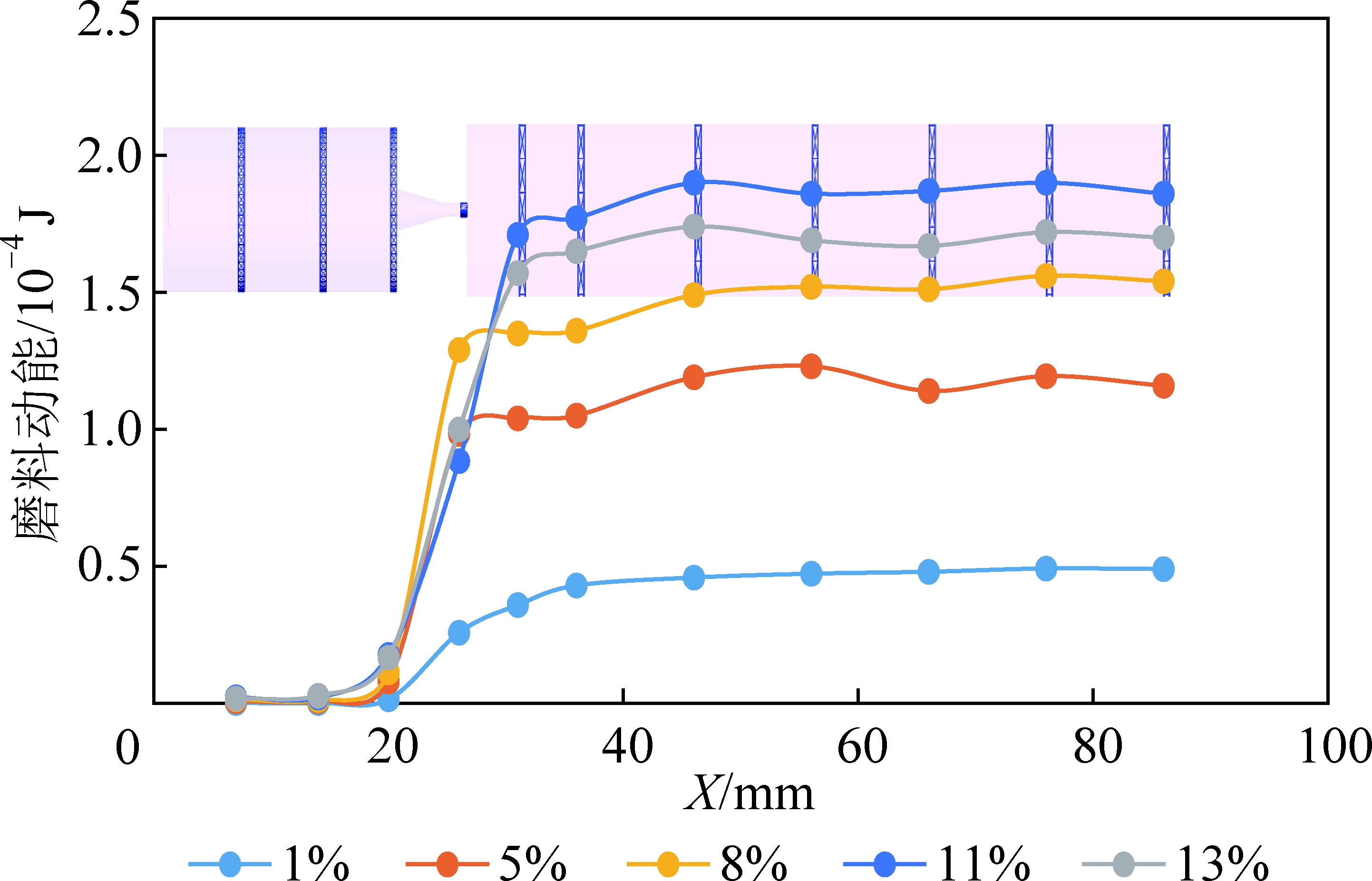
图7 磨料动能沿程变化曲线
Fig.7 Variation curves of abrasive kinetic energy along the path
磨料射流运动过程中,磨料粒子主要依靠射流与磨料两相速度产生的曳力作用完成加速,在没有外力作用下,磨料动能的增加与水射流动能的变化密切相关。因此提取FLUENT模拟结果中5 MPa纯水射流与不同质量分数时水射流轴线速度,并以喷嘴出口处射流质量与速度为基础计算水射流的动能。图8为5 MPa压力下不同质量分数磨料水射流速度变化曲线,射流速度随磨料质量分数变化规律与磨料速度随质量分数变化规律一致,但射流出口速度相差较大。磨料质量分数为1%、5%、8%、11%、13%时,喷嘴出口射流速度分别为97.24、88.49、84.40、77.31、73.33 m/s,而压力5 MPa时纯水射流喷嘴出口速度为100 m/s,与前者相比,相应的最大速度差分别为2.76、11.51、15.6、22.69、26.67 m/s。根据能量守恒定律,忽略自由流场区域空气获得的能量,计算域内的磨料射流中水射流能量与磨料能量之和为相同压力下纯水射流的能量。而且,磨料射流运动中,通过液固两相的曳力,射流能量转化成为磨料能量。换言之,磨料动能的增加均来自于水射流的能量。射流速度降低其动能减少,磨料速度升高其动能增加,由此计算得到射流减少的能量与磨料增加的动能。

图8 5 MPa压力下不同质量分数射流轴线速度变化曲线
Fig.8 Axial velocity of jet with different mass fraction under 5 MPa
那么,认为射流减少能量为同压力下不同磨料质量分数射流动能与纯水射流动能的差值,定义液固能量转化效率为计算域内磨料总动能与同压力下水射流动能的比值,定义能量利用率为磨料总动能与同压力下不同质量分数射流减少能量的比值,计算出不同质量分数时的液固能量转化效率与能量利用率,计算结果见表2,为了便于分析观察,并绘制结果如图9所示。
表2 能量转化效率计算
Table 2 Calculation of energy conversion efficiency
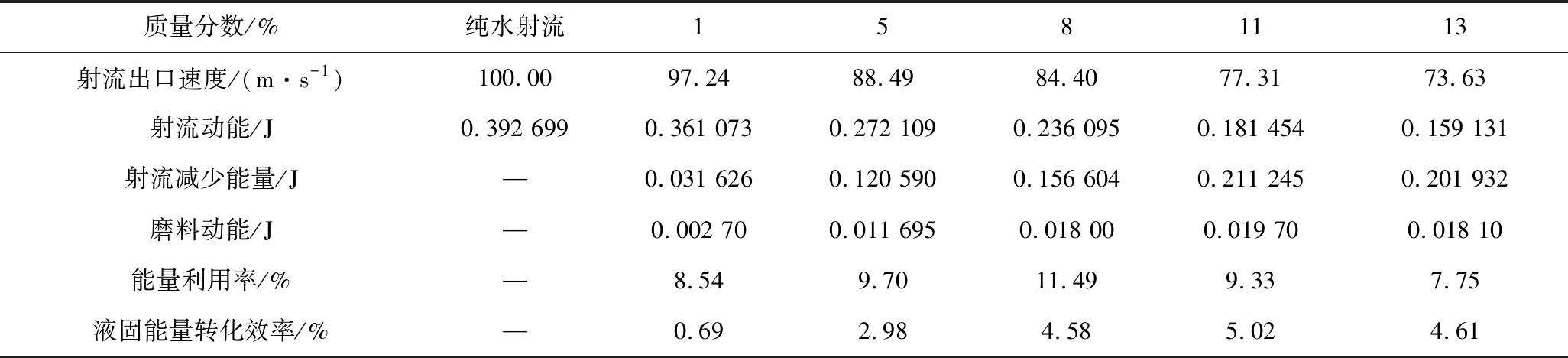
质量分数/%纯水射流1581113射流出口速度/(m·s-1)100.0097.2488.4984.4077.3173.63射流动能/J0.392 6990.361 0730.272 1090.236 0950.181 4540.159 131射流减少能量/J—0.031 6260.120 5900.156 6040.211 2450.201 932磨料动能/J—0.002 700.011 6950.018 000.019 700.018 10能量利用率/%—8.549.7011.499.337.75液固能量转化效率/%—0.692.984.585.024.61

图9 5 MPa不同质量分数磨料动能与能量转化效率
Fig.9 Kinetic energy and energy conversion efficiency of abrasives with different mass fraction under 5 MPa
由图9可以看出,射流压力5 MPa,随质量分数升高,磨料总动能先增大后减小的规律与上述断面磨料冲击动能变化一致。所以,压力一定时,磨料质量分数的增加在一定程度上使得磨料颗粒总体动能增加,但是并不能使其持续增加,这与液固能量转化效率规律相对应。不同质量分数时射流速度不同,对磨料颗粒加速能力并不相同,使得磨料总动能与能量转化效率有差异,且存在一个最优质量分数使得磨料达到此压力下最大的冲击动能,低于或超过这一最优质量分数,磨料均不能得到最大的冲击动能。压力5 MPa时,11%质量分数磨料粒子整体的加速最为充分,磨料冲击动能最大。由能量利用率曲线可以看出,随着质量分数增加,能量利用率同样呈现先增后减的趋势,8%质量分数时射流减少能量转化成磨料动能的效率最高,为11.49%,其他质量分数时能量利用率较低,射流减少能量没有充分转化为磨料动能。说明根本改变磨料动能的原因是液固之间能量的转化效率,而磨料质量分数影响着能量利用率。
磨料射流的冲蚀性能不仅与磨料的加速规律有关,还与磨料在射流断面的分布有关。所以,分别提取不同质量分数时X轴截面的磨料粒子速度分布图,结果如图10所示。不同质量分数时的高速磨料粒子均集中于射流轴线附近,随着粒子向下游运动,射流与空气卷吸作用更加明显,颗粒沿自由流场径向出现明显扩散,磨料集束性降低,整体成钟型分布。随磨料质量分数增加,磨料颗粒碰撞概率增加,粒子流集束性更差,磨料在射流分布中不断发散引起夹角θ增大,导致射流断面单位面积冲击动能逐渐减小。当夹角增加到一定程度后,断面单位面积冲击动能低于破岩临界值,将不再具备破煤岩能力。因此,质量分数增加到一定程度后,磨料加速性能极低,射流无法破坏煤岩体。

图10 5 MPa不同质量分数轴面磨料粒子速度分布
Fig.10 Velocity profile of abrasive particles at the axis of different mass fraction under 5 MPa
根据上述分析,认为该射流压力下存在一个最优质量分数使得液固能量转化效率最高。低质量分数时,增加磨料数量,虽然磨料速度降低但磨料整体冲击动能增加;高质量分数时,磨料颗粒之间碰撞概率增大并消耗了其动能,降低了能量转化效率及能量利用率。以冲击动能为标准评判,5 MPa时磨料最优质量分数为11%,此时磨料整体加速最为充分,液固两相能量转化效率最高。
1.6.2 压力对最优质量分数的影响
射流压力是影响磨料水射流破煤岩效果的重要因素,基于射流压力对磨料质量分数的影响,进行压力10 MPa的数值模拟。除压力变化外,其余数值模拟设置与压力5 MPa时保持一致。射流压力10 MPa磨料随质量分数变化的加速规律基本与5 MPa时保持一致,随质量分数增大,单颗磨料粒子速度逐渐降低,但是10 MPa压力下射流速度与磨料粒子速度相差较大,对磨料产生更大的曳力,因此磨料加速更加充分,速度更大。按照上述分析方法,分别提取10 MPa压力下的磨料动能与轴线射流速度,计算液固能量转化效率与能量利用率,相关结果如图11所示。由图11可知,随质量分数增加,磨料最大冲击动能先增后减,在12%时达到峰值,此质量分数下液固能量转化效率最高,为4.61%,而在质量分数9%时能量利用率最高,为10.15%。由于不同压力时射流速度与磨料速度差值不尽相同,射流压力愈大其作用于磨料的曳力愈大,磨料粒子加速愈充分,所以每一压力都存在与之相适应的最优质量分数,5 MPa压力时最优质量分数为11%,10 MPa压力时最优质量分数为12%。
对比图9与图11可知,同一质量分数下,压力由5 MPa提高至10 MPa,磨料动能有所提高,但射流能量未能有效转化为磨料动能,液固能量转化效率与能量利用率不增反减。虽然射流压力大时射流速度较大,磨料所受曳力提高,磨料颗粒加速效果更好,但是同时由于射流速度增大导致射流与磨料颗粒接触时间缩短,射流与磨料粒子作用时间的减少大幅降低了射流能量的转化效率与能量利用率。因此,相较于提高射流压力,适当增加磨料质量分数以提高液固能量转化效率与能量利用率,是增加磨料冲击动能的更经济、低能耗的方式。

图11 10 MPa压力不同质量分数磨料动能与转化效率
Fig.11 Kinetic energy and energy conversion efficiency of abrasives with different mass fraction under 10 MPa
2 破岩试验研究
2.1 实验系统
相比于传统的前混合磨料水射流,预混合磨料水射流不仅能够实现磨料的连续供给,还能使磨料与水混合更加均匀,充分利用成熟的高压注浆技术,巧妙地将高压浆液转化为磨料射流,使得磨料加速更加充分,具有更大的冲击力。实验系统采用自行研制的预混合磨料水射流破煤岩实验系统,主要由磨料供给系统、加压系统参数控制系统及喷射系统组成。实验时,预先将磨料和水按照比例注入磨料罐,在离心泵的作用下均匀混合,浆液通过柱塞泵加压经高压管路泵送至喷嘴,形成预混合磨料水射流,实验装置如图12所示。其中,橙色管路的红色箭头表示循环制浆模式下浆液的循环路线,灰色管路中的红色箭头表示高压切割模式下浆液的供料循环路线,黄色箭头表示高压浆液的流动。

图12 预混合磨料水射流实验装置
Fig.12 Experimental facility of premixed abrasive water jet
此过程中,磨料-水在开放环境中混合,激励形式简单,能够连续供给;磨料-水在升压前混合,混合更均匀,磨料能够充分得到加速,能够提高磨料水射流冲击破煤岩的能量转化率,具有更高的冲击能力,从而实现高效破岩;设备工艺的简易性也使其适用于井下受限作业空间,磨料射流还可通过钻杆输送至割缝器,根据需要随着钻杆旋转对煤岩进行割缝、扩孔、造穴等增透措施。实验系统可调节射流压力范围0~40 MPa,流量范围0~60 L/min,形成高、中和低压射流,可进行射流压力、质量分数等不同参数条件下的煤岩冲蚀实验。
2.2 预混合磨料水射流破岩实验
前期实验中预混合磨料水射流破煤效果比较好,但实验煤样冲击破坏后直接劈裂、破碎,无法定量表征进行系统分析,因此笔者以玄武岩作为实验试样进行预混合磨料水射流冲蚀实验。实验采用的玄武岩加工成标准试样(φ50 mm×100 mm),采用实验室的MTS进行力学强度测试,玄武岩试样单轴抗压强度为270 MPa。
实验选用磨料种类为80目(0.178 mm)石榴石,射流靶距为20 mm,喷嘴选择直径为1 mm的圆锥形合金制喷嘴。入口压力分别为5、10 MPa,冲蚀时间为60 s,磨料质量分数与数值模拟实验设置相同,分别为1%、3%、5%、7%、8%、9%、11%、12%、13%。
2.3 破岩实验结果分析与讨论
实验前磨料罐中的磨料和水混合均匀,在实验中保证预混合磨料水射流的连续供料。根据实验方案,进行不同压力、不同质量分数预混合磨料水射流的破岩实验研究,图13为5 MPa与10 MPa压力下不同质量分数、冲蚀时间60 s时玄武岩冲蚀效果,其中H为冲蚀深度,d为冲蚀孔径。实验结果表明,射流压力5 MPa时,3%质量分数磨料射流可以使煤体破碎、玄武岩形成冲蚀坑。此外,由于预混合磨料水射流磨料与水混合均匀,且磨料整体加速效果较好,冲蚀坑并非传统的“V”型,而是呈现圆柱状。表明预混合磨料水射流磨料整体加速更为充分,获得较大的能量转化效率以及能量利用率,能够实现对坚硬岩石的破碎,有力证明了其在煤矿卸压增透广泛的应用前景。
射流压力、磨料质量流量和冲蚀时间是影响预混合磨料水射流冲蚀效果的关键因素。图14为不同射流压力和质量分数对冲蚀效果的影响规律。由图13和图14可知,5 MPa时,质量分数3%时冲蚀坑深度为3.12 mm,质量分数11%时冲蚀坑深度为10.36 mm,相比于质量分数3%时,质量分数为11%时的冲蚀深度提高了7.24 mm。说明在磨料质量分数为3%时,磨料射流的能量未被充分利用,没有转化为磨料的冲击动能。提高磨料的质量分数,能够有效地提高预混合磨料水射流能量转化效率与能量利用率,使磨料冲击动能增加,从而提高冲蚀效果。但是当质量分数超过最优质量分数后,质量分数13%时磨料冲击动能降低,冲蚀效果减弱。相比于射流压力5 MPa,射流压力至10 MPa,质量分数3%时冲蚀坑深度为4.53 mm,提高了1.41 mm,质量分数13%时冲蚀坑深度提高了5.75 mm。低质量分数时提高压力能够提高冲蚀深度,但冲蚀深度增幅并不明显。提高射流压力能够提高冲蚀效果,但与提高射流压力相比,提高磨料质量分数的效果更为明显。在低磨料分数的情况下,增加磨料,对冲蚀起主要作用的是磨料数量,单颗磨料速度的稍微下降对冲蚀性能影响不大,而当磨料分数增大到一定值时,磨料粒子整体的动能开始降低。因此,持续提高磨料质量分数,并不能使冲蚀效果持续增加,每一射流压力条件下,均有与之相匹配的最优的质量分数,当超过该临界值时,冲蚀效果开始降低。实验结果与模拟结果一致,证明了数值模拟方法的可行性以及模拟结果的准确性。

图13 预混合磨料水射流冲蚀玄武岩效果
Fig.13 Effect of premixed abrasive water jet on basalt erosion

图14 不同压力、不同质量分数对冲蚀效果的影响规律
Fig.14 Eerosion depth of basalt under different pressure and mass fraction
磨料射流冲蚀效果不仅与磨料加速规律相关,也与射流断面磨料分布密切联系。从图13可观察到,5 MPa压力时,质量分数3%时冲蚀半径为2.30 mm,质量分数11%时冲蚀半径为3.98 mm,而质量分数13%时冲蚀半径为3.68 mm。磨料质量分数增加,冲蚀孔径也在增加,这由射流断面磨料分布状态决定。质量分数增加,射流集束性降低磨料分布更分散,导致冲蚀孔径增大。但当断面单位面积磨料动能降低至破岩临界值,冲蚀孔径减小,因此质量分数13%时冲蚀半径较11%降低。这与磨料在射流断面分布的模拟分析结论相验证,进一步验证数值模拟结果的可靠性。
3 结 论
(1)考虑颗粒间的摩擦、碰撞,通过添加颗粒相体积分数和动量源相修正VOF模型,开发用户自定义函数(UDF)通信接口,精确计算磨料质量分数对磨料颗粒加速运动与分布的影响,准确描述了磨料粒子对水射流流场的影响。
(2)在固定压力下,不同质量分数的射流液固能量转化效率不同,导致磨料冲击动能不同。提高磨料质量分数,能够提高破岩效果,但存在最优值。每一压力条件下都有与之相适配的最优质量分数,此质量分数下能量转化效率最高。以冲击动能为标准,射流压力为5 MPa时,80目(0.178 mm)石榴石最优质量分数为11%。
(3)提高射流压力可提高磨料冲击动能,但是能量转化率和利用率降低。提高压力使射流速度增加,曳力增大,但射流与磨料接触时间缩短,导致射流能量未能及时转化为磨料的能量。因此,相较于提高射流压力,适当增加磨料质量分数以提高能量转化效率以及能量利用率,是达到最佳破煤岩效果的更经济低能耗的方式。
[1] 管华双,姜晨,李佳音,等.微通道反应器沟槽底面的磨料水射流抛光研究[J].流体机械,2021,49(3):8-13.
GUAN Huashuang,JIANG Chen,LI Jiayin,et al.Research on abrasive waterjet polishing of groove bottom surface in microchannel reactor[J].Fluid Machinery,2021,49(3):8-13.
[2] ANISH Nair,ADAM Khan M,SIVAKUMAR M,et al.Geometric cha-
racteristics analysis of hole making through abrasive water jet drilling[J].Materials Today:Proceedings,2021,39(1):338-347.
[3] 王相蕊,缪小进,武美萍.Ti6Al4V/CFRP叠层材料的磨料水射流孔加工机理与实验[J].机械设计与研究,2021,37(4):135-139.
WANG Xiangrui,MIAO Xiaojin,WU Meiping.Research on the mechanism and strategy of abrasive water jet drilling Ti6AI4V/CFRP stacks[J].Machine Design &Research,2021,37(4):135-139.
[4] PADMAKAR J Pawar,UMESH S Vidhate,MANGESH Y Khalkar.Improving the quality characteristics of abrasive water jet machining of marble material using multi-objective artificial bee colony algorithm[J].Journal of Computational Design and Engineering,2018,5(3):319-328.
[5] GABRIELE Pozzetti,BERNHARD Peters.A numerical approach for the evaluation of particle-induced erosion in an abrasive waterjet focusing tube[J].Powder Technology,2018,333:229-242.
[6] 章文峰,卢义玉,汤积仁.磨料射流喷嘴外流场磨料速度模型及分析[J].煤炭学报,2017,42(S2):576-584.
ZHANG Wenfeng,LU Yiyu,TANG Jiren.Analysis and modeling of particle in the outer flow field of the nozzle of AWJ[J].Journal of China Coal Society,2017,42(S2):576-584.
[7] 王耀锋,何学秋,王恩元,等.水力化煤层增透技术研究进展及发展趋势[J].煤炭学报,2014,39(10):1945-1955.
WANG Yaofeng,HE Xueqiu,WANG Enyuan,et al.Research progress and development tendency of the hydraulic technology for increasing the permeability of coal seams[J].Journal of China Coal Society,2014,39(10):1945-1955.
[8] 闫发志,朱传杰,郭畅,等.割缝与压裂协同增透技术参数数值模拟与试验[J].煤炭学报,2015,40(4):823-829.
YAN Fazhi,ZHU Chuanjie,GUO Chang,et al.Numerical simulation parameters and test of cutting and fracturing collaboration permeability-increasing technology[J].Journal of China Coal Society,2015,40(4):823-829.
[9] 卢义玉,沈晓莹,杨晓峰,等.新型磨料水射流钻头岩石钻进过程关键水力学参数研究[J].应用基础与工程科学学报,2012,20(5):837-845.
LU Yiyu,SHEN Xiaoying,YANG Xiaofeng,et al.Investigations on main hydraulic parameters of a new abrasive water jets assisted bit for rock drilling[J].Journal of Basic Science and Engineering,2012,20(5):837-845.
[10] 卢义玉,黄杉,葛兆龙,等.我国煤矿水射流卸压增透技术进展与战略思考[J].煤炭学报,2022,47(9):3189-3211.
LU Yiyu,HUANG Shan,GE Zhaolong,et al.Research progress and strategic thinking of coal mine water jet technology to enhance coal permeability in China[J].Journal of China Coal Society,2022,47(9):3189-3211.
[11] 冯仁俊.脉冲射流割缝控制压裂技术关键参数研究及应用[J].煤炭工程,2022,54(1):63-69.
FENG Renjun.Research on key technical parameters of control fracturing with pulse jet slotting and its application[J].Coal Engineering,2022,54(1):63-69.
[12] 张成光,张勇,张飞虎,等.新型后混合式磨料水射流系统的研制[J].机械工程学报,2015,51(5):205-212.
ZHANG Chengguang,ZHANG Yong,ZHANG Feihu,et al.Development of new entrainment abrasive waterjet system[J].Journal of Mechanical Engineering,2015,51(5):205-212.
[13] 左伟芹,卢义玉,夏彬伟,等.前混合磨料射流新型连续加砂系统设计与实验[J].应用基础与工程科学学报,2013,21(2):328-335.
ZUO Weiqin,LU Yiyu,XIA Binwei,et al.System design of continuous feeding abrasive for pre-mixed abrasive jet and its experiment[J].Journal of Basic Science and Engineering,2013,21(2):328-335.
[14] 卢义玉,李良伟,汤积仁,等.前混合磨料水射流连续加料系统设计与实验研究[J].重庆大学学报(自然科学版),2018,41(8):111-120.
LU Yiyu,LI Liangwei,TANG Jiren,et al.Design and experimental research of the continuous feeding system of premixed abrasive water jet[J].Journal of Chongqing University (Natural Science Edition),2018,41(8):111-120.
[15] LIU Yong,CHEN Changjiang,WEI Jianping,et al.Influence of abrasive hardness on erosion wear of abrasive air jets[J].Journal of Central South University,2020,27(2):356-371.
[16] LIU Yong,GUO Xinhui,WEI Jianping,et al.Application of supercritical carbon dioxide jet:A parametric study using numerical simulation model[J].Journal of Petroleum Science and Engineering,2021,201(1):108422.
[17] REN Fushen,FANG Tiancheng,CHENG Xiaoze.Study on rock da-
mage and failure depth under particle water-jet coupling impact[J].International Journal of Impact Engineering,2020,139:103504.
[18] 刘勇,李志飞,魏建平,等.磨料空气射流破煤冲蚀模型研究[J].煤炭学报,2020,45(5):1733-1742.
LIU Yong,LI Zhifei,WEI Jianping,et al.Erosion model of abrasive air jet used in coal breaking[J].Journal of China Coal Society,2020,45(5):1733-1742.
[19] 高耀东,周同.基于三维FEM-SPH转换算法的截齿冲击结核体仿真分析[J].煤炭学报,2017,42(S2):568-575.
GAO Yaodong,ZHOU Tong.Numerical simulation and analysis for bit impact on pyrites based on 3D FEM-SPH conversion algorithm[J].Journal of China Coal Society,2017,42(S2):568-575.
[20] 林晓东,卢义玉,汤积仁,等.前混合式磨料水射流磨料粒子加速过程数值模拟[J].振动与冲击,2015,34(16):19-24,47.
LIN Xiaodong,LU Yiyu,TANG Jiren,et al.Numerical simulation of abrasive particles acceleration process in pre-mixed abrasive water jet[J].Journal of Vibration and Shock,2015,34(16):19-24,47.
[21] DEEPAK,JODEL,ABRAHAM M M,et al.Numerical analysis of
the effect of nozzle geometry on flow parameters in abrasive water jet machines[J].Pertanika Journal of Science and Technology,2017,25(2):497-506.
[22] 施红辉,张一博,王天雨,等.不同喷嘴结构下高压脉冲水射流的数值模拟[J].浙江理工大学学报:自然科学版,2021,45(3):343-350.
SHI Honghui,ZHANG Yibo,WANG Tianyu,et al.Numerical simulation of high pressure pulsed water jet generated by different nozzle structures[J].Journal of Zhejiang Sci-Tech University (Natural Sciences Edition),2021,45(3):343-350.
[23] 赵佳乐,任连城,王圣林,等.旋流井眼净化工具携岩性能影响因素研究[J].重庆科技学院学报(自然科学版),2021,23(5):64-69.
ZHAO Jiale,REN Liancheng,WANG Shenglin,et al.Research on influencing factors of rock carrying performance of swirl wellbore purification tool[J].Journal of Chongqing University of Science and Technology (Natural Sciences Edition),2021,23(5):64-69.
[24] 陈逢军,尹业青,胡天.仿形喷嘴磨料射流抛光微结构仿真及试验研究[J].机械工程学报,2022,58(15):177-187.
CHEN Fengjun,YIN Yeqing,HU Tian.Simulation and experimental research on polishing microstructure by using abrasive water jet with profiling nozzle[J].Journal of Mechanical Engineering,2022,58(15):177-187.
[25] 米建宇,黄飞,李树清,等.基于SPH-FEM耦合算法的后混合磨料水射流冲击破岩数值模拟研究[J].振动与冲击,2021,40(16):132-139.
MI Jianyu,HUANG Fei,LI Shuqing,et al.Numerical simulation of rock breaking by rear-mixed abrasive water jet based on an SPH-FEM coupling algorithm[J].Journal of Vibration and Shock,2021,40(16):132-139.
[26] 吴亮.含固体颗粒的两相流界面变化的数值研究[D].天津:天津大学,2018:24-25.
WU Liang.Development of a DEM-VOF model for the turbulent free-surface flows with particle[D].Tianjin:Tianjin University,2018:24-25.
[27] CHEN Changjiang,LIU Yong,TANG Jiren.Effect of nozzle pre-ssure ratios on the flow and distribution of abrasive particles in abrasive air jet machining[J].Powder Technology,2022,397:117114.
[28] 徐启文.前混合磨料射流外部流场的数值模拟与实验研究[D].徐州:中国矿业大学,2019:43-56.
XU Qiwen.Numerical simulation and experimental research on external flow field of abrasive water suspension jet[D].Xuzhou:China University of Mining and Technology,2019:43-56.
[29] JIANG Wan,XU Xiangyu,WEN Zhihui,et al.Applying the similarity theory to model dust dispersion during coal-mine tunneling[J].Process Safety and Environmental Protection,2021,148(4):415-427.
